A Divestment Model: Migration to Green Energy Investment Portfolio Concept
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. The Divestment Model
- A2: In this study, we have adopted the Gurol 1978 [25] coefficients given below by:
2.1.1. Derivation of Equations for the Statistical Moments
- 1.
- From Equation (9), we can see that the first moment decays exponentially. The investment in the risky asset (fossil fuel investment) declines exponentially, a feature which describes divestment from the stock asset.
- 2.
- From Equation (10), one can find the second moment which provides the reflecting boundaries within which the risky asset must evolve.
2.1.2. Derivation of the Total Wealth Equation
- If , then .
- If for all then .
3. Results and Simulations
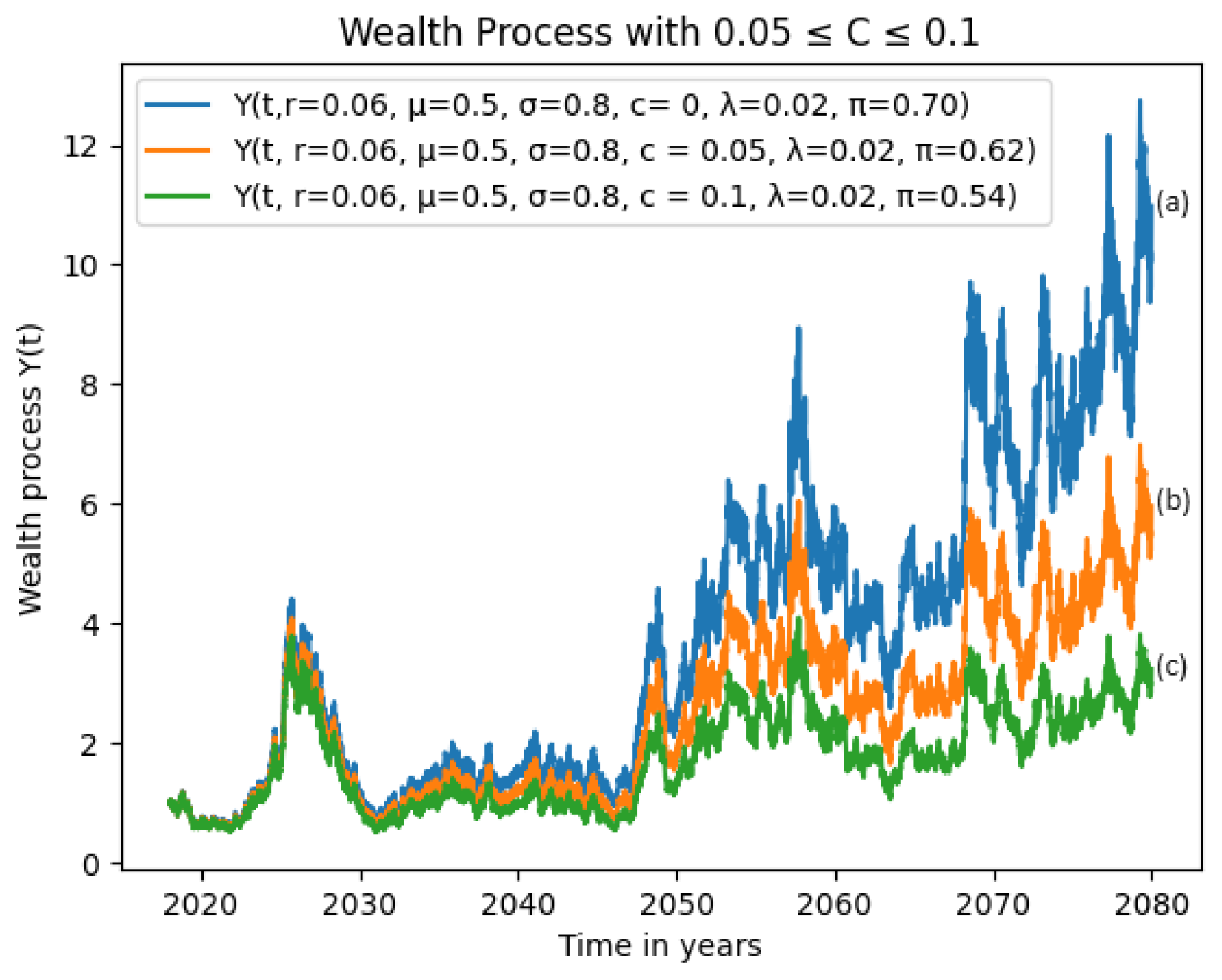
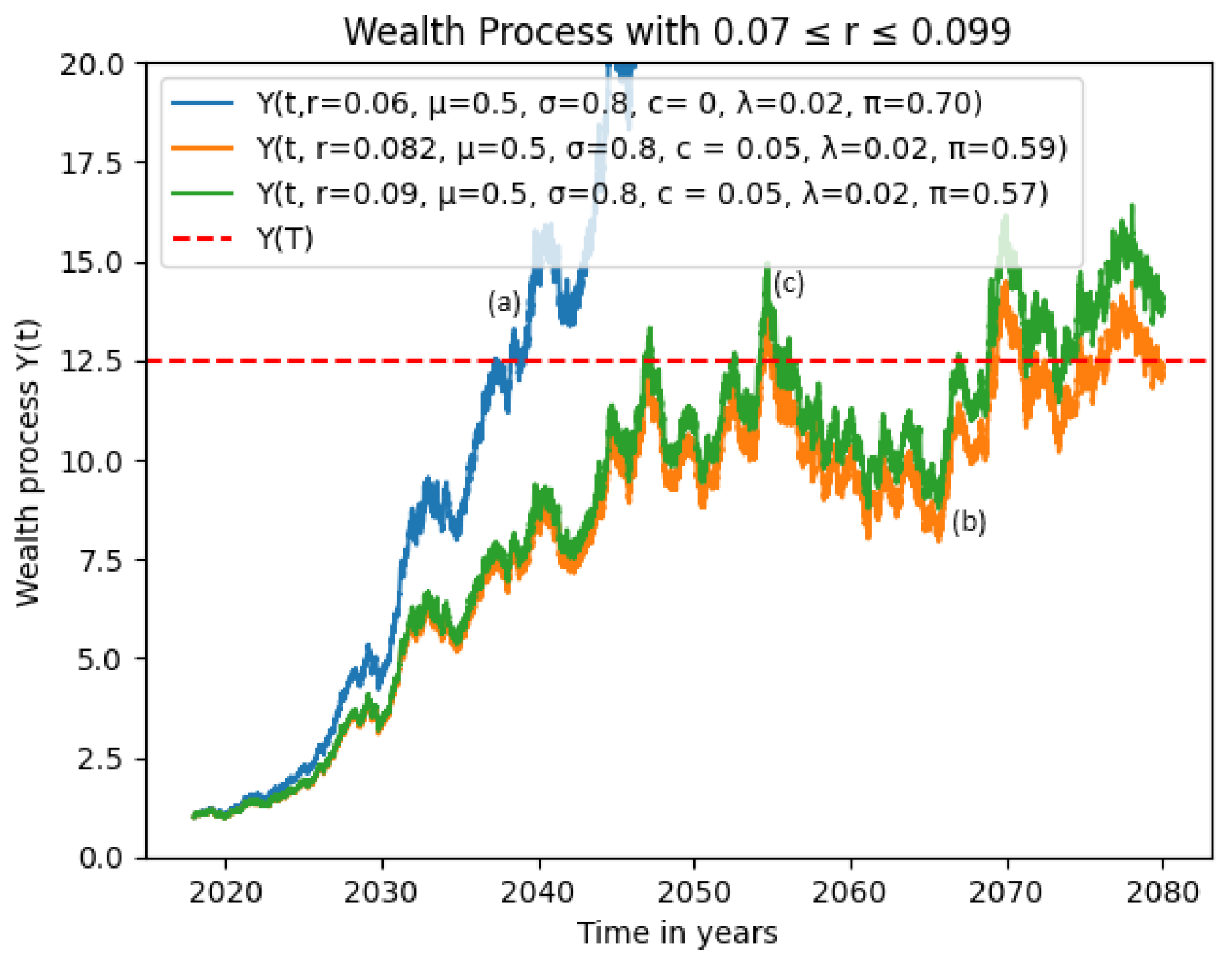
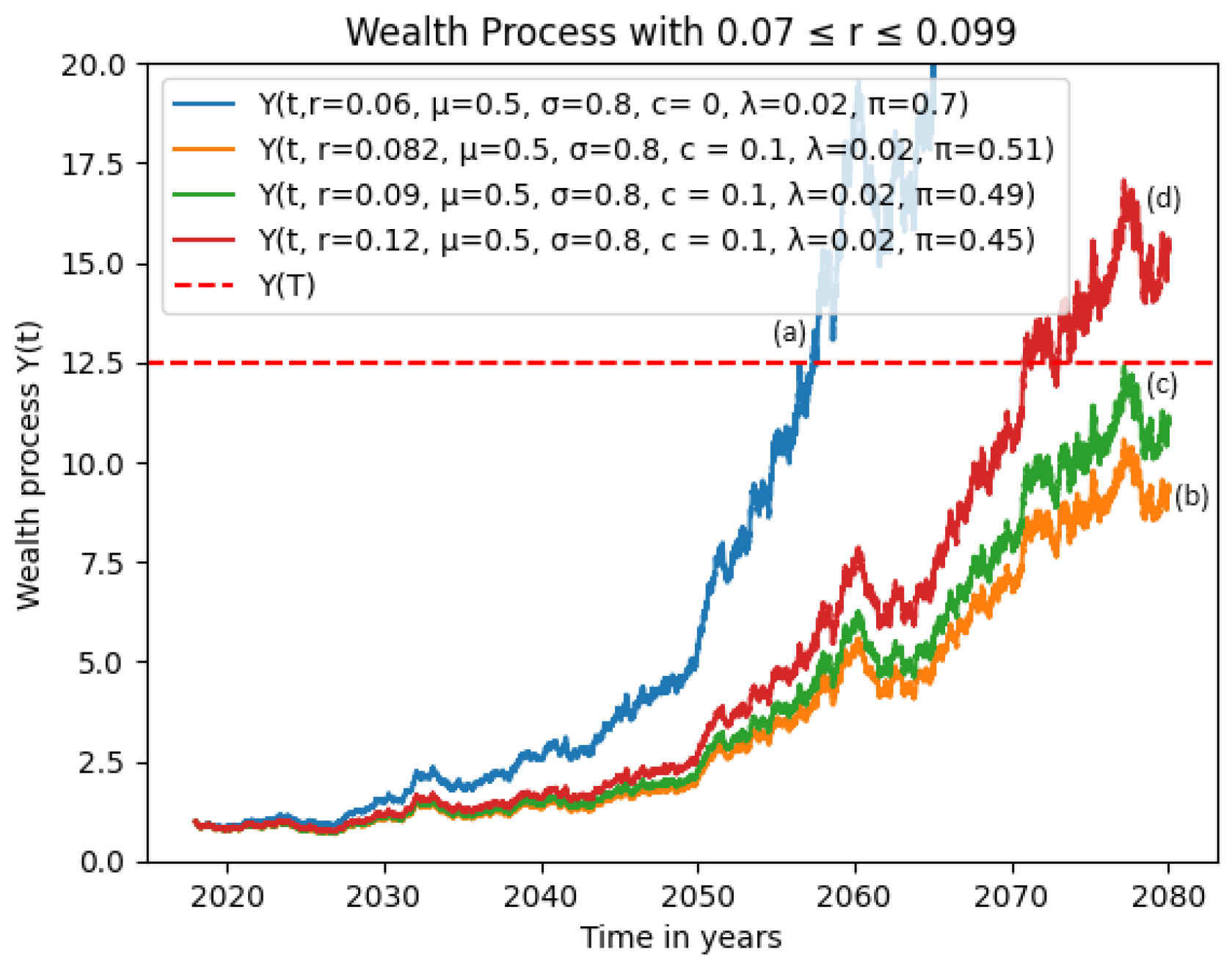
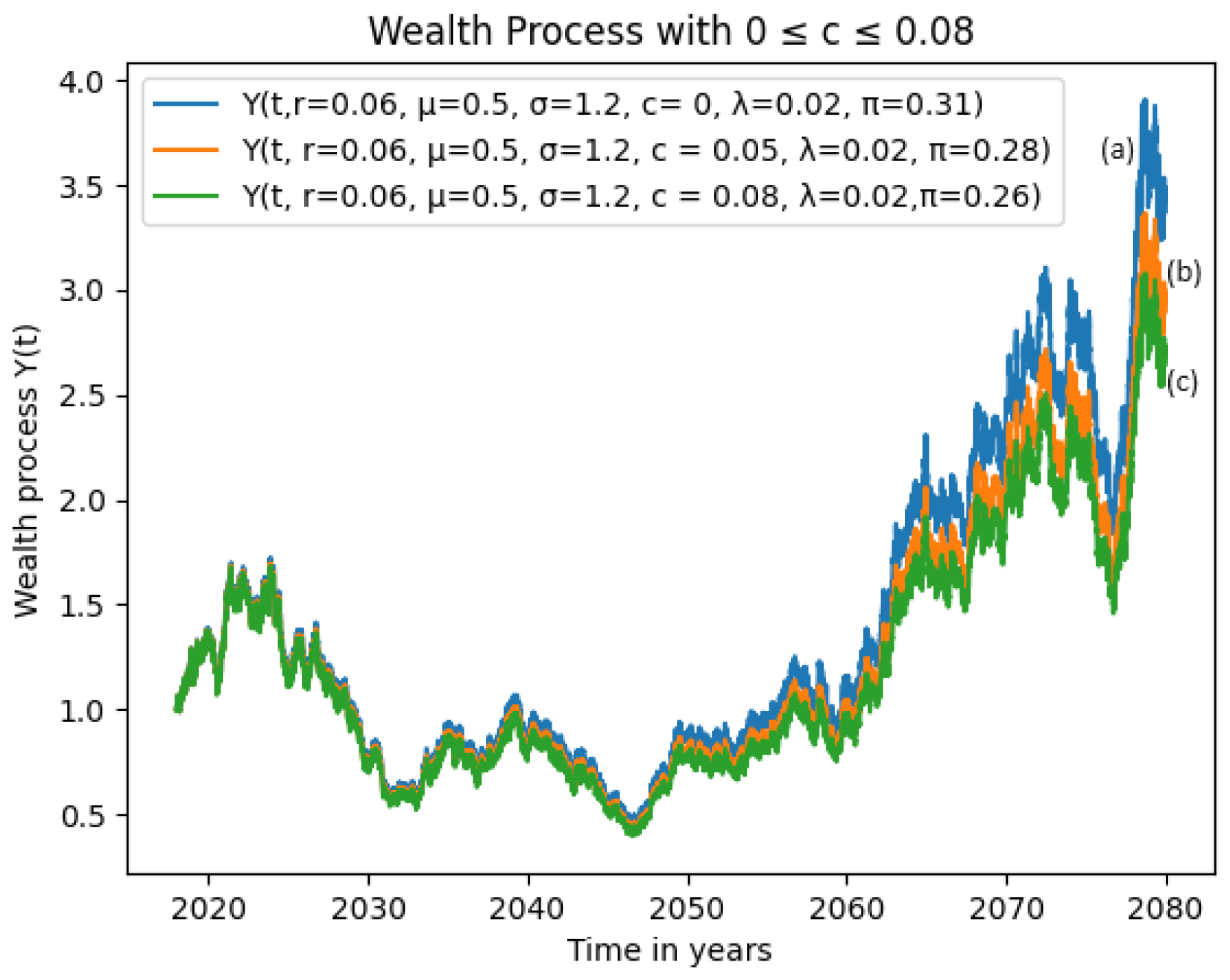
3.1. Hypothetical Examples of Increased Volatility with Varying Phase-Down Rate
3.1.1. Effects of Fixed Interest and Varying Phase-Down Rates
3.1.2. Effects of High Interest Rate
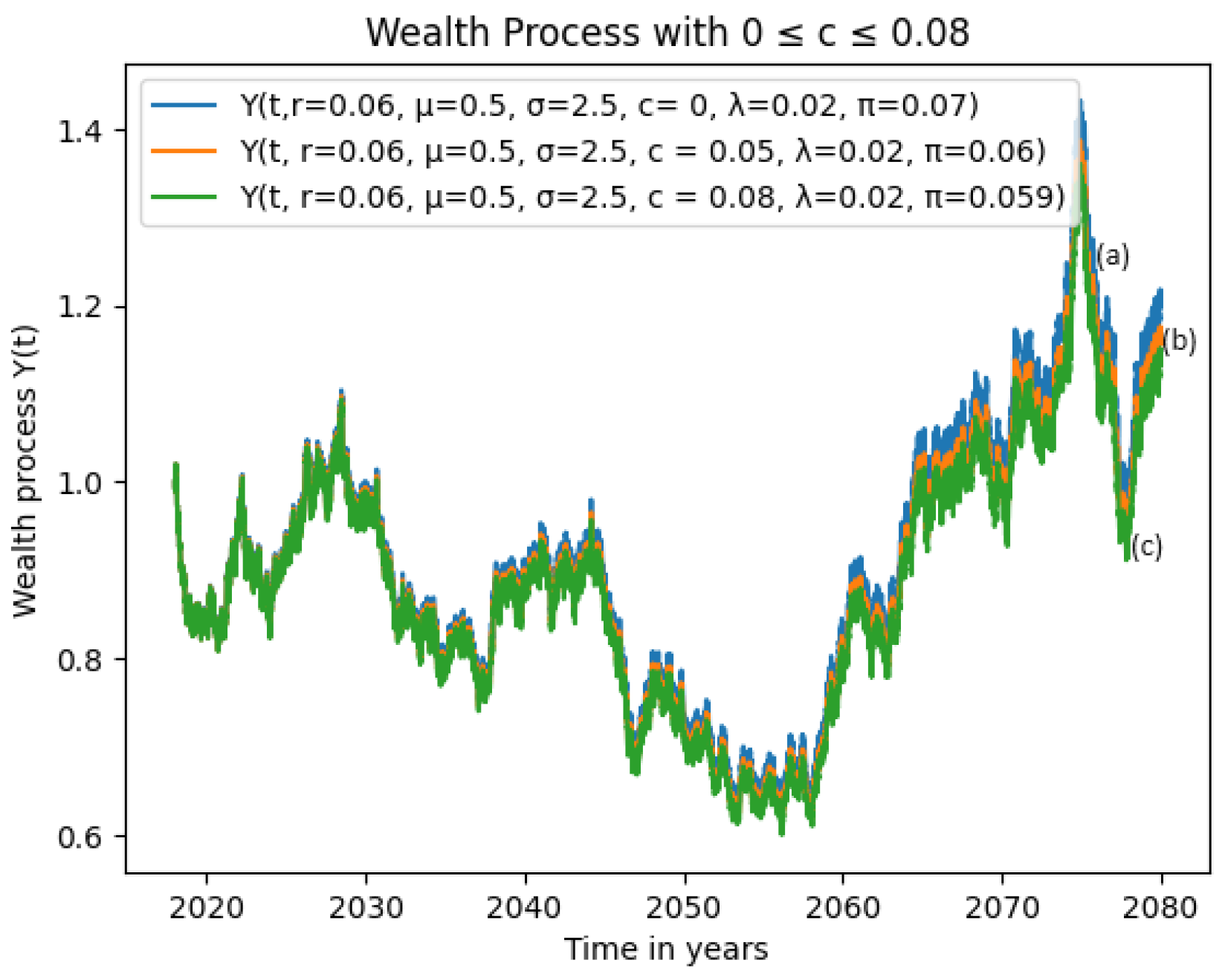
3.1.3. Effects of High Volatility
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Das, R.C.; Chatterjee, T.; Ivaldi, E. Co-movements of income and urbanization through energy use and pollution: An investigation for world’s leading polluting countries. Ecol. Indic. 2023, 153, 110381. [Google Scholar] [CrossRef]
- Trencher, G.; Rinscheid, A.; Rosenbloom, D.; Truong, N. The rise of phase-out as a critical decarbonisation approach: A systematic review. Environ. Res. Lett. 2022, 17, 123002. [Google Scholar] [CrossRef]
- The Sustainable Development Goals (Sdgs). Available online: https://www.un.org/sustainabledevelopment/sustainable-development-goals/ (accessed on 1 January 2022).
- Hyun, M.; Cherp, A.; Jewell, J.; Kim, Y.J.; Eom, J. Feasibility trade-offs in decarbonising the power sector with high coal dependence: The case of korea. Renew. Sustain. Energy Transit. 2023, 3, 100050. [Google Scholar] [CrossRef]
- Zohuri, B.; Mossavar-Rahmani, F.; Behgounia, F. Global electricity demand and clean energy source growth scenario. J. Energy Power Eng. 2022, 16, 156–165. [Google Scholar] [CrossRef]
- Kou, J.; Sun, F.; Li, W.; Jin, J. Could China declare a “coal phase-out”? an evolutionary game and empirical analysis involving the government, enterprises, and the public. Energies 2022, 15, 531. [Google Scholar] [CrossRef]
- Cosgrove, A.; Byrne, D.; Khan, F.; Castro, L.; Irwin, S. Air Pollution and Its Impact on the Energy Sector, A Final Report Submitted for the Course SEDV 609, Impact of Proposed Phasing out of Coal-Based Power Plants in Alberta, 16 October 2017. Available online: https://www.researchgate.net/publication/320407265_Impact_of_Proposed_Phasing_Out_of_Coal-Based_Power_Plants_in_Alberta (accessed on 26 February 2022).
- Hauser, P.; Görlach, B.; Umpfenbach, K.; Perez, R.; Gaete, R. Phasing Out Coal in Chile and Germany. A Comparative Analysis; Agora Energiewende: Berlin, Germany, 2021. [Google Scholar]
- Liu, X.; Peerally, J.A.; Fuentes, C.D.; Ince, D.; Vredenburg, H. Who makes or breaks energy policymaking in the caribbean small island jurisdictions? a study of stakeholders’ perceptions. Sustainability 2022, 14, 1902. [Google Scholar] [CrossRef]
- Tesche, M.; Kruger, A. Is the summer season losing potential for solar energy applications in south africa? J. Energy South. 2017, 28, 52–60. [Google Scholar] [CrossRef]
- Masubelele, M.L.; Masubelele, M.L. Carbon Footprint Assessment in Nature-Based Conservation Management Estates Using South African National Parks as a Case Study. Sustainability 2021, 13, 13969. [Google Scholar] [CrossRef]
- Lin, S.-J.; Beidari, M.; Lewis, C.E. Energy consumption trends and decoupling effects between carbon dioxide and gross domestic product in south africa. Aerosol Air Qual. Res. 2015, 15, 2676–2687. [Google Scholar] [CrossRef]
- Nel, E.; Marais, L.; Mqotyana, Z. The regional implications of just transition in the world’s most coal-dependent economy: The case of mpumalanga, south africa. Front. Sustain. Cities 2023, 4, 1059312. [Google Scholar] [CrossRef]
- Global Oil Supply-and-Demand Outlook to 2040|Mckinsey. Available online: https://www.mckinsey.com/industries/oil-and-gas/our-insights/global-oil-supply-and-demand-outlook-to-2040 (accessed on 26 February 2022).
- L-Rubaye, A.H.A.; Suwaid, M.A.; Al-Muntaser, A.A.; Varfolomeev, M.A.; Rakhmatullin, I.Z.; Hakimi, M.H.; Saeed, S.A. Intensification of the steam stimulation process using bimetallic oxide catalysts of mfe2o4 (m = cu, co, ni) for in-situ upgrading and recovery of heavy oil. J. Pet. Explor. Prod. Technol. 2021, 12, 577–587. [Google Scholar] [CrossRef]
- Executive Summary—World Energy Investment 2021—Analysis-Iea. Available online: https://www.iea.org/reports/world-energy-investment-2021/executive-summary (accessed on 1 June 2022).
- Cockerill, S.; Martin, C. Are Biofuels Sustainable? The eu Perspective. Biotechnol. Biofuels 2008, 1, 9. [Google Scholar] [CrossRef] [PubMed]
- Velenturf, A.P. A framework and baseline for the integration of a sustainable circular economy in offshore wind. Energies 2021, 14, 5540. [Google Scholar] [CrossRef]
- Li, D. A Study for Development Suitability of Biomass Power Generation Technology Based on Ghg Emission Reduction Benefits and Growth Potential. Comput. Intell. Neurosci. 2022, 2022, 7961573. [Google Scholar] [CrossRef] [PubMed]
- Ringim, S.; Alhassan, A.; Güngör, H.; Victor Bekun, F. Economic policy uncertainty and energy prices: Empirical evidence from multivariate dcc-garch models. Energies 2022, 15, 3712. [Google Scholar] [CrossRef]
- Øksendal, B.; Sulem, A. Backward Stochastic Differential Equations and Risk Measures; Springer: Berlin/Heidelberg, Germany, 2019; pp. 75–91. ISBN 978-1-4939-8930-0. [Google Scholar] [CrossRef]
- Øksendal, B. Stochastic Differential Equations, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-04758-2. [Google Scholar] [CrossRef]
- Frenkel, J. Kinetic Theory of Liquids; Oxford at the Claredon Press: Oxford, UK, 1946. [Google Scholar]
- Goodrich, F. Nucleation rates and the kinetics of particle growth. i. the pure birth process. Proc. R. Soc. London. Ser. Math. Phys. Sci. 1964, 277, 155–166. [Google Scholar]
- Gurol, H. Transport Theory Formulation of the Rate Equations, (Univ. of Carlifonia, Santa Barbora). Trans. Am. Nucl. Soc. 1978, 30, 151–159. [Google Scholar]
- Xu, C. Global threshold dynamics of a stochastic differential equation sis model. J. Math. Anal. Appl. 2017, 447, 736–757. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moagi, G.S.; Doctor, O.; Lungu, E. A Divestment Model: Migration to Green Energy Investment Portfolio Concept. Mathematics 2024, 12, 915. https://doi.org/10.3390/math12060915
Moagi GS, Doctor O, Lungu E. A Divestment Model: Migration to Green Energy Investment Portfolio Concept. Mathematics. 2024; 12(6):915. https://doi.org/10.3390/math12060915
Chicago/Turabian StyleMoagi, Gaoganwe Sophie, Obonye Doctor, and Edward Lungu. 2024. "A Divestment Model: Migration to Green Energy Investment Portfolio Concept" Mathematics 12, no. 6: 915. https://doi.org/10.3390/math12060915
APA StyleMoagi, G. S., Doctor, O., & Lungu, E. (2024). A Divestment Model: Migration to Green Energy Investment Portfolio Concept. Mathematics, 12(6), 915. https://doi.org/10.3390/math12060915





