Distributed Adaptive Tracking Control of Hidden Leader-Follower Multi-Agent Systems with Unknown Parameters
Abstract
1. Introduction
2. Preparatory Knowledge and Modeling
2.1. Graph Theory
2.2. Multi-Agent Modeling
3. Multi-Model Adaptive Method
3.1. The Projection Algorithm
3.2. Multi-Model Adaptive Parameter Estimate
- (1)
- ;
- (2)
- ;
- (3)
- For , let and represent the centre and radius of , respectively, that is to say, , and for any , one has
3.3. Multi-Model Adaptive Optimal Parameter
- (1)
- When , let
- (2)
- When , the index switching functions are calculated
4. Distributed Adaptive Control Strategy
5. Auxiliary Lemmas
- (1)
- ∃ s.t.
- (2)
- (3)
- where
- (1)
- Selectas the Lyapunov function. Then, the difference isSince , we haveThe infinitesimal of the higher-order does not affect the sign of the function ; that is,So, we can conclude . In other words, s.t. .
- (2)
- Applying some simple manipulations to (26), we can obtainIt is easy to see that the left side of (27) is a convergent series; that is
- (3)
- According to (2) of Lemma 1, it follows from one necessary condition for the convergence of the series that
- (1)
- , and
- (2)
- (3)
6. Tracking Performance of The Multi-Agent System
- (1)
- the desired reference signal is tracked by the hidden leader agent, and each follower agent follows the average value of its own neighbors’ history outputs; that isand
- (2)
- the strong synchronization in the sense of the mean of all the follower agents to the hidden leader agent is achieved; that is,
- (3)
- all the agents track the desired reference signal; that is
- (1)
- From Lemma 2, we can writewhere . Based on Assumption 4 and the Lipschitz condition of , the order estimation is obtainedthus, we can obtainFrom (28), one hasAccording to , and (29), one haswhere I is an identity matrix and is an adjacency matrix of MAS; that isAfter calculation, it can be found thatwhereIt is clear that as ,From Assumption 3, and the bounded sequence , thenThus, (6) can be written asIt is clear to see is a sub-stochastic and irreducible matrix; and , which clearly indicates that
- (2)
- Define the error as follows:By (18), we haveSincethen, we can haveFurthermore, we havewhich can be written asBased on Assumption 3, we can suppose . In other words, for every real number , there is , if , thenwhich yieldsThen,In particular, . There is a matrix norm such thatfor . That iswhere ; that is, for , , if , then . Obviously, the first T terms of this sequence are bounded by a constant , i.e., Thus, (38) can be written asSince , one hasandBased on the equivalence among norms, we haveFrom (34), it is clear to see that
- (3)
- Denote the error ; thus,which leads to
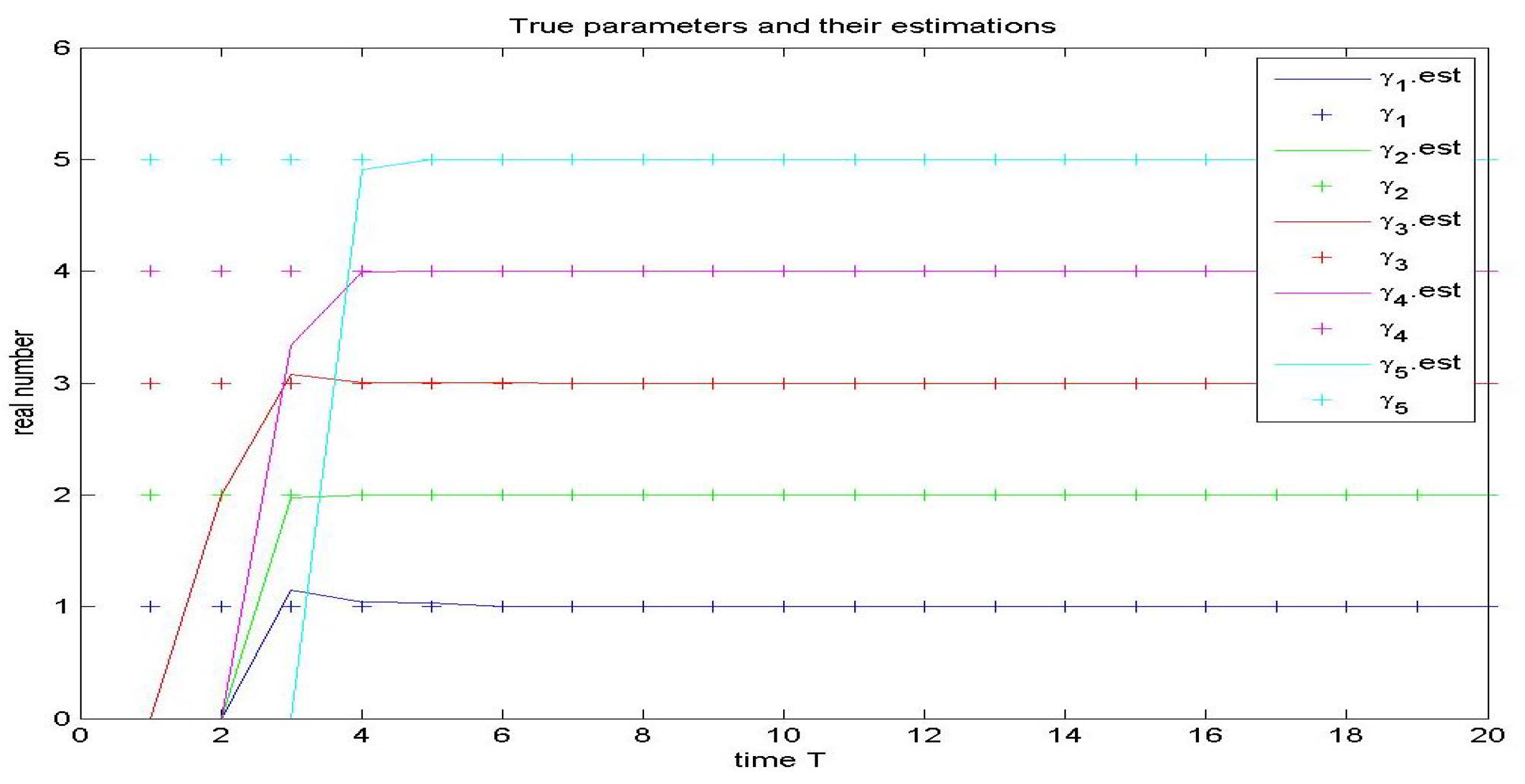
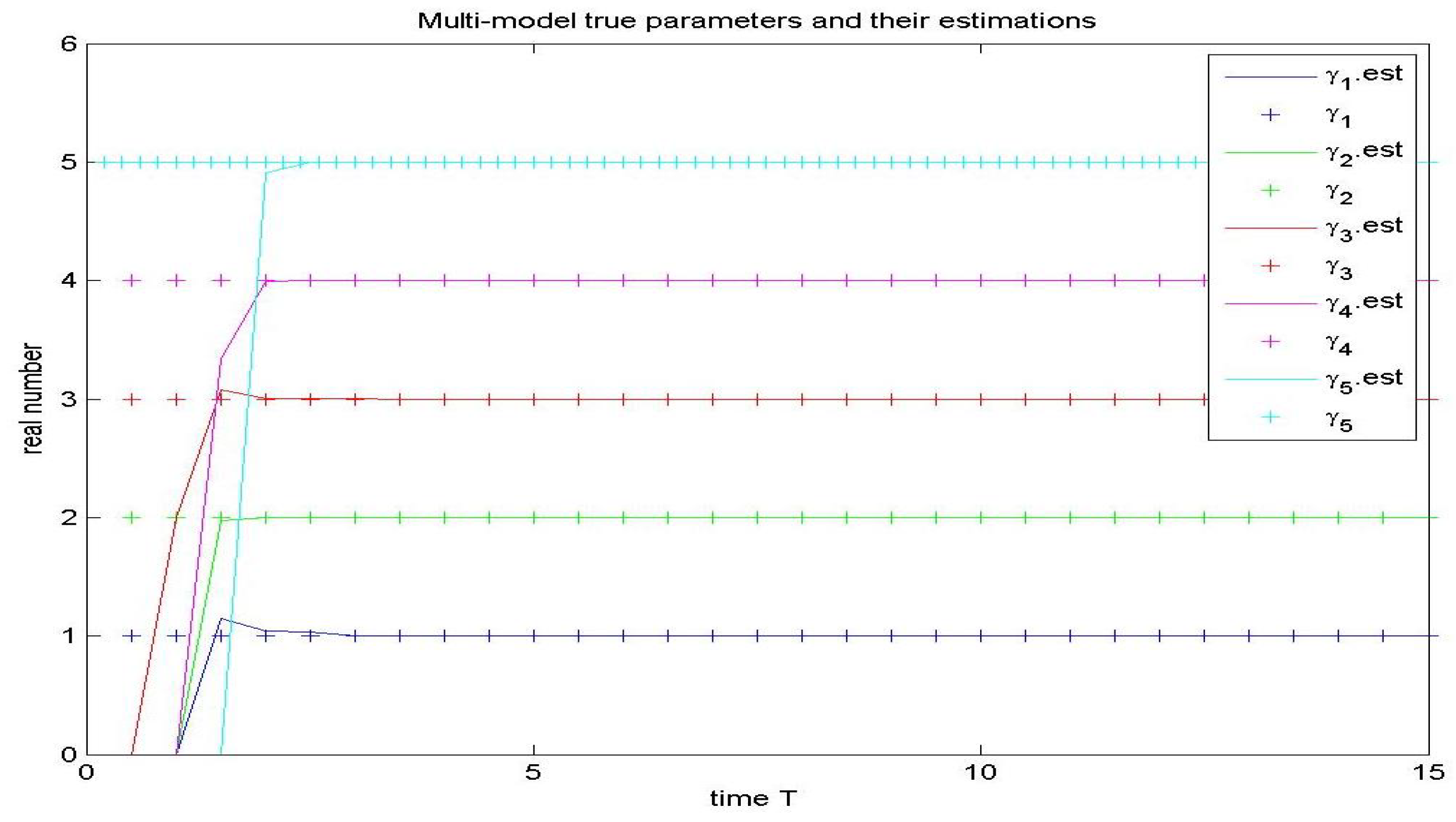
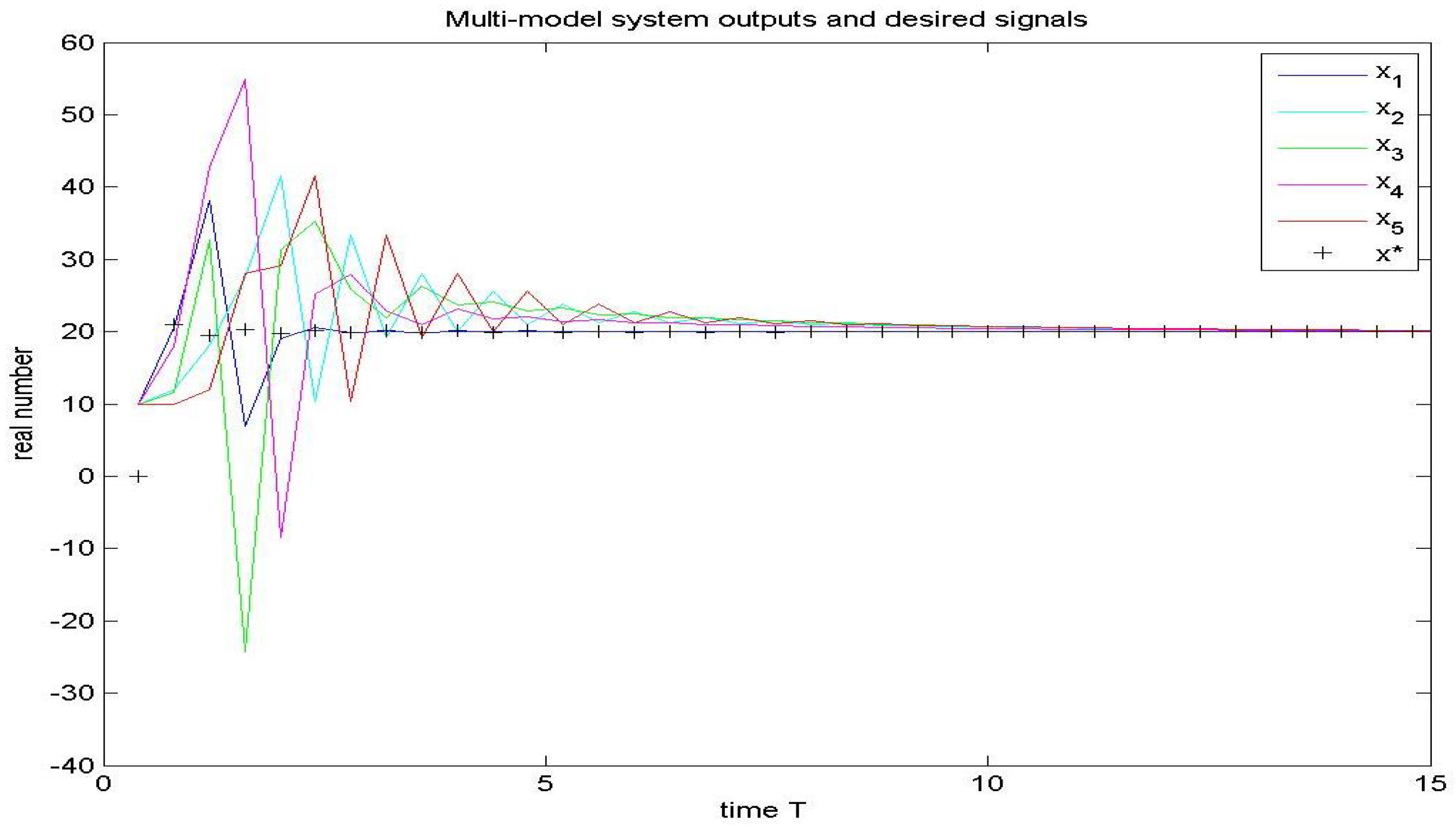
7. Simulations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.L.; Yan, J.G.; Lv, M.L.; Kong, X.J.; Zhang, P. UAV Formation Flight Cooperative Tracking Controller Design. In Proceedings of the International Conference on Control, Automation, Robotics and Vision, Singapore, 18–21 November 2018. [Google Scholar]
- Zhang, J.L.; Xiao, B.; Lv, M.L.; Zhang, Q. Design and Flight-Stability Analysis of a Closed Fixed-Wing Unmanned Aerial Vehicle Formation Controller. Proc. Inst. Mech. Eng. 2019, 233, 1045–1054. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Li, Y.Z.; Wu, Y.Q.; He, S.H. Formation Control of Nonholonomic Unmanned Ground Vehicles via Unscented Kalman Filter-based Sensor Fusion Approach. ISA Trans. 2022, 125, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.L.; Chang, N.W. Fuzzy Decentralized Sliding-Mode Control of a Car-Like Mobile Robot in Distributed Sensor-Network Spaces. IEEE Trans. Fuzzy Syst. 2008, 16, 97–109. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, G. Distributed Tracking Control of Mobile Sensor Networks with Intermittent Communications. J. Frankl. Inst. 2017, 354, 3634–3647. [Google Scholar] [CrossRef]
- Meng, M.; Xiao, G.X.; Li, B.B. Adaptive Consensus for Heterogeneous Multi-Agent Systems Under Sensor and Actuator Attacks. Automatica 2020, 122, 109242. [Google Scholar] [CrossRef]
- Rouzegar, H.; Khosravi, A.; Sarhadi, P. Spacecraft Formation Flying Control Around L2 Sun-Earth Libration Point Using On-Off SDRE Approach. Adv. Space Res. 2021, 67, 2172–2184. [Google Scholar] [CrossRef]
- Gao, Z.F.; Wang, S. Fault Estimation and Fault Tolerance Control for Spacecraft Formation Systems with Actuator Fault and Saturation. Optim. Control Appl. Methods 2021, 42, 1591–1611. [Google Scholar] [CrossRef]
- Ma, X.P.; Yang, P.L.; Dong, H.Y.; Yang, J.; Yao, Z. Secondary Control Strategy of Islanded Micro-grid Based on Multi-agent Consistency. In Proceedings of the IEEE Conference on Energy Internet and Energy System Integration, Beijing, China, 26–28 November 2017. [Google Scholar]
- Chen, X. Multimode Coordination Control Method for Microgrid Cluster Based on Adaptive Power Control and Routing Algorithm. J. Nanoelectron. Optoelectron. 2022, 17, 72–81. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Liu, C.G.; Liu, X.P.; Wang, H.Q.; Zhou, Y.C. Adaptive Tracking Control for Stochastic Nonlinear Systems with Unknown Virtual Control Coefficients. Int. J. Robust Nonlinear Control 2022, 32, 1331–1354. [Google Scholar] [CrossRef]
- Yan, C.H.; Zhang, W.; Guo, H.; Zhu, F.L.; Qian, Y.C. Distributed Adaptive Time-Varying Formation Control for Lipschitz Nonlinear Multi-agent Systems. Trans. Inst. Meas. Control 2022, 44, 272–285. [Google Scholar] [CrossRef]
- Wang, X.M.; Sun, J.S.; Wu, Z.X.; Li, Z.T. Robust Integral of Sign of Error-Based Distributed Flocking Control of Double-Integrator Multi-Agent Systems with a Varying Virtual Leader. Int. J. Robust Nonlinear Control 2022, 32, 286–303. [Google Scholar] [CrossRef]
- Hu, W.; Wen, G.G.; Rahmani, A.; Yang, G.Y. Distributed Consensus Tracking of Unknown Nonlinear Chaotic Delayed Fractional-order Multi-Agent Systems with External Disturbances Based on ABC Algorithm. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 101–117. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Zhang, Z.H.; Li, X.B.; Yang, X.L. Event-Triggered Adaptive NN Tracking Control with Dynamic Gain for a Class of Unknown Nonlinear Systems. Neurocomputing 2022, 467, 292–299. [Google Scholar] [CrossRef]
- Bian, Y.G.; Zhang, J.J.; Hu, Q.J.; Ding, R.J. Self-Triggered Distributed Model Predictive Control for Cooperative Diving of Multi-AUV System. Ocean Eng. 2023, 267, 113262. [Google Scholar] [CrossRef]
- Distributed Pinning Controllers Design for Set Stabilization of k-Valued Logical Control Networks. Math. Model. Control 2023, 3, 61–72. [CrossRef]
- Davis, J.H.; Dryden, G.H. Centralized Traffic Control and Train Control of the Baltimore and Ohio Railroad. Trans. Am. Inst. Electr. Eng. 2009, 52, 308–312. [Google Scholar] [CrossRef]
- Narmanlioglu, O.; Uysal, M. Event-Triggered Adaptive Handover for Centralized Hybrid VLC/MMW Networks. IEEE Trans. Commun. 2022, 70, 455–468. [Google Scholar] [CrossRef]
- Hui, Y.; Xia, X.H. Adaptive Leaderless Consensus of Agents in Jointly Connected Networks. Neurocomputing 2017, 241, 64–70. [Google Scholar] [CrossRef]
- Chen, C.; Lewis, F.L.; Li, X.L. Event-Triggered Coordination of Multi-Agent Systems via a Lyapunov-Based Approach for Leaderless Consensus. Automatica 2022, 136, 109936. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J. Adaptive Leader-Following Consensus for a Class of Higher-order Nonlinear Multi-Agent Systems with Directed Switching Networks. Automatica 2017, 79, 84–92. [Google Scholar] [CrossRef]
- Zhao, M.J.; Peng, Y.; Wang, Y.Y.; Zhang, D.; Luo, J.; Pu, H.Y. Concise Leader-follower Formation Control of Under Actuated Unmanned Surface Vehicle with Output Error Constraints. Trans. Inst. Meas. Control 2022, 44, 1081–1094. [Google Scholar] [CrossRef]
- Zhang, P.; Xue, H.F.; Gao, S.; Zhang, J.L. Distributed Adaptive Consensus Tracking Control for Multi-Agent System with Communication Constraints. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1293–1306. [Google Scholar] [CrossRef]
- Yang, R.H.; Zhou, D.Y. Distributed Event-Triggered Tracking Control of Heterogeneous Discrete-Time Multi-Agent Systems with Unknown Parameters. J. Syst. Sci. Complex. 2022, 35, 1330–1347. [Google Scholar] [CrossRef]
- Lu, Y.R.; Liao, F.C.; Liu, H.Y.; Usman. Cooperative Preview Tracking Problem of Discrete-Time Linear Multi-Agent Systems: A Distributed Output Regulation Approach. ISA Trans. 2019, 85, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jiang, B.; Wang, X.F.; Yang, H.L.; Xie, S.R. Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks. IEEE/CAA J. Autom. Sin. 2022, 9, 1037–1048. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.L.; Zhang, Y.S. Distributed Continuous-Time Containment Control of Heterogeneous Multiagent Systems with Nonconvex Control Input Constraints. Complexity 2022, 2022, 7081091. [Google Scholar] [CrossRef]
- Hamdan, T.B.; Mercere, G.; Dairay, T.; Meunier, R.; Tremblay, P.; Coirault, P. Tracking Distributed Parameters System Dynamics with Recursive Dynamic Mode Decomposition with Control. SIAM J. Appl. Dyn. Syst. 2023, 22, 37–64. [Google Scholar] [CrossRef]
- Wen, N.Q.; Wu, A.G.; Dong, R.Q. Distributed Adaptive Neural Network Fixed-Time Leader-Follower Attitude Consensus Control for Multiple Rigid Spacecraft. Int. J. Adapt. Control Signal Process. 2023, 37, 553–582. [Google Scholar] [CrossRef]
- Lainiotis, D.G. Optimal Adaptive Estimation: Structure and Parameter Adaption. IEEE Trans. Autom. Control 1971, 16, 160–170. [Google Scholar] [CrossRef]
- Middleton, R.H.; Goodwin, G.C.; Hill, D.J.; Mayne, D.Q. Design Issues in Adaptive Control. IEEE Trans. Autom. Control 1988, 33, 50–58. [Google Scholar] [CrossRef]
- Zhivoglyadov, P.V.; Middleton, R.H.; Fu, M. Localization Based Switching Adaptive Control for Time-Varying Discrete-Time Systems. IEEE Trans. Autom. Control 2000, 45, 752–755. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Chai, T.Y.; Wang, H.; Fu, J.; Zhang, L.Y.; Wang, Y.G. An Adaptive Generalized Predictive Control Method for Nonlinear Systems Based on ANFIS and Multiple Models. IEEE Trans. Fuzzy Syst. 2010, 18, 1070–1082. [Google Scholar] [CrossRef]
- Narendra, K.S.; Xiang, C. Adaptive Control of Discrete-Time Systems Using Multiple Models. IEEE Trans. Autom. Control 2000, 45, 1669–1686. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Fei, S.M. Multiple Models Adaptive Control Based on Online Optimization. Syst. Eng. Electron. 2009, 31, 2185–2188. [Google Scholar]
- Yue, F.; Chai, T.Y. Nonlinear Multivariable Adaptive Control Using Multiple Models and Neural Networks. Automatica 2007, 43, 1101–1110. [Google Scholar] [CrossRef]
- Miao, H.; Wang, X.; Wang, Z.L.; Feng, Q. Multiple Models Adaptive Control Based on Cluster-optimization for a Class of Nonlinear System. In Proceedings of the Intelligent Control and Automation, Beijing, China, 6–8 July 2011. [Google Scholar] [CrossRef]
- Niu, Y.G.; Li, X.M.; Lin, Z.W.; Li, M.Y. Multiple Models Decentralized Coordinated Control of Doubly Fed Induction Generator. Int. J. Electr. Power Energy Syst. 2015, 64, 921–930. [Google Scholar] [CrossRef]
- Zhang, X.H.; Chang, Z.Y.; Wang, Y.H. Multi-Model Method Decentralized Adaptive Control for a Class of Discrete-Time Multi-Agent Systems. IEEE Access 2020, 8, 193717–193727. [Google Scholar] [CrossRef]
- Zhang, X.H.; Ma, H.B.; Yang, C.G. Decentralised Adaptive Control of a Class of Hidden Leader-follower Non-linearly Parameterised Coupled MASs. IET Control Theory Appl. 2017, 11, 3016–3025. [Google Scholar] [CrossRef]
- Ge, S.S.; Yang, C.G.; Li, Y.N.; Tong, H.L. Decentralized Adaptive Control of a Class of Discrete-time Multi-agent Systems for Hidden Leader Following Problem. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009. [Google Scholar] [CrossRef]
- Zhang, X.H.; Ma, H.B.; Wang, J.N. Decentralized Adaptive Control of a Class of Discrete-Time Nonlinear Hidden-Leader Follower Multi-Agent Systems. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Lee, B.G. Distributed Adaptive Tracking Control of Hidden Leader-Follower Multi-Agent Systems with Unknown Parameters. Mathematics 2024, 12, 1013. https://doi.org/10.3390/math12071013
Yang J, Lee BG. Distributed Adaptive Tracking Control of Hidden Leader-Follower Multi-Agent Systems with Unknown Parameters. Mathematics. 2024; 12(7):1013. https://doi.org/10.3390/math12071013
Chicago/Turabian StyleYang, Jie, and Byung Gook Lee. 2024. "Distributed Adaptive Tracking Control of Hidden Leader-Follower Multi-Agent Systems with Unknown Parameters" Mathematics 12, no. 7: 1013. https://doi.org/10.3390/math12071013
APA StyleYang, J., & Lee, B. G. (2024). Distributed Adaptive Tracking Control of Hidden Leader-Follower Multi-Agent Systems with Unknown Parameters. Mathematics, 12(7), 1013. https://doi.org/10.3390/math12071013




