A Risk-Structured Model for the Transmission Dynamics of Anthrax Disease
Abstract
1. Introduction
2. Model Formulation
- There is no vertical transmission in both populations.
- High-risk susceptibles can become low-risk susceptibles due to their adoption of protective measures as a result of educational and enlightenment campaigns.
- A fraction of the recruited animals are effectively vaccinated.
- Susceptible humans and animals get infected by coming into contact with infected livestock, infected carcasses, and spores.
- There is no human-to-human infection.
- Recovered humans and animals can lose infection-acquired immunity.
- Animal vaccination is perfect.
- Only healthy animals are recruited into the population.
3. Analyses of the Model
3.1. Boundedness of Solutions
3.2. Non-Negativity of Solutions
3.3. Existence and Uniqueness of the Solution
- ;
- , where M is Lipschitz constant.
3.4. The Disease-Free Equilibrium (DFE)
3.5. Effective Reproduction Number ()
3.6. The Disease-Endemic Equilibrium (DEE)
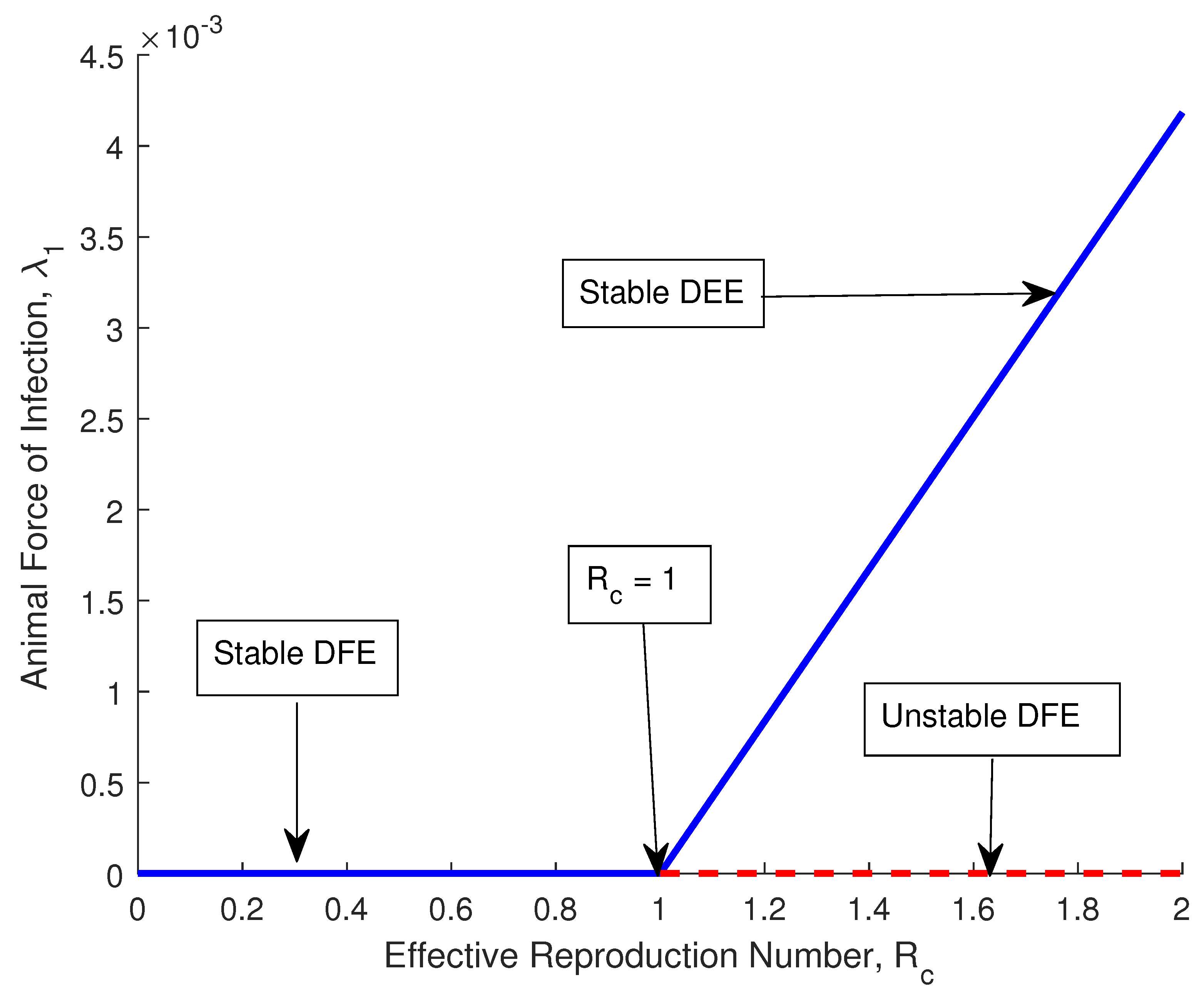
3.7. Bifurcation Analysis
3.8. Global Stability Analysis
4. Parameterization and Scenario Simulations
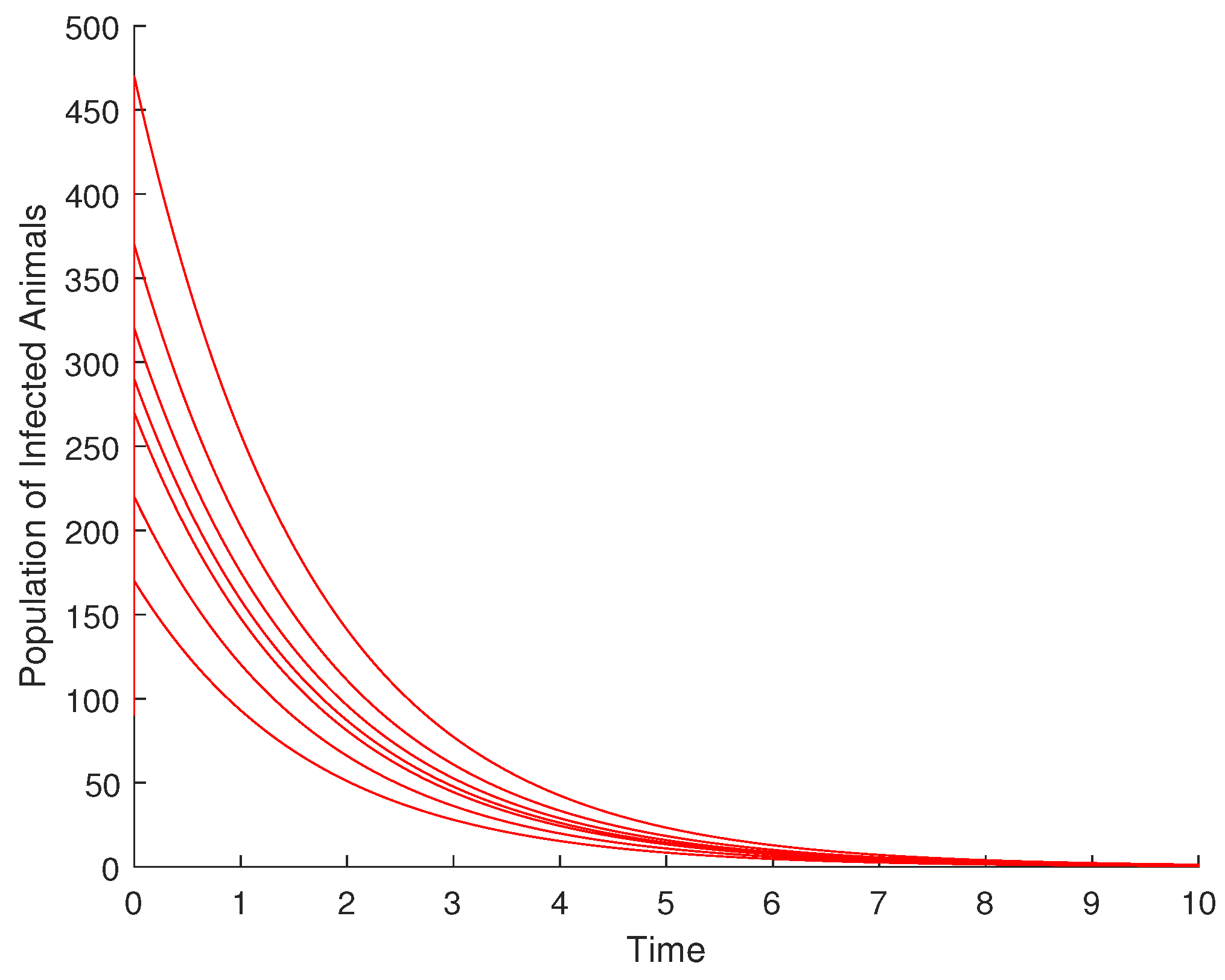
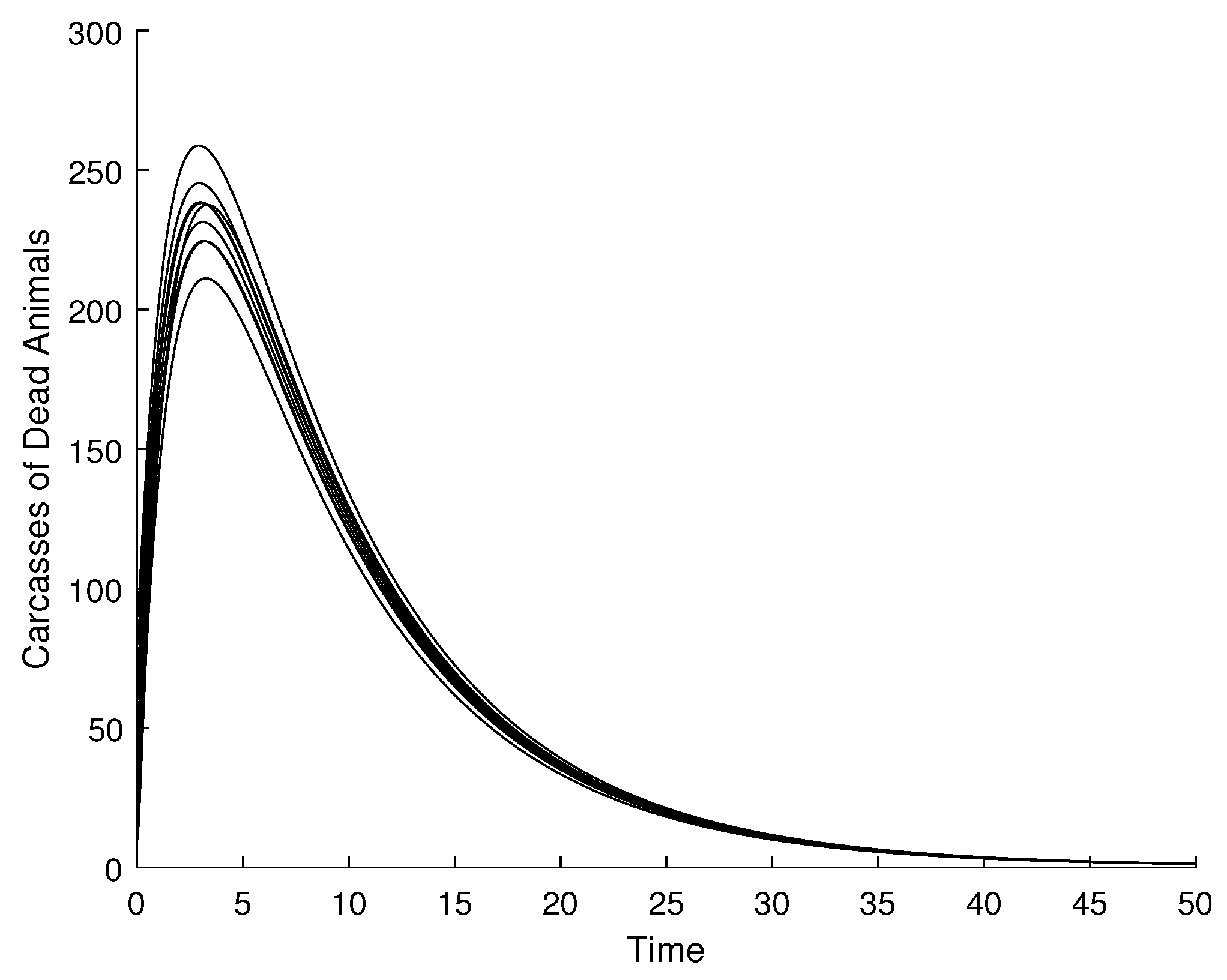
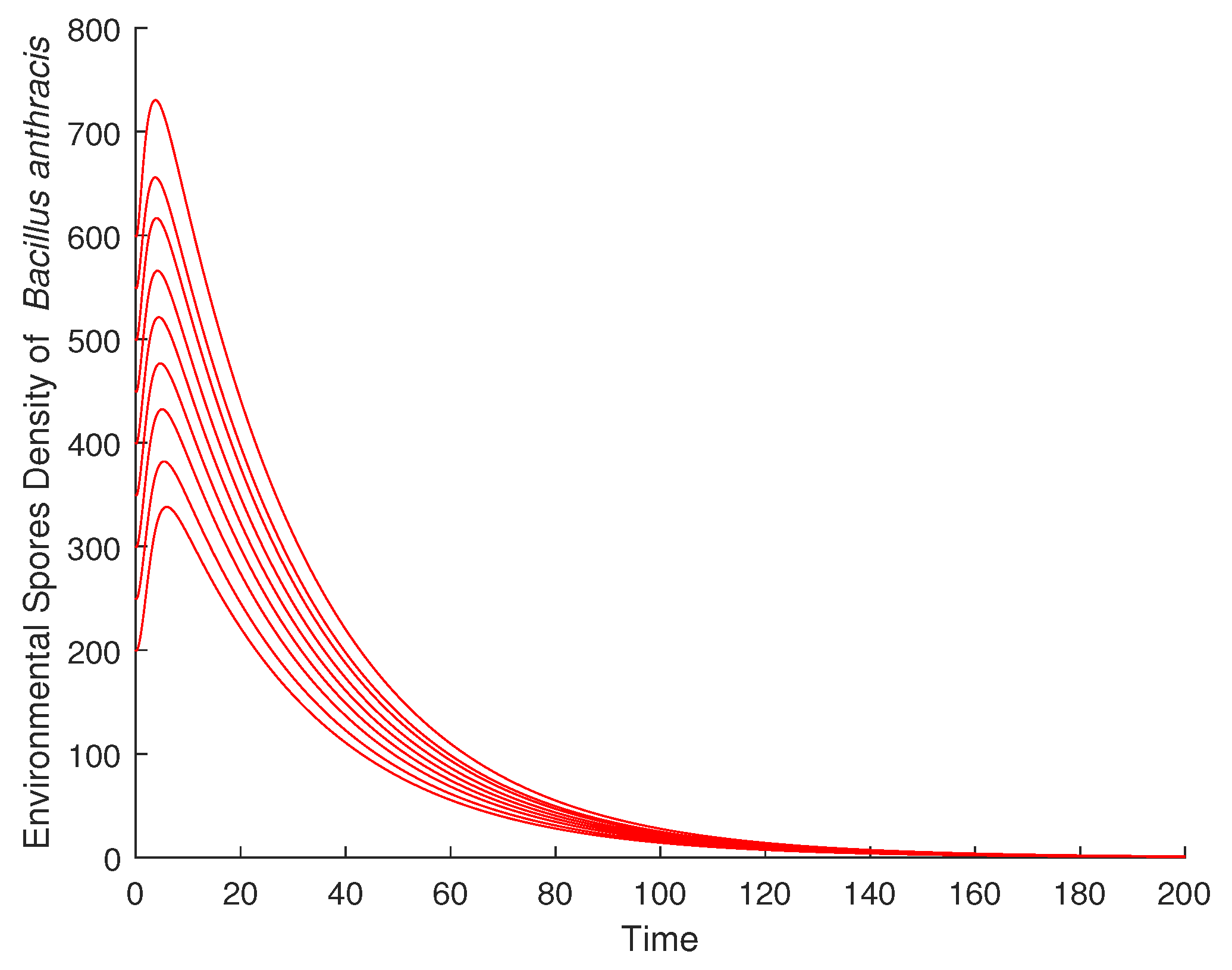
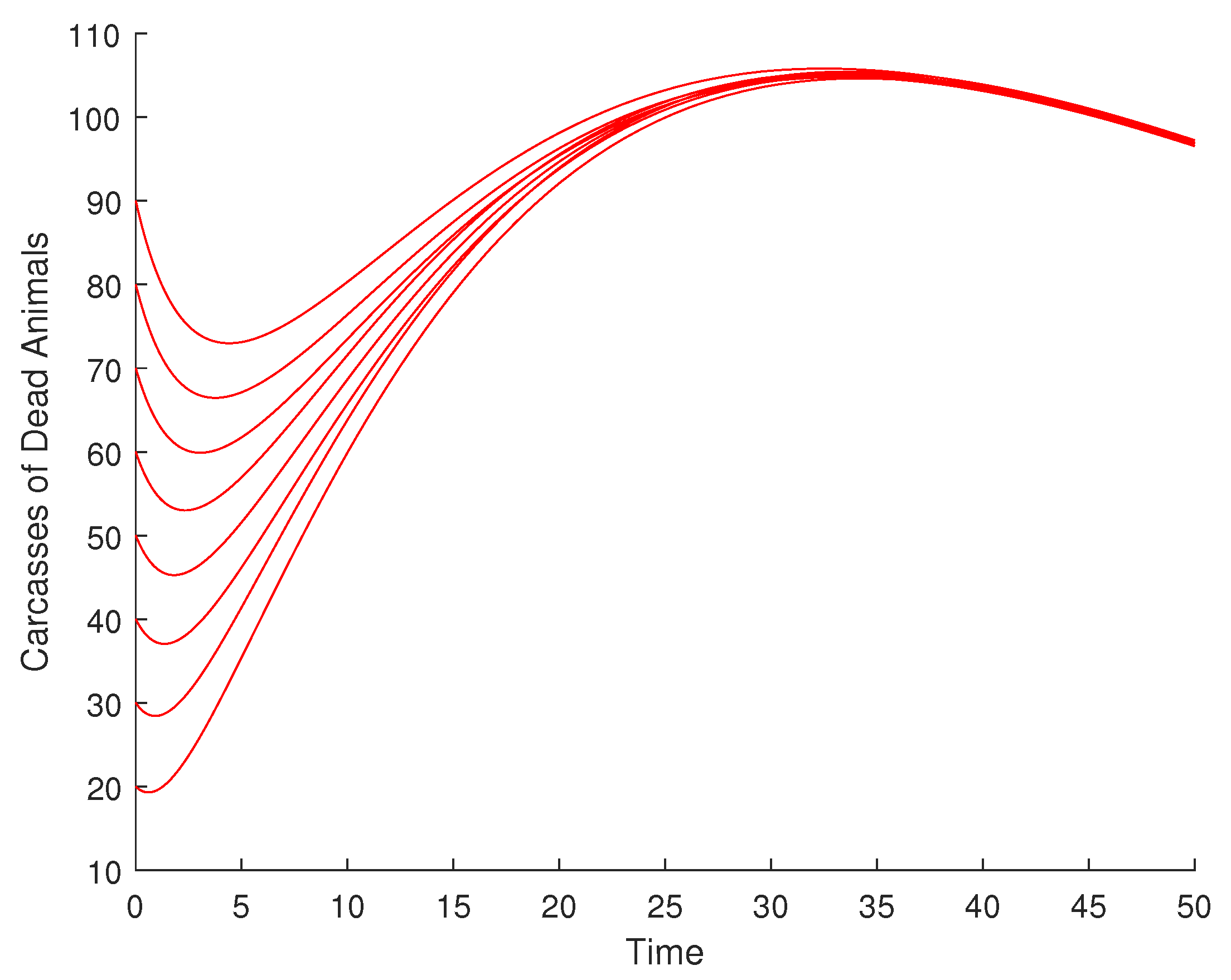
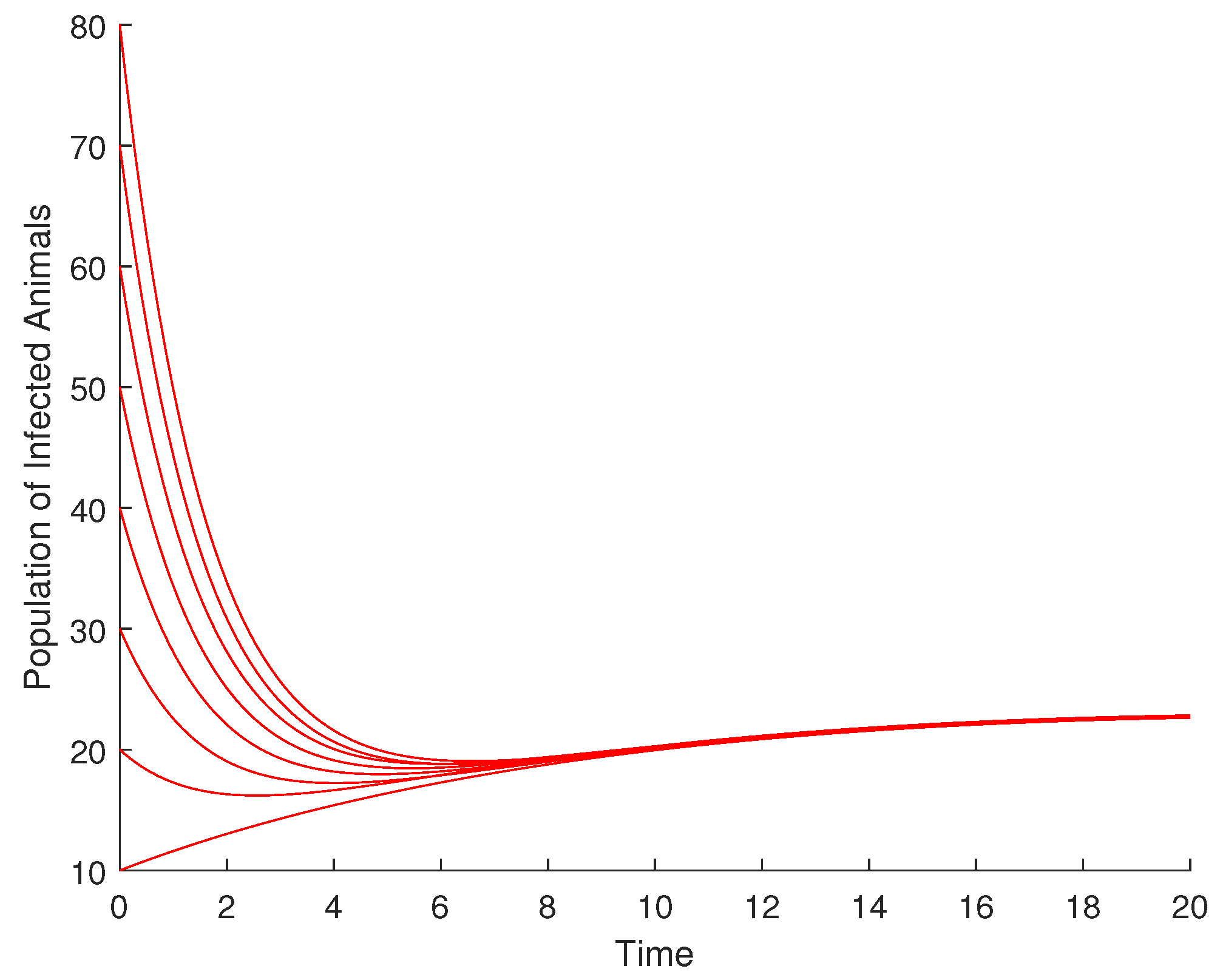
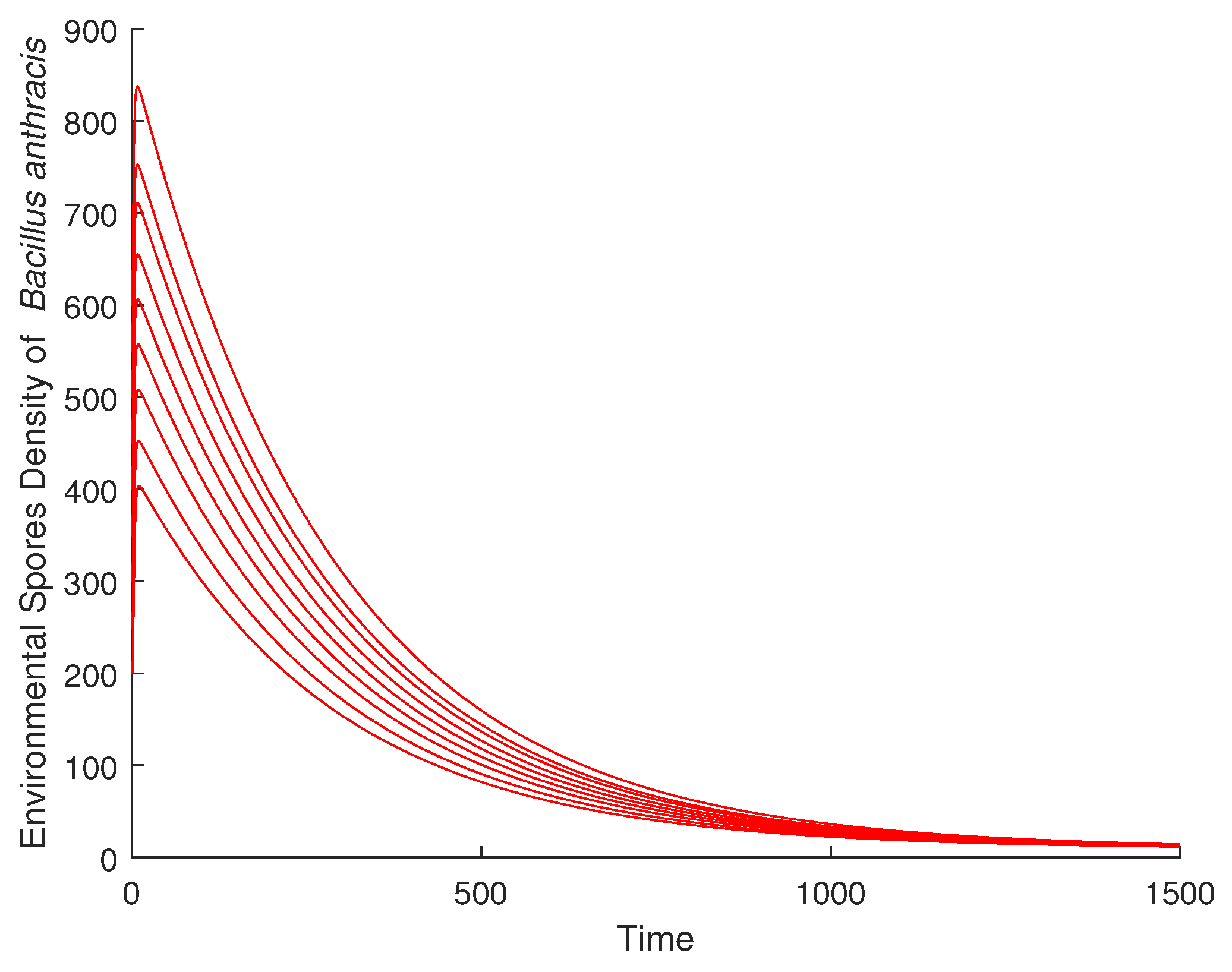
4.1. Validation of the Qualitative Analysis
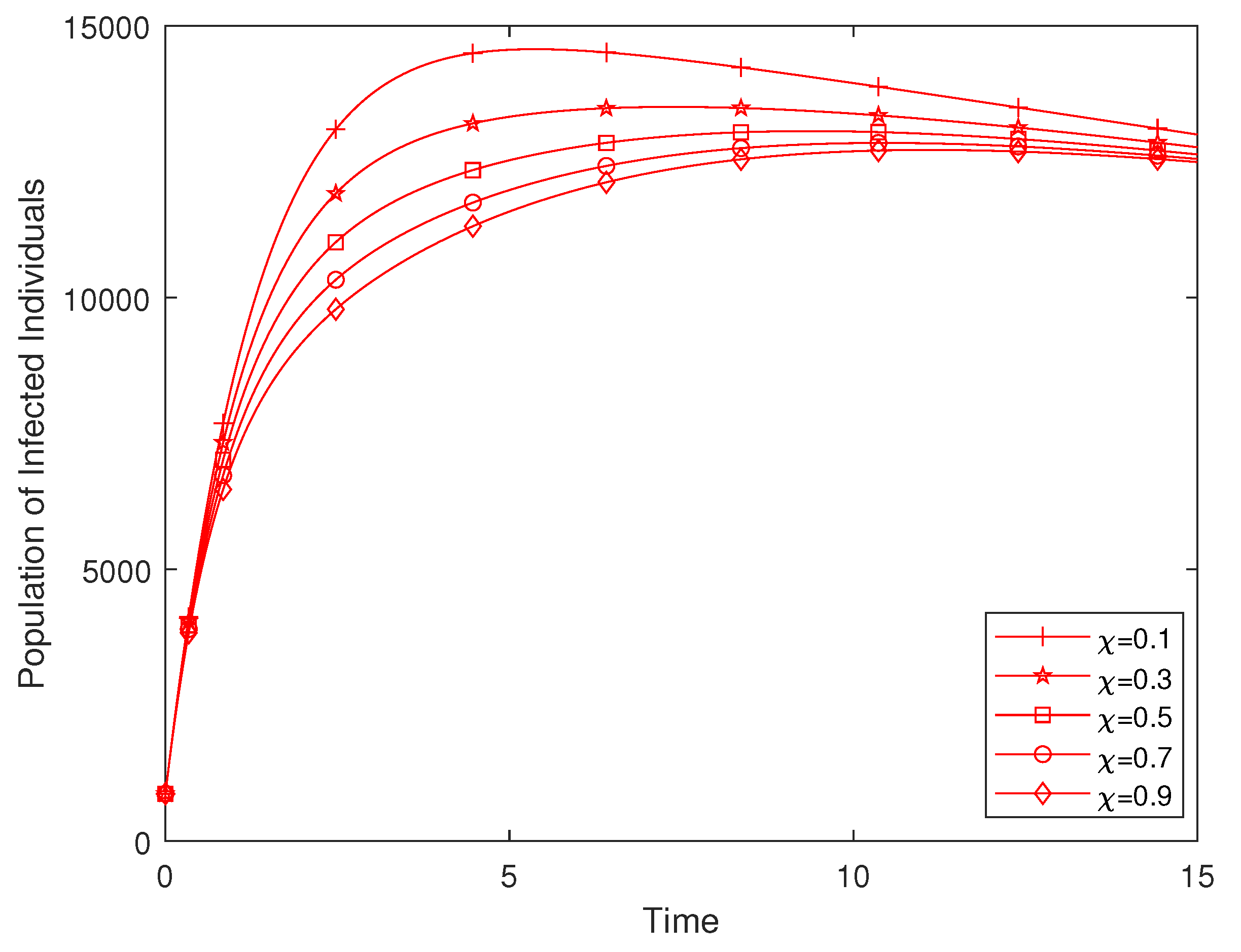
4.2. Effect of Enlightenment Campaign on the Disease Dynamics
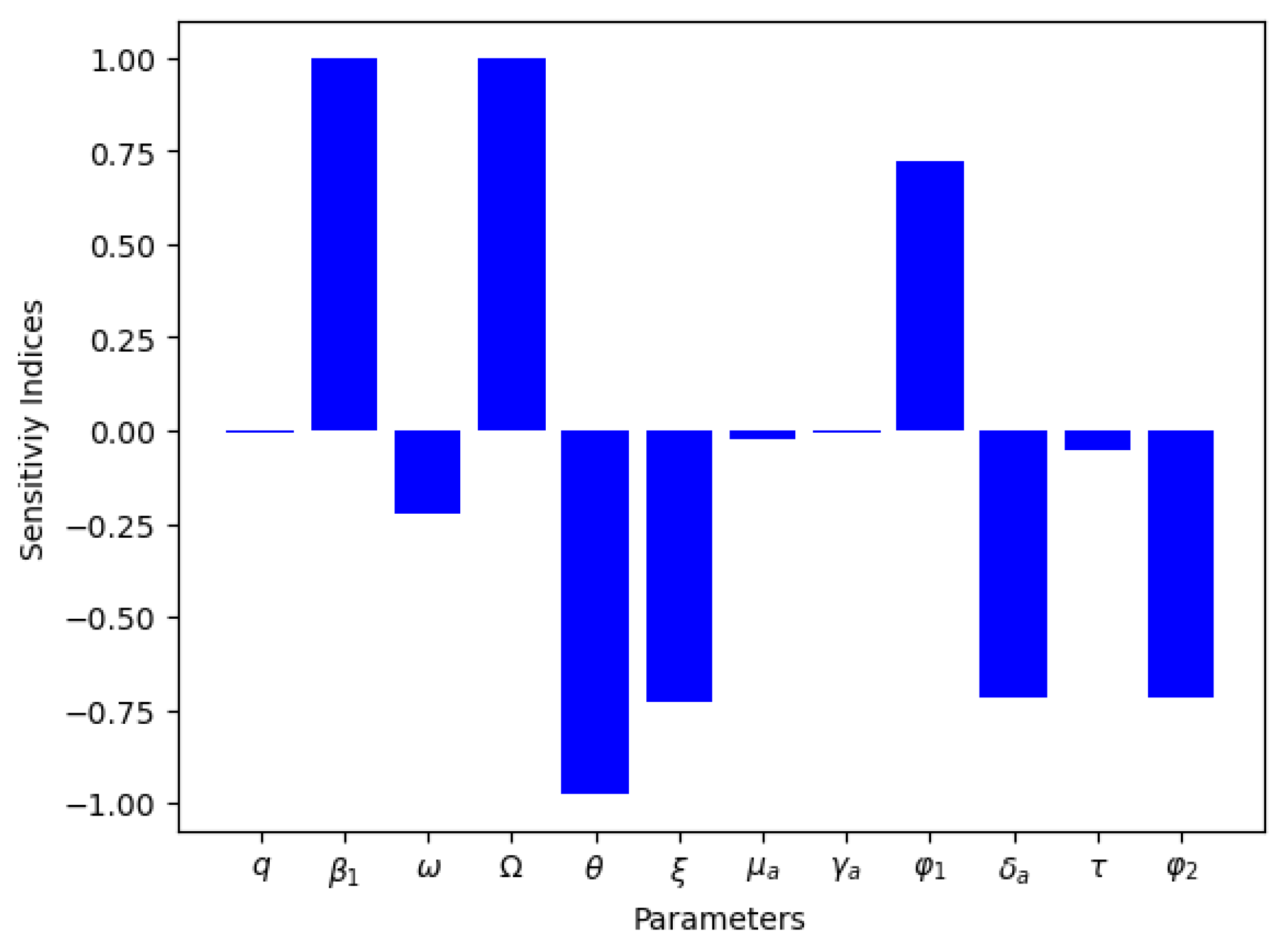
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Center for Disease Control (CDC). National Center for Emerging and Zoonotic Infectious Diseases (NCEZID), Division of High-Consequence Pathogens and Pathology (DHCPP). Available online: https://www.cdc.gov/anthrax/basics/index.html (accessed on 8 November 2023).
- Doganay, M.; Metan, G.; Alp, E. A review of cutaneous anthrax and its outcome. J. Infect. Public Health 2010, 3, 98–105. [Google Scholar] [CrossRef]
- Alam, M.E.; Kamal, M.M.; Moizur, R.; Aurangazeb, K.; Islam, M.S.; Hassan, J. Review of anthrax: A disease of farm animals. J. Adv. Vet. Anim. Res. 2022, 9, 323. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization; International Office of Epizootics. Anthrax in Humans and Animals; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Dragon, D.C.; Rennie, R.P. The ecology of anthrax spores: Tough but not invincible. Can. Vet. J. 1995, 36, 295–301. [Google Scholar] [PubMed]
- Martcheva, M. Methods for deriving necessary and sufficient conditions for backward bifurcation. J. Biol. Dyn. 2019, 13, 538–566. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization (WHO). Available online: https://www.who.int/news-room/fact-sheets/detail/climate-change-and-health (accessed on 8 November 2023).
- Baloba, E.B.; Seidu, B.; Bornaa, C.S.; Okyere, E. Optimal control and cost-effectiveness analysis of anthrax epidemic model. J. Inform. Med. Unlocked 2023, 42, 101355. [Google Scholar] [CrossRef]
- Akinyemi, S.T.; Idisi, I.O.; Rabiu, M.; Okeowo, V.I.; Iheonu, N.; Dansu, E.J.; Abah, R.T.; Mogbojuri, O.A.; Audu, A.M.; Yahaya, M.M.; et al. A tale of two countries: Optimal control and cost-effectiveness analysis of monkeypox disease in Germany and Nigeria. Healthc. Anal. 2023, 2023, 100258. [Google Scholar] [CrossRef]
- Iheonu, N.O.; Nwajeri, U.K.; Omame, A. A non-integer order model for Zika and Dengue co-dynamics with cross-enhancement. Healthc. Anal. 2023, 2023, 100276. [Google Scholar] [CrossRef]
- Waku, J.; Oshinubi, K.; Adam, U.M.; Demongeot, J. Forecasting the Endemic/Epidemic Transition in COVID-19 in Some Countries: Influence of the Vaccination. Diseases 2023, 11, 135. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Bahl, P.; Silva, C.D.; Heslop, D.; Doolan, C.; Lim, S.; MacIntyre, C. Systematic Review and Evaluation of Mathematical Attack Models of Human Inhalational Anthrax for Supporting Public Health Decision Making and Response. Prehospital Disaster Med. 2020, 35, 412–419. [Google Scholar] [CrossRef]
- Mushayabasa, S.; Marijani, T.; Masocha, M. Dynamical analysis and control strategies in modeling anthrax. Comp. Appl. Math. 2017, 36, 1333–1348. [Google Scholar] [CrossRef]
- Saad-Roy, C.M.; Driessche, P.v.; Yakubu, A.A. A Mathematical Model of Anthrax Transmission in Animal Populations. Bull. Math. Biol. 2017, 79, 303–324. [Google Scholar] [CrossRef] [PubMed]
- Otieno, F.T.; Gachohi, J.; Gikuma-Njuru, P.; Kariuki, P.; Oyas, H.; Canfield, S.A.; Bett, B.; Njenga, M.K.; Blackburn, J.K. Modeling the Potential Future Distribution of Anthrax Outbreaks under Multiple Climate Change Scenarios for Kenya. Int. J. Environ. Res. Public Health 2021, 18, 4176. [Google Scholar] [CrossRef] [PubMed]
- Osman, S.; Makinde, O.D.; Theuri, D.M. Mathematical modeling of Transmission Dynamics of Anthrax in Human and Animal Population. Math. Theory Model. 2018, 8, 201847. [Google Scholar]
- Raza, A.; Baleanu, D.; Yousaf, M.; Akhter, N.; Mahmood, S.K.; Rafiq, M. Modeling of Anthrax Disease via Efficient Computing Techniques. Intell. Autom. Soft Comput. (IASC) 2022, 32, 1109–1124. [Google Scholar] [CrossRef]
- Baloba, E.B.; Seidu, B. A Mathematical Model of Anthrax Epidemic with Behavioural Change. J. Math. Model. Control. (MMC) AIMS 2022, 2, 243–256. [Google Scholar] [CrossRef]
- Gomez, J.P.; Nekorchuk, D.M.; Mao, L.; Ryan, S.J.; Ponciano, J.M.; Blackburn, J.K. Decoupling Environmental Effects and Host Population Dynamics for Anthrax, a Classic Reservoir-Driven Disease. PLoS ONE 2018, 13, e0208621. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, A.J.; Bordoloi, A.J.; Mohan, F.; Devi, A. Dynamical Analysis of an Anthrax Disease Model in Animals with Nonlinear Transmission. Math. Model. Control. 2023, 3, 370–386. [Google Scholar] [CrossRef]
- Efraim, J.E.; Irunde, J.I.; Kuznetsov, D. Modeling the Transmission Dynamics of Anthrax Disease in Cattle and Humans. J. Math. Comput. Sci. 2018, 8, 654–672. [Google Scholar] [CrossRef]
- Zerihun, M.S.; Narasimha, M.S. Modeling and Simulation Study of Anthrax Attack On Environment. J. Multidiscip. Eng. Sci. Technol. (JMEST) 2016, 3, 4574–4578. [Google Scholar]
- Denekew, Z.A.; Sunita, G.; Kumar, G.S. Model for Transmission and Optimal Control of Anthrax Involving Human and Animal Population. J. Biol. Syst. 2022, 30, 605–630. [Google Scholar] [CrossRef]
- Prawandani, N.; Toaha, S.; Kasbawati, S. VSEIR Mathematical Model on Anthrax Disease Dissemination in Animal Population with Vaccination and Treatment Effects. J. Mat. Stat. Komputari 2020, 17, 14–25. [Google Scholar] [CrossRef]
- Alfwzan, W.F.; Abuasbe, K.; Raza, A.; Rafiq, M.; Awadalla, M.; Almulla, M.A. A Non-standard Computational Method for Stochastic Anthrax Epidemic Model. AIP Adv. 2023, 3, 075022. [Google Scholar] [CrossRef]
- Den Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Data from United Nations. 2023. Available online: https://population.un.org/wpp/Download/Standard/MostUsed (accessed on 8 November 2023).
- Macrotrends. Africa Life Expectancy 1950–2023. Available online: https://www.macrotrends.net/countries/AFR/africa/life-expectancy#:~:text=The%20life%20expectancy%20for%20Africa,a%200.46%25%20increase%20from%202019 (accessed on 8 November 2023).
- La Salle, J.P. The stability of dynamical systems. In Society of Industrial and Applied Mathematics—SIAM; E-book: Rijeka, Croatia, 1976. [Google Scholar]
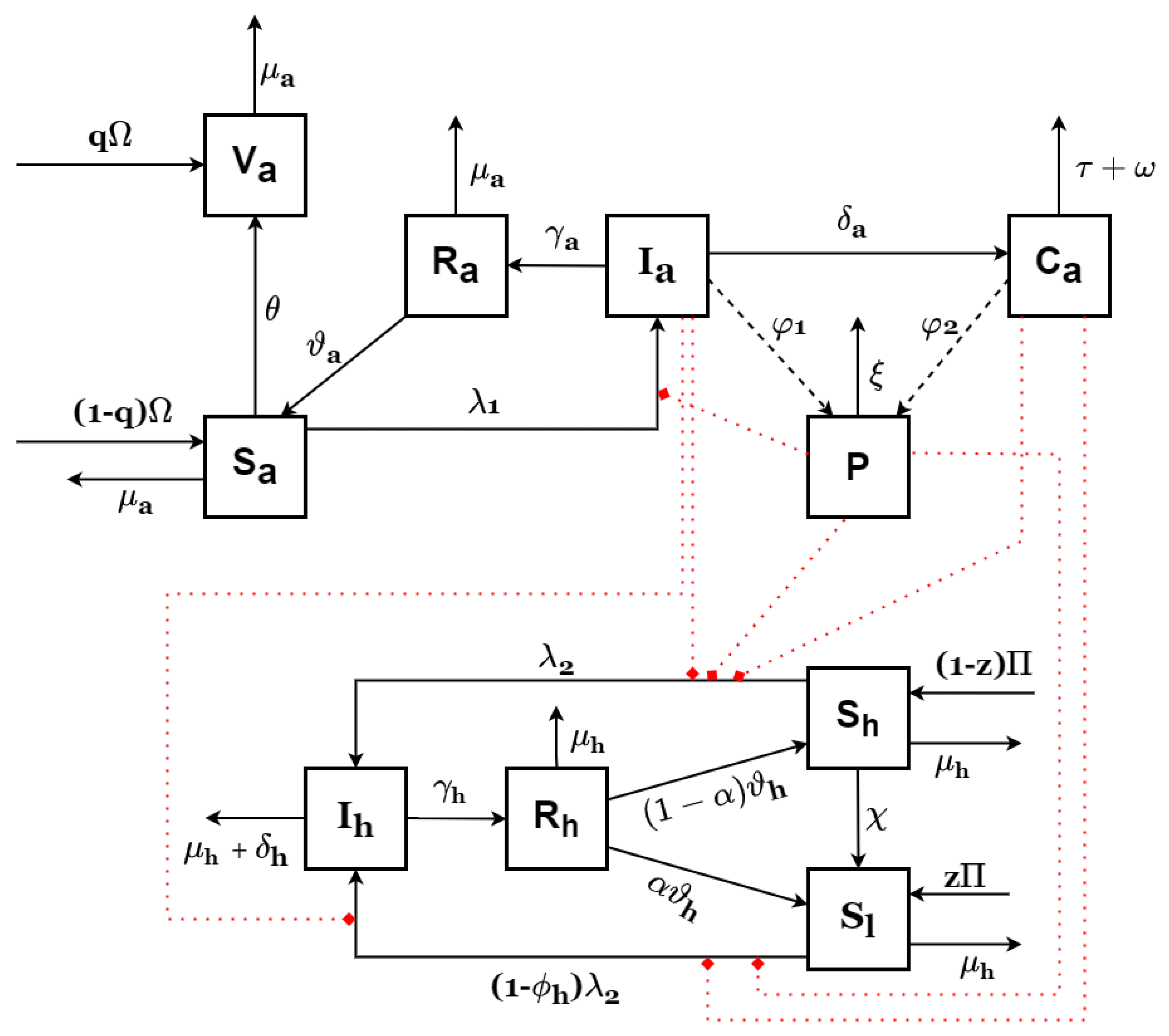


| Variable | Interpretation |
|---|---|
| Population of susceptible animals | |
| Population of vaccinated animals | |
| Population of infected animals | |
| Population of recovered animals | |
| Carcasses of dead animals | |
| P | Environmental spore density of Bacillus anthracis |
| Population of susceptible high-risk individuals | |
| Population of susceptible low-risk individuals | |
| Population of infected individuals | |
| Population of recovered individuals | |
| Parameter | Interpretation |
| Recruitment rates into animal and human populations, respectively | |
| Effective disease transmission rate for animals and humans, respectively | |
| Effective vaccination rate of animals | |
| Proportion of recovered individuals that become low-risk susceptibles | |
| z | Fraction of recruited humans categorized to be low-risk |
| q | Fraction of recruited animals that come into the population already vaccinated |
| Rate of carcass consumption by scavengers | |
| Natural decomposition rate of carcasses | |
| Modification parameter for behavioral dispositions of low-risk susceptibles | |
| Enlightenment/educational campaign efforts at controlling the disease | |
| Removal/natural decay rate of spores | |
| Pathogen release rate from infected animals and decaying carcasses, respectively | |
| Recovery rate for humans and animals, respectively | |
| Natural death rates of humans and animals | |
| Disease-induced death rates for humans and animals, respectively | |
| Rate of loss of infection-acquired immunity by individuals and animals, respectively |
| S/N | Parameter | Values | Source |
|---|---|---|---|
| 1 | 0.001–0.009 | [25] | |
| 2 | q | 0.003 | [24] |
| 3 | 0.05 | [25] | |
| 4 | 0.035 | [25] | |
| 5 | 0.45 | [18,21] | |
| 6 | 0.6 | [22] | |
| 7 | 0.001125 | [22] | |
| 8 | 0.025 | [25] | |
| 9 | 0.1 | [17] | |
| 10 | 0.0001 | [18] | |
| 11 | 0.004 | [24] | |
| 12 | 0.92 | [18] | |
| 13 | 0.0001 | [8] | |
| 14 | 0.6 | Assumed | |
| 15 | z | 0.6 | Assumed |
| 16 | 0.6 | [18] | |
| 17 | [0, 0.9] | Assumed & [8] | |
| 18 | 0.04 | [18] | |
| 19 | 0.000042734 | [27,28] | |
| 20 | 0.5 | [18] | |
| 21 | 0.07 | [24] | |
| 22 | 0.02 | [24] | |
| 23 | 0.0025 | [18] |
| Parameter | Sensitivity Index |
|---|---|
| 1 | |
| q | −0.0030 |
| 1 | |
| −0.7305 | |
| 0.7218 | |
| −0.7175 | |
| −0.0556 | |
| −0.2225 | |
| −0.0246 | |
| −0.0041 | |
| −0.7175 | |
| −0.9756 |
| Par | ||||||
|---|---|---|---|---|---|---|
| −0.9993 | −0.9867 | 0.3280 | 0.3280 | 0.3286 | 0.3281 | |
| q | ||||||
| 1.329 | 1.327 | 1.327 | 1.330 | |||
| 0.9275 | 0.9159 | −0.3036 | −0.3051 | −0.3057 | −1.304 | |
| −0.9248 | −0.9134 | 0.3036 | 0.3041 | 0.3029 | 1.301 | |
| 0.1999 | 0.1973 | −0.2697 | −0.2695 | −0.2695 | ||
| 0.7996 | 0.7893 | −1.079 | −1.077 | −1.080 | −1.030 | |
| −0.999 | ||||||
| −0.9876 | −0.3195 | −0.3195 | −0.3195 | −0.3195 | ||
| 0 | -0.9959 | |||||
| 1.019 | 1.616 |
| Par | ||||
|---|---|---|---|---|
| 0.6474 | 0.3845 | 0.7137 | 0.7137 | |
| q | ||||
| 2.880 | 2.880 | |||
| −2.427 | −1.443 | −2.679 | −2.677 | |
| 2.418 | 1.436 | 2.666 | 2.665 | |
| −0.5314 | −0.3157 | −0.5858 | −0.5853 | |
| −2.125 | −1.263 | −2.343 | −2.343 | |
| −0.6297 | −0.3740 | |||
| −3.257 | −3.255 | −3.588 | −3.588 | |
| 7.330 | 6.976 | 6.976 | 6.976 | |
| 1.968 | 1.168 | 2.169 | 2.168 | |
| 2.641 | 2.909 | 2.910 | 2.910 | |
| z | 5.355 | |||
| 3.257 | 3.257 | 2.590 | 3.589 | |
| −2.176 | −2.179 | |||
| −6.329 | −5.981 | −5.981 | −6.976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akande, K.B.; Akinyemi, S.T.; Iheonu, N.O.; Audu, A.M.; Jimoh, F.M.; Ojoma, A.A.; Okeowo, V.I.; Suleiman, A.L.; Oshinubi, K. A Risk-Structured Model for the Transmission Dynamics of Anthrax Disease. Mathematics 2024, 12, 1014. https://doi.org/10.3390/math12071014
Akande KB, Akinyemi ST, Iheonu NO, Audu AM, Jimoh FM, Ojoma AA, Okeowo VI, Suleiman AL, Oshinubi K. A Risk-Structured Model for the Transmission Dynamics of Anthrax Disease. Mathematics. 2024; 12(7):1014. https://doi.org/10.3390/math12071014
Chicago/Turabian StyleAkande, Kazeem Babatunde, Samuel Tosin Akinyemi, Nneka O. Iheonu, Alogla Monday Audu, Folashade Mistura Jimoh, Atede Anne Ojoma, Victoria Iyabode Okeowo, Abdulrahaman Lawal Suleiman, and Kayode Oshinubi. 2024. "A Risk-Structured Model for the Transmission Dynamics of Anthrax Disease" Mathematics 12, no. 7: 1014. https://doi.org/10.3390/math12071014
APA StyleAkande, K. B., Akinyemi, S. T., Iheonu, N. O., Audu, A. M., Jimoh, F. M., Ojoma, A. A., Okeowo, V. I., Suleiman, A. L., & Oshinubi, K. (2024). A Risk-Structured Model for the Transmission Dynamics of Anthrax Disease. Mathematics, 12(7), 1014. https://doi.org/10.3390/math12071014







