A Hybrid Adaptive Simulated Annealing and Tempering Algorithm for Solving the Half-Open Multi-Depot Vehicle Routing Problem
Abstract
1. Introduction
- (1)
- A mixed-integer programming model for HOMDVRP to minimize the total transportation distance is formulated by analyzing vehicle routing problems in the collaborative logistics under the sharing economy;
- (2)
- A hybrid adaptive simulated annealing and tempering algorithm (HASATA) based on an improved simulated annealing (ISA) algorithm and an improved large neighborhood search (ILNS) algorithm is proposed, in which an adaptive Markov chain length mechanism and a neighborhood-based searching mechanism are designed considering the features of HOMDVRP;
- (3)
- The effectiveness and computation efficiency of HASATA in this paper for solving the HOMDVRP are verified by comparing the results obtained by one commercial solver and three existing heuristic algorithms in different scale computational experiments.
2. Problem Description and Mathematical Modeling
2.1. Problem Description
- (1)
- The distance between each node is known;
- (2)
- Each customer’s demand is satisfied by one vehicle service only once;
- (3)
- The number of vehicles is sufficient;
- (4)
- The vehicle’s departure and termination depots can be inconsistent;
- (5)
- Vehicles cannot travel directly between depots;
- (6)
- The total customer demand on the route does not exceed the loading capacity of the vehicle.
2.2. Mathematical Modeling
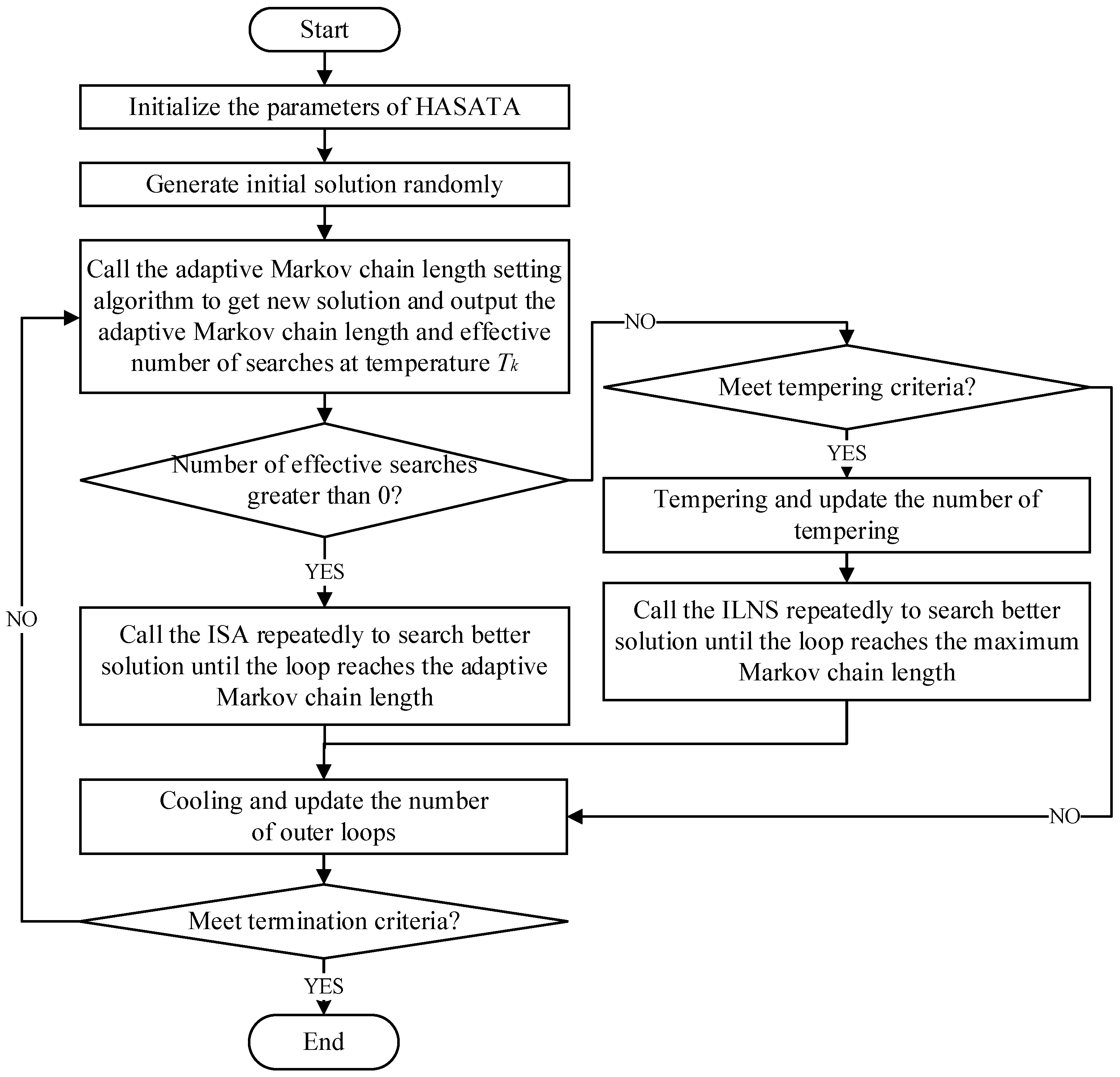
3. Hybrid Adaptive Simulated Annealing and Tempering Algorithm
3.1. Initialization of the Parameters
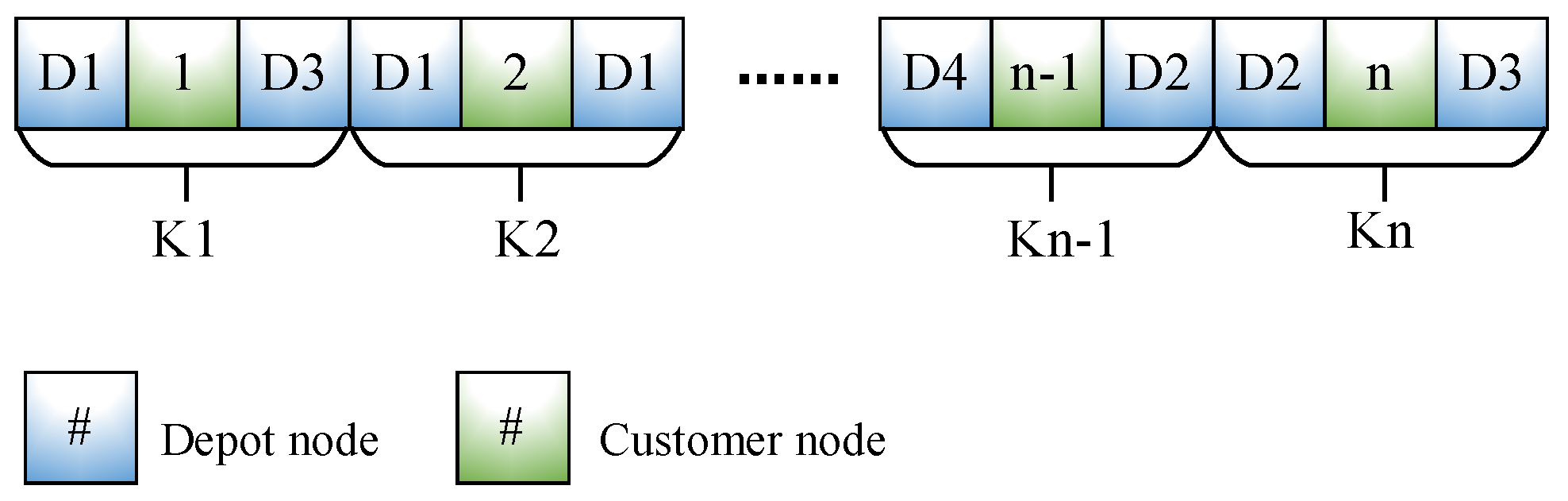
3.2. Initial Solution Representation
3.3. Adaptive Markov Chain Length Mechanism
| Algorithm 1 The pseudo-code of adaptive Markov chain length setting algorithm | |
| 1: | Input, , |
| 2: | Initialization: |
| 3: | while do |
| 4: | |
| 5: | if then |
| 6: | |
| 7: | then |
| 8: | |
| 9: | end if |
| 10: | |
| 11: | |
| 12: | end if |
| 13: | else if and then |
| 14: | |
| 15: | |
| 16: | |
| 17: | end else if |
| 18: | |
| 19: | end while |
| 20: | if then |
| 21: | |
| 22: | end if |
| 23: | if then |
| 24: | |
| 25: | end if |
| 26: | Output |
3.4. Tempering Mechanism
3.5. Perturbations in the ISA
- (1)
- Reverse: As shown in Figure 4, two customers, 1 and 3, are first randomly selected within a path and then the customer segments containing customers 1 and 3 are sorted in reverse order.
- (2)
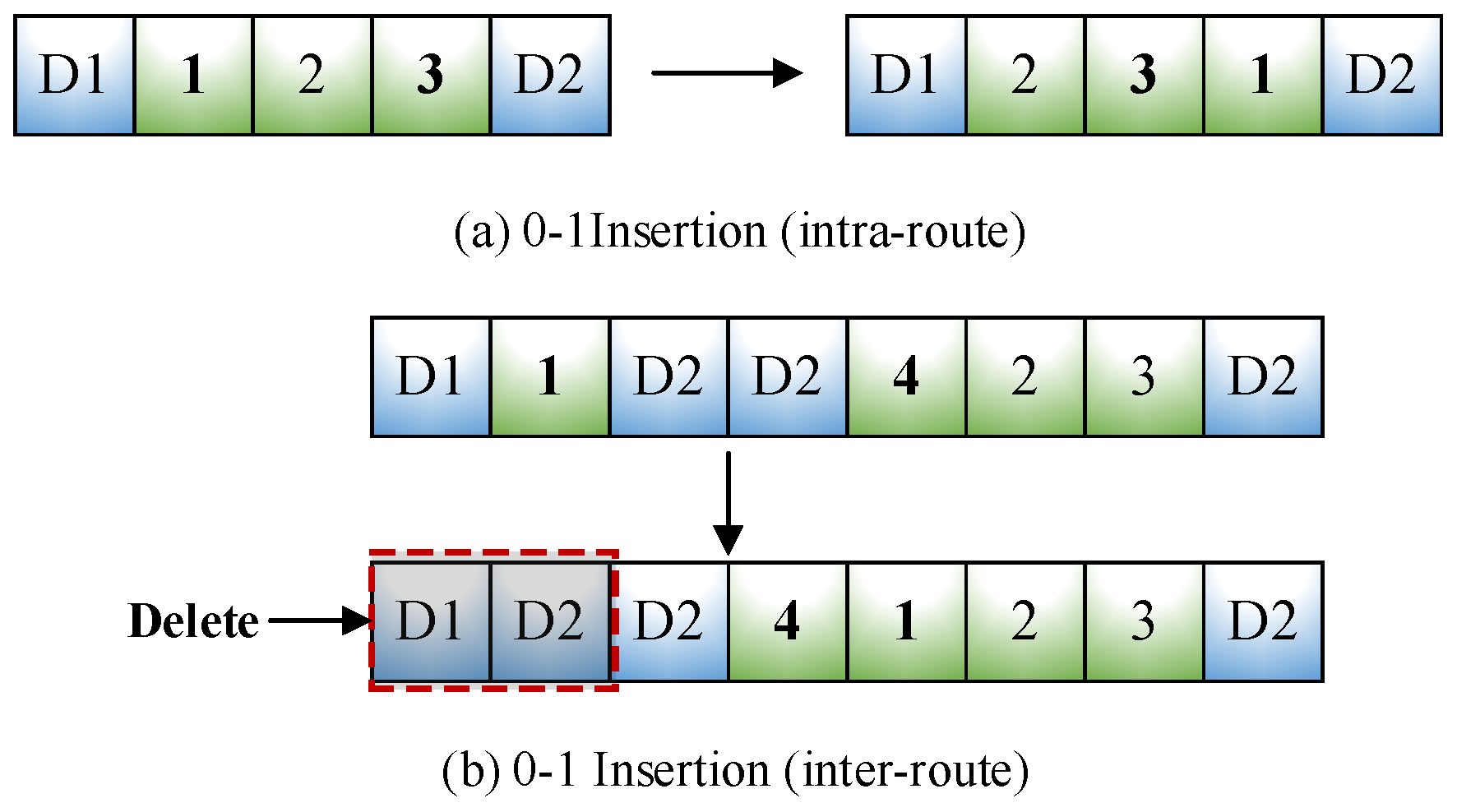
- 0-1 Insertion: Select two customers randomly and then insert the first selected customer to the right neighboring position of the second customer. As shown in Figure 5a, when the selected customers are all on the same path, then it is an intra-route 0-1 insertion, otherwise, it is inter-route 0-1 insertion, as shown in Figure 5b, under the premise of satisfying the vehicle load constraints, the inter-route 0-1 insertion may produce an infeasible solution situation of direct access between two depots, so after executing the inter-route 0-1 insertion, it is necessary to judge and delete the infeasible vehicle path in solution.
- (3)
- 1-1 Exchange: Figure 6a,b shows examples of intra-route and inter-route exchanges, respectively. Notably, the inter-route 1-1 exchange needs to ensure that vehicle load constraints are not violated.
- (4)
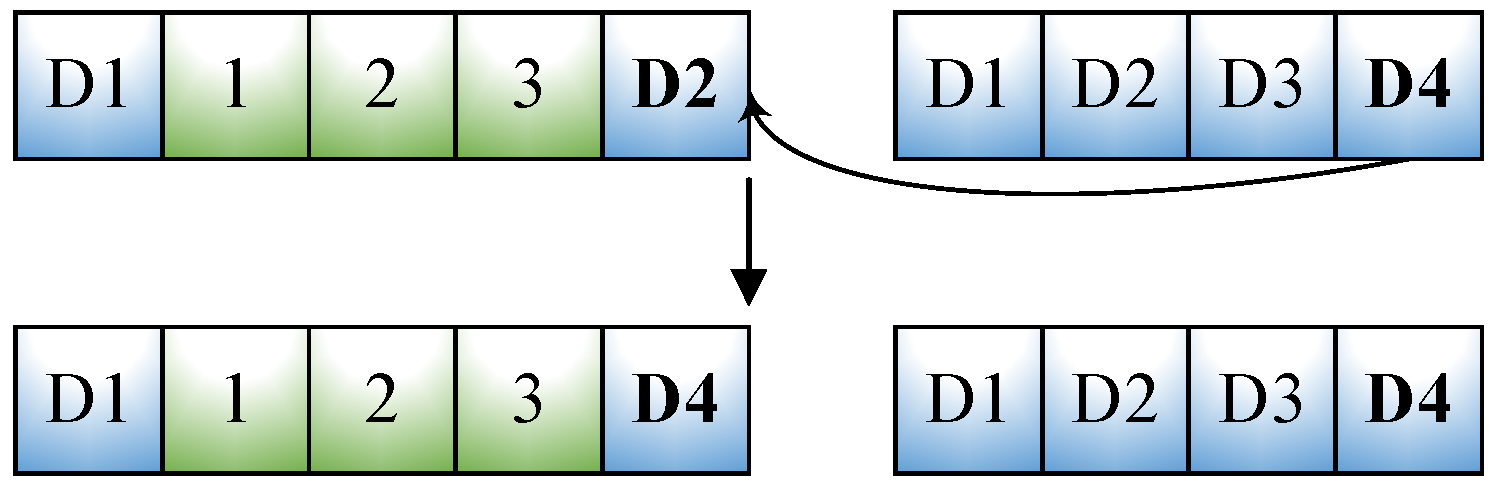
- Depot mutation: in order to search for the optimal combination solution of vehicles and depots in a half-open vehicle path structure, we design the depot mutation perturbation method. As shown in Figure 7, a better solution in HOMDVRP is searched by randomly selecting a depot in a route and then replacing it with any depot in the depot set.
| Algorithm 2 The pseudo-code of ISA algorithm | |
| 1: | Input |
| 2: | while do |
| 3: | while is infeasible do |
| 4: | |
| 5: | end while |
| 6: | if then |
| 7: | |
| 8: | if then |
| 9: | |
| 10: | end if |
| 11: | end if |
| 12: | else if and then |
| 13: | |
| 14: | end else if |
| 15: | |
| 16: | end while |
| 17: | ; |
| 18: | if or then |
| 19: | Computation terminated |
| 20: | else |
| 21: | Turn to Algorithm 1 |
| 22: | end if |
| 23: | Output |
3.6. Destroy and Repair Operators in ILNS
- (1)
- Random customer removal: this operator removes customers from the current solution at random, with the percentage of removal ranging from 0% to 10% of all customers;
- (2)
- Cluster removal: the operator randomly selects a customer and set as the distance between customer and its farthest neighborhood and then remove customer and all customers within its radius;
- (3)
- Route removal: the operator calculates the average number of customers across all routes, if the number of customers on a randomly selected route is greater than , then customers will be removed randomly, otherwise, the entire route will be removed;
- (4)
- Relevance removal: a customer is randomly selected, then the relevance values of customer with other customer are calculated by Equation (13) and finally customer c and the first customers with the highest relevance are removed.
- (5)
- Random depot removal: similar to the depot mutation in ISA, this operator randomly selects and records the indexes of certain warehouses and then deletes them.
- (1)
- Random insertion: this operator randomly inserts a customer into an arbitrarily chosen route, and if the generated solution is not feasible, a new route is created for that customer. This operation is repeated until all customers are inserted into the route;
- (2)
- Sequential greedy repair: this operator randomly selects a customer from the customer pool and inserts it into the best position, then updates the current solution. Repeat this operation until all customers are inserted into the route;
- (3)
- Random depot repair: this operator randomly selects a depot from the pool and inserts it into the current position of the destroyed depot. Repeat this operation until all depots have been repaired;
- (4)
- Greedy depot repair: the operator selects a depot from the depot set and inserts it into the current position of the destroyed depot according to the principle of minimum cost increase.
| Algorithm 3 The pseudo-code of ILNS algorithm | |
| 1: | Input |
| 2: | if meet tempering criteria then |
| 3: | ; |
| 4: | while do |
| 5: | |
| 6: | if then |
| 7: | |
| 8: | if then |
| 9: | |
| 10: | end if |
| 11: | end if |
| 12: | else if and then |
| 13: | |
| 14: | end else if |
| 15: | |
| 16: | end while |
| 17: | ; |
| 18: | if or then |
| 19: | Computation terminated |
| 20: | else |
| 21: | Turn to Algorithm 1 |
| 22: | end if |
| 23: | else |
| 24: | ; |
| 25: | if or then |
| 26: | Computation terminated |
| 27: | else |
| 28: | Turn to Algorithm 1 |
| 29: | end if |
| 30: | end if |
| 31: | Output |
3.7. Termination Criteria
4. Computational Experiments and Analysis
4.1. Experiment Setting
4.2. The Comparison Algorithms
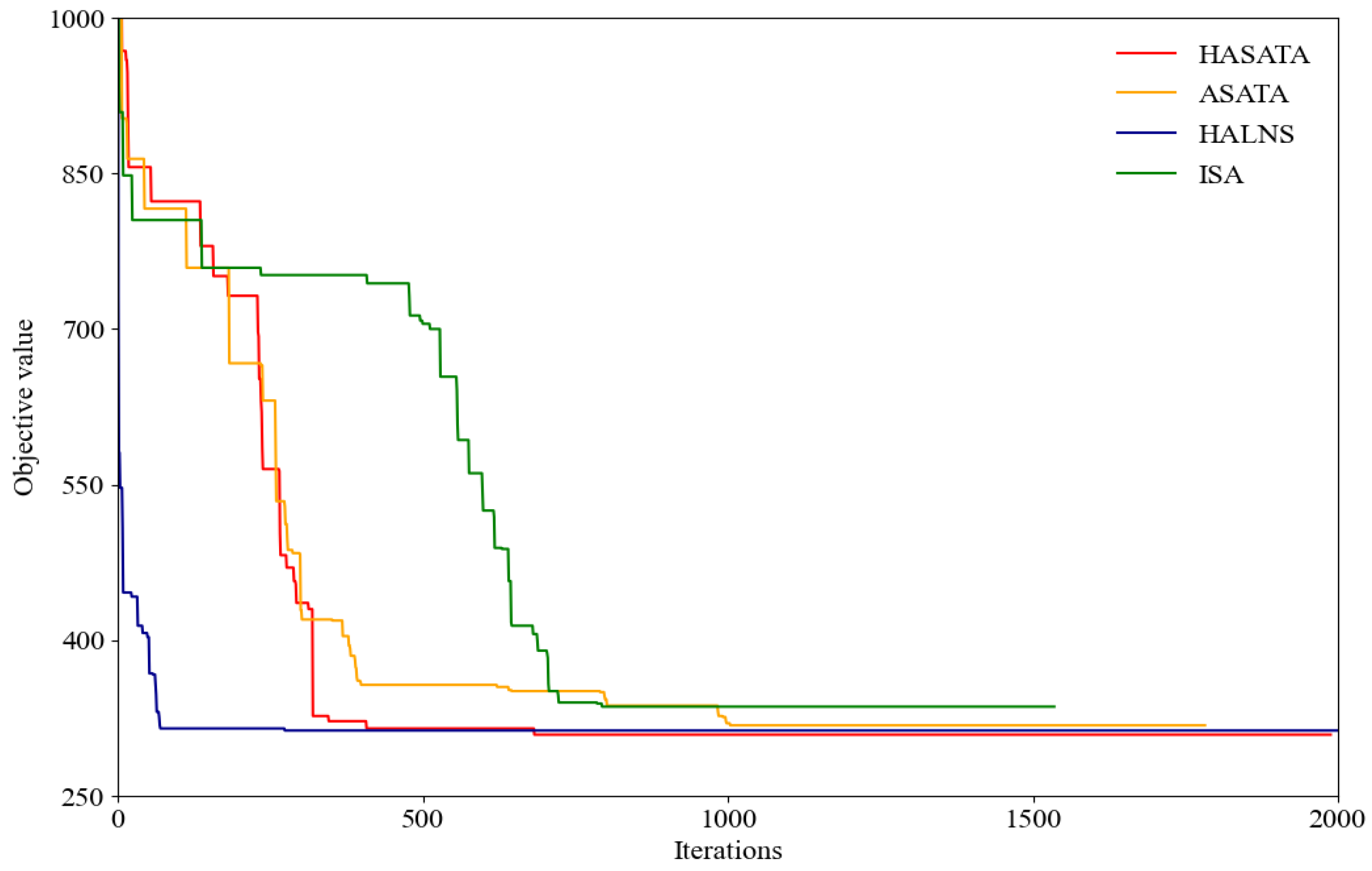
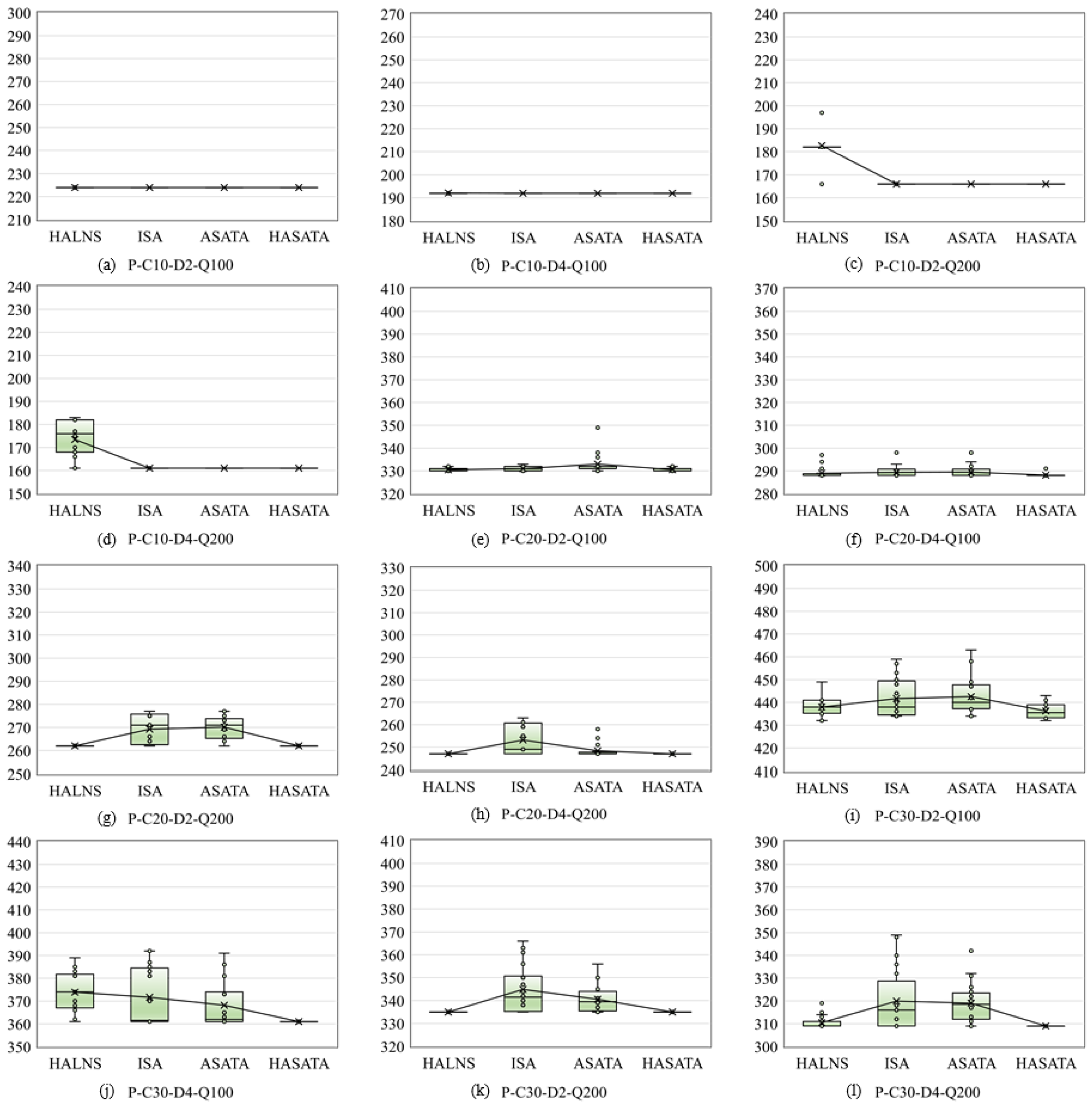
4.3. Experimental Results of Small-Scale Instances
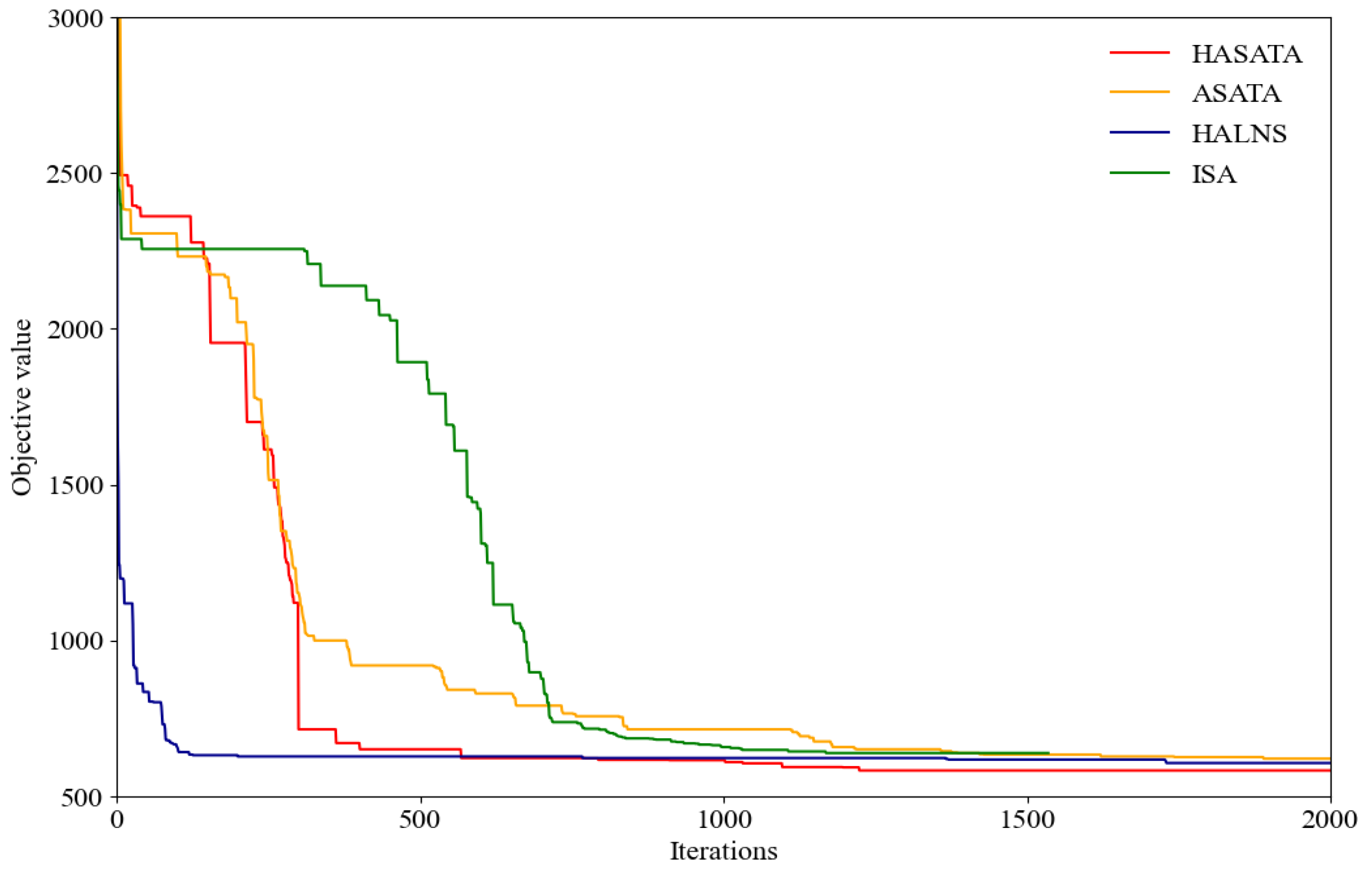
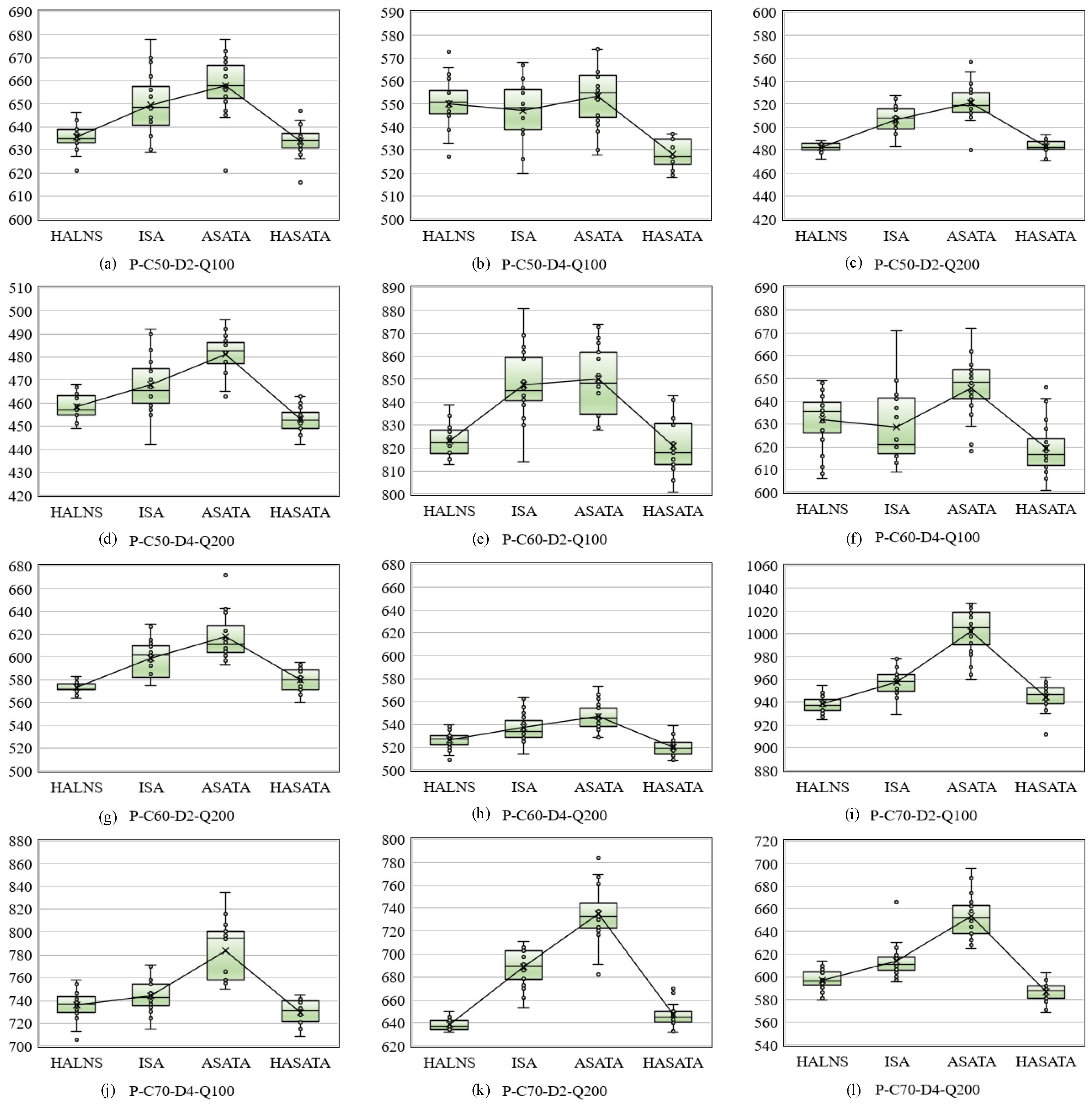
4.4. Experimental Results of Large-Scale Instances
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, H.; Sun, Y.; Yun, L.; Yu, R. A Joint distribution pricing model of express enterprises based on dynamic game theory. Mathematics 2023, 11, 4054. [Google Scholar] [CrossRef]
- Ferrell, W.; Ellis, K.; Kaminsky, P.; Rainwater, C. Horizontal collaboration: Opportunities for improved logistics planning. Int. J. Prod. Res. 2020, 58, 4267–4284. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Collaborative vehicle routing: A survey. Eur. J. Oper. Res. 2018, 268, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Y.; Tang, J. Compensation and profit distribution for cooperative green pickup and delivery problem. Transp. Res. Part B Methodol. 2018, 113, 54–69. [Google Scholar] [CrossRef]
- Li, J.; Wang, R.; Li, T.T.; Lu, Z.X.; Pardalos, P.M. Benefit analysis of shared depot resources for multi-depot vehicle routing problem with fuel consumption. Transp. Res. Part D Transp. Environ. 2018, 59, 417–432. [Google Scholar] [CrossRef]
- Liu, G.; Hu, J.; Yang, Y.; Xia, S.; Lim, K.M. Vehicle routing problem in cold Chain logistics: A joint distribution model with carbon trading mechanisms. Resour. Conserv. Recycl. 2020, 156, 104715. [Google Scholar] [CrossRef]
- Fan, H.; Yang, X.; Li, D.; Li, Y.; Liu, P.; Wu, J. Half-open multi-depot vehicle routing problem based on joint distribution mode of fresh food. Comput. Integr. Manuf. Syst. 2019, 25, 256–266. [Google Scholar] [CrossRef]
- Zhou, Z.; Ha, M.; Hu, H.; Ma, H. Half open multi-depot heterogeneous vehicle routing problem for hazardous materials transportation. Sustainability 2021, 13, 1262. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, L.; Guan, X.; Fan, J.; Sun, Y.; Wang, H. Collaborative multicenter vehicle routing problem with time windows and mixed deliveries and pickups. Expert Syst. Appl. 2022, 197, 116690. [Google Scholar] [CrossRef]
- Chen, Y.; Gan, H.; Chen, L. Cold chain logistics model based on joint distribution and its optimization algorithm under the background of double carbon. Control Decis. 2023, 38, 1951–1959. [Google Scholar] [CrossRef]
- Ma, B.; Hu, D.; Chen, X.; Hu, H. An optimization of pure electric vehicle routing problem on half-open multi-distribution center. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 199–205. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Montazeri, Z.; Niknam, T.; Aghaei, J.; Malik, O.P.; Dehghani, M.; Dhiman, G. Golf optimization algorithm: A new game-based metaheuristic algorithm and its application to energy commitment problem considering resilience. Biomimetics 2023, 8, 386. [Google Scholar] [CrossRef] [PubMed]
- Ho, W.; Ho, G.T.S.; Ji, P.; Lau, H.C.W. A hybrid genetic algorithm for the multi-depot vehicle routing problem. Eng. Appl. Artif. Intel. 2008, 21, 548–557. [Google Scholar] [CrossRef]
- Venkata Narasimha, K.; Kivelevitch, E.; Sharma, B.; Kumar, M. An ant colony optimization technique for solving min–max multi-depot vehicle routing problem. Swarm Evol. Comput. 2013, 13, 63–73. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Hosny, M.; Braekers, K.; Dammak, A. Three effective metaheuristics to solve the multi-depot multi-trip heterogeneous dial-a-ride problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 96, 60–80. [Google Scholar] [CrossRef]
- Li, J.; Pardalos, P.M.; Sun, H.; Pei, J.; Zhang, Y. Iterated local search embedded adaptive neighborhood selection approach for the multi-depot vehicle routing problem with simultaneous deliveries and pickups. Expert Syst. Appl. 2015, 42, 3551–3561. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Exact and meta-heuristic approach for a general heterogeneous dial-a-ride problem with multiple depots. Transp. Res. Part B Methodol. 2014, 67, 166–186. [Google Scholar] [CrossRef]
- Hesam Sadati, M.E.; Çatay, B.; Aksen, D. An efficient variable neighborhood search with tabu shaking for a class of multi-depot vehicle routing problems. Comput Oper. Res. 2021, 133, 105269. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; López Franco, J.; Nieto Isaza, S.; Felizzola Jiménez, H.; Herazo-Padilla, N. A literature review on the vehicle routing problem with multiple depots. Comput. Ind. Eng. 2015, 79, 115–129. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Z.; Geng, N.; Liu, T. The half open multi-depot vehicle routing problem. J. Shanghai Jiaotong Univ. 2010, 44, 1539–1545. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Pardalos, P.M. Multi-depot vehicle routing problem with time windows under shared depot resources. J. Comb. Optim. 2014, 31, 515–532. [Google Scholar] [CrossRef]
- Ge, X.; Xu, M.; Wang, X. Route optimization of urban logistics in joint distribution. Control Decis. 2016, 31, 503–512. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.X.; Xu, M.Z.; Liu, Y.; Wang, H.Z. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Gu, Y.; Yuan, Y.; Zhang, L.; Duan, J. Multi-depot half open vehicle routing problem with time windows. China Mech. Eng. 2020, 13, 1733–1740. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, P.; Lv, Y.; Fan, H. Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance. Comput Oper. Res. 2021, 129, 105211. [Google Scholar] [CrossRef]
- Fan, H.; Liu, P.; Liu, H.; Hou, D. The multi-depot vehicle routing problem with simultaneous deterministic delivery and stochastic pickup based on joint distribution. Acta Autom. Sin. 2021, 47, 1646–1660. [Google Scholar] [CrossRef]
- Hasanpour Jesri, Z.S.; Eshghi, K.; Rafiee, M.; Van Woensel, T. The multi-depot traveling purchaser problem with shared resources. Sustainability 2022, 14, 10190. [Google Scholar] [CrossRef]
- Bai, X.; Ma, N.; Chin, K.-S. Hybrid heuristic for the multi-depot static bike rebalancing and collection problem. Mathematics 2022, 10, 4583. [Google Scholar] [CrossRef]
- Xiao, Y.; Konak, A. A simulating annealing algorithm to solve the green vehicle routing & scheduling problem with hierarchical objectives and weighted tardiness. Appl. Soft Comput. 2015, 34, 372–388. [Google Scholar] [CrossRef]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Li, Y.; Xiang, Z.; Zhang, W. A relaxation model and time complexity analysis for simulated annealing algorithm. Chin. J. Comput. 2020, 43, 16. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, W.; Xiang, Z.; Zhang, W. Relaxation model based temperature setting methods for simulated annealing algorithm. Chin. J. Comput. 2020, 43, 17. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transport. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. A unified heuristic for a large class of vehicle routing problems with backhauls. Eur. J. Oper. Res. 2006, 171, 750–775. [Google Scholar] [CrossRef]
- Ge, D.; Huangfu, Q.; Wang, Z.; Wu, J.; Ye, Y. Cardinal Optimizer (COPT) User Guide. Available online: https://guide.coap.online/copt/en-doc (accessed on 18 February 2024).
- Lahyani, R.; Gouguenheim, A.L.; Coelho, L.C. A hybrid adaptive large neighbourhood search for multi-depot open vehicle routing problems. Int. J. Prod. Res. 2019, 57, 6963–6976. [Google Scholar] [CrossRef]




| Reference | Algorithms | Problems | Objectives | Algorithms Designed for Half-Open Path? | Other Issues |
|---|---|---|---|---|---|
| [21] | Heuristic | HOMDVRP | Distance | - | - |
| [22] | Hybrid heuristic | HOMDVRPTW | Distance | √ | Shared depot resources |
| [23] | Meta-heuristic | UL-JD | Fuel cost | - | Urban logistics; Joint distribution |
| [7] | Meta-heuristic | HOMDVRP | Total cost | - | Fresh logistics; Joint distribution |
| [11] | Meta-heuristic; Exact algorithm | HOMDEVRPTW | Total cost | - | - |
| [24] | Hybrid heuristic | MDGVRP | carbon emission; Total cost | - | Collaborative logistics; Shared transportation resource; Time-dependent speed |
| [25] | Meta-heuristic | HOMDVRPTW | Total cost | √ | - |
| [26] | Hybrid meta-heuristic | TDMDGVRPTW | Total cost | - | Time-varying road network; Vehicle fuel consumption |
| [27] | Hybrid meta-heuristic | MDVRPSDDSPJD | Distance | √ | - |
| [8] | Hybrid meta-heuristic | HOMDHVRP | Risk; Cost | - | Hazardous material transportation |
| [9] | Hybrid heuristic | CMVRPTWMDP | Total cost | - | Collaborative logistics; Shared transportation resource |
| [28] | Hybrid heuristic | MDTPPSR | Distance | - | Sustainable logistics |
| [29] | Hybrid heuristic; Exact algorithm | BRP | Working time; Fixed cost | - | Multi-depot; Broken bike collection |
| [10] | Hybrid meta-heuristic | CCL-JD | Total cost | - | Cold chain logistics; Carbon trading mechanism |
| This work | Hybrid meta-heuristic; Exact algorithm | HOMDVRP | Distance | √ | Collaborative logistics |
| Abbreviations | Problems |
|---|---|
| HOMDVRPTW | Half-open multi-depot vehicle routing problem with time windows |
| UL-JD | Urban logistics based on joint distribution |
| HOMDEVRPTW | Half-open multi-depot electric vehicle routing problem with time windows |
| MDGVRP | Multi-depot green vehicle routing problem |
| TDMDGVRPTW | Time-dependent multi-depot green vehicle routing problem with time windows |
| MDVRPSDDSPJD | Multi-depot vehicle routing problem with simultaneous deterministic delivery and stochastic pickup based on joint distribution |
| HOMDHVRP | Half-open multi-depot heterogeneous vehicle routing problem |
| CMVRPTWMDP | Collaborative multi-center vehicle routing problem with time windows and mixed deliveries and pickups |
| MDTPPSR | Multi-depot traveling purchaser problem under shared resources |
| BRP | Bike rebalancing problem |
| CCL-JD | Cold chain logistics based on joint distribution |
| Notations | Definitions |
|---|---|
| Sets | |
| Index set of customers, where | |
| Index set of all nodes, where | |
| Index set of depots | |
| Index set of dummy depots | |
| Index set of vehicles, where | |
| Parameters | |
| The demand of the customer | |
| The distance from node to node | |
| The maximum load capacity of the vehicle | |
| The sum of the number of actual depot nodes and customer nodes, where | |
| Variables | |
| equals 1 if vehicle drives from node to node , otherwise equals 0 | |
| The sequence of vehicle arrivals at nodes | |
| Algorithmic Parameter | Description |
|---|---|
| The initial temperature | |
| The final temperature | |
| The current temperature | |
| The cooling rate | |
| The current solution | |
| The best solution | |
| The new solution | |
| is updated) | |
| The number of tempering | |
| The tempering factor | |
| The adaptive Markov chain length | |
| in pre-annealing phase | |
| The maximum Markov chain length | |
| The outer maximum number of loops |
| Parameters | Low Level | Medium Level | High Level | Selected Level |
|---|---|---|---|---|
| 2000 | 5000 | 8000 | Low level | |
| 0.97 | 0.98 | 0.99 | Medium level | |
| 2 | 3 | 4 | Medium level | |
| 200 | 250 | 300 | Medium level |
| Instances | COPT | HALNS | ISA | ASATA | HASATA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(s) | (s) | (s) | (s) | (s) | ||||||||||
| S1-C10-D2-Q100 | 224.0 | 0.7 | 224.0 | 9.4 | 0.00% | 224.0 | 9.5 | 0.00% | 224.0 | 2.0 | 0.00% | 224.0 | 5.5 | 0.00% |
| S2-C10-D4-Q100 | 192.0 | 0.4 | 192.1 | 9.9 | 0.05% | 192.0 | 9.1 | 0.00% | 192.0 | 1.9 | 0.00% | 192.0 | 5.2 | 0.00% |
| S3-C10-D2-Q200 | 166.0 | 0.1 | 182.6 | 18.9 | 10.00% | 166.0 | 5.8 | 0.00% | 166.0 | 1.3 | 0.00% | 166.0 | 2.4 | 0.00% |
| S4-C10-D4-Q200 | 161.0 | 0.1 | 173.5 | 15.4 | 7.76% | 161.0 | 5.6 | 0.00% | 161.0 | 1.3 | 0.00% | 161.0 | 2.4 | 0.00% |
| S5-C20-D2-Q100 | 330.0 | 7200.0 | 330.5 | 15.5 | 0.15% | 331.0 | 35.6 | 0.30% | 333.0 | 6.8 | 0.91% | 330.6 | 5.8 | 0.17% |
| S6-C20-D4-Q100 | 288.0 | 799.2 | 289.0 | 15.6 | 0.35% | 289.4 | 25.6 | 0.47% | 289.5 | 4.6 | 0.52% | 288.2 | 5.9 | 0.07% |
| S7-C20-D2-Q200 | 262.0 | 6.8 | 262.0 | 22.3 | 0.00% | 269.3 | 11.8 | 2.77% | 270.1 | 2.5 | 3.09% | 262.0 | 5.0 | 0.00% |
| S8-C20-D4-Q200 | 247.0 | 1.1 | 247.0 | 23.0 | 0.00% | 253.2 | 11.7 | 2.49% | 248.4 | 2.4 | 0.55% | 247.0 | 4.9 | 0.00% |
| S9-C30-D2-Q100 | 463.0 | 7200.0 | 438.0 | 30.2 | −5.40% | 441.7 | 22.9 | −4.60% | 442.6 | 6.0 | −4.41% | 436.3 | 12.4 | −5.78% |
| S10-C30-D4-Q100 | 361.0 | 7200.0 | 373.9 | 30.0 | 3.57% | 371.7 | 22.4 | 2.95% | 368.2 | 7.7 | 1.99% | 361.0 | 14.8 | 0.00% |
| S11-C30-D2-Q200 | 335.0 | 7200.0 | 335.0 | 44.7 | 0.00% | 344.9 | 15.2 | 2.96% | 340.6 | 4.8 | 1.66% | 335.0 | 12.9 | 0.00% |
| S12-C30-D4-Q200 | 309.0 | 126.1 | 310.5 | 44.4 | 0.47% | 319.9 | 15.0 | 3.53% | 319.0 | 8.8 | 3.24% | 309.0 | 13.4 | 0.00% |
| Average | 278.2 | 2477.9 | 279.8 | 23.3 | 1.41% | 280.3 | 15.9 | 0.91% | 279.5 | 4.2 | 0.63% | 276.0 | 7.5 | −0.46% |
| Instances | COPT | HALNS | ISA | ASATA | HASATA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(s) | (s) | (s) | (s) | (s) | ||||||||||
| L1-C50-D2-Q100 | 941.0 | 7200.0 | 635.5 | 58.9 | −32.47% | 649.4 | 34.9 | −30.99% | 658.0 | 14.0 | −30.08% | 633.8 | 31.6 | −32.65% |
| L2-C50-D4-Q100 | 847.0 | 7200.0 | 550.0 | 60.9 | −35.06% | 547.3 | 33.9 | −35.38% | 553.6 | 10.8 | −34.64% | 528.3 | 34.4 | −37.63% |
| L3-C50-D2-Q200 | 589.0 | 7200.0 | 482.6 | 76.3 | −18.07% | 506.8 | 22.5 | −13.96% | 521.3 | 7.9 | −11.50% | 483.1 | 26.1 | −17.99% |
| L4-C50-D4-Q200 | 488.0 | 7200.0 | 458.6 | 76.8 | −6.02% | 468.2 | 22.4 | −4.07% | 481.2 | 6.6 | −1.39% | 452.9 | 27.2 | −7.19% |
| L5-C60-D2-Q100 | 2044.0 | 7200.0 | 823.1 | 48.7 | −59.73% | 847.6 | 49.7 | −58.53% | 850.0 | 21.8 | −58.41% | 821.0 | 37.1 | −59.83% |
| L6-C60-D4-Q100 | 962.0 | 7200.0 | 631.9 | 51.7 | −34.32% | 628.8 | 48.6 | −34.64% | 645.8 | 16.8 | −32.87% | 619.4 | 41.5 | −35.62% |
| L7-C60-D2-Q200 | 1089.0 | 7200.0 | 573.0 | 66.9 | −47.38% | 599.0 | 31.8 | −45.00% | 618.1 | 9.4 | −43.24% | 579.6 | 29.0 | −46.78% |
| L8-C60-D4-Q200 | 854.0 | 7200.0 | 526.3 | 67.7 | −38.37% | 537.5 | 30.3 | −37.06% | 547.2 | 8.2 | −35.93% | 520.2 | 33.8 | −39.09% |
| L9-C70-D2-Q100 | 1698.0 | 7200.0 | 938.4 | 87.7 | −44.73% | 957.5 | 73.9 | −43.61% | 1002.6 | 17.8 | −40.96% | 944.9 | 60.1 | −44.36% |
| L10-C70-D4-Q100 | 1162.0 | 7200.0 | 735.7 | 90.8 | −36.69% | 743.9 | 51.6 | −35.98% | 783.4 | 17.7 | −32.58% | 729.8 | 65.2 | −37.19% |
| L11-C70-D2-Q200 | 1424.0 | 7200.0 | 638.7 | 115.6 | −55.15% | 688.7 | 33.7 | −51.64% | 735.3 | 11.5 | −48.36% | 647.0 | 51.7 | −54.57% |
| L12-C70-D4-Q200 | 1041.0 | 7200.0 | 597.3 | 120.3 | −42.63% | 614.0 | 33.0 | −41.02% | 653.3 | 11.1 | −37.25% | 586.8 | 56.7 | −43.64% |
| Average | 1094.9 | 7200.0 | 632.6 | 76.9 | −37.55% | 649.0 | 38.9 | −35.99% | 670.8 | 12.8 | −33.94% | 628.9 | 41.2 | −38.04% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Peng, P.; Zheng, P.; Wu, Z. A Hybrid Adaptive Simulated Annealing and Tempering Algorithm for Solving the Half-Open Multi-Depot Vehicle Routing Problem. Mathematics 2024, 12, 947. https://doi.org/10.3390/math12070947
Xiao S, Peng P, Zheng P, Wu Z. A Hybrid Adaptive Simulated Annealing and Tempering Algorithm for Solving the Half-Open Multi-Depot Vehicle Routing Problem. Mathematics. 2024; 12(7):947. https://doi.org/10.3390/math12070947
Chicago/Turabian StyleXiao, Shichang, Pan Peng, Peng Zheng, and Zigao Wu. 2024. "A Hybrid Adaptive Simulated Annealing and Tempering Algorithm for Solving the Half-Open Multi-Depot Vehicle Routing Problem" Mathematics 12, no. 7: 947. https://doi.org/10.3390/math12070947
APA StyleXiao, S., Peng, P., Zheng, P., & Wu, Z. (2024). A Hybrid Adaptive Simulated Annealing and Tempering Algorithm for Solving the Half-Open Multi-Depot Vehicle Routing Problem. Mathematics, 12(7), 947. https://doi.org/10.3390/math12070947






