The Nonlinear Bending of Sector Nanoplate via Higher-Order Shear Deformation Theory and Nonlocal Strain Gradient Theory
Abstract
1. Introduction
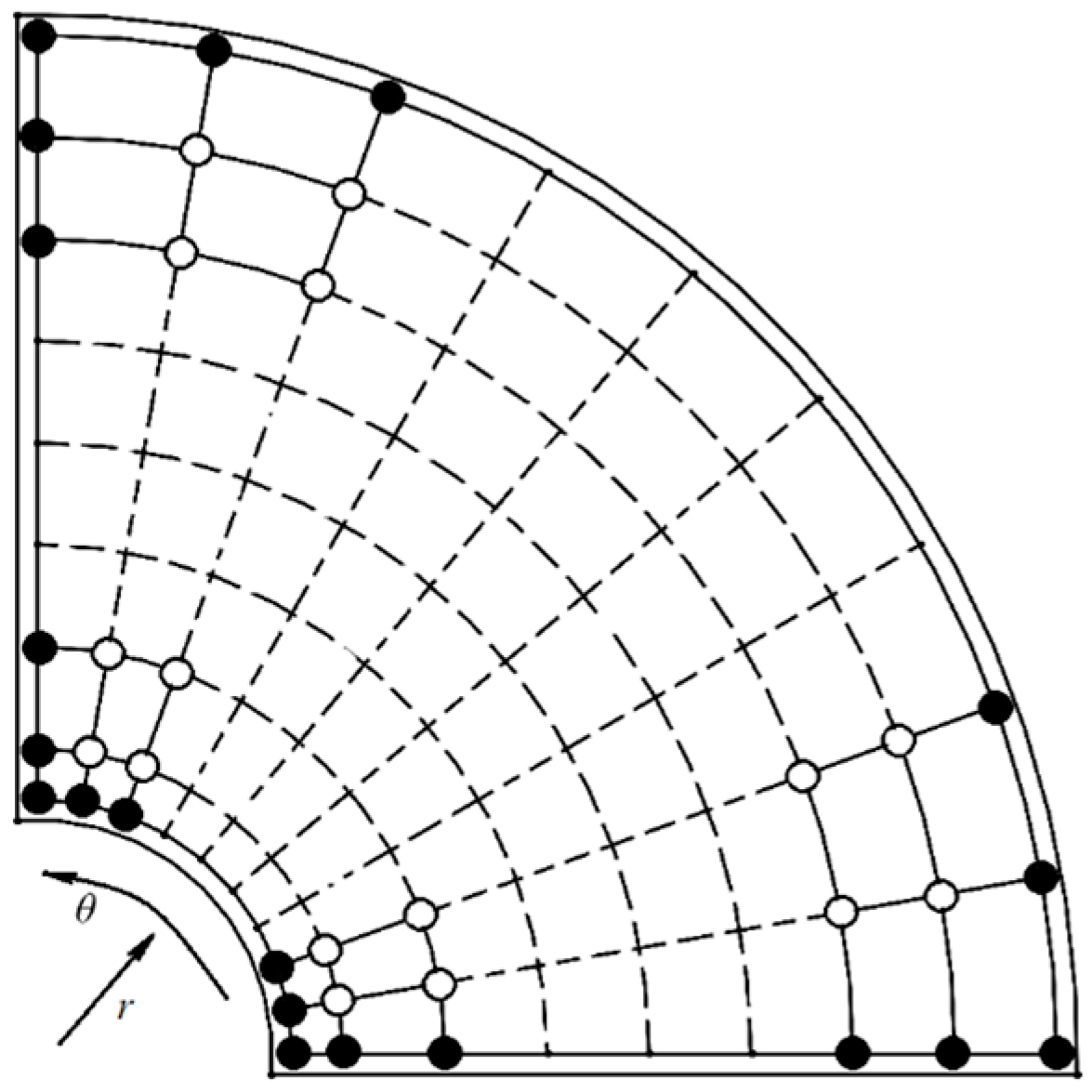
2. The Governing Equations
3. The Computational Procedure
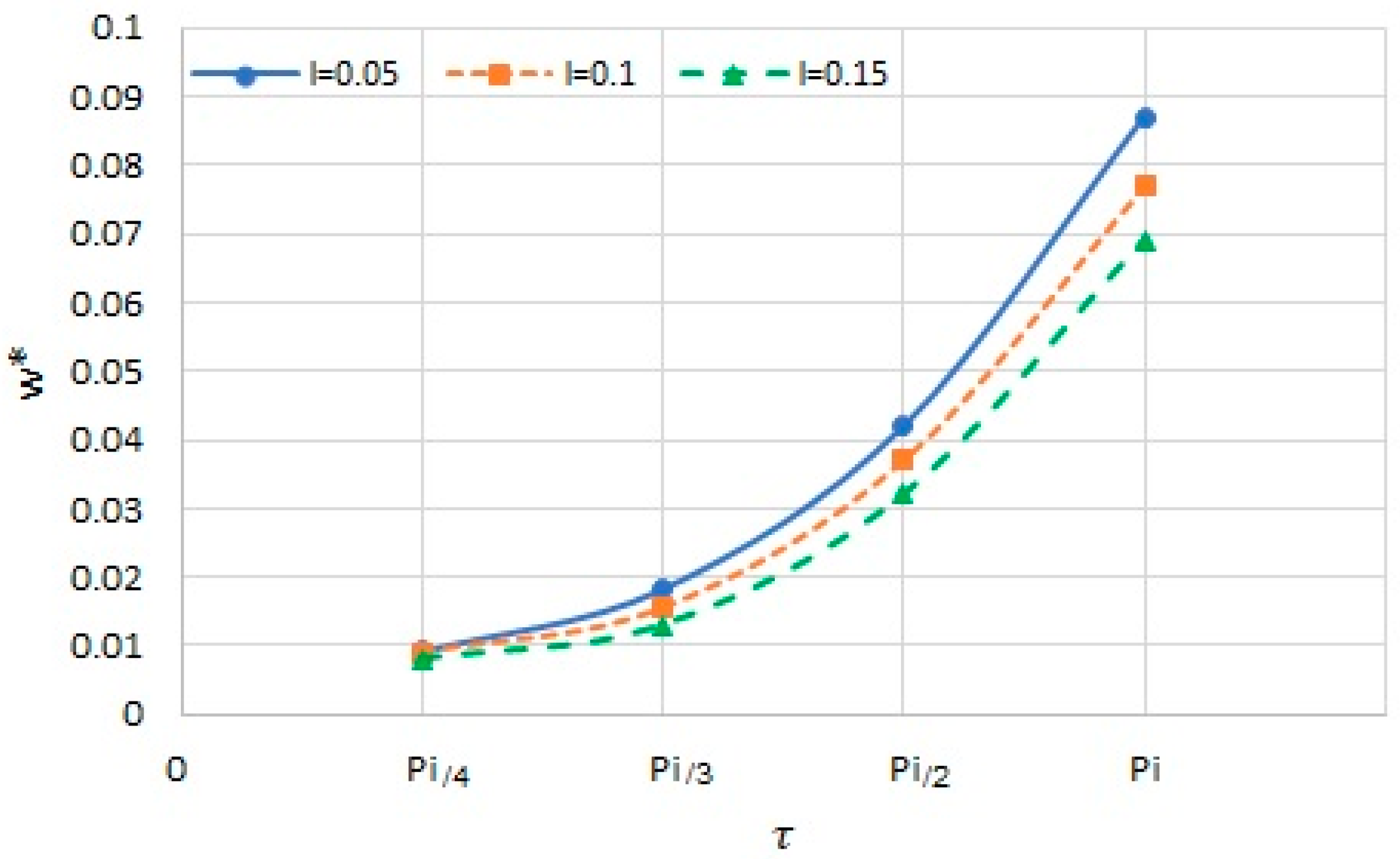
4. Results and Discussions
5. Conclusions
- ∗
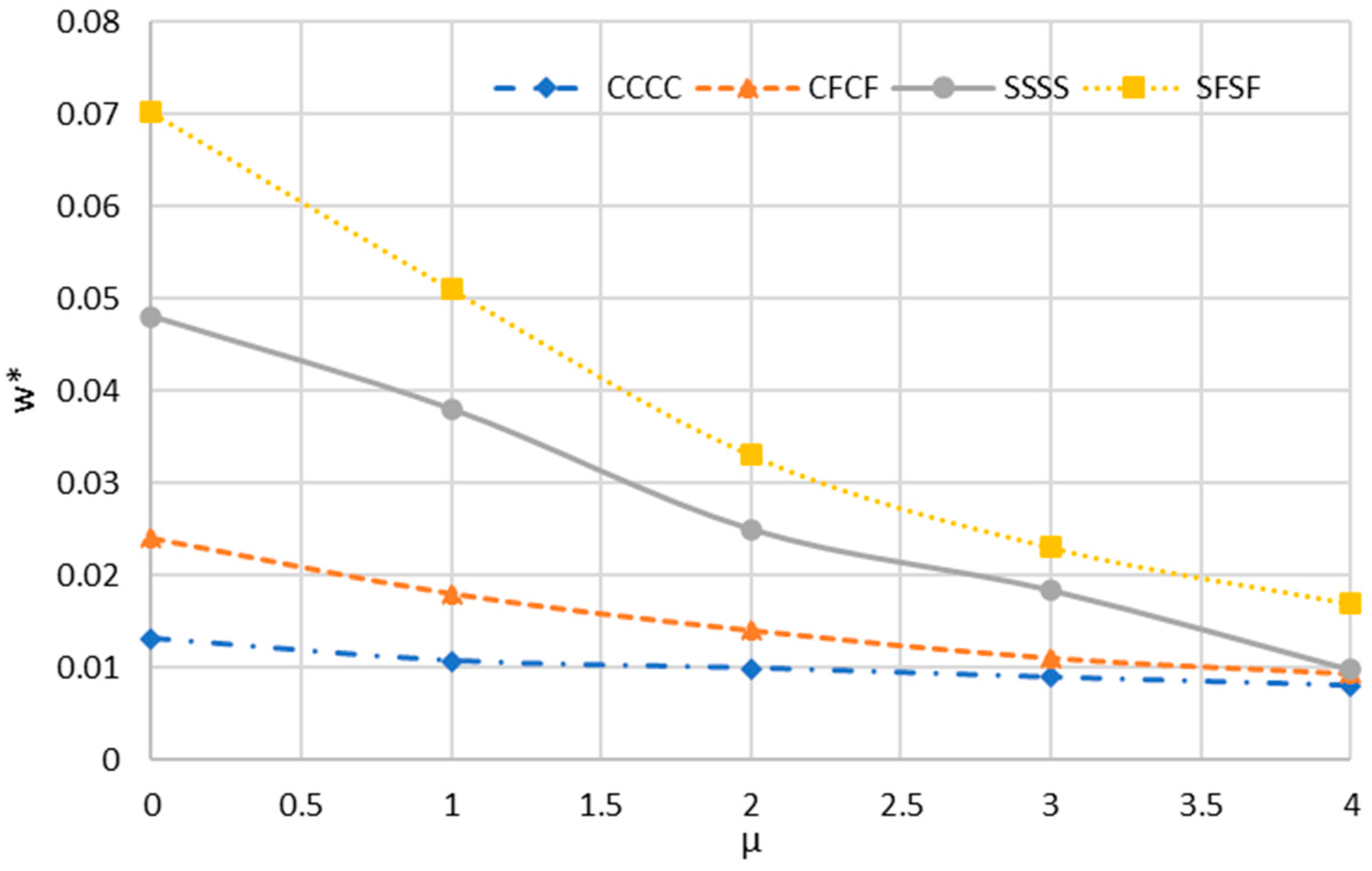
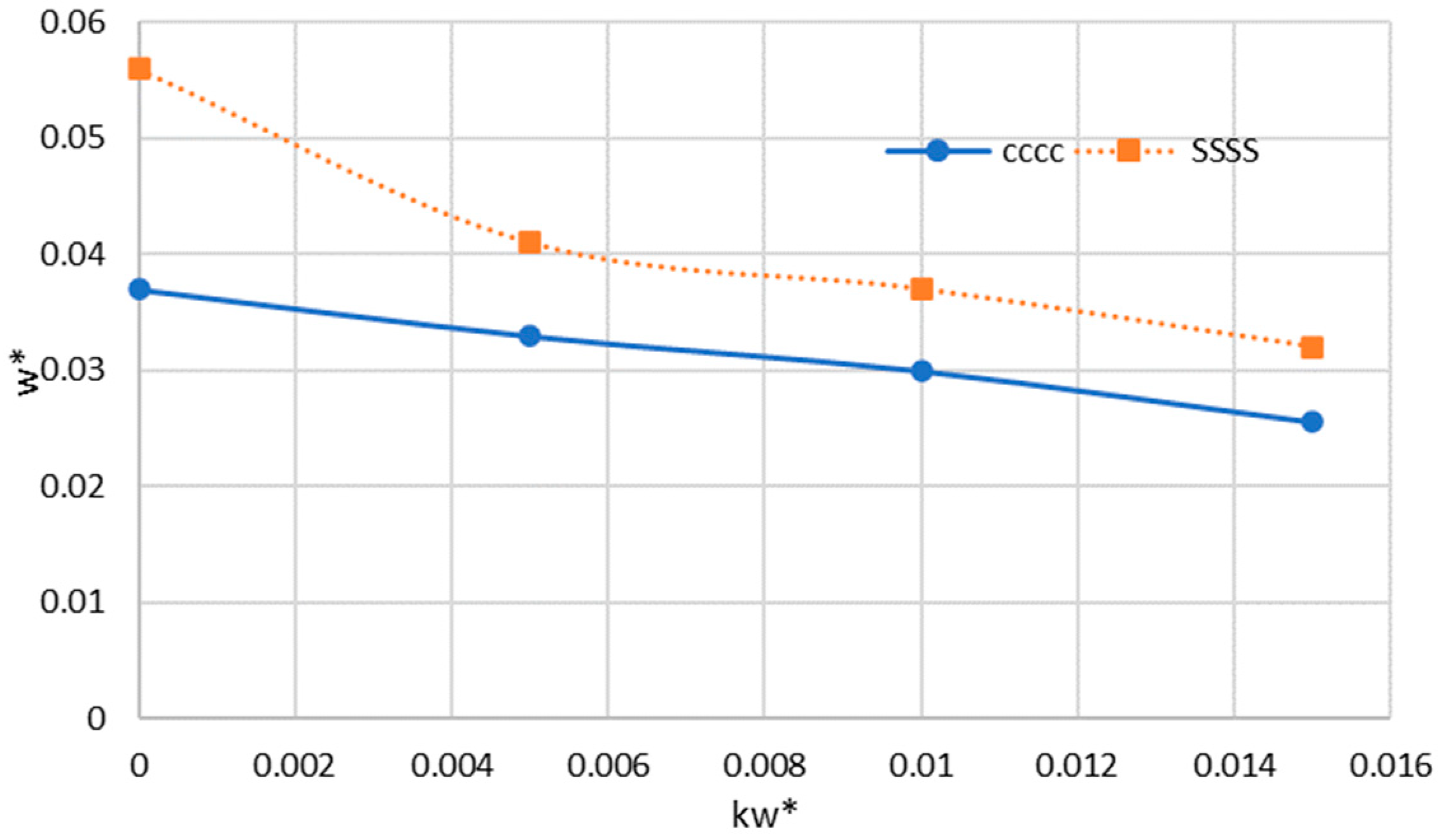
- Small-scale parameters significantly influence the deflection of the sector nanoplate.
- ∗
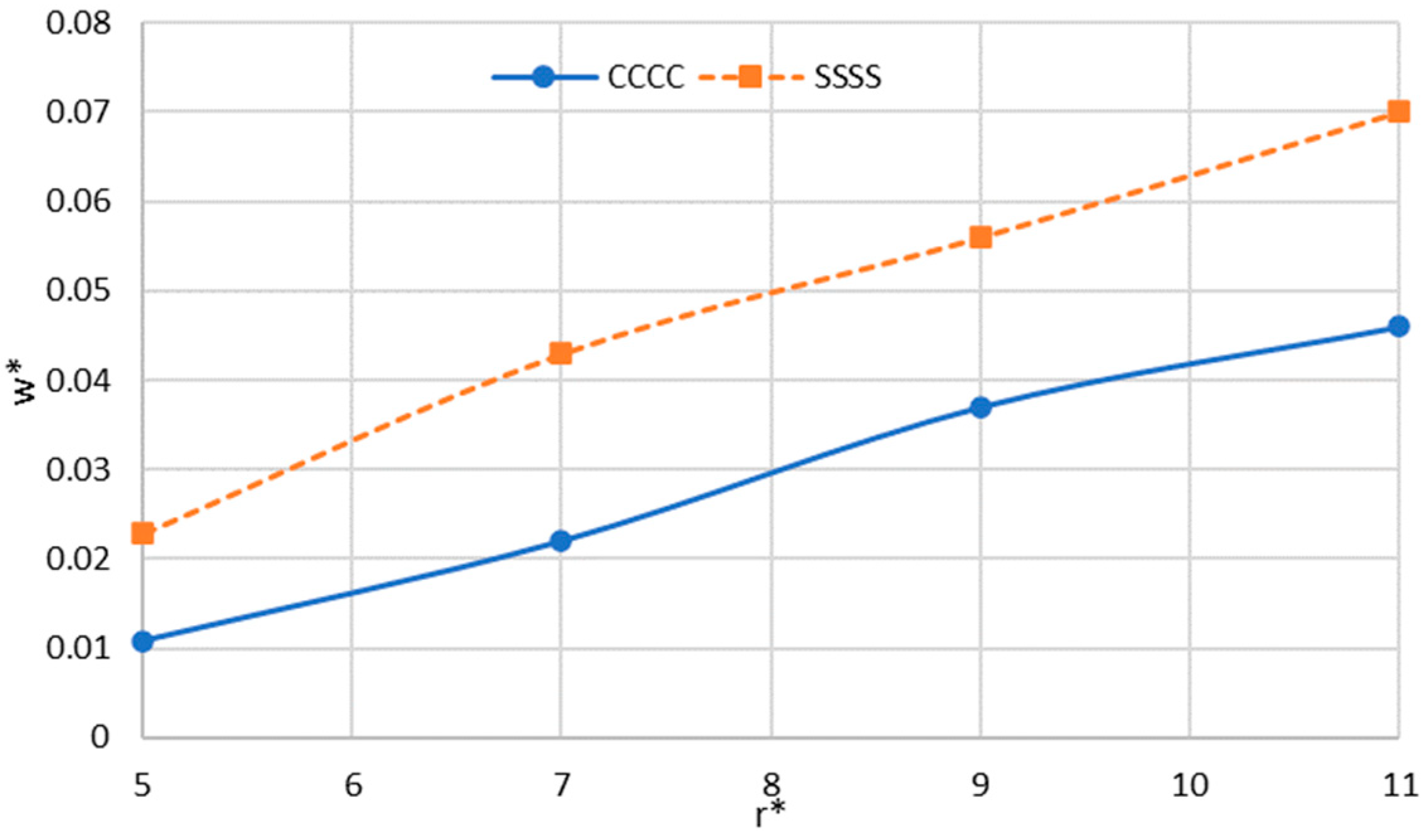
- Factors such as radius, flexibility of boundary conditions, load, and sector angle have direct influences on the deflection of the sector plate.
- ∗
- By increasing load, radius, and sector angle, the values of the deflection for different boundary conditions converge.
- ∗
- The strain gradient parameter has a relatively more significant effect at larger angles of the sector nanoplate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupta, R.; Kumar, A.; Biswas, A.; Singh, R.; Gehlot, A.; Akram, S.V.; Verma, A.S. Advances in micro and nano-engineered materials for high-value capacitors for miniaturized electronics. J. Energy Storage 2022, 55, 105591. [Google Scholar] [CrossRef]
- Manolis, G.D.; Dineva, P.S.; Rangelov, T.; Sfyris, D. Mechanical models and numerical simulations in nanomechanics: A review across the scales. Eng. Anal. Bound. Elem. 2021, 128, 149–170. [Google Scholar] [CrossRef]
- Schiavo, L.; Cammarano, A.; Carotenuto, G.; Longo, A.; Palomba, M.; Nicolais, L. An overview of the advanced nanomaterials science. Inorganica Chim. Acta 2024, 559, 121802. [Google Scholar] [CrossRef]
- Farajpour, A.; Mohammadi, M.; Shahidi, A.R.; Mahzoon, M. Axisymmetric buckling of the circular graphene sheets with the nonlocal continuum plate model. Phys. E Low-Dimens. Syst. Nanostructures 2011, 43, 1820–1825. [Google Scholar] [CrossRef]
- Huang, Z.; Shao, G.; Li, L. Micro/nano functional devices fabricated by additive manufacturing. Prog. Mater. Sci. 2023, 131, 101020. [Google Scholar] [CrossRef]
- Collaert, N.; Alian, A.; Arimura, H.; Boccardi, G.; Eneman, G.; Franco, J.; Ivanov, T.; Lin, D.; Loo, R.; Merckling, C.; et al. Ultimate nano-electronics: New materials and device concepts for scaling nano-electronics beyond the Si roadmap. Microelectron. Eng. 2015, 132, 218–225. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Smitt, J. Bending and Vibration Analysis of the FG Circular Nanoplates Subjected to Hygro-Thermo-Electrical Loading Based on Nonlocal Strain Gradient Theory. Int. J. Struct. Stab. Dyn. 2022, 23, 2350017. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Axial postbuckling analysis of multilayer functionally graded composite nanoplates reinforced with GPLs based on nonlocal strain gradient theory. Eur. Phys. J. Plus 2017, 132, 490. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Aifantis, E.C. Strain gradient interpretation of size effects. Int. J. Fract. 1999, 95, 299–314. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Gui, Y.; Wu, R. Buckling analysis of embedded thermo-magneto-electro-elastic nano cylindrical shell subjected to axial load with nonlocal strain gradient theory. Mech. Res. Commun. 2023, 128, 104043. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model. 2019, 68, 583–602. [Google Scholar] [CrossRef]
- Arefi, M.; Kiani, M.; Rabczuk, T. Application of nonlocal strain gradient theory to size dependent bending analysis of a sandwich porous nanoplate integrated with piezomagnetic face-sheets. Compos. Part B Eng. 2019, 168, 320–333. [Google Scholar] [CrossRef]
- Farajpour, A.; Yazdi, M.R.H.; Rastgoo, A.; Mohammadi, M. A higher-order nonlocal strain gradient plate model for buckling of orthotropic nanoplates in thermal environment. Acta Mech. 2016, 227, 1849–1867. [Google Scholar] [CrossRef]
- Nematollahi, M.S.; Mohammadi, H. Geometrically nonlinear vibration analysis of sandwich nanoplates based on higher-order nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 156, 31–45. [Google Scholar] [CrossRef]
- Thai, C.H.; Hung, P.T.; Nguyen-Xuan, H.; Phung-Van, P. A size-dependent meshfree approach for magneto-electro-elastic functionally graded nanoplates based on nonlocal strain gradient theory. Eng. Struct. 2023, 292, 116521. [Google Scholar] [CrossRef]
- Thai, C.H.; Fereira, A.M.J.; Nguyen-Xuan, H.; Hung, P.T.; Phung-Van, P. A nonlocal strain gradient isogeometric model for free vibration analysis of magneto-electro-elastic functionally graded nanoplates. Compos. Struct. 2023, 316, 117005. [Google Scholar] [CrossRef]
- Alghanmi, R.A. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials 2022, 15, 8601. [Google Scholar] [CrossRef]
- Kumar, D.; Ali, S.F.; Arockiarajan, A. Theoretical and experimental studies on large deflection analysis of double corrugated cantilever structures. Int. J. Solids Struct. 2021, 228, 111126. [Google Scholar] [CrossRef]
- Han, P.; Tian, F.; Babaei, H. Thermally induced large deflection analysis of graphene platelet reinforced nanocomposite cylindrical panels. Structures 2023, 53, 1046–1056. [Google Scholar] [CrossRef]
- Bertóti, E. Primal- and Dual-Mixed Finite Element Models for Geometrically Nonlinear Shear-Deformable Beams—A Comparative Study. Comput. Assist. Methods Eng. Sci. 2020, 27, 285–315. [Google Scholar] [CrossRef]
- Liu, L.; Zhong, X.; Liao, S. Accurate solutions of a thin rectangular plate deflection under large uniform loading. Appl. Math. Model. 2023, 123, 241–258. [Google Scholar] [CrossRef]
- Gao, F.; Liao, W.-H.; Wu, X. Being gradually softened approach for solving large deflection of cantilever beam subjected to distributed and tip loads. Mech. Mach. Theory 2022, 174, 104879. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, J. Analytical solutions of bending analysis and vibration of rectangular nano laminates with surface effects. Appl. Math. Model. 2022, 110, 663–673. [Google Scholar] [CrossRef]
- Krysko, V.A.; Awrejcewicz, J.; Kalutsky, L.A.; Krysko, V.A. Quantification of various reduced order modelling computational methods to study deflection of size-dependent plates. Comput. Math. Appl. 2023, 133, 61–84. [Google Scholar] [CrossRef]
- Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate. Micromachines 2023, 14, 1052. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. Bending response of functionally graded plates by using a new higher order shear deformation theory. Compos. Struct. 2012, 94, 714–723. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Hu, Y. The effect of thickness on the mechanics of nanobeams. Int. J. Eng. Sci. 2018, 123, 81–91. [Google Scholar] [CrossRef]
- Ambartsumian, S. On the theory of bending plates. Izv. Otd. Tech. Nauk AN SSSR 1958, 5, 69–77. [Google Scholar]
- Ambartsumian, S.A. On the theory of bending of anisotropic plates and shallow shells. J. Appl. Math. Mech. 1960, 24, 500–514. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Reissner, E. On transverse bending of plates, including the effect of transverse shear deformation. Int. J. Solids Struct. 1975, 11, 569–573. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B Eng. 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Kerr, A.D.; Alexander, H. An application of the extended Kantorovich method to the stress analysis of a clamped rectangular plate. Acta Mech. 1968, 6, 180–196. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Harik, I.E. Analytical Solution to Orthotropic Sector. J. Eng. Mech. 1984, 110, 554–568. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Tahani, M. Analytical solution for bending of moderately thick radially functionally graded sector plates with general boundary conditions using multi-term extended Kantorovich method. Compos. Part B Eng. 2012, 43, 1405–1416. [Google Scholar] [CrossRef]
- Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model. Micromachines 2023, 14, 1790. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghian, M.; Jamil, A.; Palevicius, A.; Janusas, G.; Naginevicius, V. The Nonlinear Bending of Sector Nanoplate via Higher-Order Shear Deformation Theory and Nonlocal Strain Gradient Theory. Mathematics 2024, 12, 1134. https://doi.org/10.3390/math12081134
Sadeghian M, Jamil A, Palevicius A, Janusas G, Naginevicius V. The Nonlinear Bending of Sector Nanoplate via Higher-Order Shear Deformation Theory and Nonlocal Strain Gradient Theory. Mathematics. 2024; 12(8):1134. https://doi.org/10.3390/math12081134
Chicago/Turabian StyleSadeghian, Mostafa, Asif Jamil, Arvydas Palevicius, Giedrius Janusas, and Vytenis Naginevicius. 2024. "The Nonlinear Bending of Sector Nanoplate via Higher-Order Shear Deformation Theory and Nonlocal Strain Gradient Theory" Mathematics 12, no. 8: 1134. https://doi.org/10.3390/math12081134
APA StyleSadeghian, M., Jamil, A., Palevicius, A., Janusas, G., & Naginevicius, V. (2024). The Nonlinear Bending of Sector Nanoplate via Higher-Order Shear Deformation Theory and Nonlocal Strain Gradient Theory. Mathematics, 12(8), 1134. https://doi.org/10.3390/math12081134







