Analysis of an Interface Crack between Piezoelectric Semiconductor Coating and Elastic Substrate Structure
Abstract
1. Introduction
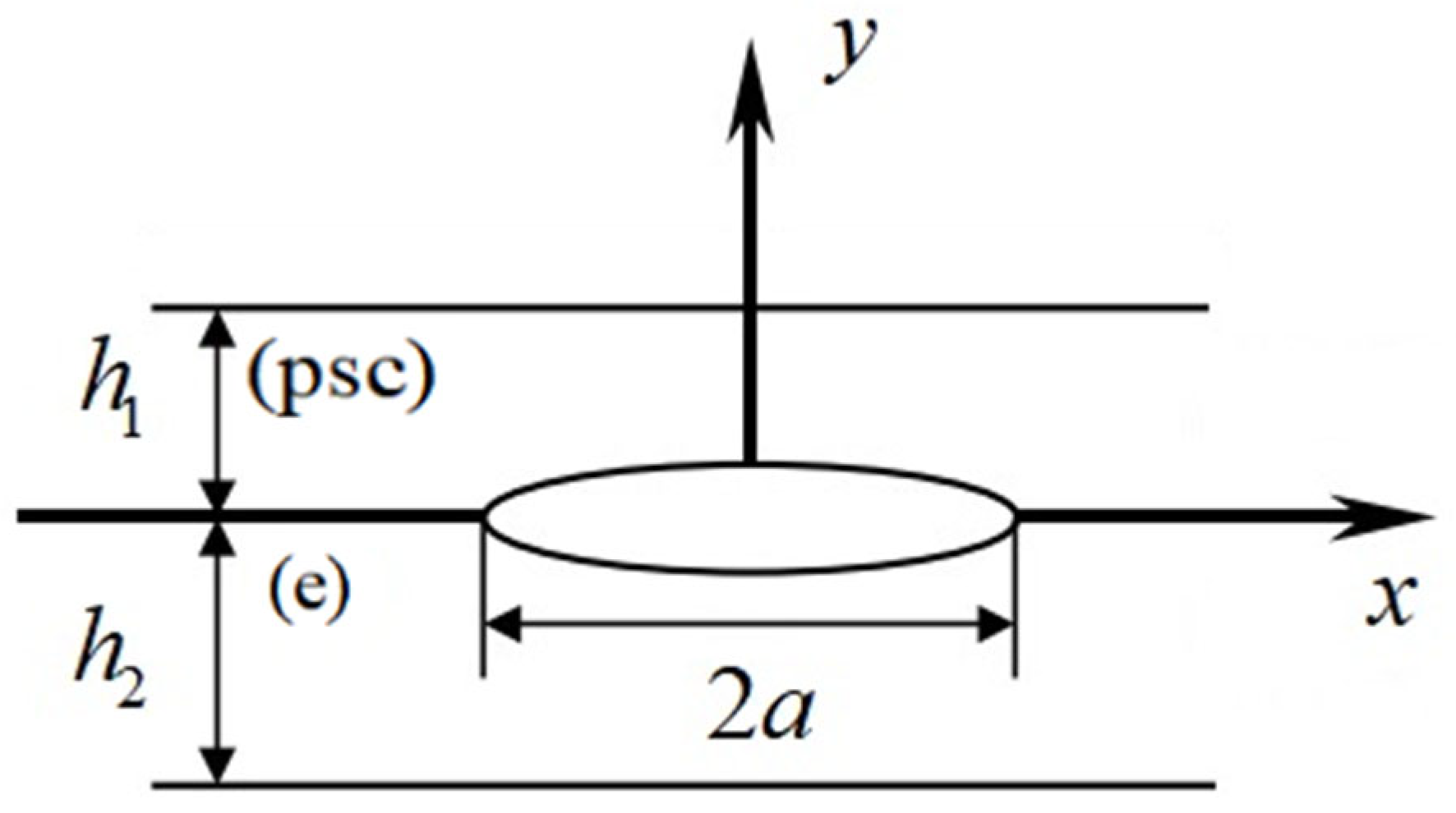
2. Description of the Problem
3. Boundary Conditions
4. Theoretical Analysis and Solution
5. Field Intensity Factors and Energy Release Rates
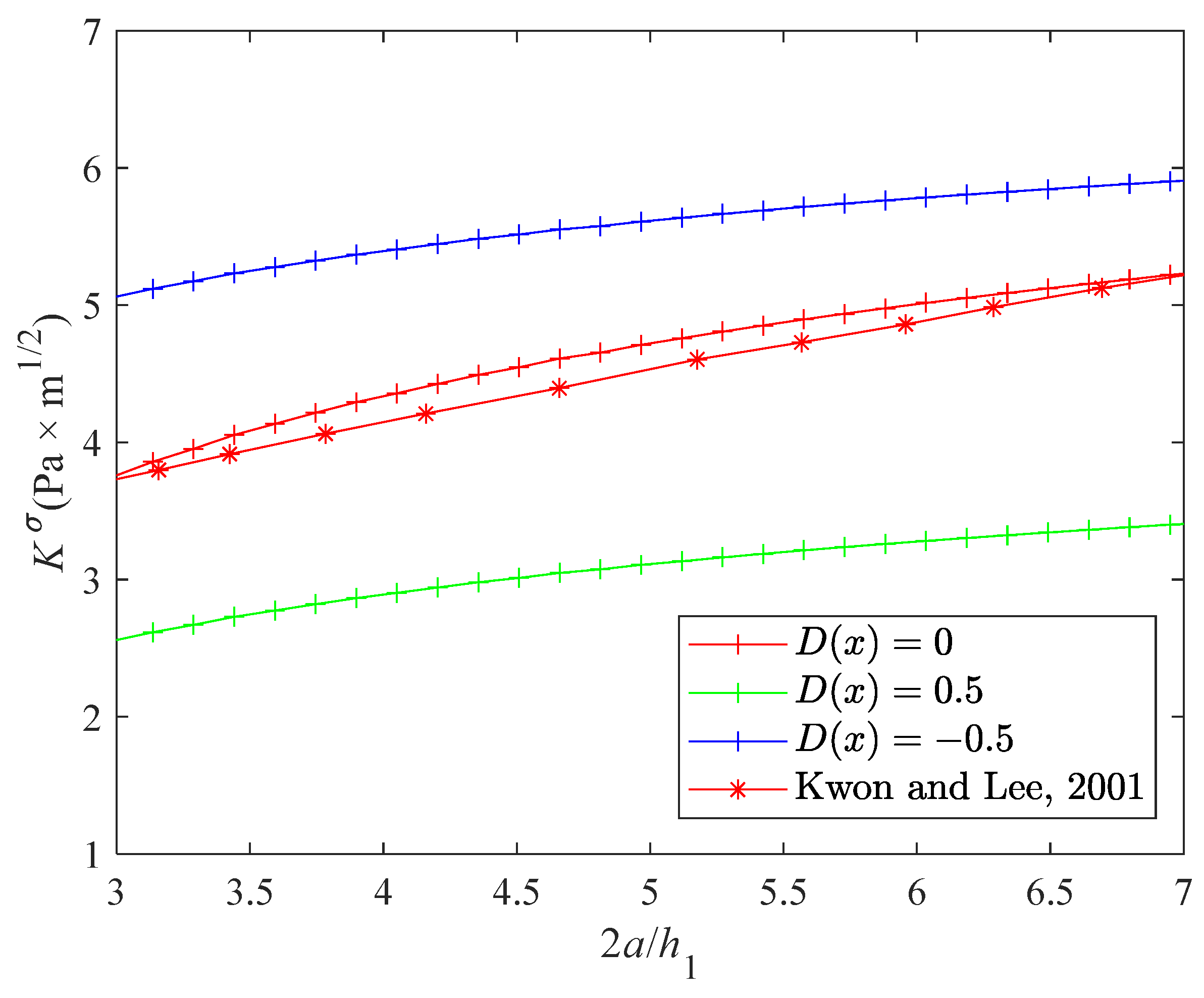
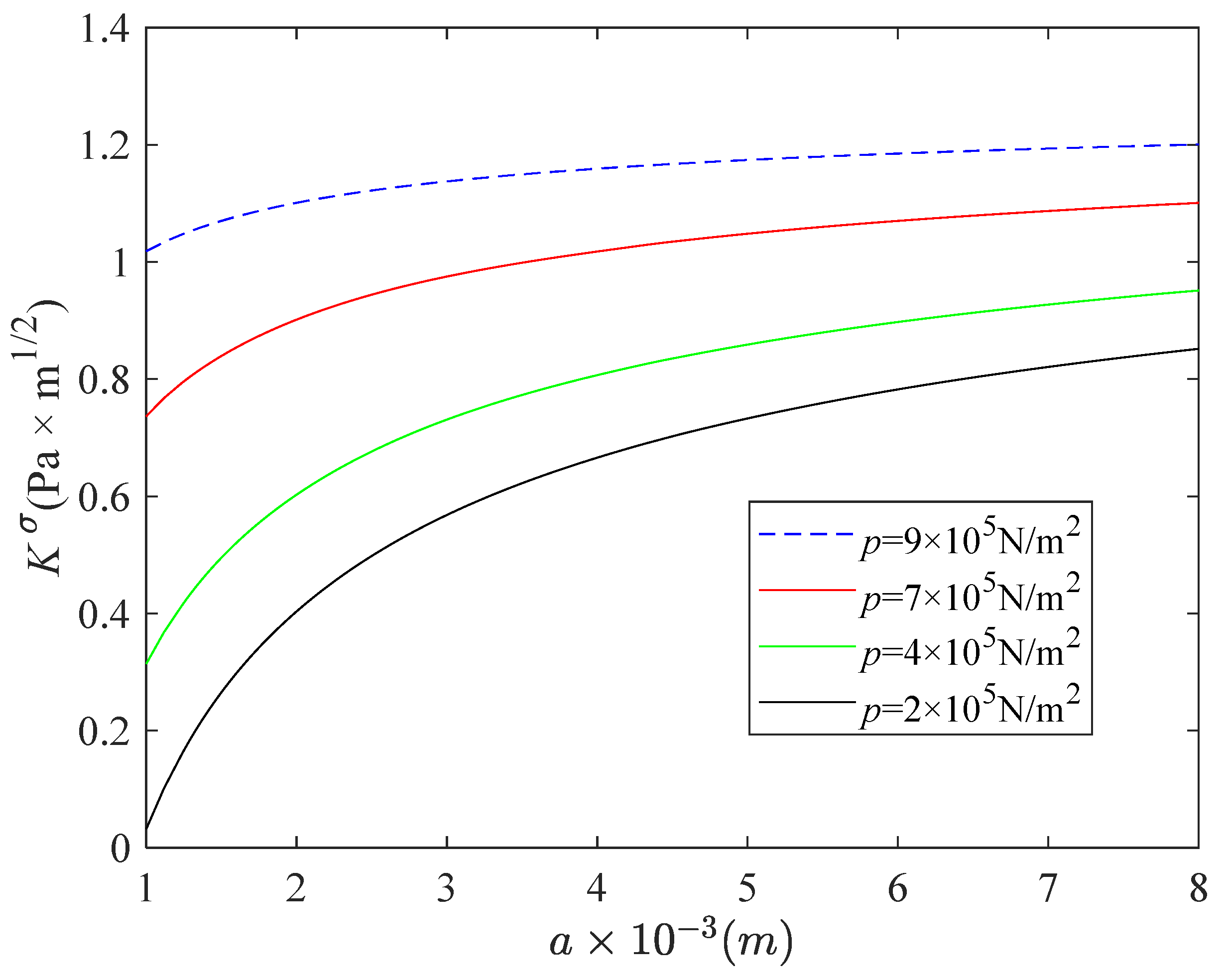
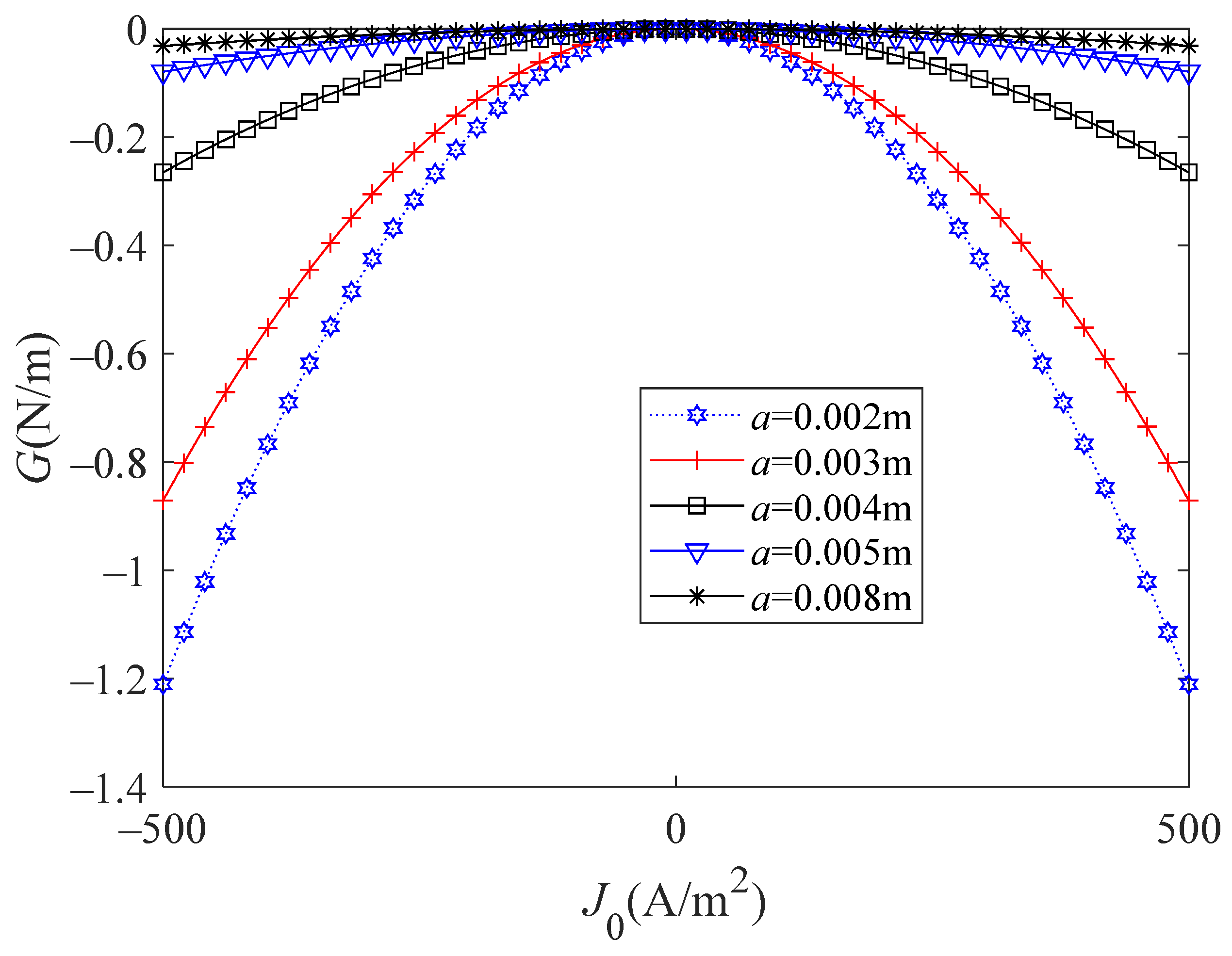
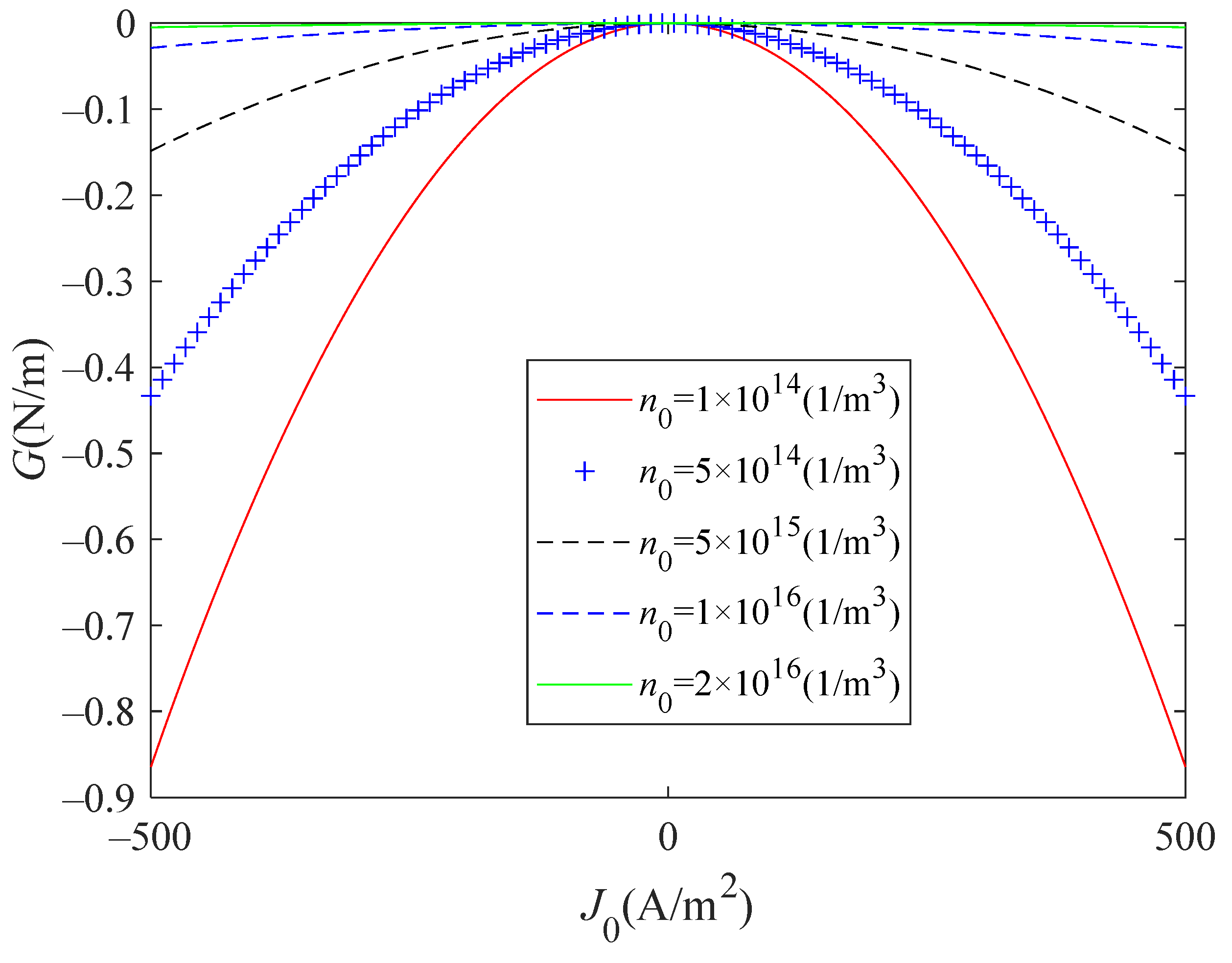
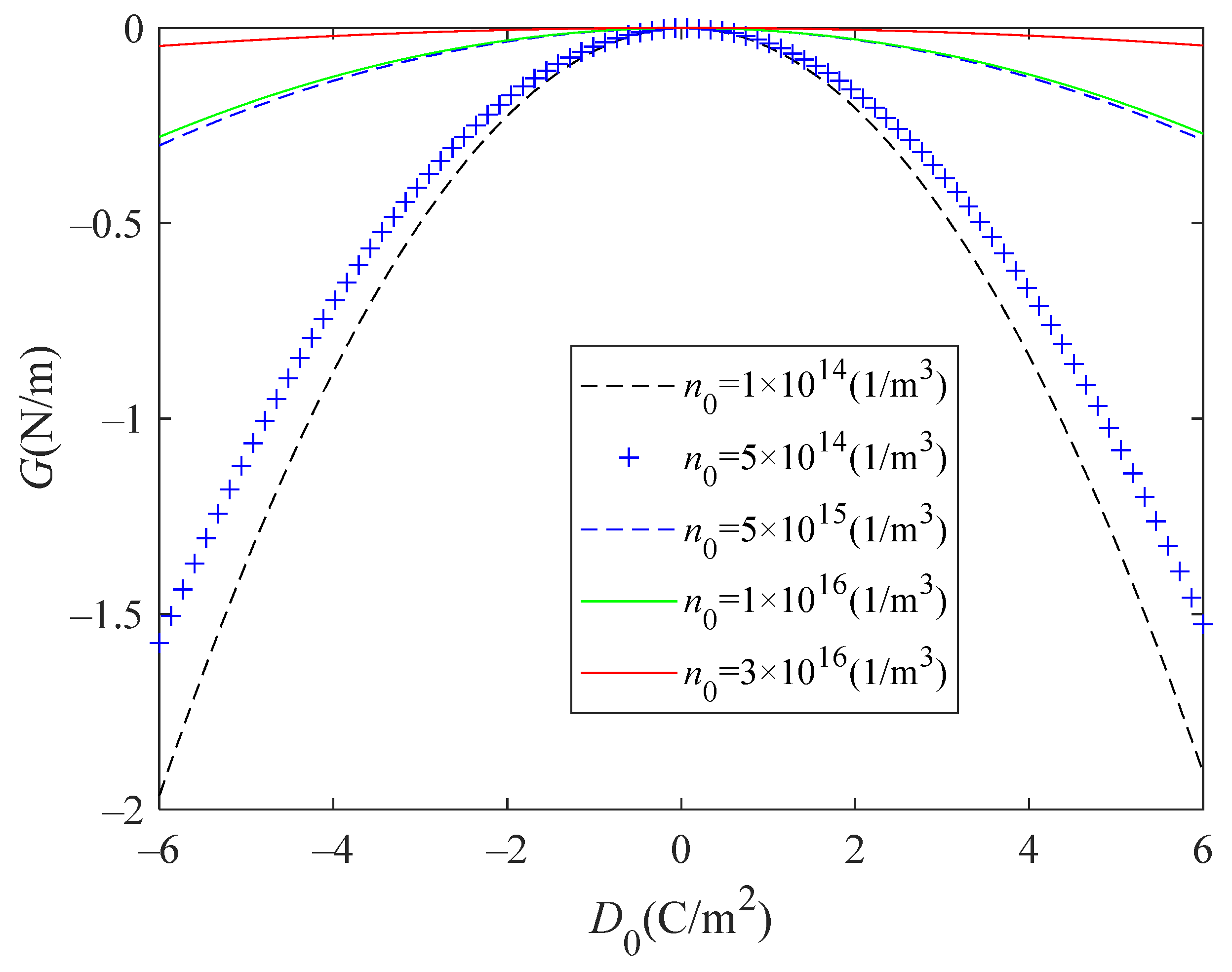
6. Numerical Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J. Analysis of Piezoelectric Semiconductor Structures; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Sun, L.; Zhang, Z.; Gao, C.; Zhang, C. Effect of flexoelectricity on piezotronic responses of a piezoelectric semiconductor bilayer. J. Appl. Phys. 2021, 129, 244102. [Google Scholar] [CrossRef]
- Tian, R.; Nie, G.; Liu, J.; Pan, E.; Wang, Y. On Rayleigh waves in a piezoelectric semiconductor thin film over an elastic half-space. Int. J. Mech. Sci. 2021, 204, 106565. [Google Scholar] [CrossRef]
- Guo, X.; Wei, P. Dispersion relations of in-plane elastic waves in nano-scale one dimensional piezoelectric semiconductor/piezoelectric dielectric phononic crystal with the consideration of interface effect. Appl. Math. Model. 2021, 96, 189–214. [Google Scholar] [CrossRef]
- Tian, R.; Nie, G.; Liu, J.; Pan, E.; Wang, Y. Love waves in a piezoelectric semiconductor thin film on an elastic dielectric half-space. Acta Mech. Solida Sin. 2023, 36, 45–54. [Google Scholar] [CrossRef]
- Han, C.; Lu, C.; Zhao, M.; Zhang, Q. Nonlinear finite element analysis of electromechanical behaviors in a piezoelectric semiconductor beam. Int. J. Non-Linear Mech. 2023, 149, 104311. [Google Scholar] [CrossRef]
- Fu, S.; Wu, H.; He, W.; Li, Q.; Shan, C.; Wang, J.; Du, Y.; Du, S.; Huang, Z.; Hu, C. Conversion of dielectric surface effect into volume effect for high output energy. Adv. Mater. 2023, 35, 2302954. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, Z.; Li, X.; Deng, S.; Liu, Y.; Zhou, H.; Peng, M.; Fu, Z.; Chen, R.; Meng, D.; et al. Gamma-Ray Irradiation Induced Dielectric Loss of SiO2/Si Heterostructures in Through-Silicon Vias (TSVs) by Forming Border Traps. ACS Appl. Electron. Mater. 2024, 6, 1339–1346. [Google Scholar] [CrossRef]
- Yang, J. A semi-infinite anti-plane crack in a piezoelectric semiconductor. Int. J. Fract. 2004, 130, L169–L174. [Google Scholar] [CrossRef]
- Hu, Y.; Zeng, Y.; Yang, J. A mode III crack in a piezoelectric semiconductor of crystals with 6 mm symmetry. Int. J. Solids Struct. 2007, 44, 3928–3938. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y. Analysis on the anti-plane deformations of a piezoelectric semiconductor plate with a hole. In Proceedings of the 2014 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, Beijing, China, 30 October–2 November 2014; IEEE: New York, NY, USA, 2014; pp. 106–109. [Google Scholar]
- Fan, C.; Yan, Y.; Xu, G.; Zhao, M. Piezoelectric-conductor iterative method for analysis of cracks in piezoelectric semiconductors via the finite element method. Eng. Fract. Mech. 2016, 165, 183–196. [Google Scholar] [CrossRef]
- Qin, G.; Lu, C.; Zhang, X.; Zhao, M. Electric current dependent fracture in GaN piezoelectric semiconductor ceramics. Materials 2018, 11, 2000. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhou, C.; Zhao, M.; Pan, E.; Fan, C. Penny-shaped cracks in three-dimensional piezoelectric semiconductors via Green’s functions of extended displacement discontinuity. J. Intell. Mater. Syst. Struct. 2017, 28, 1775–1788. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, C.; Xu, G.; Zhao, M. Iterative boundary element method for crack analysis of two-dimensional piezoelectric semiconductor. Eng. Anal. Bound. Elem. 2017, 83, 87–95. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Lu, C.; Zhang, Q. Nonlinear analysis of a crack in 2D piezoelectric semiconductors with exact electric boundary conditions. J. Intell. Mater. Syst. Struct. 2021, 32, 632–639. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, L.; Liu, J. Transient responses of a mode-III crack in a piezoelectric semiconductor material. In Proceedings of the 2023 17th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 10–12 November 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar]
- Sladek, J.; Sladek, V.; Pan, E.; Young, D.L. Dynamic anti-plane crack analysis in functional graded piezoelectric semiconductor crystals. CMES-Comput. Model. Eng. Sci. 2014, 99, 273–296. [Google Scholar]
- Sladek, J.; Sladek, V.; Pan, E.; Wünsche, M. Fracture analysis in piezoelectric semiconductors under a thermal load. Eng. Fract. Mech. 2014, 126, 27–39. [Google Scholar] [CrossRef]
- Beom, H.G.; Jang, H.S. Interfacial wedge cracks in dissimilar anisotropic materials under antiplane shear. Int. J. Eng. 2012, 56, 49–62. [Google Scholar] [CrossRef]
- Ding, S.H.; Zhou, Y.T.; Li, X. Interface crack problem in layered orthotropic materials under thermo-mechanical loading. Int. J. Solids Struct. 2014, 51, 4221–4229. [Google Scholar] [CrossRef]
- Arshid, E.; Amir, S.; Loghman, A. On the vibrations of FG GNPs-RPN annular plates with piezoelectric/metallic coatings on Kerr elastic substrate considering size dependency and surface stress effects. Acta Mech. 2023, 234, 4035–4076. [Google Scholar] [CrossRef]
- Kwon, J.H.; Lee, K.Y. Crack problem at interface of piezoelectric strip bonded to elastic layer under anti-plane shear. KSME Int. J. 2001, 15, 61–65. [Google Scholar] [CrossRef]
- Ou, Z.C.; Chen, Y.H. Interface crack problem in elastic dielectric/piezoelectric bimaterials. Int. J. Fract. 2004, 130, 427–454. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Wünsche, M.; Zhang, C. Analysis of an interface crack between two dissimilar piezoelectric solids. Eng. Fract. Mech. 2012, 89, 114–127. [Google Scholar] [CrossRef]
- Pamnani, G.; Bhattacharya, S.; Sanyal, S. Analysis of interface crack in piezoelectric materials using extended finite element method. Mech. Adv. Mater. Struct. 2019, 26, 1447–1457. [Google Scholar] [CrossRef]
- Hu, S.; Li, J. Interaction between screw dislocation and interfacial crack in fine-grained piezoelectric coatings under steady-state thermal loading. Appl. Sci. 2021, 11, 11922. [Google Scholar] [CrossRef]
- Herrmann, K.P.; Loboda, V.V. Fracture mechanical assessment of interface cracks with contact zones in piezoelectric bimaterials under thermoelectromechanical loadings: I. Electrically permeable interface cracks. Int. J. Solids Struct. 2003, 40, 4191–4217. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B.; Li, X.; Ding, S. A closed-form solution to the mechanism of interface crack formation with one contact area in decagonal quasicrystal bi-materials. Crystals 2024, 14, 316. [Google Scholar] [CrossRef]
- Rizzoni, R.; Serpilli, M.; Raffa, M.L.; Lebon, F. A micromechanical model for damage evolution in thin piezoelectric films. Coatings 2023, 13, 82. [Google Scholar] [CrossRef]
- Golub, M.V.; Doroshenko, O.V. Analysis of eigenfrequencies of a circular interface delamination in elastic media based on the boundary integral equation method. Mathematics 2021, 10, 38. [Google Scholar] [CrossRef]
- Gu, B.; Yu, S.W.; Feng, X.Q. Transient response of an interface crack between dissimilar piezoelectric layers under mechanical impacts. Int. J. Solids Struct. 2002, 39, 1743–1756. [Google Scholar] [CrossRef]
- Kwon, J.H.; Lee, K.Y. Moving interfacial crack between piezoelectric ceramic and elastic layers. Eur. J. Mech. A/Solids 2000, 19, 979–987. [Google Scholar] [CrossRef]
- Gao, C.F.; Häusler, C.; Balke, H. Periodic permeable interface cracks in piezoelectric materials. Int. J. Solids Struct. 2004, 41, 323–335. [Google Scholar] [CrossRef]
- Feng, F.X.; Lee, K.Y.; Li, Y.D. Multiple cracks on the interface between a piezoelectric layer and an orthotropic substrate. Acta Mech. 2011, 221, 297–308. [Google Scholar] [CrossRef]
- Loboda, V.; Sheveleva, A.; Chapelle, F.; Lapusta, Y. Multiple electrically limited permeable cracks in the interface of piezoelectric materials. Mech. Adv. Mater. Struct. 2023, 54, 1–13. [Google Scholar]
- Zhu, S.; Yu, H.; Guo, L. Analysis of an interfacial crack between two nonhomogeneous piezoelectric materials using a new domain-independent interaction integral. Compos. Struct. 2024, 331, 117873. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, S.; Ma, H.; Wang, J. Interface crack analysis of piezoelectric laminates considering initial strain. Int. J. Mech. Sci. 2024, 271, 109104. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, C.; Chen, W.; Yang, J. Piezotronic effect of a thin film with elastic and piezoelectric semiconductor layers under a static flexural loading. J. Appl. Mech. 2019, 86, 051003. [Google Scholar] [CrossRef]
- Ren, C.; Wang, K.F.; Wang, B.L. Electromechanical analysis of a piezoelectric semiconductor bilayer system with imperfect interface. Eur. J. Mech. -A/Solids 2024, 103, 105173. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear solid mechanics: A continuum approach for engineering science. Meccanica 2002, 37, 489–490. [Google Scholar] [CrossRef]
- Vasileska, D.; Goodnick, S.M.; Klimeck, G. Computational Electronics: Semiclassical and Quantum Device Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hutson, A.R.; White, D.L. Elastic wave propagation in piezoelectric semiconductors. J. Appl. Phys. 1962, 33, 40–47. [Google Scholar] [CrossRef]
- White, D.L. Amplification of ultrasonic waves in piezoelectric semiconductors. J. Appl. Phys. 1962, 33, 2547–2554. [Google Scholar] [CrossRef]
- Pak, Y.E. Crack extension force in a piezoelectric materia. J. Appl. Mech. 1990, 57, 647–653. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley and Sons: Hoboken, NJ, USA, 1973; pp. 357–382. [Google Scholar]
- Goodge, M.E. Semiconductor Device Technology; The Macmillan Press: New York, NY, USA, 1983. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Zhang, Y.; Ma, H.; Li, X.; Ding, S. Analysis of an Interface Crack between Piezoelectric Semiconductor Coating and Elastic Substrate Structure. Mathematics 2024, 12, 1208. https://doi.org/10.3390/math12081208
Tian X, Zhang Y, Ma H, Li X, Ding S. Analysis of an Interface Crack between Piezoelectric Semiconductor Coating and Elastic Substrate Structure. Mathematics. 2024; 12(8):1208. https://doi.org/10.3390/math12081208
Chicago/Turabian StyleTian, Xiangru, Yali Zhang, Hailiang Ma, Xing Li, and Shenghu Ding. 2024. "Analysis of an Interface Crack between Piezoelectric Semiconductor Coating and Elastic Substrate Structure" Mathematics 12, no. 8: 1208. https://doi.org/10.3390/math12081208
APA StyleTian, X., Zhang, Y., Ma, H., Li, X., & Ding, S. (2024). Analysis of an Interface Crack between Piezoelectric Semiconductor Coating and Elastic Substrate Structure. Mathematics, 12(8), 1208. https://doi.org/10.3390/math12081208




