Study on the Vibration Characteristics of the Helical Gear-Rotor-Bearing Coupling System of a Wind Turbine with Composite Faults
Abstract
:1. Introduction
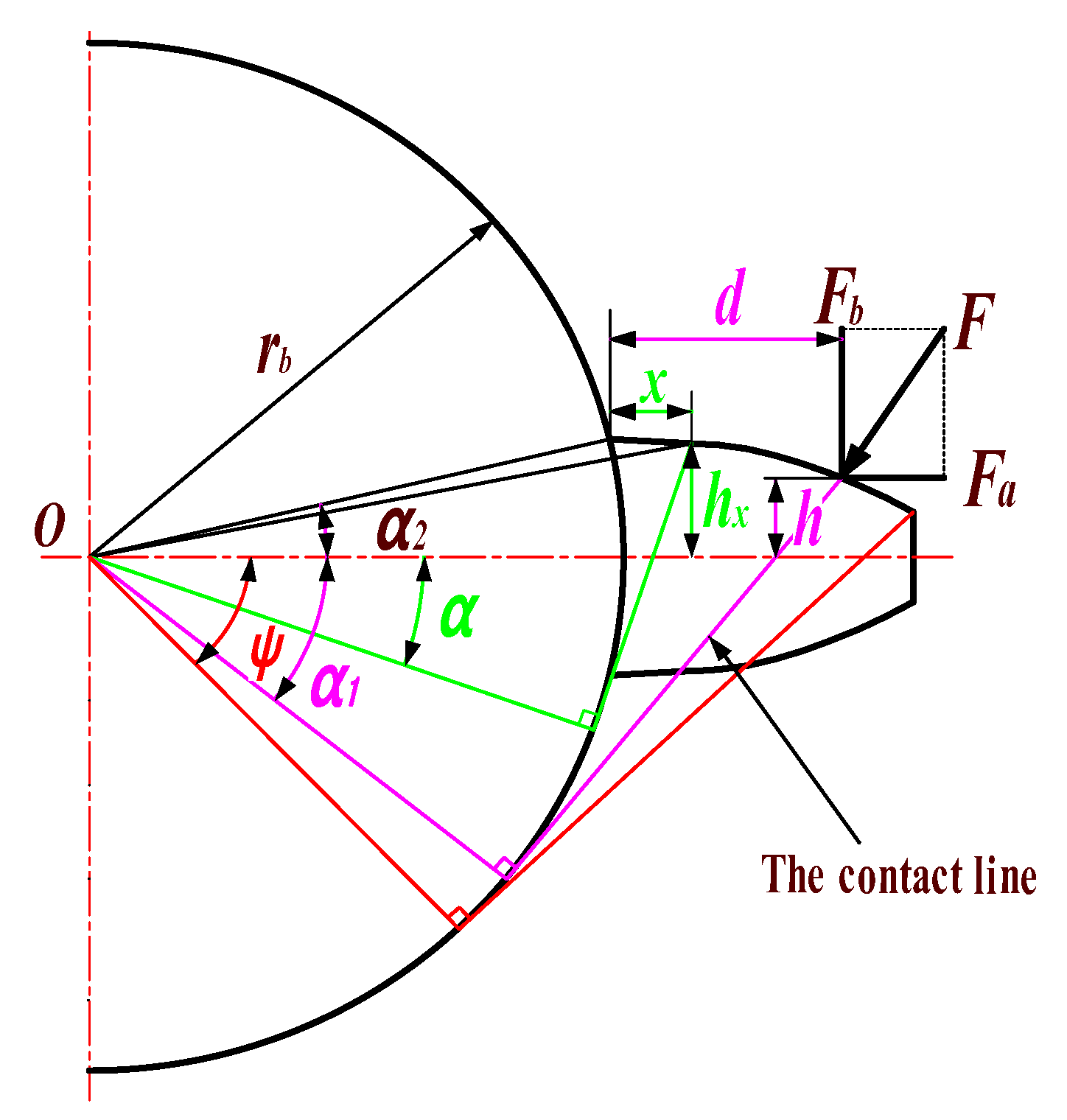
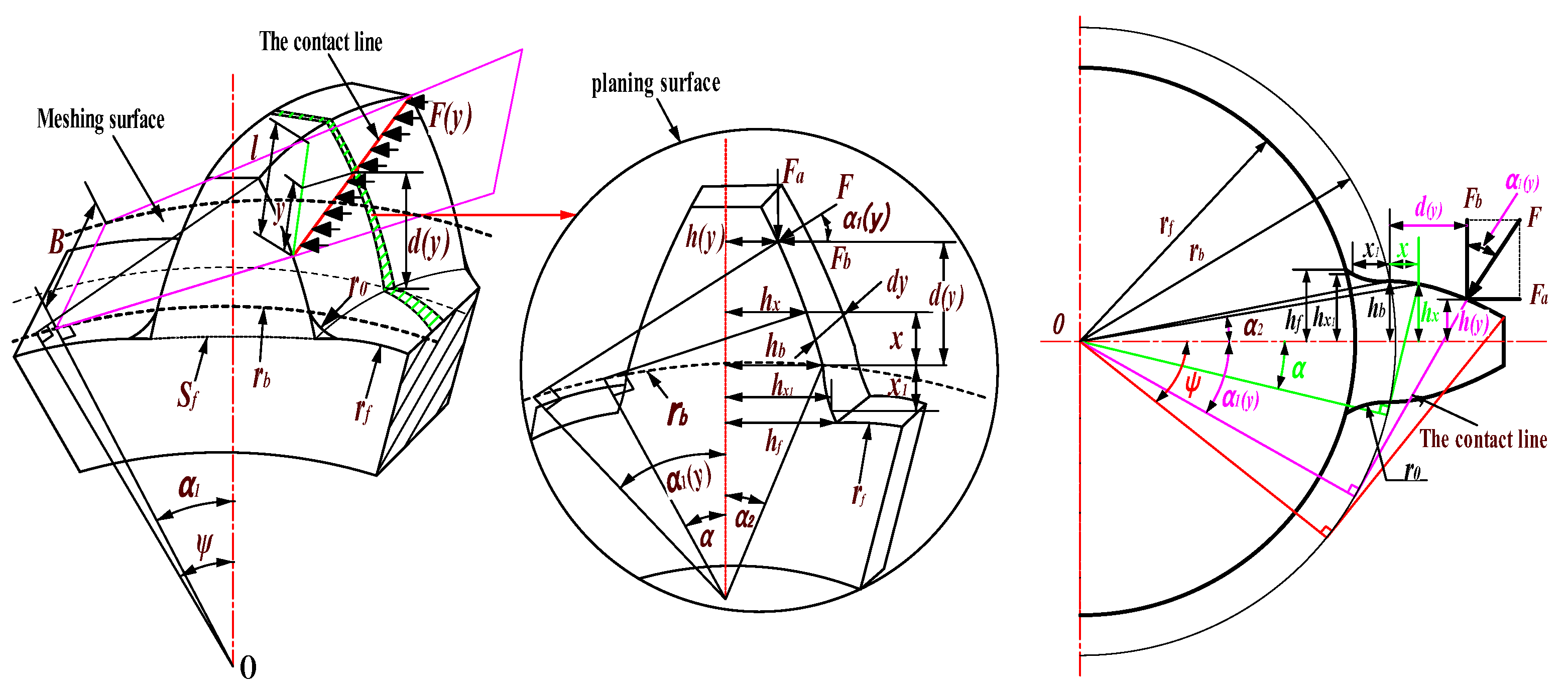
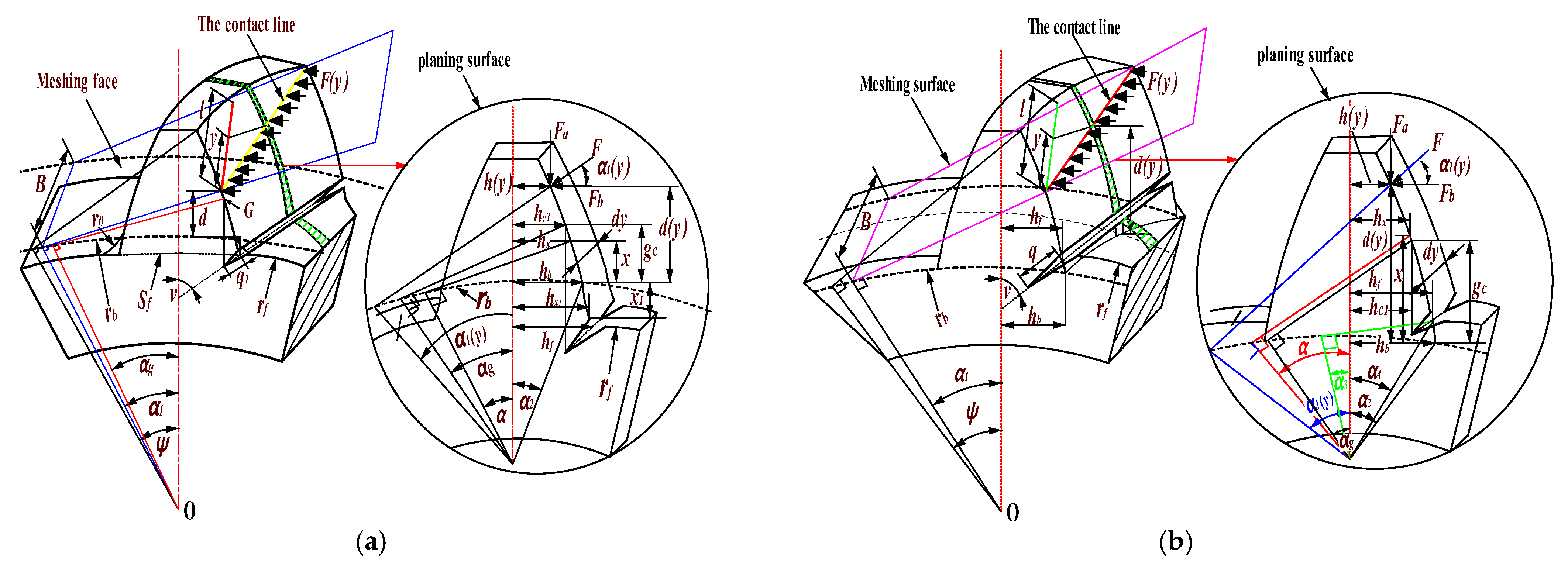
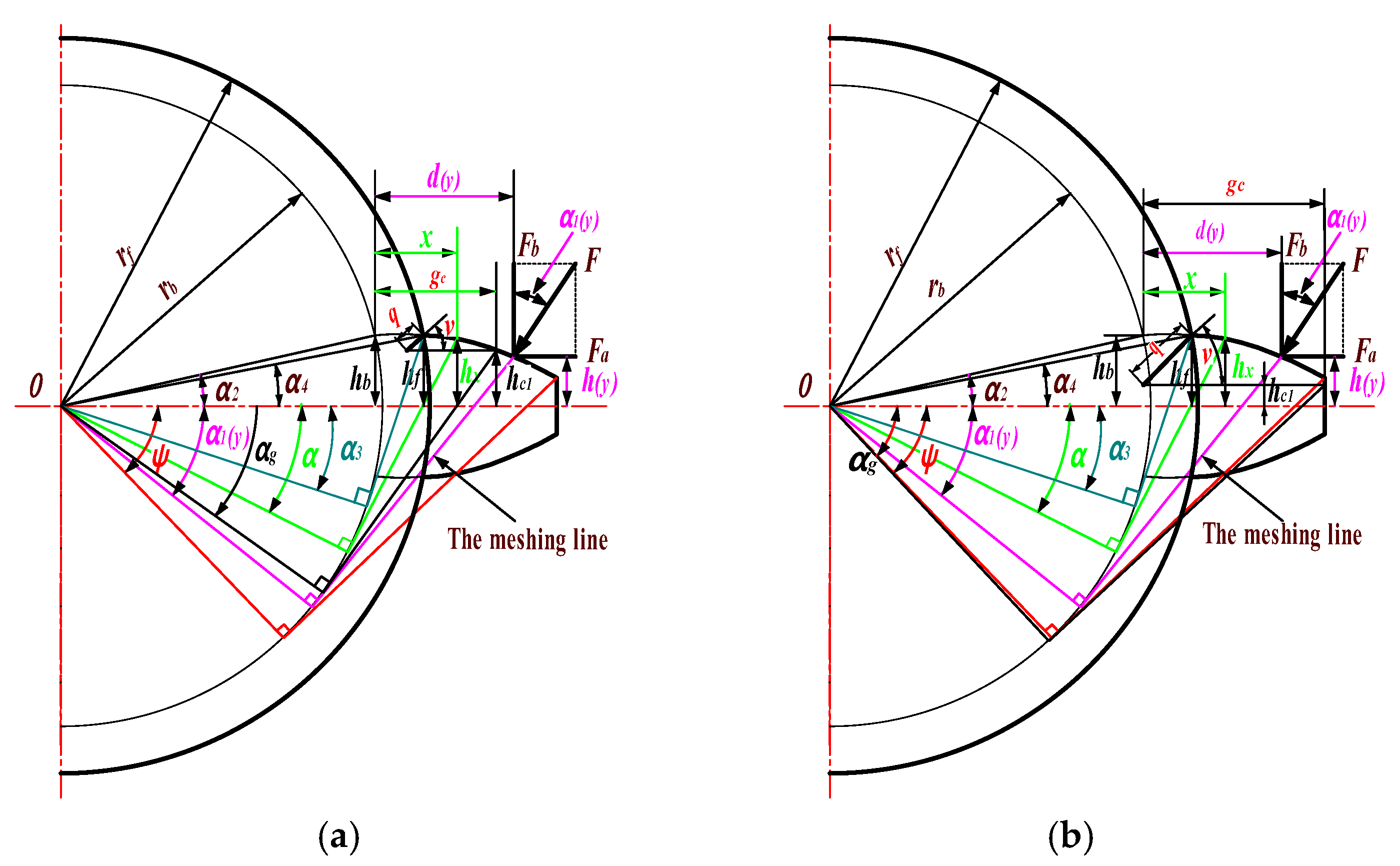
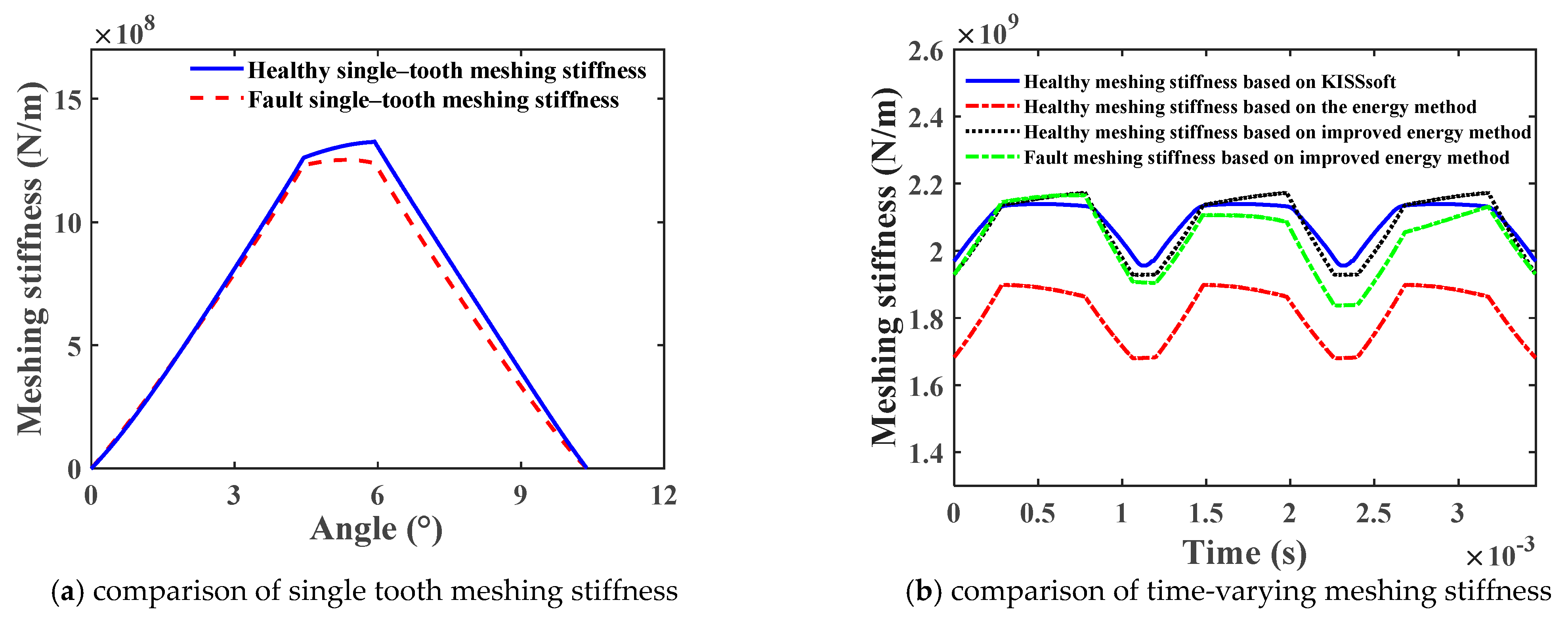
2. Calculation of Meshing Stiffness of Helical Gears with Root Cracks Based on Improved Energy Method
- (1)
- As in the case of Figure 5a, , , and :
- (2)
- As in the case of Figure 5b, and or and :
- (3)
- As in the case of Figure 6a, , , and :
- (4)
- As in the case of Figure 6b, , or , and :
3. Dynamics Modeling of the Helical Gear-Rotor-Bearing Coupling System with Compound Faults
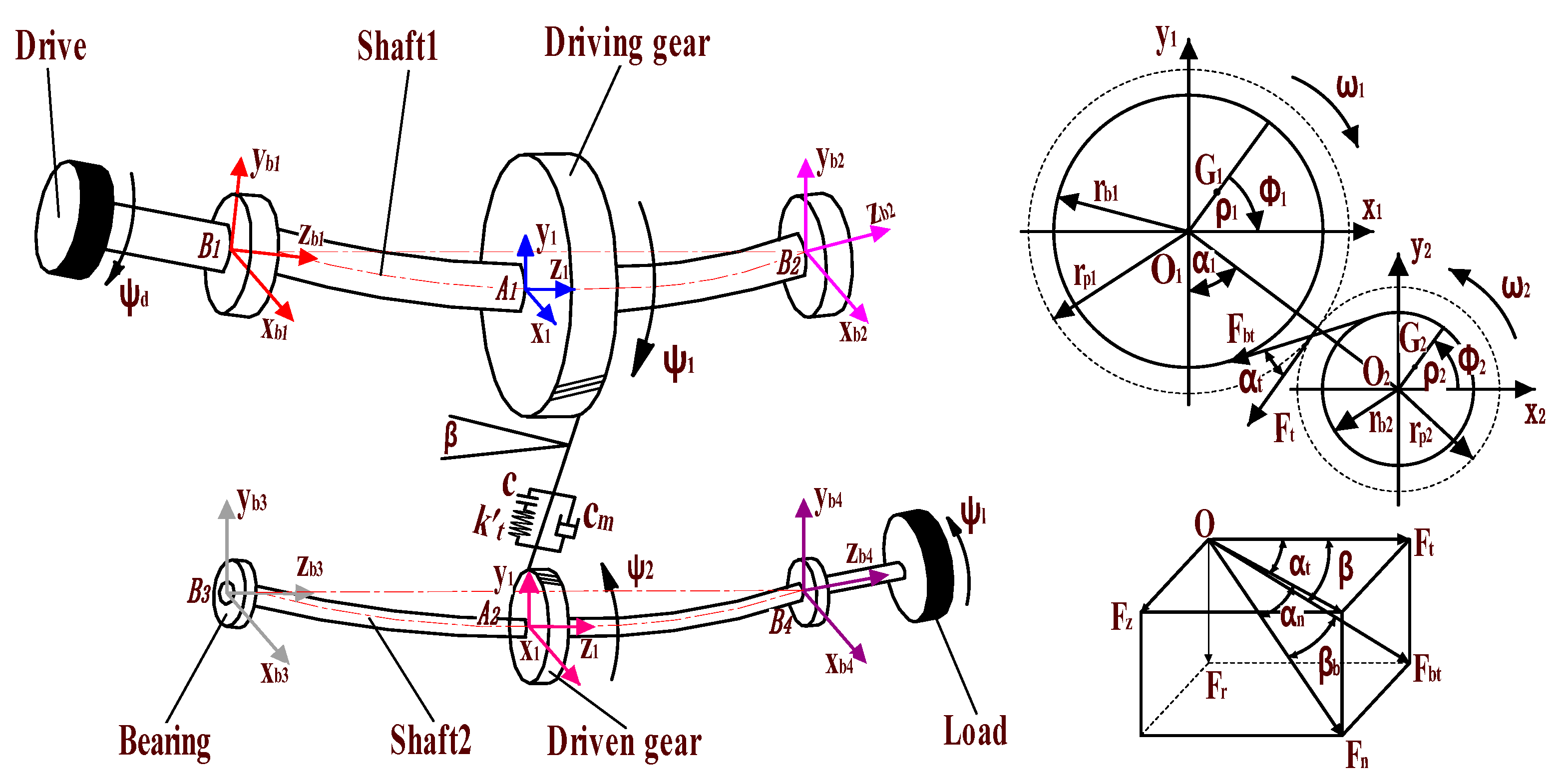
3.1. Dynamic Modeling of Helical Gear System
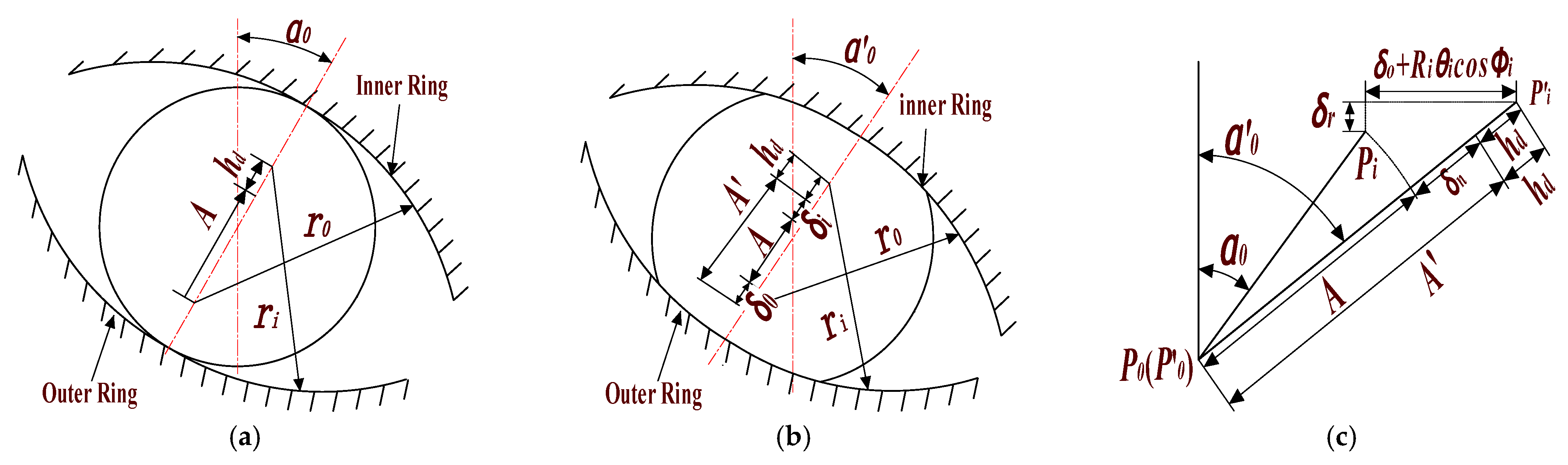
3.2. Vibration Analysis Model of Angular Contact Ball Bearings with Faults
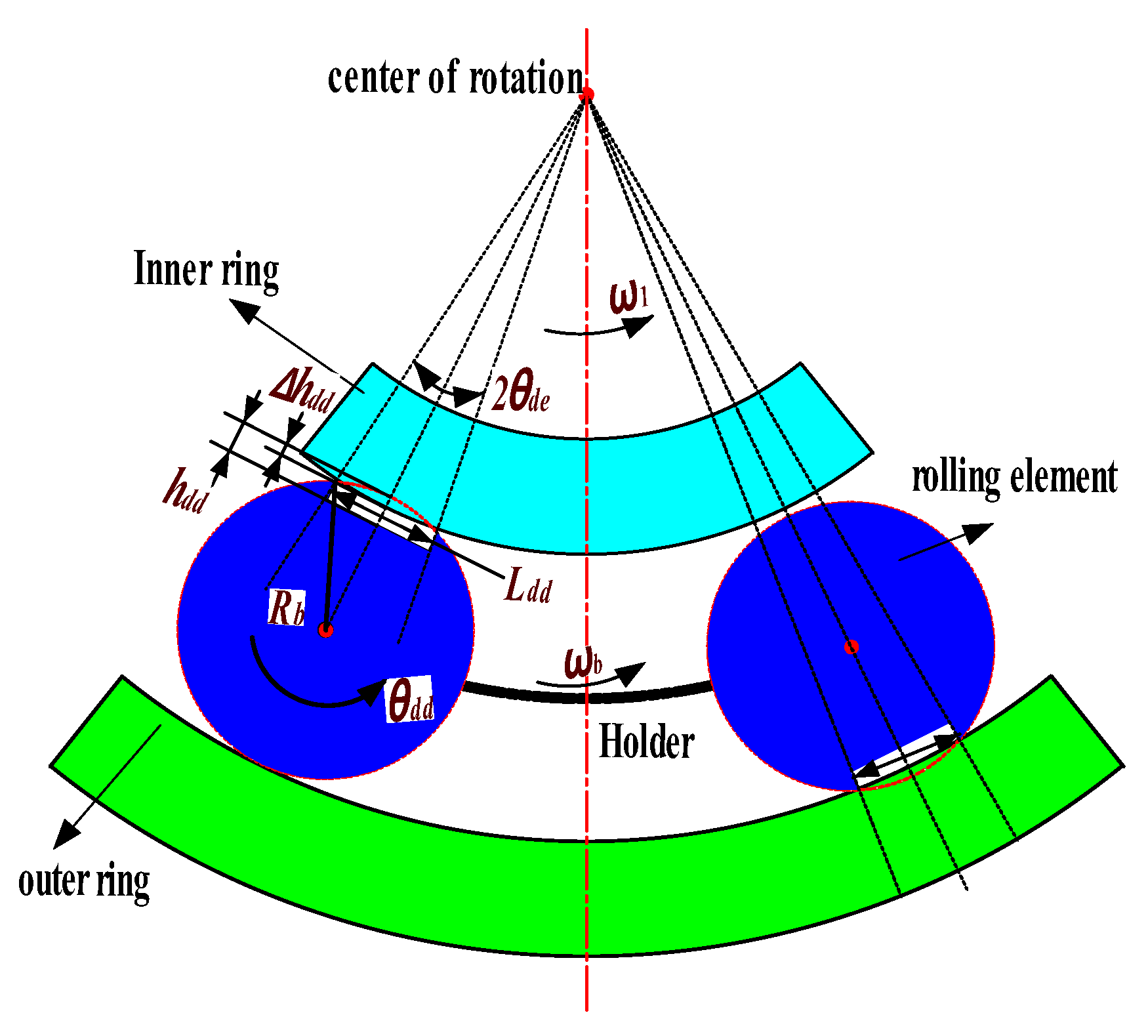
3.3. Establishment of Bearing Excitation Model with Typical Faults
3.4. Compound Fault Helical Gear-Rotor-Bearing Coupling Dynamic Equation
4. Analysis of Vibration Characteristics of Helical Gear-Rotor-Bearing System with Faults
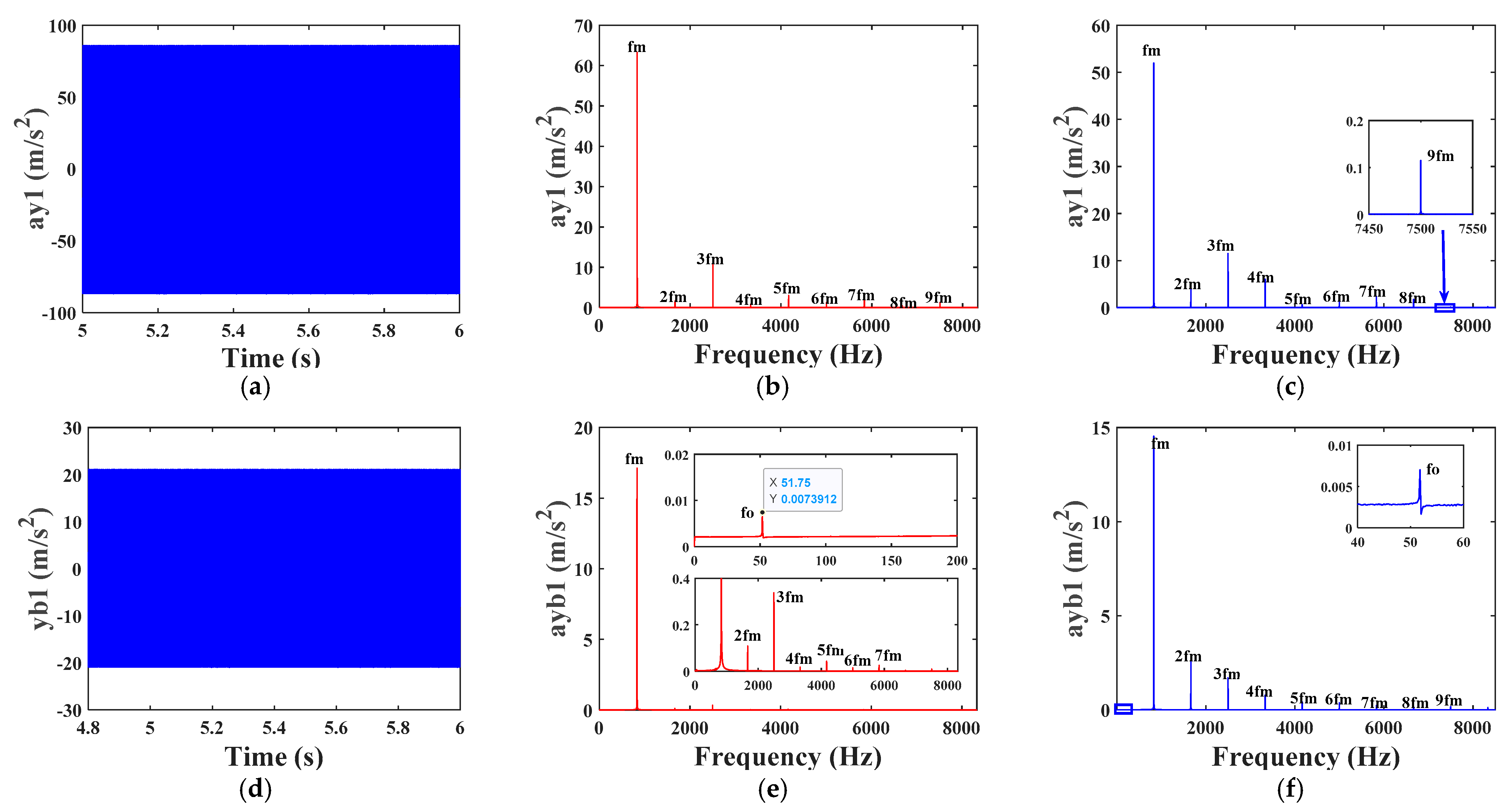
4.1. Analysis of Vibration Characteristics of Health Systems
4.2. Analysis of Vibration Response and Parameter Effects of a Single Fault System with Gear Eccentricity
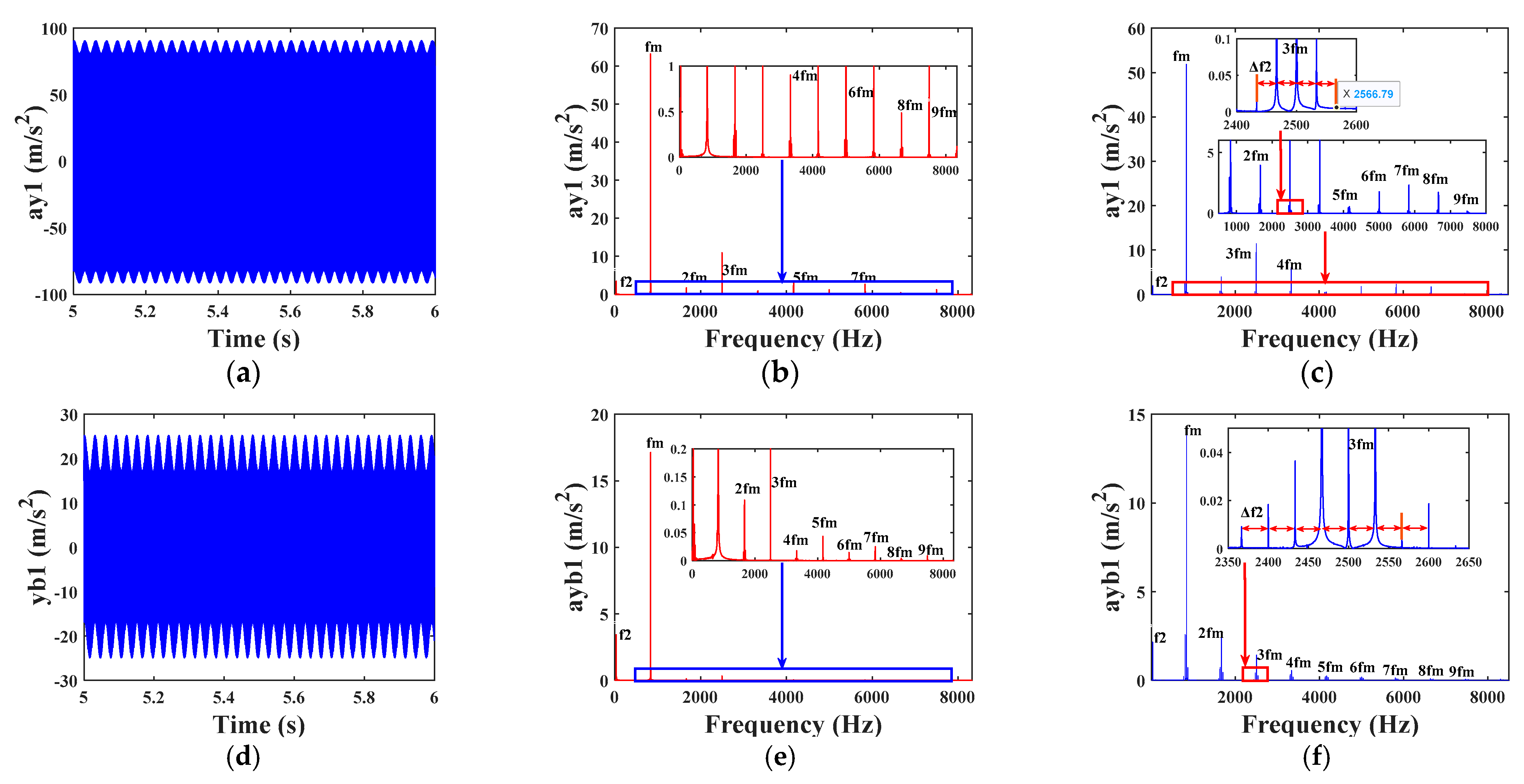
4.2.1. Analysis of Vibration Characteristics of a Single Fault System with Eccentricity
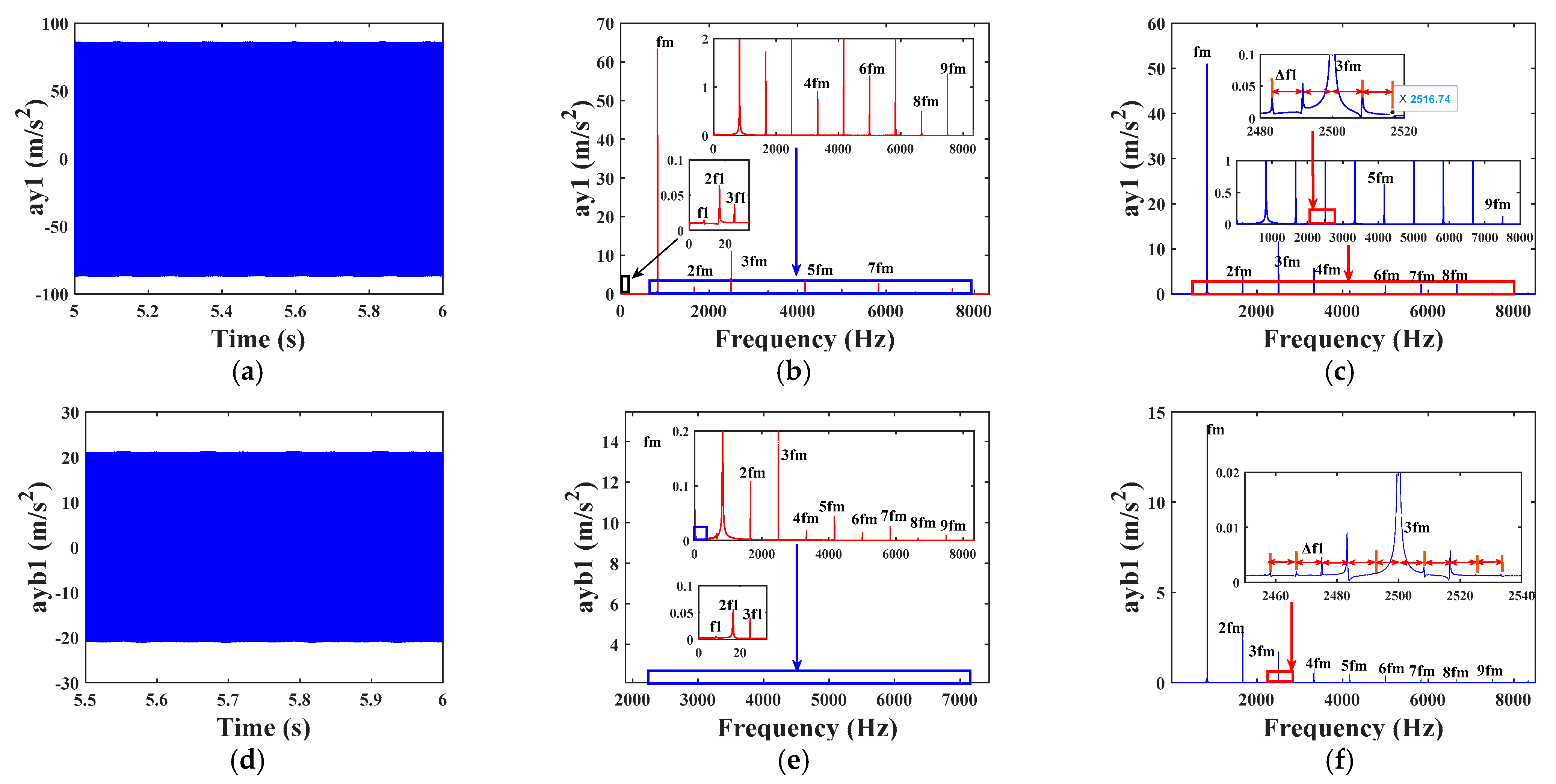
4.2.2. Analysis of Vibration Characteristics of a Single Fault System with Root Cracks
4.2.3. Analysis of Vibration Characteristics of a Single Fault System with Bearing Outer Ring
4.2.4. Analysis of Vibration Characteristics of a Single Fault System of Bearing Inner Ring
4.2.5. Analysis of Vibration Characteristics of a Single Fault System of Bearing Rolling Element
4.3. Analysis of Vibration Characteristics of a System with Composite Faults of Gears and Bearings
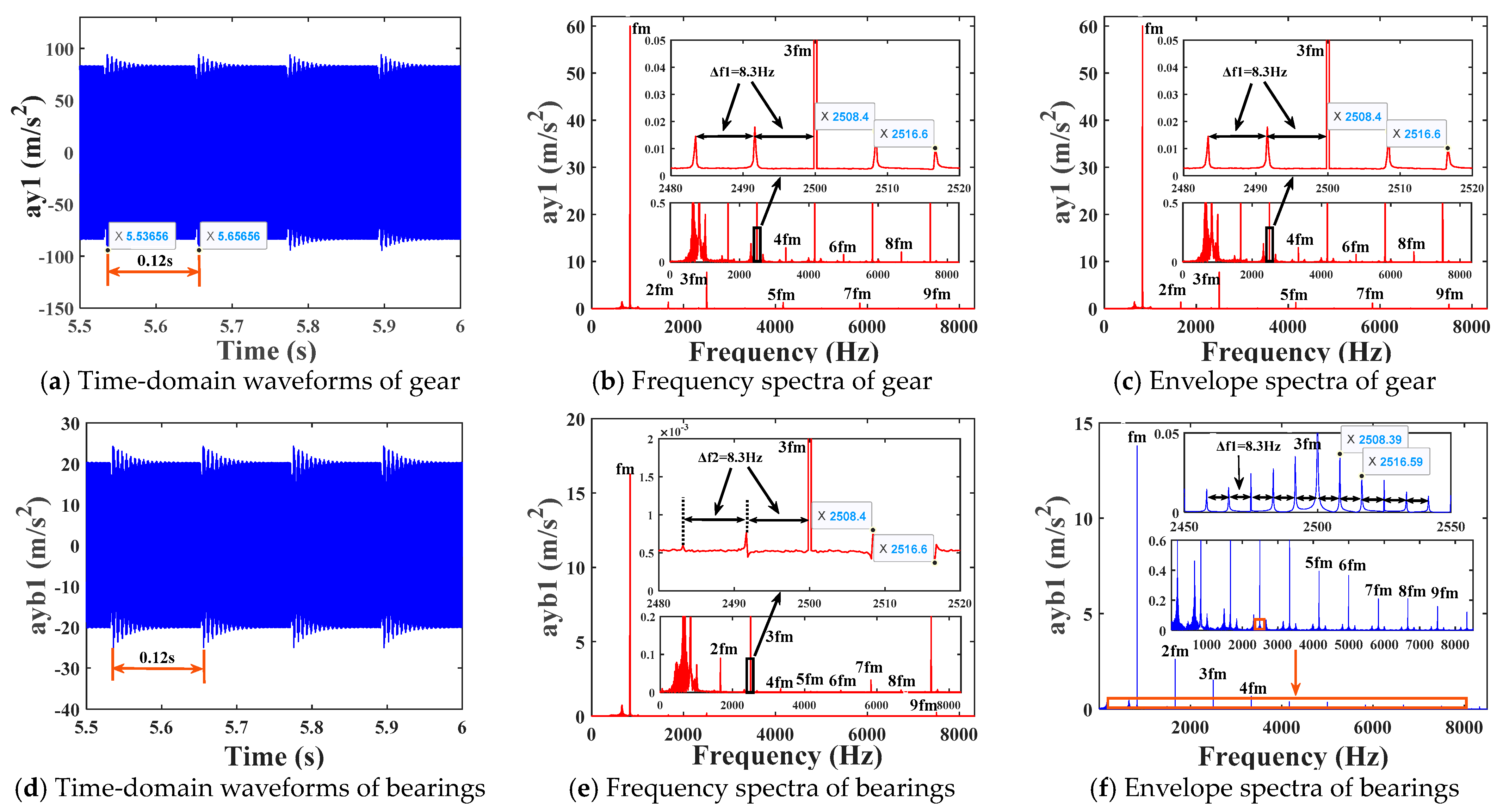
4.3.1. Vibration Response of a System with Root Cracks and Bearing Outer Ring Composite Faults
4.3.2. Vibration Response of a System with Root Cracks and Bearing Inner Ring Composite Faults
4.3.3. Vibration Response of a Composite Fault System with Root Cracks and Bearing Rolling Elements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Hertz contact stiffness | |
| Bending stiffness | |
| Shear stiffness | |
| Axial compression stiffness | |
| Elastic stiffness of matrix | |
| Hertz contact deformation potential energy | |
| Bending deformation potential energy | |
| Shear deformation potential energy | |
| Axial deformation potential energy | |
| The meshing force in the meshing line direction | |
| Young’s modulus | |
| Shear modulus | |
| Poisson ratio | |
| The distance from the meshing point to the base circle | |
| The distance from the meshing point to the centerline of the gear | |
| Tooth width | |
| The distance of inertia of the tooth from the cross-section at the base circle | |
| The cross-sectional area of the tooth from the cross-section at the base circle | |
| The distance from the point at the base circle from the centerline of the single tooth of the gear | |
| The angle between the meshing force and the direction of the perpendicular line of the centerline of the gear | |
| The radius of the root transition curve | |
| The root circle pressure angle | |
| The crack depth | |
| The crack angle | |
| The perpendicular distance from the crack tip to the gear centerline | |
| Number of teeth | |
| Pressure angle | |
| Spiral angle | |
| modulus | |
| The mass of helical gear | |
| The moment of inertia relative to the center of mass | |
| The eccentricity | |
| The base circle radius | |
| Respectively, the tangential force | |
| Radial force | |
| Rxial force | |
| The torsional vibration angular displacement of the input device, the driving and driven gears, and the load, respectively | |
| The center of mass | |
| The center of rotation | |
| The horizontal, vertical, and axial vibrational displacements of the driving and driven gears, respectively | |
| The mean value of error | |
| The amplitude of error | |
| The linear velocity of the contact points between the rolling elements and the inner and outer rings of the bearing | |
| Angular velocity of the inner and outer rings of the bearing | |
| The number of bearing rollers | |
| The angle at which the gear is located | |
| The rolling body diameter of the bearing | |
| The diameter of the axis | |
| Groove diameters of inner/outer rings of bearings, respectively | |
| The pitch diameter of the bearing | |
| , | The distance between the centers of curvature of the grooves of the inner and outer rings of the bearing before and after loading |
| The contact angles before and after loading | |
| The position of bearing outer ring raceway curvature center before/after the force, respectively, because the bearing outer ring is fixed | |
| The position of the center of curvature of the inner ring raceway of the bearing before/after the force, respectively | |
| The radial deformation, axial deformation, and angular deformation caused by the force and torque, respectively | |
| The radius of the inner ring raceway curvature center track | |
| The contact deformation and total deformation of the inner and outer channel of the ball bearing, respectively | |
| The additional displacement caused by localized bearing failure | |
| The distance between the initial inner and outer ring channel curvature centers | |
| The Hertzian contact stiffness | |
| The Heaviside function | |
| The component of the nonlinear support force generated by angular contact ball bearings in three directions | |
| The diameter and depth of the inner and outer ring fault areas are represented | |
| The actual depths at which the rolling element of the bearing falls into the inner and outer rings of the bearing | |
| Half of the center angles corresponding to the inner and outer fault areas | |
| The rotation angles of the center of the damaged area in the inner and outer rings | |
| The radius of the rolling element | |
| The rotational speed of the rolling element | |
| Bending stiffness of the main and driven shafts | |
| Torsional stiffness of driven shafts and driven shafts | |
| Bending damping of main and driven shafts | |
| Torsional damping of the main and driven shafts | |
| Damping in the direction of the bearing | |
| Nonlinear support force in the direction of the bearing |
References
- Li, Y.; Yuan, S.; Wu, W.; Liu, K.; Lian, C.; Song, X. Vibration Analysis of Two-Stage Helical Gear Transmission with Cracked Fault Based on an Improved Mesh Stiffness Model. Machines 2022, 10, 1052. [Google Scholar] [CrossRef]
- Wu, G.; Wu, H.; Li, D. Review of Automotive Transmission Gear Rattle. J. Tongji Univ. (Nat. Sci. Ed.) 2016, 44, 276–285. (In English) [Google Scholar]
- Chen, X.F.; Li, J.M.; Cheng, H.; He, Z.J. Research and Development of Condition Monitoring and Fault Diagnosis Technology for Wind Turbines. J. Mech. Eng. 2011, 47, 45–52. (In Chinese) [Google Scholar] [CrossRef]
- Hu, Z.; Tang, J.; Zhong, J.; Chen, S.; Yan, H. Effects of tooth profile modification on dynamic responses of a high speed gear-rotor-bearing system. Mech. Syst. Signal Process. 2016, 76, 294–318. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, W.; Liu, W. Frequency and vibration characteristics of high-speed gear-rotor-bearing system with tooth root crack considering compound dynamic backlash. Shock. Vib. 2019, 2019, 1854263. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Lin, J.Y. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics. J. Mech. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of spur gear dynamics and estimation of fault growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; Chen, Y. Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech. Mach. Theory 2015, 92, 447–463. [Google Scholar] [CrossRef]
- Ma, H.; Song, R.; Pang, X.; Wen, B. Time-varying mesh stiffness calculation of cracked spur gears. Eng. Fail. Anal. 2014, 44, 179–194. [Google Scholar] [CrossRef]
- Huangfu, Y.F.; Chen, K.K.; Ma, H.; Che, L.; Li, Z.; Wen, B. Deformation and meshing stiffness analysis of cracked helical gear pairs. Eng. Fail. Anal. 2019, 95, 30–46. [Google Scholar] [CrossRef]
- Huangfu, Y.F.; Chen, K.K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. Meshing and dynamic characteristics analysis of spalled gear systems, A theoretical and experimental study. Mech. Syst. Signal Process. 2020, 139, 106640. [Google Scholar] [CrossRef]
- Choy, F.K.; Ruan, Y.F.; Tu, R.K.; Zakrajsek, J.J.; Townsend, D.P. Modal analysis of multistage gear systems coupled with gearbox vibrations. J. Mech. Des. 1992, 114, 486–497. [Google Scholar] [CrossRef]
- Howard, I.; Jia, S.; Wang, J. The dynamic modelling of a spur gear in mesh including friction and a crack. Mech. Syst. Signal Process. 2001, 15, 831–853. [Google Scholar] [CrossRef]
- Jia, S.; Howard, I. Comparison of localised spalling and crack damage from dynamic modelling of spur gear vibrations. Mech. Syst. Signal Process. 2006, 20, 332–349. [Google Scholar] [CrossRef]
- Ma, H.; Li, Z.; Feng, M. Time-varying mesh stiffness calculation of spur gears with spalling defect. Eng. Fail. Anal. 2016, 66, 166–176. [Google Scholar] [CrossRef]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; He, Z. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Eng. Fail. Anal. 2014, 42, 157–177. [Google Scholar] [CrossRef]
- Han, L.; Qi, H. Dynamics responses analysis in frequency domain of helical gear pair under multi-fault conditions. J. Mech. Sci. Technol. 2019, 33, 5117–5127. [Google Scholar] [CrossRef]
- Ma, H.; Song, R.; Pang, X.; Wen, B. Fault feature analysis of a cracked gear coupled rotor system. Math. Probl. Eng. 2014, 2014, 832192. [Google Scholar] [CrossRef]
- Cui, L.; Cai, C. Nonlinear dynamics analysis of a gear-shaft-bearing system with breathing crack and tooth wear faults. Open Mech. Eng. J. 2015, 9, 483–491. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, X.; Li, T.; Zhang, H. Analysis of coupling fault correlation and nonlinear vibration of multi-stage gear transmission system. J. Vibroeng. 2021, 23, 114–126. [Google Scholar] [CrossRef]
- Cao, P.; Li, Q.; Feng, K.; Qin, Y. Dynamic modeling of spur gear transmission system with evolutive coupling fault of fatigue crack and wear. Eng. Fail. Anal. 2024, 156, 107820. [Google Scholar] [CrossRef]
- Dai, P.; Wang, J.; Yan, S.; Jiang, B.; Wang, F.; Niu, L. Effects of localized defects of gear-shaft-bearing coupling system on the meshing stiffness of gear pairs. J. Vib. Eng. Technol. 2022, 10, 1153–1173. [Google Scholar] [CrossRef]
- Patel, V.N.; Tandon, N.; Pandey, R.K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races. J. Tribol. 2010, 132, 041101. [Google Scholar] [CrossRef]
- Patel, U.K.A.; Upadhyay, S.H. Nonlinear dynamic response of cylindrical roller bearing–rotor system with 9 degree of freedom model having a combined localized defect at inner–outer races of bearing. Tribol. Trans. 2017, 60, 284–299. [Google Scholar] [CrossRef]
- Jafari, S.M.; Rohani, R.; Rahi, A. Experimental and numerical study of an angular contact ball bearing vibration response with spall defect on the outer race. Arch. Appl. Mech. 2020, 90, 2487–2511. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Lu, W.; Yang, Z. Research on time-varying stiffness of bearing based on local defect and varying compliance coupling. Measurement 2019, 143, 155–179. [Google Scholar] [CrossRef]
- Ogundare, A.A.; Ojolo, S.J.; Adelaja, A.; Mba, D.; Zhou, L.; Li, X. Study of the Vibration Characteristics of SA 330 Helicopter Planetary Main Gearbox. J. Appl. Comput. Mech. 2023, 9, 1093–1106. [Google Scholar]
- Li, C.F.; Zhou, S.H.; Liu, J. Coupled lateral-torsional-axial vibrations of a helical gear-rotor-bearing system. Acta Mech. Sin. 2014, 30, 746–761. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. A review of gear fault diagnosis using various condition indicators. Procedia Eng. 2016, 144, 253–263. [Google Scholar] [CrossRef]
- Reuben, L.C.K.; Mba, D. Bearing time-to-failure estimation using spectral analysis features. Struct. Health Monit. 2014, 13, 219–230. [Google Scholar] [CrossRef]






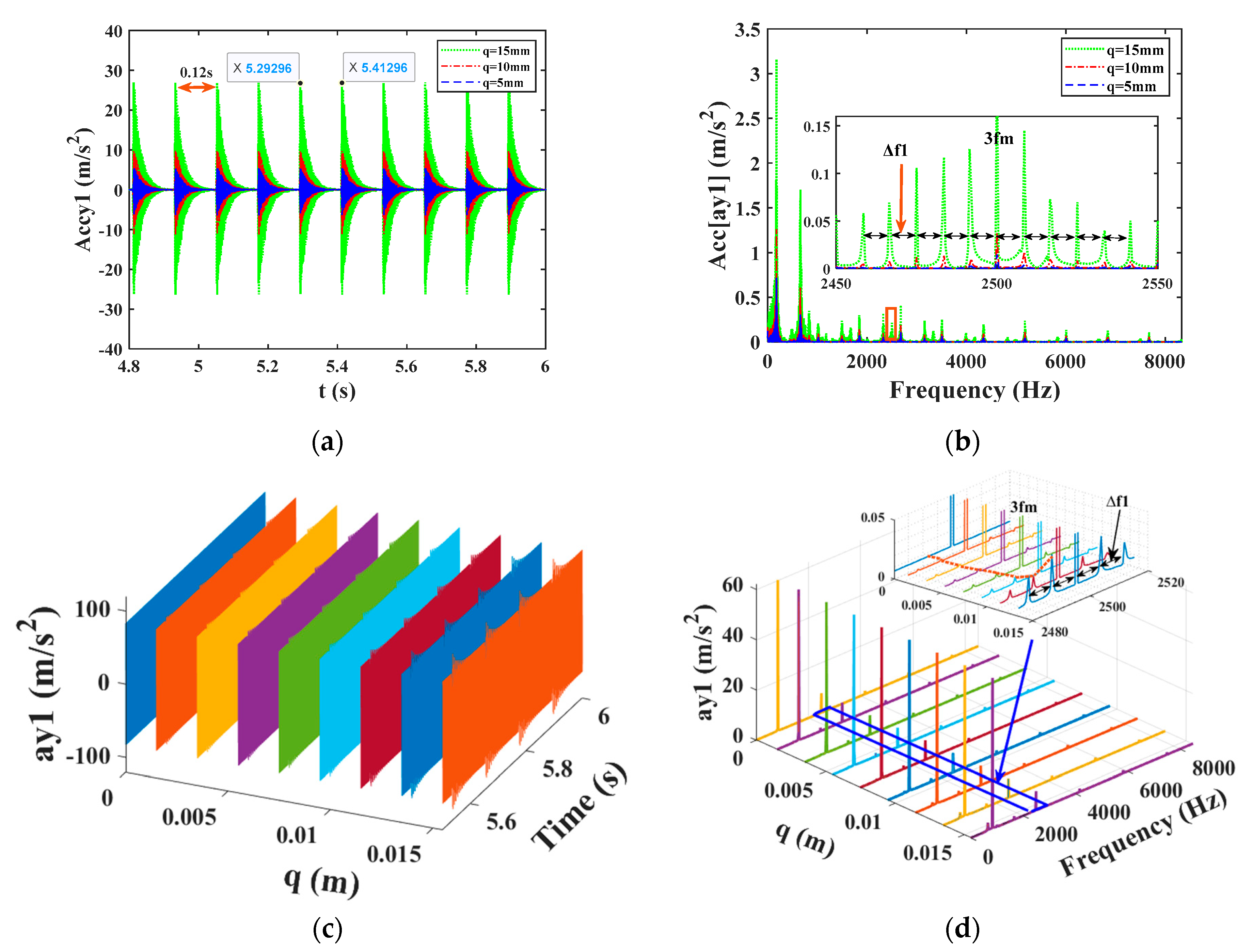
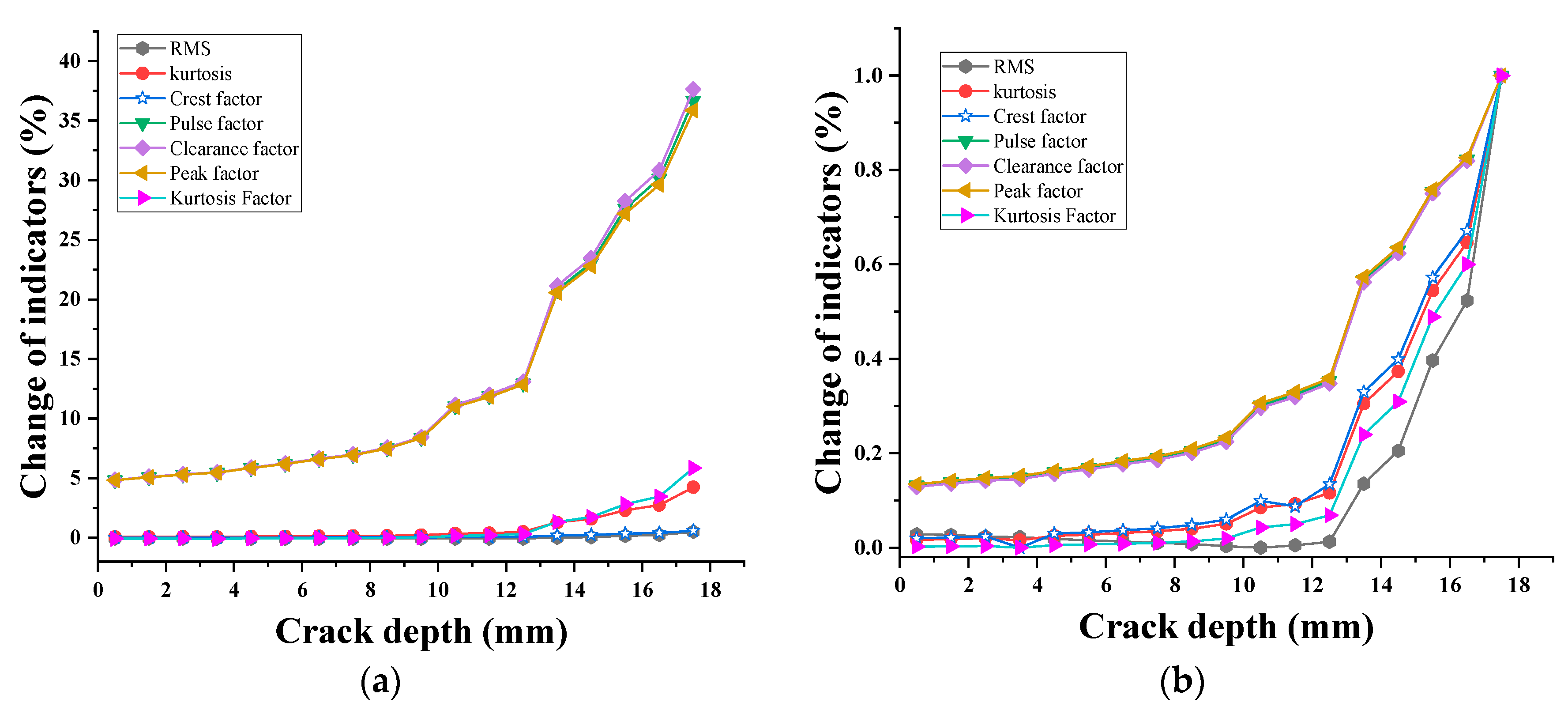
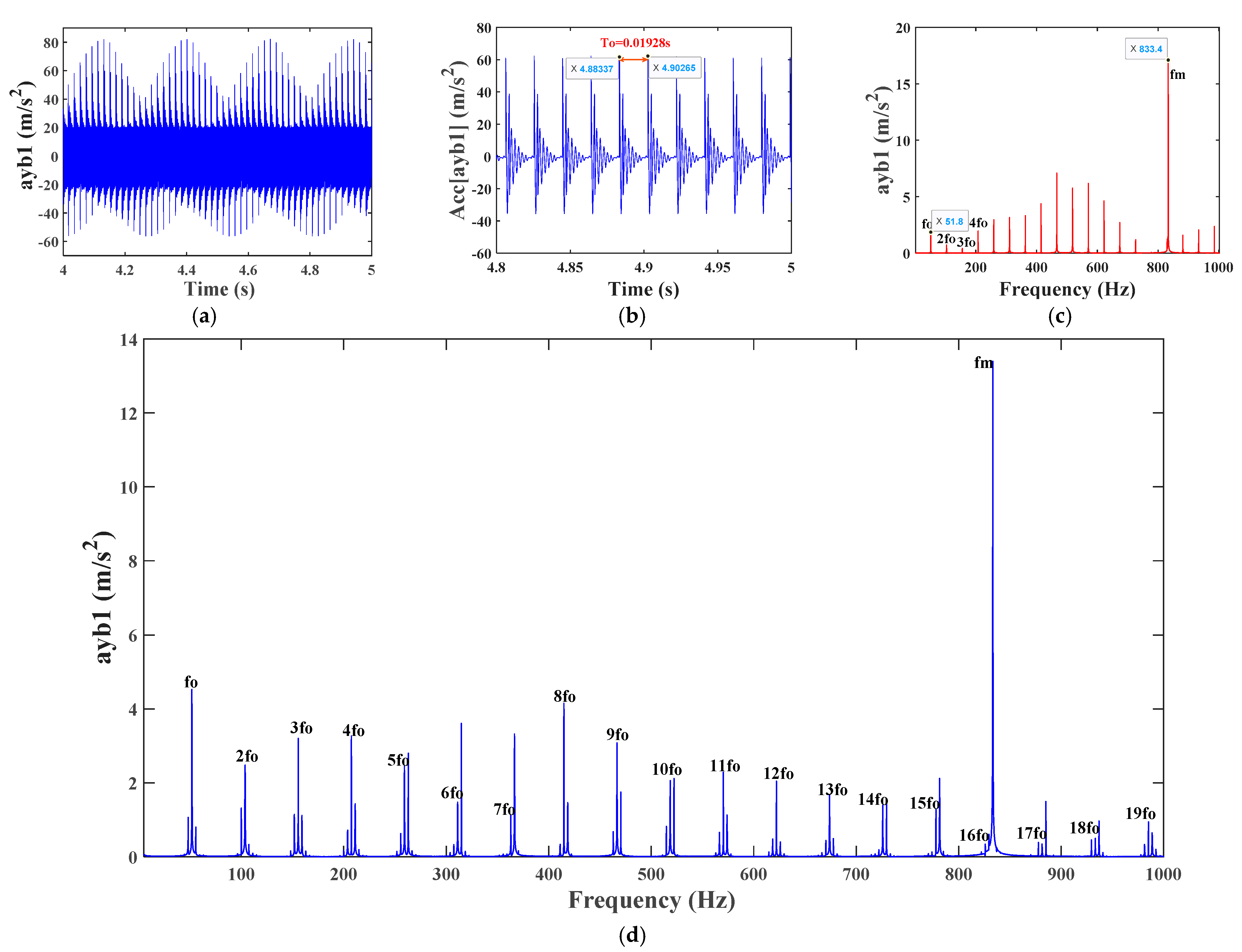
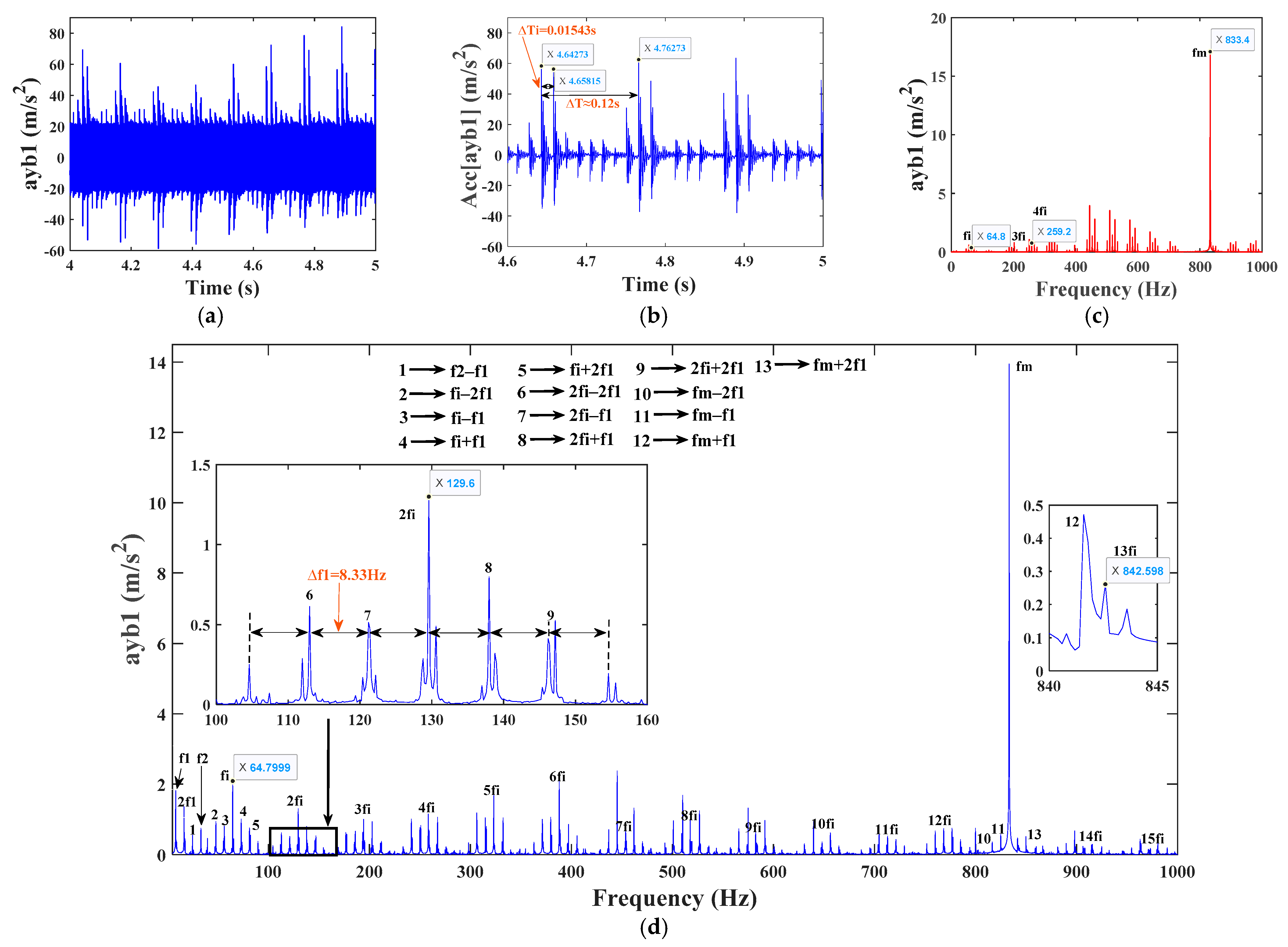
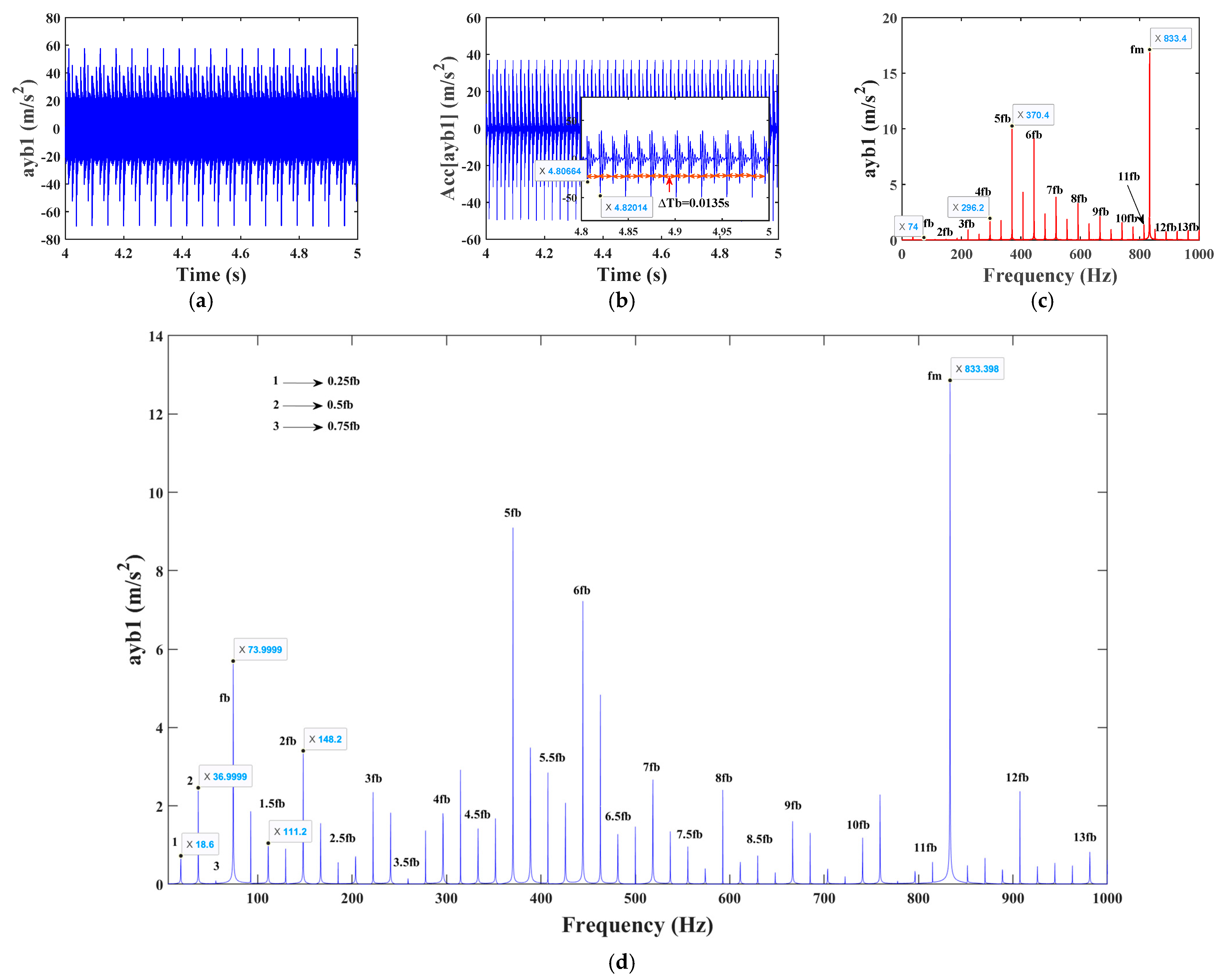
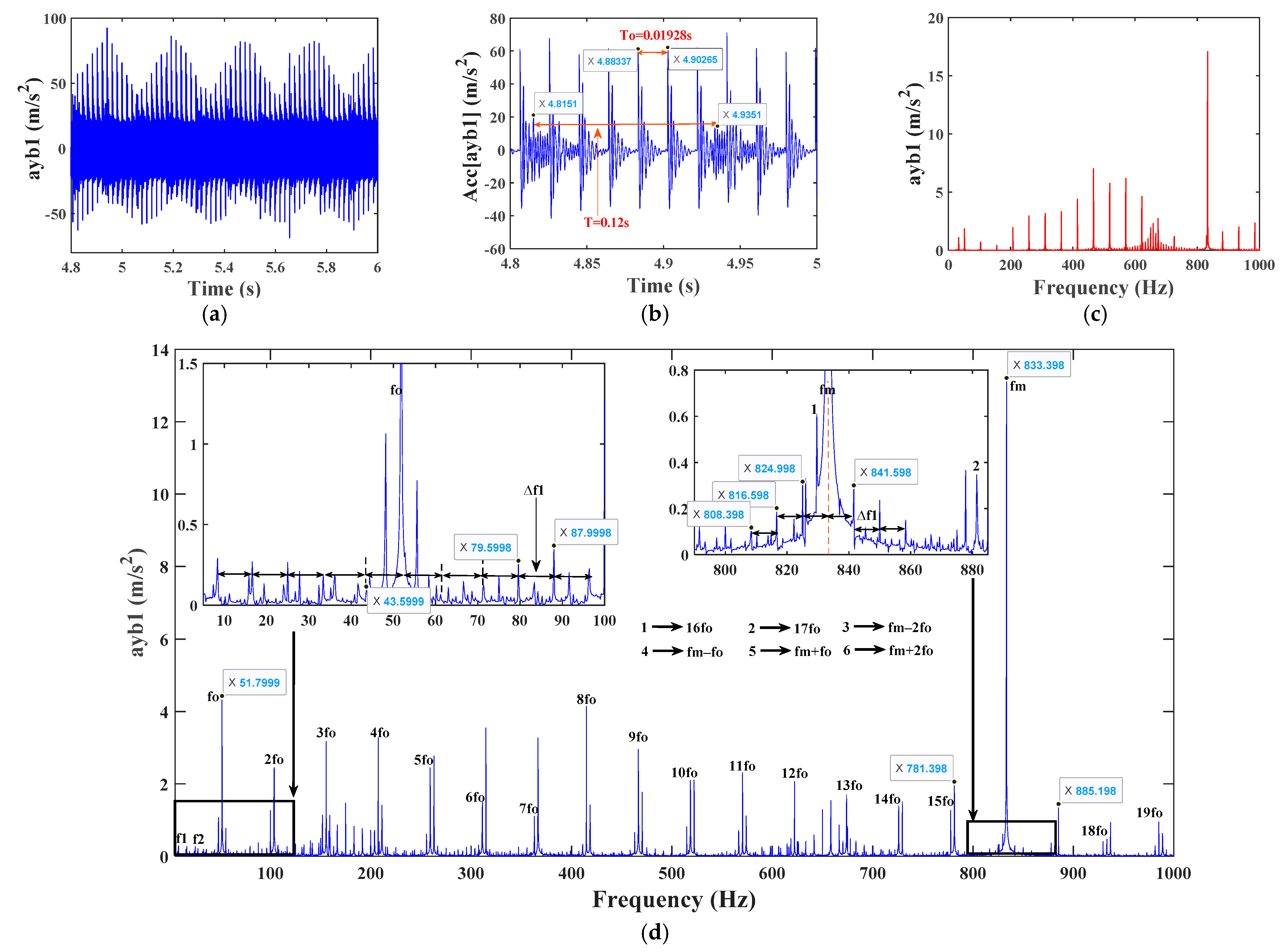
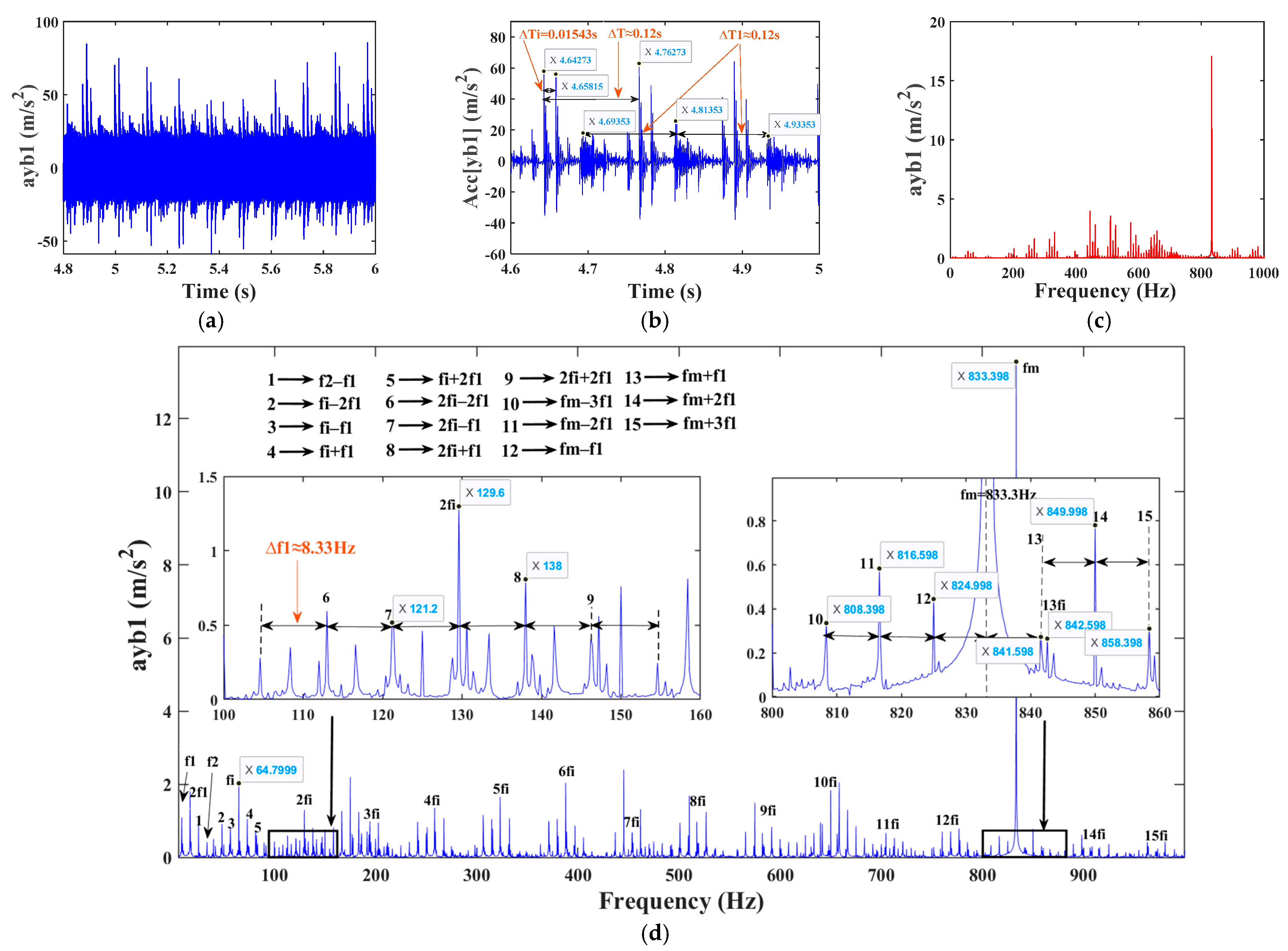
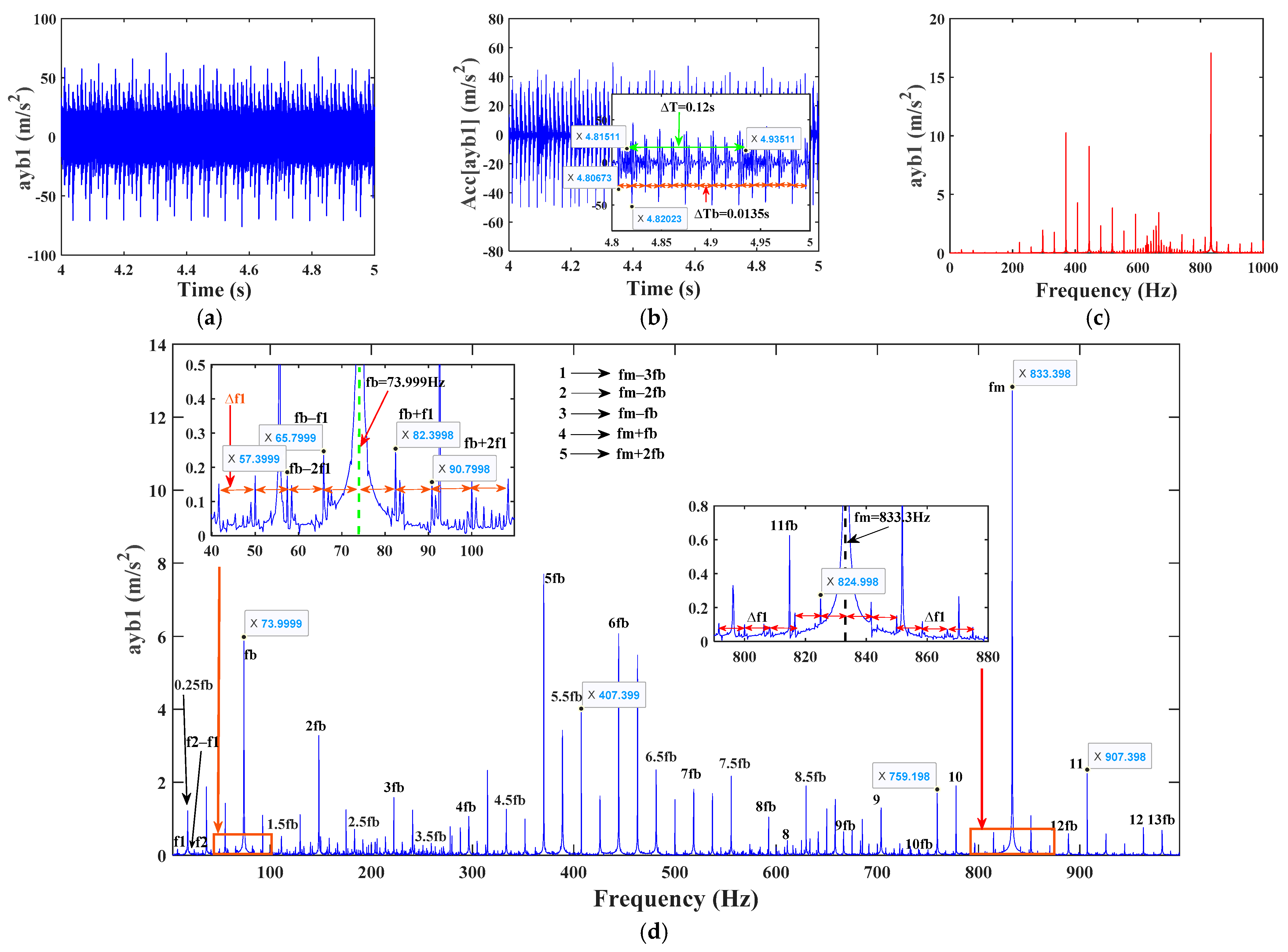
| Parameter Name | Parameter Symbol | Value |
|---|---|---|
| Number of teeth | data | |
| Pressure angle | /(°) | 20 |
| Spiral angle | /(°) | 15 |
| modulus | 8 | |
| Tooth width | /(mm) | 120 |
| Poisson’s ratio | 0.25 | |
| modulus of elasticity | /(Gpa) | 207 |
| Parameter Name | Parameter Symbol | Value |
|---|---|---|
| Driving/Driven gear mass | /(kg) | 668, 141 |
| Rotational inertia of driving/driven gear | m2) | 44.35, 0.21 |
| Meshing damping ratio | 0.1 | |
| Error mean/magnitude value | /(m) | 10−5 |
| Lateral clearance | /(um) | 10 |
| Parameter Name | Parameter Symbol | Value |
|---|---|---|
| Shaft I and II bending stiffness | m−1) | 6 × 108, 6 × 108, 1.5 × 108, 1.5 × 108 |
| Bending damping ratio | 0.07 | |
| Shaft I and II torsional stiffness | m−1) | 8 × 108, 1.5 × 108 |
| Torsional damping ratio | 0.07 | |
| Moment of inertia of the driving and load device | m2) | 20, 5 |
| Input and output revolutions | min−1) | 500, 2000 |
| Parameters | Bearing 1/Bearing 2 | Bearing 3/Bearing 4 |
|---|---|---|
| (r/min) | 500 | 2000 |
| /Hz | 8.33 | 33.33 |
| /Hz | 51.85 | 148.15 |
| /Hz | 64.81 | 185.19 |
| /Hz | 74.07 | 296.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, S.; Sun, H. Study on the Vibration Characteristics of the Helical Gear-Rotor-Bearing Coupling System of a Wind Turbine with Composite Faults. Mathematics 2024, 12, 1410. https://doi.org/10.3390/math12091410
Zhang H, Li S, Sun H. Study on the Vibration Characteristics of the Helical Gear-Rotor-Bearing Coupling System of a Wind Turbine with Composite Faults. Mathematics. 2024; 12(9):1410. https://doi.org/10.3390/math12091410
Chicago/Turabian StyleZhang, Hongyuan, Shuo Li, and Hongyun Sun. 2024. "Study on the Vibration Characteristics of the Helical Gear-Rotor-Bearing Coupling System of a Wind Turbine with Composite Faults" Mathematics 12, no. 9: 1410. https://doi.org/10.3390/math12091410
APA StyleZhang, H., Li, S., & Sun, H. (2024). Study on the Vibration Characteristics of the Helical Gear-Rotor-Bearing Coupling System of a Wind Turbine with Composite Faults. Mathematics, 12(9), 1410. https://doi.org/10.3390/math12091410





