The Multi-Soliton Solutions for the (2+1)-Dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada Equation
Abstract
1. Introduction
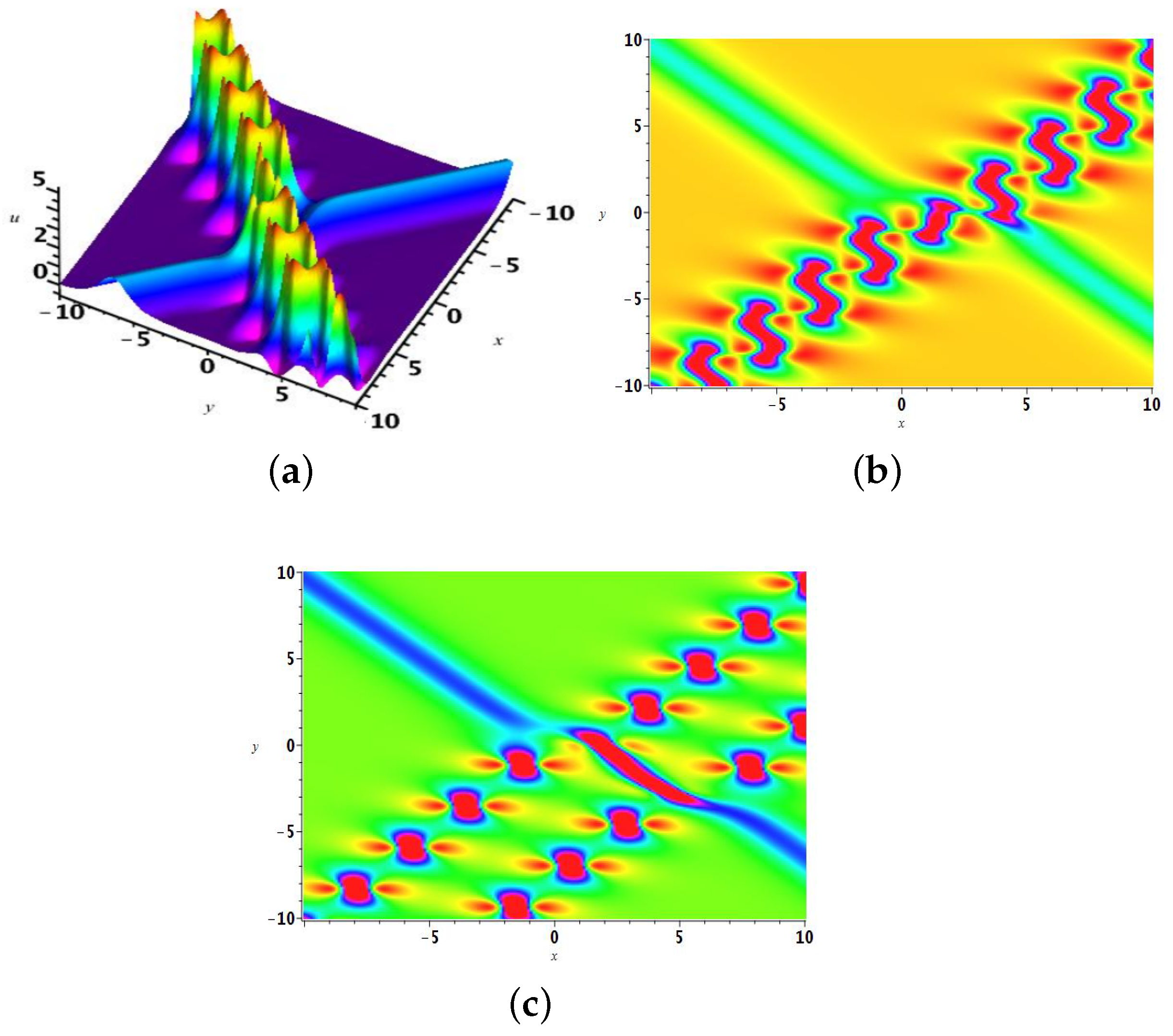
2. The Multi-Soliton Solutions and Their Hybrid Structures
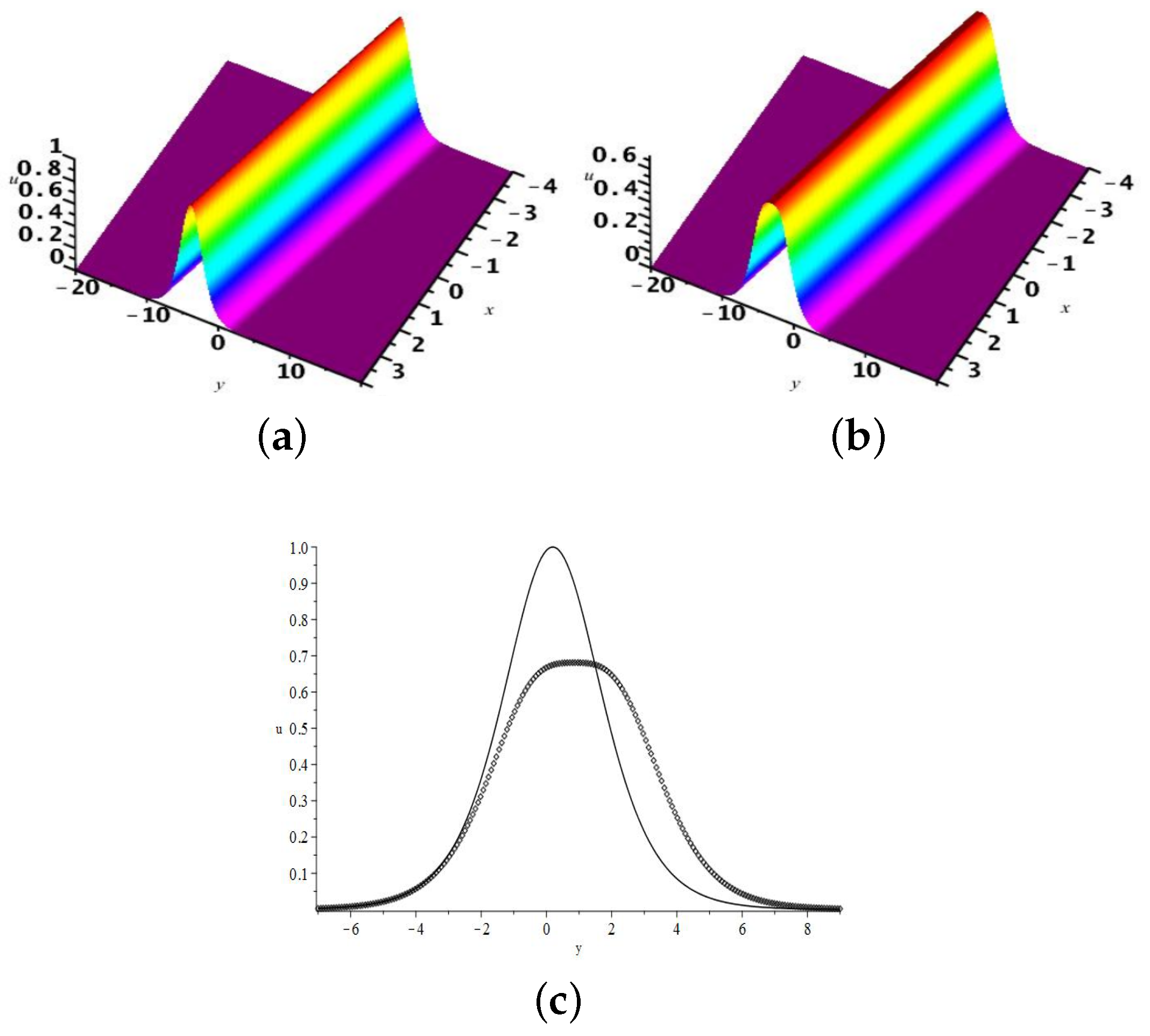
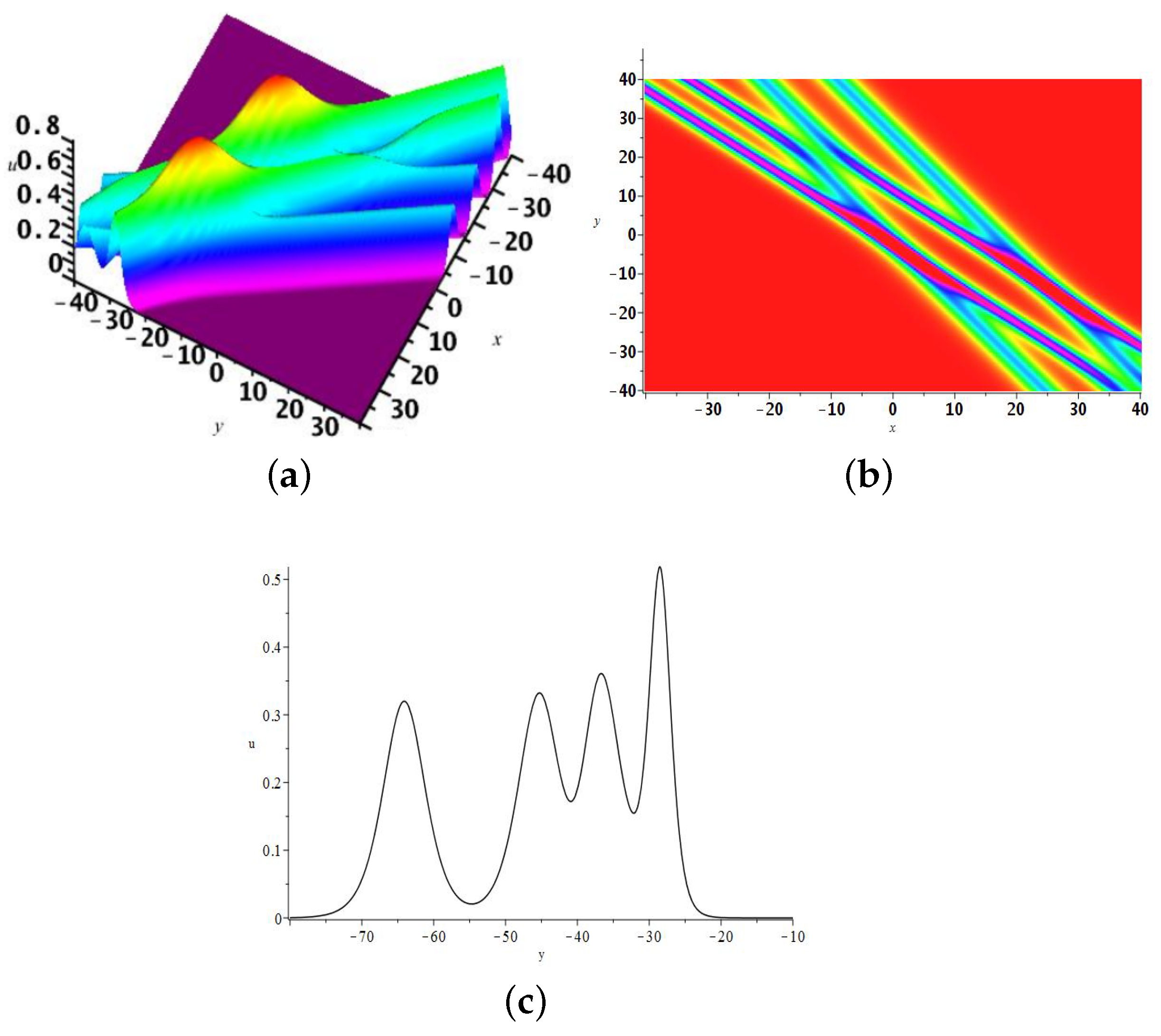
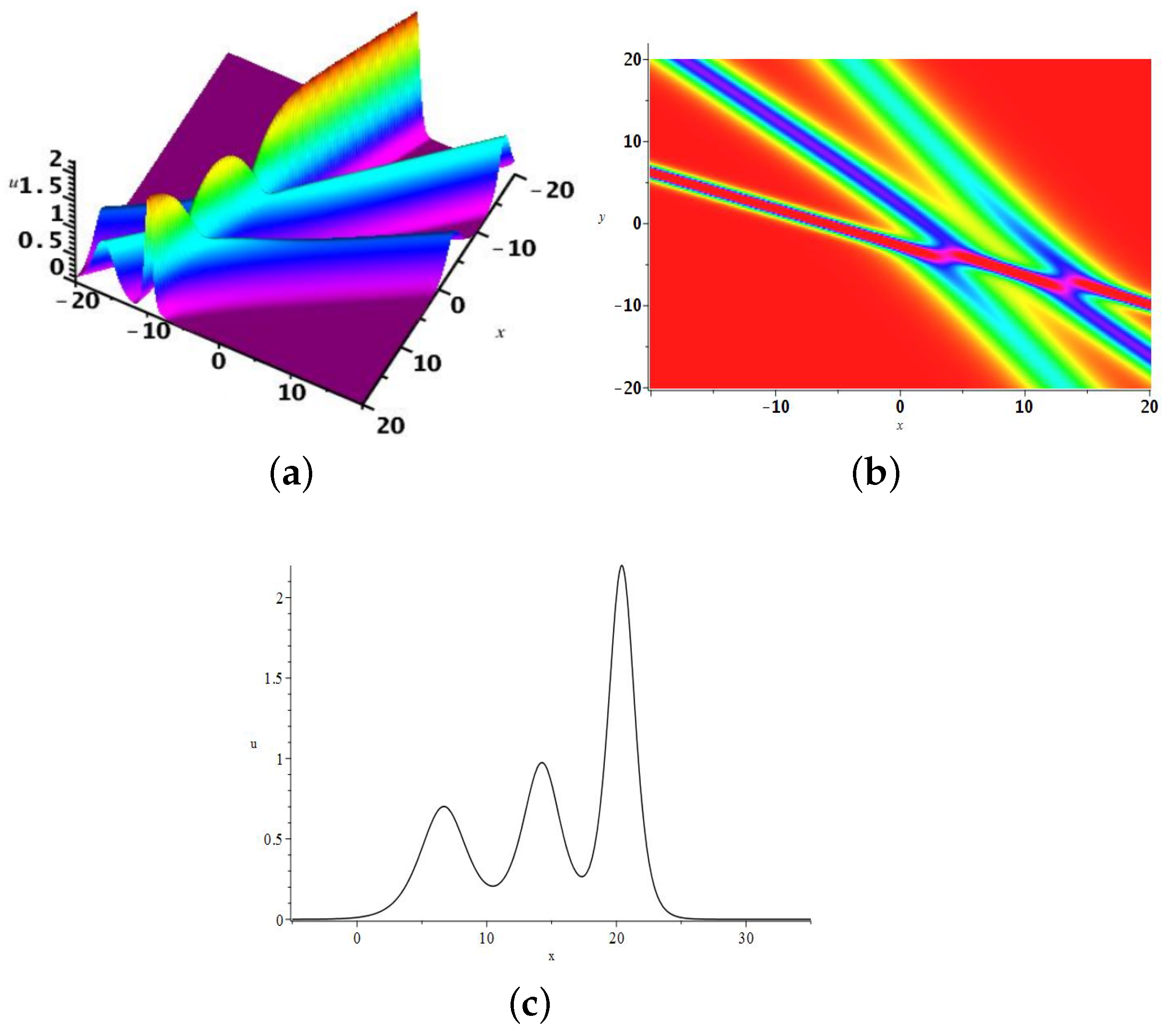
2.1. The One-Soliton Solution
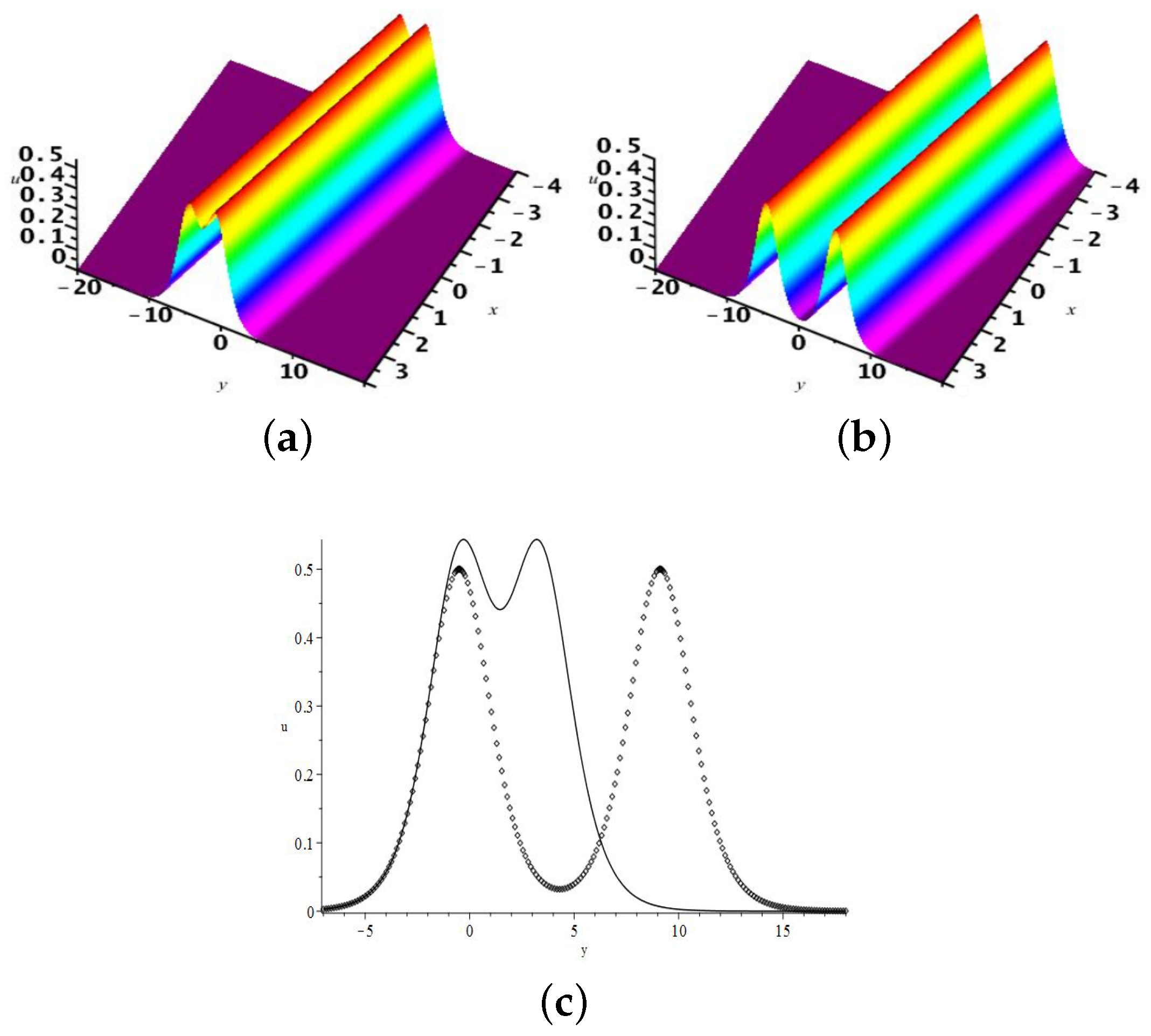
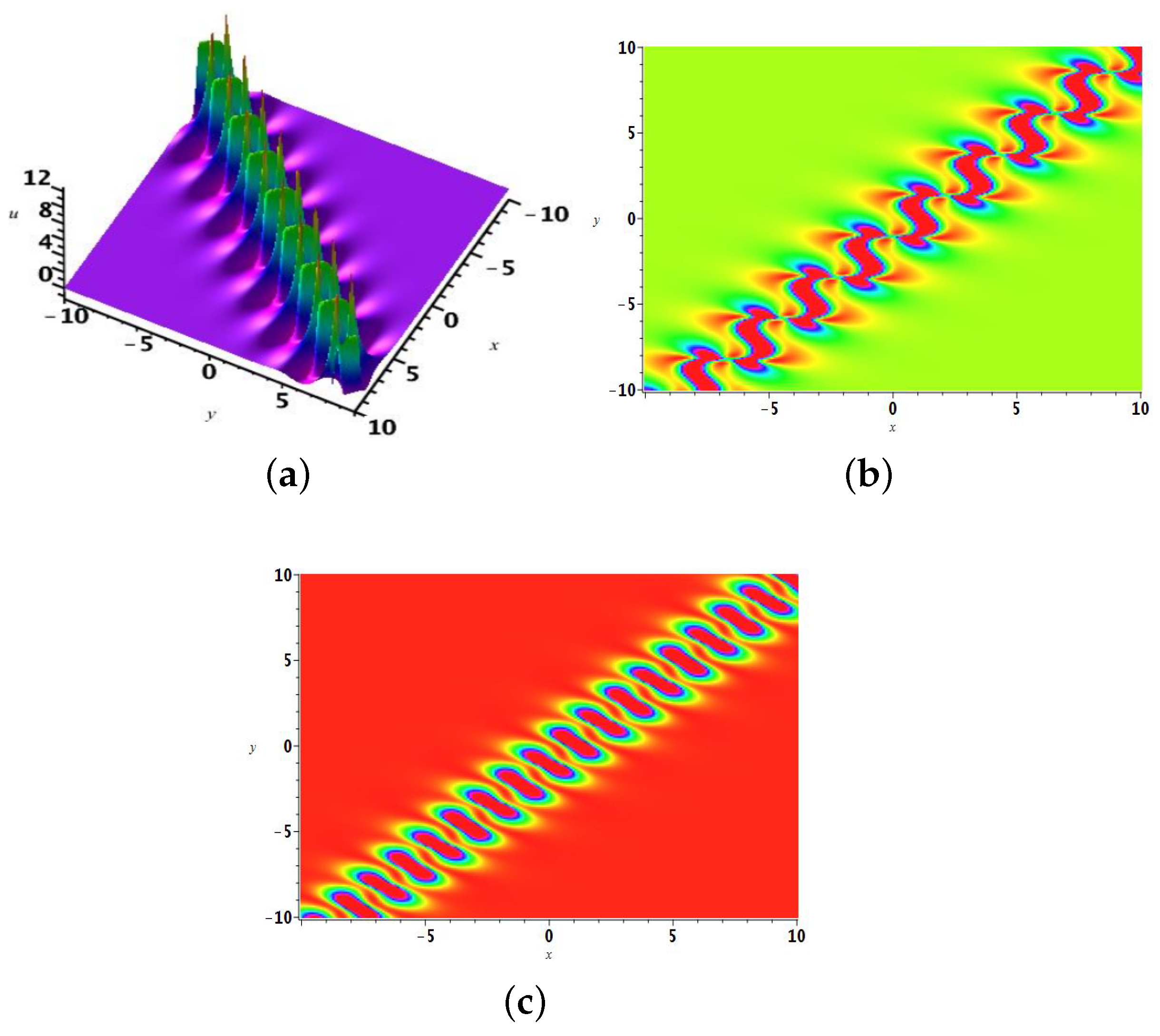
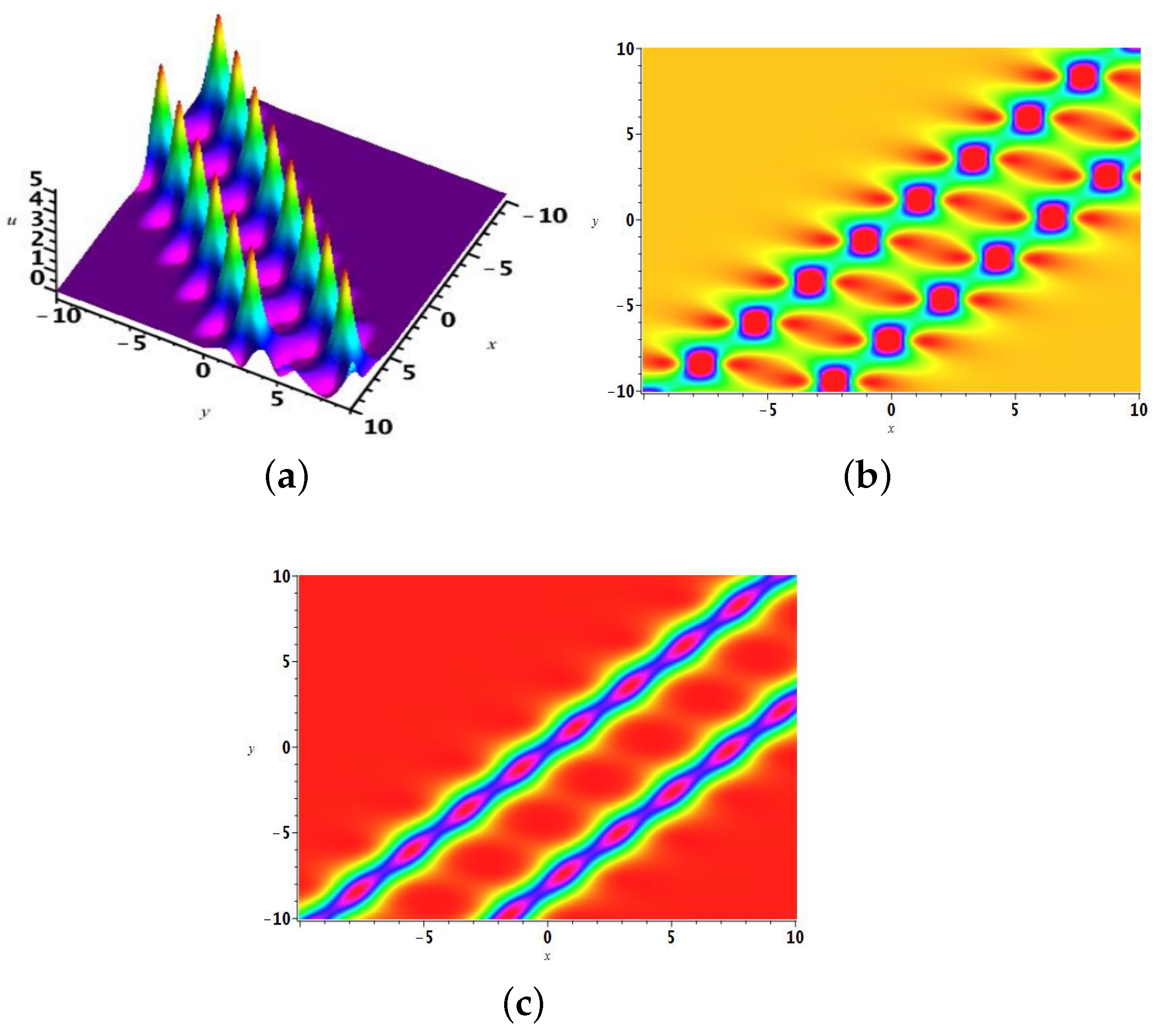
2.2. The Two-Soliton Solution
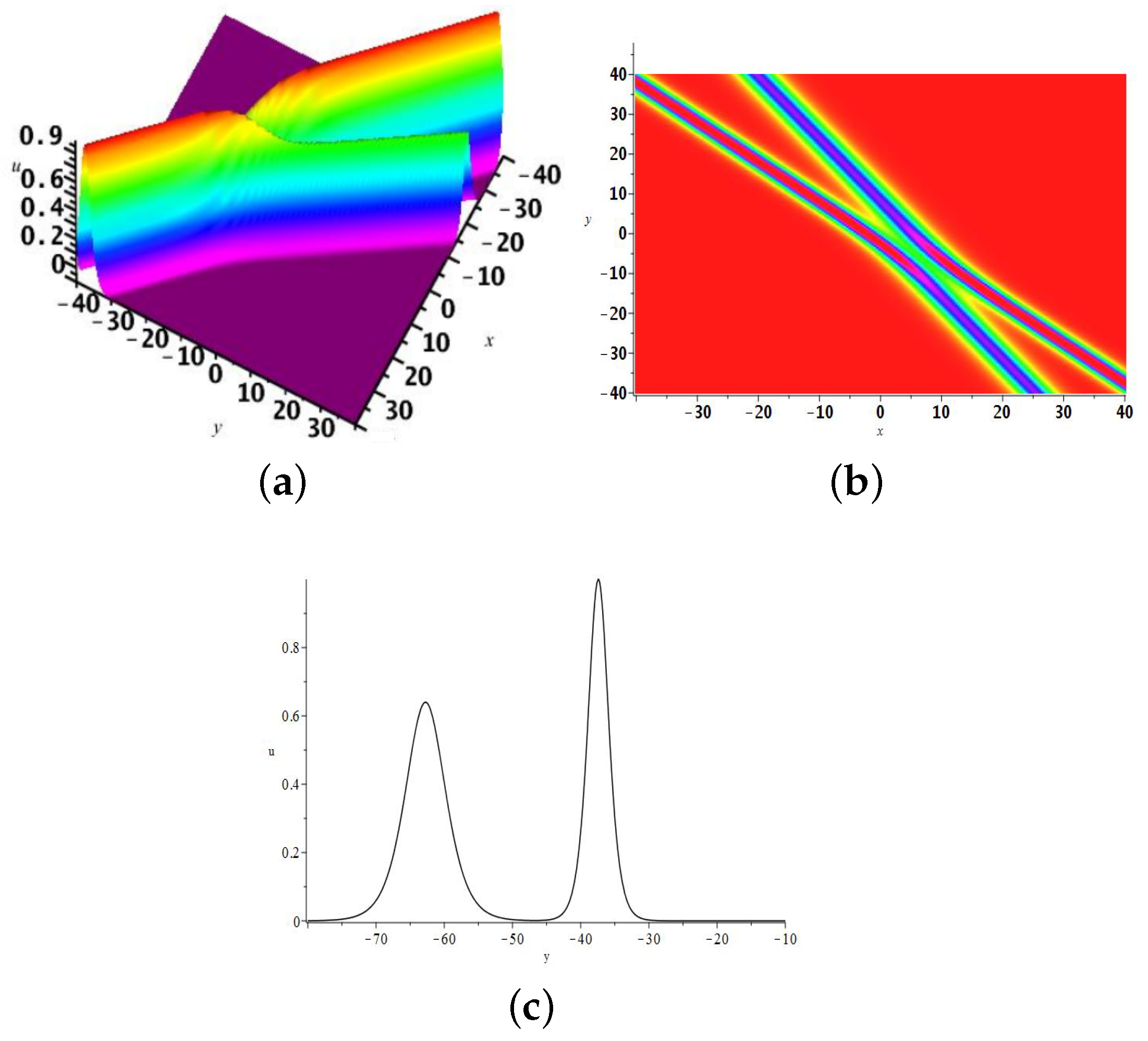
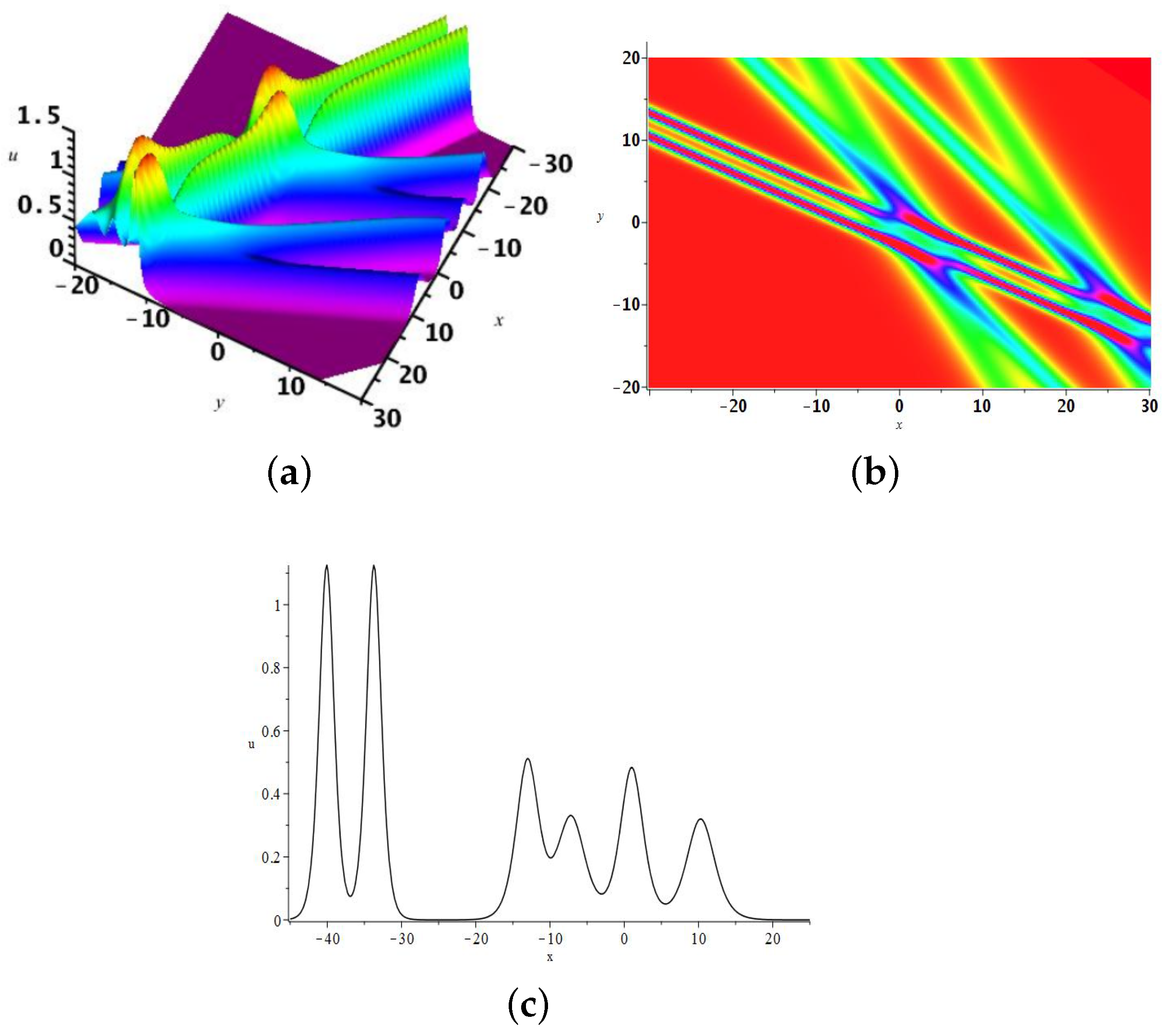
2.3. The 3-Soliton Solution
3. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Konopelchenko, B.G.; Dubrovsky, V.G. Some new integrable nonlinear evolution equations in 2+1 dimensions. Phys. Lett. A 1984, 102, 15–17. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Y.S. Constraints of the 2+1 dimensional integrable soliton systems. J. Phys. A Math. Gen. 1992, 25, 419–431. [Google Scholar] [CrossRef]
- Hu, X.B.; Li, Y. Some results on the Caudrey-Dodd-Gibbon-Kotera- Sawada equation. J. Phys. A Math. Gen. 1991, 24, 3205–3212. [Google Scholar] [CrossRef]
- Cao, C.W.; Wu, Y.T.; Geng, X.G. On quasi-periodic solutions of the 2+1 dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada equation. Phys. Lett. A 1999, 256, 59–65. [Google Scholar] [CrossRef]
- Pu, J.C.; Chen, Y. Double and triple-pole solutions for the third-order flow equation of the Kaup-Newell system with zero/nonzero boundary conditions. arXiv 2022, arXiv:2105.06098v3. [Google Scholar] [CrossRef]
- Tang, Y.N.; Tao, S.Q.; Guan, Q. Lump solitons and the interaction phenomena of them for two classes of nonlinear evolution equations. Comput. Math. Appl. 2016, 72, 2334–2342. [Google Scholar] [CrossRef]
- Peng, W.Q.; Tian, S.F.; Zou, L.; Zhang, T.T. Characteristics of the solitary waves and lump waves with interaction phenomena in a (2+1)-dimensional generalized Caudrey-Dodd-Gibbon-Kotera-Sawada equation. Nonlinear Dyn. 2018, 93, 1841–1851. [Google Scholar] [CrossRef]
- Fang, T.; Gao, C.N.; Wang, H.; Wang, Y.H. Lumpt-ype solution, rogue wave, fusion and fission phenomena for the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada equation. Mod. Phys. Lett. B 2019, 33, 1950198. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Albishari, M.; Zheng, F.C.; Lan, Z.Z. Generalized lump solutions, classical lump solutions and rogue waves of the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada-like equation. Appl. Math. Comput. 2021, 403, 126201. [Google Scholar] [CrossRef]
- Ma, H.C.; Yue, S.P.; Deng, A.P. Resonance Y-shape solitons and mixed solutions for a (2+1)-dimensional generalized Caudrey-Dodd-Gibbon-Kotera -Sawada equation in fluid mechanics. Nonlinear Dyn. 2022, 108, 505–519. [Google Scholar] [CrossRef]
- Ma, H.C.; Yue, S.P.; Deng, A.P. Nonlinear superposition between lump and other waves of the (2+1)-dimensional generalized Caudrey-Dodd-Gibbon -Kotera-Sawada equation in fluid dynamics. Nonlinear Dyn. 2022, 109, 1969–1983. [Google Scholar] [CrossRef]
- Zhuang, J.H.; Liu, Y.Q.; Zhuang, P. Variety interaction solutions comprising lump solitons for the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera -Sawada equation. AIMS Math. 2021, 6, 5370–5386. [Google Scholar] [CrossRef]
- Liu, F.Y.; Gao, Y.T.; Yu, X.; Hu, L.; Wu, X.H. Hybrid solutions for the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-Kotera-Sawada equation in fluid mechanics. Chaos Soliton. Fract. 2021, 152, 111355. [Google Scholar] [CrossRef]
- Wang, T.T.; Liu, X.Q.; Yu, J.Q. Symmetries, exact solutions and conservation laws of Caudrey-Dodd-Gibbon-Kotera-Sawada equation. Chin. J. Quant. Elect. 2011, 28, 385–390. [Google Scholar]
- Li, L.F.; Xie, Y.Y.; Wang, M.C. Characteristics of the interaction behavior between solitons in (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada equation. Results Phys. 2020, 19, 103697. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the KdV equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Zheng, Y.B.; Ma, W.X.; Shao, Y. Two binary Darboux transformations for the KdV hierarchy with self-consistent sources. J. Math. Phys. 2001, 42, 2113–2128. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ramini, A.; Segur, H. A connection between nonlinear evolution equations and ordinary differential equations of P-type. J. Math. Phys. 1980, 21, 1006–1015. [Google Scholar] [CrossRef]
- Burdik, C.; Shaikhova, G.; Rakhimzhanov, B. Soliton solutions and traveling wave solutions for the two-dimensional generalized nonlinear Schrödinger equations. Eur. Phys. J. Plus 2021, 136, 1095. [Google Scholar] [CrossRef]
- Mandal, U.K.; Malik, S.; Kumar, S.; Das, A. A generalized (2+1)-dimensional Hirota bilinear equation: Integrability, solitons and invariant solutions. Nonlinear Dyn. 2023, 111, 4593–4611. [Google Scholar] [CrossRef]
- Qin, C.Y.; Zhang, R.F.; Li, Y.H. Various exact solutions of the (4+1)-dimensional Boiti–Leon–Manna–Pempinelli-like equation by using bilinear neural network method. Chaos Soliton. Fract. 2024, 187, 115438. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Cherraf, A.; Vadyala, S.R. The interference wave and the bright and dark soliton for two integro-differential equation by using BNNM. Nonlinear Dyn. 2023, 111, 8637–8646. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Xu, T.; Tian, B. Bright N-soliton solutions innterms of the triple Wronskia for the coupled nonlinear Schödinger equations in optical fibers. J. Phys. A Math. Theor. 2010, 43, 245205. [Google Scholar] [CrossRef]
- Zhang, C.C.; Chen, A.H. Bilinear form and new multi-soliton solutions of the classical Boussinesq-Burgers system. Appl. Math. Lett. 2016, 58, 133–139. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Chen, Y. A new form of general soliton solutions and multiple zeros solutions for a higher-order Kaup-Newell equation. J. Math. Phys. 2021, 62, 123501. [Google Scholar] [CrossRef]
- Li, Y.; Yao, R.X.; Lou, S.Y. An extended Hirota bilinear method and new wave structures of (2+1)-dimensional Sawada-Kotera equation. Appl. Math. Lett. 2023, 145, 1087608. [Google Scholar] [CrossRef]
- Dai, Z.D.; Liu, Z.J.; Li, D.L. Exact periodic solitary-wave solution for KdV equation. Chin. Phys. Lett. 2008, 25, 1531–1533. [Google Scholar]
- Wang, C.J.; Fang, H.; Tang, X.X. State transition of lump-type waves for the (2+1)-dimensional generalized KdV equation. Nonlinear Dyn. 2019, 95, 2943–2961. [Google Scholar] [CrossRef]
- Wu, H.L.; Wu, H.Y.; Zhu, Q.Y.; Fei, J.X.; Ma, Z.Y. Soliton, breather and lump molecules in the (2+1)-dimensional B-type Kadomtsev-Petviashvili-Korteweg de-Vries equation. J. Appl. Anal. Comput. 2022, 12, 230–244. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Fei, J.X.; Cao, W.P. The N-soliton solutions of the (2+1)-dimensional Hirota–Satsuma–Ito equation. Results Phys. 2022, 43, 106090. [Google Scholar] [CrossRef]
- Camassa, R.; Hyman, J.M.; Luce, B.E. Nonlinear waves and solitons in physical systems. Physica D 1998, 123, 1–20. [Google Scholar] [CrossRef]
- Lou, S.Y. Soliton molecules and asymmetric solitons in three fifth order systems via velocity resonance. J. Phys. Commun. 2020, 4, 041002. [Google Scholar] [CrossRef]
- Yan, Z.W.; Lou, S.Y. Soliton molecules in Sharma-Tasso-Olver-Burgers equation. Appl. Math. Lett. 2020, 104, 106271. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.-J.; Ma, Z.-Y.; Fei, J.-X.; Wu, H.-L.; Cheng, L. The Multi-Soliton Solutions for the (2+1)-Dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada Equation. Mathematics 2025, 13, 236. https://doi.org/10.3390/math13020236
Xu L-J, Ma Z-Y, Fei J-X, Wu H-L, Cheng L. The Multi-Soliton Solutions for the (2+1)-Dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada Equation. Mathematics. 2025; 13(2):236. https://doi.org/10.3390/math13020236
Chicago/Turabian StyleXu, Li-Jun, Zheng-Yi Ma, Jin-Xi Fei, Hui-Ling Wu, and Li Cheng. 2025. "The Multi-Soliton Solutions for the (2+1)-Dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada Equation" Mathematics 13, no. 2: 236. https://doi.org/10.3390/math13020236
APA StyleXu, L.-J., Ma, Z.-Y., Fei, J.-X., Wu, H.-L., & Cheng, L. (2025). The Multi-Soliton Solutions for the (2+1)-Dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada Equation. Mathematics, 13(2), 236. https://doi.org/10.3390/math13020236