New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method
Abstract
1. Introduction
2. Literature Review
3. Method
3.1. Preliminaries
- (1)
- If E(L1) > E(L2), then L1 is bigger than L2;
- (2)
- If E(L1) = E(L2), then L1 is equal to L2.
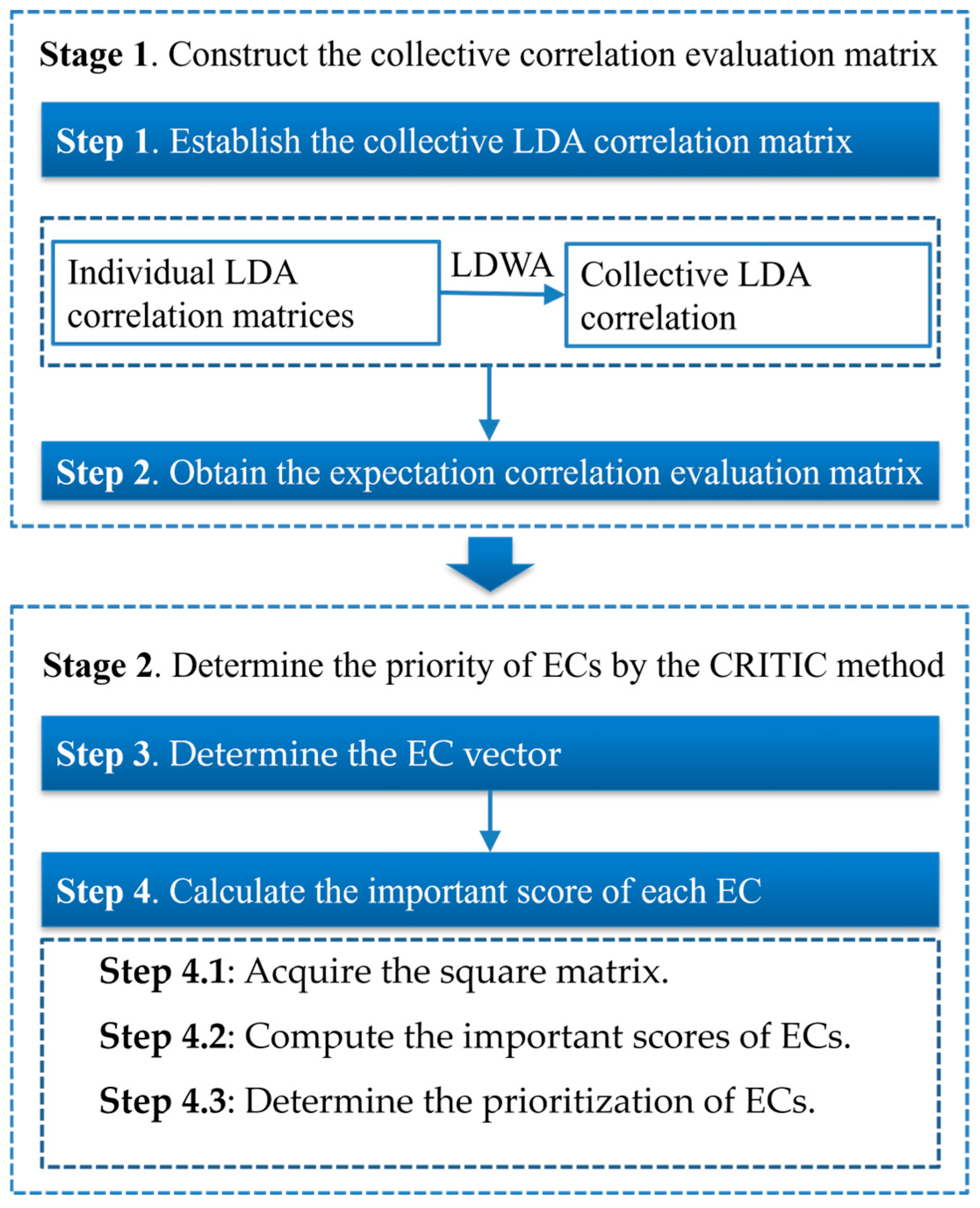
3.2. The Proposed QFD Approach
- (1)
- If rji is a beneficial criterion, then
- (2)
- If rji is a non-beneficial criterion, then
4. Findings and Discussion
4.1. Application
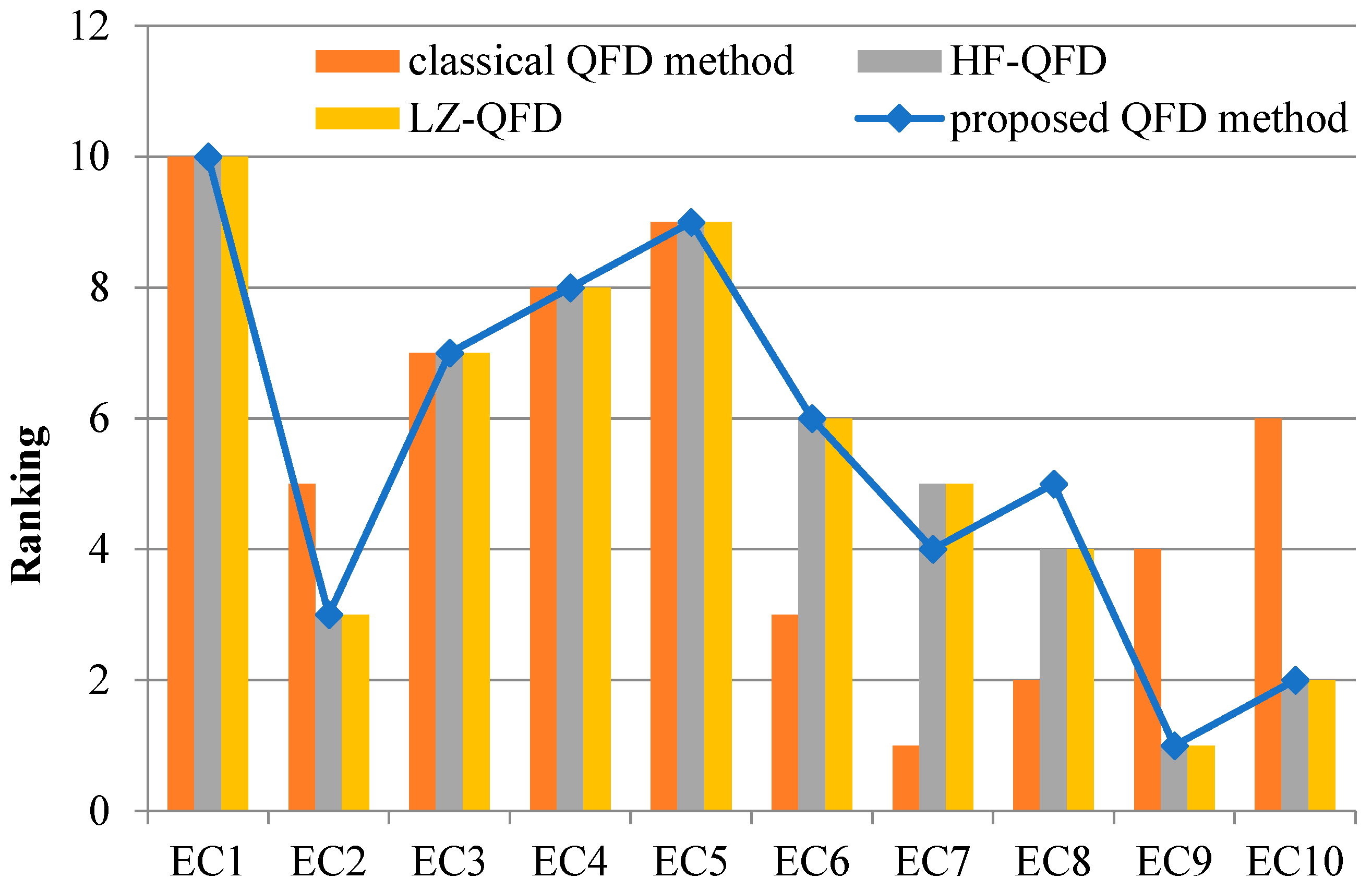
4.2. Comparative Analysis
4.3. Managerial Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mehrjerdi, Y.Z. Quality function deployment and its extensions. Int. J. Qual. Reliab. Manag. 2010, 27, 616–640. [Google Scholar] [CrossRef]
- Chan, L.K.; Wu, M.L. Quality function deployment: A literature review. Eur. J. Oper. Res. 2002, 143, 463–497. [Google Scholar]
- Song, W.; Ming, X.; Han, Y. Prioritising technical attributes in QFD under vague environment: A rough-grey relational analysis approach. Int. J. Prod. Res. 2014, 52, 5528–5545. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Chin, K.-S. Technical importance ratings in fuzzy QFD by integrating fuzzy normalization and fuzzy weighted average. Comput. Math. Appl. 2011, 62, 4207–4221. [Google Scholar] [CrossRef]
- Huang, J.; You, X.-Y.; Liu, H.-C.; Si, S.-L. New approach for quality function deployment based on proportional hesitant fuzzy linguistic term sets and prospect theory. Int. J. Prod. Res. 2019, 57, 1283–1299. [Google Scholar] [CrossRef]
- Seker, S.; Aydin, N. Fermatean fuzzy based Quality Function Deployment methodology for designing sustainable mobility hub center. Appl. Soft Comput. 2023, 134, 110001. [Google Scholar] [CrossRef]
- Erol, I.; Ar, I.M.; Peker, I.; Searcy, C. Alleviating the Impact of the barriers to circular economy adoption through blockchain: An investigation using an integrated MCDM-based QFD with hesitant fuzzy linguistic term sets. Comput. Ind. Eng. 2022, 165, 107962. [Google Scholar] [CrossRef]
- Liu, H.-C.; Wu, S.-M.; Wang, Z.-L.; Li, X.-Y. A new method for quality function deployment with extended prospect theory under hesitant linguistic environment. IEEE Trans. Eng. Manag. 2021, 68, 442–451. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A novel spherical fuzzy QFD method and its application to the linear delta robot technology development. Eng. Appl. Artif. Intell. 2020, 87, 103348. [Google Scholar] [CrossRef]
- Nisha, G.R.; Ravi, V. Implementation of Quality 4.0 framework in the electronics sector using ANP and QFD methodologies. Int. J. Qual. Reliab. Manag. 2024. [Google Scholar] [CrossRef]
- Moktadir, M.A.; Ren, J. Global semiconductor supply chain resilience challenges and mitigation strategies: A novel integrated decomposed fuzzy set Delphi, WINGS and QFD model. Int. J. Prod. Econ. 2024, 273, 109280. [Google Scholar] [CrossRef]
- Gangadhari, R.K.; Tarei, P.K.; Chand, P.; Rabiee, M.; Delen, D. Navigating the new normal: Redefining N95 respirator design with an integrated text mining and quality function deployment-based optimization model. Comput. Ind. Eng. 2024, 189, 109962. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.-C.; Zhang, J.; Shi, H.; Zhang, Q.-Z. New approach for quality function development based on cooperative game-based consensus mechanism and three-way decision method. Int. J. Prod. Econ. 2024, 276, 109380. [Google Scholar] [CrossRef]
- Gai, T.; Wu, J.; Liang, C.; Cao, M.; Zhang, Z. A quality function deployment model by social network and group decision making: Application to product design of e-commerce platforms. Eng. Appl. Artif. Intell. 2024, 133, 108509. [Google Scholar] [CrossRef]
- Hariri, A.; Domingues, P.; Sampaio, P. Integration of multi-criteria decision-making approaches adapted for quality function deployment: An analytical literature review and future research agenda. Int. J. Qual. Reliab. Manag. 2023, 40, 2326–2350. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.-C.; Shi, H.; Guo, W.; Zhu, J.-Y. New approach for quality function deployment based on social network analysis and interval 2-tuple Pythagorean fuzzy linguistic information. Comput. Ind. Eng. 2023, 183, 109554. [Google Scholar] [CrossRef]
- Finger, G.S.W.; Lima-Junior, F.R. A hesitant fuzzy linguistic QFD approach for formulating sustainable supplier development programs. Int. J. Prod. Econ. 2022, 247, 108428. [Google Scholar] [CrossRef]
- Zhang, G.; Dong, Y.; Xu, Y. Consistency and consensus measures for linguistic preference relations based on distribution assessments. Inf. Fusion 2014, 17, 46–55. [Google Scholar] [CrossRef]
- Tian, Z.P.; Xu, F.X.; Nie, R.X.; Wang, X.K.; Wang, J.Q. An adaptive consensus model for multi-criteria sorting under linguistic distribution group decision making considering decision-makers’ attitudes. Inf. Fusion 2024, 108, 102406. [Google Scholar] [CrossRef]
- Ding, X.; Chang, W.; Liao, B. A group stability-based consensus model for multi-criteria group decision-making problems with linguistic distribution assessments. J. Oper. Res. Soc. 2024. [Google Scholar] [CrossRef]
- Tian, Y.; Song, S.; Bao, S.; Zhou, D.; Wei, C. Canonical triangular interval type-2 fuzzy linguistic distribution assessment EDAS approach with its application to production supplier evaluation and ranking. Appl. Soft Comput. 2024, 154, 111309. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, T.; Tu, Y.; Zhao, Q. A group consensus reaching model balancing individual satisfaction and group fairness for distributed linguistic preference relations. Appl. Intell. 2024, 54, 12697–12724. [Google Scholar] [CrossRef]
- Jia, X.; Wang, Y.M.; Martínez, L. Enhancing reliability of failure modes and effects analysis dealing with linguistic distribution assessments: A consistency based approach. Eng. Appl. Artif. Intell. 2024, 133, 108333. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Zhu, Y.; Zhang, H. A consensus-based 360 degree feedback evaluation method with linguistic distribution assessments. Mathematics 2024, 12, 1883. [Google Scholar] [CrossRef]
- Han, Y.-J.; Cao, M.-M.; Liu, H.-C. New approach for quality function deployment based on multi-granular unbalanced linguistic information and consensus reaching process. Appl. Soft Comput. 2023, 144, 110490. [Google Scholar] [CrossRef]
- Huang, J.; Mao, L.X.; Liu, H.C.; Song, M.S. Quality function deployment improvement: A bibliometric analysis and literature review. Qual. Quant. 2022, 56, 1347–1366. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Bilişik, Ö.N.; Duman, N.H.; Taş, E. A novel interval-valued intuitionistic fuzzy CRITIC-TOPSIS methodology: An application for transportation mode selection problem for a glass production company. Expert Syst. Appl. 2024, 235, 121134. [Google Scholar] [CrossRef]
- Xiao, S.; Kremantzis, M.D.; Kyrgiakos, L.S.; Vlontzos, G.; Pardalos, P.M. Embracing fairness within a cross-efficiency hierarchical network DEA system. Oper. Res. 2024, 24, 4. [Google Scholar] [CrossRef]
- Atawi, I.E.; Abuelrub, A.; Al-Shetwi, A.Q.; Albalawi, O.H. Design of a wind-PV system integrated with a hybrid energy storage system considering economic and reliability assessment. J. Energy Storage 2024, 81, 110405. [Google Scholar] [CrossRef]
- Tripathi, D.K.; Nigam, S.K.; Cavallaro, F.; Rani, P.; Mishra, A.R.; Hezam, I.M. A novel CRITIC-RS-VIKOR group method with intuitionistic fuzzy information for renewable energy sources assessment. Group Decis. Negot. 2023, 32, 1437–1468. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Wang, Y.; Deveci, M.; Moslem, S.; Coffman, D.M. Unveiling the implementation barriers to the digital transformation in the energy sector using the Fermatean cubic fuzzy method. Appl. Energy 2024, 360, 122756. [Google Scholar] [CrossRef]
- Song, W.; Rong, W.; Tang, Y. Quantifying risk of service failure in customer complaints: A textual analysis-based approach. Adv. Eng. Inform. 2024, 60, 102377. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Y.; Chai, S.L.; Niu, S.F.; Yang, M.L.; Wu, G.R. Product design evaluation based on improved CRITIC and comprehensive cloud-TOPSIS—Applied to automotive styling design evaluation. Adv. Eng. Inform. 2024, 60, 102361. [Google Scholar] [CrossRef]
- Krishankumar, R.; Dhruva, S.; Ravichandran, K.S.; Kar, S. Selection of a viable blockchain service provider for data management within the internet of medical things: An MCDM approach to Indian healthcare. Inf. Sci. 2024, 657, 119890. [Google Scholar] [CrossRef]
- Hou, J.; Gao, T.; Yang, Y.; Wang, X.; Yang, Y.; Meng, S. Battery inconsistency evaluation based on hierarchical weight fusion and fuzzy comprehensive evaluation method. J. Energy Storage 2024, 84, 110878. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, Q.; Lu, X.; Hu, T.; Wang, Y.; Pan, J. Interval-valued spherical fuzzy quality function deployment methodology: Metaverse collaborative system design application. Eng. Appl. Artif. Intell. 2024, 133, 108644. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, X.; Tang, X. Spherical fuzzy bipartite graph based QFD methodology (SFBG-QFD): Assistive products design application. Expert Syst. Appl. 2024, 239, 122279. [Google Scholar] [CrossRef]
- Du, J.L.; Liu, S.F.; Javed, S.A.; Goh, M.; Chen, Z.S. Enhancing quality function deployment through the integration of rough set and ordinal priority approach: A case study in electric vehicle manufacturing. IEEE Trans. Eng. Manag. 2024, 71, 7541–7552. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Yildiz, A.; Taskin, A.; Ozkan, C. An interval valued Pythagorean fuzzy AHP integrated quality function deployment methodology for hazelnut production in Turkey. Expert Syst. Appl. 2023, 231, 120708. [Google Scholar] [CrossRef]
- Wang, Z.-L.; Liu, H.-C.; Xu, J.-Y.; Ping, Y.-J. A new method for quality function deployment using double hierarchy hesitant fuzzy linguistic term sets and axiomatic design approach. Qual. Eng. 2021, 33, 511–522. [Google Scholar] [CrossRef]
- Mao, L.-X.; Liu, R.; Mou, X.; Liu, H.-C. New approach for quality function deployment using linguistic Z-numbers and EDAS method. Informatica 2021, 32, 565–582. [Google Scholar] [CrossRef]
- Shi, H.; Mao, L.-X.; Li, K.; Wang, X.-H.; Liu, H.-C. Engineering characteristics prioritization in quality function deployment using an improved ORESTE method with double hierarchy hesitant linguistic information. Sustainability 2022, 14, 9771. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, X. An optimization method for handling incomplete and conflicting opinions in quality function deployment based on consistency and consensus reaching process. Comput. Ind. Eng. 2024, 187, 109779. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, X.; Zhang, B.; Zhang, H. Consensus-driven methodology to managing diversity and complex linguistic ratings in quality function deployment: An optimization-based approach. J. Oper. Res. Soc. 2022, 74, 2165–2186. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, X.; Zhang, H. Coping with diversity ratings in prioritizing design requirements in quality function deployment: A consensus-based approach with minimum-maximum adjustments. Comput. Ind. Eng. 2022, 163, 107799. [Google Scholar] [CrossRef]
- Agarwal, A. Investigating design targets for effective performance management system: An application of balance scorecard using QFD. J. Adv. Manag. Res. 2021, 18, 353–367. [Google Scholar] [CrossRef]
- Bauwens, R.; Audenaert, M.; Decramer, A. Performance management systems, innovative work behavior and the role of transformational leadership: An experimental approach. J. Organ. Eff. 2024, 11, 178–195. [Google Scholar] [CrossRef]
- Culasso, F.; Broccardo, L.; Giordino, D.; Crocco, E. Performance management systems and digital technologies: An exploratory analysis of practitioners and academics’ perspectives. Ind. Manag. Data Syst. 2024, 124, 2870–2898. [Google Scholar] [CrossRef]
- Wang, J.; Yu, L.; Rong, Y. A new CoCoSo ranking-based QFD approach in Pythagorean fuzzy environment and its application on evaluating design attributes of mobile medical App. J. Intell. Fuzzy Syst. 2024, 46, 3677–3700. [Google Scholar] [CrossRef]
| Authors | Years | Correlation Assessment Methods | EC Ranking Methods | Research Aims | Main Results |
|---|---|---|---|---|---|
| Fu et al. [37] | 2024 | Interval-valued spherical fuzzy sets | VIKOR method | To develop an interval-valued spherical fuzzy QFD method for metaverse collaborative system design | The proposed QFD approach for metaverse collaborative systems is able to handle uncertainty and vagueness in design processes |
| Liu et al. [38] | 2024 | Spherical fuzzy sets | Bipartite graph prioritization | To introduce a spherical fuzzy bipartite graph-based QFD method for assistive product design | The proposed QFD method can enhance product design efficiency in assistive technologies |
| Kumar Gangadhari et al. [12] | 2024 | Spherical fuzzy sets | Weighted average method | To redefine N95 respirator design using QFD-based optimization model | The presented optimized design method can improving functionality and compliance with new standards for N95 respirators |
| Du et al. [39] | 2024 | Rough sets | Ordinal priority mehtod | To enhancing QFD through the integration of rough sets and ordinal priority method | The proposed QFD can effectively prioritize engineering characteristics in the electric vehicle manufacturing |
| Seker and Aydin [6] | 2023 | Fermatean fuzzy sets | Weighted average method | To apply fermatean fuzzy QFD method to sustainable mobility hub center design | The proposed method is helpful for the related authorities while designing mobility hubs to meet passenger needs and requirements |
| Ayyildiz et al. [40] | 2023 | Interval-valued Pythagorean fuzzy sets | Weighted average method | To integrate interval-valued Pythagorean fuzzy AHP with QFD for hazelnut production optimization | The proposd method is practical for farmers and companies to improve the quality of hazelnut production |
| Wang et al. [41] | 2021 | Double hierarchy hesitant fuzzy linguistic term sets | Axiomatic design method | To develop a QFD methodology using double hierarchy hesitant fuzzy linguistic term sets and axiomatic design | The new method can capture the ambiguity and hesitancy in experts’ evaluation information and obtain a accurate prioritization of ECs |
| Mao et al. [42] | 2021 | Linguistic Z-numbers | Evaluation based on distance from average solution (EDAS) method | To propose a linguistic Z-numbers-based QFD approach integrated with EDAS | The method can represent experts’ evaluation information flexibly and produce a reasonable prioritization of ECs |
| Shi et al. [43] | 2022 | Double hierarchy hesitant linguistic term sets | Improved ORESTE method | To prioritize ECs in QFD using improved ORESTE with hesitant linguistic information | The proposed method is flexibility in handling experts’ hesitant evaluations and effective in ranking ECs |
| Xiao and Wang [44] | 2024 | Incomplete linguistic distribution assessments | Multi-criteria optimization | To handle incomplete and conflicting opinions in QFD through consistency and consensus-reaching processes | Improved the robustness of QFD methodologies in scenarios with incomplete and conflicting stakeholder inputs |
| Wang et al. [13] | 2024 | Probabilistic linguistic term sets | Three-way decision method | To develop a new QFD approach combining cooperative game-based consensus and three-way decision making | The proposed method can help domain experts acquire more consensual correlation evaluations between CRs and ECs |
| Gai et al. [14] | 2024 | Hesitant fuzzy linguistic term sets | Prospect theory | To enhance QFD using social network and group decision-making techniques | The proposed method can generate effective and stable results for QFD implementation |
| Wang et al. [16] | 2023 | Interval 2-tuple Pythagorean fuzzy linguistic sets | Extended CoCoSo method | To propose a new QFD approach based on social network analysis and interval 2-tuple Pythagorean fuzzy linguistic information | The new QFD can express experts’ uncertain linguistic assessments and deal with experts’ consensus in correlation assessment process |
| Han et al. [25] | 2023 | Multi-granular unbalanced linguistic term sets | Extended CoCoSo method | To develop a QFD method based on multi-granular unbalanced linguistic information and consensus reaching process | The proposed approach can represent complex linguistic relationship assessments and determine accurate priority orders of ECs |
| Xiao et al. [45] | 2022 | Two-tuple linguistic method | Weighted average method | To propose a QFD using a consensus-based approach with minimum-maximum adjustments | The propsoed method can manage diversity and complex linguistic ratings in QFD |
| Xiao et al. [46] | 2022 | Two-tuple linguistic method; Comparative linguistic expressions | Extended TOPSIS method | To propose a consensus-based QFD to derive the consensual prioritization of ECs | The proposed method is able to deal with diverse and conflicting ratings in QFD prioritization tasks |
| The current study | 2025 | Linguistic distribution assessments | Extended CRITIC method | To develop a QFD based on linguistic distribution assessments and CRITIC method | The proposed approach can represent experts’ uncertain linguistic relationship evaluations and determine reliable importance ranking of ECs |
| CRs | Customer Requirements | ECs | Engineering Characteristics | Units |
|---|---|---|---|---|
| CR1 | Budget adherence | EC1 | Realistic budget | Deviation from budget allocated |
| CR2 | Right compensation for responsibility level | EC2 | Appropriate compensation for the role and responsibility | Comparing with industry average |
| CR3 | Contribution in increase in overall profit | EC3 | Clear objectives derived from company’s vision | Extent to which goals are assigned to the employees |
| CR4 | Successful internal customer relationships | EC4 | Clearly defined policies and organizational hierarchy | Number of deviations when the policy documents could not be linked to decisions made |
| CR5 | Successful external customer relationships | EC5 | Improved post-sale service/supplier relationships | Number of customer/supplier complaints |
| CR6 | Task completed on schedule | EC6 | Improved departmental communication and coordination system | Number of events of miscommunication/delays due to lack of coordination |
| CR7 | Task success rate | EC7 | Quality of production/service process | Number of deviations |
| CR8 | Resource efficiency | EC8 | Clarity in product/service specifications | Quantity of rejected products |
| CR9 | Trainings undertaken | EC9 | Access to training and growth opportunities inside or outside the company | Number of relevant training opportunities provided by company |
| CR10 | Number of improvement suggestions made | EC10 | Employee empowerment | Number of employee suggestions applied/executed |
| EC1 | EC2 | EC3 | EC4 | EC5 | EC6 | EC7 | EC8 | EC9 | EC10 | |
| CR1 | ||||||||||
| CR2 | ||||||||||
| CR3 | ||||||||||
| CR4 | ||||||||||
| CR5 | ||||||||||
| CR6 | ||||||||||
| CR7 | ||||||||||
| CR8 | ||||||||||
| CR9 | ||||||||||
| CR10 |
| EC1 | EC2 | EC3 | EC4 | EC5 | EC6 | EC7 | EC8 | EC9 | EC10 | |
| CR1 | ||||||||||
| CR2 | ||||||||||
| CR3 | ||||||||||
| CR4 | ||||||||||
| CR5 | ||||||||||
| CR6 | ||||||||||
| CR7 | ||||||||||
| CR8 | ||||||||||
| CR9 | ||||||||||
| CR10 |
| 0.44 | 0.28 | −0.29 | −0.18 | 0.38 | 0.24 | 0.28 | −0.31 | −0.30 | |
| 0.44 | 1.00 | 0.01 | −0.54 | −0.35 | −0.35 | −0.41 | −0.33 | −0.58 | 0.32 |
| 0.28 | 0.01 | 1.00 | −0.08 | 0.46 | 0.36 | 0.38 | 0.27 | −0.19 | 0.02 |
| −0.29 | −0.54 | −0.08 | 1.00 | 0.67 | 0.07 | −0.27 | −0.13 | 0.04 | −0.35 |
| −0.18 | −0.35 | 0.46 | 0.67 | 1.00 | 0.38 | −0.02 | −0.13 | −0.39 | −0.42 |
| 0.38 | −0.35 | 0.36 | 0.07 | 0.38 | 1.00 | 0.47 | 0.31 | −0.01 | −0.62 |
| 0.24 | −0.41 | 0.38 | −0.27 | −0.02 | 0.47 | 1.00 | 0.68 | 0.36 | −0.37 |
| 0.28 | −0.33 | 0.27 | −0.13 | −0.13 | 0.31 | 0.68 | 1.00 | 0.56 | −0.50 |
| −0.31 | −0.58 | −0.19 | 0.04 | −0.39 | −0.01 | 0.36 | 0.56 | 1.00 | 0.02 |
| −0.30 | 0.32 | 0.02 | −0.35 | −0.42 | −0.62 | −0.37 | −0.50 | 0.02 | 1.00 |
| H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 |
|---|---|---|---|---|---|---|---|---|---|
| 2.54 | 8.25 | 6.37 | 4.86 | 3.74 | 6.86 | 7.69 | 7.62 | 9.73 | 8.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, L.-X.; Lan, J.; Chen, A.; Shi, H.; Liu, H.-C. New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method. Mathematics 2025, 13, 240. https://doi.org/10.3390/math13020240
Mao L-X, Lan J, Chen A, Shi H, Liu H-C. New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method. Mathematics. 2025; 13(2):240. https://doi.org/10.3390/math13020240
Chicago/Turabian StyleMao, Ling-Xiang, Jing Lan, Anqi Chen, Hua Shi, and Hu-Chen Liu. 2025. "New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method" Mathematics 13, no. 2: 240. https://doi.org/10.3390/math13020240
APA StyleMao, L.-X., Lan, J., Chen, A., Shi, H., & Liu, H.-C. (2025). New Approach for Quality Function Deployment Based on Linguistic Distribution Assessments and CRITIC Method. Mathematics, 13(2), 240. https://doi.org/10.3390/math13020240






