The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization
Abstract
:1. Introduction
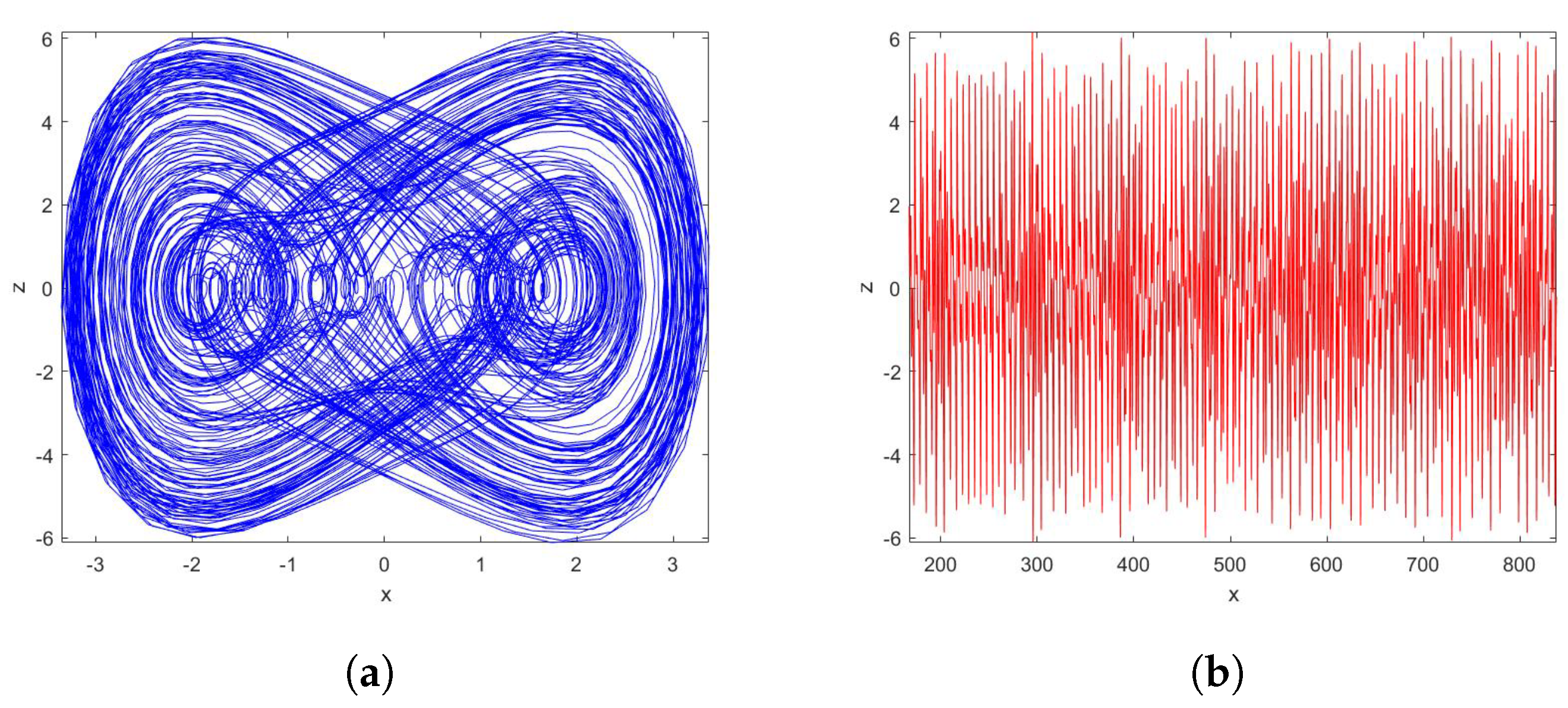
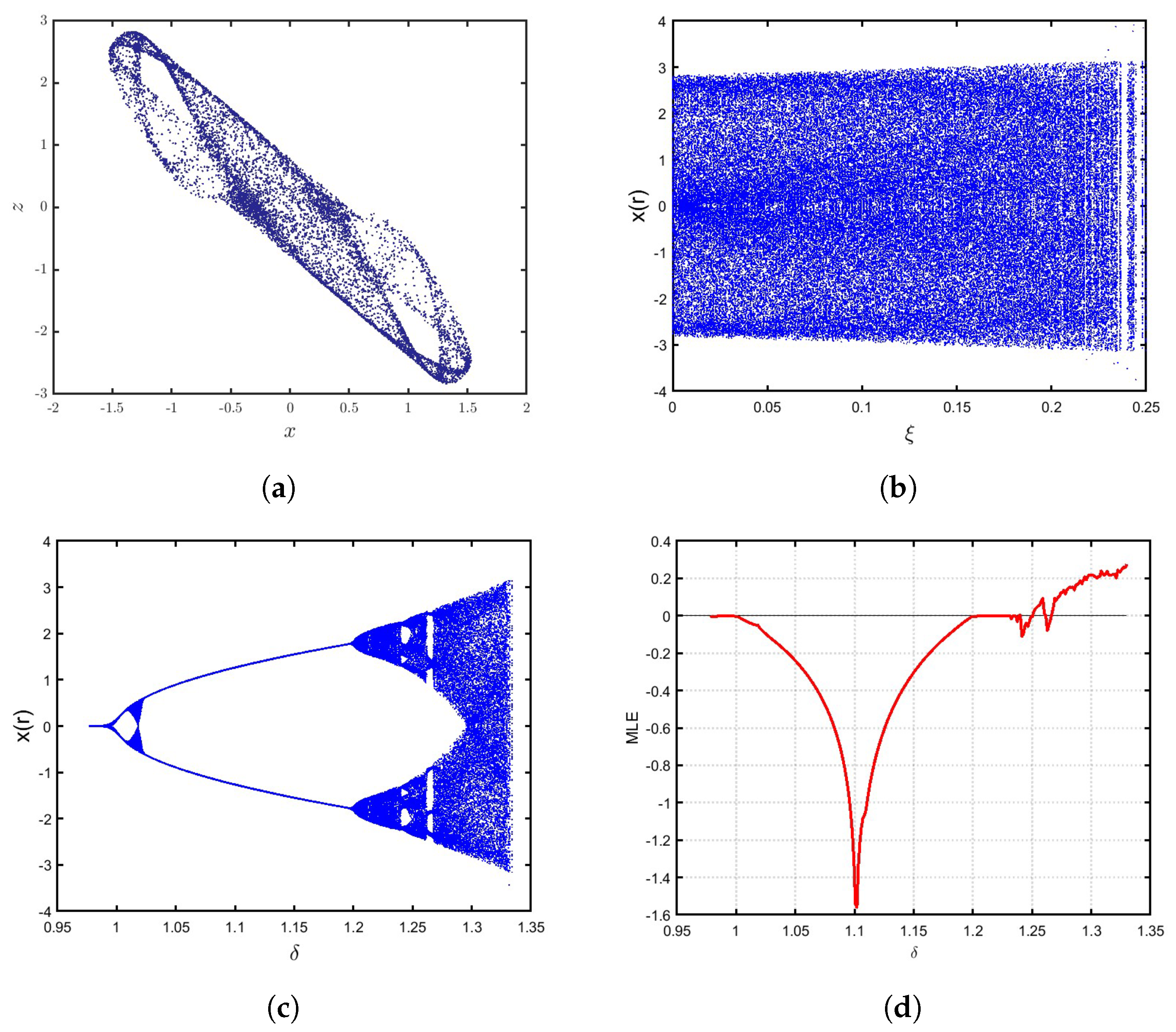
2. The Discrete-Time of Integer-Order Ueda System
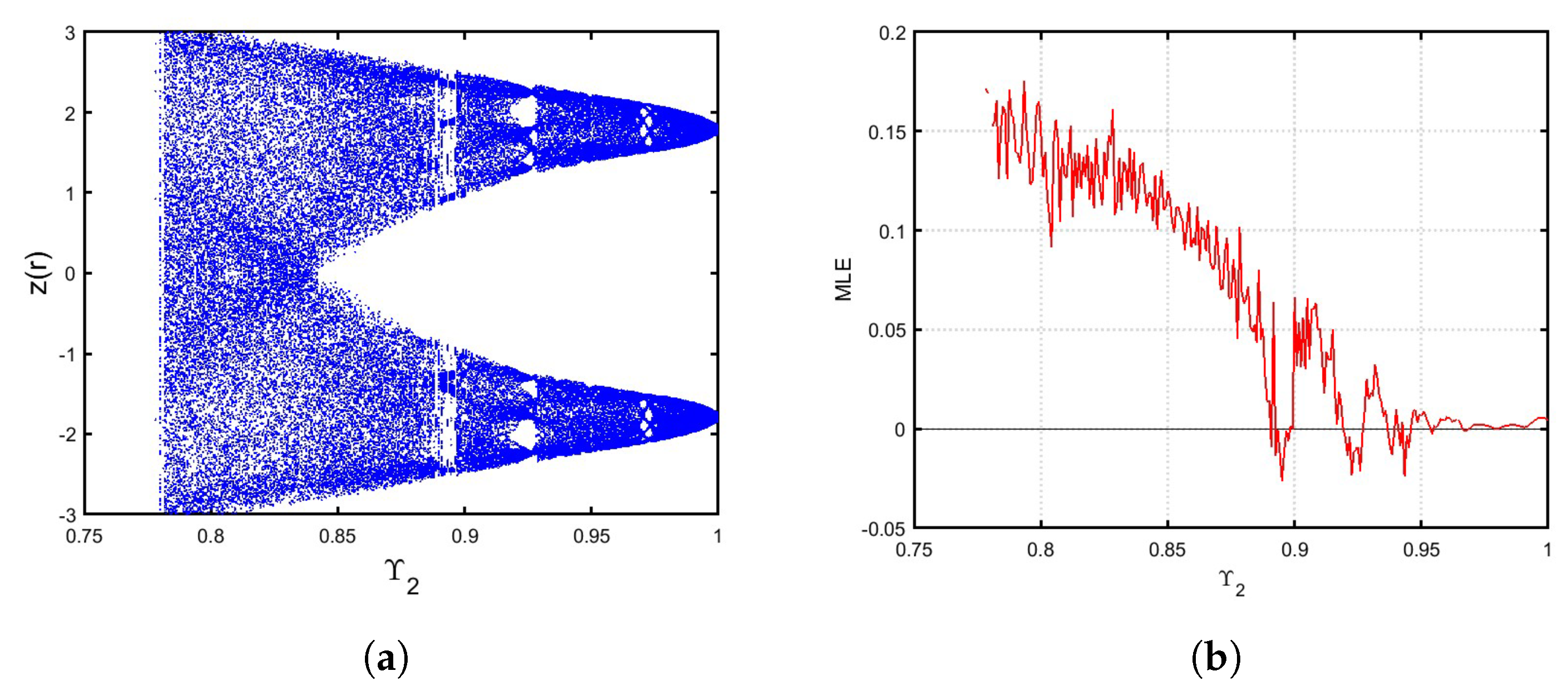
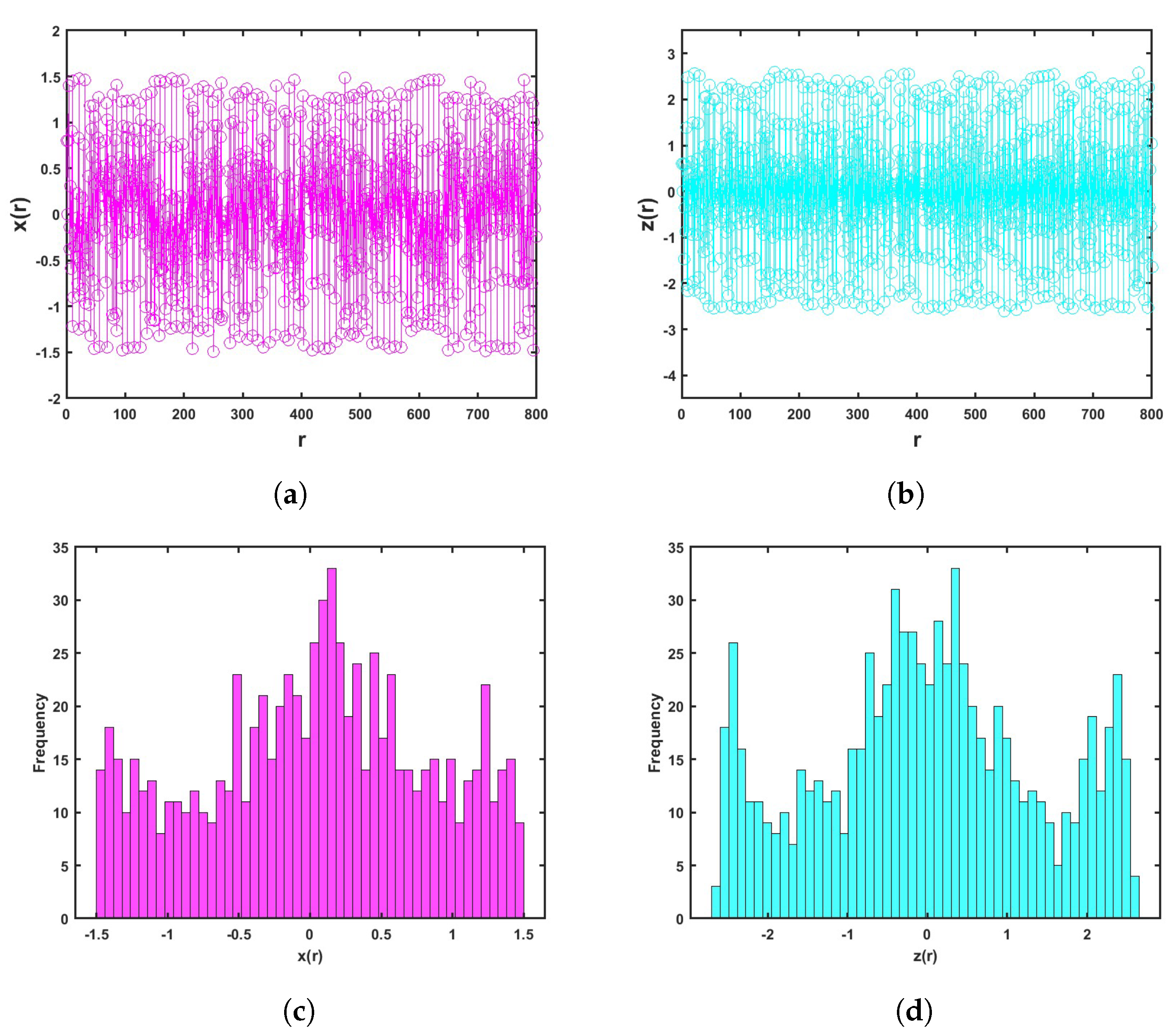
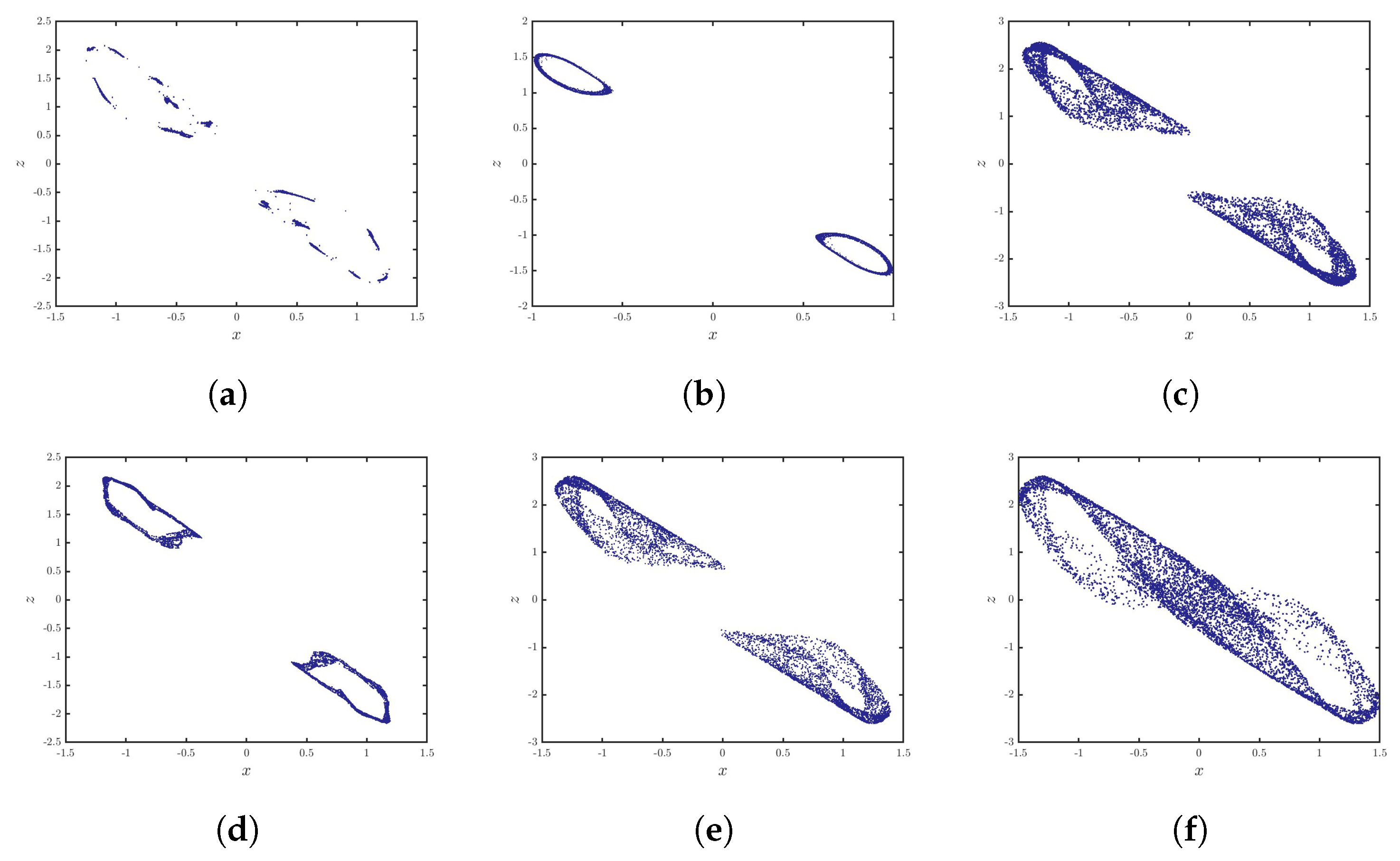
3. The Fractional Ueda Map
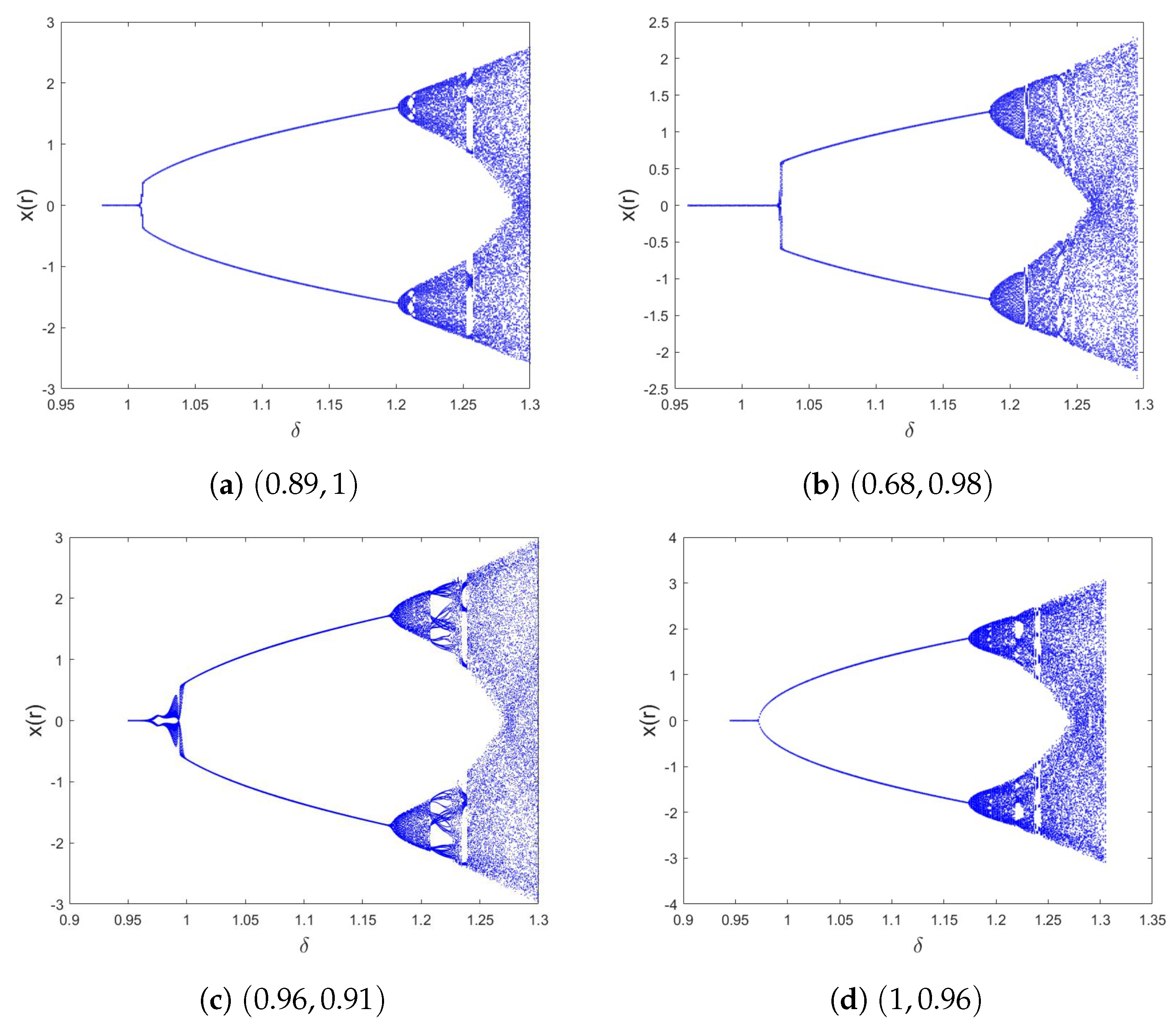
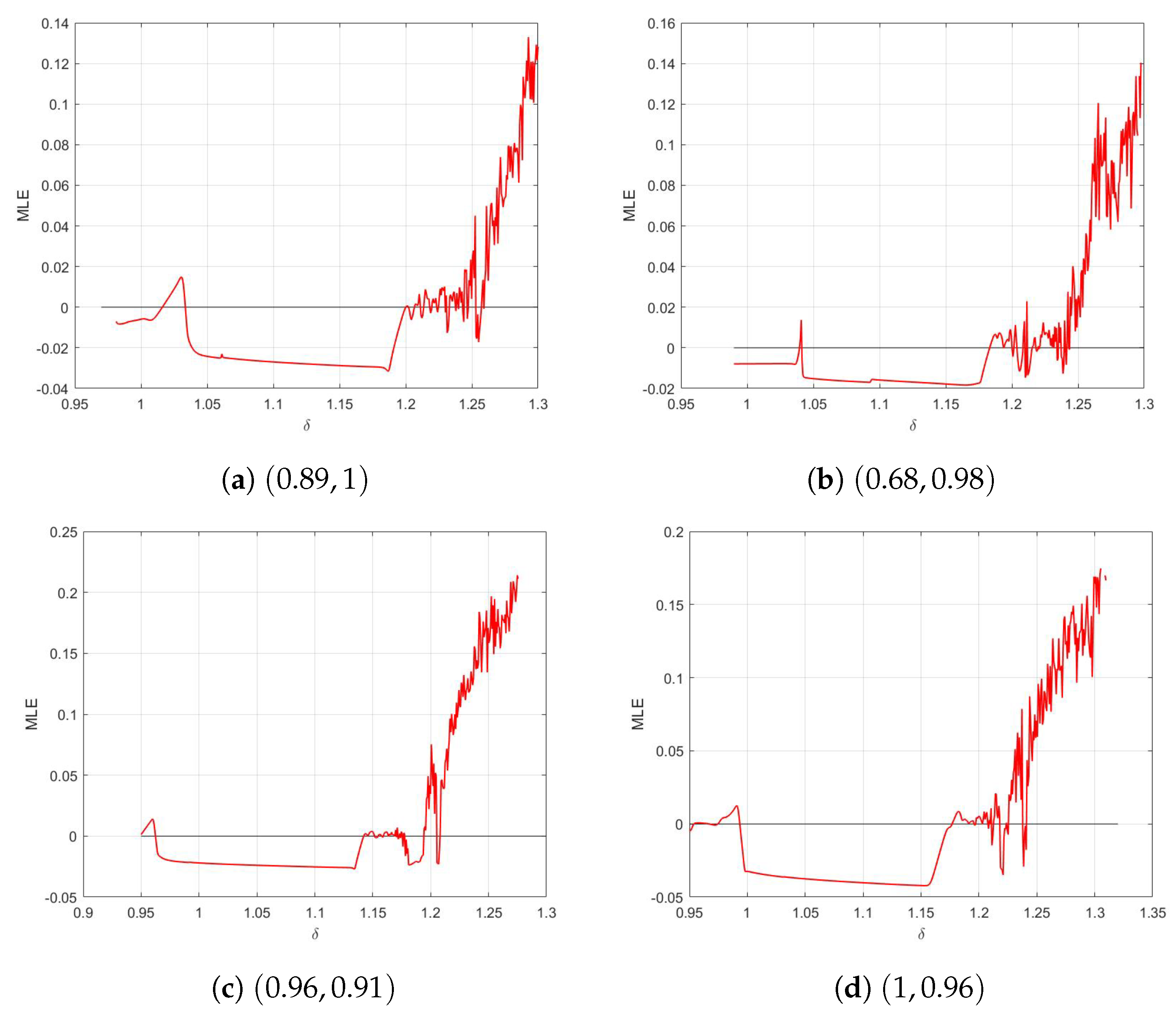
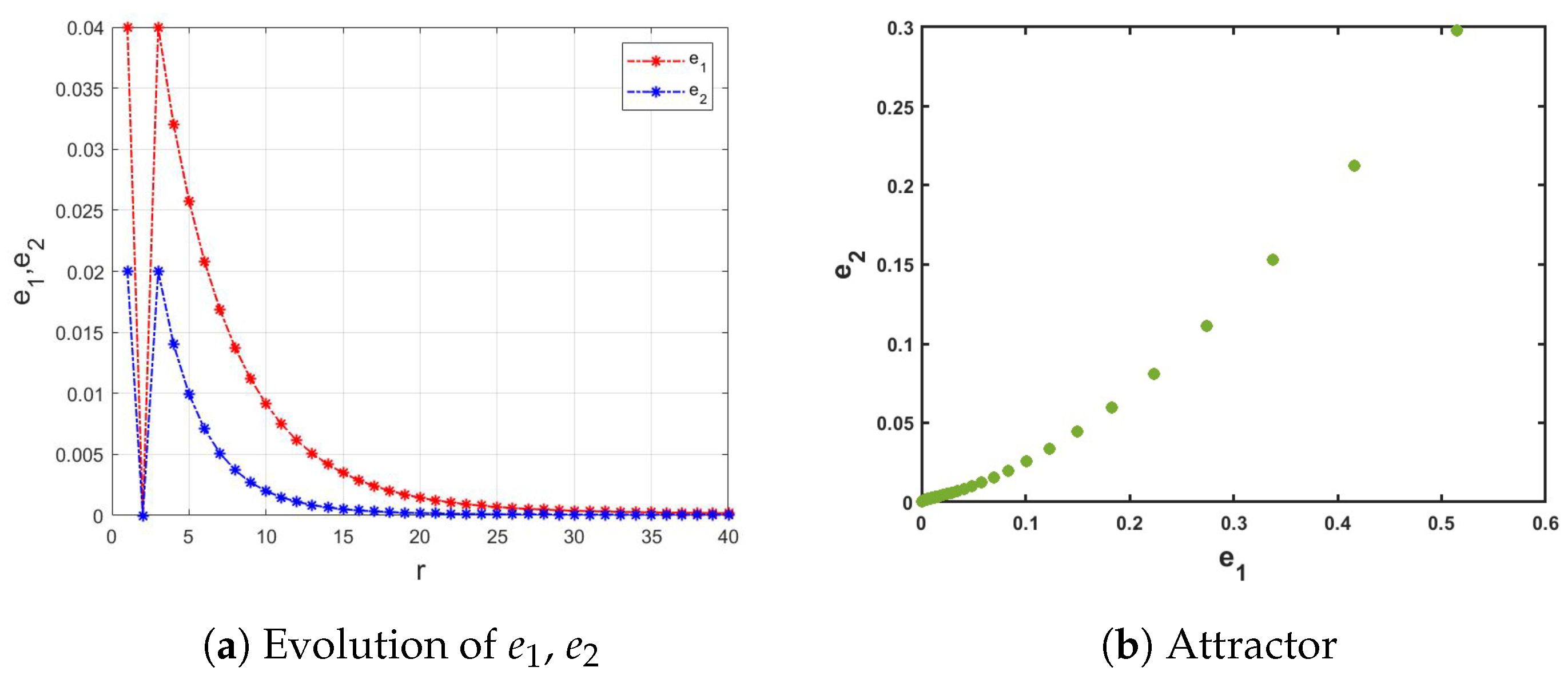
3.1. Commensurate Case
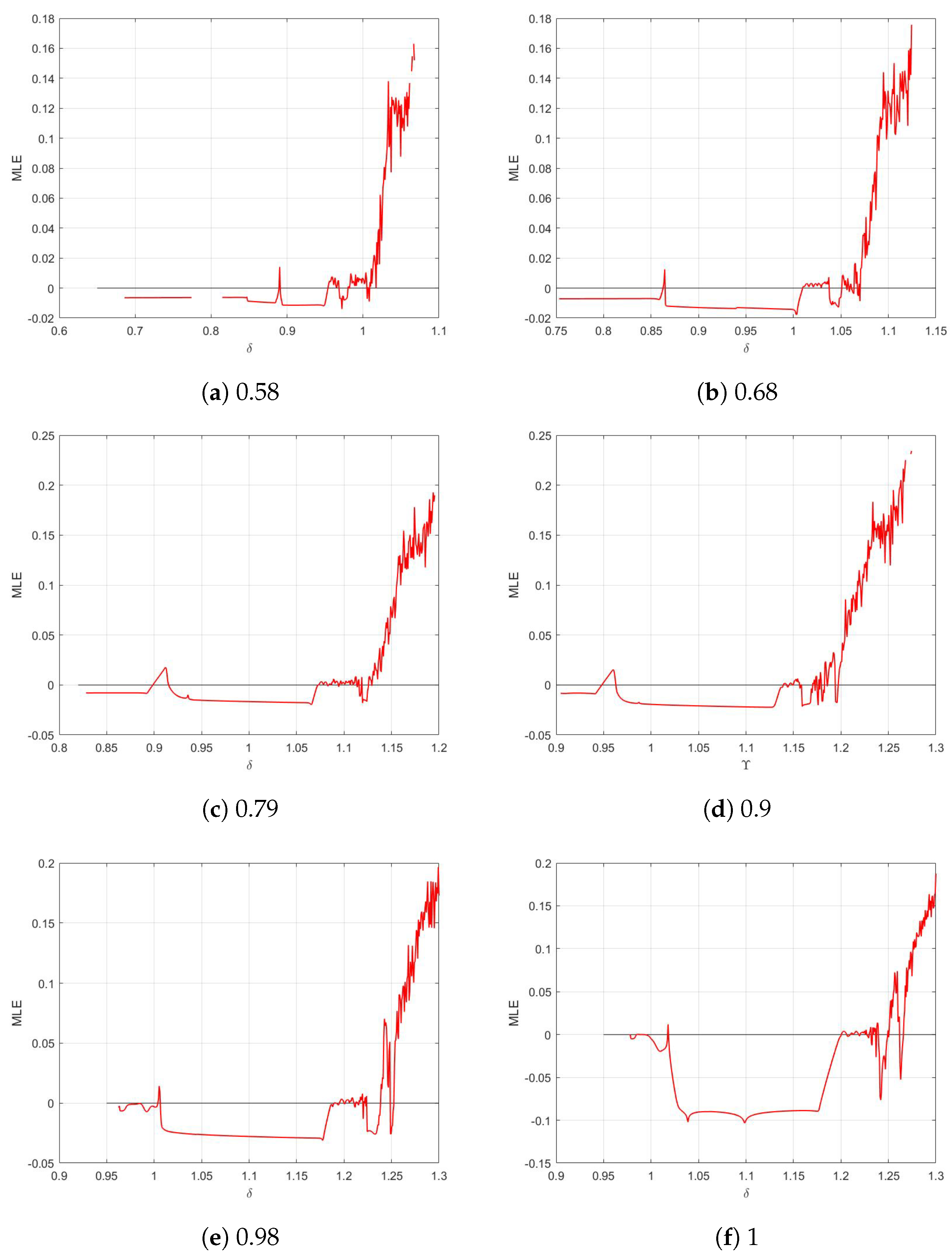
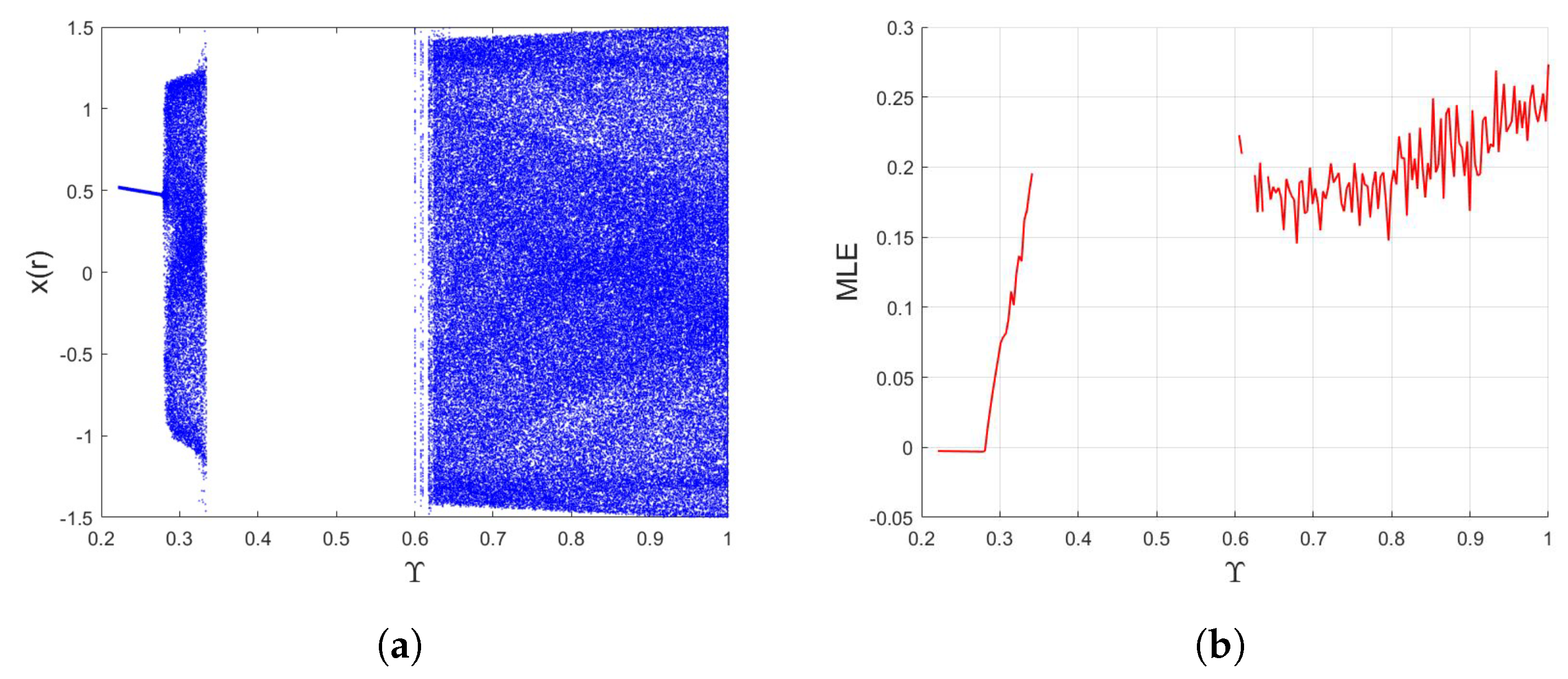
3.2. Incommensurate Case
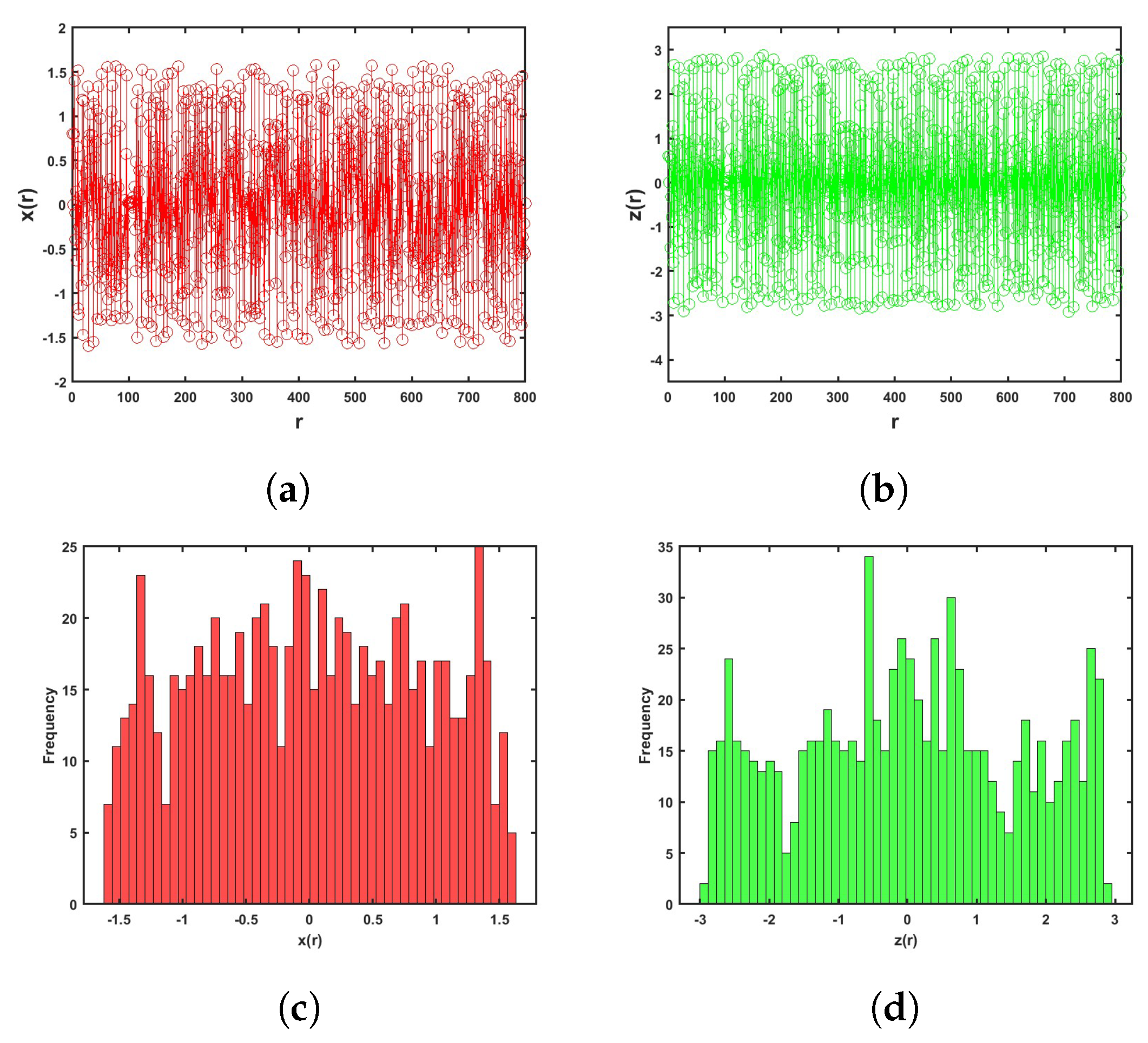
4. Entropy and Complexity
4.1. Approximate Entropy
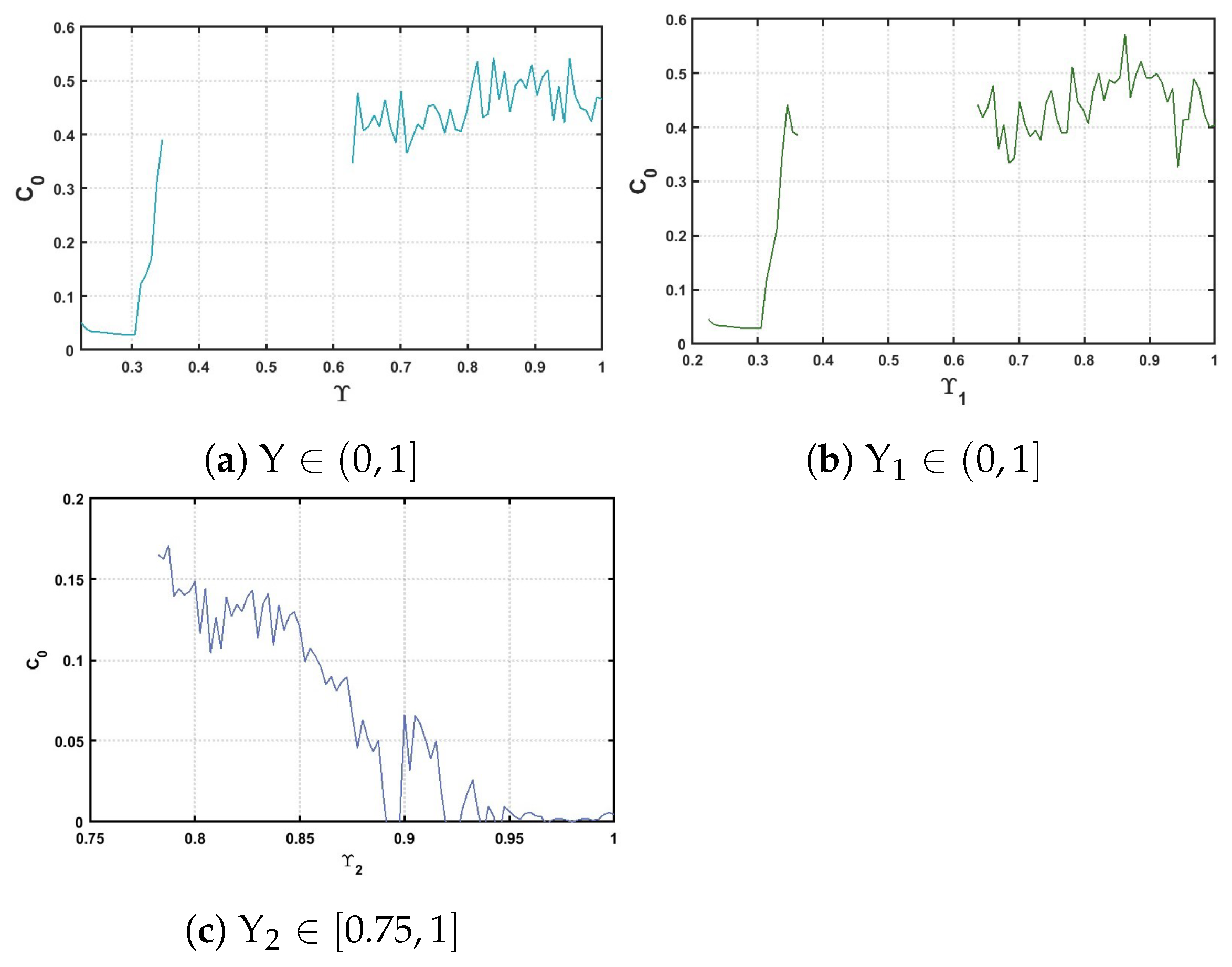
4.2. Complexity
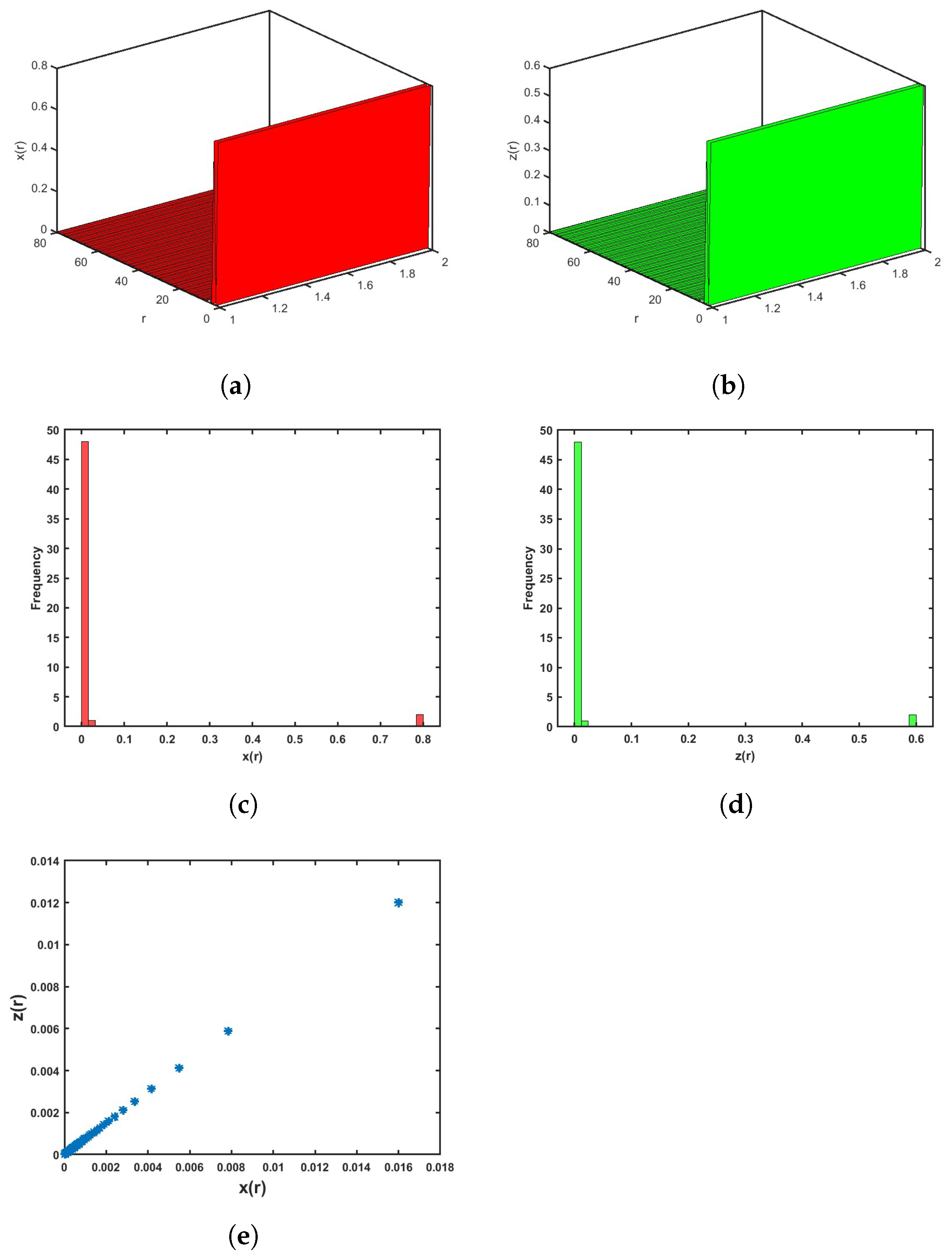
5. Control Methods
5.1. Stabilization of the Fractional Ueda Maps
5.1.1. Stabilization of the Commensurate Version
5.1.2. Stabilization of the Incommensurate Version
5.2. Synchronization Between Fractional Ueda Map
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, C.H.; Tian, D.; Moatimid, G.M.; Salman, H.F.; Zekry, M.H. Hybrid Rayleigh-van der pol-duffing oscillator: Stability analysis and controller. J. Low Freq. Noise, Vib. Act. Control 2022, 41, 244–268. [Google Scholar] [CrossRef]
- Ueda, Y. Randomly transitional phenomena in the system governed by Duffing’s equation. J. Stat. Phys. 1979, 20, 181–196. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
- Zhang, X.; Li, C.; Chen, Y.; Herbert, H.C.; Lei, T. A memristive chaotic oscillator with controllable amplitude and frequency. Chaos Solitons Fractals 2020, 139, 110000. [Google Scholar] [CrossRef]
- Houas, M.; Samei, M.E.; Sundar Santra, S.; Alzabut, J. On a Duffing-type oscillator differential equation on the transition to chaos with fractional q-derivatives. J. Inequalities Appl. 2024, 2024, 12. [Google Scholar] [CrossRef]
- Kassim, S.; Hamiche, H.; Djennoune, S.; Bettayeb, M. A novel secure image transmission scheme based on synchronization of fractional-order discrete-time hyperchaotic systems. Nonlinear Dyn. 2017, 88, 2473–2489. [Google Scholar] [CrossRef]
- Jain, K.; Aji, A.; Krishnan, P. Medical image encryption scheme using multiple chaotic maps. Pattern Recognit. Lett. 2021, 152, 356–364. [Google Scholar] [CrossRef]
- Alhamadani, B.N. Implement image encryption on chaotic and discrete transform domain encryption. Inform. J. Appl. Mach. Electr. Electron. Comput. Sci. Commun. Syst. 2021, 2, 36–41. [Google Scholar]
- Sun, K.; Duo Li-kun, A.; Dong, Y.; Wang, H.; Zhong, K. Multiple coexisting attractors and hysteresis in the generalized Ueda oscillator. Math. Probl. Eng. 2013, 2013, 256092. [Google Scholar] [CrossRef]
- Huang, L.L.; Baleanu, D.; Wu, G.C.; Zeng, S.D. A new application of the fractional logistic map. Rom. J. Phys. 2016, 61, 1172–1179. [Google Scholar]
- Ostalczyk, P. The non-integer difference of the discrete-time function and its application to the control system synthesis. Int. J. Syst. Sci. 2000, 31, 1551–1561. [Google Scholar] [CrossRef]
- Ferreira, R.A. Discrete Fractional Calculus and Fractional Difference Equations; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Tavazoei, M.; Asemani, M.H. On robust stability of incommensurate fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105344. [Google Scholar] [CrossRef]
- Fiaz, M.; Aqeel, M.; Marwan, M.; Sabir, M. Integer and fractional order analysis of a 3D system and generalization of synchronization for a class of chaotic systems. Chaos Solitons Fractals 2022, 155, 111743. [Google Scholar] [CrossRef]
- Ouannas, A.; Batiha, I.M.; Pham, V.T. Fractional discrete chaos: Theories, methods and applications. In World Scientific; World Scientific Publishing: Singapore, 2023; Volume 3. [Google Scholar]
- Zhang, Y.; Li, J.; Zhu, S.; Zhao, H. Bifurcation and chaos detection of a fractional Duffing-van der Pol oscillator with two periodic excitations and distributed time delay. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 083153. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Oussaeif, T.E.; Pham, V.T.; Grassi, G.; Dibi, Z. Hyperchaotic fractional Grassi-Miller map and its hardware implementation. Integration 2021, 80, 13–19. [Google Scholar] [CrossRef]
- Wang, Z.R.; Shiri, B.; Baleanu, D. Discrete fractional watermark technique. Front. Inf. Technol. Electron. Eng. 2020, 21, 880–883. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V.T. The discrete fractional duffing system: Chaos, 0-1 test, C complexity, entropy, and control. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083131. [Google Scholar] [CrossRef] [PubMed]
- Ramroodi, N.; Tehrani, H.A.; Skandari, M.N. Numerical behavior of the variable-order fractional Van der Pol oscillator. J. Comput. Sci. 2023, 74, 102174. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. [Electron. Only] 2009, 62, 12. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J.-Physiol. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Shen, E.-H.; Cai, Z.-J.; Gu, F.-J. Mathematical foundation of a new complexity measure. Appl. Math. Mech. 2005, 26, 1188–1196. [Google Scholar]
- Čermák, J.; Győri, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Electron. J. Qual. Theory Differ. Equ. [Electron. Only] 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G. Novel convenient conditions for the stability of nonlinear incommensurate fractional-order difference systems. Alex. Eng. J. 2022, 61, 1655–1663. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diabi, L.; Ouannas, A.; Hioual, A.; Grassi, G.; Momani, S. The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization. Mathematics 2025, 13, 239. https://doi.org/10.3390/math13020239
Diabi L, Ouannas A, Hioual A, Grassi G, Momani S. The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization. Mathematics. 2025; 13(2):239. https://doi.org/10.3390/math13020239
Chicago/Turabian StyleDiabi, Louiza, Adel Ouannas, Amel Hioual, Giuseppe Grassi, and Shaher Momani. 2025. "The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization" Mathematics 13, no. 2: 239. https://doi.org/10.3390/math13020239
APA StyleDiabi, L., Ouannas, A., Hioual, A., Grassi, G., & Momani, S. (2025). The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization. Mathematics, 13(2), 239. https://doi.org/10.3390/math13020239