Modeling, Analysis, and Transmission Dynamics of Cassava Mosaic Disease Through Stochastic Fractional Delay Differential Equations
Abstract
:1. Introduction
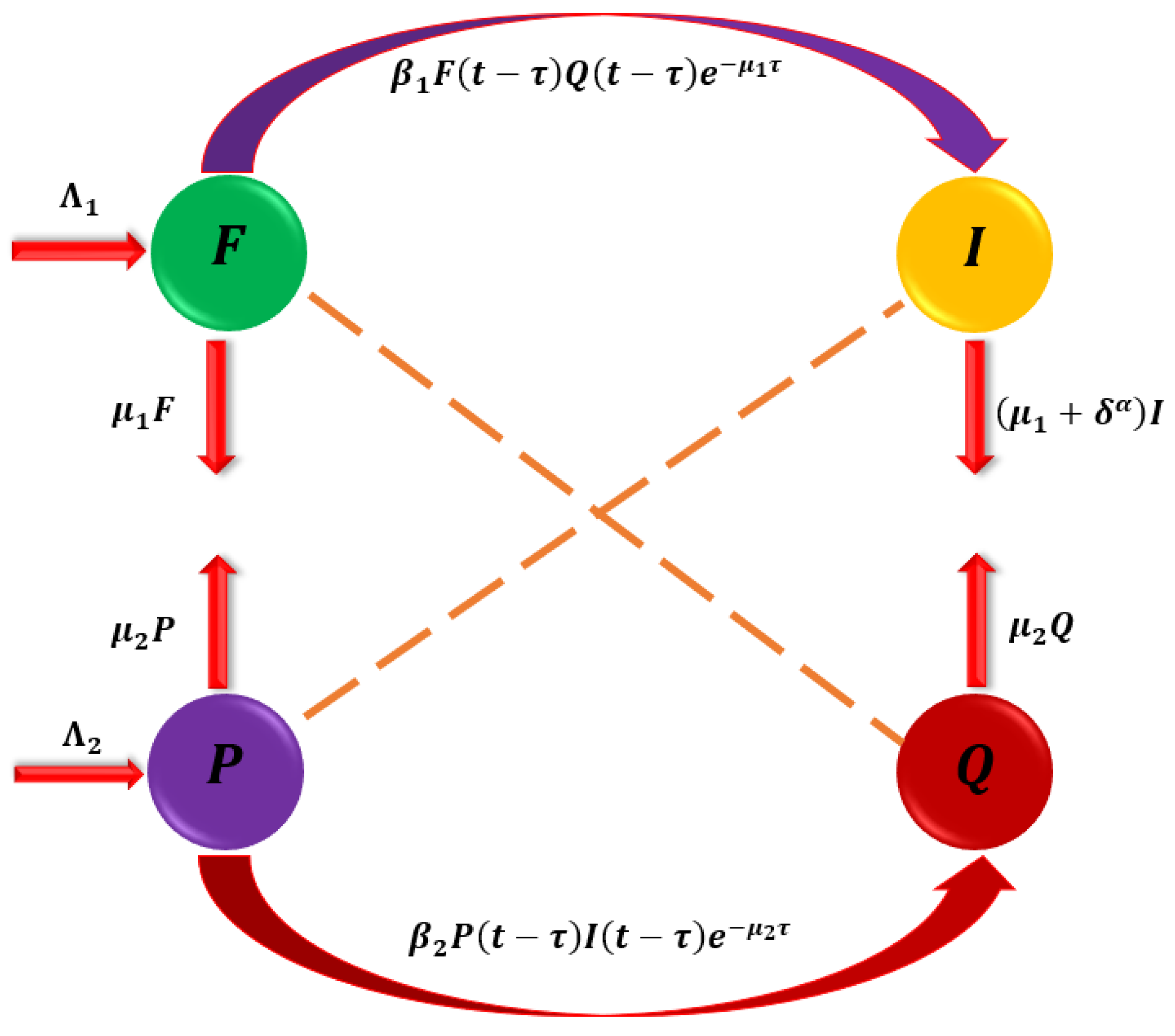
2. Model Formulation
2.1. Existence and Uniqueness of the Stochastic Fractional Delayed Model
2.2. Model Equilibria and Reproduction Number
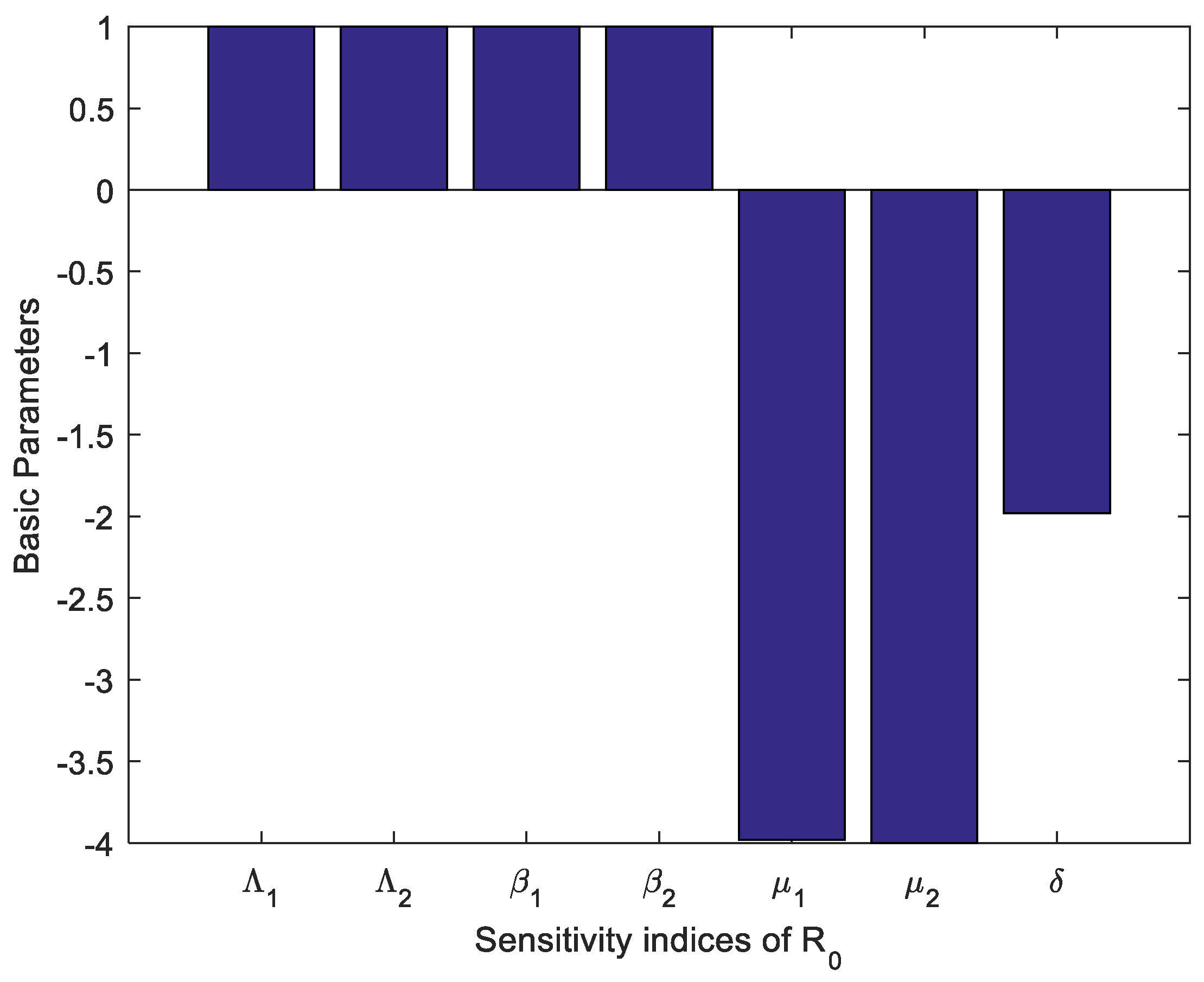
3. Sensitivity Analysis
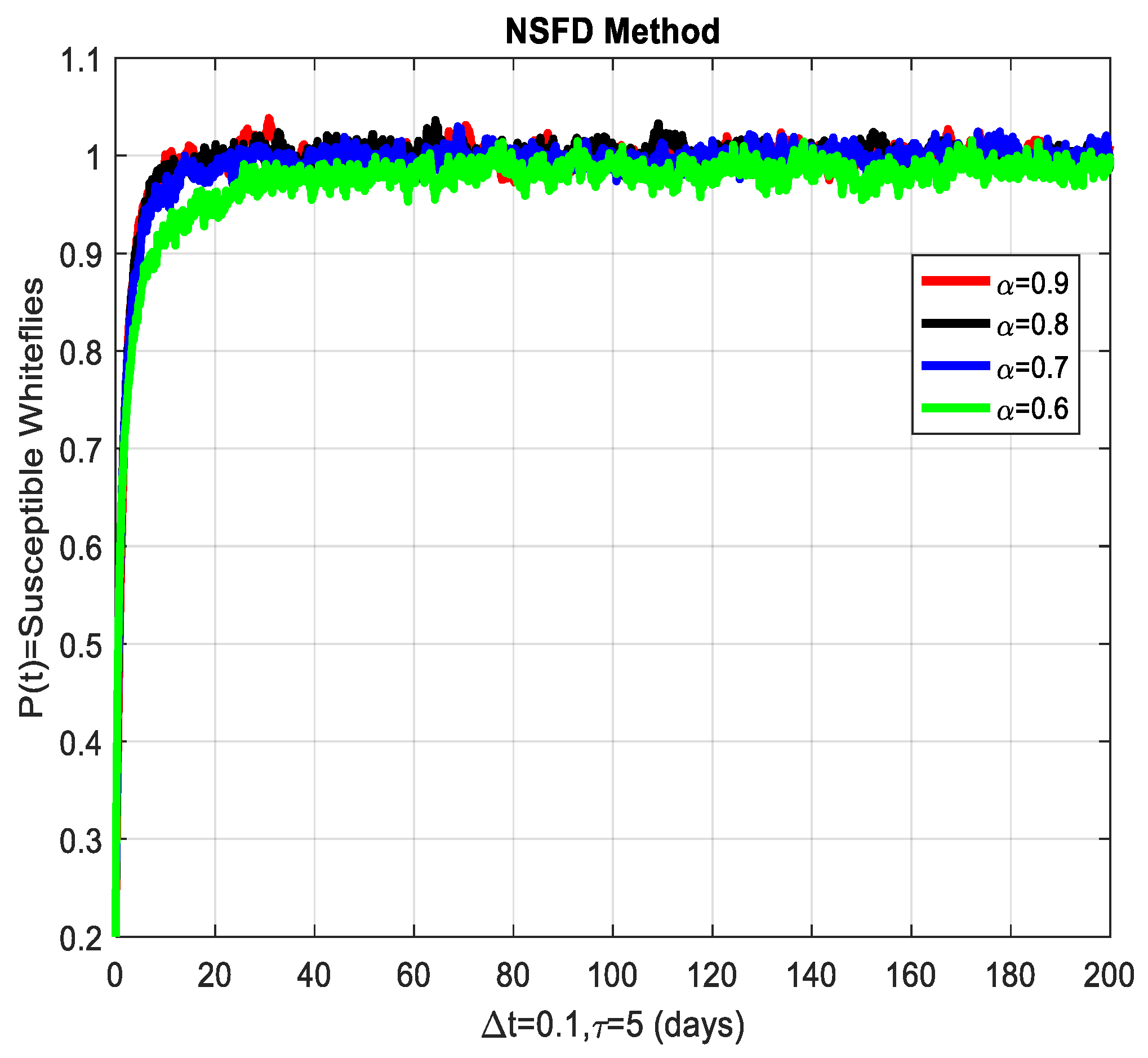
4. NSFD Method
5. Properties
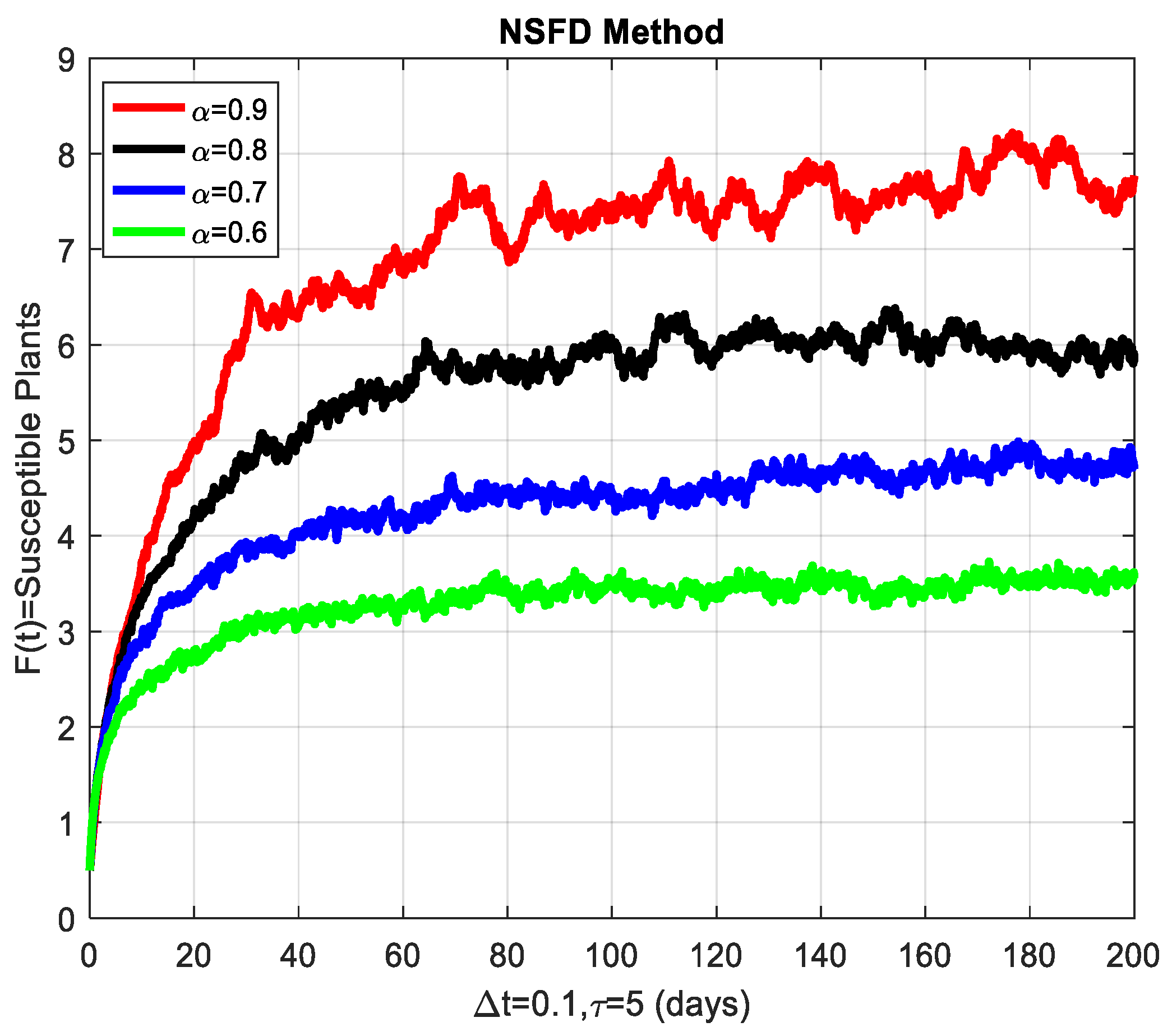
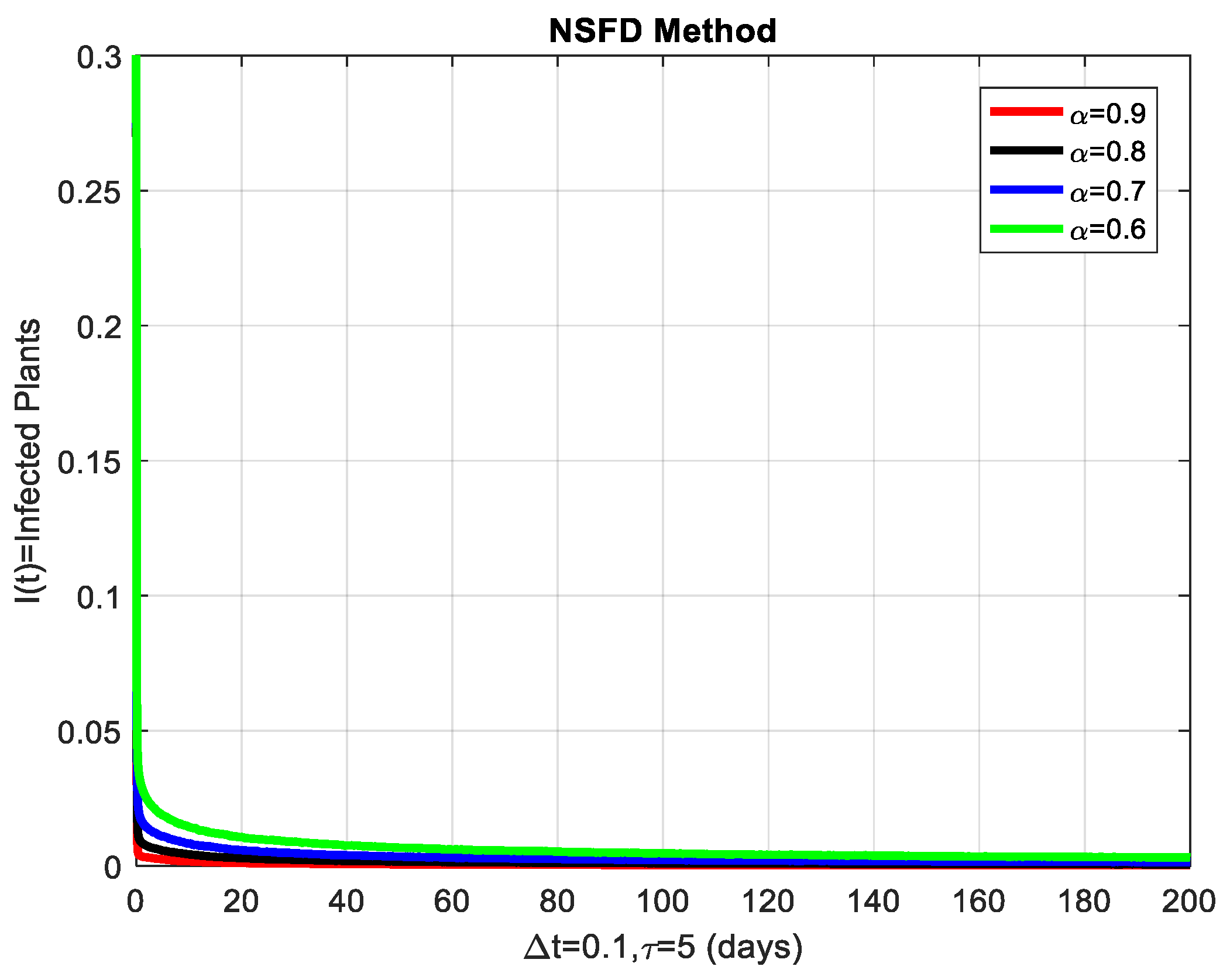
6. Numerical Simulations
Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holt, J.; Jeger, M.J.; Thresh, J.M.; Otim-Nape, G.W. An epidemilogical model incorporating vector population dynamics applied to african cassava mosaic virus disease. J. Appl. Ecol. 2024, 34, 793–806. [Google Scholar] [CrossRef]
- Abdullah, T.Q.; Huang, G.; Al-Sadi, W.; Aboelmagd, Y.; Mobarak, W. Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme. Mathematics 2024, 12, 2386. [Google Scholar] [CrossRef]
- Sangsawang, S.; Khan, A.; Pongsumpun, P. Sensitivity analysis and optimal control for the dynamic mathematical model of cassava mosaic disease. AIP Adv. 2024, 14, 065230. [Google Scholar] [CrossRef]
- Erick, B.; Mayengo, M.M. Optimization Framework for the Dynamics of Cassava Mosaic Disease in the Presence of Non-Cassava Host Plants. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4866552 (accessed on 19 January 2025).
- Yasaswini, M.D.; Babu, B.V. Effective detection of cassava mosaic disease (cmd) in cassava plants using drnn technique. Mach. Intell. Res. 2024, 18, 125–138. [Google Scholar]
- Andersen Onofre, K.; Delaquis, E.; Newby, J.; de Haan, S.; Thuy, C.T.L.; Minato, N.; Legg, J.P.; Cuellar, W.J.; Briseño, R.I.A.; Garrett, K.A. Decision support for managing an invasive pathogen through efficient clean seed systems: Cassava mosaic disease in Southeast Asia. bioRxiv 2024. [Google Scholar] [CrossRef]
- Ferris, A.C.; Stutt, R.O.; Godding, D.S.; Mohammed, I.U.; Nkere, C.K.; Eni, A.O.; Pita, J.S.; Gilligan, C.A. Computational models for improving surveillance for the early detection of direct introduction of cassava brown streak disease in Nigeria. PLoS ONE 2024, 19, e0304656. [Google Scholar] [CrossRef] [PubMed]
- Chaowongdee, S.; Vannatim, N.; Malichan, S.; Kuncharoen, N.; Tongyoo, P.; Siriwan, W. Comparative transcriptomics analysis reveals defense mechanisms of Manihot esculenta Crantz against Sri Lanka Cassava MosaicVirus. BMC Genom. 2024, 25, 436. [Google Scholar] [CrossRef] [PubMed]
- Robson, F.; Hird, D.L.; Boa, E. Cassava brown streak: A deadly virus on the move. Plant Pathol. 2024, 73, 221–241. [Google Scholar] [CrossRef]
- Niño-Jimenez, D.P.; López-López, K.; Cuervo-Ibáñez, M. Quantitative detection of cassava common mosaic virus for health certification of cassava (Manihot esculenta Crantz) germplasm using qPCR analysis. Heliyon 2024, 10, e27604. [Google Scholar] [CrossRef] [PubMed]
- Sikazwe, G.; epse Yocgo, R.E.; Landi, P.; Richardson, D.M.; Hui, C. Current and future scenarios of suitability and expansion of cassava brown streak disease, Bemisia tabaci species complex, and cassava planting in Africa. PeerJ 2024, 12, e17386. [Google Scholar] [CrossRef] [PubMed]
- Allado, S.S.; Adjata, K.D.; Pita, J.S.; Atassé, K.; Sé, A.; Tozo, K. East African Cassava Mosaic Virus and East African Cassava Mosaic Cameroon Virus: Two Species Emerging in Togo. Agric. Sci. 2024, 15, 864–876. [Google Scholar] [CrossRef]
- Kaushik, P.; Jain, E.; Gill, K.S.; Upadhyay, D.; Devliyal, S. Comparative Analysis of Cassava Leaf Disease Prediction Using the Deep Learning Approach. In Proceedings of the 2024 2nd International Conference on Sustainable Computing and Smart Systems (ICSCSS), Coimbatore, India, 10–12 July 2024; pp. 1369–1373.
- Sichalwe, K.L.; Kayondo, S.I.; Edema, R.; Omari, M.A.; Kulembeka, H.; Rubaihayo, P.; Kanju, E. Unlocking Cassava Brown Streak Disease Resistance in Cassava: Insights from Genetic Variability and Combining Ability. Agronomy 2024, 14, 2122. [Google Scholar] [CrossRef]
- Sikazwe, G.; Yocgo, R.E.; Landi, P.; Richardson, D.M.; Hui, C. Managing whitefly development to control cassava brown streak virus coinfections. Ecol. Model. 2024, 493, 110753. [Google Scholar] [CrossRef]
- Wei, Y.; Xie, H.; Xu, L.; Cheng, X.; Zhu, B.; Zeng, H.; Shi, H. The coat protein of cassava common mosaic virus targets RAV1 and RAV2 transcription factors to subvert immunity in cassava. Plant Physiol. 2024, 194, 1218–1232. [Google Scholar] [CrossRef] [PubMed]
- Zanini, A.; Dominguez, M.C.; Rodriguez, M.S. Unraveling the Plant-Pathogen Interaction Clock: Circadian Disruptions in Sugar Metabolism Induced by Cassava Common Mosaic Virus (CsCMV). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4737291 (accessed on 19 January 2025).
- Gopi, A. Disclosing the Potential of Deep Learning in Cassava Leaf Disease Analysis by using CNN and Neural Networks Approach. In Proceedings of the 2024 International Conference on Inventive Computation Technologies (ICICT), Lalitpur, Nepal, 24–26 April 2024; pp. 188–193. [Google Scholar]
- Wosula, E.N.; Shirima, R.R.; Amour, M.; Woyengo, V.W.; Otunga, B.M.; Legg, J.P. Occurrence and Distribution of Major Cassava Pests and Diseases in Cultivated Cassava Varieties in Western Kenya. Viruses 2024, 16, 1469. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, B.; Qi, C.; Nyalala, I.; Mecha, P.; Chen, K.; Gao, J. MAIANet: Signal modulation in cassava leaf disease classification. Comput. Electron. Agric. 2024, 225, 109351. [Google Scholar] [CrossRef]
- Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infect. Dis. Model. 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]
- Mamis, K.; Farazmand, M. Modeling correlated uncertainties in stochastic compartmental models. Math. Biosci. 2024, 374, 109226. [Google Scholar] [CrossRef] [PubMed]
- Allen, E.J.; Allen, L.J.; Arciniega, A.; Greenwood, P.E. Construction of equivalent stochastic differential equation models. Stoch. Anal. Appl. 2008, 26, 274–297. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Mickens, R.E. (Ed.) Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1993. [Google Scholar]
- Arenas, A.J.; González-Parra, G.; Chen-Charpentier, B.M. Construction of nonstandard finite difference schemes for the SI and SIR epidemic models of fractional order. Math. Comput. Simul. 2015, 121, 48–63. [Google Scholar] [CrossRef]

| Parameters | Signs |
|---|---|
| Positive | |
| Positive | |
| Positive | |
| Positive | |
| Negative | |
| Negative | |
| Negative |
| Parameters | Values |
|---|---|
| Parameters | Values | Source [1] |
|---|---|---|
| Estimated | ||
| 0.5 | Fitted | |
| Estimated | ||
| Fitted | ||
| Fitted | ||
| Estimated | ||
| Estimated | ||
| Fitted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minhós, F.; Raza, A.; Shafique, U.; Mohsin, M. Modeling, Analysis, and Transmission Dynamics of Cassava Mosaic Disease Through Stochastic Fractional Delay Differential Equations. Mathematics 2025, 13, 383. https://doi.org/10.3390/math13030383
Minhós F, Raza A, Shafique U, Mohsin M. Modeling, Analysis, and Transmission Dynamics of Cassava Mosaic Disease Through Stochastic Fractional Delay Differential Equations. Mathematics. 2025; 13(3):383. https://doi.org/10.3390/math13030383
Chicago/Turabian StyleMinhós, Feliz, Ali Raza, Umar Shafique, and Muhammad Mohsin. 2025. "Modeling, Analysis, and Transmission Dynamics of Cassava Mosaic Disease Through Stochastic Fractional Delay Differential Equations" Mathematics 13, no. 3: 383. https://doi.org/10.3390/math13030383
APA StyleMinhós, F., Raza, A., Shafique, U., & Mohsin, M. (2025). Modeling, Analysis, and Transmission Dynamics of Cassava Mosaic Disease Through Stochastic Fractional Delay Differential Equations. Mathematics, 13(3), 383. https://doi.org/10.3390/math13030383








