Limit Theorems for Kernel Regression Estimator for Quasi-Associated Functional Censored Time Series Within Single Index Structure
Abstract
1. Introduction
2. Model and Estimator
2.1. Quasi-Associated Dependence
- 1.
- Associated but not mixing sequences: Consider the sequence , where are i.i.d. random variables with . Let . The linear process is associated (see and in [16]) but not mixing, as (refer to [53]). Furthermore, follows a uniform distribution on , and its covariance function satisfiesexhibiting exponential decay. The associated empirical process converges, as demonstrated in [54].
- 2.
- Associated and mixing sequences: When the conditions of Theorem 2.1 in [50] hold, and for all , the linear process exhibits both association and β-mixing properties.
- 3.
- Mixing but not associated sequences: Consider a sequence satisfying and for . Then, is not associated, asviolating the association condition. However, the sequence is mixing due to its m-dependence.
2.2. The Single Functional Index Model
3. Strong Uniform Consistency
3.1. Results
- (A0)
- The random variables and C are independent.
- (A1)
- (i)
- The probability , denoted by , is positive for all , and satisfies
- (ii)
- There exists a differentiable function such that for all and ,and there exists a constant for which
- (A2)
- The function satisfies a Hölder condition. Specifically, for all and for all ,where .
- (A3)
- The function is bounded and continuous, and satisfies the following conditions:
- (i)
- There exist constants such that
- (ii)
- For all ,
- (A4)
- Let . The sequences and satisfy
- (i)
- (ii)
- (iii)
- (A5)
- The process is quasi-associated with a covariance coefficient that satisfies
- (A6)
- (A7)
- (i)
- There exists a constant such that
- (ii)
3.2. Methodology for Estimating a Single Functional Index
4. Asymptotic Distribution
- (A1’)
- The probability measure satisfiesand there exists a function such that
- (A3’)
- The kernel function is a continuous and bounded function supported on . Moreover, is differentiable, and its derivative exists, satisfying the condition that there exist constants C and such that
- (A4’)
- The bandwidth sequence and the function satisfy the following conditions:
- (i)
- and .
- (ii)
- (A7’)
- There exists a sequence that diverges to infinity while satisfying , such that
Confidence Interval
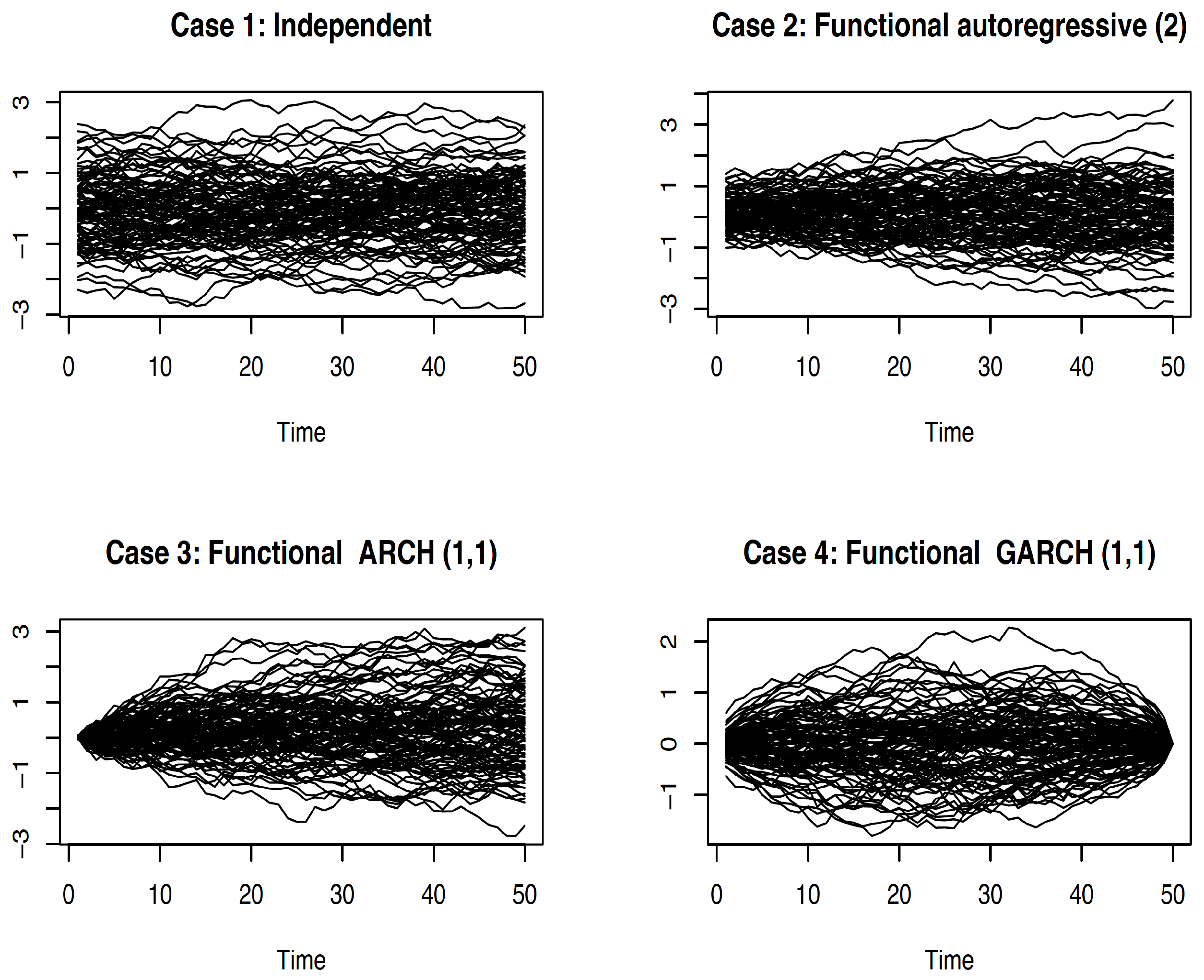
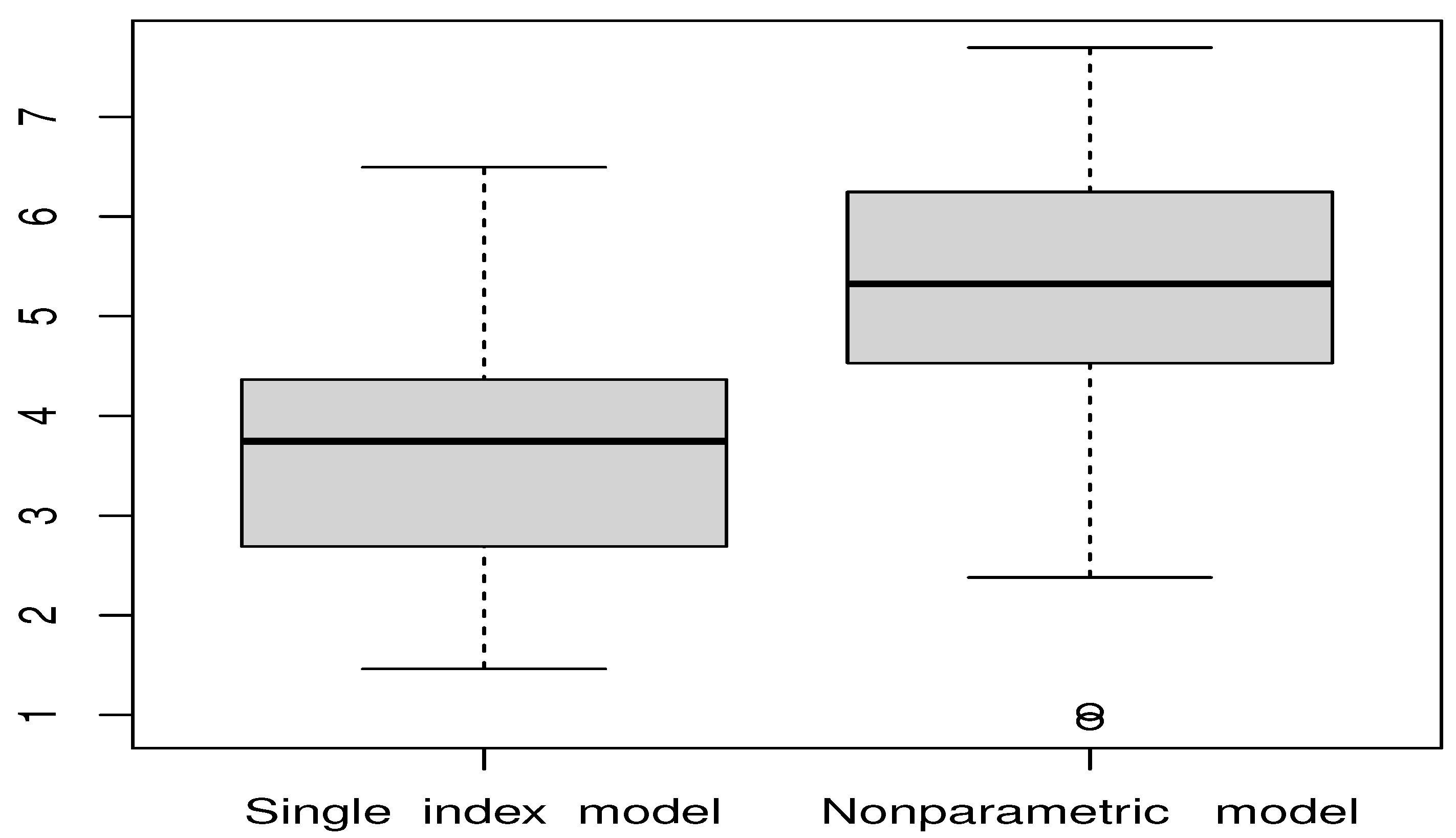
5. Numerical Results
6. Real Data Example
7. Concluding Remarks
8. Proofs
- If , we obtain
- If , we apply the quasi-association condition to show
- Proof of (35):
- Proof of : Using stationarity and basic covariance bounds, we have
- Bound for :
- Proof of : Since , we haveThen,
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Härdle, W.; Hall, P.; Ichimura, H. Optimal smoothing in single-index models. Ann. Statist. 1993, 21, 157–178. [Google Scholar] [CrossRef]
- Hristache, M.; Juditsky, A.; Spokoiny, V. Direct estimation of the index coefficient in a single-index model. Ann. Statist. 2001, 29, 595–623. [Google Scholar] [CrossRef]
- Ferraty, F.; Peuch, A.; Vieu, P. Modèle à indice fonctionnel simple. Comptes Rendus Math. 2003, 336, 1025–1028. [Google Scholar] [CrossRef]
- Chen, D.; Hall, P.; Müller, H.G. Single and multiple index functional regression models with nonparametric link. Ann. Statist. 2011, 39, 1720–1747. [Google Scholar] [CrossRef]
- Ding, H.; Liu, Y.; Xu, W.; Zhang, R. A class of functional partially linear single-index models. J. Multivar. Anal. 2017, 161, 68–82. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. The functional nonparametric model and application to spectrometric data. Comput. Statist. 2002, 17, 545–564. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis. Theory and Practice; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Ferraty, F.; Park, J.; Vieu, P. Estimation of a functional single index model. In Recent Advances in Functional Data Analysis and Related Topics; Contributions to Statistics; Physica-Verlag/Springer: Berlin/Heidelberg, Germany, 2011; pp. 111–116. [Google Scholar] [CrossRef]
- Bouzebda, S. Limit Theorems in the Nonparametric Conditional Single-Index U-Processes for Locally Stationary Functional Random Fields under Stochastic Sampling Design. Mathematics 2024, 12, 1996. [Google Scholar] [CrossRef]
- Bouzebda, S. General tests of conditional independence based on empirical processes indexed by functions. Jpn. J. Stat. Data Sci. 2023, 6, 115–177. [Google Scholar] [CrossRef]
- Bouzebda, S. Uniform in Number of Neighbor Consistency and Weak Convergence of k-Nearest Neighbor Single Index Conditional Processes and k-Nearest Neighbor Single Index Conditional U-Processes Involving Functional Mixing Data. Symmetry 2024, 16, 1576. [Google Scholar] [CrossRef]
- Bouzebda, S.; Taachouche, N. Oracle inequalities and upper bounds for kernel conditional U-statistics estimators on manifolds and more general metric spaces associated with operators. Stochastics 2024, 96, 2135–2198. [Google Scholar] [CrossRef]
- Bouzebda, S.; Taachouche, N. On the variable bandwidth kernel estimation of conditional U-statistics at optimal rates in sup-norm. Phys. A 2023, 625, 129000. [Google Scholar] [CrossRef]
- Bulinski, A.; Suquet, C. Normal approximation for quasi-associated random fields. Statist. Probab. Lett. 2001, 54, 215–226. [Google Scholar] [CrossRef]
- Esary, J.D.; Proschan, F.; Walkup, D.W. Association of random variables, with applications. Ann. Math. Statist. 1967, 38, 1466–1474. [Google Scholar] [CrossRef]
- Doukhan, P.; Louhichi, S. A new weak dependence condition and applications to moment inequalities. Stoch. Process. Appl. 1999, 84, 313–342. [Google Scholar] [CrossRef]
- Richard, E.; Barlow, F.P. Statistical Theory of Reliability and Life Testing: Probability Models; International Series in Decision Processes Series in Quantitative Methods for Decision Making; Rinehart and Winston: Holt, MI, USA, 1975; p. 290. [Google Scholar]
- Ichimura, H. Semiparametric least squares (SLS) and weighted SLS estimation of single-index models. J. Econ. 1993, 58, 71–120. [Google Scholar] [CrossRef]
- Delecroix, M.; Härdle, W.; Hristache, M. Efficient estimation in conditional single-index regression. J. Multivar. Anal. 2003, 86, 213–226. [Google Scholar] [CrossRef]
- Huang, Z. Empirical likelihood for single-index varying-coefficient models with right-censored data. J. Korean Statist. Soc. 2010, 39, 533–544. [Google Scholar] [CrossRef]
- Li, T.T.; Yang, H.; Wang, J.L.; Xue, L.G.; Zhu, L.X. Estimation for a partial-linear single-index model [correction on MR2589322]. Ann. Statist. 2011, 39, 3441–3443. [Google Scholar] [CrossRef]
- Strzalkowska-Kominiak, E.; Cao, R. Maximum likelihood estimation for conditional distribution single-index models under censoring. J. Multivar. Anal. 2013, 114, 74–98. [Google Scholar] [CrossRef]
- Saidi, A.A.; Ferraty, F.; Kassa, R. Single functional index model for a time series. Rev. Roum. Math. Pures Appl. 2005, 50, 321–330. [Google Scholar]
- Masry, E. Nonparametric regression estimation for dependent functional data: Asymptotic normality. Stoch. Process. Appl. 2005, 115, 155–177. [Google Scholar] [CrossRef]
- Ait-Saïdi, A.; Ferraty, F.; Kassa, R.; Vieu, P. Cross-validated estimations in the single-functional index model. Statistics 2008, 42, 475–494. [Google Scholar] [CrossRef]
- Shang, H.L. Estimation of a functional single index model with dependent errors and unknown error density. arXiv 2018, arXiv:1810.08714. [Google Scholar] [CrossRef]
- Novo, S.; Aneiros, G.; Vieu, P. Automatic and location-adaptive estimation in functional single-index regression. J. Nonparametr. Stat. 2019, 31, 364–392. [Google Scholar] [CrossRef]
- Li, J.; Huang, C.; Zhu, H. A functional varying-coefficient single-index model for functional response data. J. Amer. Statist. Assoc. 2017, 112, 1169–1181. [Google Scholar] [CrossRef]
- Attaoui, S.; Ling, N. Asymptotic results of a nonparametric conditional cumulative distribution estimator in the single functional index modeling for time series data with applications. Metrika 2016, 79, 485–511. [Google Scholar] [CrossRef]
- Wang, G.; Feng, X.N.; Chen, M. Functional partial linear single-index model. Scand. J. Stat. 2016, 43, 261–274. [Google Scholar] [CrossRef]
- Attaoui, S.; Bentata, B.; Bouzebda, S.; Laksaci, A. The strong consistency and asymptotic normality of the kernel estimator type in functional single index model in presence of censored data. AIMS Math. 2024, 9, 7340–7371. [Google Scholar] [CrossRef]
- Elmezouar, Z.C.; Alshahrani, F.; Almanjahie, I.M.; Bouzebda, S.; Kaid, Z.; Laksaci, A. Strong consistency rate in functional single index expectile model for spatial data. AIMS Math. 2024, 9, 5550–5581. [Google Scholar] [CrossRef]
- Douge, L. Théorèmes limites pour des variables quasi-associées hilbertiennes. Ann. ISUP 2010, 54, 51–60. [Google Scholar]
- Attaoui, S.; Laksaci, A.; Ould Said, E. A note on the conditional density estimate in the single functional index model. Statist. Probab. Lett. 2011, 81, 45–53. [Google Scholar] [CrossRef]
- Ling, N.; Xu, Q. Asymptotic normality of conditional density estimation in the single index model for functional time series data. Statist. Probab. Lett. 2012, 82, 2235–2243. [Google Scholar] [CrossRef]
- Ye, Z.; Hooker, G. Local Quadratic Estimation of the Curvature in a Functional Single Index Model. arXiv 2018, arXiv:1803.09321. [Google Scholar] [CrossRef]
- Douge, L. Nonparametric regression estimation for quasi-associated Hilbertian processes. arXiv 2018, arXiv:1805.02422. [Google Scholar]
- Kallabis, R.S.; Neumann, M.H. An exponential inequality under weak dependence. Bernoulli 2006, 12, 333–350. [Google Scholar] [CrossRef]
- Bouzebda, S.; Laksaci, A.; Mohammedi, M. The k-nearest neighbors method in single index regression model for functional quasi-associated time series data. Rev. Mat. Complut. 2023, 36, 361–391. [Google Scholar] [CrossRef]
- Harris, T.E. A lower bound for the critical probability in a certain percolation process. Proc. Camb. Philos. Soc. 1960, 56, 13–20. [Google Scholar] [CrossRef]
- Lehmann, E.L. Some concepts of dependence. Ann. Math. Statist. 1966, 37, 1137–1153. [Google Scholar] [CrossRef]
- Joag-Dev, K.; Proschan, F. Negative association of random variables, with applications. Ann. Statist. 1983, 11, 286–295. [Google Scholar] [CrossRef]
- Bulinski, A.; Sabanovitch, E. Asymptotical behaviour of some functionals of positively and negatively random fields. Fundam. Appl. Math. 1998, 4, 479–492. [Google Scholar]
- Shashkin, A.P. Quasi-associatedness of a Gaussian system of random vectors. Uspekhi Mat. Nauk 2002, 57, 199–200. [Google Scholar] [CrossRef]
- Bulinskii, A.V.; Shashkin, A.P. Rates in the CLT for sums of dependent multiindexed random vectors. J. Math. Sci. 2004, 122, 3343–3358. [Google Scholar] [CrossRef]
- Newman, C.M. Asymptotic independence and limit theorems for positively and negatively dependent random variables. In Inequalities in Statistics and Probability (Lincoln, Neb., 1982); IMS Lecture Notes Monograph Series; Institute of Mathematical Statistics: Hayward, CA, USA, 1984; Volume 5, pp. 127–140. [Google Scholar] [CrossRef]
- Pitt, L.D. Positively correlated normal variables are associated. Ann. Probab. 1982, 10, 496–499. [Google Scholar] [CrossRef]
- Doukhan, P. Mixing; Lecture Notes in Statistics; Springer: New York, NY, USA, 1994; Volume 85, pp. xii+142. [Google Scholar] [CrossRef]
- Pham, T.D.; Tran, L.T. Some mixing properties of time series models. Stoch. Process. Appl. 1985, 19, 297–303. [Google Scholar] [CrossRef]
- Andrews, D.W.K. Nonstrong mixing autoregressive processes. J. Appl. Probab. 1984, 21, 930–934. [Google Scholar] [CrossRef]
- Louhichi, S. Weak convergence for empirical processes of associated sequences. Ann. Inst. H. Poincaré Probab. Statist. 2000, 36, 547–567. [Google Scholar] [CrossRef]
- Bradley, R.C. Basic properties of strong mixing conditions. A survey and some open questions. Probab. Surv. 2005, 2, 107–144. [Google Scholar] [CrossRef]
- Yu, H. A Glivenko-Cantelli lemma and weak convergence for empirical processes of associated sequences. Probab. Theory Relat. Fields 1993, 95, 357–370. [Google Scholar] [CrossRef]
- Nadaraja, E.A. On a regression estimate. Teor. Verojatnost. Primenen. 1964, 9, 157–159. [Google Scholar]
- Watson, G.S. Smooth regression analysis. Sankhyā Ser. A 1964, 26, 359–372. [Google Scholar]
- Carbonez, A.; Györfi, L.; van der Meulen, E.C. Partitioning-estimates of a regression function under random censoring. Statist. Decis. 1995, 13, 21–37. [Google Scholar] [CrossRef]
- Kohler, M.; Máthé, K.; Pintér, M. Prediction from randomly right censored data. J. Multivar. Anal. 2002, 80, 73–100. [Google Scholar] [CrossRef]
- Bouzebda, S.; Chaouch, M. Uniform limit theorems for a class of conditional Z-estimators when covariates are functions. J. Multivar. Anal. 2022, 189, 104872. [Google Scholar] [CrossRef]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Deheuvels, P.; Einmahl, J.H.J. Functional limit laws for the increments of Kaplan-Meier product-limit processes and applications. Ann. Probab. 2000, 28, 1301–1335. [Google Scholar] [CrossRef]
- Hall, P.; Hosseini-Nasab, M. On properties of functional principal components analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 109–126. [Google Scholar] [CrossRef]
- Ferraty, F.; Mas, A.; Vieu, P. Nonparametric regression on functional data: Inference and practical aspects. Aust. N. Z. J. Stat. 2007, 49, 267–286. [Google Scholar] [CrossRef]
- Karhunen, K. Über lineare Methoden in der Wahrscheinlichkeitsrechnung. Ann. Acad. Sci. Fenn. Ser. A I Math.-Phys. 1947, 1947, 79. [Google Scholar]
- Loève, M. Probability Theory II, 4th ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1978; Volume 46, pp. xvi+413. [Google Scholar]
- Loève, M. Probability Theory. Foundations. Random Sequences; D. Van Nostrand Co., Inc.: Toronto, ON, Canada; New York, NY, USA; London, UK, 1955; pp. xv+515. [Google Scholar]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 1989; pp. xix+511. [Google Scholar] [CrossRef]
- Yao, W. A bias corrected nonparametric regression estimator. Statist. Probab. Lett. 2012, 82, 274–282. [Google Scholar] [CrossRef]
- Karlsson, A. Bootstrap methods for bias correction and confidence interval estimation for nonlinear quantile regression of longitudinal data. J. Stat. Comput. Simul. 2009, 79, 1205–1218. [Google Scholar] [CrossRef]
- Bouzebda, S.; Nezzal, A.; Zari, T. Uniform Consistency for Functional Conditional U-Statistics Using Delta-Sequences. Mathematics 2023, 11, 161. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Wu, H.T. Local linear regression on manifolds and its geometric interpretation. J. Amer. Statist. Assoc. 2013, 108, 1421–1434. [Google Scholar] [CrossRef]
- Soukarieh, I.; Bouzebda, S. Weak convergence of the conditional U-statistics for locally stationary functional time series. Stat. Inference Stoch. Process. 2024, 27, 227–304. [Google Scholar] [CrossRef]
- Bouzebda, S.; Didi, S. Multivariate wavelet density and regression estimators for stationary and ergodic discrete time processes: Asymptotic results. Comm. Statist. Theory Methods 2017, 46, 1367–1406. [Google Scholar] [CrossRef]
- Doob, J.L. Stochastic Processes; John Wiley & Sons, Inc.: New York, NY, USA; Chapman & Hall, Ltd.: London, UK, 1953; pp. viii+654. [Google Scholar]
- Cai, Z. Estimating a distribution function for censored time series data. J. Multivar. Anal. 2001, 78, 299–318. [Google Scholar] [CrossRef]

| Functional Time Series Case | n | Bias | Var | |
|---|---|---|---|---|
| 50 | 2 | 0.1436 | 0.783 | |
| 50 | 0.5 | 0.230 | 0.952 | |
| 50 | 0.05 | 0.111 | 0.998 | |
| 100 | 2 | 0.196 | 0.874 | |
| Independent case | 100 | 0.5 | 0.112 | 0.831 |
| 100 | 0.05 | 0.051 | 0.967 | |
| 350 | 2 | 0.121 | 0.697 | |
| 350 | 0.5 | 0.101 | 0.715 | |
| 350 | 0.05 | 0.022 | 0.881 | |
| 50 | 2 | 0.247 | 0.861 | |
| 50 | 0.5 | 0.331 | 0.753 | |
| 50 | 0.05 | 0.102 | 0.977 | |
| 100 | 2 | 0.166 | 0.699 | |
| FAR(1) | 100 | 0.5 | 0.126 | 0.702 |
| 100 | 0.05 | 0.099 | 0.913 | |
| 350 | 2 | 0.135 | 0.578 | |
| 350 | 0.5 | 0.881 | 0.677 | |
| 350 | 0.05 | 0.085 | 0.863 | |
| 50 | 2 | 0.281 | 0.841 | |
| 50 | 0.5 | 0.173 | 0.919 | |
| 50 | 0.05 | 0.184 | 0.942 | |
| 100 | 2 | 0.169 | 0.768 | |
| FARCH(1,1) | 100 | 0.5 | 0.142 | 0.823 |
| 100 | 0.05 | 0.106 | 0.893 | |
| 350 | 2 | 0.117 | 0.673 | |
| 350 | 0.5 | 0.110 | 0.671 | |
| 350 | 0.05 | 0.098 | 0.855 | |
| 50 | 2 | 0.357 | 1.811 | |
| 50 | 0.5 | 0.175 | 1.182 | |
| 50 | 0.05 | 0.194 | 1.121 | |
| 100 | 2 | 0.2126 | 1.630 | |
| FGARCH(1,1) | 100 | 0.5 | 0.143 | 1.071 |
| 100 | 0.05 | 0.136 | 1.018 | |
| 350 | 2 | 0.181 | 1.541 | |
| 350 | 0.5 | 0.121 | 1.131 | |
| 350 | 0.05 | 0.119 | 1.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attaoui, S.; Benouda, O.E.; Bouzebda, S.; Laksaci, A. Limit Theorems for Kernel Regression Estimator for Quasi-Associated Functional Censored Time Series Within Single Index Structure. Mathematics 2025, 13, 886. https://doi.org/10.3390/math13050886
Attaoui S, Benouda OE, Bouzebda S, Laksaci A. Limit Theorems for Kernel Regression Estimator for Quasi-Associated Functional Censored Time Series Within Single Index Structure. Mathematics. 2025; 13(5):886. https://doi.org/10.3390/math13050886
Chicago/Turabian StyleAttaoui, Said, Oum Elkheir Benouda, Salim Bouzebda, and Ali Laksaci. 2025. "Limit Theorems for Kernel Regression Estimator for Quasi-Associated Functional Censored Time Series Within Single Index Structure" Mathematics 13, no. 5: 886. https://doi.org/10.3390/math13050886
APA StyleAttaoui, S., Benouda, O. E., Bouzebda, S., & Laksaci, A. (2025). Limit Theorems for Kernel Regression Estimator for Quasi-Associated Functional Censored Time Series Within Single Index Structure. Mathematics, 13(5), 886. https://doi.org/10.3390/math13050886







