Computationally Efficient Design of 16-Poles and 24-Slots IPMSM for EV Traction Considering PWM-Induced Iron Loss Using Active Transfer Learning
Abstract
:1. Introduction
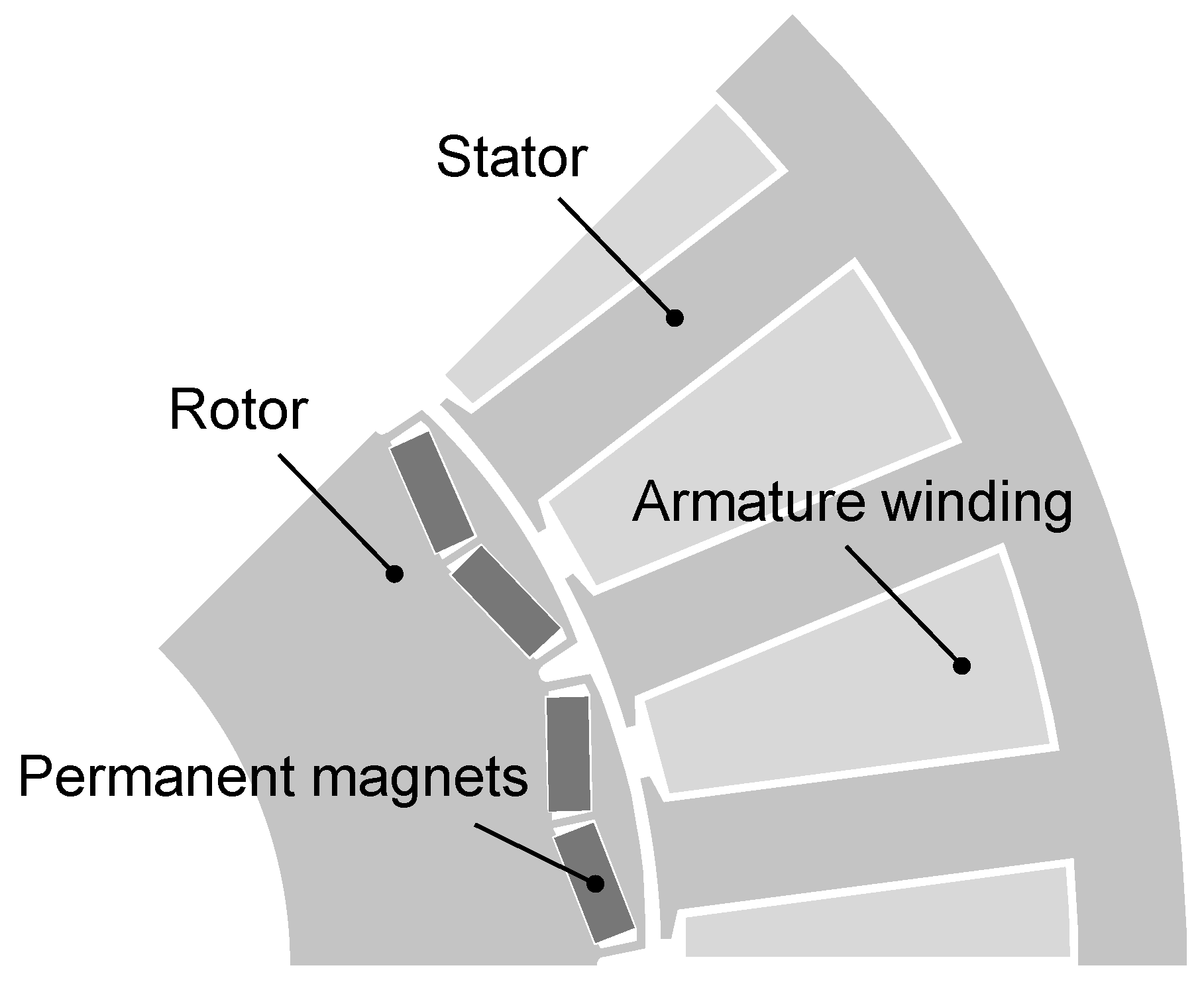
2. Mathematical Model of OEW-PMSM
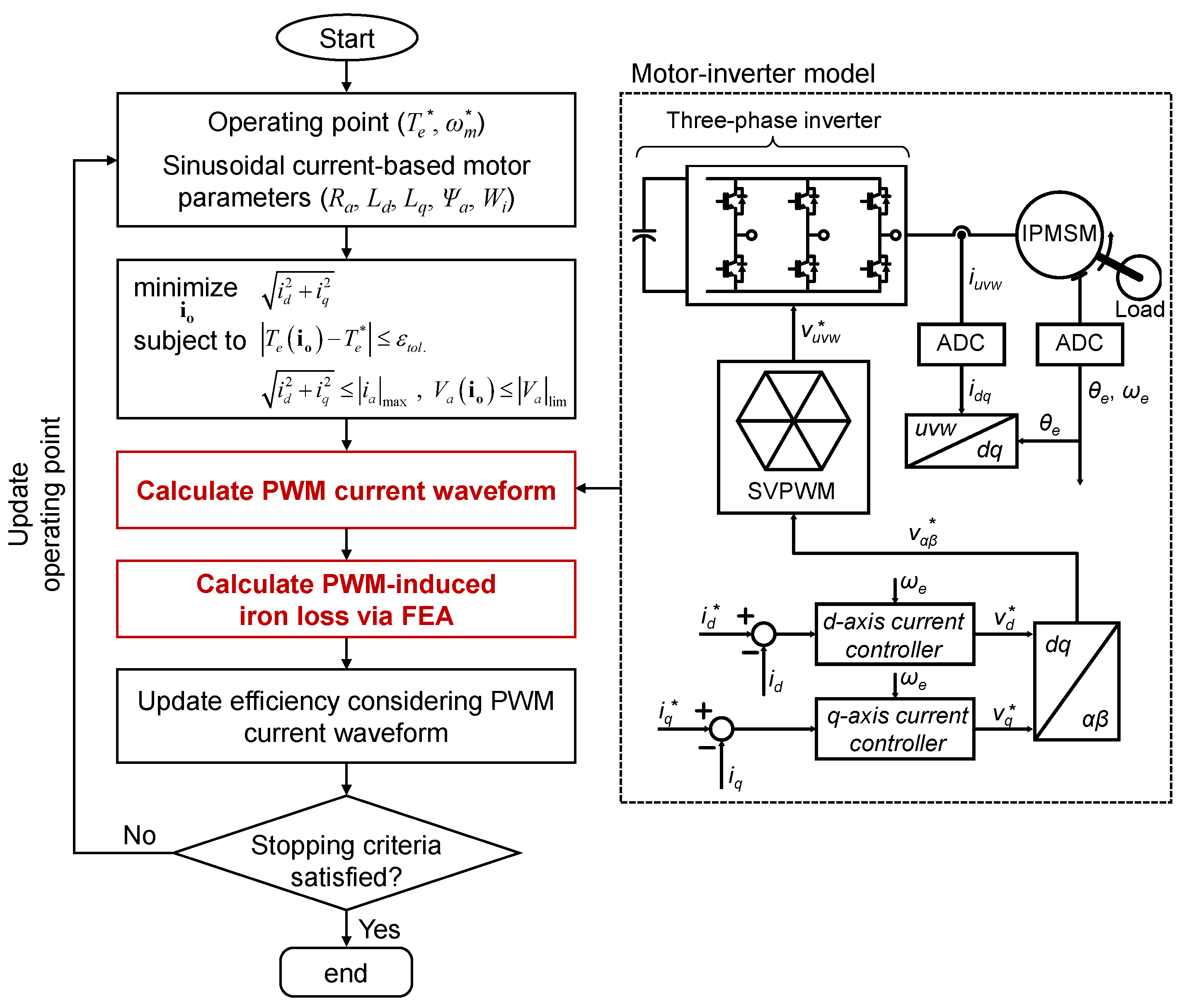
2.1. Procedure for Calculating PWM-Induced Iron Loss
2.2. Effect of PWM-Induced Iron Loss on Efficiency of IPMSM
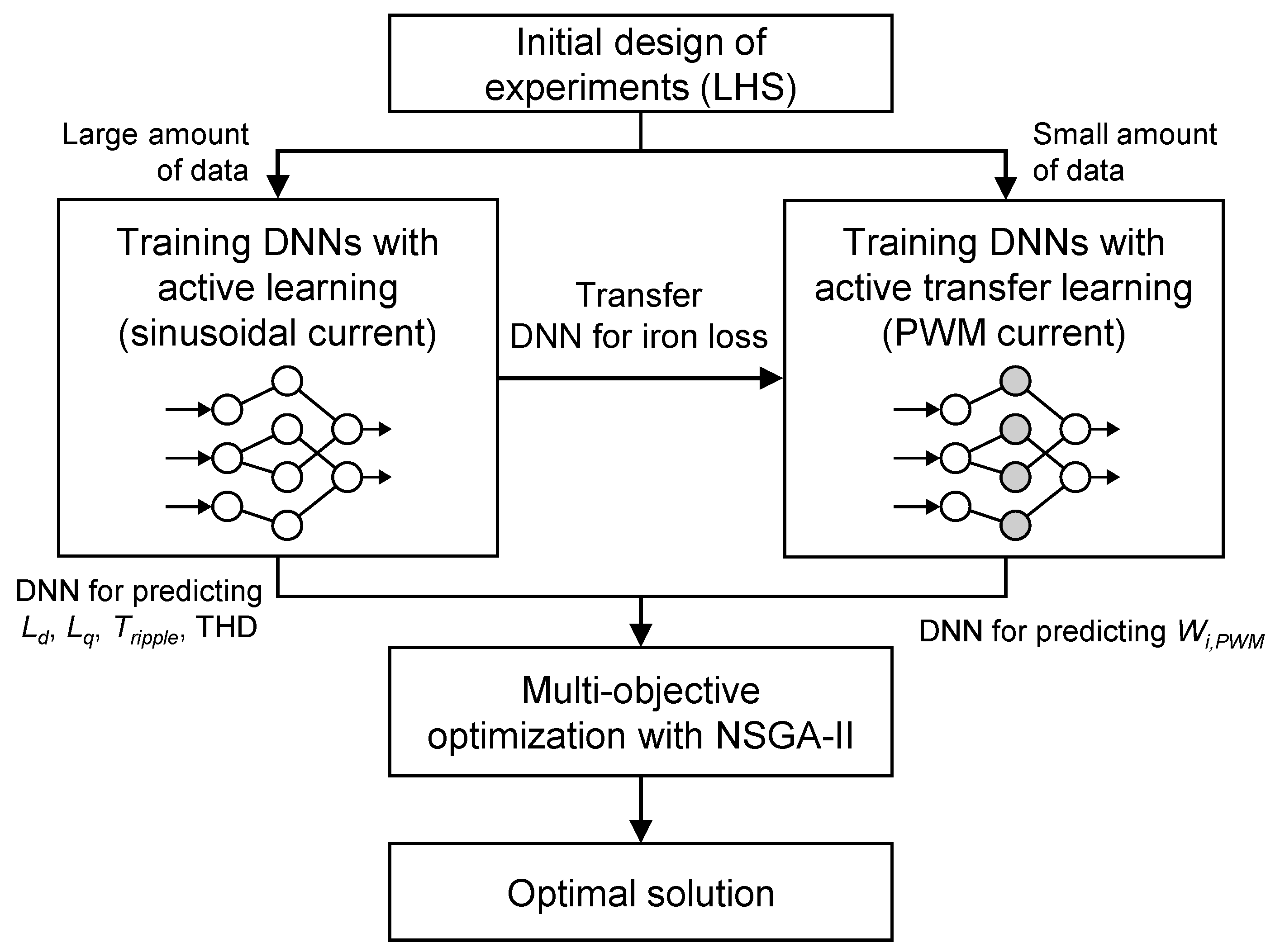
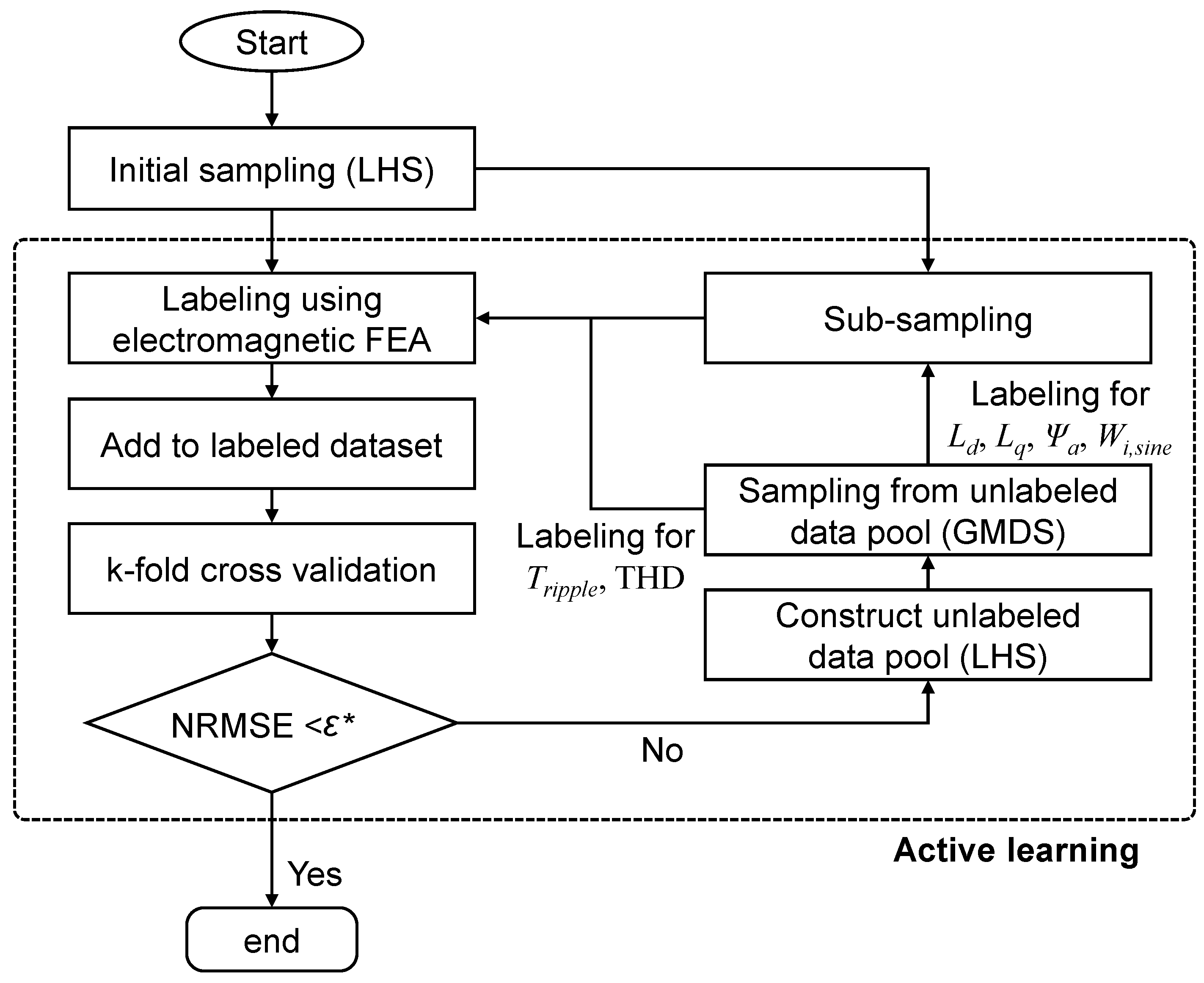
3. Design Optimization of Traction Motor Using Active Transfer Learning
3.1. Formulation of Design Optimization Problem
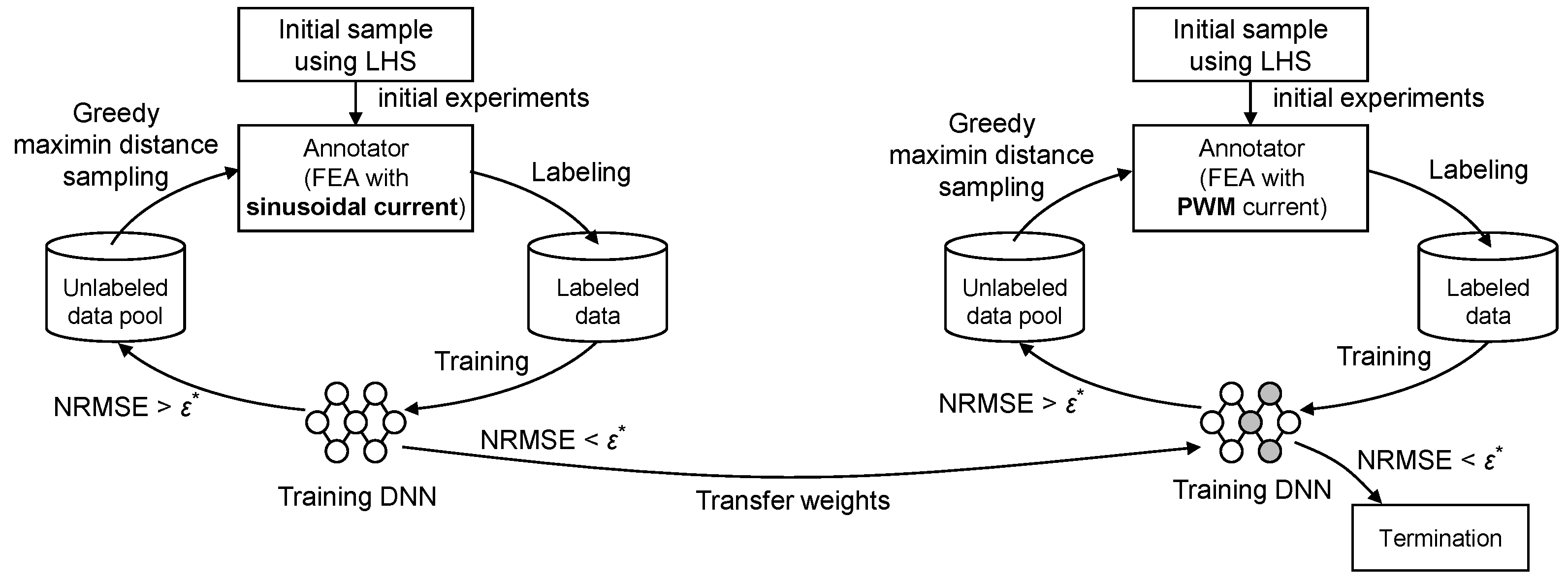
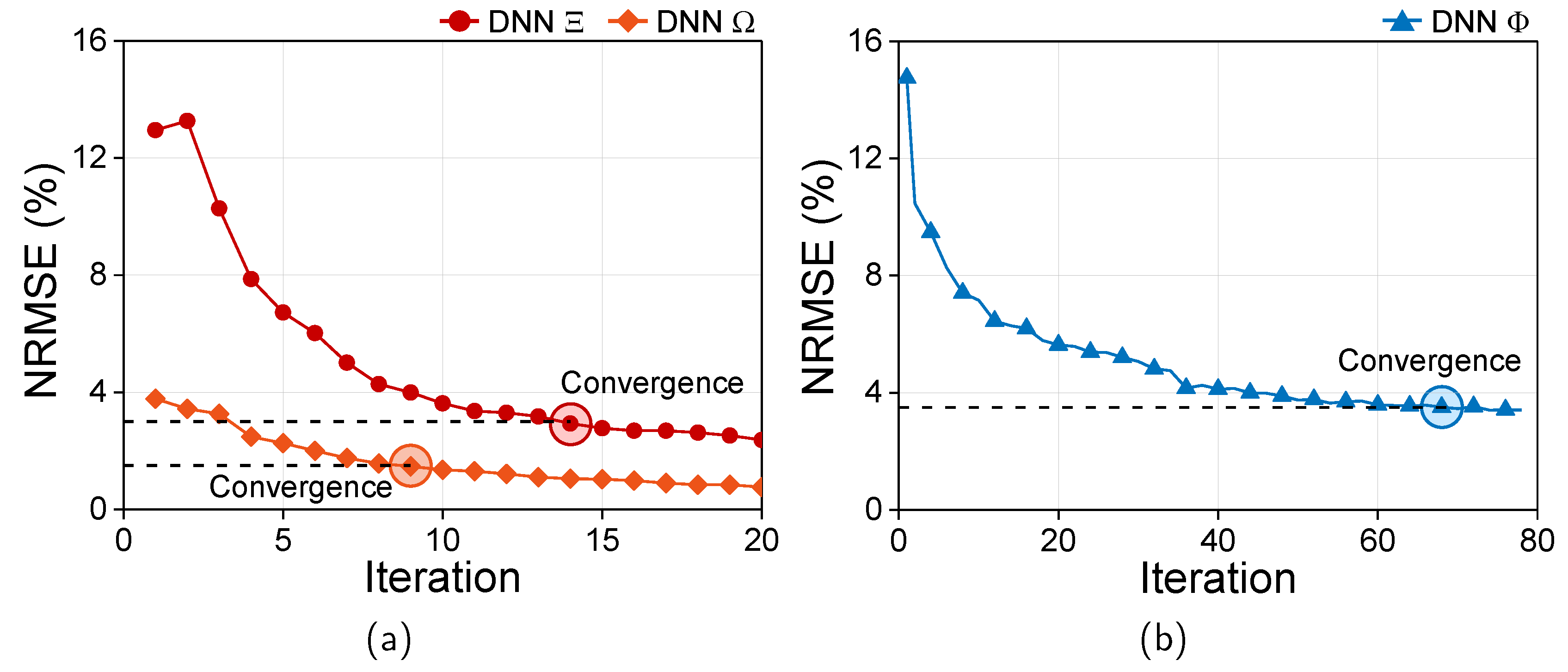
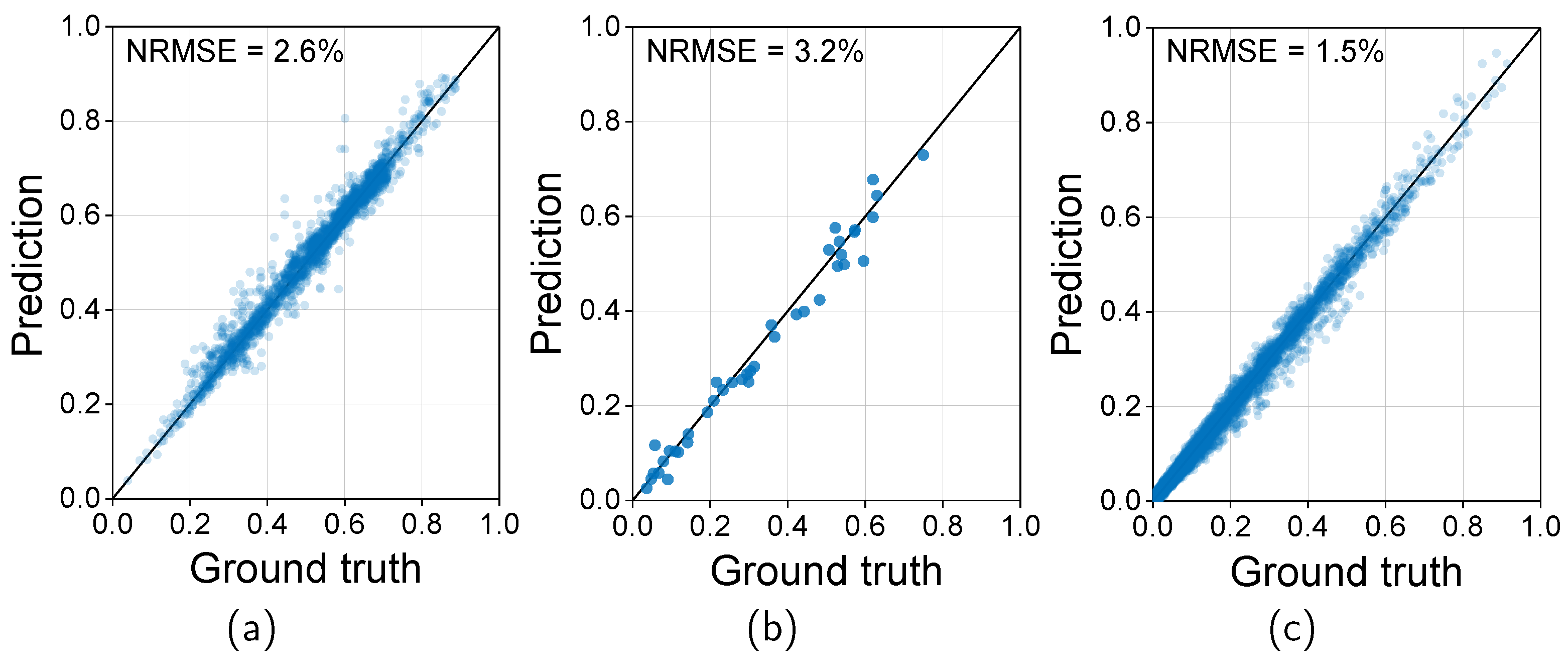
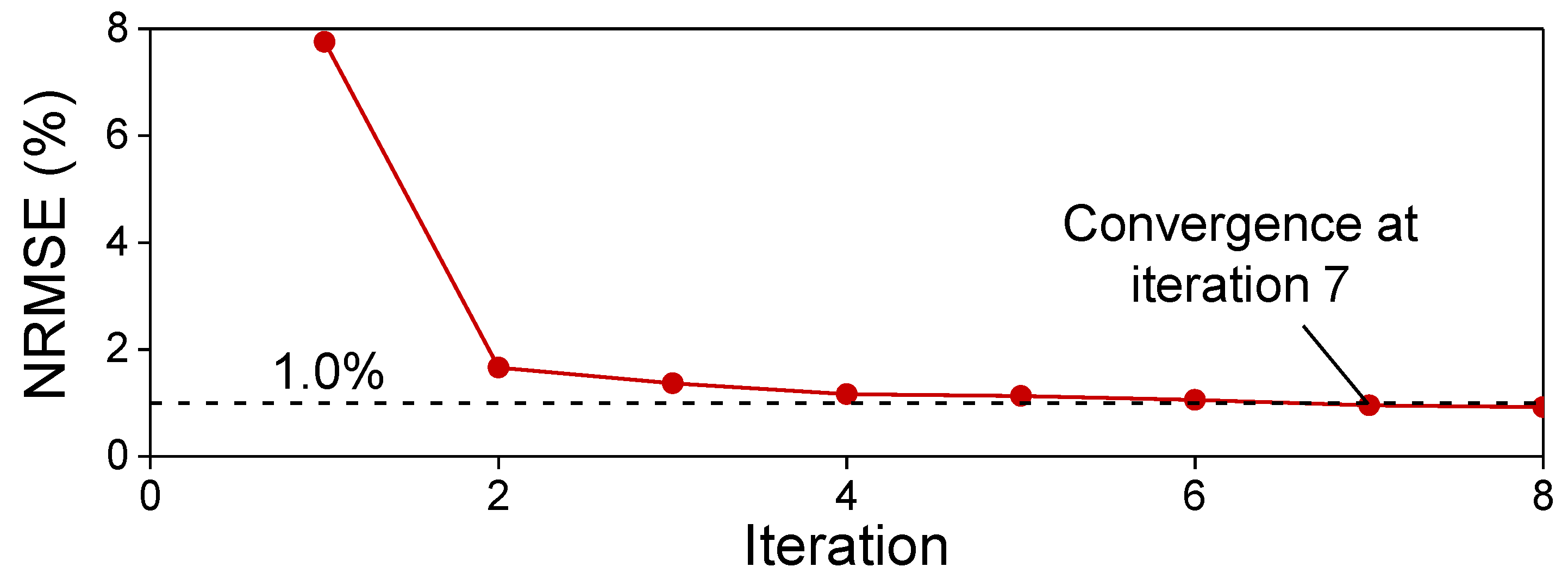
3.2. Training of DNNs for Sinusoidal and PWM Current-Based Motor Performance Using Active Transfer Learning
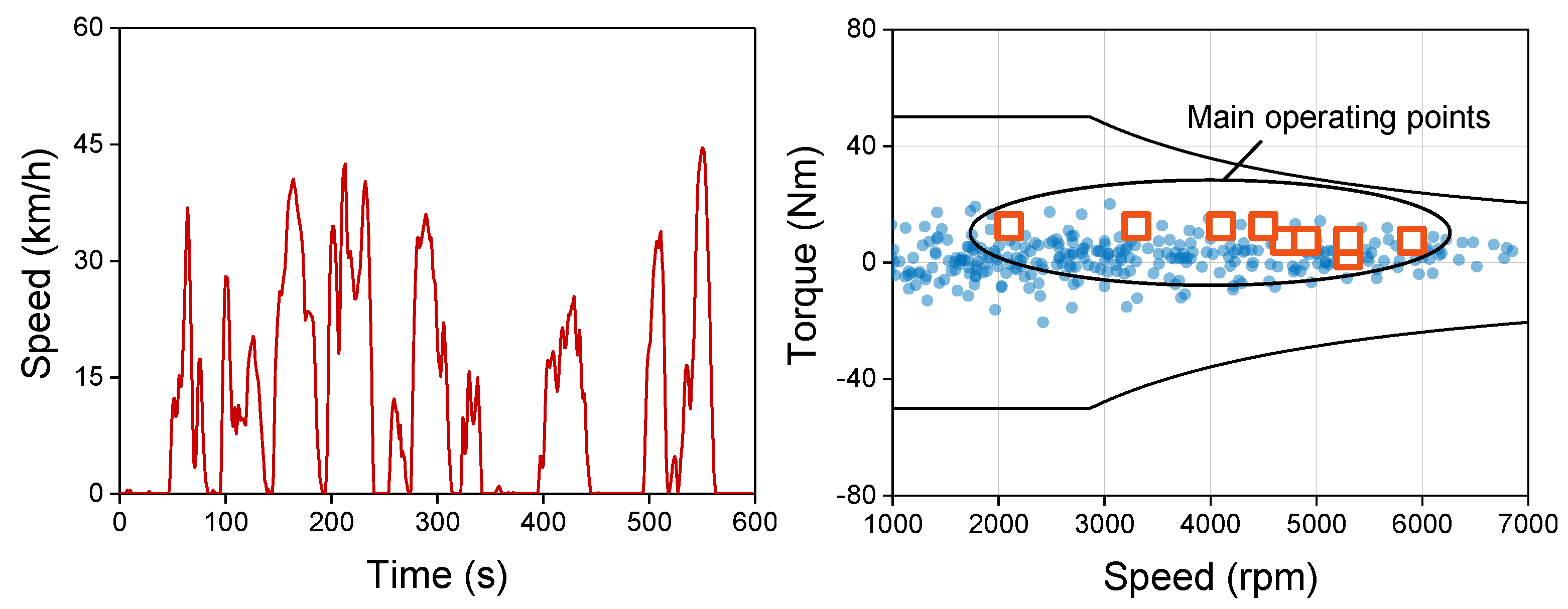
3.3. Design Results
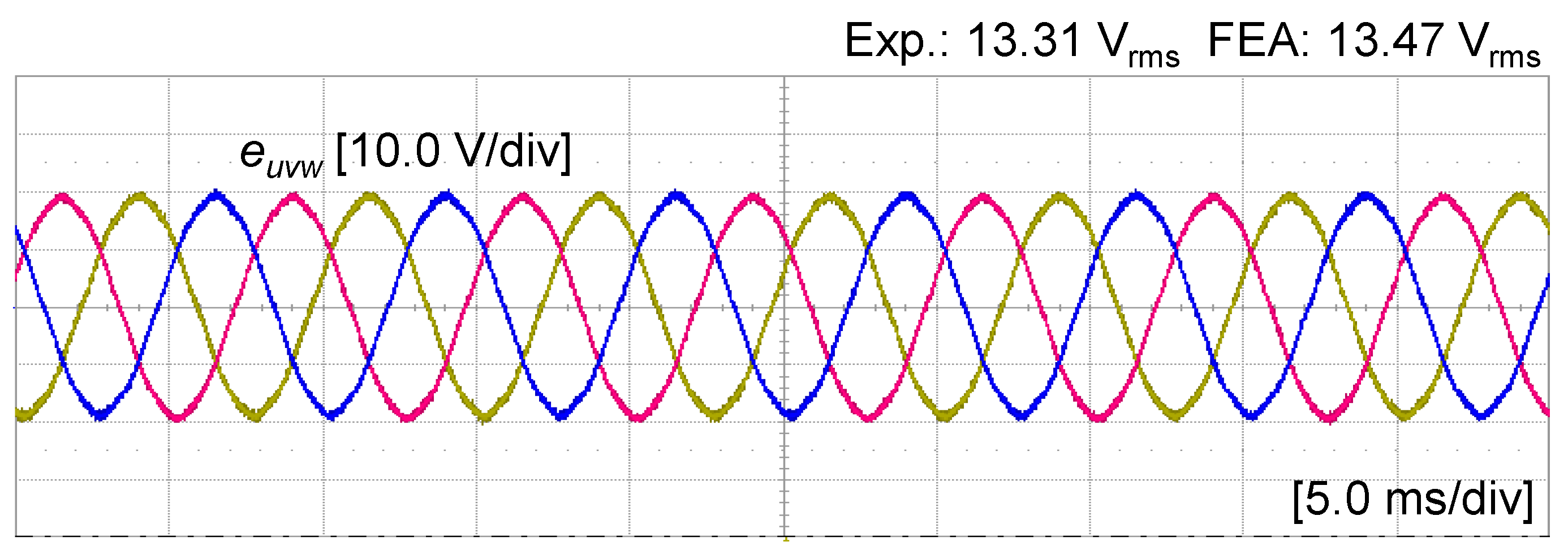
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krings, A.; Monissen, C. Review and Trends in Electric Traction Motors for Battery Electric and Hybrid Vehicles. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 1807–1813. [Google Scholar]
- Yang, Y.; Castano, S.M.; Yang, R.; Kasprzak, M.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. Design and Comparison of Interior Permanent Magnet Motor Topologies for Traction Applications. IEEE Trans. Transp. Electrif. 2017, 3, 86–97. [Google Scholar] [CrossRef]
- Husain, I.; Ozpineci, B.; Islam, M.S.; Gurpinar, E.; Su, G.J.; Yu, W.; Chowdhury, S.; Xue, L.; Rahman, D.; Sahu, R. Electric Drive Technology Trends, Challenges, and Opportunities for Future Electric Vehicles. Proc. IEEE 2021, 109, 1039–1059. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, E.C.; Park, J.C.; Hwang, S.W.; Lim, M.S. Prediction of Mechanical Loss for High-Power-Density PMSM Considering Eddy Current Loss of PMs and Conductors. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Fischer, M.; Werber, M.; Schwartz, P.V. Batteries: Higher Energy Density Than Gasoline? Energy Policy 2009, 37, 2639–2641. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, Y.G.; Lai, M.C. Effects of Battery Pack Capacity on Fuel Economy of Hybrid Electric Vehicles. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Brasov, Romania, 25–28 September 2022; IEEE: Piscataway, NJ, USA, 2021; pp. 771–775. [Google Scholar]
- Zhou, S.; Chen, Z.; Huang, D.; Lin, T. Model Prediction and Rule Based Energy Management Strategy for a Plug-In Hybrid Electric Vehicle with Hybrid Energy Storage System. IEEE Trans. Power Electron. 2021, 36, 5926–5940. [Google Scholar] [CrossRef]
- Shao, L.; Karci, A.E.H.; Tavernini, D.; Sorniotti, A.; Cheng, M. Design Approaches and Control Strategies for Energy-Efficient Electric Machines for Electric Vehicles—A Review. IEEE Access 2020, 8, 116900–116913. [Google Scholar] [CrossRef]
- Lee, J.D.; Park, D.H.; Kim, R.Y. Novel Variable Switching Frequency PWM Strategy for a SiC-MOSFET-Based Electric Vehicle Inverter to Increase Battery Usage Time. IEEE Access 2022, 10, 21929–21940. [Google Scholar] [CrossRef]
- Xue, S.; Feng, J.; Guo, S.; Chen, Z.; Peng, J.; Chu, W.; Xu, P.; Zhu, Z. Iron loss model for electrical machine fed by low switching frequency inverter. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, B. Modeling of PWM-induced iron losses with frequency-domain methods and low-frequency parameters. IEEE Trans. Ind. Electron. 2022, 69, 2402–2413. [Google Scholar] [CrossRef]
- Ahn, D.G.; Yoon, M.H.; Hong, J.P.; Jung, J.W. Finite-Element Analysis of Local Flux Density Variation Considering PWM Current Harmonics. IEEE Trans. Magn. 2018, 54, 8201804. [Google Scholar] [CrossRef]
- Jeong, T.C.; Kim, W.H.; Kim, M.J.; Lee, K.D.; Lee, J.J.; Han, J.H.; Sung, T.H.; Kim, H.J.; Lee, J. Current Harmonics Loss Analysis of 150-kW Traction Interior Permanent Magnet Synchronous Motor Through Co-Analysis of d, q-Axis Current Control and Finite Element Method. IEEE Trans. Magn. 2013, 49, 2343–2346. [Google Scholar] [CrossRef]
- Akatsu, K.; Narita, K.; Sakashita, Y.; Yamada, T. Impact of Flux Weakening Current to the Iron Loss in an IPMSM Including PWM Carrier Effect. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1927–1932. [Google Scholar]
- Yamazaki, K.; Abe, A. Loss Investigation of Interior Permanent-Magnet Motors Considering Carrier Harmonics and Magnet Eddy Currents. IEEE Trans. Ind. Appl. 2009, 45, 659–665. [Google Scholar] [CrossRef]
- Sarigiannidis, A.G.; Kladas, A.G. Switching Frequency Impact on Permanent Magnet Motors Drive System for Electric Actuation Applications. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Park, S.H.; Chin, J.W.; Cha, K.S.; Ryu, J.Y.; Lim, M.S. Investigation of AC Copper Loss Considering Effect of Field and Armature Excitation on IPMSM with Hairpin Winding. IEEE Trans. Ind. Electron. 2023, 70, 12102–12112. [Google Scholar] [CrossRef]
- Yamazaki, K.; Seto, Y. Iron Loss Analysis of Interior Permanent-Magnet Synchronous Motors-Variation of Main Loss Factors due to Driving Condition. IEEE Trans. Ind. Appl. 2006, 42, 1045–1052. [Google Scholar] [CrossRef]
- Cheong, B.; Giangrande, P.; Zhang, X.; Galea, M.; Zanchetta, P.; Wheeler, P. Evolutionary Multiobjective Optimization of a System-Level Motor Drive Design. IEEE Trans. Ind. Appl. 2020, 56, 6904–6913. [Google Scholar] [CrossRef]
- Godbehere, J.; Popescu, M.; Michon, M. Optimization of an IPM Traction Motor Considering the Electric Drive Unit System Requirements. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3667–3674. [Google Scholar]
- Duan, Y.; Ionel, D.M. A Review of Recent Developments in Electrical Machine Design Optimization Methods with a Permanent-Magnet Synchronous Motor Benchmark Study. IEEE Trans. Ind. Appl. 2013, 49, 1268–1275. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design Optimization, and Applications of Switched Reluctance Machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Shimizu, Y.; Morimoto, S.; Sanada, M.; Inoue, Y. Investigation of Irreversible Demagnetization Constraints in Magnet Volume Minimization Design of IPMSM for Automotive Applications Using Machine Learning. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Park, S.H.; Chin, J.W.; Cha, K.S.; Lim, M.S. Deep Transfer Learning-Based Sizing Method of Permanent Magnet Synchronous Motors Considering Axial Leakage Flux. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Barmada, S.; Fontana, N.; Sani, L.; Thomopulos, D.; Tucci, M. Deep Learning and Reduced Models for Fast Optimization in Electromagnetics. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Ibrahim, I.; Silva, R.; Mohammadi, M.H.; Ghorbanian, V.; Lowther, D.A. Surrogate Models for Design and Optimization of Inverter-Fed Synchronous Motor Drives. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Wu, D.; Lin, C.T.; Huang, J. Active learning for regression using greedy sampling. Inf. Sci. 2019, 474, 90–105. [Google Scholar] [CrossRef]






| Item | Unit | Value |
|---|---|---|
| Number of poles | - | 16 |
| Number of slots | - | 24 |
| Nominal battery voltage | V | 144 |
| Max. output power | kW | 14.5 |
| Peak torque | Nm | 45 |
| Max. speed | rpm | 7000 |
| Max. current deisnty | Arms/mm2 | 15.0 |
| Switching frequency | kHz | 12 |
| Operating temperature | °C | 50 |
| Drag coefficient | - | 0.64 |
| Frontal area | m2 | 1.59 |
| Vehicle weight | kg | 690 |
| Drive cycle | - | NYCC |
| Design Variables | Unit | Min. | Max. |
|---|---|---|---|
| Slot area | mm2 | 75.0 | 100.0 |
| Slot open | mm | 1.0 | 4.0 |
| Tooth tip | mm | 0.5 | 1.2 |
| Split ratio | - | 0.65 | 0.75 |
| PM thickness | mm | 2.0 | 3.5 |
| Pole arc | deg. | 7.5 | 9.0 |
| PM angle | deg. | 38.0 | 85.0 |
| Rotor eccentricity | mm | 9.8 | 33.5 |
| Item | DNN | DNN | DNN |
|---|---|---|---|
| Output | , | , THD | |
| Target accuracy | 3.0% | 3.5% | 1.5% |
| No. of samples for each iteration | 20 | 20 | 20 |
| No. of subsamples for each iteration | 35 | - | 315 |
| Total no. of data for each iteration | 700 | 20 | 6300 |
| No. of hidden layers | 4 | 4 | 4 |
| No. of hidden units | 256 | 256 | 256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Lim, M.-S. Computationally Efficient Design of 16-Poles and 24-Slots IPMSM for EV Traction Considering PWM-Induced Iron Loss Using Active Transfer Learning. Mathematics 2025, 13, 915. https://doi.org/10.3390/math13060915
Park S-H, Lim M-S. Computationally Efficient Design of 16-Poles and 24-Slots IPMSM for EV Traction Considering PWM-Induced Iron Loss Using Active Transfer Learning. Mathematics. 2025; 13(6):915. https://doi.org/10.3390/math13060915
Chicago/Turabian StylePark, Soo-Hwan, and Myung-Seop Lim. 2025. "Computationally Efficient Design of 16-Poles and 24-Slots IPMSM for EV Traction Considering PWM-Induced Iron Loss Using Active Transfer Learning" Mathematics 13, no. 6: 915. https://doi.org/10.3390/math13060915
APA StylePark, S.-H., & Lim, M.-S. (2025). Computationally Efficient Design of 16-Poles and 24-Slots IPMSM for EV Traction Considering PWM-Induced Iron Loss Using Active Transfer Learning. Mathematics, 13(6), 915. https://doi.org/10.3390/math13060915







