An Analysis of Nonlinear Axisymmetric Structural Vibrations of Circular Plates with the Extended Rayleigh–Ritz Method
Abstract
1. Introduction
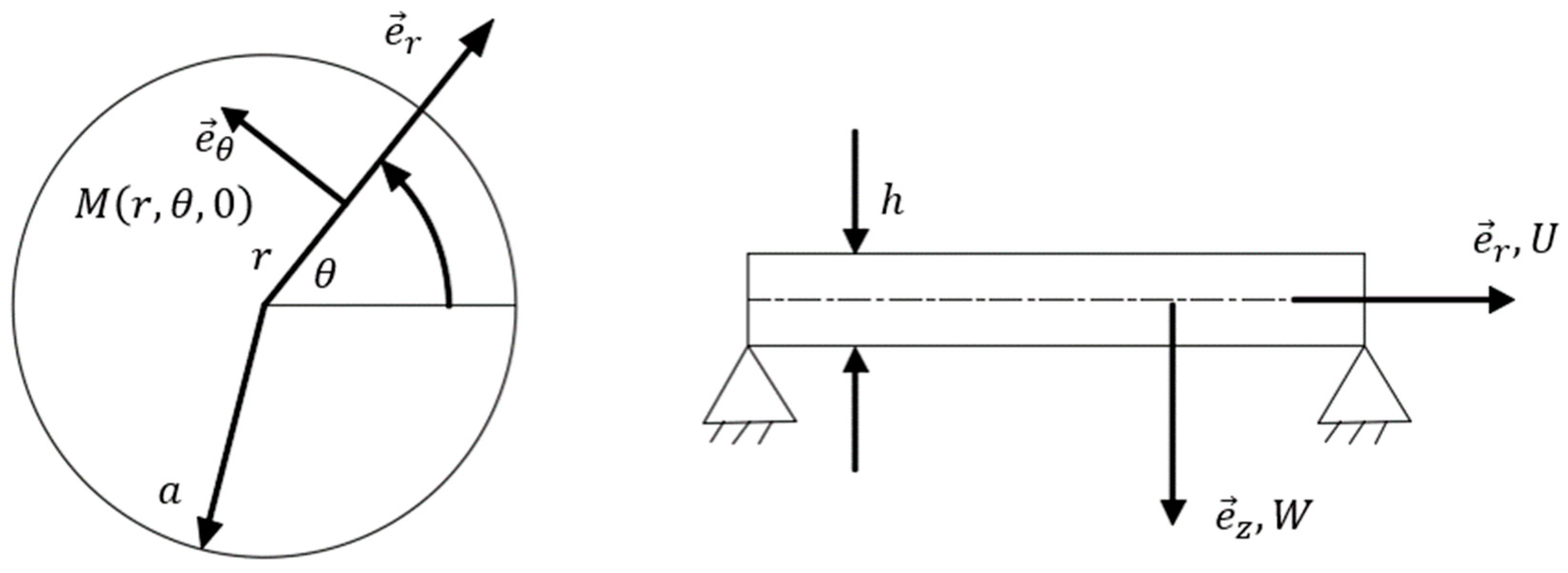
2. The ERRM for Nonlinear Axisymmetric Vibrations of Circular Plates
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Touzé, C.; Thomas, O.; Chaigne, A. Asymmetric non-linear forced vibrations of free-edge circular plates. Part 1: Theory. J. Sound. Vib. 2002, 258, 649–676. [Google Scholar] [CrossRef]
- Stoykov, S.; Ribeiro, P. Periodic geometrically nonlinear free vibrations of circular plates. J. Sound. Vib. 2008, 315, 536–555. [Google Scholar] [CrossRef]
- Hu, Y.D.; Wang, T. Nonlinear free vibration of a rotating circular plate under the static load in magnetic field. Nonlinear Dynam. 2016, 85, 1825–1835. [Google Scholar] [CrossRef]
- Tho, N.C.; Ta, N.T.; Thom, D.V. New numerical results from simulations of beams and space frame systems with a tuned mass damper. Materials 2019, 12, 1329. [Google Scholar] [CrossRef]
- Sherif, H.A. Non-linear forced flexural vibrations of a clamped circular unsymmetrical sandwich plate. J. Sound. Vib. 1995, 182, 495–503. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Geometrically nonlinear free vibration of FG-GPLRC circular plate on the nonlinear elastic foundation. Compos. Struct. 2021, 261, 113515. [Google Scholar] [CrossRef]
- Singh, B.; Saxena, V. Axisymmetric vibration of a circular plate with double linear variable thickness. J. Sound. Vib. 1995, 179, 879–897. [Google Scholar] [CrossRef]
- Elishakoff, I. Axisymmetric vibration of inhomogeneous free circular plates: An unusual exact, closed-form solution. J. Sound. Vib. 2000, 234, 167–170. [Google Scholar] [CrossRef]
- Mohammadi, M.; Farajpour, A.; Danesh, M. Buckling analysis of variable thickness nanoplates using nonlocal continuum mechanics. Phys. E 2012, 44, 719–727. [Google Scholar]
- Lee, W.M.; Chen, J.T. Free vibration analysis of a circular plate with multiple circular holes by using the multipole Trefftz method. Cmes. Comp. Model. Eng. 2009, 50, 141–160. [Google Scholar] [CrossRef]
- Avramov, K.V.; Tyshkovets, O.; Maksymenko-Sheyko, K.V. Analysis of nonlinear free vibration of circular plates with cut-outs using R-function method. J. Vib. Acoust. 2010, 132, 051001. [Google Scholar] [CrossRef]
- Srinivasan, A.V. Non-linear vibrations of beams and plates. Int. J. Nonlin Mech. 1996, 1, 179–191. [Google Scholar] [CrossRef]
- Yu, Y.Y. Vibrations of Elastic Plates; Springer: New York, NY, USA, 1996. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Haterbouch, M.; Benamar, R. Geometrically nonlinear free vibrations of simply supported isotropic thin circular plates. J. Sound. Vib. 2005, 280, 903–924. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Wu, R.; Wang, J.; Du, J.; Huang, D.; Yan, W.; Hu, Y. An analysis of nonlinear vibrations of coupled thickness-shear and flexural modes of quartz crystal plates with the Homotopy Analysis Method. IEEE T Ultrason. Ferr. 2012, 59, 30–39. [Google Scholar] [CrossRef]
- Decha-Umphai, K.; Mei, C. Finite element method for non-linear forced vibrations of circular plates. Int. J. Numer. Methods Eng. 1986, 23, 1715–1726. [Google Scholar] [CrossRef]
- Dumir, P.C.; Bhaskar, A. Some erroneous finite element formulations of non-linear vibrations of beams and plates. J. Sound. Vib. 1988, 123, 517–527. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Shirazi, K.H.; Noghrehabadi, A. Application of recent powerful analytical approaches on the non-linear vibration of cantilever beams. Int. J. Nonlinear Sci. Numer. Simul. 2012, 13, 487–494. [Google Scholar] [CrossRef]
- Ilanko, S.; Monterrubio, L.E.; Mochida, Y. The Rayleigh–Ritz Method and Simple Applications. In The Rayleigh–Ritz Method for Structural Analysis; John Wiley & Sons: New York, NY, USA, 2014; pp. 21–31. [Google Scholar]
- Wang, J. The extended Rayleigh-Ritz method for an analysis of nonlinear vibrations. Mech. Adv. Mater. Struct. 2022, 29, 3281–3284. [Google Scholar] [CrossRef]
- Jing, H.; Gong, X.; Wang, J.; Wu, R.; Huang, B. An analysis of nonlinear beam vibrations with the Extended Rayleigh-Ritz Method. J. Appl. Comput. Mech. 2022, 8, 1299–1306. [Google Scholar]
- Lian, C.; Meng, B.; Jing, H.; Wu, R.; Lin, J.; Wang, J. The analysis of higher-order nonlinear vibrations of an elastic beam with the Extended Galerkin Method. J. Vib. Eng. Technol. 2023, 12, 2743–2758. [Google Scholar] [CrossRef]
- Wang, J.; Wu, R. The extended Galerkin method for approximate solutions of nonlinear vibration equations. Appl. Sci. 2022, 12, 2979. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W.; Yang, J.; Han, Q.K. Analytical analysis of forced vibration of the hard-coating cylindrical shell with material nonlinearity and elastic constraint. Comp. Struct. 2023, 187, 281–293. [Google Scholar] [CrossRef]
- Aimmanee, S.; Chutima, S.; Hyer, M.W. Nonlinear analysis of RAINBOW actuator characteristics. Smart Mater. Struct. 2009, 18, 045002. [Google Scholar] [CrossRef]
- Amenzadeh, R.Y.; Kiyasbeyli, E.T. Critical time of a long multilayer viscoelastic shell. Mech. Comps. Mater. 2007, 43, 419–426. [Google Scholar] [CrossRef]
| Frequency Ratio of Free Vibration | ||||
|---|---|---|---|---|
| Present | HBM [15] | FEM [19] | Perturbation [20] | |
| 0.2 | 1.0268 | 1.0268 | 1.0179 | 1.0274 |
| 0.4 | 1.1032 | 1.1034 | 1.0700 | 1.1055 |
| 0.5 | 1.1572 | 1.1577 | - | - |
| 0.6 | 1.2200 | 1.2209 | 1.1518 | 1.2246 |
| 0.8 | 1.3668 | 1.3693 | 1.2577 | 1.3741 |
| 1.0 | 1.5351 | 1.5401 | 1.3826 | 1.5452 |
| 1.5 | 2.0131 | 2.0288 | - | - |
| 2.0 | 2.5351 | 2.5664 | - | - |
| 2.5 | 3.0788 | 3.1285 | - | - |
| 3.0 | 3.6345 | 3.7038 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Gong, X.; Lian, C.; Jing, H.; Huang, B.; Zhang, Y.; Wang, J. An Analysis of Nonlinear Axisymmetric Structural Vibrations of Circular Plates with the Extended Rayleigh–Ritz Method. Mathematics 2025, 13, 1356. https://doi.org/10.3390/math13081356
Han J, Gong X, Lian C, Jing H, Huang B, Zhang Y, Wang J. An Analysis of Nonlinear Axisymmetric Structural Vibrations of Circular Plates with the Extended Rayleigh–Ritz Method. Mathematics. 2025; 13(8):1356. https://doi.org/10.3390/math13081356
Chicago/Turabian StyleHan, Jie, Xianglin Gong, Chencheng Lian, Huimin Jing, Bin Huang, Yangyang Zhang, and Ji Wang. 2025. "An Analysis of Nonlinear Axisymmetric Structural Vibrations of Circular Plates with the Extended Rayleigh–Ritz Method" Mathematics 13, no. 8: 1356. https://doi.org/10.3390/math13081356
APA StyleHan, J., Gong, X., Lian, C., Jing, H., Huang, B., Zhang, Y., & Wang, J. (2025). An Analysis of Nonlinear Axisymmetric Structural Vibrations of Circular Plates with the Extended Rayleigh–Ritz Method. Mathematics, 13(8), 1356. https://doi.org/10.3390/math13081356








