Review on System Identification, Control, and Optimization Based on Artificial Intelligence

Abstract

Control engineering plays an indispensable role in enhancing safety, improving comfort, and reducing fuel consumption and emissions for various industries, for which system identification, control, and optimization are primary topics. Alternatively, artificial intelligence (AI) is a leading, multi-disciplinary technology, which tries to incorporate human learning and reasoning into machines or systems. AI exploits data to improve accuracy, efficiency, and intelligence, which is beneficial, especially in complex and challenging cases. The rapid progress of AI facilitates major changes in control engineering and is helping advance the next generation of system identification, control, and optimization methods. In this study, we review the developments, key technologies, and recent advancements of AI-based system identification, control, and optimization methods, as well as present potential future research directions.

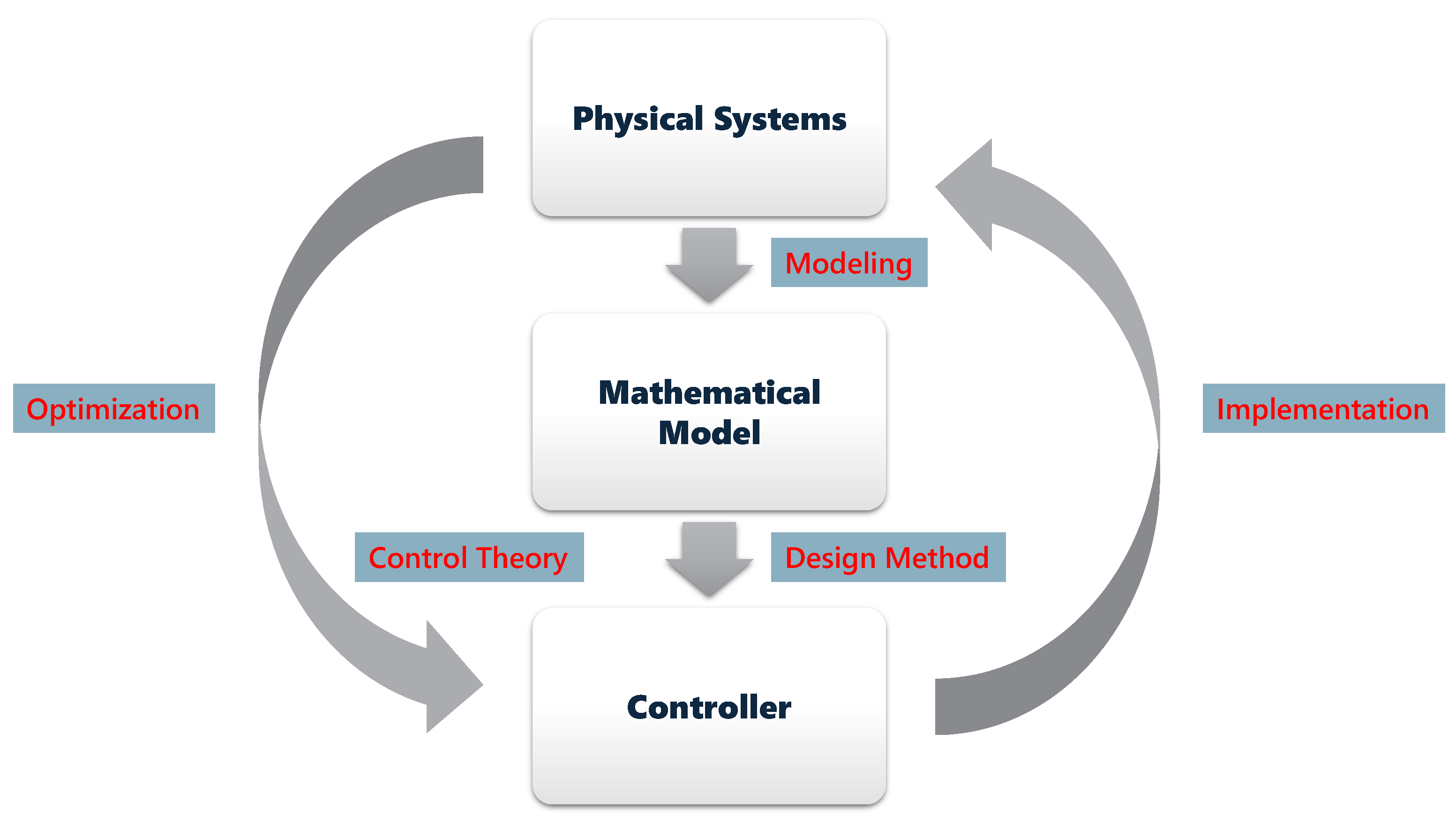
1. Introduction

Figuring out models from observations and unearthing their properties is really what science is about, and system identification is an important object of this process. System identification deals with the problem of figuring out mathematical models (such as deterministic models, stochastic models, non-parametric models, and parametric models) of dynamical systems based on the observed input-output data [1].

Although the term system identification was introduced by Lotfi Zadeh in the late 1950s [2], some progress (such as continuous functional [3], analytic functional [4]) was made by Maurice Fréchet and Vito Volterra before then. Since then, system identification has become an established research area within automatic control [5]. Considerable research has been conducted on this. Integral models can be used to describe the evolution of nonlinear dynamical systems [6]. Volterra series can be used to identify nonlinear dynamical systems [7], where integral equations play a key role in system analysis [8]. Moreover, it has been revealed that by using polynomial kernels, Volterra series can be represented implicitly as elements of a reproducing kernel Hilbert space [9]. The convex majorants method can be used to construct main solutions to nonlinear Volterra Equations [10]. A method was developed to compute the solution boundary of an interval outside which blow-up phenomena occur [11].

It is well known that when the essence, basic principles, or fundamental laws are known, mechanistic models (also called first-principles models, analytical models, or knowledge-based models) can be derived for dynamical systems. However, when dynamical systems are too complex to be understood at a fundamental level, data-driven approaches are a highly practical alternative to the first-principles approaches, which leverage computational algorithms or mathematical statistics to identify patterns in input-output data.

In general, the mechanism of dynamical systems is clear according to mechanistic models, while data-driven models are opaque because they are largely developed using mathematical methods. For this reason, mechanistic models are termed white-box models and data-driven models as black-box models. Integrating the traits of both modeling approaches yields hybrid modeling [12], which can be viewed as gray-box models. The structure of a hybrid model usually contains one part derived from first principles and the other part derived from data.

In addition to describing system dynamics, there may be other requirements, including the active manipulation of system behaviors. Control engineering involves applying control methods to design systems such that the systems behave in a desired manner, which has a wide range of applications, including aerospace [13], manufacturing [14], automotive [15], and robotics [16], where precision and reliability are imperative.

There are two main types of control methods, namely, open-loop control and closed-loop control. For simplicity, open-loop control imposes certain preplanned control logic to manipulate the systems. There is no feedback from the states or outputs of the systems. Closed-loop control uses sensors to measure the systems and then make decisions based on how the systems are responding, which allows one to deal with uncertainty and error by introducing feedback. Many methodologies have been developed for feedback control system design.

Mathematical models can be viewed as an interface between a real-world phenomenon and a mathematical world of control theory, which can be used to achieve specific control tasks by control methods. For the period of classical and/or modern control theory, model-based control is the dominant paradigm, and the framework of its control system design is shown in Figure 1. In general, mathematical models are only approximations of real plants, which cannot capture all the features. For example, high-frequency unmodeled dynamics like residual vibration modes were not considered in robotic and spacecraft models [17]. Therefore, although a model-based controller can be designed to achieve satisfactory performance in a simulation environment, it does not necessarily satisfy the predefined requirements for the real plant in practical applications due to various modeling errors or invalid prior assumptions.

Data-driven control is a promising alternative approach to control system design, using the input-output data of a plant to directly design the controller. It circumvents the necessity of system identification and has proliferated rapidly in recent decades. Consequently, data-driven control approaches are basically model-free designs, which can greatly alleviate the theory-practice gap.

Optimization refers to the problem of choosing a set of arguments that maximize or minimize a cost function or multiple cost functions. In the control community, arguments are usually related to control inputs, control parameters, etc., and a cost function or cost functions are related to the performance or requirements of a control system, like estimation errors and tracking errors. Due to various uncertainties in system dynamics, analytical solutions usually cannot be obtained for the formulated optimization problem. Various numerical optimization methods can be used to derive numerical solutions.

Alternatively, as one of the most highlighted research areas during the past decades, artificial intelligence (AI) is expanding rapidly [18,19], aiming to enable the use of systems or machines with the capability of mimicking human learning and reasoning. Much progress has been made with the help of AI technology in diversified industrial fields, including natural language processing [20], pattern recognition [21], autonomous cars [22], computer vision [23], robotics [24], etc. As the access to the data information of various sensors continues to expand and computing power becomes increasingly accessible, AI-aided or AI-based approaches have gained significant momentum. System identification, control, and optimization benefit greatly from the development of AI.

In this paper, a literature review of AI-based system identification, control, and optimization methods together with their applications and research challenges are presented. The paper is arranged as follows. The review of AI-based system identification methods is presented in Section 2. Section 3 reviews the control methods by integrating AI technology. Optimization methods are reviewed in Section 4. Section 5 presents the challenges and prospects.

2. AI-Based System Identification

In this section, we discuss parameter estimation, data-driven modeling, and hybrid modeling approaches together. Moreover, the advantages and disadvantages are discussed from a control-oriented point of view.

2.1. Parameter Estimation

To ensure mathematical models from mechanistic or data-driven modeling are capable of reflecting their physical counterparts, the parameters need to be precisely estimated. Parameter estimation usually involves the procedures of collecting data, devising estimation algorithms, and optimizing parameters to maximize the likelihood between the prediction and the observation or to minimize the error between the prediction and the observation. Although physics is able to provide knowledge for parameter estimation, the simultaneous estimation of potentially various parameters poses an exceptional challenge for high-dimensional complex systems. AI opens new avenues for the parameter estimation of dynamical systems [25].

By virtue of computational intractability, machine learning algorithms were used for the parameter estimation of complex systems following a transformation to large-scale inverse problems [26]. The stability to small changes in the data is an important property for solutions. Inverse problems that fail to satisfy this stability condition are called ill-posed as per Hadamard [27]. The strategies to solve inverse problems usually involve statistics, optimization, and regularization. Probabilistic tools (such as Bayesian inference and stochastic regularization) were mathematically introduced to address uncertainty, thus transforming ill-posedness into statistically stable solutions [28]. A neural parameter calibration method was developed to estimate parameter probability densities for large-scale multi-agent models [29]. By combining neural ordinary differential equations with physical prior knowledge, a new parameter estimation method was presented [30], which achieved a robust and accurate parameter estimation with a small sample and high noise condition. Deep learning provides an attractive strategy for solving parameter estimation problems by optimization. Regularization is usually used to avoid the ill-posed problem of parameter estimation for a large number of parameters [31]. By introducing additional constraints, a method was developed to regularize ill-posed problems into well-posed formulations [32]. A DeepBayes-based parameter estimator was devised for stochastic nonlinear dynamical models [33].

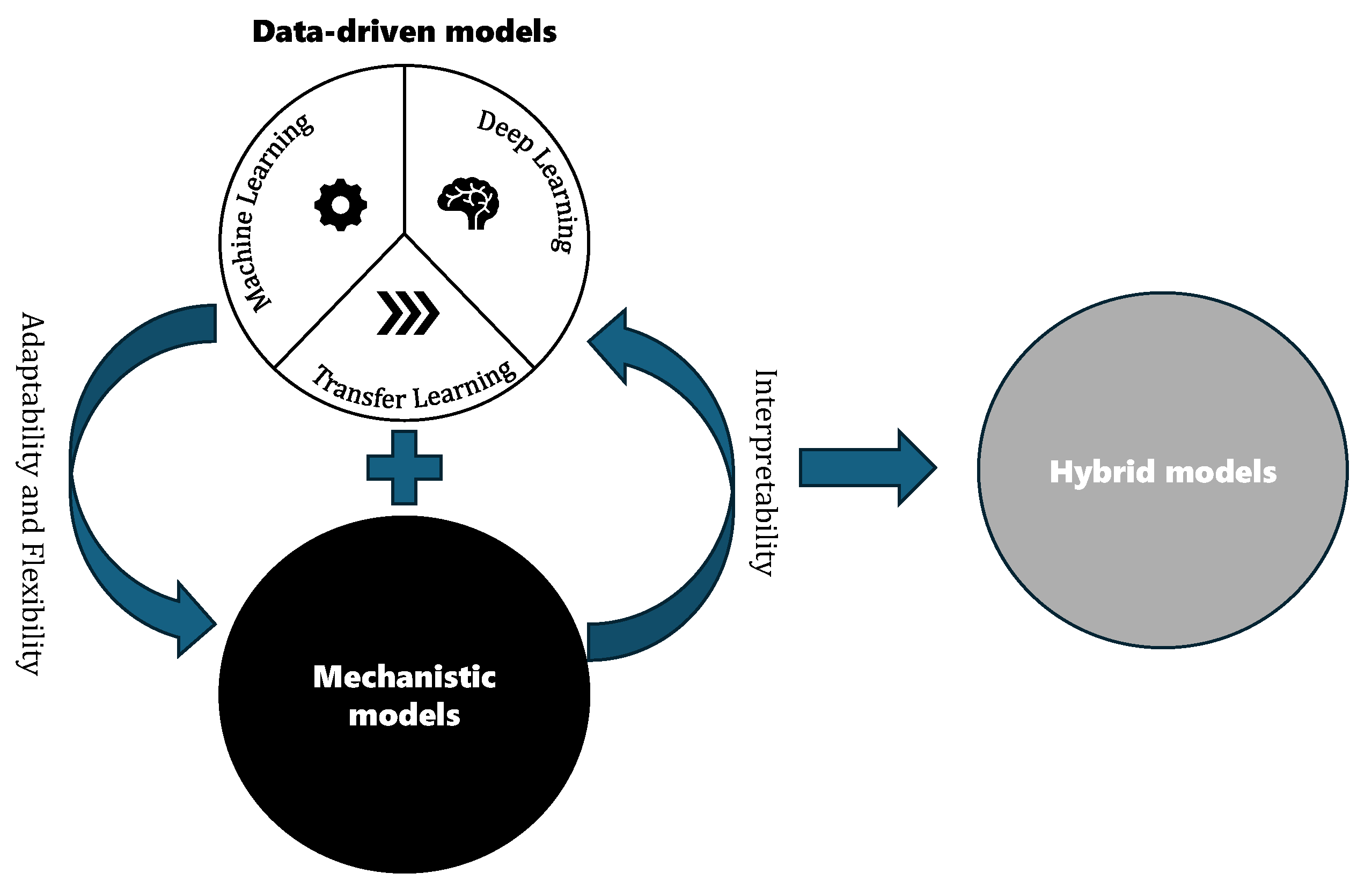
2.2. Data-Driven Modeling

The increasing complexity of dynamical systems has rendered mechanistic modeling gradually insufficient to meet the requirements due to its inherent limitations. Data-driven modeling does not rely on any prior knowledge or theoretical assumptions. It automatically learns and extracts features from a large amount of data through algorithms to establish models, which makes up for the deficiencies of mechanistic modeling. Therefore, it is increasingly favored in studies and more widely used in various industries.

2.2.1. Machine Learning

The main task of machine learning is to guide computers to learn from data and then use that experience to improve their own performance without explicit programming. In data-driven modeling, as a main learning mode of machine learning, supervised learning algorithms aim to establish the mapping and functional relationships between the inputs and outputs implicitly, with the training dataset consisting of input-and-output pairs.

Neural networks (NNs), support vector machines, logistic regression, etc., and they are supervised learning techniques with shallow structures. NNs were used to predict urban noise and to simulate car tailgating models, respectively [34,35]. Owing to the high approximation capability and the lower reliance on prior knowledge, NNs can handle more variables than traditional mathematical models, and they can deal with the nonlinear factors of dynamical systems. Due to their chaotic, unstable, or time-varying behaviors, it is more challenging to identify a dynamical system for which the observed data is nonstationary. A review about parametric system identification using neural networks was reported by [36], where the model interpretability of three types of NNs (i.e., feedforward NNs, recurrent NNs and encoder–decoder models) was summarized in modeling nonstationary time series. Support vector machines were used to model nonlinear systems [37], which reduced the impact of sample size and noise on system modeling. Furthermore, a bilinear logistic regression approach was proposed for smart grid fault modeling [38], where the parameters were trained using a real-world power grid failure dataset.

2.2.2. Deep Learning

As a breakthrough in AI, deep learning allows for the automatic processing of data by multi-level concatenation to refine highly nonlinear and complex features. Different deep learning based modeling techniques and architectures are used for system identification.

Feed-forward neural networks (FFNNs) are widely used. FFNN training entails random parameter initialization, gradient computation via back-propagation (BP) algorithms, and iterative parameter updates using stochastic gradient descent to minimize the loss function and optimize model performance. This was used to obtain the total nitrogen prediction model of effluents, with significantly improved prediction accuracy [39]. Recurrent neural networks (RNNs) have directed topological connections between neurons for learning features from sequential data [40], which were used for modeling the forward dynamics of soft robots [41]. Long and short-term memory networks are an improved version of RNNs, which were designed to solve the gradient vanishing problem and deal with complex time-series data [42]. Long and short-term memory networks were proposed to predict the acceleration distribution in car-following behavior [43]. Convolutional neural networks (CNNs) especially excel in the field of image recognition [44], where feature learning is achieved by stacking convolutional layers and pooling layers.

2.2.3. Transfer Learning

It is clear that a vast amount of data used for training is necessary for deep learning technology. When it is difficult to find sufficient training data, transfer learning is a good alternative, as it uses models trained from other data sources with certain modifications and improvements for similar fields.

Most data-driven approaches use online data to retrain models. However, unnecessary data updates and retraining are often costly and time consuming. When the studied wind–heat hybrid power system faced the issue of limited input-output data in the current scenario, transfer learning was proposed to utilize the data collected in the historical scenario to construct an online aggregated system frequency response model of the wind–heat hybrid power system operating in the current scenario [45]. A dynamic multi-source transfer learning model was proposed to effectively utilize rather than discard knowledge of historical data under similar working conditions or equipment to solve the defect of the neural network that was difficult to extrapolate [46]. Moreover, transfer learning was used in the initial feature extraction phase, where features were extracted by a pre-trained model, enabling the model to capture complex patterns in videos and extract deep features from video frames [47].

2.3. Hybrid Modeling

The idea of combining mechanistic modeling with data-driven models has emerged in the 1990s [48,49,50]. Since then, a significant amount of research has been published using the term hybrid modeling in process engineering-related research fields and gray-box modeling in the control and automation fields. Advantages with respect to modeling complex, high-dimensional, and/or computationally expensive systems could greatly benefit from hybrid modeling techniques. Hybrid modeling methodologies are reviewed from the aspect of the structure or typology of hybrid models. The relation between mechanistic modeling and data-driven modeling is shown in Figure 2.

2.3.1. Parallel Structures

When the performance of a mechanistic model is unsatisfactory due to oversimplifications, unreasonable assumptions, and unmodeled effects [51], hybrid models with parallel structures are usually appropriate. More specifically, mechanistic and data-driven models are executed simultaneously, and then, their outputs are combined in a way (e.g., voting and weighted averaging). It is well known that a mechanistic model represents the dynamics independently of a data-driven model. Consequently, a hybrid model serves to improve the quality of the predictions of the mechanistic model. Moreover, the performance of a hybrid model of a parallel structure depends on the quality of the data-driven model.

Parallel structures are able to reduce the potential bias of a single model by combining the outputs of different models. For example, a hybrid model of a mechanistic model and an FFNN for the wastewater treatment process worked well in parallel, where the output of the mechanistic model served as an input to the neural network and compensated for the model prediction error [52]. A multi-stage model consisting of a mechanistic model and a bi-directional gated recurrent unit model was developed [53], where the outputs of both models were passed by a dense neural network regressor to generate the final predictions.

Another common scenario where a parallel structure is widely used is to embed physical properties into loss functions. The loss function of a traditional data-driven model emphasizes the reduction of the loss between the estimate and the actual observation. However, it ignores the inherent physical properties, which could result in a model that is not consistent with the physics. Physics-informed loss functions are developed to address this challenge. They are constructed to constrain data-driven models to physically consistent spaces [54]. For example, Bayesian optimization algorithms were used to adjust the weighting factors in a loss function, thus optimizing model accuracy [55,56].

2.3.2. Serial Structures

Data-driven models can be advantageous when a mechanistic model is unavailable or too complex to be described mathematically [57]. Therefore, a serial structure can be chosen when a mechanistic model cannot fully map the relation between inputs and outputs because of the complexity, where the mechanistic and data-driven models are executed sequentially with the output of one model serving as the input of the other model. The performance of hybrid models of serial structures depends on how well a mechanistic model represents real phenomena. When the mechanistic model is reliable, the predictive properties of serial structures are usually better than those of parallel structures. However, parallel structures have better generalization because first-principles knowledge usually generalizes better than pure data.

A physically guided CNN was developed for the fault diagnosis of rolling element bearings [58], where the output of a mechanistic model was used as the input of a data-driven model. Deformation data were obtained by finite element simulation under different geometric gaps, and then, an FFNN prediction model was constructed for the deformation of a typical weld structure [59].

Physical information neural networks (PINNs) are a new type of networks that embed physical principles as a priori knowledge into the training process of NNs. To enable the NNs to fit the data while satisfying physical constraints, some strategies and techniques for incorporating the underlying first principles of the power grid into different types of machine learning approaches were reviewed [60]. PINNs are particularly well suited for scientific computing and engineering problems that involve solving partial differential equations or ordinary differential equations. Some newly developed techniques to enhance PINN performance while reducing training costs have been reviewed [61]. A PINN-based approach was proposed for modeling friction-inclusive dynamics of industrial robots [62], which ensured modeling accuracy while avoiding reliance on joint torque component labels and enhancing its ability to learn nonlinear features.

3. AI-Based Control Methods

The combination of AI and feedback control is an emerging research area, aiming to achieve more efficient and intelligent control systems by integrating the learning and decision-making capabilities of AI with the stability and accuracy of feedback control. The prevailing control methods have been studied extensively with the aid of AI.

3.1. Neural Network Control

Owing to universal approximation, parallel distributed processing, hardware implementation, learning and adaptation, and multivariable systems [63], neural networks are becoming particularly attractive and promising in control system design. Many neural networks with different structures have been introduced, like FFNNs [64,65,66,67,68], radial basis function neural networks (RBFNNs) [69,70,71,72,73,74], RNNs [75,76,77,78], and CNNs [79,80]. The key or challenge of using a neural network for feedback control is to select a suitable control system structure and then demonstrate how the weights of neural networks can be tuned to ensure the control performances (including stability, robustness, dynamic performance, steady-state performance, etc.) of the developed closed-loop feedback systems. Some prevailing control approaches are reviewed in the following.

3.1.1. Neural Network-Based Adaptive Control

Conventional adaptive control without neural networks is usually vulnerable to uncertainties or unknown dynamics and is challenging to deal with complex nonlinear systems. Neural network-based adaptive control is able to directly approximate unknown dynamics using neural networks, which removes the need for precise mathematical models. This is also the main reason why neural network-based adaptive control is especially suitable for complex nonlinear systems or uncertain dynamical systems.

Although promising results can be obtained for the neural network-based adaptive control methods, the closed-loop stability analysis is a burdensome task. Therefore, most of the existing neural network-based adaptive control methods rely on the Lyapunov direct method to guarantee stability. More specifically, a suitable Lyapunov candidate function is chosen first, which relates to both the neural network weights and tracking/estimation errors. Then, the update rules for the network weights are derived such that the time derivative of the Lyapunov candidate function becomes negative definite or negative semi-definite [81]. By the implicit function theorem, an observer-based direct adaptive fuzzy neural control scheme was proposed for non-affine nonlinear systems with unknown nonlinear structures [82], for which fuzzy neural networks were used to estimate the unknown nonlinear dynamics of the error system while ensuring the boundedness of all system signals by the strictly positive real Lyapunov theory. Furthermore, for highly nonlinear systems, with an online update of the layer width (e.g., neuron numbers) of the neural networks, a direct adaptive state feedback controller was used to approximate and adaptively compensate for unknown nonlinearities [83], whereby the uniform asymptotic stability of tracking errors were guaranteed via the incorporation of robust control terms.

3.1.2. Neural Network-Based Sliding-Mode Control

Owing to its robustness against structured and unstructured uncertainties, as well as its ease of implementation, sliding-mode control (SMC) has gained significant attention in the nonlinear systems control community. However, prior knowledge of the upper bounds of uncertainties or disturbances is usually required for conventional SMC methods, which may be impractical for some applications. Moreover, a large switching gain could bring about significant chattering. Therefore, numerous attempts have been made to integrate neural networks to make SMC more intelligent [84,85]. These can be mainly categorized into two types, namely, model-based and model-free ones.

Based on a mathematical model that may be inaccurate, some neural network-based adaptive SMC methods were designed for robots [86,87,88], vehicles [89,90], and aircraft [74], where the neural network was used to compensate for model uncertainties or other nonlinearities. Compared with the conventional SMC, the developed method was able to reduce chattering and improve control performance. Alternatively, to remove the prior requirement of an upper bound of uncertainties and disturbances, rather than estimating the real value, neural networks were utilized to estimate the bounds [73,91,92,93,94].

For model-free control, neural networks are designed to estimate the whole dynamics of control systems. Although there is no need to calculate mathematical models for model-free control methods, the computation complexity is challenging. For example, a recurrent fuzzy wavelet neural network was integrated into robust adaptive SMC for industrial robot manipulators [95]. An RBFNN was combined with fuzzy sliding mode to tackle the trajectory tracking control [70].

3.1.3. Neural Network-Based Backstepping Control

It is well known that it is challenging to find a suitable control Lyapunov function for a general nonlinear control system. However, for nonlinear systems of a strict feedback form, the backstepping control method is a good solution. More specifically, a recursive design procedure is used, which links finding a control Lyapunov function with the design of a feedback controller. Moreover, the global asymptotic stability of strict feedback systems is guaranteed. By integrating neural networks to estimate unknown dynamics, nonlinearities, or virtual control laws, effective control strategies have been developed for nonlinear systems with uncertainties [96,97].

Owing to their universal approximation property, neural networks were employed to construct the nonlinear mapping online in backstepping control schemes. In earlier research, an RBFNN was used for the online approximation of a linear parametric model for a nonlinear system [71]. For the case where obtaining system states was difficult or costly in practice, neural network-based observers were developed to estimate the unavailable states, which broadened the application of backstepping control [98,99]. To remove the problem of the explosion of complexity of the traditional backstepping design, neural network techniques were combined with the command-filtered control method to achieve a robust and excellent performance [100,101,102]. Virtual control laws were approximated step-by-step by neural networks and then incorporated in backstepping control design based on the Lyapunov stability method [103,104].

3.1.4. Neural Network-Based Iterative Learning Control

Iterative learning control (ILC) is widely used in practical applications, such as manufacturing [105], robotics [106], and chemical processing [107], where mass production entails repeated operations on an assembly line. It learns error knowledge from the previous iteration to improve the next iteration [108]. However, it is difficult for conventional ILCs to cope with strong nonlinearities and uncertainties in practice. Therefore, neural networks are also incorporated into ILCs to solve practical difficulties and enhance control performance.

An RBFNN was used to automatically adjust the ILC gain of a nonlinear system by a dynamic linearization technique [109]. A generalized regression neural network was developed as an estimator to calculate key parameters, and then an RBFNN was designed to find the control input by iterative training [110]. Two neural networks were used to model a nonlinear process and as a learning controller, respectively, [111]. Moreover, the convergence analysis was conducted for both P-type and D-type learning controllers. A data-driven prediction model was established by a new RBFNN to estimate non-repeating external disturbances along the iterative learning axis [112]. Based on the previous iterative control input and output error, a BP neural network was used to learn system uncertainties and disturbances and then to compensate for them [113]. To solve the zero tracking problem with inherent noise tolerance, an ILC was proposed based on a modified zeroing neural network [114], which can not only theoretically converge to the exact solution of the zero tracking problem but also eliminate the strict assumptions on the initialization conditions of each iteration [115]. Neural networks were used to estimate the nonlinear portion of an ILC output and then predicted the ILC output for multiple tasks [116]. An inverse model-based ILC method was developed for a multiple input and multiple output (MIMO) nonlinear system, for which a neural network was constructed to observe the system [117].

3.1.5. Summary

The adaptation property arises from the many characteristics of neural networks, which include learnable weights and flexible architectures. According to the mechanism of the weight update policies, neural network control methods can be broadly categorized into two types, which can be seen from Figure 3. The weight update policy of the first type is based on BP algorithms [118,119], and the second type utilizes the Lyapunov stability theory [72]. It is important to mention that the BP algorithm is a class of optimization methods based on gradient information, which is one of the core algorithms in neural network training and is very popular in the control community. Besides the gradient-based methods explained in Section 4.1, second-order optimization methods (such as Newton’s method [120], quasi-Newton methods [121]), metaheuristic optimization presented in Section 4.2, and Bayesian optimization [122] can be used to train neural networks. Furthermore, the selection of the number of hidden layers and neurons of a neural network is also important. In general, a neural network with more hidden layers and neurons is capable of providing a better control performance at the cost of higher complexity and computational cost.

Alternatively, it is clear that all the controllers mentioned above are based on standard neural networks. There are a few works based on neural ordinary differential equations. For example, a recurrent wavelet first-order neural network was developed for the multistability control of an erbium-doped fiber laser [123]. Similarly, the selection of the order number of a neural ordinary differential equation is a trade-off between performance and complexity.

3.2. Model Prediction Control

Model predictive control (MPC) is also known as receding horizon control, which belongs to the intersection fields of optimization and control. There are several notable advantages for MPC. First, it can seamlessly deal with MIMO systems, which are the main system types in complex industries. Second, various constraints including physical limitations can be well handled for MPC. Third, noting that MPC not only considers the current states and inputs but also takes into account the future states and inputs to achieve optimization control at every sampling time, it is adaptive or robust to future effects. The implementation of MPC includes three key components, namely, model prediction, optimization in a receding horizon, and feedback correction.

However, for dynamical systems requiring high-frequency control, MPC may be infeasible, especially when complex MPC schemes such as nonlinear MPC or robust MPC are used, or when the controller needs to be implemented in a low-cost embedded platform. So, the main challenge of the design and real-time implementation of MPC in practical applications is to have an accurate enough predictive model with a real-time computation capability for large-scale optimization problems. In the past two decades, a great deal of research has been carried out to utilize AI technology to facilitate the design of MPC, for which most works focus on prediction models and fast optimization for high-lever controllers.

3.2.1. Model Prediction

Machine Learning can be used to provide an accurate model at a decreased computational cost and with improved MPC performance [124]. An RNN enjoys the advantages of both high scalability and the capability of modeling multiple-output data. Therefore, RNNs have been widely used in model prediction. For example, to address the limitation of adaptive algorithms based on continuous model update processes and MPC policy redesign, which are constrained to systems with long sampling times, a novel nonlinear system identification and adaptive control method leveraging integrated neural networks was proposed [125]. Addressing at the challenges of nonlinearity, noise, and time delay in industrial processes, and a method of using RNN architectures to solve the problem of modeling and control of complex dynamical systems in industrial processes was proposed [126]. Addressing the challenge of significant hysteresis and unknown state interactions in soft robot systems, a deep-neural network-based method was proposed for modeling and controlling soft robots [127].

A nonlinear auto-regressive predictive model was built for MPC by utilizing a neural network to learn exogenous inputs, and the input-to-state stability of the closed-loop system was ensured [128]. A path-tracking MPC algorithm was developed for a vision-based mobile robot, where the disturbance was modeled as a Gaussian process [129]. To ensure the safety of the robot when operating under new conditions, a learning probabilistic model was developed by comparing a Gaussian process with a specific form of local linear regression [130]. A novel parameter adaptive MPC architecture was proposed, which enabled online tuning without recomputing large datasets and retraining [131]. To solve the problem related to the fact that the performance of nonlinear MPC models depends on the quality of the underlying model, and that the closed-loop behavior of systems may be difficult to analyze formally, a data-driven economic nonlinear MPC strategy was presented to support parameterization and approximate the action value functions [132].

3.2.2. Fast Optimization

To enable MPC strategies with fast optimization, two types of approaches are developed. The first type includes the development of fast solvers and tailored implementations to calculate formulated optimization problems in real time [133,134]. Machine learning was used to accelerate the original active set to solve the developed quadratic programming-based MPC problem [135], where a state-dependent warm-start was designed by solving the parameterized program offline.

The second type is usually called explicit MPC [136]. With feasibility and stability guarantees, a sampling-based explicit nonlinear MPC was developed for nonlinear systems, for which a support vector machine classifier was used to approximate the feasible region [137]. Neural networks were used to compute the approximate explicit MPC laws, and the feasible control inputs were generated by projecting onto a multifaceted region that was derived from the maximum control invariant set [138]. A deep-learning-based method was developed to efficiently represent an approximation of the MPC laws [133]. Neural networks with modified rectified linear units were constructed to approximate the piecewise affine explicit control laws of MPC, which allowed the approximations to effectively address large-scale problems involving thousands of parameter variables [136].

3.3. Reinforcement Learning Control

As another learning mode of machine learning, unlike supervised learning, which relies on a training dataset with predefined answers and unsupervised learning without desired answers, reinforcement learning (RL) learns a task through a lot of trials. RL is a field closely related to control theory. From the perspective of control theory, the relation of RL with dynamic programming is reviewed first. Through model-based and model-free learning, recent developments in RL in control science are summarized.

3.3.1. Approximate Dynamic Programming

Optimal control is an important branch of control theory, aiming to design controllers to optimize dynamical systems under certain performance metrics [139]. There are three pillars in optimal control, i.e., calculus of variations, Pontryagin’s maximum principle, and dynamic programming [140]. Dynamic programming was proposed by Richard Bellman to solve the Bellman equation for a discrete-time system or the Hamilton-Jacobi-Bellman (HJB) for a continuous-time system [141]. However, in practice, directly solving these equations often leads to the curse of dimensionality. In other words, it is computationally large and difficult to realize for high-dimensional systems [140].

To solve this problem, heuristic dynamic programming was developed in 1990, which approximated an optimal value function of the Bellman equation by using approximation functions or models [142]. Then HDP was developed into approximate dynamic programming [143], which is essentially equivalent to the temporal difference methods in RL [144]. In 1989, the proposal of the Q-learning approach combining dynamic programming with online learning marked the emergence of RL in the field of optimal control [145]. As a result, RL and optimal control theory began to integrate, providing a new way to solve complex optimal control problems.

In the context of the optimal control of continuous stochastic processes, the HJB equation and dynamic programming can solve the optimal solution. However, theoretical solutions are difficult to find. Thus, numerical methods such as gradient descent were employed to approximate the optimal solution [146].

3.3.2. Model-Based RL Control

In the field of control systems, with a known system model, the model information can be fully used in the RL algorithm to accelerate the learning process. Given a system model, the value and corresponding reward of each state are accurately calculated, and then, the state transfer probability matrix can be constructed [147]. Using value iteration or policy iteration, the optimal policy can be solved. When the system model is completely known, model-based RL algorithms have been widely used to solve the optimal stabilization problem [148,149], the control problem [150,151], and the tracking problem [152].

3.3.3. Model-Free RL Control

However, in practical applications, it is difficult to obtain an accurate mathematical model for an environment or a dynamic system. Even if an accurate model is obtained, it would be too complex to be used directly. Model-free RL algorithms become particularly important. They perform policy learning through interaction with the environment or system and collect data samples from interaction processes, without relying on an accurate model. There are mainly three categories of model-free RL algorithms [153], including value-based, policy-based, and actor-critic algorithms.

For value-based algorithms, a value function is estimated to evaluate the system states or control actions. An agent or controller selects the optimal policy based on the value function [139]. For example, the Q-learning algorithm is a typical value-based model-free RL algorithm [153]. It is widely used in optimal regulation control [154,155] and optimal tracking control [156,157] for nonlinear systems with unknown models. The deep Q-learning algorithm was used to optimize the energy storage management system of a wind power generator [158].

Unlike value-based algorithms, policy-based algorithms directly learn the mapping relation from states to actions, i.e., the policy function. Instead of explicitly estimating the value function, such methods maximize the long-term cumulative reward by optimizing the policy function [153]. For example, the policy gradient algorithm is a commonly used model-free RL algorithm, which uses gradient descent to optimize parameterized policies [159]. In the gait control for bipedal robots, the policy gradient algorithm learned an optimal gait control strategy in different terrains and motion states by interacting with the environment [160,161].

The actor-critic algorithm combines the advantages of both value and policy functions and learns both value and policy functions to achieve policy optimization. An actor-critic online optimal control algorithm with three neural networks was proposed for the robust control of unknown nonlinear systems [162]. To achieve the optimal synchronous tracking control of heterogeneous multi-agent systems with input-constrained and unknown nonlinearities, an off-policy RL algorithm was proposed, which utilized neural networks to build critic and actor networks, trained them by an actor-critic algorithm, and then obtained the optimal control policy [163]. An actor-critic algorithm was developed to evaluate different control strategies by learning the value function and optimizing the policy function to achieve an optimal active suspension adjustment to meet the comfort and handling requirements of the vehicle [164].

4. Performance Optimization

Satisfactory performance is one of the end goals of system design or control. Moreover, most system design or control problems can be formulated as optimization tasks. Although gradient-based algorithms are typically recognized because of their computational speed and efficiency, gradients and Hessian matrices are required for the iteration. However, the information is unavailable for black-box cases. Alternatively, when the computational cost is very cheap, the design space is noisy or discontinuous, there may be multiple optima, or when derivatives can not be calculated efficiently, gradient-free optimizers are recommended.

4.1. Gradient-Based Optimization

Gradient-based optimization is the backbone of modern machine learning. It is based on gradient descent and is crucial for training neural networks, deep learning models, and many other machine learning models.

The key idea of gradient descent is that a loss function $J\left(\theta \right)$ of parameters $\theta$ can be minimized along with the direction of the negative gradient $-\nabla J\left(\theta \right)$. In other words, the loss function value can be decreased when $\theta$ takes a step in the negative gradient direction. Gradient descent optimizers are based on first-order derivatives, which are more practical than high-order derivative-based algorithms, e.g., Newton’s method, for deep models.

Many variants are proposed. The vanilla batch gradient descent algorithm renews the parameters via the gradient of the entire training set, and while simple, it is slow for large datasets and models. Stochastic gradient descent (SGD) addresses this by updating based on the gradient of individual training examples, introducing stochasticity that can help escape suboptimal local minima. In practice, mini-batch SGD that computes the gradient over small subsets of the data is used as a happy medium.

In practice, the gradients are computed by the BP algorithm by utilizing the chain rule. The BP algorithm together with automatic differentiation tools has made gradient-based optimization the default choice for training machine learning models.

4.2. Metaheuristic Optimization

Metaheuristic optimization algorithms are a kind of computational technique widely used in complex optimization problems [165], seeking an approximate optimal solution by imitating the evolution of social behavior or natural phenomena. Moreover, they usually do not rely on the gradient information of the problems considered. Through global or local search, they reach a balance between exploration and development in search space, so as to avoid falling into a local optimal solution. Evolutionary algorithms, particle swarm optimization, ant colony optimization, and simulated annealing are examples of metaheuristic optimization algorithms. Their features are summarized in Table 1.

Genetic algorithms (GAs) are inspired by biological evolution, which simulates natural selection and genetic mechanisms to find optimal solutions. A GA was applied to automatically search for the optimal key hyperparameters of deep RL models [166], such as learning rates, discount factors, and exploration–exploitation trade-offs, which were typically difficult to fine-tune manually. A GA was used for the parameter identification of vapor-liquid thermodynamic models [167]. Differential evolution (DE) is a population-based evolutionary algorithm that guides the optimization process by exploiting the differences between solutions in a population. DE is widely used in the design optimization of power electronic systems, such as the parameter estimation of inverters [168], power converters [169], and solar photovoltaic models [170].

Particle swarm optimization (PSO) methods iteratively solve problems by moving a swarm of particles around the design space until convergence is reached [171,172]. PSO emerges as a powerful optimization technique in fields such as power system state estimation [173]. Ant colony optimization (ACO) is a kind of optimization algorithm inspired by ant foraging behavior, which is mainly used to solve combinatorial optimization problems, such as power scheduling [174], optimal path selection [175], and so on. ACO was used to identify the natural frequencies and damping ratios of mechanical systems [176]. Simulated annealing (SA) solves optimization problems iteratively by simulating the physical annealing process, which is suitable for large-scale, complex nonlinear problems and has been applied in power electronics system design [177] and other fields.

Table 1. Metaheuristic optimization algorithms.

Algorithms	Inspiration	Feature	References
GA	Evolutionary	Robust Global Search	[166,167]
DE	Evolutionary	Efficient Mutation	[168,169,170]
PSO	Swarm Intelligence	Fast Convergence	[173]
ACO	Swarm Intelligence	Positive Feedback	[177]
SA	Physics	Escape Local Optima	[174,175]

Table 1. Metaheuristic optimization algorithms.

Algorithms	Inspiration	Feature	References
GA	Evolutionary	Robust Global Search	[166,167]
DE	Evolutionary	Efficient Mutation	[168,169,170]
PSO	Swarm Intelligence	Fast Convergence	[173]
ACO	Swarm Intelligence	Positive Feedback	[177]
SA	Physics	Escape Local Optima	[174,175]

5. Challenges and Prospects

Some future challenges and directions are discussed as follows based on this literature review.

5.1. Challenges

(1)

AI models or algorithms usually rely on a large amount of high-quality training data. The means for obtaining these data, especially in dynamic and complex environments, are a significant challenge.

(2)

Data-driven techniques for system identification rely on extracted patterns from historical or experimental data. The reasoning mechanism has yet to be fully understood or explained by physics and may thus be opaque to engineers. In other words, interpretability could be a concern due to its black-box nature.

(3)

Since the mathematical foundations of AI are yet to be fully established, a practice guide to facilitate the architecture designs and implementation of AI models or algorithms for system identification, control, and optimization is still an open issue.

(4)

Although AI models or algorithms can improve the modeling accuracy or control performance of dynamical systems, computational complexity becomes correspondingly more complex. Ways to deal with the trade-off are also a crucial challenge.

5.2. Future Directions

AI is capable of making feedback control loops smarter and more adaptive to uncertainties. Several promising directions to make full use of AI in control systems are given as follows.

(1)

More models and learning methods can be used to improve the generalization ability of deep learning. Future efforts should prioritize multi-modal learning architectures that integrate heterogeneous data sources (e.g., multi-modal sensor fusion of vision, LiDAR, and inertial measurement units) to create more comprehensive system representations. Meta-learning approaches, particularly few-shot and zero-shot learning paradigms, could enable control systems to adapt rapidly to novel scenarios with minimal retraining. Foundation-scale models pre-trained on multi-domain physical system datasets demonstrate transformative potential. They can serve as universal priors for low-level control tasks while retaining domain-specific knowledge through lightweight fine-tuning. For instance, a physics-informed large language model could interpret system dynamics from textual maintenance logs and simultaneously process numerical sensor data, enabling cross-domain knowledge transfer in industrial control engineering applications.

(2)

Developing a new, effective, and more interpretable architecture to implement AI models or algorithms in feedback control systems could make the decision-making process of control systems more transparent, ensuring stability and real-time guarantees. Neural ordinary differential equation networks could be synergistically integrated with traditional MPC frameworks, where the neural component learns residual dynamics while the MPC core provides stability guarantees through convex optimization constraints. Furthermore, attention mechanisms and symbolic regression layers should be incorporated into control strategies to produce human-understandable explanations for control actions. Moreover, the integration of performance assessment tools, such as reachability analysis and Lyapunov functional synthesis, with neural network-based controllers will be essential for safety-critical applications like autonomous vehicles and medical robotics.

(3)

Exploring strategies regarding the ways machine learning is used to model and handle uncertainties can achieve more robust control. For most mechanical systems, the dominant dynamics can be obtained by first principles. Uncertainties including parameter variations (e.g., the moment of the inertia of robotic arms) and unmodeling dynamics (e.g., the aerodynamic disturbances of unmanned aerial vehicles) are the main causes of performance deterioration. A hierarchical learning framework could be developed where Bayesian neural networks quantify uncertainty distributions, while adversarial reinforcement learning agents train controllers to cope optimally under worst-case uncertainty scenarios. Physics-guided uncertainty propagation methods should be investigated, whereby learned uncertainty bounds are systematically incorporated into robust control strategies such as H infinity control and SMC. For distributed systems, federated learning architectures could enable collaborative uncertainty modeling across fleets of cyber-physical systems while preserving data privacy.

(4)

Most works focus on uncertainty estimation and compensation without considering the learning performance. Utilizing AI-based optimization algorithms to calculate the control input could be a more efficient and direct control method. Implicit neural representation networks could parameterize entire families of optimal control laws, enabling real-time solutions for nonlinear MPC problems without iterative computations. Evolutionary strategies enhanced by neural surrogates may discover non-conventional control strategies that outperform conventional PID or linear quadratic Gaussian designs in complex multi-objective scenarios. For large-scale systems, graph neural networks could solve distributed optimization problems by learning message-passing mechanisms between subsystems. Crucially, these approaches must address the duality between learning performance and control stability through novel loss functions that penalize Lyapunov function derivatives or contraction metric violations.