Exploring
Abstract
:1. Introduction, Preliminaries, and Definitions
2. Definition and Example
3. Main Results
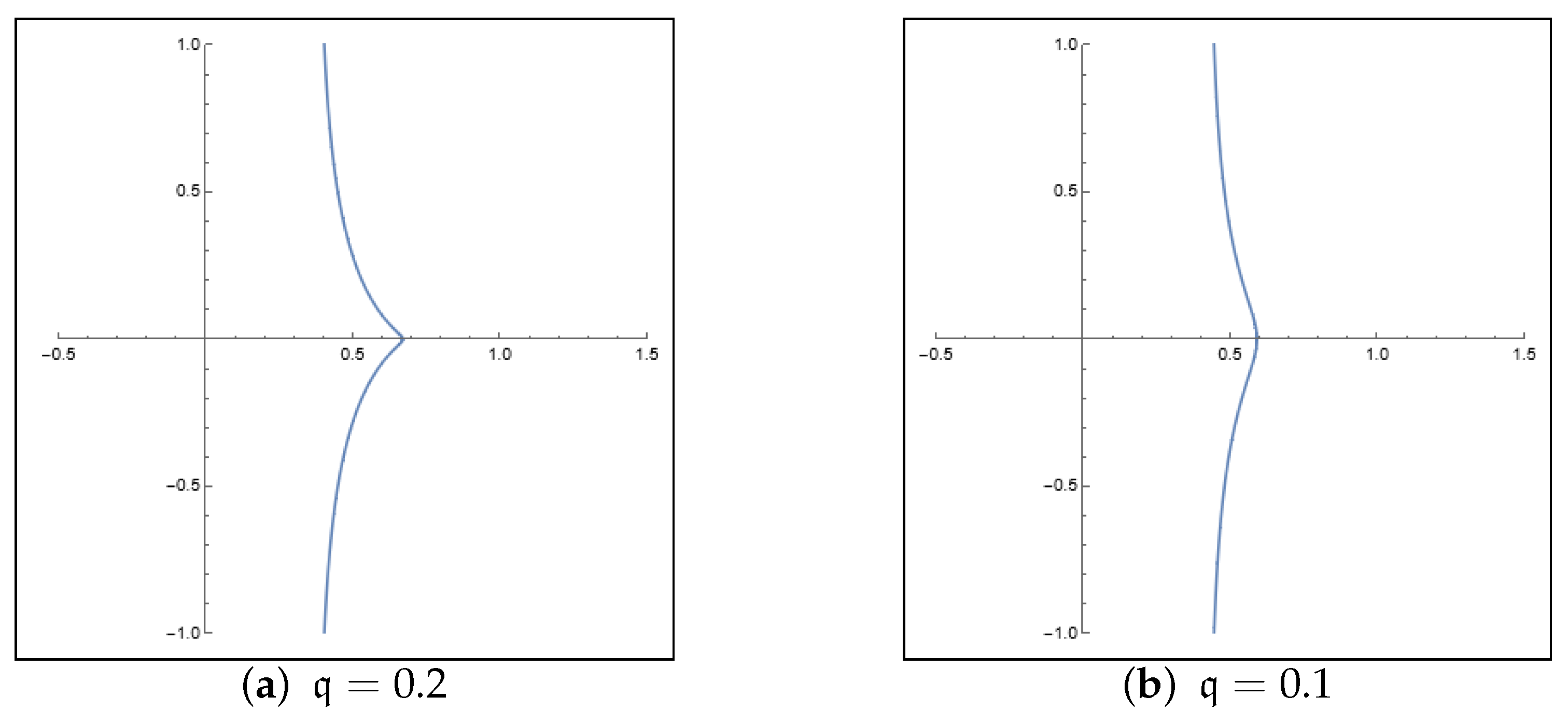
- In the range of where , the curve takes a similar appearance of a conchoid without any loops. See Figure 2 for visual representations of corresponding to various values.
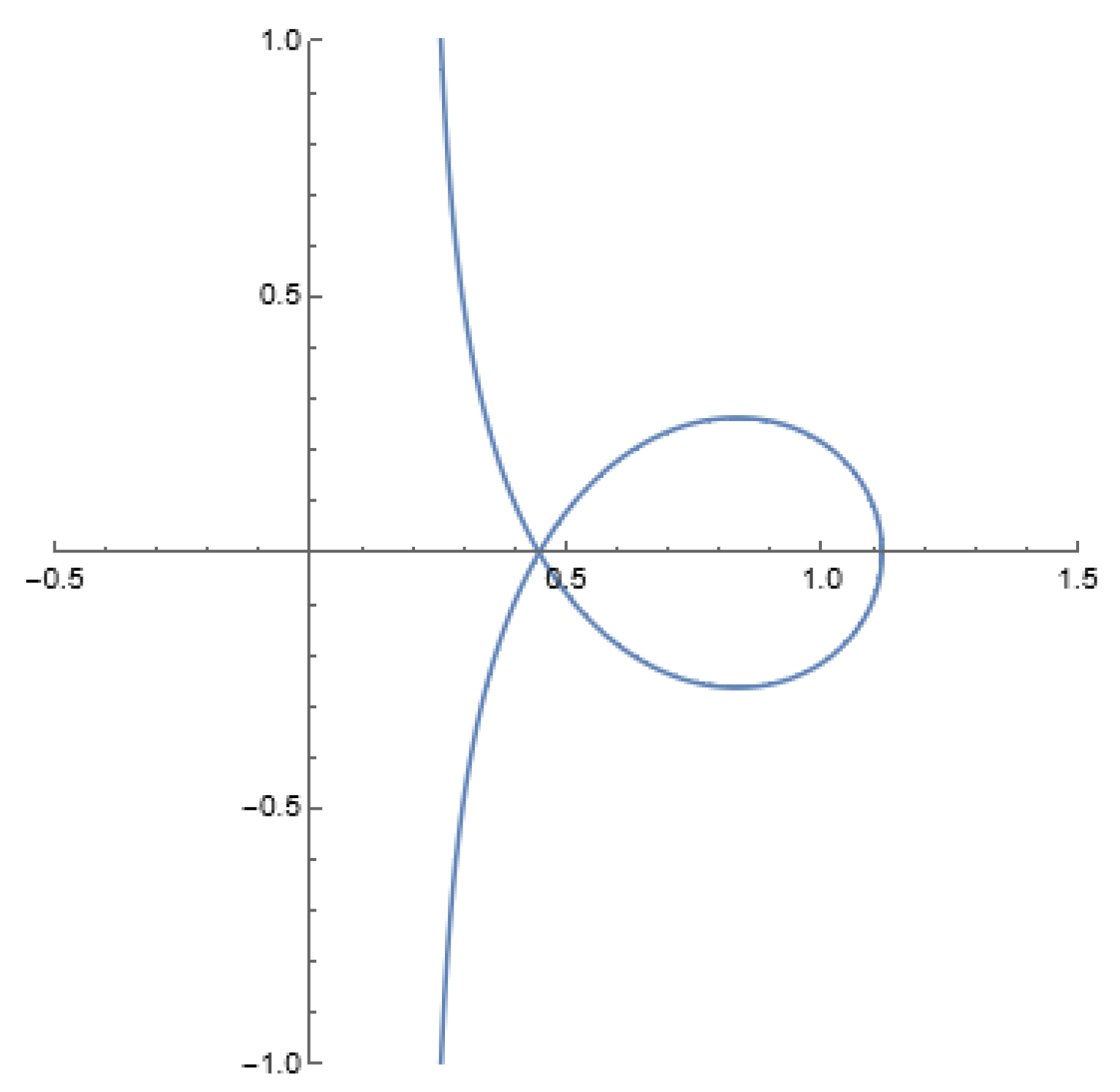
- In the range of where , we observe thatimplies that the curve intersects itself on the real axis at the point . Consequently, forms a loop that intersects the real axis at two points, and . See Figure 3 for visual representations of corresponding to various values.
- (a)
- (b)
- and
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duren, P.L. Univalent functions. In Grundlehren der Mathematischen Wissenschaften Series; Springer: New York, NY, USA, 1983. [Google Scholar]
- Ma, W.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis; International Press Inc.: Tianjin, China, 1992; pp. 157–169. [Google Scholar]
- Janowski, W. Extremal problems for a family of functions with positive real part and for some related families. Ann. Pol. Math. 1970, 23, 159–177. [Google Scholar] [CrossRef]
- Robertson, M.S. Certain classes of star-like functions. Mich. Math. J. 1985, 32, 135–140. [Google Scholar] [CrossRef]
- Sokół, J. On star-like functions connected with Fibonacci numbers. Zesz. Nauk. Politech. Rzesz. Mat. 1999, 23, 111–116. [Google Scholar]
- Sokół, J. A certain class of star-like functions. Comput. Math. Appl. 2011, 62, 611–619. [Google Scholar] [CrossRef]
- Jackson, F.H. On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 1909, 46, 253–281. [Google Scholar] [CrossRef]
- Jackson, F.H. On q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Aral, A.; Gupta, V. Generalized q-Baskakov operators. Math. Slovaca 2011, 61, 619–634. [Google Scholar] [CrossRef]
- Alsoboh; Oros, G. A Class of Bi-univalent Functions in a Leaf-Like Domain Defined through Subordination via q-calculus. Mathematics 2004, 12, 1594. [Google Scholar] [CrossRef]
- Uçar, H.; Özkan, E. Coefficient inequality for q-star-like functions. Appl. Math. Comput. 2016, 276, 122–126. [Google Scholar]
- Srivastava, H.M.; Khan, B.; Khan, N.; Tahir, M.; Ahmad, S.; Khan, N. Upper bound of the third Hankel determinant for a subclass of q-star-like functions associated with the q-exponential function. Bull. Des Sci. Math. 2021, 167, 102942. [Google Scholar] [CrossRef]
- Khan, B.; Srivastava, H.M.; Khan, N.; Darus, M.; Tahir, M.; Ahmad, Q.Z. Coefficient Estimates for a Subclass of Analytic Functions Associated with a Certain Leaf-Like Domain. Mathematics 2020, 8, 1334. [Google Scholar] [CrossRef]
- Arif, M.; Barkub, O.; Srivastava, H.M.; Abdullah, S.; Khan, S.A. Some Janowski Type Harmonic q-Star-like Functions Associated with Symmetrical Points. Mathematics 2020, 8, 629. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Aouf, M.K.; Mostafa, A.O. Some properties of analytic functions associated with fractional q-calculus operators. Miskolc Math. Notes 2019, 20, 1245–1260. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Deeb, S.M. A certain class of analytic functions of complex order connected with a q-analogue of integral operators. Miskolc Math. Notes 2020, 21, 417–433. [Google Scholar] [CrossRef]
- Shafiq, M.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Darus, M.; Kiran, S. An Upper Bound of the Third Hankel Determinant for a Subclass of q-Star-like Functions Associated with k-Fibonacci Numbers. Symmetry 2020, 12, 1043. [Google Scholar] [CrossRef]
- Mahmood, S.; Ahmad, Q.Z.; Srivastava, H.M.; Khan, N.; Khan, B.; Tahir, M. A certain subclass of meromorphically q-star-like functions associated with the Janowski functions. J. Inequal. Appl. 2019, 2019, 88. [Google Scholar] [CrossRef]
- Mahmood, S.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Khan, B.; Ali, I. Upper bound of the third Hankel determinant for a subclass of q-star-like functions. Symmetry 2019, 11, 347. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Sakar, F.M.; Ogilat, O.; Gharib, G.M.; Zomot, N. Coefficient Estimation Utilizing the Faber Polynomial for a Subfamily of Bi-Univalent Functions. Axioms 2023, 12, 512. [Google Scholar] [CrossRef]
- Al-Hawary, T.; Amourah, A.; Alsoboh, A.; Ogilat, O.; Harny, I.; Darus, M. Applications of q-Ultraspherical polynomials to bi-univalent functions defined by q-Saigo’s fractional integral operators. AIMS Math. 2024, 9, 17063–17075. [Google Scholar] [CrossRef]
- Amourah, A.; Frasin, B.; Salah, J.; Yousef, F. Subfamilies of Bi-Univalent Functions Associated with the Imaginary Error Function and Subordinate to Jacobi Polynomials. Symmetry 2025, 17, 157. [Google Scholar] [CrossRef]
- Alsoboh, A.; Darus, M. On subclasses of harmonic univalent functions defined by Jackson (p,q)-derivative. J. Anal. 2019, 10, 123–130. [Google Scholar]
- Illafe, M.; Mohd, M.H.; Yousef, F.; Supramaniam, S. Investigating inclusion, neighborhood, and partial sums properties for a general subclass of analytic functions. Int. J. Neutrosophic Sci. 2025, 25, 501–510. [Google Scholar]
- Amourah, A.; Alsoboh, A.; Breaz, D.; El-Deeb, S.M. A Bi-Star-like Class in a Leaf-like Domain Defined through Subordination via q-Calculus. Mathematics 2024, 12, 1735. [Google Scholar] [CrossRef]
- Alsoboh, A.M.; Caglar, M.; Buyankara, M. Fekete-Szeg Inequality for a Subclass of Bi-Univalent Functions Linked to q-Ultraspherical Polynomials. Contemp. Math. 2024, 5, 2531–2545. [Google Scholar]
- Elhaddad, S.; Aldweby, H.; Darus, M. Some properties on a class of harmonic univalent functions defined by q-analogue of Ruscheweyh operator. J. Math. Anal. 2018, 9, 28–35. [Google Scholar]
- Illafe, M.; Mohd, M.H.; Yousef, F.; Supramaniam, S. A Subclass of bi-univalent functions defined by aSymmetric q-derivative operator and Gegenbauer polynomials. Eur. J. Pure Appl. Math. 2024, 17, 2467–2480. [Google Scholar] [CrossRef]
- Amourah, A.; Frasin, B.A.; Swamy, S.R.; Sailaja, Y. Coefficient bounds for Al-Oboudi type bi-univalent functions connected with a modified sigmoid activation function and k-Fibonacci numbers. J. Math. Computer Sci. 2022, 27, 105–117. [Google Scholar] [CrossRef]
- Dziok, J.; Raina, R.K.; Sokół, J. Certain results for a class of convex functions related to a shell-like curve connected with Fibonacci numbers. Comput. Math. Appl. 2011, 61, 2605–2613. [Google Scholar] [CrossRef]
- Dziok, J.; Raina, R.K.; Sokół, J. On ϑq-convex functions related to a shell-like curve connected with Fibonacci numbers. Appl. Math. Comput. 2011, 218, 996–1002. [Google Scholar]
- Sundari, K.S.; Keerthi, B.S. Enhancing low-light images using Sakaguchi type function and Gegenbauer polynomial. Sci. Rep. 2024, 14, 29679. [Google Scholar] [CrossRef]
- Nithiyanandham, E.K.; Keerthi, B.S. Image edge detection enhancement using coefficients of Sakaguchi type functions mapped onto petal shaped domain. Heliyon 2024, 10, e31430. [Google Scholar] [CrossRef]
- Al-Ameedee, S.A.; Al-Hakeem, M.B.H.; Alghafil, A.K.H. Fekete-Szegö inequalities for higher-order derivatives of multivalent analytic function with application to stealth combat aircraft. J. Int. Math. 2024, 27, 721–727. [Google Scholar] [CrossRef]

| The Family of Star-like Functions | Author/s | Ref. |
|---|---|---|
| Janowski | [3] | |
| Robertson | [4] | |
| Sokół | [5] | |
| Sokół | [6] |
| The -Analogue of Fibonacci Numbers | The Classical Fibonacci Numbers |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsoboh, A.; Amourah, A.; Alnajar, O.; Ahmed, M.; Seoudy, T.M.
Exploring
Alsoboh A, Amourah A, Alnajar O, Ahmed M, Seoudy TM.
Exploring
Alsoboh, Abdullah, Ala Amourah, Omar Alnajar, Mamoon Ahmed, and Tamer M. Seoudy.
2025. "Exploring
Alsoboh, A., Amourah, A., Alnajar, O., Ahmed, M., & Seoudy, T. M.
(2025). Exploring









