Exploring $\mathfrak{q}$-Fibonacci Numbers in Geometric Function Theory: Univalence and Shell-like Starlike Curves

Abstract

Emphasising their connection with shell-like star-like curves, this work investigates a new subclass of star-like functions defined by $\mathfrak{q}$-Fibonacci numbers and $\mathfrak{q}$-polynomials. We study the geometric and analytic properties of this subclass, including the computation of intervals of univalence and nonunivalence for some functions. Moreover, we define a sufficient condition for functions in this subclass to satisfy the criteria of the famous class of analytic functions with positive real components. This work improves our understanding of the link between Fibonacci-type sequences and the geometric properties of analytic functions by using subordination ideas and the features of $\mathfrak{q}$-Fibonacci sequences. Emphasising the possibility for diverse research in combinatorial and analytical mathematics, the results offer fresh insights and support further study on the applications of calculus in geometric function theory.

1. Introduction, Preliminaries, and Definitions

The Fibonacci sequence is a widely regarded numerical series in mathematics. The sequence is defined by the recurrence relation ${\phi }_{\mathsf{s}}={\phi }_{\mathsf{s}-1}+{\phi }_{\mathsf{s}-2},(\mathsf{s}\ge 2),$ with initial conditions ${\phi }_0=0$ and ${\phi }_1=1$. It is prevalent in nature and art and is utilised in computer science, mathematics, and various other fields. The Fibonacci sequence, intricately linked to generating functions, is essential for comprehending the characteristics of sequences. The generating function is explicitly defined as

$$G\left(\varkappa \right)=\sum _{\mathsf{s}=0}^{\infty }{\phi }_{\mathsf{s}}{\varkappa }^{\mathsf{s}}={\displaystyle \frac{\varkappa }{1-\varkappa -{\varkappa }^2}}.$$

Aside from its mathematical importance, the Fibonacci sequence appears in natural occurrences, affecting development patterns and structural formations in the physical realm. Its recursive structure renders it a potent instrument for analysing sequences, series, and issues related to iterative processes, highlighting its versatility and significance in both theoretical and practical domains.

Denote the family of all analytic functions defined on the open unit disk as $\mathcal{O}$, where $\mathcal{O}$ is the set of all complex numbers $\mathsf{z}=a+ib$ (with $a,b\in \mathbb{R}$) satisfying $\left|\mathsf{z}\right|<1$. Geometrically, $\mathcal{O}$ represents the collection of all points in the complex plane that lie strictly inside the unit circle centered at the origin.

The functions $\mathsf{f}\in \mathcal{A}$ are normalized to satisfy the following initial conditions:

$$\mathsf{f}\left(0\right)=0\mathrm{and}\mathsf{f}\prime \left(0\right)=1.$$

These normalization conditions ensure that the functions are uniquely determined and facilitate the study of their properties within the unit disk. This framework provides a foundation for exploring the analytical and geometric properties of functions in various mathematical contexts, which are central to the broader mathematical investigations discussed in this work.

For every function $\mathrm{f}\in \mathcal{A}$, the Taylor–Maclaurin series expansion can be expressed in the following form:

$$\mathsf{f}\left(\mathsf{z}\right)=\mathsf{z}+\sum _{\mathsf{s}=2}^{\infty }{\alpha }_{\mathsf{s}}{\mathsf{z}}^s,(\mathsf{z}\in \mathcal{O}).$$

(1)

This class of functions has numerous significant subclasses, defined as follows:

$$\begin{array}{cc}\hfill \mathcal{S}& =\left\{\mathsf{f}\in \mathcal{A}:\mathsf{f} \mathrm{is} \mathrm{univalent} \left(\mathrm{injective}\right) \mathrm{in} \mathrm{the} \mathrm{open} \mathrm{unit} \mathrm{disk} \mathcal{O}\right\},\hfill \\ \hfill \mathsf{P}& =\left\{\mathsf{p}\in \mathcal{A}:\mathsf{p}\left(\mathsf{z}\right)=1+\sum _{\mathsf{s}=1}^{\infty }{\mathsf{p}}_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}\mathrm{with}\Re e\left(\mathsf{p}\left(\mathsf{z}\right)\right)>0,\mathsf{z}\in \mathcal{O}\right\},\hfill \\ \hfill \mathsf{P}\left(\beta \right)& =\left\{\mathsf{p}\in \mathcal{A}:\mathsf{p}\left(0\right)=1\mathrm{and}\Re e\left(\mathsf{p}\right(\mathsf{z}\left)\right)>\gamma ,(0\le \gamma <1),\mathsf{z}\in \mathcal{O}\right\}.\hfill \end{array}$$

Geometric function theory extensively utilises the class $\mathsf{P}$ of Caratheodory functions, which pertains to functions possessing positive real components alongside certain analytic characteristics [1]. A function p is classified within $\mathcal{P}$ if and only if it can be represented as

$$\mathsf{p}\left(\mathsf{z}\right)=\left(1+\hslash \left(\mathsf{z}\right)\right){\left(1-\hslash \left(\mathsf{z}\right)\right)}^{-1},(\mathsf{z}\in \mathcal{O}).$$

The function ℏ is categorised as a Schwartz function, fulfilling the criterion $|\hslash (\mathsf{z}\left)\right|<1$ for every $\mathsf{z}\in \mathcal{O}$. The class $\mathcal{S}$ of univalent functions, which is very pertinent to conformal mappings, along with the generalised class $\mathsf{P}\left(\beta \right)$, demonstrates substantial applicability in complex analysis, particularly in geometric function theory.

The class of star-like functions, represented as ${\mathcal{S}}^{*}$, can be defined by multiple methodologies employing the principle of subordination. In 1992, Ma and Minda [2] established the class ${\mathcal{S}}^{*}\left(\mathsf{\Omega }\right)$ derived from this idea, articulated as follows:

$${\mathsf{s}}^{*}\left(\mathsf{\Omega }\right)=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}\mathsf{f}\prime \left(\mathsf{z}\right)}{\mathsf{f}\left(\mathsf{z}\right)}}\prec \mathsf{\Omega }\left(\mathsf{z}\right),\mathrm{where}\mathsf{\Omega }\in \mathsf{P}\mathrm{and}\mathsf{z}\in \mathcal{O}\right\}.$$

Contemporary research has produced several subclasses of star-like functions with the application of specific forms of $\mathsf{\Omega }$. Scholars demonstrate adaptability in their research by employing several methodologies.

Table 1. Lists several of the star-like classes defined by the subordination principle.

The Family of Star-like Functions	Author/s	Ref.
${\mathsf{s}}^{*}\left({\displaystyle \frac{1+\mathsf{z}}{1-\mathsf{z}}}\right)=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}\mathsf{f}\prime \left(\mathsf{z}\right)}{\mathsf{f}\left(\mathsf{z}\right)}}\prec {\displaystyle \frac{1+\mathsf{z}}{1-\mathsf{z}}}\right\}$	Janowski	[3]
${\mathsf{s}}^{*}\left(\vartheta \right)=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}\mathsf{f}\prime \left(\mathsf{z}\right)}{\mathsf{f}\left(\mathsf{z}\right)}}\prec {\displaystyle \frac{1+(1-2\vartheta )\mathsf{z}}{1-\mathsf{z}}},0\le \vartheta <1\right\}$	Robertson	[4]
$\mathsf{SL}\left(\vartheta \right)=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}\mathsf{f}\prime \left(\mathsf{z}\right)}{\mathsf{f}\left(\mathsf{z}\right)}}\prec {\displaystyle \frac{1+{\vartheta }^2{\mathsf{z}}^2}{1-\vartheta \mathsf{z}-{\vartheta }^2{\mathsf{z}}^2}},\vartheta ={\displaystyle \frac{1-\sqrt{5}}{2}}\right\}$	Sokół	[5]
$\mathcal{SK}\left(\vartheta \right)=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}\mathsf{f}\prime \left(\mathsf{z}\right)}{\mathsf{f}\left(\mathsf{z}\right)}}\prec {\displaystyle \frac{3}{3+(\vartheta -3)\mathsf{z}-{\vartheta }^2{\mathsf{z}}^2}},\vartheta \in (-3,1]\right\}$	Sokół	[6]

delineates these subfamilies and underscores the many star-like characteristics arising from distinct $\mathsf{\Omega }$ choices.

Recently, quantum calculus, also known as $\mathfrak{q}$-calculus, has garnered significant interest in the fields of physics and mathematics. Its historical origins date back to the 19th century when Jackson [7,8] introduced the $\mathfrak{q}$-difference operator and integral. Subsequently, Aral and Gupta [9] expanded upon this foundational research by examining $\mathfrak{q}$ analogues of many operators, particularly in the realm of geometric function theory. Quantum calculus, grounded in $\mathfrak{q}$-differences, extends classical calculus and offers a robust framework for exploring specific subclasses of analytic functions, such as star-like and convex functions. In this context, the parameter $\mathfrak{q}$ is anticipated to satisfy $0<\mathfrak{q}<1$, ensuring the requisite convergence and essential attributes necessary for these analyses.

Definition 1 

([10]). The $\mathfrak{q}$-bracket ${\lceil \kappa \rfloor }_{\mathfrak{q}}$ is defined as follows:

$${\lceil \kappa \rfloor }_{\mathfrak{q}}=\left\{\begin{array}{cc}{\displaystyle \frac{1-{\mathfrak{q}}^{\lambda }}{1-\mathfrak{q}}},\hfill & 0<\mathfrak{q}<1,\lambda \in {\mathbb{C}}^{*}=\mathbb{C}\setminus \left\{0\right\}\hfill \\ 1,\hfill & \mathfrak{q}\mapsto 0^{+},\lambda \in {\mathbb{C}}^{*}\hfill \\ \lambda ,\hfill & \mathfrak{q}\mapsto 1^{-},\lambda \in {\mathbb{C}}^{*}\hfill \\ {\mathfrak{q}}^{\gamma -1}+{\mathfrak{q}}^{\gamma -2}+\cdots +\mathfrak{q}+1={\displaystyle \sum _{\mathsf{s}=0}^{\gamma -1}}{\mathfrak{q}}^{\mathsf{s}},\hfill & 0<\mathfrak{q}<1,\lambda =\gamma \in \mathbb{N}.\hfill \end{array}\right.$$

Definition 2 

([10]). The $\mathfrak{q}-$derivative, also known as the $\mathfrak{q}-$difference operator, of a function f is defined by

$${ð}_{\mathfrak{q}}\langle \mathsf{f}\left(\mathsf{z}\right)\rangle =\left\{\begin{array}{cc}{\mathsf{f}\left(\mathsf{z}\right)-f\left(\mathfrak{q}\mathsf{z}\right))(\mathsf{z}-\mathfrak{q}\mathsf{z})}^{-1},\hfill & \mathit{if}0<\mathfrak{q}<1,\mathsf{z}\ne 0,\hfill \\ & \\ \mathsf{f}\prime \left(0\right),\hfill & \mathit{if}\mathsf{z}=0,\hfill \\ & \\ \mathsf{f}\prime \left(\mathsf{z}\right),\hfill & \mathit{if}\mathfrak{q}\mapsto 1^{-},\mathsf{z}\ne 0.\hfill \end{array}\right..$$

Additionally, Jackson [8] introduced the concept of the $\mathfrak{q}$-integral concerning any function $\mathrm{f}$, characterising it as

$$\begin{array}{c}\hfill {\displaystyle \underset{0}{\overset{\mathsf{z}}{\int }}\mathsf{f}(\zeta ){ð}_{\mathfrak{q}}\zeta =(1-\mathfrak{q})\mathsf{z}\sum _{\mathsf{s}=1}^{\infty }{\mathfrak{q}}^{\mathsf{s}-1}\mathsf{f}({\mathfrak{q}}^{\mathsf{s}-1}\mathsf{z}).}\end{array}$$

(2)

As a specific instance of the $\mathfrak{q}$-Jackson integral, we obtain the following equation:

$$\begin{array}{c}\hfill {\displaystyle \underset{0}{\overset{\mathsf{z}}{\int }}\frac{{ð}_{\mathfrak{q}}\langle \mathsf{f}\left(\zeta \right)\rangle }{\mathsf{f}\left(\zeta \right)}{ð}_{\mathfrak{q}}\zeta =\frac{\mathfrak{q}-1}{log\mathfrak{q}}{log}_{\mathfrak{q}}\mathsf{f}\left(\mathsf{z}\right).}\end{array}$$

(3)

By employing the $\mathfrak{q}$-Jackson difference operators, Uçar and Özkan [11] introduced a novel class of functions known as $\mathfrak{q}$-star-like functions, denoted by ${\mathsf{s}}_{\mathfrak{q}}^{*}$. This class is formally defined as

$${\mathsf{s}}_{\mathfrak{q}}^{*}=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathsf{f}\left(\mathsf{z}\right)\rangle }{\mathsf{f}\left(\mathsf{z}\right)}}\prec {\displaystyle \frac{1+\mathsf{z}}{1-\mathfrak{q}\mathsf{z}}}(\mathsf{z}\in \mathcal{O})\right\}.$$

This definition extends the classical concept of star-like functions by incorporating the $\mathfrak{q}$-difference operator, thereby providing a more generalized framework for studying geometric properties of analytic functions.

Similarly, Srivastava et al. [12] proposed another class of $\mathfrak{q}$ star-like functions, denoted by ${\mathsf{s}}^{*}(\mathcal{L},\mathfrak{q})$, defined as

$${\mathsf{s}}^{*}(\mathcal{L},\mathfrak{q})=\left\{\mathsf{f}\in \mathcal{A}:{\displaystyle \frac{\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathsf{f}\left(\mathsf{z}\right)\rangle }{\mathsf{f}\left(\mathsf{z}\right)}}\prec ex{p}_{\mathfrak{q}}\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{z}}{{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}!}}(\mathsf{z}\in \mathcal{O})\right\},$$

where $ex{p}_{\mathfrak{q}}\left(z\right)$ represents the $\mathfrak{q}$-exponential function, which plays a central role in $\mathfrak{q}$-calculus. This class generalizes the concept of star-like functions by incorporating the $\mathfrak{q}$-exponential function into the subordination condition, providing a broader framework for analysis. The use of $\mathfrak{q}$-calculus has facilitated the exploration of new subclasses of analytic functions, leading to significant progress in understanding their geometric and analytic properties. These advancements demonstrate the versatility and depth of $\mathfrak{q}$-calculus, showcasing its ability to enrich the theory of analytic functions and reveal new mathematical insights. Such developments highlight the growing importance of $\mathfrak{q}$-calculus in both theoretical and applied contexts, opening avenues for further research and innovation in the field, as discussed in [13,14,15,16,17,18,19]. The study of univalent functions is essential in geometric function theory, especially for investigating functions that are univalent in both a domain and its inverse. These functions are linked to orthogonal polynomials, such as $\mathfrak{q}$-Fibonacci numbers, which facilitate the analysis of coefficient bounds and structural properties [20,21,22,23,24,25,26,27,28,29,30,31]. Their applications extend across various fields, including low-light imaging for improved contrast, image edge detection for greater precision, and stealth combat aircraft for optimizing radar signatures (see [32,33,34]).

2. Definition and Example

Motivated by the $\mathfrak{q}$-Fibonacci numbers, this section introduces a novel subclass of analytic functions. This subclass not only unifies aspects of the conventional theory of analytic functions but also highlights new geometric and analytic properties that emerge through the use of $\mathfrak{q}$-Fibonacci numbers. By incorporating $\mathfrak{q}$-Fibonacci numbers, this subclass provides fresh perspectives on the connections between geometric analytic functions, Fibonacci-type sequences, and $\mathfrak{q}$-calculus, thereby advancing and enriching the existing theory.

Definition 3. 

The function $\mathrm{f}$ belongs to the class ${\mathrm{SL}}_{\mathfrak{q}}$ if and only if

$${\displaystyle \frac{\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle }{\mathrm{f}\left(\mathsf{z}\right)}}\prec \mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q}),$$

where

$$\begin{array}{c}\hfill \mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})={\displaystyle \frac{1+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}},\end{array}$$

(4)

and ${\vartheta }_{\mathfrak{q}}=\frac{1-\sqrt{4\mathfrak{q}+1}}{2\mathfrak{q}}$ is the $\mathfrak{q}$-analogue of the Fibonacci numbers, defined recursively by the relation

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\phi }_0\left(\mathfrak{q}\right)& ={\phi }_1\left(\mathfrak{q}\right)-1=0,\hfill \\ \hfill {\phi }_n\left(\mathfrak{q}\right)& ={\phi }_{\mathsf{s}-1}\left(\mathfrak{q}\right)+\mathfrak{q}{\phi }_{\mathsf{s}-2}\left(\mathfrak{q}\right),\mathit{for}(\mathsf{s}\ge 2).\hfill \end{array}\end{array}$$

(5)

The initial terms of the $\mathfrak{q}$-Fibonacci numbers, which serve as a generalization of the classical Fibonacci numbers in the limit as approaches $\mathfrak{q}\mapsto 1^{-}$, are provided in

Table 2. The first initial terms of the $\mathfrak{q}$-Fibonacci sequence.

The $\mathfrak{q}$-Analogue of Fibonacci Numbers	The Classical Fibonacci Numbers
${\phi }_0\left(\mathfrak{q}\right)=0$	${\phi }_0=0$
${\phi }_1\left(\mathfrak{q}\right)=1$	${\phi }_1=1$
${\phi }_2\left(\mathfrak{q}\right)=1$	${\phi }_2=1$
${\phi }_3\left(\mathfrak{q}\right)=1+\mathfrak{q}$	${\phi }_3=2$
${\phi }_4\left(\mathfrak{q}\right)=1+2\mathfrak{q}$	${\phi }_4=3$
${\phi }_5\left(\mathfrak{q}\right)=1+3\mathfrak{q}+{\mathfrak{q}}^2$	${\phi }_5=5$

.

We aim to establish a novel link between the $\mathfrak{q}$-analogue of Fibonacci numbers and their corresponding Fibonacci polynomials. We define a function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ in the following approach:

$$\begin{array}{cc}\hfill \mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})& ={\displaystyle \frac{1+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}}\hfill \\ \hfill & =1+{\vartheta }_{\mathfrak{q}}\mathsf{z}+(2\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2+(3\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^3{\mathsf{z}}^3+(2{\mathfrak{q}}^2+4\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^4{\mathsf{z}}^4+\cdots .\hfill \end{array}$$

(6)

It is worth noting that the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is not univalent in the domain $\mathcal{O}$. Specifically, it attains the same value at two distinct points:

$$\mathsf{{\rm Y}}(0;\mathfrak{q})=1\mathrm{and}\mathsf{{\rm Y}}\left(-{\displaystyle \frac{1}{2\mathfrak{q}{\vartheta }_{\mathfrak{q}}}};\mathfrak{q}\right)=1.$$

Example 1. 

If $\mathfrak{q}\to 1^{-}$ in Definition 3, we obtain the class $\mathsf{SL}=\underset{\mathfrak{q}\to 1^{-}}{lim}{\mathsf{SL}}_{\mathfrak{q}}$ defined as follows:  A function f belongs to the class $\mathsf{SL}$ if and only if

$${\displaystyle \frac{\mathsf{z}\mathrm{f}\prime \left(\mathsf{z}\right)}{\mathrm{f}\left(\mathsf{z}\right)}}\prec \mathsf{{\rm Y}}\left(\mathsf{z}\right),$$

where

$$\mathsf{{\rm Y}}(\mathsf{z};1)=\mathsf{{\rm Y}}\left(\mathsf{z}\right)={\displaystyle \frac{1+{\vartheta }^2{\mathsf{z}}^2}{1-\vartheta \mathsf{z}-{\vartheta }^2{\mathsf{z}}^2}},$$

(7)

and $\vartheta ={\displaystyle \frac{1-\sqrt{5}}{2}}$ corresponds to the classical Fibonacci numbers.

3. Main Results

Theorem 1. 

Let

$${\phi }_{\mathsf{s}}\left(\mathfrak{q}\right)={\displaystyle \frac{{\left(1-\mathfrak{q}{\vartheta }_{\mathfrak{q}}\right)}^{\mathsf{s}}-{\left({\vartheta }_{\mathfrak{q}}\right)}^{\mathsf{s}}}{\sqrt{4\mathfrak{q}+1}}},$$

denotes the sequence of $\mathfrak{q}$-Fibonacci numbers, defined in recurrence relation as

$${\phi }_{\mathsf{s}+2}\left(\mathfrak{q}\right)={\phi }_{\mathsf{s}+1}\left(\mathfrak{q}\right)+\mathfrak{q}{\phi }_{\mathsf{s}-1}\left(\mathfrak{q}\right),\mathsf{s}=0,1,2,3,\cdots .$$

If the generating function

$$\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})={\displaystyle \frac{1+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}}=1+\sum _{\mathsf{s}=1}^{\infty }{\mathsf{p}}_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}},$$

then

$${\mathsf{p}}_{\mathsf{s}}=\left({\phi }_{\mathsf{s}+1}\left(\mathfrak{q}\right)+\mathfrak{q}{\phi }_{\mathsf{s}-1}\left(\mathfrak{q}\right)\right){\vartheta }_{\mathfrak{q}},\mathsf{s}\in \mathbb{N}.$$

Proof. 

Let us denote ${\vartheta }_{\mathfrak{q}}\mathsf{z}=\varpi$ and $\left|\varpi \right|<|{\vartheta }_{\mathfrak{q}}|$. Now, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{1+\mathfrak{q}{\varpi }^2}{1-\varpi -\mathfrak{q}{\varpi }^2}}& =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right){\displaystyle \frac{\varpi }{1-\varpi -\mathfrak{q}{\varpi }^2}}\hfill \\ & =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right){\displaystyle \frac{1}{\sqrt{4\mathfrak{q}+1}}}\left({\displaystyle \frac{{\vartheta }_{\mathfrak{q}}}{\varpi +{\vartheta }_{\mathfrak{q}}}}+{\displaystyle \frac{\mathfrak{q}{\vartheta }_{\mathfrak{q}}-1}{\mathfrak{q}\varpi +(1-\mathfrak{q}{\vartheta }_{\mathfrak{q}})}}\right)\hfill \\ & =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right){\displaystyle \frac{1}{\sqrt{4\mathfrak{q}+1}}}\left({\displaystyle \frac{1}{1+\frac{\varpi }{{\vartheta }_{\mathfrak{q}}}}}-{\displaystyle \frac{1}{1+\frac{\mathfrak{q}\varpi }{1-\mathfrak{q}{\vartheta }_{\mathfrak{q}}}}}\right)\hfill \\ & =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right){\displaystyle \frac{1}{\sqrt{4\mathfrak{q}+1}}}\sum _{\mathsf{s}=1}^{\infty }{(-1)}^{\mathsf{s}}\left[{\left({\displaystyle \frac{\varpi }{{\vartheta }_{\mathfrak{q}}}}\right)}^{\mathsf{s}}-{\left({\displaystyle \frac{\mathfrak{q}\varpi }{1-\mathfrak{q}{\vartheta }_{\mathfrak{q}}}}\right)}^{\mathsf{s}}\right]\hfill \\ & =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right)\sum _{\mathsf{s}=1}^{\infty }{\displaystyle \frac{{\left(1-\mathfrak{q}{\vartheta }_{\mathfrak{q}}\right)}^{\mathsf{s}}-{\left({\vartheta }_{\mathfrak{q}}\right)}^{\mathsf{s}}}{\sqrt{4\mathfrak{q}+1}}}{t}^{\mathsf{s}}\hfill \\ & =\left(\mathfrak{q}\varpi +{\displaystyle \frac{1}{\varpi }}\right)\sum _{\mathsf{s}=1}^{\infty }{\phi }_{\mathsf{s}}\left(\mathfrak{q}\right){\varpi }^{\mathsf{s}}=1+\sum _{\mathsf{s}=1}^{\infty }\left({\phi }_{\mathsf{s}+1}\left(\mathfrak{q}\right)+\mathfrak{q}{\phi }_{\mathsf{s}-1}\left(\mathfrak{q}\right)\right){\vartheta }_{\mathfrak{q}}^{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}.\hfill \end{array}\end{array}$$

(8)

□

Theorem 2. 

A function $\mathrm{f}$ of the form (1) is in the class $\mathrm{SL}\mathfrak{q}$ if and only if there exists a function $\mu \prec \mathsf{{\rm Y}}$, where

$$\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})={\displaystyle \frac{1+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}}.$$

In this case, f can be expressed in the integral form

$$\begin{array}{c}\hfill \mathrm{f}\left(\mathsf{z}\right)=\mathsf{z}·{exp}_{\mathfrak{q}}\left({\displaystyle \frac{log\mathfrak{q}}{\mathfrak{q}-1}}{\int }_0^{\mathsf{z}}{\displaystyle \frac{\mu \left(\zeta \right)-1}{\zeta }}{\mathfrak{d}}_{\mathfrak{q}}\zeta \right),\mathsf{z}\in \mathcal{O}.\end{array}$$

(9)

Proof. 

If $\mathrm{f}\in {\mathsf{SL}}_{\mathfrak{q}}$, then

$${\displaystyle \frac{\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle }{\mathrm{f}\left(\mathsf{z}\right)}}=\mathsf{{\rm Y}}(\hslash \left(\mathsf{z}\right);\mathfrak{q}),|\hslash \left(\mathsf{z}\right)|<1,\mathsf{z}\in \mathcal{O}.$$

(10)

Let $\mu \left(\mathsf{z}\right)=\mathsf{{\rm Y}}(\hslash (\mathsf{z});q)$. By applying the $\mathfrak{q}$-Jackson integral, as defined in Equation (3), we establish the equivalence between Equations (9) and (10). Specifically, the $\mathfrak{q}$-Jackson integral provides a framework through which the transformation from (9) to (10) can be rigorously derived, ensuring consistency and mathematical validity. □

Theorem 3. 

Let $\mathrm{f}$ be given by (1) and belong to the class ${\mathrm{SL}}_{\mathfrak{q}}$ Then, the coefficients satisfy the bound

$$\begin{array}{c}\hfill |{\alpha }_{\mathsf{s}}|\le |{\vartheta }_{\mathfrak{q}}{|}^{\mathsf{s}-1}{\phi }_{\mathsf{s}}\left(\mathfrak{q}\right),\end{array}$$

(11)

where ${\phi }_{\mathsf{s}}\left(\mathfrak{q}\right)$ represents the sequence of q-Fibonacci numbers, and ${\vartheta }_{\mathfrak{q}}$ is given by

$${\vartheta }_{\mathfrak{q}}={\displaystyle \frac{1-\sqrt{4q+1}}{2\mathfrak{q}}}.$$

Moreover, this bound is sharp and is attained by the function

$${\mathsf{{\rm Y}}}_0(\mathsf{z};\mathfrak{q})={\displaystyle \frac{\mathsf{z}}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}}.$$

Proof. 

From the definition of ${\mathsf{SL}}_{\mathfrak{q}}$, there exists a function ℏ, with $|\hslash (\mathsf{z}\left)\right|<1$ for $\mathsf{z}\in \mathcal{O}$, such that for $\mathrm{f}\in {\mathsf{SL}}_{\mathfrak{q}}$ given by (1), the following holds:

$${\displaystyle \frac{\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle }{\mathrm{f}\left(\mathsf{z}\right)}}={\displaystyle \frac{1+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\hslash }^2\left(\mathsf{z}\right)}{1-{\vartheta }_{\mathfrak{q}}\hslash \left(\mathsf{z}\right)-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\hslash }^2\left(\mathsf{z}\right)}}.$$

Therefore, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathsf{z}{ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle -\mathrm{f}\left(\mathsf{z}\right)& ={\vartheta }_{\mathfrak{q}}\mathsf{z}\hslash \left(\mathsf{z}\right){ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle +{\vartheta }_{\mathfrak{q}}^2\hslash {\left(\mathsf{z}\right)}^2\left[\mathsf{z}{ð}_{\mathfrak{q}}\langle \mathrm{f}\left(\mathsf{z}\right)\rangle +\mathrm{f}\left(\mathsf{z}\right)\right]\hfill \end{array}\end{array}$$

which equivalent to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{\mathsf{s}=1}^{\infty }\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}-1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}& ={\vartheta }_{\mathfrak{q}}\hslash \left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\infty }{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+{\vartheta }_{\mathfrak{q}}^2{\hslash }^2\left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\infty }\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}+1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}\hfill \end{array}\end{array}$$

and so

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{\mathsf{s}=1}^{\tau }\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}-1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+\sum _{\mathsf{s}=\tau +1}^{\infty }{c}_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}& ={\vartheta }_{\mathfrak{q}}\hslash \left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+{\vartheta }_{\mathfrak{q}}^2{\hslash }^2\left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\tau -2}\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}+1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}.\hfill \end{array}\end{array}$$

Hence, for $m\ge 2,$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\left|\sum _{\mathsf{s}=1}^{\tau }\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}-1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+\sum _{\mathsf{s}=\tau +1}^{\infty }{c}_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}\right|}^2\hfill \\ \hfill & ={\left|{\vartheta }_{\mathfrak{q}}\hslash \left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+{\vartheta }_{\mathfrak{q}}^2{\hslash }^2\left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\tau -2}\left({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}+1\right){\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}\right|}^2\hfill \\ \hfill & \le {\left|{\vartheta }_{\mathfrak{q}}\sum _{\mathsf{s}=1}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+{\vartheta }_{\mathfrak{q}}^2\hslash \left(\mathsf{z}\right)\sum _{\mathsf{s}=1}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}-1}{\mathsf{z}}^{\mathsf{s}-1}\right|}^2\hfill \\ \hfill & \le \sum _{\mathsf{s}=1}^{\tau -1}|{\vartheta }_{\mathfrak{q}}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}+{\vartheta }_{\mathfrak{q}}^2{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}-1}\hslash \left(z\right){\mathsf{z}}^{\mathsf{s}-1}{|}^2\hfill \\ \hfill & \le \sum _{\mathsf{s}=1}^{\tau -1}|{\vartheta }_{\mathfrak{q}}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}}{\mathsf{z}}^{\mathsf{s}}{|}^2+|{\vartheta }_{\mathfrak{q}}^2{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}{\alpha }_{\mathsf{s}-1}{\mathsf{z}}^{\mathsf{s}-1}{|}^2+2|{\vartheta }_{\mathfrak{q}}^3{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}^2{\alpha }_{\mathsf{s}}{\alpha }_{\mathsf{s}-1}{\mathsf{z}}^{2\mathsf{s}-1}{|}^2\hfill \end{array}\end{array}$$

By integrating this inequality over the contour defined by $\mathsf{z}=\mathsf{r}exp\left(i\varphi \right)$ and taking the limit as $\mathsf{r}\mapsto 1^{-}$, we derive the following:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill & \sum _{\mathsf{s}=1}^{\tau }{\left({[n-1]}_{\mathfrak{q}}\right)}^2|{\alpha }_{\mathsf{s}}{|}^2+\sum _{\mathsf{s}=\tau +1}^{\infty }|c_{\mathsf{s}}{|}^2\hfill & \hfill \le {\vartheta }_{\mathfrak{q}}^2\sum _{\mathsf{s}=1}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}^2|{\alpha }_{\mathsf{s}}{|}^2+{\vartheta }_{\mathfrak{q}}^4\sum _{\mathsf{s}=1}^{\tau -2}{\lceil \mathsf{s}+1\rfloor }_{\mathfrak{q}}^2|{\alpha }_{\mathsf{s}}{|}^2+2{\vartheta }_{\mathfrak{q}}^3\sum _{\mathsf{s}=2}^{\tau -1}{\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}^2\left|{\alpha }_{\mathsf{s}}\right|\left|{\alpha }_{\mathsf{s}-1}\right|.\end{array}\end{array}$$

Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\alpha }_{\mathsf{s}}|& \le {\displaystyle \frac{1}{{({\lceil \mathsf{s}\rfloor }_{\mathfrak{q}}-1)}^2}}\left(\sum _{\kappa =1}^{\mathsf{s}-1}\left({\vartheta }_{\mathfrak{q}}^2{\lceil \kappa \rfloor }_{\mathfrak{q}}^2-{({\lceil \kappa \rfloor }_{\mathfrak{q}}-1)}^2\right)|{\alpha }_{\kappa }{|}^2+{\vartheta }_{\mathfrak{q}}^4\sum _{\kappa =1}^{\mathsf{s}-2}{({\lceil \kappa \rfloor }_{\mathfrak{q}}+1)}^2|{\alpha }_{\kappa }{|}^2+2{\vartheta }_{\mathfrak{q}}^3\sum _{\kappa =1}^{\mathsf{s}-1}{\lceil \kappa \rfloor }_{\mathfrak{q}}^2|{\alpha }_{\kappa }\left|\right|{\alpha }_{\kappa -1}|\right).\hfill \end{array}\end{array}$$

(12)

For $\mathsf{s}=1$, the estimation (11) holds true. Let the inequality in (11) hold for $\mathsf{s}$, $1<\mathsf{s}\le \tau$. Then, from (12), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\alpha }_{\tau +1}{|}^2& \le {\displaystyle \frac{1}{{\lceil \tau \rfloor }_{\mathfrak{q}}^2}}\left\{\sum _{\kappa =1}^{\tau }\left({\vartheta }_{\mathfrak{q}}^2{\lceil \kappa \rfloor }_{\mathfrak{q}}^2-{({\lceil \kappa \rfloor }_{\mathfrak{q}}-1)}^2\right)|{\alpha }_{\kappa }{|}^2+{\vartheta }_{\mathfrak{q}}^4\sum _{\kappa =1}^{\tau -1}{({\lceil \kappa \rfloor }_{\mathfrak{q}}+1)}^2|{\alpha }_{\kappa }{|}^2+2\sum _{\kappa =1}^{\tau }\left|{\vartheta }_{\mathfrak{q}}^3\right|{\lceil \kappa \rfloor }_{\mathfrak{q}}^2|{\alpha }_{\kappa }\left|\right|{\alpha }_{\kappa -1}|\right\}.\hfill \end{array}\end{array}$$

Therefore, we have $|{\alpha }_{\tau +1}{|}^2\le$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\left({\displaystyle \frac{{\lceil \tau \rfloor }_{\mathfrak{q}}-1}{{\lceil \tau \rfloor }_{\mathfrak{q}}}}\right)}^2{\displaystyle \frac{1}{{({\lceil \tau \rfloor }_{\mathfrak{q}}-1)}^2}}\left\{\begin{array}{c}{\displaystyle \sum _{\kappa =1}^{\tau -1}}\left({\vartheta }_{\mathfrak{q}}^2{\lceil \kappa \rfloor }_{\mathfrak{q}}^2-{({\lceil \kappa \rfloor }_{\mathfrak{q}}-1)}^2\right)|{\alpha }_{\kappa }{|}^2+{\vartheta }_{\mathfrak{q}}^4{\displaystyle \sum _{\kappa =1}^{\tau -2}}{({\lceil \kappa \rfloor }_{\mathfrak{q}}+1)}^2{\left|{\alpha }_{\kappa }\right|}^2\\ +2\left|{\vartheta }_{\mathfrak{q}}^3\right|{\displaystyle \sum _{\kappa =1}^{\tau -1}}{\lceil \kappa \rfloor }_{\mathfrak{q}}^2|{\alpha }_{\kappa }\left|\right|{\alpha }_{\kappa -1}|+\left({\vartheta }_{\mathfrak{q}}^2{\lceil \tau \rfloor }_{\mathfrak{q}}^2-{({\lceil \tau \rfloor }_{\mathfrak{q}}-1)}^2\right){\left|{\alpha }_{\tau }\right|}^2\\ +{\vartheta }_{\mathfrak{q}}^4{\left({\lceil \tau \rfloor }_{\mathfrak{q}}\right)}^3|{\alpha }_{\tau -1}{|}^2+2\left|{\vartheta }_{\mathfrak{q}}^3\right|{\lceil \tau \rfloor }_{\mathfrak{q}}^2|{\alpha }_{\tau }\left|\right|{\alpha }_{\tau -1}|\end{array}\right\}\hfill \\ & ={\left({\displaystyle \frac{{\lceil \tau \rfloor }_{\mathfrak{q}}-1}{{\lceil \tau \rfloor }_{\mathfrak{q}}}}\right)}^2\left\{\begin{array}{c}|{\alpha }_{\tau }{|}^2+{\displaystyle \frac{1}{{\left({\lceil \tau \rfloor }_{\mathfrak{q}}-1\right)}^2}}({\vartheta }_{\mathfrak{q}}^2{\left[\tau \right]}_{\mathfrak{q}}^2+{\vartheta }_{\mathfrak{q}}^4{\lceil \tau \rfloor }_{\mathfrak{q}}^2{\left|{\alpha }_{\tau -1}\right|}^2\\ +2{\vartheta }_{\mathfrak{q}}^3{\lceil \tau \rfloor }_{\mathfrak{q}}^2|{\alpha }_{\tau }\left|\right|{\alpha }_{\tau -1}|-{({\lceil \tau \rfloor }_{\mathfrak{q}}-1)}^2{\left|{\alpha }_{\tau }\right|}^2)\end{array}\right\}\hfill \\ & ={\displaystyle \frac{1}{{\lceil \tau \rfloor }_{\mathfrak{q}}^2}}{\left({\vartheta }_{\mathfrak{q}}{\lceil \tau \rfloor }_{\mathfrak{q}}|{\alpha }_{\tau }|+{\vartheta }_{\mathfrak{q}}^2{\lceil \tau \rfloor }_{\mathfrak{q}}\left|{\alpha }_{\tau -1}\right|\right)}^2\le {\left({\vartheta }_{\mathfrak{q}}|{\alpha }_{\tau }|+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2\left|{\alpha }_{\tau -1}\right|\right)}^2\hfill \\ & ={\left({\vartheta }_{\mathfrak{q}}^{\tau }{\phi }_{\tau }\left(\mathfrak{q}\right)+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^{\tau }{\phi }_{\tau -1}\left(\mathfrak{q}\right)\right)}^2={\vartheta }_{\mathfrak{q}}^{\tau }{\left({\phi }_{\tau }\left(\mathfrak{q}\right)+\mathfrak{q}{\vartheta }_{\mathfrak{q}}^{\tau }{\phi }_{\tau -1}\left(\mathfrak{q}\right)\right)}^2={\left({\vartheta }_{\mathfrak{q}}^{\tau }{\phi }_{\tau +1}\left(\mathfrak{q}\right)\right)}^2.\hfill \end{array}\end{array}$$

This is because ${\phi }_{\tau }\left(\mathfrak{q}\right)$ represents the sequence of the $\mathfrak{q}$-analog of Fibonacci numbers. We have proven the inequality in (11) by induction, which establishes a key property of this sequence. In addition, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\displaystyle \frac{\mathsf{z}}{1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2}}=& \mathsf{z}+{\vartheta }_{\mathfrak{q}}{\mathsf{z}}^2+(\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^3+(2\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^3{\mathsf{z}}^4+\hfill & \hfill ({\mathfrak{q}}^2+3\mathfrak{q}+1){\vartheta }_{\mathfrak{q}}^4{\mathsf{z}}^5+\cdots .\end{array}\end{array}$$

□

Corollary 1 

([5]). If the function belongs to the class $\mathrm{SL}$, then

$$\underset{n\to \infty }{lim}|{\alpha }_{\mathsf{s}}{|\le |\vartheta |}^{\mathsf{s}-1}{\phi }_{\mathsf{s}}.$$

This result is sharp for the function

$${\mathsf{{\rm Y}}}_0(\mathsf{z};1)={\displaystyle \frac{\mathsf{z}}{1-\vartheta \mathsf{z}-{\vartheta }^2{\mathsf{z}}^2}},\vartheta ={\displaystyle \frac{1-\sqrt{5}}{2}}.$$

Theorem 4. 

Consider the function ${\mathsf{{\rm Y}}}_0(\mathsf{z};\mathfrak{q})$ given by the form in (4). The image of the unit circle under this function traces out the curve ${\mathsf{\Omega }}_{\mathfrak{q}}$, which satisfies the following parametric equations:

$$\begin{array}{cc}\hfill \varkappa & ={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(1+2\mathfrak{q}-2\mathfrak{q}cos\varphi )}}\mathit{and}\mathsf{y}={\displaystyle \frac{\frac{sin\varphi }{2(1+cos\varphi )}(4\mathfrak{q}cos\varphi -1)}{(1+2\mathfrak{q}-2\mathfrak{q}cos\varphi )}},\left(\varphi \in [0,2\pi )\setminus \left\{\pi \right\}\right).\hfill \end{array}$$

(13)

Proof. 

The proof is established through a series of straightforward calculations, which rely on fundamental properties and techniques from the underlying mathematical framework. Recall that the curve known as the conchoid of Sluze is described by the following equation:

$$\varrho (\varkappa -\varrho )\left({\varkappa }^2+{\mathsf{y}}^2\right)+{\eta }^2{\varkappa }^2=0,(\varrho ,\eta >0).$$

(14)

When $\eta =2\varrho$, the equation for the conchoid of Sluze (14) simplifies to the following form:

$${\varkappa }^3+(\varkappa -\varrho ){\mathsf{y}}^2+3\varrho {\varkappa }^2=0,$$

(15)

which represents the well-known trisectrix of Maclaurin, as shown in Figure 1.

Derived from Equation (13), the Cartesian equation for the curve is

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_{\mathfrak{q}}:\left[2(1+4\mathfrak{q})\varkappa -\sqrt{1+4\mathfrak{q}}\right]{\mathsf{y}}^2& =\left(\sqrt{4\mathfrak{q}+1}-2\varkappa \right){\left(\sqrt{4\mathfrak{q}+1},\varkappa -1\right)}^2.\hfill \end{array}$$

(16)

If we express Equation (16) in the form

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\left({\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}-\varkappa \right)}^3+{\displaystyle \frac{(4\mathfrak{q}-1)\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}{\left({\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}-\varkappa \right)}^2+\left[\left({\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}-\varkappa \right)-{\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}\right]{\mathsf{y}}^2=0,\hfill \end{array}\end{array}$$

(17)

then we can observe that the image of a unit circle under the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is translated into a curve with Equation (15), where

$$a={\displaystyle \frac{1-2\mathfrak{q}{\vartheta }_q}{2(4\mathfrak{q}+1)}}={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}.$$

As a result, the curve ${\mathsf{\Omega }}_{\mathfrak{q}}$ displays a shell-like configuration and is symmetric about the real axis, as illustrated in Figure 1. The symmetry and geometric structure originate from the analytical properties of the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ and its dependence on the parameter $\mathfrak{q}$.

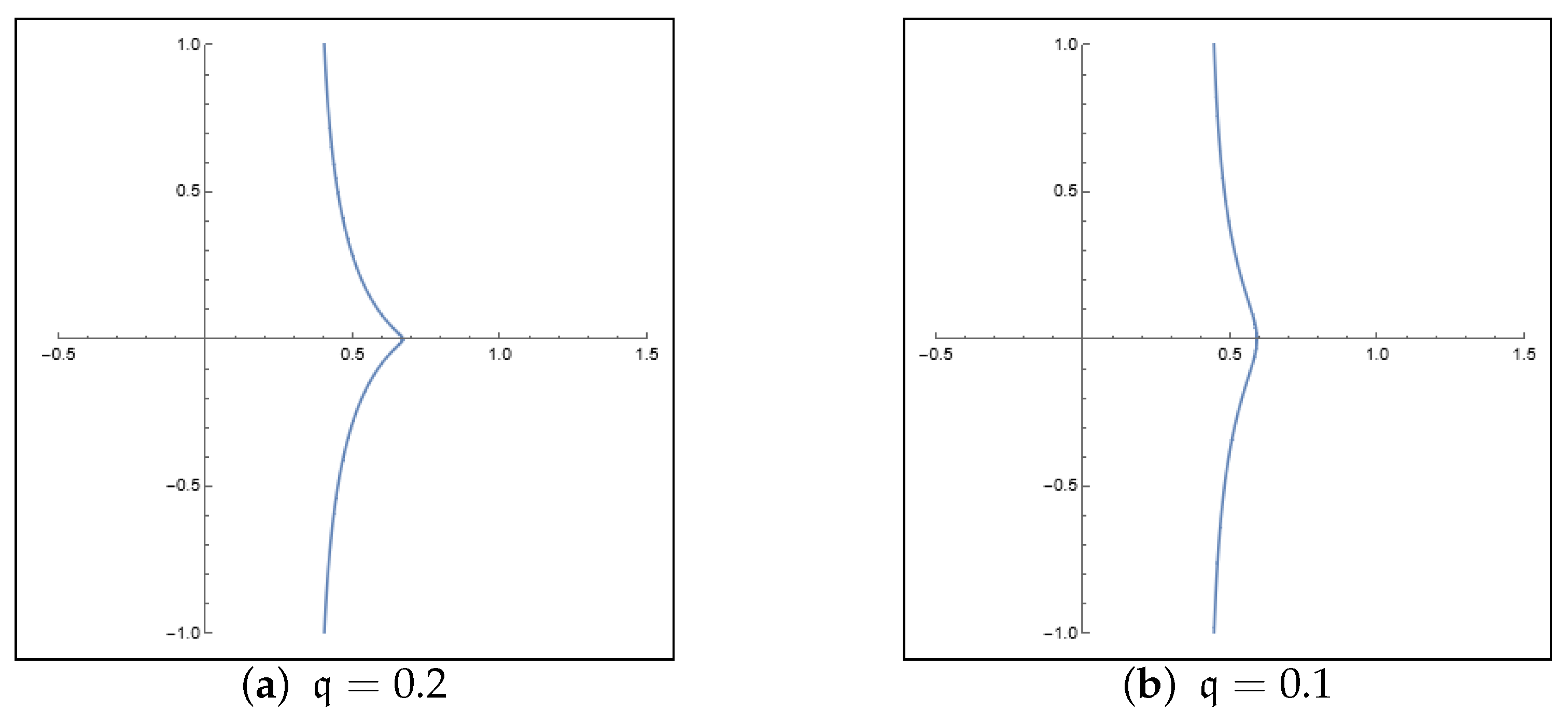
• In the range of $\mathfrak{q}$ where $\mathfrak{q}\in \left(0,{\displaystyle \frac{1}{4}}\right)$, the curve takes a similar appearance of a conchoid without any loops. See Figure 2 for visual representations of ${\mathsf{\Omega }}_{\mathfrak{q}}$ corresponding to various $\mathfrak{q}$ values.
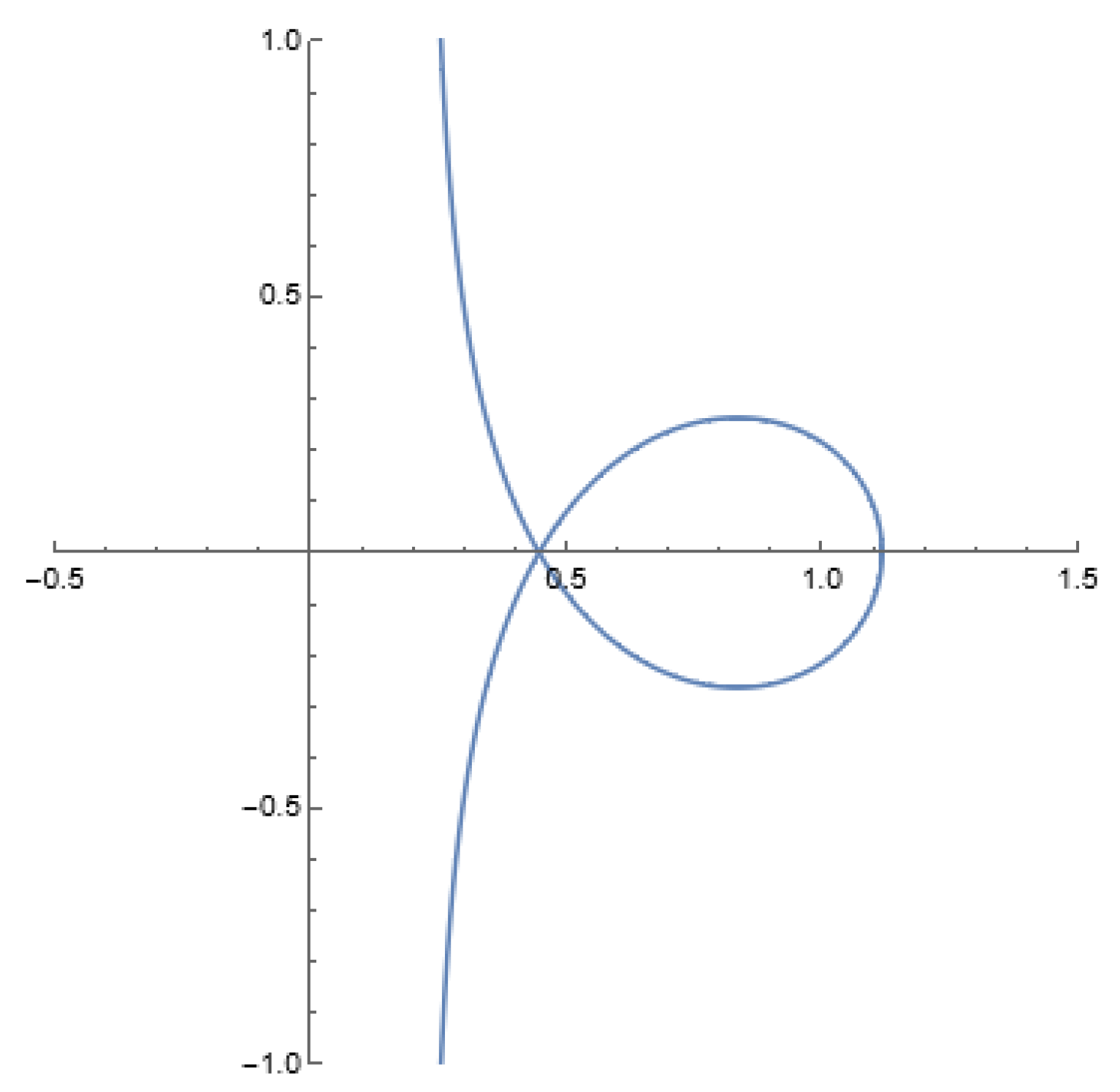
• In the range of $\mathfrak{q}$ where $\mathfrak{q}\in \left({\displaystyle \frac{1}{4}},1\right)$, we observe that

  $$\mathsf{{\rm Y}}\left(exp\left(\pm iarccos{\left(4\mathfrak{q}\right)}^{-1}\right)\right)={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}},$$

  implies that the curve ${\mathsf{\Omega }}_{\mathfrak{q}}$ intersects itself on the real axis at the point ${\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}$. Consequently, ${\mathsf{\Omega }}_{\mathfrak{q}}$ forms a loop that intersects the real axis at two points, $e_1={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2}}$ and $e_2={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}$. See Figure 3 for visual representations of ${\mathsf{\Omega }}_{\mathfrak{q}}$ corresponding to various $\mathfrak{q}$ values.

The curve $\mathsf{{\rm Y}}(e^{i\varphi };\mathfrak{q})$, where $\varphi \in [0,2\pi )\setminus \left\{\pi \right\}$, exhibits a vertical asymptote and a loop, arising from the characteristics of Υ. Furthermore, the curve intersects itself at the coordinates

$$\mathsf{{\rm Y}}\left(e^{\pm iarccos(1/4\mathfrak{q})}\right)={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{4\mathfrak{q}+1}}.$$

These intersections, along with the presence of the asymptote and loop, highlight the intricate geometric structure of the curve, which is influenced by the parameter $\mathfrak{q}$ and the functional properties of Υ. Furthermore, we have the following limits:

(a)

$\underset{\xi \to \pi }{lim}\Re e\left(\mathsf{{\rm Y}}\left(e^{i\xi }\right);\mathfrak{q}\right)=ϵ.$

(b)

$\underset{\xi \to {\pi }^{-}}{lim}\Im m\left(\mathsf{{\rm Y}}\left(e^{i\xi }\right);\mathfrak{q}\right)=-\infty$ and $\underset{\xi \to {\pi }^{+}}{lim}\Im m\left(\mathsf{{\rm Y}}\left(e^{i\xi }\right);\mathfrak{q}\right)=\infty .$

□

In the following theorem, we establish a sufficient condition for the function ${\mathsf{{\rm Y}}}_0(\mathsf{z};\mathfrak{q})$ to belong to the class $\mathsf{{\rm Y}}\left(\beta \right)$.

Theorem 5. 

The function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ belongs to the class $\mathsf{P}\left(\beta \right)$, with the parameter

$$\beta ={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}.$$

Proof. 

The proof is direct. Let us examine the image of the unit circle under the mapping ${\mathsf{{\rm Y}}}_0$. From Theorem 4 (after performing the necessary calculations), we derive the following relationship:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Re e\left\{\mathsf{{\rm Y}}\left(e^{it};\mathfrak{q}\right)\right\}& ={\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(1+2\mathfrak{q}-2\mathfrak{q}cos\varphi )}}\ge {\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}=\beta ,\hfill \end{array}\end{array}$$

(18)

where $\varphi \in [0,2\pi )$, since $\mathsf{{\rm Y}}(0;\mathfrak{q})=1$—it follows that $\mathsf{{\rm Y}}\in \mathsf{P}\left({\displaystyle \frac{\sqrt{4\mathfrak{q}+1}}{2(4\mathfrak{q}+1)}}\right)$. □

We construct a sufficient condition for the univalency of the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ in the following theorem within a well-defined disk.

Theorem 6. 

The function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is univalent within the disk

$${\mathbb{D}}_{\mathfrak{q}}=\left\{\mathsf{z}:\left|\mathsf{z}\right|<{\mathsf{r}}_{\mathfrak{q}}={\displaystyle \frac{1+\mathfrak{q}-\sqrt{{(1+\mathfrak{q})}^2+1}}{\mathfrak{q}{\vartheta }_{\mathfrak{q}}}}\right\},$$

(19)

and is not univalent in any disk with a radius equal to or greater than ${\mathsf{r}}_{\mathfrak{q}}$.

Proof. 

Let $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})=\mathsf{{\rm Y}}(w;\mathfrak{q})\mathrm{for}\mathrm{some}\mathsf{z},\omega \in \mathcal{O}$. By performing the necessary calculations, we arrive at the following equation:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\vartheta }_{\mathfrak{q}}(\mathsf{z}-\omega )\left[\omega -{\displaystyle \frac{2\mathfrak{q}{\vartheta }_{\mathfrak{q}}\mathsf{z}+1}{\mathfrak{q}{\vartheta }_{\mathfrak{q}}({\vartheta }_{\mathfrak{q}}\mathsf{z}-2)}}\right]=0.\hfill \end{array}\end{array}$$

(20)

The function $g_{\mathfrak{q}}\left(\mathsf{z}\right)={\displaystyle \frac{2\mathfrak{q}{\vartheta }_{\mathfrak{q}}\mathsf{z}+1}{\mathfrak{q}{\vartheta }_{\mathfrak{q}}({\vartheta }_{\mathfrak{q}}\mathsf{z}-2)}},$ transforms the circle $\left|\mathsf{z}\right|=r_{\mathfrak{q}}$ (where $r_{\mathfrak{q}}<2/{\vartheta }_{\mathfrak{q}}$) into another a circle, with its diameter extending between the points $g_{\mathfrak{q}}(-r_{\mathfrak{q}})$ and $g_{\mathfrak{q}}\left(r_{\mathfrak{q}}\right)$. The center of the result circle is positioned at

$$m={\displaystyle \frac{-r_{\mathfrak{q}}}{\mathfrak{q}}}\left({\displaystyle \frac{4\mathfrak{q}+1}{4-{\vartheta }_{\mathfrak{q}}^2{r}_{\mathfrak{q}}^2}}\right),$$

and its radius is given by

$$\rho ={\displaystyle \frac{-2\left(\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{r}_{\mathfrak{q}}^2+1\right)}{\mathfrak{q}{\vartheta }_{\mathfrak{q}}\left(4-{\vartheta }_{\mathfrak{q}}^2{\mathsf{r}}_{\mathfrak{q}}^2\right)}}.$$

Consequently, the function $g_{\mathfrak{q}}$ transforms the circle $\left|\mathsf{z}\right|={\mathsf{r}}_{\mathfrak{q}}$ into another circle with a diameter stretching from the point $g_{\mathfrak{q}}\left({\mathsf{r}}_{\mathfrak{q}}\right)={\mathsf{r}}_{\mathfrak{q}}$ to the point $g_{\mathfrak{q}}(-{\mathsf{r}}_{\mathfrak{q}})$. For all $\mathfrak{q}\in (0,1)$, we have $g_{\mathfrak{q}}(-{\mathsf{r}}_{\mathfrak{q}})>g_{\mathfrak{q}}\left({\mathsf{r}}_{\mathfrak{q}}\right)={\mathsf{r}}_{\mathfrak{q}}$, which follows from the inequality

$${ð}_{\mathfrak{q}}\langle f\left(g_{\mathfrak{q}}\left(\varkappa \right)\right)\rangle >0,\forall \varkappa \in \mathbb{R},$$

where

$$f\left(g_{\mathfrak{q}}\left(\mathsf{z}\right)\right)={\displaystyle \frac{-(4\mathfrak{q}+1)}{\mathfrak{q}(2-q{\vartheta }_{\mathfrak{q}}\mathsf{z})(2-{\vartheta }_{\mathfrak{q}}\mathsf{z})}}.$$

Thus, if $\left|w\right|\le r_{\mathfrak{q}}$ and $\left|\mathsf{z}\right|\le {\mathsf{r}}_{\mathfrak{q}}$, the third factor in Equation (20) vanishes only when $\omega =\mathsf{z}-{\mathsf{r}}_{\mathfrak{q}}$. As a result, Equation (20) cannot hold for $\left|w\right|<{\mathsf{r}}_{\mathfrak{q}}$ and $\left|\mathsf{z}\right|<{\mathsf{r}}_{\mathfrak{q}}$. This confirms that the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is univalent in the disk ${\mathbb{D}}_{\mathfrak{q}}$, as defined by Equation (19).

On the other hand, the derivative of the function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {ð}_{\mathfrak{q}}\langle f\left(\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})\right)\rangle & ={\displaystyle \frac{{\vartheta }_{\mathfrak{q}}\left(1+2q{\left[2\right]}_{\mathfrak{q}}{\vartheta }_{\mathfrak{q}}\mathsf{z}-{\mathfrak{q}}^2{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2\right)}{\left(1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-\mathfrak{q}{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2\right)\left(1-\mathfrak{q}{\vartheta }_{\mathfrak{q}}\mathsf{z}-{\mathfrak{q}}^3{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2\right)}}\hfill \\ \hfill & ={\displaystyle \frac{{\vartheta }_{\mathfrak{q}}(\mathsf{z}-r_{\mathfrak{q}})\left(\mathsf{z}-\frac{1+\mathfrak{q}+\sqrt{{(1+\mathfrak{q})}^2+1}}{q{\vartheta }_{\mathfrak{q}}}\right)}{\left(1-{\vartheta }_{\mathfrak{q}}\mathsf{z}-q{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2\right)\left(1-q{\vartheta }_{\mathfrak{q}}\mathsf{z}-q^3{\vartheta }_{\mathfrak{q}}^2{\mathsf{z}}^2\right)}}.\hfill \end{array}\end{array}$$

(21)

The function $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ vanishes at the point $z=r_{\mathfrak{q}}$, and therefore it follows that $\mathsf{{\rm Y}}(\mathsf{z};\mathfrak{q})$ is not univalent to $\left|\mathsf{z}\right|\ge {\mathsf{r}}_{\mathfrak{q}}$. □

4. Conclusions

Emphasising their connection with shell-like star-like curves, this work presents a fresh method for exploring $\mathfrak{q}$-Fibonacci numbers and their corresponding polynomials. We investigated the geometric and analytic characteristics of a newly defined subclass of star-like functions by using the interval of univalence and nonunivalence for some functions. We also developed a sufficient condition for functions in this subclass such that they may be labelled as analytic functions with positive real components. Using subordination ideas and the natural properties of Fibonacci sequences helped us to obtain the results, therefore providing a strong analytical foundation for our findings.

This work highlights the critical connection between Geometric Function Theory and $\mathfrak{q}$-calculus, offering fresh insights into the structural properties of functions defined by $\mathfrak{q}$-Fibonacci sequences. By bridging sequential and analytical domains, it enhances the theoretical understanding of Fibonacci numbers and paves the way for multidisciplinary research opportunities. The study establishes a novel framework that links Fibonacci-type sequences with the geometric properties of analytic functions, uncovering new geometric and analytical features that enrich the field. This approach not only advances the theoretical foundation of Geometric Function Theory but also opens new avenues for exploration, such as extending the results to higher-dimensional spaces, applying them in mathematical physics, or developing computational techniques inspired by this theory. Additionally, the work lays the groundwork for future investigations and encourages researchers to further explore the applications of $\mathfrak{q}$-calculus in geometric function theory and related fields, ensuring its continued relevance and fostering innovation within the mathematical community.