Data-Driven Robust Attitude Tracking Control of Unmanned Underwater Vehicles with Performance Constraints
Abstract
1. Introduction
- (i)
- In comparison to most FTPFs in [23,25,26] operating with an exponential form, where the computation number increases as the exponential term increases, a new polynomial FTPF is adopted in this paper, where the calculation number of the polynomial FTPF is invariable, effectually reducing the computation burden. Additionally, different from the traditional error transformation function in [17,21], which causes a singularity problem since the denominator has a negative sign, a new transformed function is adopted to avoid the singularity problem in the error transformation.
- (ii)
- In contrast to the current results in [30,31,32,33,34] involving the system model, the constructed disturbance observer only uses data information without involving system models. In addition, different from the disturbance observer in [36], where the large overshoot tends to occur when the observed gain is large, a DNDO from [16] is adopted in this paper to avoid the large overshoot by introducing a saturated function.
- (iii)
- By means of the constrained error and the DNDO, a data-driven robust control strategy with performance constraints is designed to fulfill accurate attitude tracking control of UUVs, which ensures that the error draws into a prescribed region in a predetermined time.
2. Problem Statement
2.1. Notation
2.2. System Model
2.3. Control Target
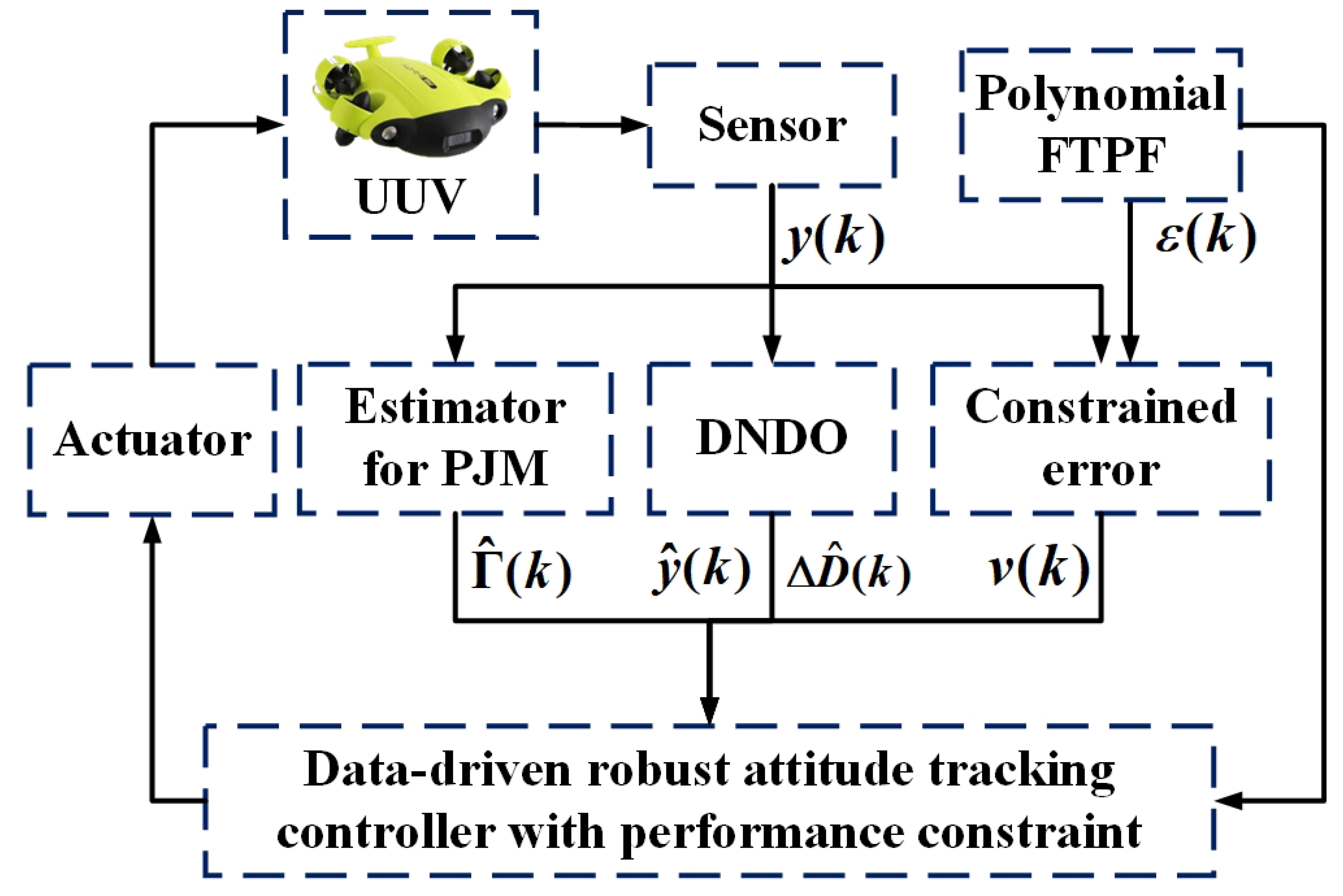
3. Control Strategy Design
3.1. Polynomial FTPF and Error Transformation
3.2. Estimator Design for PJM and Disturbance Observer Design
3.3. Control Law Design and Stability Analysis
4. Numerical Simulations
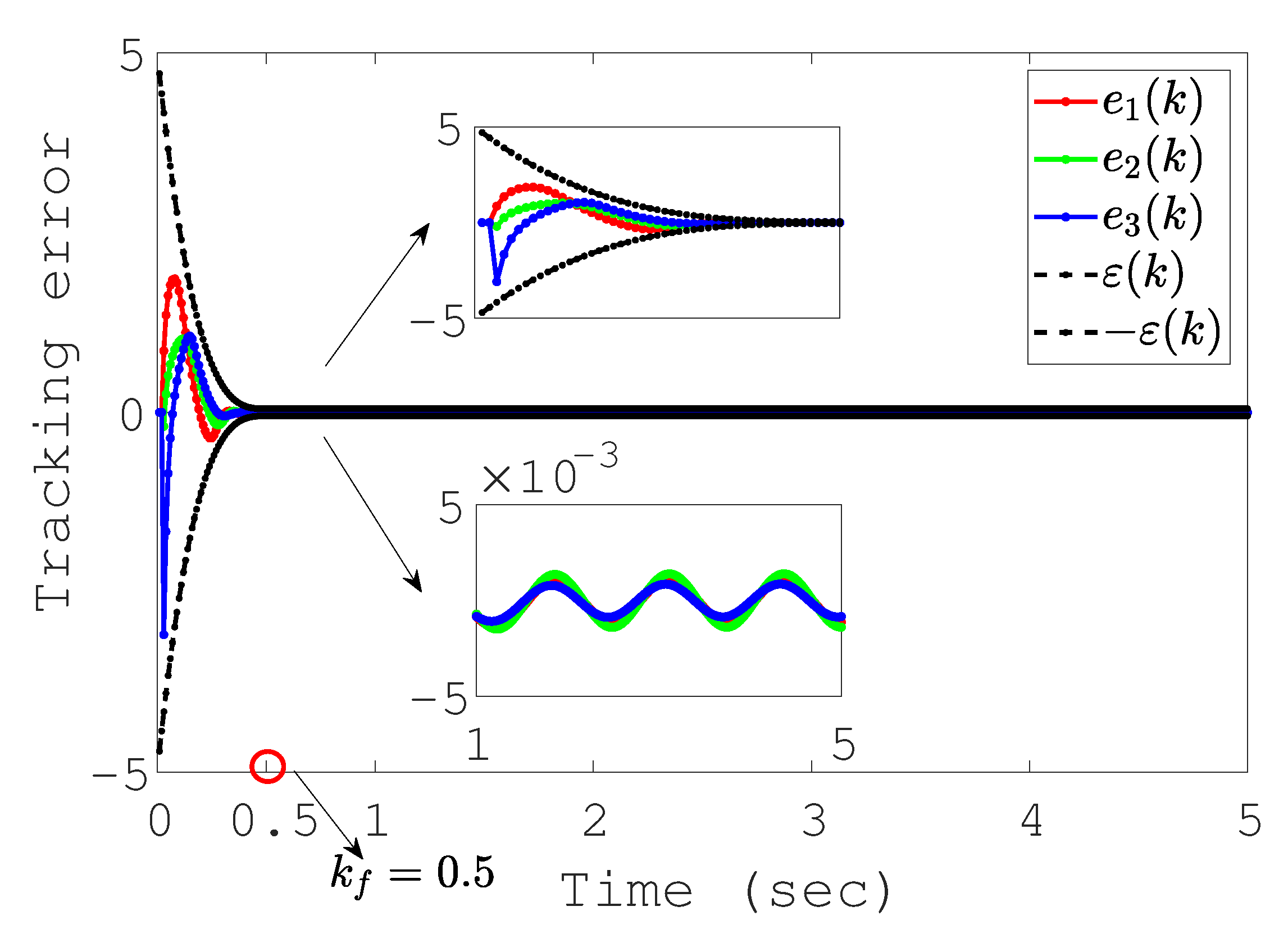
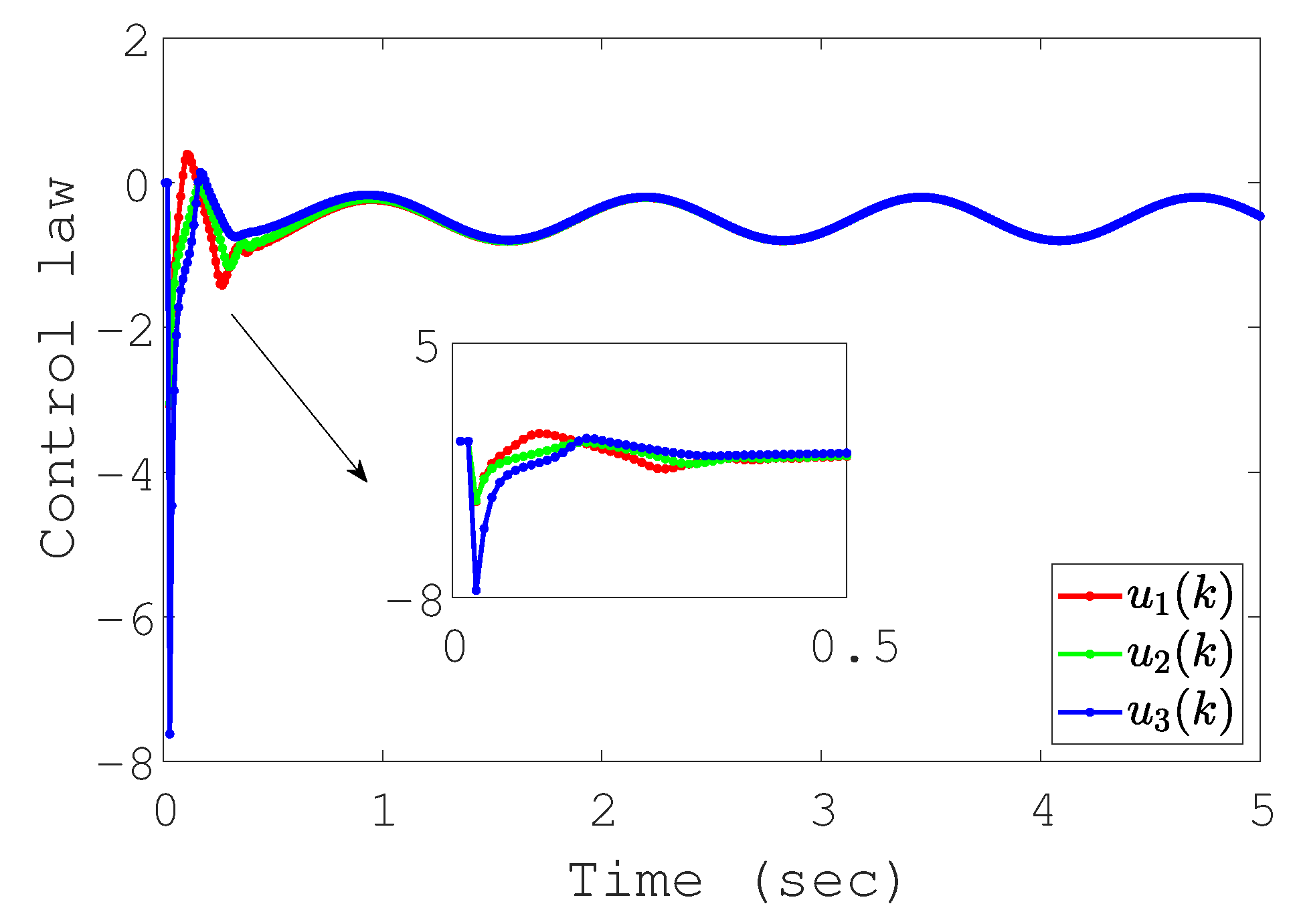
4.1. Tracking Results
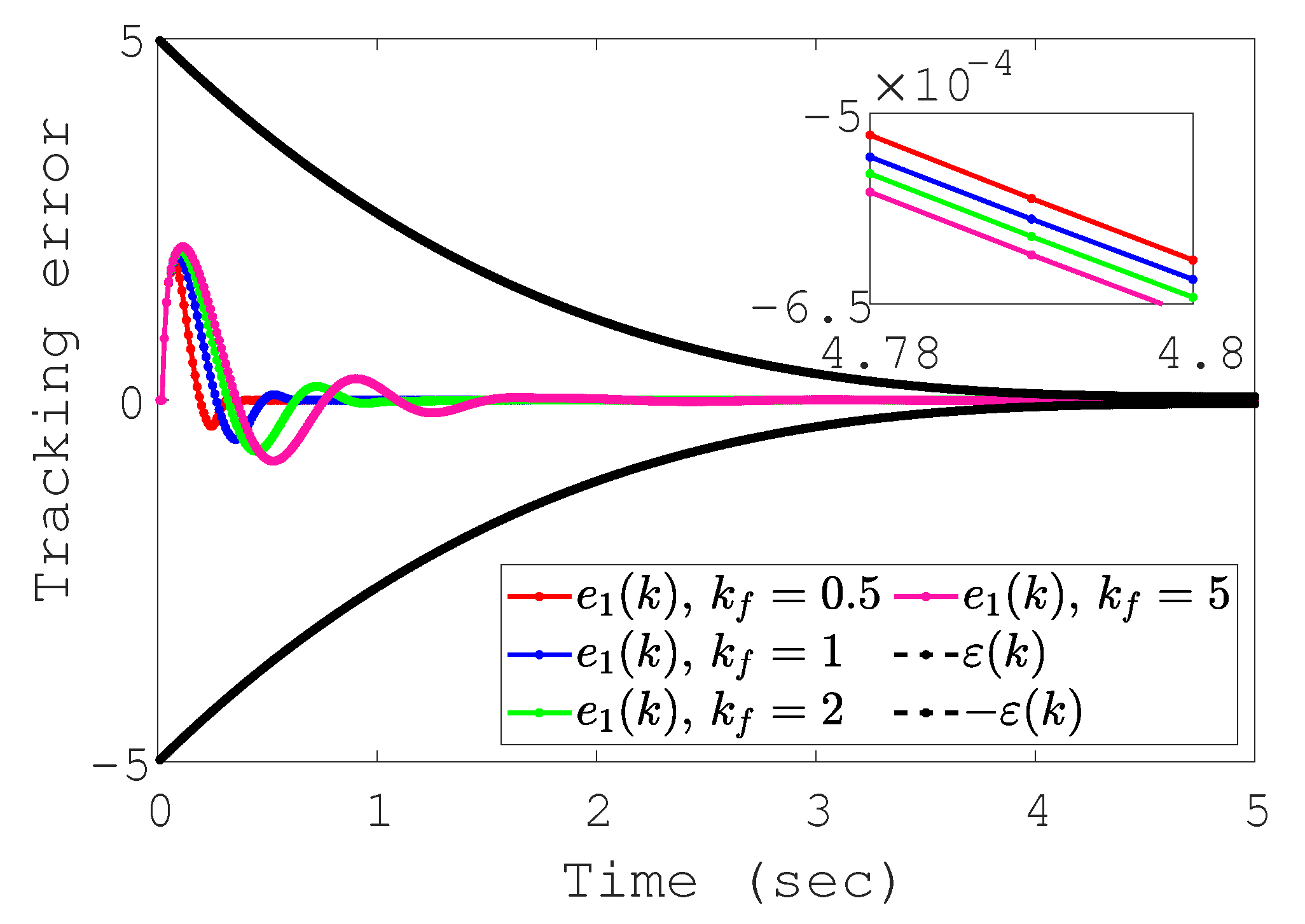
4.2. Comparative Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, H.; Ahn, H.; Chung, Y.; You, K. Quadrotor position and attitude tracking using advanced second-order sliding mode control for disturbance. Mathematics 2023, 11, 4786. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Z.; Che, W. Adaptive sliding mode attitude-tracking control of spacecraft with prescribed time performance. Mathematics 2022, 23, 401. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.B.; Ali, Z.A. A review of different designs and control models of remotely operated underwater vehicle. Meas. Control. 2020, 53, 1561–1570. [Google Scholar] [CrossRef]
- Cho, H.; Jeong, S.K.; Ji, D.H.; Tran, N.H.; Vu, M.T.; Choi, H.S. Study on control system of integrated unmanned surface vehicle and underwater vehicle. Sensors 2020, 20, 2633. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Han, Y.; Li, R.; Zhang, Y.; He, Z. Coupling dynamics study on multi-body separation process of underwater vehicles. Drones 2024, 8, 533. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. PID Control; Springer-Verlag London Limited: London, UK, 2005; pp. 47–107. [Google Scholar]
- Wang, L.; Zhang, W.; Zhang, Q.; Shi, H.; Zhang, R.; Gao, F. Terminal constrained robust hybrid iterative learning model predictive control for complex time-delayed batch processes. Nonlinear Anal. Hybrid Syst. 2023, 47, 101276. [Google Scholar] [CrossRef]
- Wang, L.; Yu, J.; Li, P.; Li, H.; Zhang, R. A 2D-FM model-based robust iterative learning model predictive control for batch processes. ISA Trans. 2021, 110, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shen, Y.; Yu, J.; Li, P.; Zhang, R.; Gao, F. Robust iterative learning control for multi-phase batch processes: An average dwell-time method with 2D convergence indexes. Int. J. Syst. Sci. 2018, 49, 324–343. [Google Scholar] [CrossRef]
- Bontempi, G.; Birattari, M.; Bersini, H. Lazy learning for local modelling and control design. Int. J. Control 1999, 72, 643–658. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. Model Free Adaptive Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Xu, D.; Jiang, B.; Shi, P. A novel model-free adaptive control design for multivariable industrial processes. IEEE Trans. Ind. Electron. 2014, 61, 6391–6398. [Google Scholar] [CrossRef]
- Hou, Z.; Xiong, S. On model-free adaptive control and its stability analysis. IEEE Trans. Autom. Control 2019, 64, 4555–4569. [Google Scholar] [CrossRef]
- Yu, X.; Hou, Z.; Polycarpou, M.M. Distributed data-driven iterative learning consensus tracking for nonlinear discrete-time multiagent systems. IEEE Trans. Autom. Control 2021, 67, 3670–3677. [Google Scholar] [CrossRef]
- Ma, Y.S.; Che, W.W.; Deng, C.; Wu, Z.G. Distributed model-free adaptive control for learning nonlinear MASs under DoS attacks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1146–1155. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.Z.; Guo, X.G.; Li, Q.; Wang, J.L.; Guo, L. Disturbance-observer-based model-free adaptive active fault-tolerant consensus control for MASs with TVDAF. Automatica 2025, 173, 112114. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems. IEEE Trans. Autom. Control 2010, 55, 1220–1226. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust partial-state feedback prescribed performance control of cascade systems with unknown nonlinearities. IEEE Trans. Autom. Control 2011, 56, 2224–2230. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Prescribed performance fault-tolerant control of uncertain nonlinear systems with unknown control directions. IEEE Trans. Autom. Control 2017, 62, 6529–6535. [Google Scholar] [CrossRef]
- Liu, D.; Yang, G.H. Data-driven adaptive sliding mode control of nonlinear discrete-time systems with prescribed performance. IEEE Trans. Syst. Man, Cybern. Syst. 2017, 49, 2598–2604. [Google Scholar] [CrossRef]
- Huang, K.; Wang, H.; Pei, P.; Sun, H.; Shao, K. Preset trajectory based prescribed performance control for active anti-roll of automotives. Veh. Syst. Dyn. 2025, 1–22. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Jing, Y.; Zhang, Z. A novel finite-time adaptive fuzzy tracking control scheme for nonstrict feedback systems. IEEE Trans. Fuzzy Syst. 2018, 27, 646–658. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J. Predefined-time sliding mode control with prescribed convergent region. IEEE/CAA J. Autom. Sin. 2022, 9, 934–936. [Google Scholar] [CrossRef]
- Wang, H.; Bai, W.; Zhao, X.; Liu, P.X. Finite-time-prescribed performance-based adaptive fuzzy control for strict-feedback nonlinear systems with dynamic uncertainty and actuator faults. IEEE Trans. Cybern. 2021, 52, 6959–6971. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Niu, B.; Wang, H.; Zhao, X.; Chen, W. Prescribed performance-based finite-time consensus technology of nonlinear multiagent systems and application to FDPs. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 591–595. [Google Scholar] [CrossRef]
- Åström, K.J. Adaptive control. In Mathematical System Theory: The Influence of RE Kalman; Springer: Berlin/Heidelberg, Germany, 1995; pp. 437–450. [Google Scholar]
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Liu, J.; Wang, X. Advanced Sliding Mode Control; Springer: Berlin/Heidelberg, Germany, 2011; pp. 81–96. [Google Scholar]
- Han, J.Q. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 676–697. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Guo, B.Z. On active disturbance rejection control for nonlinear systems using time-varying gain. Eur. J. Control. 2015, 23, 62–70. [Google Scholar] [CrossRef]
- Ran, M.; Li, J.; Xie, L. A new extended state observer for uncertain nonlinear systems. Automatica 2021, 131, 109772. [Google Scholar] [CrossRef]
- Cao, P.; Gan, Y.; Dai, X. Finite-time disturbance observer for robotic manipulators. Sensors 2019, 131, 1943. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, J.; Liu, X. Finite-time variable-gain ADRC for master–slave teleoperated parallel manipulators. IEEE Trans. Ind. Electron. 2023, 71, 9234–9243. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H. Improved ADRC with a cascade extended state observer based on quasi-generalized integrator for PMSM current disturbances attenuation. IEEE Trans. Transp. Electrif. 2023, 10, 2145–2157. [Google Scholar] [CrossRef]
- Chi, R.H.; Yu, H.; Zhang, S.H.; Huang, B.; Hou, Z.S. Active disturbance rejection control for nonaffined globally Lipschitz nonlinear discrete-time systems. IEEE Trans. Autom. Control. 2023, 66, 5955–5967. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control. 2011, 21, 686–702. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.-N.; Chen, R.-Z.; Liu, Z.-Y.; Zhang, Z.-F.; Huang, Y.-Z. Data-Driven Robust Attitude Tracking Control of Unmanned Underwater Vehicles with Performance Constraints. Mathematics 2025, 13, 1350. https://doi.org/10.3390/math13081350
Zhang H-N, Chen R-Z, Liu Z-Y, Zhang Z-F, Huang Y-Z. Data-Driven Robust Attitude Tracking Control of Unmanned Underwater Vehicles with Performance Constraints. Mathematics. 2025; 13(8):1350. https://doi.org/10.3390/math13081350
Chicago/Turabian StyleZhang, He-Ning, Run-Ze Chen, Zi-Yi Liu, Zhi-Fu Zhang, and Yi-Zhe Huang. 2025. "Data-Driven Robust Attitude Tracking Control of Unmanned Underwater Vehicles with Performance Constraints" Mathematics 13, no. 8: 1350. https://doi.org/10.3390/math13081350
APA StyleZhang, H.-N., Chen, R.-Z., Liu, Z.-Y., Zhang, Z.-F., & Huang, Y.-Z. (2025). Data-Driven Robust Attitude Tracking Control of Unmanned Underwater Vehicles with Performance Constraints. Mathematics, 13(8), 1350. https://doi.org/10.3390/math13081350








