Direct Solution of Inverse Steady-State Heat Transfer Problems by Improved Coupled Radial Basis Function Collocation Method
Abstract
:1. Introduction
2. ICRBF and PSO Method
2.1. ICRBF
2.2. Particle Swarm Optimization Algorithm
3. ICRBF Method for Inverse Problem
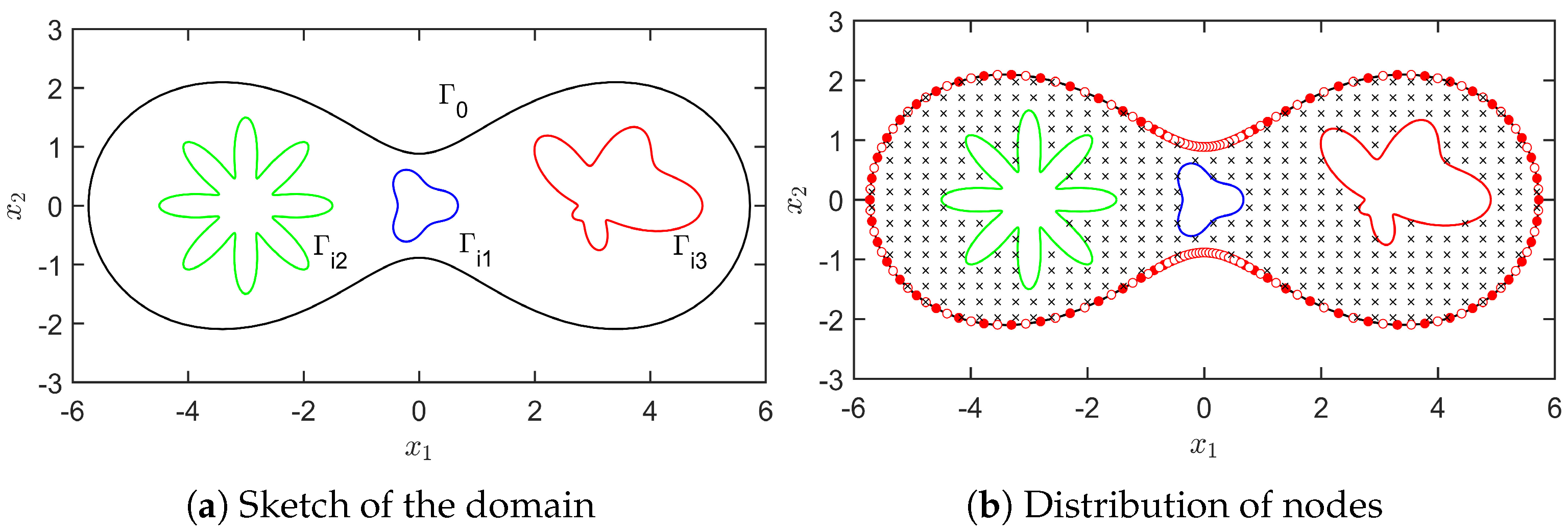
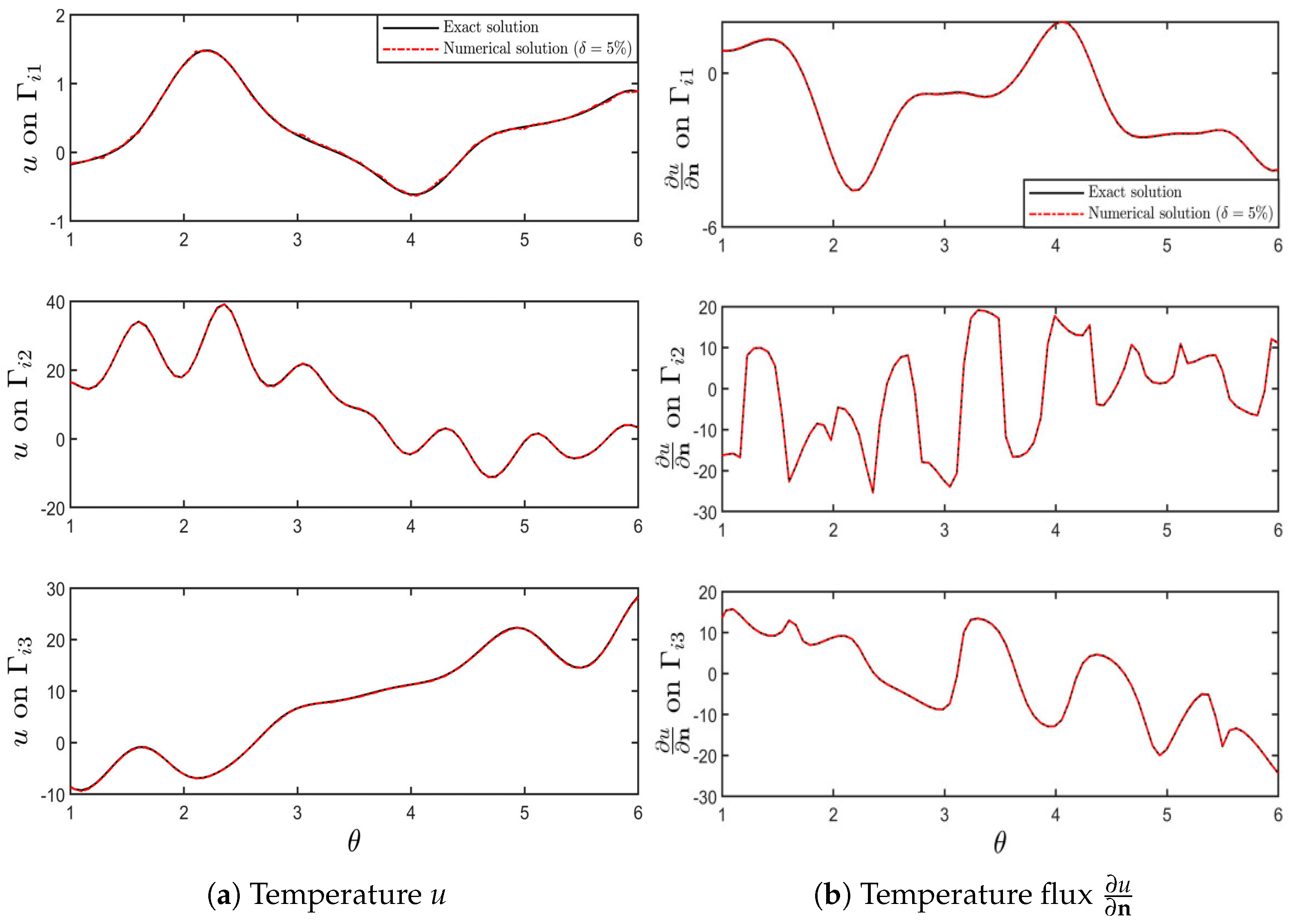
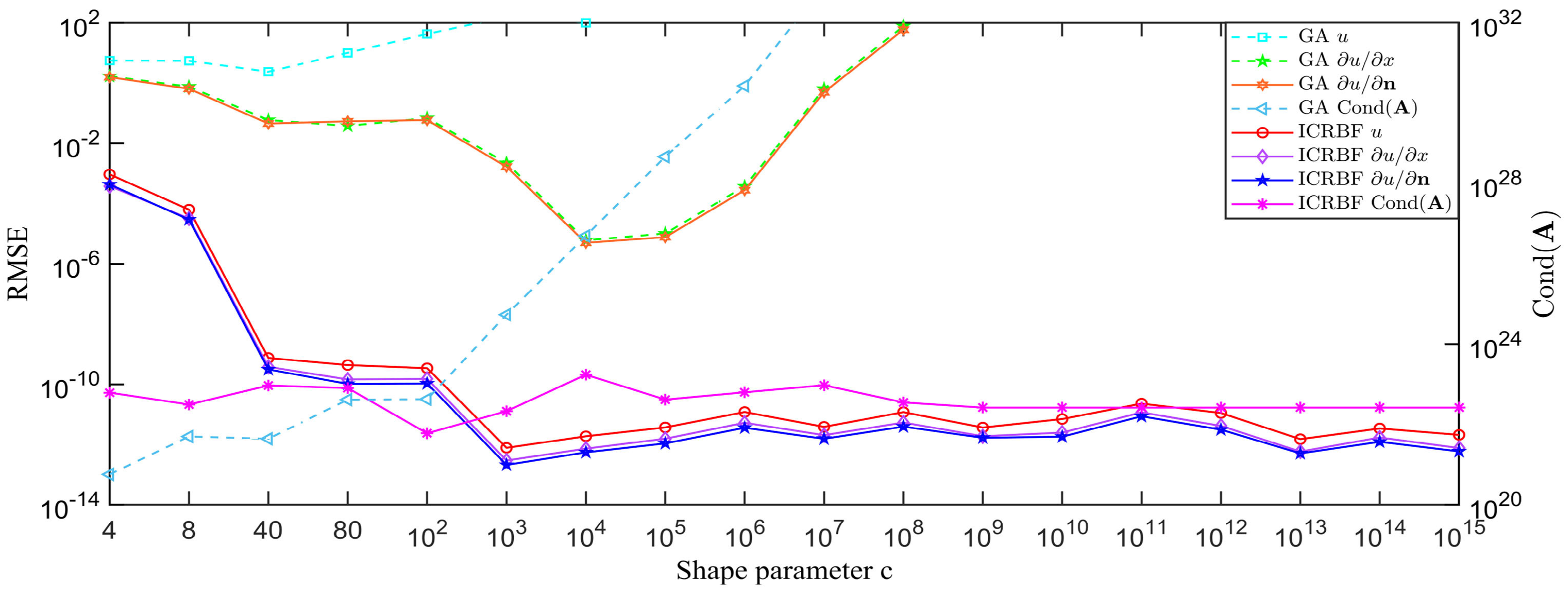
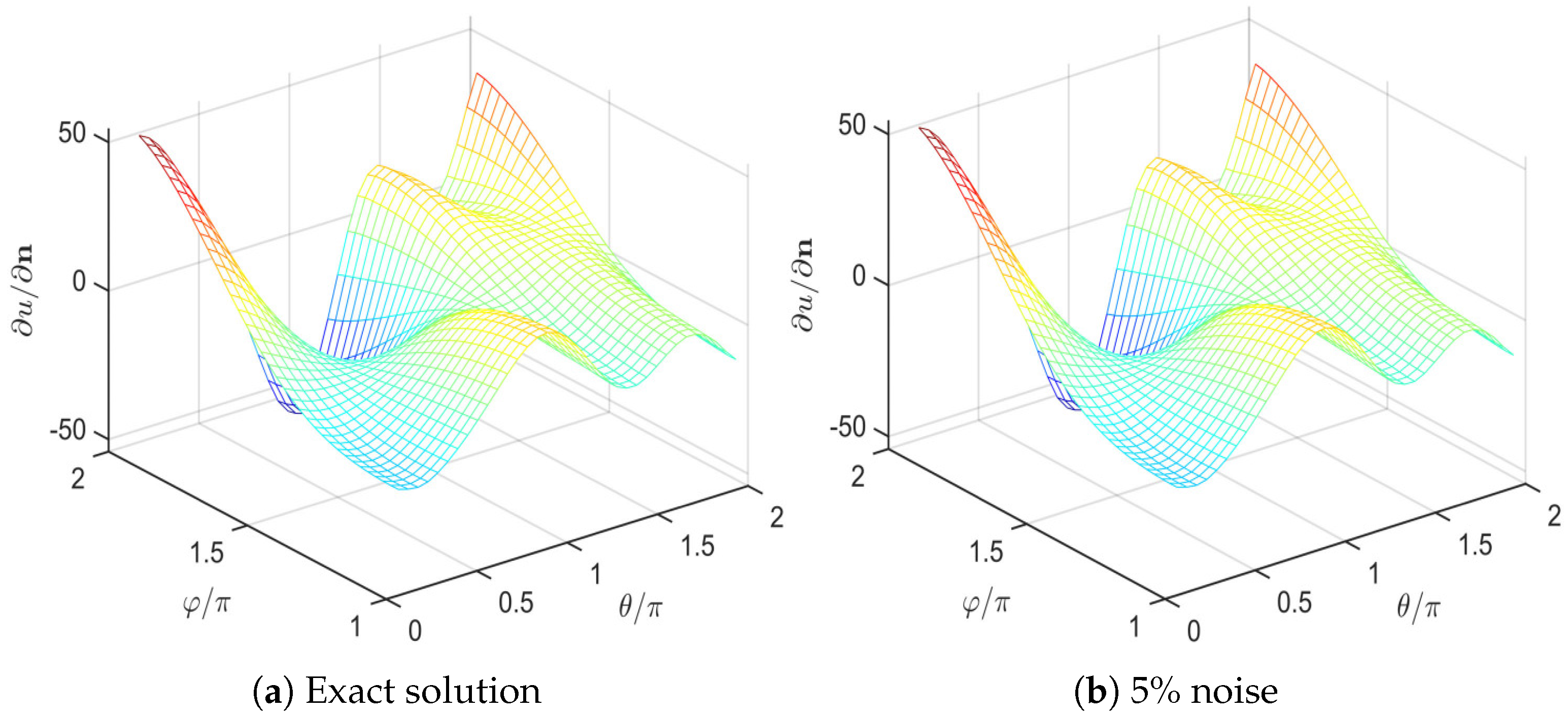
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory; Springer: New York, NY, USA, 1998; pp. 195–206. [Google Scholar]
- Balaban, A.; Grechikhin, V.; Yufanova, J. Inverse problems in the design of electromagnetic mechanisms of ground vehicle magnetic levitation systems. Transp. Res. Procedia 2022, 63, 1171–1179. [Google Scholar] [CrossRef]
- Laves, M.H.; Tölle, M.; Schlaefer, A.; Engelhardt, S. Posterior temperature optimized Bayesian models for inverse problems in medical imaging. Med. Image Anal. 2022, 78, 102382. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Al-Mamun, A.; Pereira, F.; Rahunanthan, A. Multiscale sampling for the inverse modeling of partial differential equations. J. Comput. Phys. 2024, 497, 112609. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Zhang, C.Z. Boundary particle method for Cauchy inhomogeneous potential problems. Inverse Probl. Sci. Eng. 2012, 20, 189–207. [Google Scholar] [CrossRef]
- Li, Y.X.; Hu, X.L. Artificial neural network approximations of Cauchy inverse problem for linear PDEs. Appl. Math. Comput. 2022, 414, 126678. [Google Scholar] [CrossRef]
- Hu, W.; Fu, Z.J.; Tang, Z.C.; Gu, Y. A meshless collocation method for solving the inverse Cauchy problem associated with the variable-order fractional heat conduction model under functionally graded materials. Eng. Anal. Bound. Elem. 2022, 140, 132–144. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Tuan, N.H.; Yang, C. On Cauchy problem for fractional parabolic-elliptic Keller-Segel model. Adv. Nonlinear Anal. 2023, 12, 97–116. [Google Scholar] [CrossRef]
- Aronson, D.G.; Besala, P. Uniqueness of solutions of the Cauchy problem for parabolic equations. J. Math. Anal. Appl. 1966, 13, 516–526. [Google Scholar] [CrossRef]
- Chakib, A.; Nachaoui, A. Convergence analysis for finite element approximation to an inverse Cauchy problem. Inverse Probl. 2006, 22, 1191–1206. [Google Scholar] [CrossRef]
- Cheng, A.H.D.; Cabral, J.J.S.P. Direct solution of ill-posed boundary value problems by radial basis function collocation method. Int. J. Numer. Methods Eng. 2005, 64, 45–64. [Google Scholar] [CrossRef]
- Ly, I. An iterative method for solving Cauchy problems for the p-Laplace operator. Complex Var. Elliptic Equ. 2010, 55, 1079–1088. [Google Scholar] [CrossRef]
- Wang, F.J.; Fan, C.M.; Hua, Q.S.; Gu, Y. Localized MFS for the inverse Cauchy problems of two-dimensional Laplace and biharmonic equations. Appl. Math. Comput. 2020, 364, 124658. [Google Scholar] [CrossRef]
- Gong, R.F.; Wang, M.; Huang, Q.; Zhang, Y. A CCBM-based generalized GKB iterative regularization algorithm for inverse Cauchy problems. J. Comput. Appl. Math. 2023, 432, 115282. [Google Scholar] [CrossRef]
- Hu, X.Z.; Mu, L.; Ye, X. A simple finite element method of the Cauchy problem for Poisson equation. Int. J. Numer. Anal. Model. 2017, 14, 591–603. [Google Scholar]
- Bakushinsky, B.A.; Kokurin, Y.M.; Kokurin, M.M. On a class of finite difference methods for ill-posed Cauchy problems with noisy data. J. Inverse Ill-Posed Probl. 2011, 18, 959–977. [Google Scholar] [CrossRef]
- Ellabib, A.; Nachaoui, A.; Ousaadane, A. Mathematical analysis and simulation of fixed point formulation of Cauchy problem in linear elasticity. Math. Comput. Simul. 2021, 187, 231–247. [Google Scholar] [CrossRef]
- Li, W.; Liu, X.Y.; Yao, G.M. A local meshless collocation method for solving certain inverse problems. Eng. Anal. Bound. Elem. 2015, 57, 9–15. [Google Scholar] [CrossRef]
- Safari, F. Solving multi-dimensional inverse heat problems via an accurate RBF-based meshless technique. Int. J. Heat Mass Transf. 2023, 209, 124100. [Google Scholar] [CrossRef]
- Lamm, P.K. Future-sequential regularization methods for III-posed Volterra equations: Applications to the inverse heat conduction problem. J. Math. Anal. Appl. 1995, 195, 469–494. [Google Scholar] [CrossRef]
- Dreglea, A.; Sidorov, N. Integral equations in identification of external force and heat source density dynamics. Bull. Acad. Științe Repub. Mold. Mat. 2018, 88, 68–77. [Google Scholar]
- Dardé, J.; Hannukainen, A.; Hyvönen, N. An hdiv-based mixed quasi-reversibility method for solving elliptic Cauchy problems. SIAM J. Numer. Anal. 2013, 51, 2123–2148. [Google Scholar] [CrossRef]
- Chen, C.S.; Amuzu, L.; Acheampong, K.; Zhu, H. Improved geometric modeling using the method of fundamental solutions. Eng. Anal. Bound. Elem. 2021, 130, 49–57. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Qin, Q.H. Boundary knot method for heat conduction in nonlinear functionally graded material. Eng. Anal. Bound. Elem. 2011, 35, 729–734. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Sun, F.L.; Qu, W.Z.; Gu, Y.; Young, D.L. A meshless average source boundary node method for steady-state heat conduction in general anisotropic media. Comput. Math. Appl. 2018, 75, 1739–1755. [Google Scholar] [CrossRef]
- Kovářík, K.; Mužík, J.; Gago, F.; Sitányiová, D. Modified local singular boundary method for solution of two-dimensional diffusion equation. Eng. Anal. Bound. Elem. 2022, 143, 525–534. [Google Scholar] [CrossRef]
- Fu, Z.J.; Yang, L.W.; Xi, Q.; Liu, C.S. A boundary collocation method for anomalous heat conduction analysis in functionally graded materials. Comput. Math. Appl. 2021, 88, 91–109. [Google Scholar] [CrossRef]
- Borkowska, D.; Borkowski, M. A numerical analysis of the generalised collocation Trefftz method for some 2D Laplace problems. Eng. Anal. Bound. Elem. 2023, 152, 608–626. [Google Scholar] [CrossRef]
- Li, J.C. A radial basis meshless method for solving inverse boundary value problems. Commun. Numer. Methods Eng. 2003, 20, 51–61. [Google Scholar] [CrossRef]
- Liu, C.S.; Chen, W.; Fu, Z.J. A multiple-scale MQ-RBF for solving the inverse Cauchy problems in arbitrary plane domain. Eng. Anal. Bound. Elem. 2016, 68, 11–16. [Google Scholar] [CrossRef]
- Chen, Y.T.; Li, C.; Yao, L.Q.; Cao, Y. A hybrid RBF collocation method and its application in the elastostatic symmetric problems. Symmetry 2022, 14, 1476. [Google Scholar] [CrossRef]
- Mostajeran, F.; Hosseini, S.M. Radial basis function neural network (RBFNN) approximation of Cauchy inverse problems of the Laplace equation. Comput. Math. Appl. 2023, 141, 129–144. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Multiquadric and its shape parameter-a numerical investigation of error estimate, condition number, and round-offerror by arbitrary precision computation. Eng. Anal. Bound. Elem. 2012, 36, 220–239. [Google Scholar] [CrossRef]
- Chen, W.; Hong, Y.; Lin, J. The sample solution approach for determination of the optimal shape parameter in the multiquadric function of the Kansa method. Comput. Math. Appl. 2018, 75, 2942–2954. [Google Scholar] [CrossRef]
- Wang, F.; Chen, W.; Zhang, C.; Hua, Q. Kansa method based on the Hausdorff fractal distance for Hausdorff derivative Poisson equations. Fractals 2018, 26, 1850084. [Google Scholar] [CrossRef]
- Liu, C.-S.; Liu, D. Optimal shape parameter in the MQ-RBF by minimizing an energy gap functional. Appl. Math. Lett. 2018, 86, 157–165. [Google Scholar] [CrossRef]
- Zhang, Y.M. An accurate and stable RBF method for solving partial differential equations. Appl. Math. Lett. 2019, 97, 93–98. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, Z.J.; Zhang, Y.M. A novel global RBF direct collocation method for solving partial differential equations with variable coefficients. Eng. Anal. Bound. Elem. 2024, 160, 14–27. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Fasshauer, G.E.; Zhang, J.G. On choosing optimal shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Onishi, K. Boundary inverse problems in seepage and viscous fluid flows. In Proceedings of the Computer Methods and Water Resources III, Chalkis, Greece, 26–28 September 1995; pp. 457–468. [Google Scholar]
- Moazami, D.; Esmaeilbeigi, M. Enhanced stability and accuracy in solving nonlinear fredholm integral equations using hybrid radial kernels and particle swarm optimization. Comput. Appl. Math. 2025, 44, 78. [Google Scholar] [CrossRef]


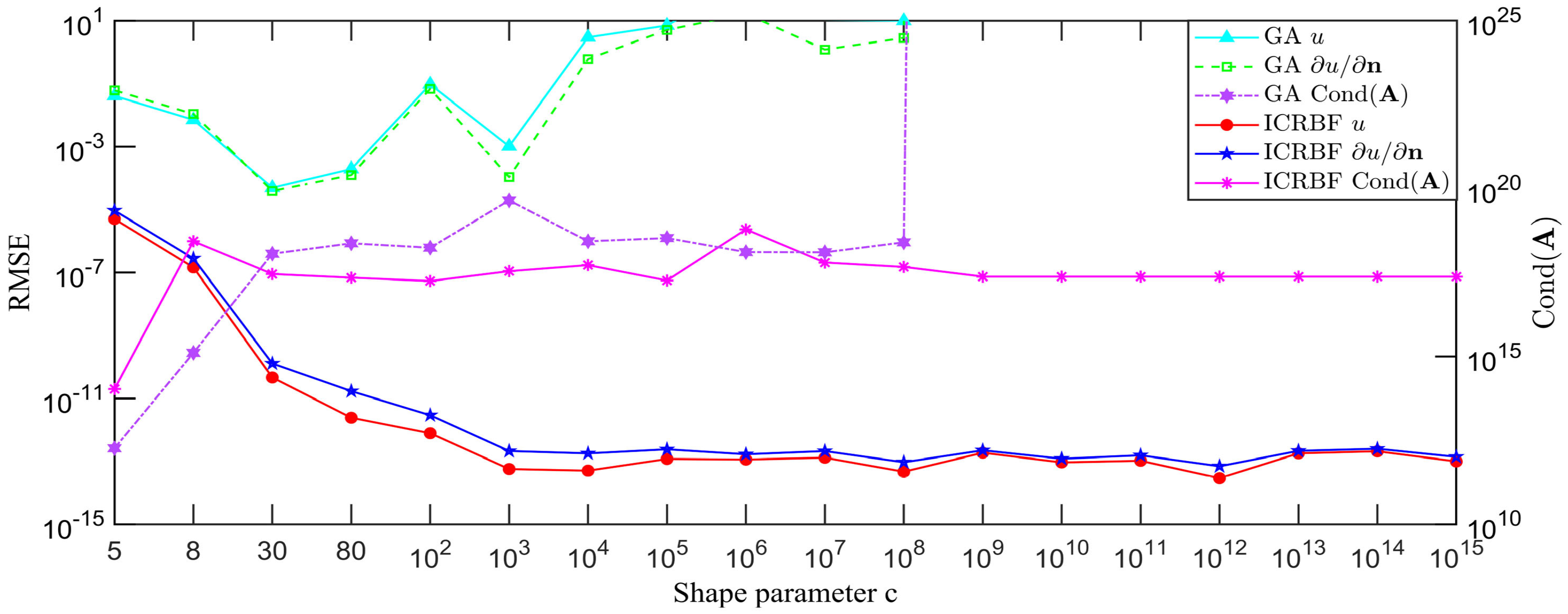
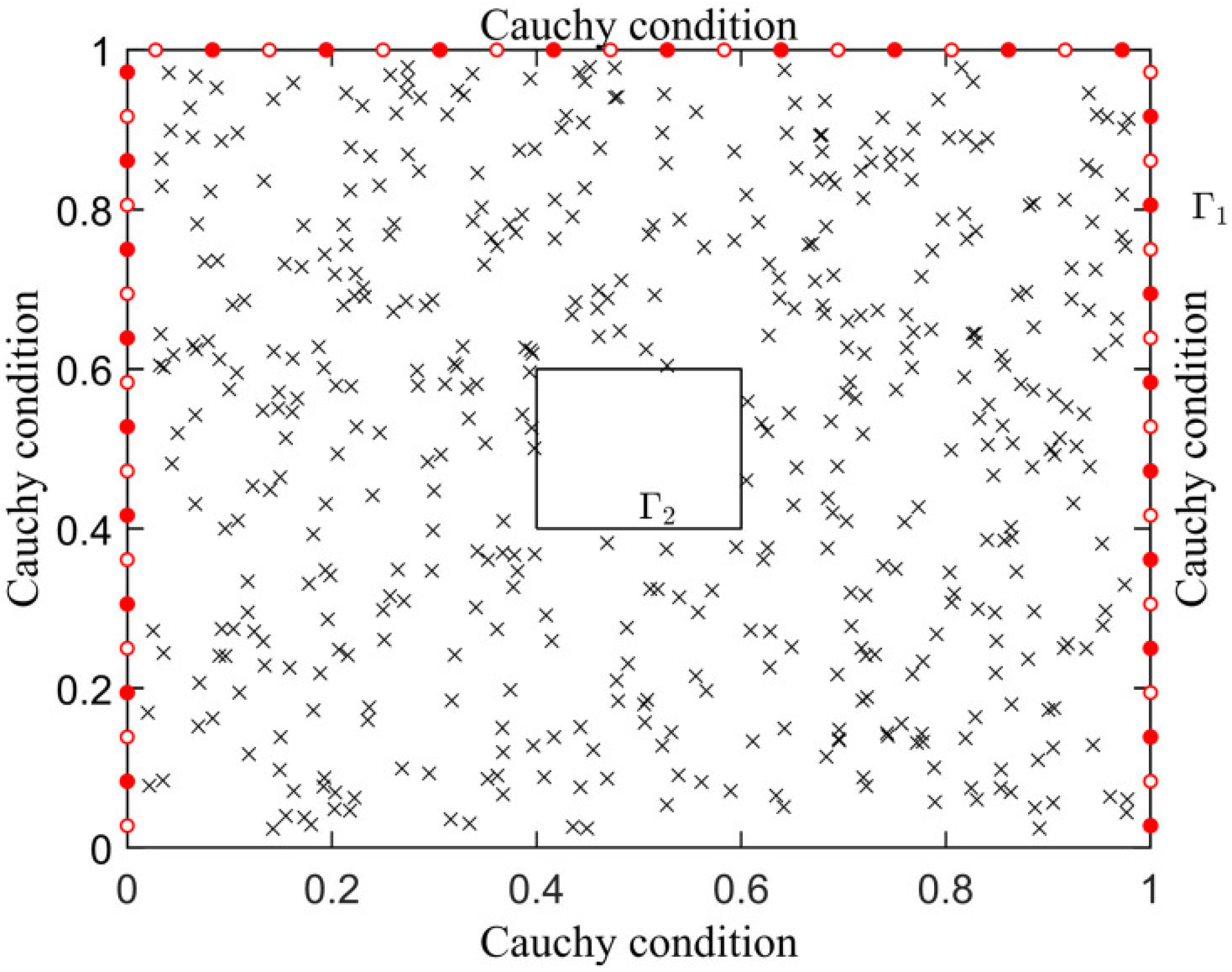

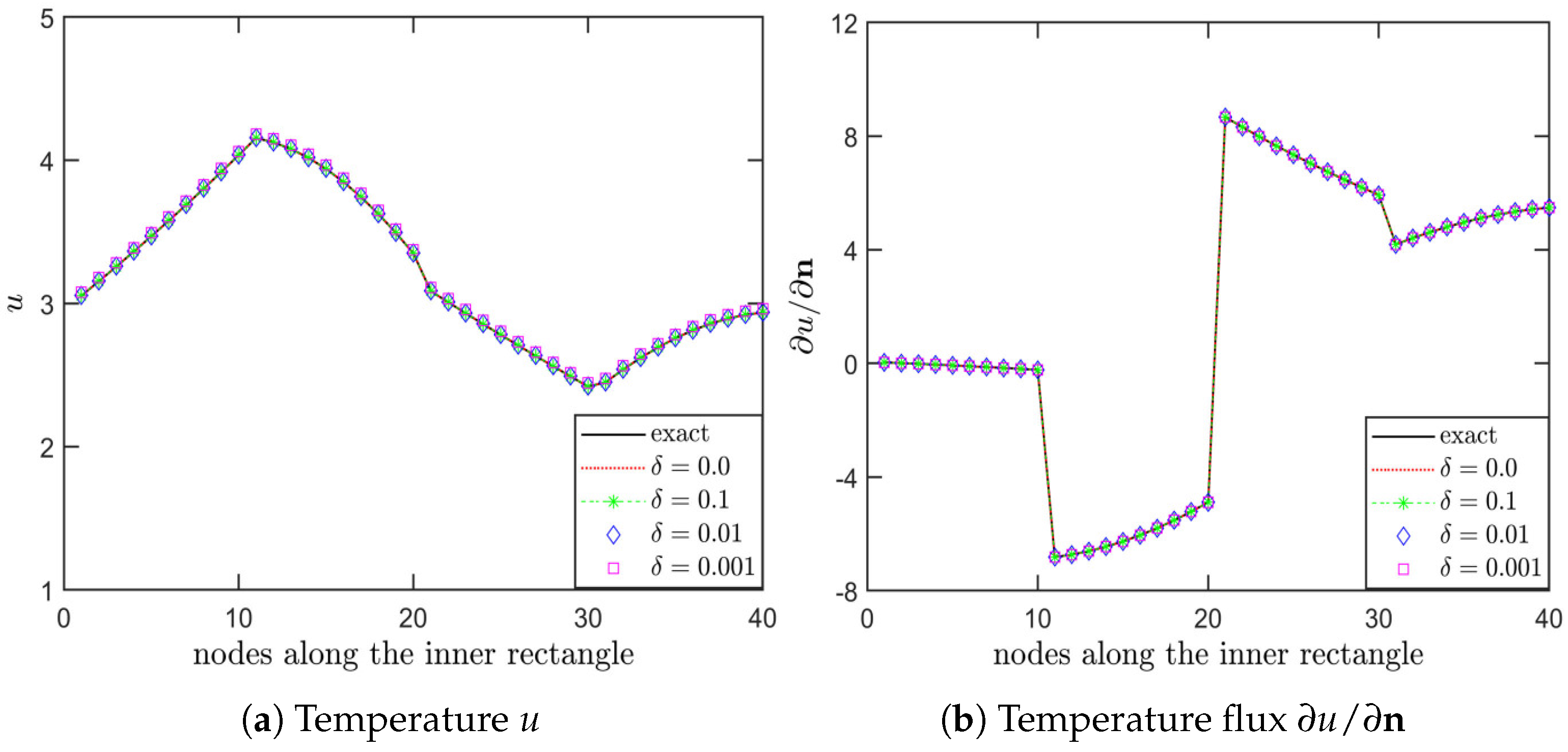
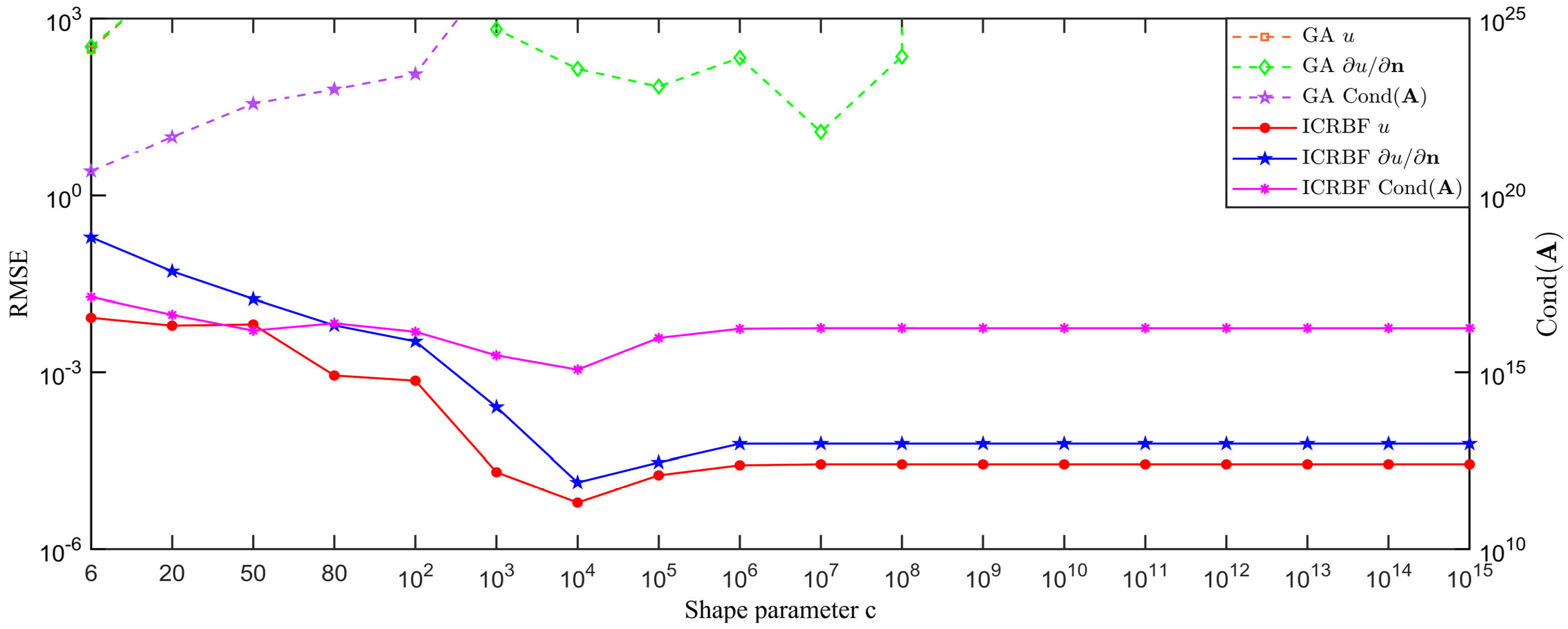






| Method | Temperature Value | Error (%) |
|---|---|---|
| Exact solution | 2.250 | 0 |
| Onishi, FEM 36 elements [42] | 2.323 | 3.2 |
| Onishi, FEM 144 elements [42] | 2.341 | 4.0 |
| RBF, 49 elements () [11] | 2.296 | 2.0 |
| RBF, 49 elements () [11] | 2.251 | 0.04 |
| GA + CU () [43] | 2.2501 | 6.4741 × |
| GA + CU () [43] | 2.2499 | 2.9952 × |
| ICRBF () | 2.2495 | 0.02170 |
| ICRBF () | 2.2514 | 0.062391 |
| ICRBF () | 2.2499 | 5.2558 × |
| ICRBF () | 2.2500 | 1.6185 × |
| Noise Levels () | |||
|---|---|---|---|
| 0.01% | 3.38 × | 1.70 × | 1.85 × |
| 0.1% | 4.42 × | 1.79 × | 2.80 × |
| 1% | 3.10 × | 2.01 × | 1.01 × |
| ni | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|
| ARE | 5.55 × | 3.21 × | 2.82 × | 2.81 × | 3.20 × | 3.37 × |
| ICRBF | ||||
|---|---|---|---|---|
| Temperature | Heat Flux | Temperature | Heat Flux | |
| 0 | 1.18 × | 1.37 × | 4.63 × | 5.99 × |
| 1% | 4.04 × | 3.69 × | 4.03 × | 4.82 × |
| 3% | 7.54 × | 1.05 × | 1.37 × | 1.58 × |
| 5% | 1.60 × | 1.66 × | 2.24 × | 2.61 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Zhang, C.; Zhang, Y. Direct Solution of Inverse Steady-State Heat Transfer Problems by Improved Coupled Radial Basis Function Collocation Method. Mathematics 2025, 13, 1423. https://doi.org/10.3390/math13091423
Yuan C, Zhang C, Zhang Y. Direct Solution of Inverse Steady-State Heat Transfer Problems by Improved Coupled Radial Basis Function Collocation Method. Mathematics. 2025; 13(9):1423. https://doi.org/10.3390/math13091423
Chicago/Turabian StyleYuan, Chunting, Chao Zhang, and Yaoming Zhang. 2025. "Direct Solution of Inverse Steady-State Heat Transfer Problems by Improved Coupled Radial Basis Function Collocation Method" Mathematics 13, no. 9: 1423. https://doi.org/10.3390/math13091423
APA StyleYuan, C., Zhang, C., & Zhang, Y. (2025). Direct Solution of Inverse Steady-State Heat Transfer Problems by Improved Coupled Radial Basis Function Collocation Method. Mathematics, 13(9), 1423. https://doi.org/10.3390/math13091423





