Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary
Abstract
:1. Introduction
2. Literature Review
2.1. Theoretical Framework
2.2. Fiscal and Monetary Policy Interactions
2.3. Empirical Studies on Policy Coordination
2.4. Historical Perspective on Fiscal and Monetary Policies
3. Methodology
3.1. Research Design
3.2. Analytical Framework
3.3. Estimation Strategy
4. Results and Discussion
4.1. Descriptive Analysis
4.2. Estimation of Model Parameters
4.3. Derivation and Simulation of Best Response Functions
- Derivation of best response functions:
- 2.
- Simulation of best response strategies
4.4. Computation of Nash Equilibrium Strategies
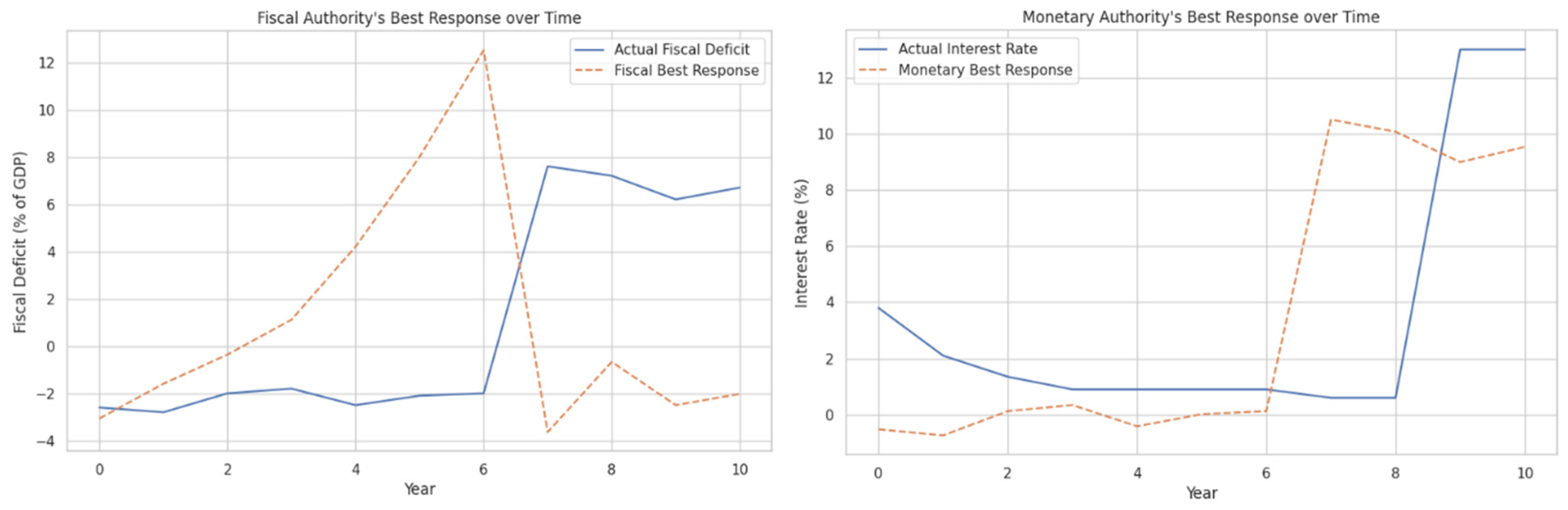
4.5. Comparison with Actual Policy Decisions and Discussion of Findings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blinder, A.S. Issues in the Coordination of Monetary and Fiscal Policy; National Bureau of Economic Research: Cambridge, MA, USA, 1982. [CrossRef]
- Afonso, A.; Alves, J.; Balhote, R. Interactions between monetary and fiscal policies. J. Appl. Econ. 2019, 22, 132–151. [Google Scholar] [CrossRef]
- Bucacos, E. The interdependence of Fiscal and Monetary Policies in an Emerging economy: The case of Uruguay. Int. J. Financ. Bank. Stud. 2022, 11, 19–33. [Google Scholar] [CrossRef]
- Di Bartolomeo, G.; Di Gioacchino, D. Fiscal-monetary policy coordination and debt management: A two-stage analysis. Empirica 2008, 35, 433–448. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, H.; Chen, H. Learning correlated stackelberg equilibrium in general-sum multi-leader-single-follower games. arXiv 2022, arXiv:2210.12470. [Google Scholar] [CrossRef]
- Ferrari, M.M.; Pagliari, M.S. DSGE Nash: Solving Nash Games in Macro Models; ECB Working Paper; European Central Bank: Frankfurt am Main, Germany, 2022. [Google Scholar] [CrossRef]
- Stawska, J.; Malaczewski, M.; Szymańska, A. Combined monetary and fiscal policy: The Nash Equilibrium for the case of non-cooperative game. Econ. Res.-Ekon. Istraživanja 2019, 32, 3554–3569. [Google Scholar] [CrossRef]
- Saulo, H.; Rêgo, L.C.; Divino, J.A. Fiscal and monetary policy interactions: A game theory approach. Ann. Oper. Res. 2013, 206, 341–366. [Google Scholar] [CrossRef]
- Bennett, H.; Loayza, N. Policy Biases When the Monetary and Fiscal Authorities Have Different Objectives; Banco Central de Chile: Santiago, Chile, 2002.
- Leeper, E.M. Equilibria under ‘active’ and ‘passive’ monetary and fiscal policies. J. Monet. Econ. 1991, 27, 129–147. [Google Scholar] [CrossRef]
- Sargent, T.J.; Wallace, N. Some unpleasant monetarist arithmetic. Fed. Reserve Bank Minneap. Q. Rev. 1981, 5, 1–7. [Google Scholar] [CrossRef]
- Blanchard, O.J.; Summers, L.H. Rethinking Stabilization Policy: Evolution or Revolution? National Bureau of Economic Research: Cambridge, MA, USA, 2018. [Google Scholar] [CrossRef]
- Hungarian National Bank. Economic and Financial Statistics. Available online: https://www.mnb.hu (accessed on 1 February 2025).
- Chortareas, G.; Mavrodimitrakis, C. Strategic fiscal policies and leadership in a monetary union. Eur. J. Political Econ. 2017, 47, 133–147. [Google Scholar] [CrossRef]
- Kreps David, M. Nash equilibrium. In Game Theory; Palgrave Macmillan: London, UK, 1989; pp. 167–177. [Google Scholar]
- Holt, C.A.; Roth, A.E. The Nash equilibrium: A perspective. Proc. Natl. Acad. Sci. USA 2004, 101, 3999–4002. [Google Scholar] [CrossRef]
- Alderborn, J. The Impact of Coordination and Targets on Monetary and Fiscal Policy. Master’s Thesis, Universitat de Barcelona, Barcelona, Spain, 2018. [Google Scholar]
- Shannon, B.N.; McGee, Z.A.; Jones, B.D. Bounded rationality and cognitive limits in political decision making. Oxf. Res. Encycl. Politics 2019. [Google Scholar] [CrossRef]
- Blueschke, D.; Neck, R.; Behrens, D.A. OPTGAME3: A dynamic game solver and an economic example. In Advances in Dynamic Games: Theory, Applications, and Numerical Methods; Springer: Cham, Switzerland, 2013; pp. 29–51. [Google Scholar]
- Yeboah, S. A Systematic Review of the Association between Fiscal Policy and Monetary Policy: Interactions, Challenges, and Implications. Munich Pers. RePEc Arch. 2022, 17530. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/117530 (accessed on 15 March 2025).
- Chibi, A.; Chekouri, S.M.; Benbouziane, M. Interaction between monetary and fiscal policy in Algeria: An application of a model with Markovian regime switching. Les Cah. Cread 2021, 37, 173–210. [Google Scholar]
- Reinhart, C.M.; Rogoff, K.S. Growth in a Time of Debt. Am. Econ. Rev. 2010, 100, 573–578. [Google Scholar] [CrossRef]
- Engwerda, J.; van Aarle, B.; Anevlavis, T. Debt stabilization games in a monetary union: What are the effects of introducing eurobonds. J. Macroecon. 2019, 59, 78–102. [Google Scholar] [CrossRef]
- Ortega-Argilés, R. The evolution of regional entrepreneurship policies: “no one size fits all”. Ann. Reg. Sci. 2022, 69, 585–610. [Google Scholar] [CrossRef]
- Echeverri, A.; Furumo, P.R.; Moss, S.; Figot Kuthy, A.G.; García Aguirre, D.; Mandle, L.; Valencia, I.D.; Ruckelshaus, M.; Daily, G.C.; Lambin, E.F. Colombian biodiversity is governed by a rich and diverse policy mix. Nat. Ecol. Evol. 2023, 7, 382–392. [Google Scholar] [CrossRef]
- Andor, L. Hungary in the financial crisis: A (basket) case study. Debatte J. Contemp. Cent. East. Eur. 2009, 17, 285–296. [Google Scholar] [CrossRef]
- Palotai, G.M. The interaction between fiscal and monetary policy in Hungary over the past decade and a half. Financ. Econ. Rev. 2016, 15, 5–32. [Google Scholar]
- Polackova, H.; Papp, A.; Schick, A. Fiscal Risks and the Quality of Fiscal Adjustment in Hungary; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Banai, Á.; Lang, P.; Nagy, G.; Stancsics, M. Waste of money or growth opportunity: The causal effect of EU subsidies on Hungarian SMEs. Econ. Syst. 2020, 44, 100742. [Google Scholar] [CrossRef]
- Eurostat and International Monetary Fund, Respective Publications and Datasets. 2013–2023. Available online: https://dsbb.imf.org/sdds/eurostat-note (accessed on 15 March 2025).
- Smets, F.; Wouters, R. An estimated dynamic stochastic general equilibrium model of the euro area. J. Eur. Econ. Assoc. 2003, 1, 1123–1175. [Google Scholar] [CrossRef]
- Reiss, P.C.; Wolak, F.A. Structural econometric modeling: Rationales and examples from industrial organization. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 2007; Volume 6, pp. 4277–4415. [Google Scholar] [CrossRef]
- Asso, P.F.; Kahn, G.A.; Leeson, R. The Taylor Rule and the Transformation of Monetary Policy; Hoover Institute Press Publication: Stanford, CA, USA, 2007. [Google Scholar]
- Dismuke, C.; Lindrooth, R. Ordinary least squares. Methods Des. Outcomes Res. 2006, 93, 93–104. [Google Scholar]
- Ferdinandusse, M.; Palaiodimos, G.; Politsidis, P.N. Non-Linearities in Fiscal Policy: Evidence from the Eurozone; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Stawska, J.; Malaczewski, M.; Malaczewska, P.; Stawasz-Grabowska, E. The Nash equilibrium in the policy mix model for Czechia, Hungary, and Romania. Cogent Econ. Financ. 2021, 9, 1869380. [Google Scholar] [CrossRef]
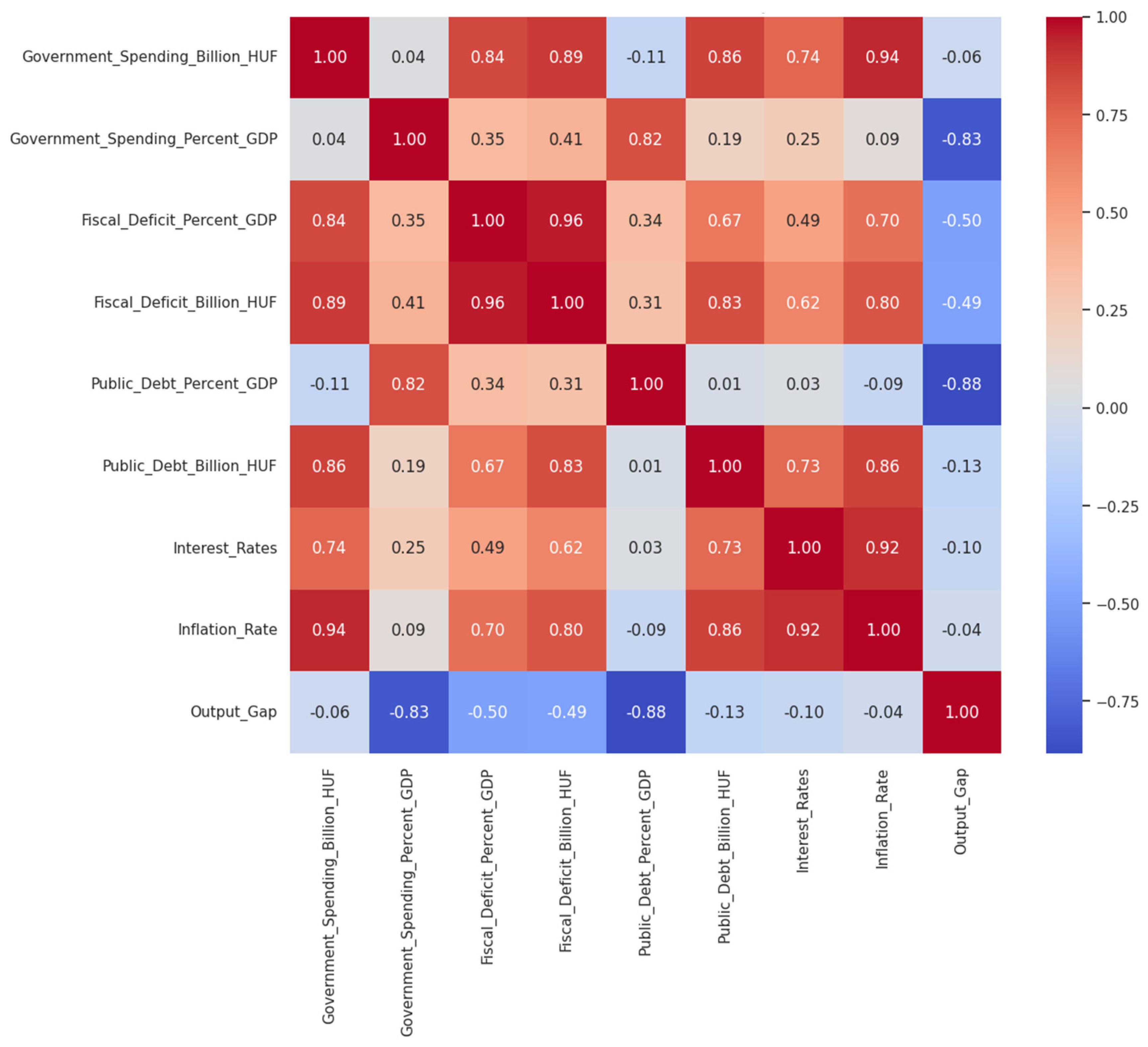

| Selected Variables * | Symbol | Mean | Std | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|
| Interest Rates | 3.46 | 4.8 | 0.6 | 0.9 | 0.9 | 2.95 | 13 | |
| Government Spending (HUF Billion) | 9417.27 | 3048.42 | 5985 | 7056 | 8540 | 10,941 | 15,386 | |
| Government Spending (Percent GDP) | 48.44 | 1.92 | 45.8 | 46.65 | 48.7 | 50.05 | 51 | |
| Inflation Rate | 4.58 | 5.82 | −0.2 | 1.05 | 2.9 | 4.2 | 17.1 | |
| Output Gap | −0.076 | 2.57 | −4.85 | −1.21 | 0.0 | 1.35 | 3.5 | |
| Fiscal Deficit (Percent GDP) | 1.08 | 4.65 | −2.8 | −2.30 | −2.0 | 6.45 | 7.6 | |
| Fiscal Deficit (HUF Billion) | 2119.82 | 1546.62 | 900 | 1000 | 1100 | 3500 | 5018 | |
| Public Debt (Percent GDP) | 73.8 | 3.98 | 65 | 72.7 | 74.6 | 76.35 | 78.7 | |
| Public Debt (HUF Billion) | 29,057.64 | 9196.2 | 23,000 | 24,250 | 25,500 | 30,500 | 55,134 |
| Parameter | Estimate | Std. Error | t-Statistic | p-Value |
|---|---|---|---|---|
| Fiscal Authority Regression | ||||
| Constant | 41.0969 | 54.349 | 0.756 | 0.471 |
| (Output Gap) | −1.6451 | 1.140 | −1.443 | 0.187 |
| (Public Debt) | 0.5438 | 0.737 | 0.738 | 0.482 |
| Monetary Authority Regression | ||||
| Constant | 2.2573 | 0.665 | 3.392 | 0.009 |
| (Inflation Gap) | 0.7548 | 0.115 | 6.544 | 0.000 |
| (Output Gap) | −0.1034 | 0.261 | −0.396 | 0.702 |
| Year | Actual Fiscal Deficit (% GDP) | Fiscal Best Response (% GDP) | Actual Interest Rate (%) | Monetary Best Response (%) |
|---|---|---|---|---|
| 2013 | −2.6 | −3.06 | 3.80 | −0.52 |
| 2014 | −2.8 | −1.59 | 2.10 | −0.74 |
| 2015 | −2.0 | −0.36 | 1.35 | 0.13 |
| 2016 | −1.8 | 1.12 | 0.90 | 0.34 |
| 2017 | −2.5 | 4.20 | 0.90 | −0.41 |
| 2018 | −2.1 | 8.00 | 0.90 | 0.02 |
| 2019 | −2.0 | 12.51 | 0.90 | 0.13 |
| 2020 | 7.6 | −3.64 | 0.60 | 10.51 |
| 2021 | 7.2 | −0.67 | 0.60 | 10.07 |
| 2022 | 6.2 | −2.50 | 13.00 | 8.99 |
| 2023 | 6.7 | −2.02 | 13.00 | 9.53 |
| Year | Nash Fiscal Strategy (% GDP) | Nash Monetary Strategy (%) | Iterations |
|---|---|---|---|
| 2013 | −1.77 | 0.37 | 19 |
| 2014 | −1.18 | 1.01 | 17 |
| 2015 | −0.51 | 1.74 | 16 |
| 2016 | 0.42 | 2.74 | 18 |
| 2017 | 2.61 | 5.11 | 19 |
| 2018 | 5.31 | 8.03 | 19 |
| 2019 | 8.52 | 11.50 | 20 |
| 2020 | −3.04 | −0.99 | 18 |
| 2021 | −0.93 | 1.29 | 17 |
| 2022 | 1.09 | 3.47 | 20 |
| 2023 | 1.43 | 3.84 | 20 |
| Year | Actual Fiscal Deficit (% GDP) | Nash Fiscal Strategy (% GDP) | Difference | Actual Interest Rate (%) | Nash Monetary Strategy (%) | Difference |
|---|---|---|---|---|---|---|
| 2013 | −2.6 | −1.77 | 0.83 | 3.80 | 0.37 | −3.43 |
| 2014 | −2.8 | −1.18 | 1.62 | 2.10 | 1.01 | −1.09 |
| 2015 | −2.0 | −0.51 | 1.49 | 1.35 | 1.74 | 0.39 |
| 2016 | −1.8 | 0.42 | 2.22 | 0.90 | 2.74 | 1.84 |
| 2017 | −2.5 | 2.61 | 5.11 | 0.90 | 5.11 | 4.21 |
| 2018 | −2.1 | 5.31 | 7.41 | 0.90 | 8.03 | 7.13 |
| 2019 | −2.0 | 8.52 | 10.52 | 0.90 | 11.50 | 10.60 |
| 2020 | 7.6 | −3.04 | −10.64 | 0.60 | −0.99 | −1.59 |
| 2021 | 7.2 | −0.93 | −8.13 | 0.60 | 1.29 | 0.69 |
| 2022 | 6.2 | 1.09 | −5.11 | 13.00 | 3.47 | −9.53 |
| 2023 | 6.7 | 1.43 | −5.27 | 13.00 | 3.84 | −9.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salimi, S.; Kazinczy, E.; Tatay, T.; Amini, M. Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary. Mathematics 2025, 13, 1427. https://doi.org/10.3390/math13091427
Salimi S, Kazinczy E, Tatay T, Amini M. Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary. Mathematics. 2025; 13(9):1427. https://doi.org/10.3390/math13091427
Chicago/Turabian StyleSalimi, Sara, Eszter Kazinczy, Tibor Tatay, and Mehran Amini. 2025. "Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary" Mathematics 13, no. 9: 1427. https://doi.org/10.3390/math13091427
APA StyleSalimi, S., Kazinczy, E., Tatay, T., & Amini, M. (2025). Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary. Mathematics, 13(9), 1427. https://doi.org/10.3390/math13091427






