Numerical Methods for a Two-Species Competition-Diffusion Model with Free Boundaries
Abstract
:1. Introduction
- For any point , it moves with velocity , where is the unit outward normal of at , and is a given positive constant.
2. Numerical Methods for 1D Two-Species Competition-Diffusion Model
2.1. Method 1: Front-Tracking Method for 1D Two-Species Competition-Diffusion Model
- 1
- When as depicted in Figure 1, denoting . Let us first consider the symmetric point of respect to the position , which is denoted by . In particular, when , . We use the Lagrange interpolation to construct polynomial from the value of d, h, , , and , thus at , we use the value of at instead of ,
- 2
- When , the central scheme approximation of the spatial derivatives to approximate involves the fictitious value at the point . The value can be estimated from the second-order discretization of the boundary condition (10),which implies that . It is obvious that all the values of on the grid points are equal to 0 except . Numerically, we take , and this can be explained by the fact the species is only located inside one grid mesh. The simulation should stop here indicating that a more refined mesh is needed.
- 3
- When as shown in Figure 2, denoting . Let us first consider the symmetric point of with respect to the position , which is denoted by . Then we consider the value of , and use the Lagrange interpolation to construct polynomial from the value of h, d, , , and . Then at , we use the value of at instead of .
- 4
- When , it implies that the spreading of the populations already goes out of the computational domain , and the simulation should stop here.
- 1
- When and , then we know that . Let , , for and , , for . We consider the central approximation of the spatial derivatives at , for , and the central approximation of the spatial derivatives at , for , where U and V are updated by the backward EulerThen use the Iteration (or Newton Iteration) to solve the nonlinear system (12).
- 2
- When and , denoting and , we use the Lagrange interpolation to construct polynomial from the value of h, , , , and and polynomial from the value of h, , , , and . Then at and , we use the value of at instead of and the value of at instead of . For the solution u at , for , a standard central approximation in space with backward Euler in time will be employed. , for . For the solution v at , for , a standard central approximation in space with backward Euler in time will be employed. , for . U and V is updated by the backward Euler in timeIteration (or Newton Iteration) will be applied to solve the nonlinear system (13).
- 3
- When and , then we know that . Let , , for . We consider the central approximation of the spatial derivatives at , for . Denoting , we use the Lagrange interpolation to construct polynomial from the value of h, , , , and . Then at , we use the value of at instead of , where U and V is updated by the backward Euler in timeThen use the Iteration (or Newton Iteration) to solve the nonlinear system (14).
- 4
- When and , denoting , we use the Lagrange interpolation to construct polynomial from the value of h, , , , Then at , we use the value of at instead of . For the solution u at , for , a standard central approximation in space with backward Euler in time will be employed. , for . For the solution v at , for , a standard central approximation in space with backward Euler in time will be employed. , for , where U and V is updated by the backward Euler in timeIteration (or Newton Iteration) will be applied to solve the nonlinear system (15).
2.2. Method 2: Front-Fixing Method for 1D Two-Species Competition-Diffusion Model
- 1
- When , then we know that . Let , , for . We consider the central approximation of the spatial derivatives at , for , where is updated by the backward Euler
- 2
- When , denoting , we use the Lagrange interpolation to construct polynomial from the value of h, R, , , and , We consider to use the value of at instead of .
- 3
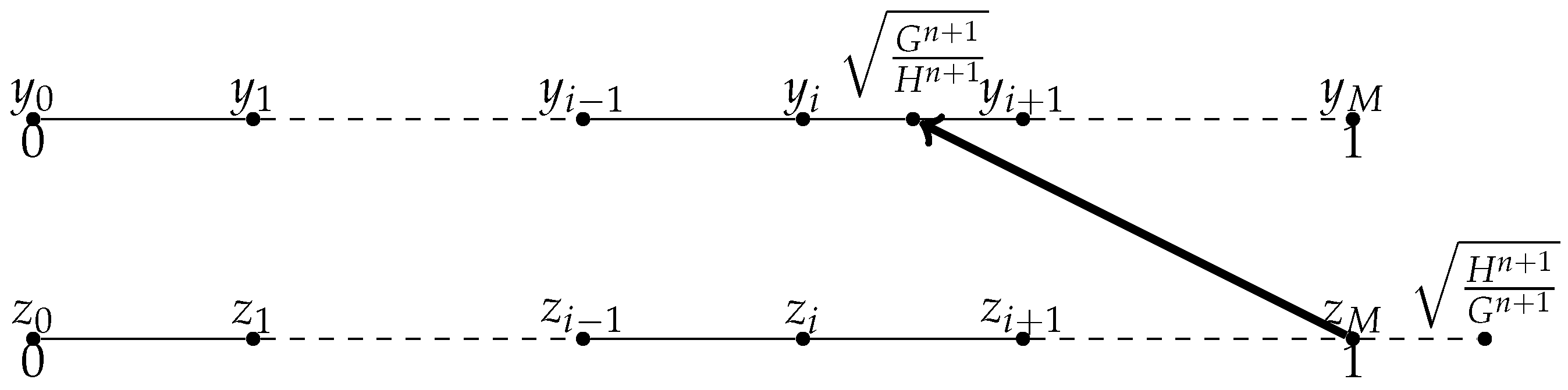
- When as shown in Figure 3, we consider the central approximation of the spatial derivatives at , for , for , we know that , let us approximate instead of approximating . Suppose , we use the Lagrange interpolation to construct polynomial P from the value of , , , , , and , then .
- 1
- When , then we know that . Let , , for . We consider the central approximation of the spatial derivatives at , for , where M is updated by the backward Euler
- 2
- When , denoting , we use the Lagrange interpolation to construct polynomial from the value of h, R, , , and , We consider to use the value of at instead of .
- 3
- When as illustrated in Figure 4, we consider the central approximation of the spatial derivatives at , for , for , we know that , let us approximate instead of approximating . Suppose , we use the Lagrange interpolation to construct polynomial P from the value of , , , , , and , then .
3. Level Set Method for 2D Two-Species Competition-Diffusion Model
- At points away from the front, which means the nearby four grid points are all inside the domain , we solve the nonlinear parabolic partial difference equation (53) by combining the forward Euler method and the five-point stencil scheme.
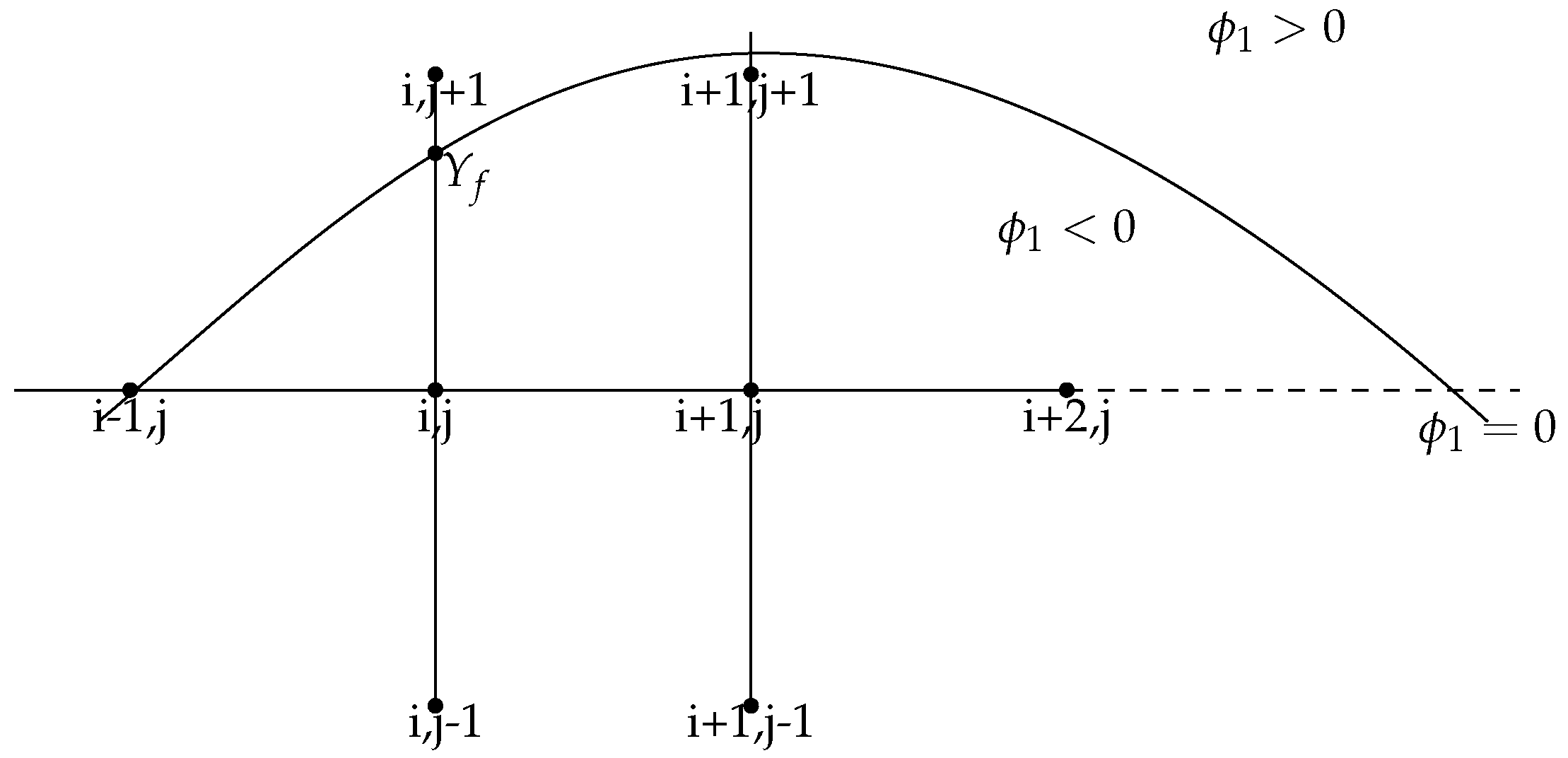
- For points near the front , some special care should be taken. We effectively capture the front using the level set function . We can use the one-sided different sign of to incorporate the distances between a point on the front and grid points neighboring it in either the vertical or horizontal direction. For example, , we consider two grid points and which border . In y-direction, we have . We introduceand use and to construct interpolating polynomial P. When updating , we use a standard five-point stencil combing forward Euler method by employing instead of , i.e.,For the case when front interacts with x-axis, we use the same process in x-direction. In the special case where we cannot find enough grid points inside the domain to construct interpolating polynomial P, we employ the nearby grid points and intersect points of the front and x and y-axis to construct quadratic polynomial or straight line as the interpolating polynomial P to update U. For the extreme configuration, where there are only intersect points of the front and x and y-axis near the grid point, we update at the grid point.
- If a grid point lies on the front, we set the value at that point (in view of (53)). For example, we set =0 for the grid point .
4. Numerical Experiments
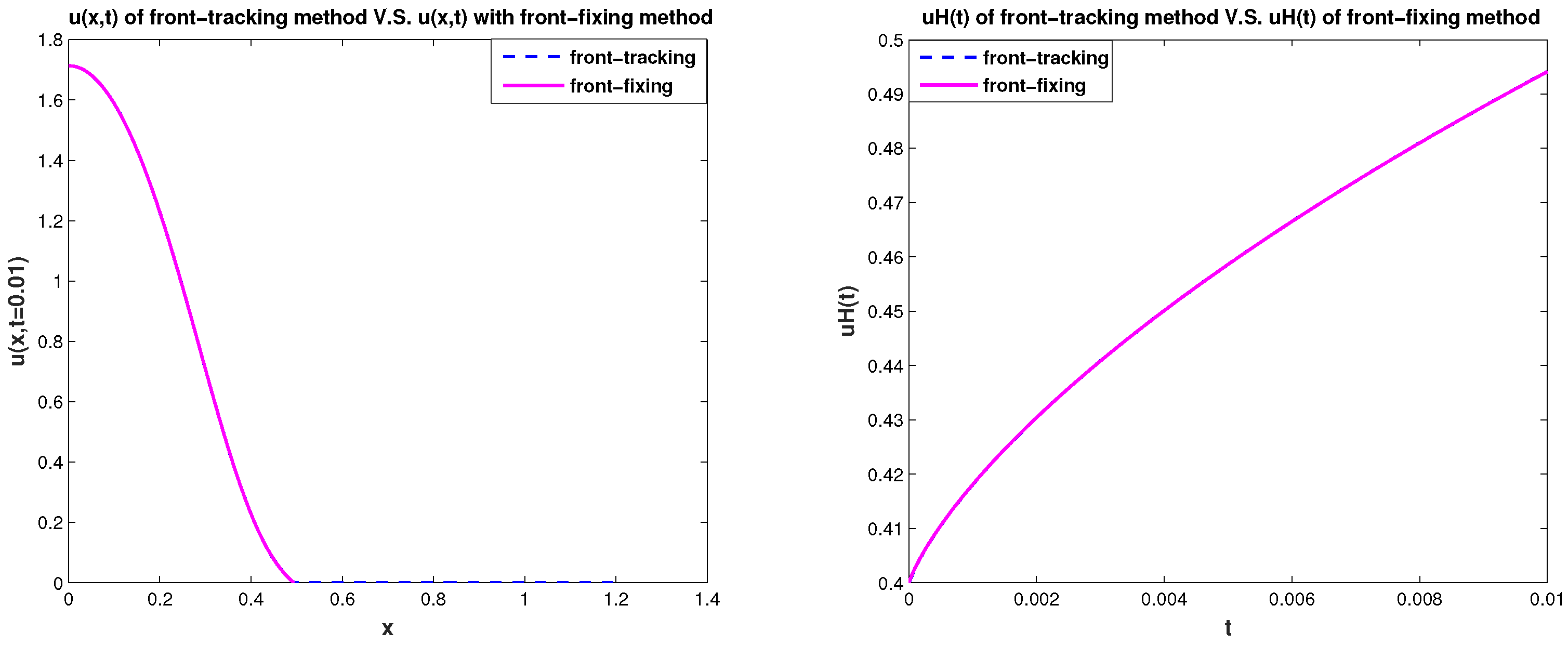
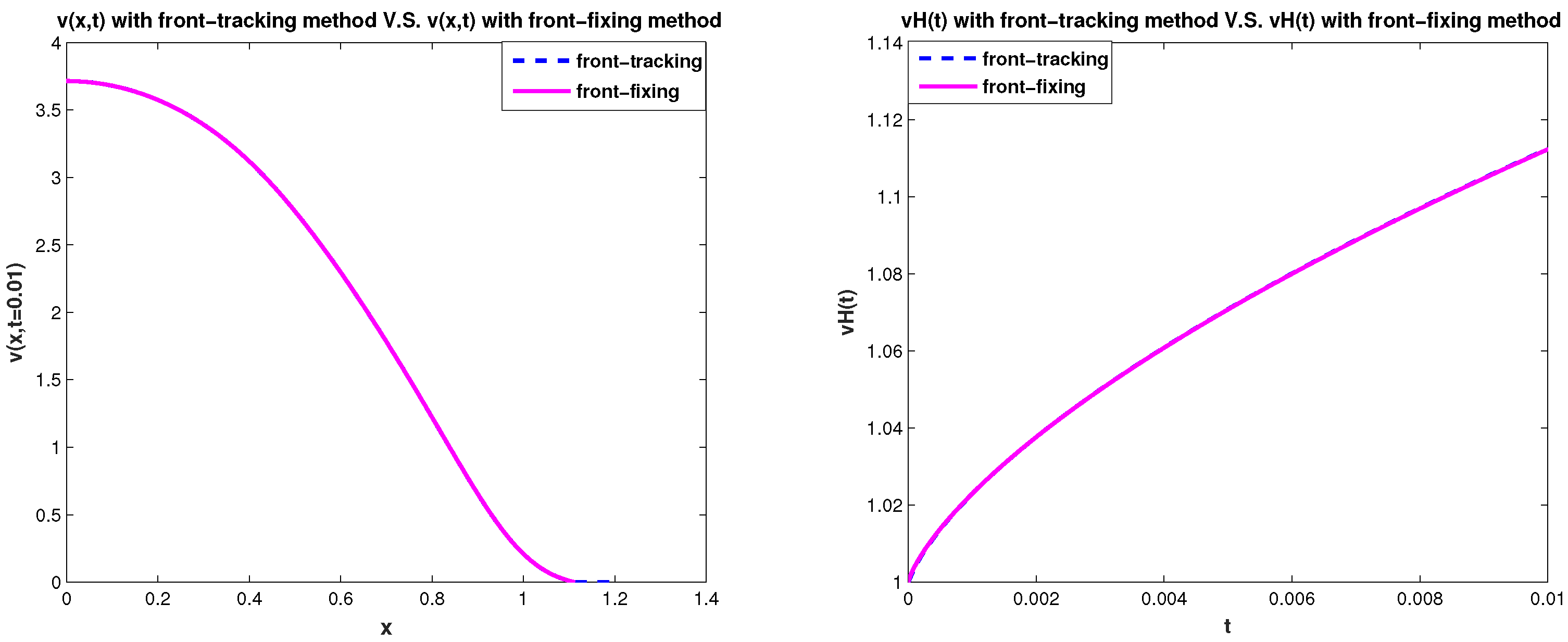
4.1. Numerical Tests of 1D Problem: Front-Fixing Method and Front-Tracking Method
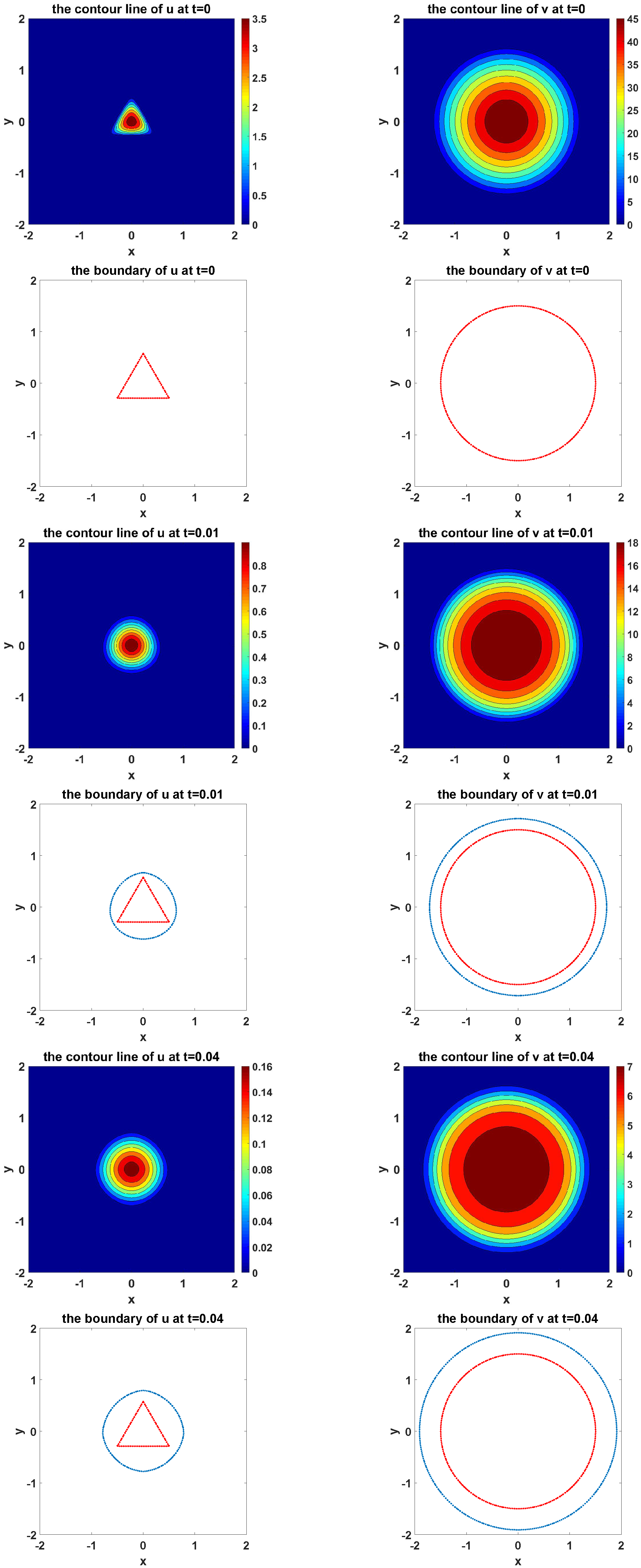
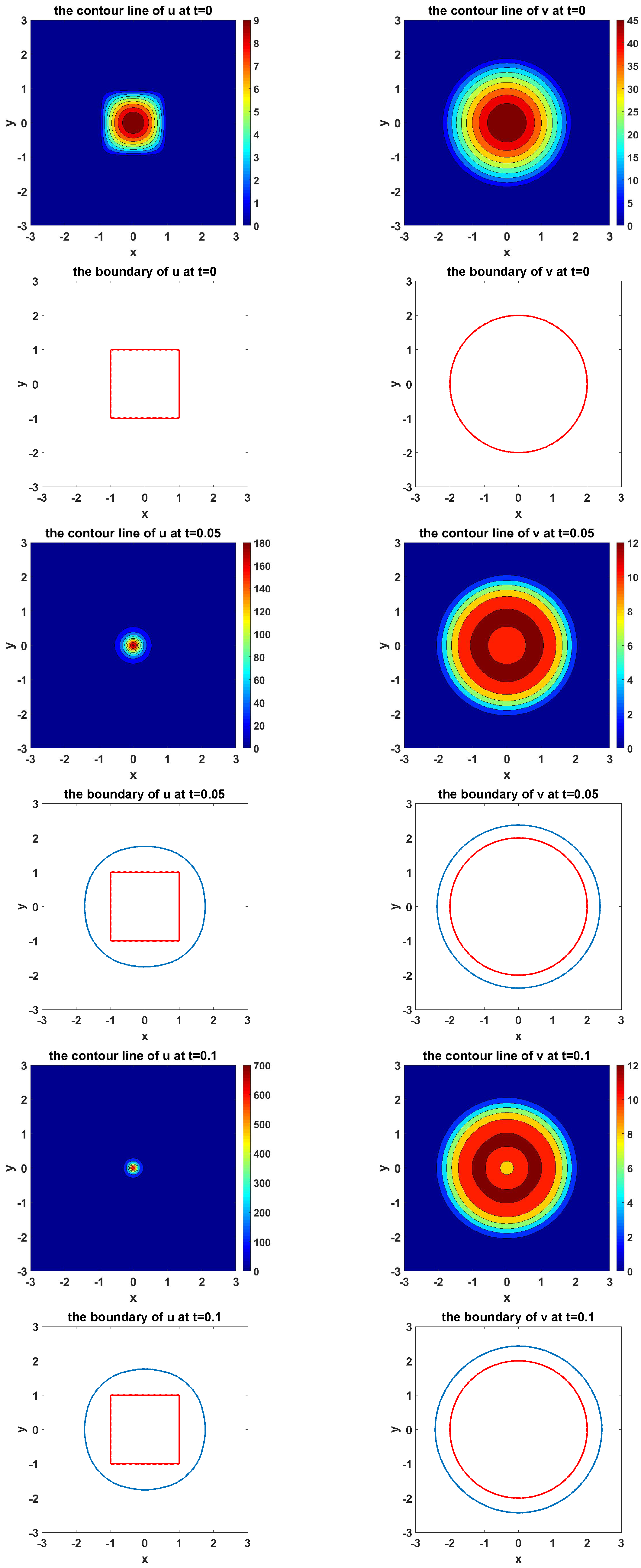
4.2. Numerical Tests of Level Set Methods for 2D Model With Different Initial Configuration
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Wang, M.; Zhang, Y. Note on a two-species competition-diffusion model with two free boundaries. Nonlinear Anal. Theory Methods Appl. 2017, 159, 458–467. [Google Scholar] [CrossRef]
- Guo, J.S.; Wu, C.H. Dynamics for a two-species competition—Diffusion model with two free boundaries. Nonlinearity 2014, 28, 1. [Google Scholar] [CrossRef]
- Guo, J.S.; Wu, C.H. On a free boundary problem for a two-species weak competition system. J. Dyn. Differ. Equ. 2012, 24, 873–895. [Google Scholar] [CrossRef]
- Wu, C.H. The minimal habitat size for spreading in a weak competition system with two free boundaries. J. Differ. Equ. 2015, 259, 873–897. [Google Scholar] [CrossRef]
- Hilhorst, D.; Iida, M.; Mimura, M.; Ninomiya, H. A competition-diffusion system approximation to the classical two-phase Stefan problem. Jpn. J. Ind. Appl. Math. 2001, 18, 161. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J. Free boundary problems for a Lotka-Volterra competition system. J. Dyn. Differ. Equ. 2014, 26, 655–672. [Google Scholar] [CrossRef]
- Hosono, Y. The minimal speed of traveling fronts for a diffusive Lotka-Volterra competition model. Bull. Math. Biol. 1998, 60, 435–448. [Google Scholar] [CrossRef]
- Conley, C.; Gardner, R. An Application of the Generalized Morse Index to Travelling Wave Solutions of a Competitive Reaction-Diffusion Model; Technical Report; Wisconsin Univ-Madison Mathematics Research Center: Madison, WI, USA, 1980. [Google Scholar]
- Gardner, R.A. Existence and stability of travelling wave solutions of competition models: A degree theoretic approach. J. Differ. Equ. 1982, 44, 343–364. [Google Scholar] [CrossRef]
- Lewis, M.A.; Li, B.; Weinberger, H.F. Spreading speed and linear determinacy for two-species competition models. J. Math. Biol. 2002, 45, 219–233. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Weinberger, H.F.; Lewis, M.A. Spreading speeds as slowest wave speeds for cooperative systems. Math. Biosci. 2005, 196, 82–98. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, H.F.; Lewis, M.A.; Li, B. Analysis of linear determinacy for spread in cooperative models. J. Math. Biol. 2002, 45, 183–218. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Guo, Z. The Stefan problem for the Fisher–KPP equation. J. Differ. Equ. 2012, 253, 996–1035. [Google Scholar] [CrossRef]
- Dong, X.; Li, H.; Derdowski, A.; Ding, L.; Burnett, A.; Chen, X.; Peters, T.; Dermody, T.; Woodruff, E.; Wang, J.; et al. AP-3 directs the intracellular trafficking of HIV-1 Gag and plays a key role in particle assembly. Cell 2005, 120, 663–674. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Lou, B. Spreading and vanishing in nonlinear diffusion problems with free boundaries. J. Eur. Math. Soc. 2015, 17, 2673–2724. [Google Scholar] [CrossRef]
- Du, Y.; Lou, B.; Zhou, M. Nonlinear diffusion problems with free boundaries: convergence, transition speed, and zero number arguments. SIAM J. Math. Anal. 2015, 47, 3555–3584. [Google Scholar] [CrossRef]
- Du, Y.; Matano, H.; Wang, K. Regularity and asymptotic behavior of nonlinear Stefan problems. Arch. Ration. Mech. Anal. 2014, 212, 957–1010. [Google Scholar] [CrossRef]
- Liu, S.; Du, Y.; Liu, X. Numerical methods for a class of reaction-diffusion equations with free boundaries. 2018; preprint. [Google Scholar]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces; Springer Verlag: Berlin, Germany, 2002. [Google Scholar]
- Osher, S.; Sethian, J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef] [PubMed]
- Sethian, J.A. Level Set Methods and Fast Marching Methods; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Xu, J.; Li, Z.; Lowengrub, J.; Zhao, H. A level-set method for interfacial flows with surfactant. J. Comput. Phys. 2006, 212, 590–616. [Google Scholar] [CrossRef]
- Zhao, H.; Chan, T.; Merriman, B.; Osher, S. A variational level set approach to multiphase motion. J. Comput. Phys. 1996, 127, 179–195. [Google Scholar] [CrossRef]
- Leveque, R.; Li, Z. The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 1994, 31, 1019–1044. [Google Scholar] [CrossRef]
- Peskin, C. The immersed boundary method. Acta Numer. 2003, 11, 479–517. [Google Scholar]
- Wiegmann, A.; Bube, K. The immersed interface method for nonlinear differential equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 1998, 35, 177–200. [Google Scholar] [CrossRef]
- Zhu, L.; Peskin, C. Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 2002, 179, 452–468. [Google Scholar] [CrossRef]
- Chern, I.; Glimm, J.; McBryan, O.; Plohr, B.; Yaniv, S. Front tracking for gas dynamics. J. Comput. Phys. 1986, 62, 83–110. [Google Scholar] [CrossRef]
- Glimm, J.; Li, X.; Liu, Y.; Zhao, N. Conservative front tracking and level set algorithms. Proc. Natl. Acad. Sci. USA 2001, 98, 14198–14201. [Google Scholar] [CrossRef] [PubMed]
- Hilditch, J.; Colella, P. A front tracking method for compressible flames in one dimension. SIAM J. Sci. Comput. 1995, 16, 755–772. [Google Scholar] [CrossRef]
- Hua, J.; Stene, J.; Lin, P. Numerical simulation of 3D bubbles rising in viscous liquids using a front tracking method. J. Comput. Phys. 2007, 227, 3358–3382. [Google Scholar] [CrossRef]
- LeVeque, R.; Shyue, K. Two-dimensional front tracking based on high resolution wave propagation methods. J. Comput. Phys. 1996, 123, 354–368. [Google Scholar] [CrossRef]
- Unverdi, S.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Crank, J. Free and Moving Boundary Problems; Oxford Science Publications: Oxford, UK, 1984. [Google Scholar]
- Landau, H.G. Heat conduction in a melting solid. Q. Appl. Math. 1950, 8, 81–94. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
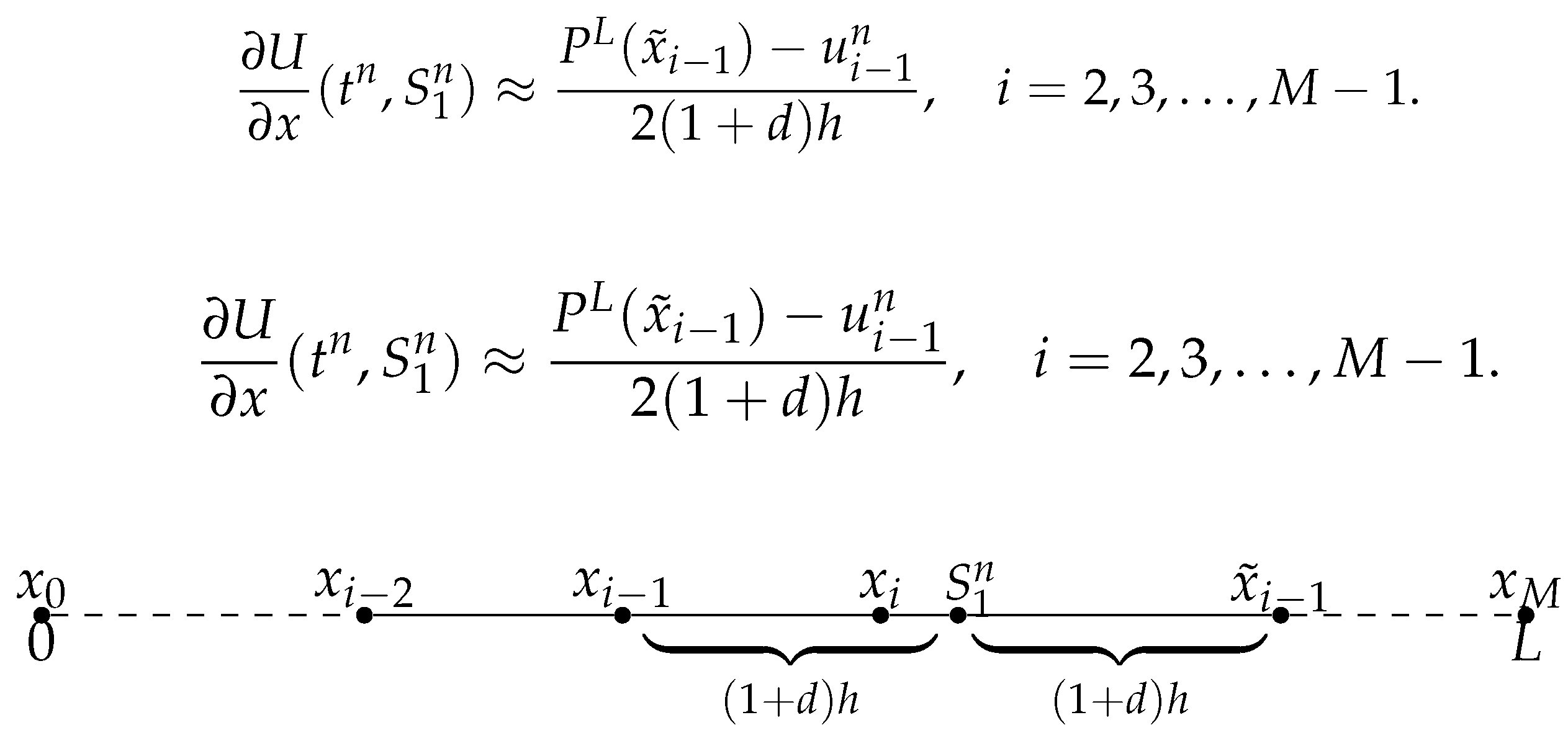




| Order | Order | |||
|---|---|---|---|---|
| Accuracy test of U of front-fixing method | ||||
| 101 × | 1.195× | 2.119× | ||
| 201 | 3.142 | 1.93 | 5.424 | 1.97 |
| 401 | 8.233 | 1.93 | 1.314 | 2.05 |
| 801 | 1.956 | 2.07 | 3.983 | 1.72 |
| 1601 | Reference | |||
| Accuracy test of the front of U of front-fixing method | ||||
| 101 | 3.178 | 9.366 | ||
| 201 | 7.880 | 2.01 | 2.424 | 1.95 |
| 401 | 1.880 | 2.07 | 5.927 | 2.03 |
| 801 | 3.800 | 2.32 | 1.202 | 2.30 |
| 1601 | Reference | |||
| Order | Order | |||
|---|---|---|---|---|
| Accuracy test of V of front-fixing method | ||||
| 101 | 1.038 | 2.115 | ||
| 201 | 2.776 | 1.90 | 5.609 | 1.91 |
| 401 | 6.861 | 2.02 | 1.381 | 2.02 |
| 801 | 1.398 | 2.30 | 2.807 | 2.30 |
| 1601 | Reference | |||
| Accuracy test of the front of V of front-fixing method | ||||
| 101 | 2.890 | 7.595 | ||
| 201 | 7.700 | 1.91 | 2.123 | 1.84 |
| 401 | 1.910 | 2.01 | 5.454 | 1.96 |
| 801 | 3.900 | 2.29 | 1.141 | 2.26 |
| 1601 | Reference | |||
| Order | Order | |||
|---|---|---|---|---|
| Accuracy test of U of front-tracking method | ||||
| 61 | 5.637 | 1.699 | ||
| 121 | 1.035 | 2.45 | 3.260 | 2.38 |
| 241 | 1.850 | 2.48 | 6.019 | 2.44 |
| 481 | 2.987 | 2.63 | 9.833 | 2.61 |
| 961 | Reference | |||
| Accuracy test of the front of U of front-tracking method | ||||
| 61 | 1.222 | 2.233 | ||
| 121 | 2.280 | 2.42 | 5.672 | 1.98 |
| 241 | 4.300 | 2.39 | 1.296 | 2.13 |
| 481 | 8.000 | 2.50 | 2.494 | 2.38 |
| 961 | Reference | |||
| Order | Order | |||
|---|---|---|---|---|
| Accuracy test of V of front-tracking method | ||||
| 61 | 4.443 | 1.373 | ||
| 121 | 7.882 | 2.49 | 2.493 | 2.46 |
| 241 | 1.396 | 2.50 | 4.254 | 2.55 |
| 481 | 2.378 | 2.55 | 9.871 | 2.11 |
| 961 | Reference | |||
| Accuracy test of the front of V of front-tracking method | ||||
| 61 | 1.385 | 3.268 | ||
| 121 | 2.721 | 2.35 | 8.504 | 1.94 |
| 241 | 6.000 | 2.19 | 1.922 | 2.15 |
| 481 | 1.200 | 2.30 | 3.788 | 2.34 |
| 961 | Reference | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Liu, X. Numerical Methods for a Two-Species Competition-Diffusion Model with Free Boundaries. Mathematics 2018, 6, 72. https://doi.org/10.3390/math6050072
Liu S, Liu X. Numerical Methods for a Two-Species Competition-Diffusion Model with Free Boundaries. Mathematics. 2018; 6(5):72. https://doi.org/10.3390/math6050072
Chicago/Turabian StyleLiu, Shuang, and Xinfeng Liu. 2018. "Numerical Methods for a Two-Species Competition-Diffusion Model with Free Boundaries" Mathematics 6, no. 5: 72. https://doi.org/10.3390/math6050072
APA StyleLiu, S., & Liu, X. (2018). Numerical Methods for a Two-Species Competition-Diffusion Model with Free Boundaries. Mathematics, 6(5), 72. https://doi.org/10.3390/math6050072




