Consistent Sets of Soft Contexts Defined by Soft Sets

Abstract

We introduce the notion of consistent sets of soft contexts and investigate its characterizations. For the purpose of studying the characterizations of consistent sets, we introduce the notions of $1^0$ and $2^0$ classes of independent attributes. By studying the characterizations, we determined that every consistent set has to contain the special class $1^0$ called the Essential Zone of consistent sets. This is very important information that we should consider when constructing consistent sets of a given soft context. Additionally, we study the fundamental theorems necessary to construct the consistent sets of a given soft context. In particular, we apply the Fundamental Theorem 2 to obtain the consistent sets of a given soft context, and show that this fundamental theorem provides a more effective way of constructing the consistent sets of a formal context.

1. Introduction

In 1982, Wille introduced formal concept analysis (FCA) [1], which is an important theory for the research of hierarchical structures induced by a binary relation between the set of objects and attributes. The three basic notions of FCA are formal context, formal concept, and concept lattice. A formal context is a kind of information system, which is a tabular form of an object–attribute value relationship [2,3,4,5]. The formal concept consists of two parts called expansion and tension. The expansion contains all objects belonging to this concept and the tension contains all attributes that are valid for all of those objects.

The subconcept–superconcept order relation between two formal concepts can be defined by the inclusion relation on objects and attributes. Furthermore, the set of all formal concepts together with the order relation forms a complete lattice called a concept lattice [5]. A formal concept analysis has been widely applied to many fields and generalized to other types for requirements of real word applications [5,6,7,8,9,10,11,12,13].

The soft set concept was introduced by Molodtsov in 1999 [14], to deal with complicated problems and uncertainties as follows: Let U be an initial universe set (simply, universe set) and A be a collection of characteristics of objects in U. A pair $(F,A)$ is called a soft set over U if F is a set-valued mapping from A into the set $P\left(U\right)$ of all subsets of U. In [15], Maji et al. introduced several operators (equality, subset, superset, complement, null, and absolute soft set, etc.) for soft set theory. In [16], Ali et al. introduced new operations that modified some concepts introduced by Maji.

In [17], we studied the new notions such as soft contexts, soft concepts and soft concept lattices, which are closely related to formal contexts and formal concept lattices. The main purpose of studying these new notions was to obtain a more effective method than the traditional method of constructing all formal concepts in a formal context. So, we introduced the soft context, combining the formal contexts and soft sets, and investigated the notions of soft concepts, independent soft concepts, dependent soft concepts and bases. Furthermore, we obtained important results: (1) The set of all soft concepts can be decomposed into the set of all independent soft concepts and the set of all dependent soft concepts; (2) All dependent soft concepts are generated by independent soft concepts; (3) There exists a bijective mapping between the set of all formal concepts and the set of all associated soft concepts in a given formal context.

Based on the above facts, we intend to obtain a more effective method of finding a consistent set in a formal context using soft contexts. So, in this paper, we introduce the notion of consistent sets of soft context and investigate its characterizations. For the purpose of studying the characterizations of consistent sets, we investigate the independence and dependence for attributes in a given soft context, and introduce the notions of $1^0$ and $2^0$ classes of independent attributes. By studying the characterizations, we determine that every consistent set has to contain a special set called the Essential Zone of Consistent Sets. In fact, this is very important information that we should consider when constructing consistent sets of a given soft context. Additionally, we study the fundamental theorems necessary to construct the consistent sets of a given soft context. Finally, we apply the above-mentioned fundamental theorem to obtain the consistent sets of a given soft context. In particular, by using an example, we show that this fundamental theorem provides a more effective way of constructing the consistent sets of a given formal context.

2. Preliminaries

A formal context is a triplet $(U,A,I)$, where X and Y are finite sets, and $I\subseteq U\times A$ is a relation from U to A. In a formal context $(U,A,I)$, U is a finite set of objects, A is a finite set of attributes or properties, and if $(x,a)\in I$, we simply write $xIa$ and say that x has the property a, or a is possessed by object x. The set of all attributes possessed by $x\in U$ and the set of all objects having an attribute $a\in A$ were represented as [1,5]:

$$x^{*}=\{a\in A|xIa\}; a^{*}=\{x\in U|xIa\}.$$

For a set of objects $X\subseteq U$, $X^{*}$ is the maximal set of properties shared by all objects in X; for a set of properties $B\subseteq A$, $B^{*}$ is the maximal set of objects that all have properties in B; that is,

$$X^{*}=\{a\in A|\forall x\in X,xIa\}; B^{*}=\{x\in U|\forall b\in B,xIb\}.$$

Let us define two operators $I_{\uparrow },I^{\downarrow }$ between the power sets of U and A as follows:

$I_{\uparrow }:2^U\to 2^A, I_{\uparrow }\left(X\right)=X^{*}$;

$I^{\downarrow }:2^A\to 2^U, I^{\downarrow }\left(B\right)=B^{*}$.

Then, obviously, the pair of operators $(I_{\uparrow },I^{\downarrow })$ is a contravariant Galois connection between the power sets of U and A.

A pair $(X,B)$, $X\subseteq U$, $B\subseteq A$, is called a formal concept of the context $(U,A,I)$ if $X=B^{*}$ and $B=X^{*}$ [1,5]. X is called the extension of the concept, and B is called the extension of the concept.

For a formal context $(U,A,I)$, the concepts of $(U,A,I)$ are ordered by the following: For two concepts $(X,B),(Y,C)$,

$$(X,B)\le (Y,C)\iff X\subseteq Y(\iff C\subseteq B).$$

The ordered set of all concepts in $(U,A,I)$ is a complete lattice and the ordered set is denoted by $L(U,A,I)$ and called the formal concept lattice of $(U,A,I)$.

Let U be a universe set and E be a set of parameters with respect to U. In general, parameters are properties or attributes of objects in U.

A pair $(F,A)$ is called a soft set [14] over U if F is a set-valued mapping of A into $2^U$, that is, $F:A\to 2^U$ is a mapping defined by $F\left(a\right)\in 2^U$ for $a\in A$.

Let $U=\{x_1,x_2,\dots ,x_n\}$ be a non-empty finite set of objects, $A=\{a_1,a_2,\dots ,a_m\}$ a non-empty finite set of attributes, and $F:A\to 2^U$ a soft set. Then, the triple $(U,A,F)$ is called a soft context [17].

Let $(U,A,F)$ be a soft context, $P\left(U\right)$ denote the power set of U and $A\subseteq E$. Then, in [17], ${\mathbf{F}}^{+}$ and ${\mathbf{F}}^{-}$ are defined as the following:

(1)

${\mathbf{F}}^{+}:P\left(A\right)\to P\left(U\right)$ is a mapping defined as ${\mathbf{F}}^{+}\left(B\right)={\cap }_{b\in B}F\left(b\right)$;

(2)

${\mathbf{F}}^{-}:P\left(U\right)\to P\left(A\right)$ is a mapping defined as ${\mathbf{F}}^{-}\left(X\right)=\{a\in A:X\subseteq F\left(a\right)\}$.

Let $\mathbf{Im}\left({\mathbf{F}}^{+}\right)=\left\{{\mathbf{F}}^{+}\left(B\right)\right|B\in P\left(A\right)\}$ and $\mathbf{Im}\left({\mathbf{F}}^{-}\right)=\left\{{\mathbf{F}}^{-}\left(X\right)\right|X\in P\left(U\right)\}$. For $a\in A$ and $x\in U$, simply, ${\mathbf{F}}^{+}\left(\left\{a\right\}\right)={\mathbf{F}}^{+}\left(a\right)$ and ${\mathbf{F}}^{-}\left(\left\{x\right\}\right)={\mathbf{F}}^{-}\left(x\right)$.

Then, we showed the following facts:

Theorem 1

([17]). Let $(U,A,F)$ be a soft context, $X,Y\subseteq U$ and $C,D\subseteq A$.

(1) 

If $X\subseteq Y$, then ${\mathbf{F}}^{-}\left(Y\right)\subseteq {\mathbf{F}}^{-}\left(X\right)$; if $C\subseteq D$, then ${\mathbf{F}}^{+}\left(D\right)\subseteq {\mathbf{F}}^{+}\left(C\right)$;

(2) 

$X\subseteq {\mathbf{F}}^{+}{\mathbf{F}}^{-}\left(X\right)$; $C\subseteq {\mathbf{F}}^{-}{\mathbf{F}}^{+}\left(C\right)$;

(3) 

${\mathbf{F}}^{-}(X\cup Y)={\mathbf{F}}^{-}\left(X\right)\cap {\mathbf{F}}^{-}\left(Y\right)$, ${\mathbf{F}}^{+}(C\cup D)={\mathbf{F}}^{+}\left(C\right)\cap {\mathbf{F}}^{+}\left(D\right)$;

(4) 

${\mathbf{F}}^{-}\left(X\right)={\mathbf{F}}^{-}{\mathbf{F}}^{+}{\mathbf{F}}^{-}\left(X\right)$, ${\mathbf{F}}^{+}\left(C\right)={\mathbf{F}}^{+}{\mathbf{F}}^{-}{\mathbf{F}}^{+}\left(C\right);$

(5) 

${\mathbf{F}}^{-}\left(X\right)\cup {\mathbf{F}}^{-}\left(Y\right)\subseteq {\mathbf{F}}^{-}(X\cap Y)$, ${\mathbf{F}}^{+}\left(C\right)\cup {\mathbf{F}}^{+}\left(D\right)\subseteq {\mathbf{F}}^{+}(C\cap D)$.

In a soft context $(U,A,F)$, the associated operation $\mathsf{\Psi }$ [17] was induced by ${\mathbf{F}}^{+},{\mathbf{F}}^{+}$ as follows: For each $X\in P\left(U\right)$,

$$\mathsf{\Psi }:P\left(U\right)\to P\left(U\right) \mathrm{is} \mathrm{a} \mathrm{mapping} \mathrm{defined} \mathrm{as} \mathsf{\Psi }\left(X\right)={\mathbf{F}}^{+}{\mathbf{F}}^{-}\left(X\right):$$

Then, X is called a soft concept in $(U,A,F)$ if $\mathsf{\Psi }\left(X\right)={\mathbf{F}}^{+}{\mathbf{F}}^{-}\left(X\right)=X$.

The set of all soft concepts is denoted by $sC(U,A,F)$. The important properties of soft concepts are obtained as follows:

Theorem 2

([17]). Let $(U,A,F)$ be a soft context. Then

(1) 

∅, U, $\mathsf{\Psi }\left(X\right)$ are soft concepts.

(2) 

For each $B\subseteq A$, ${\mathbf{F}}^{+}\left(B\right)$ is a soft concept.

(3) 

For each $a\in A$, $F\left(a\right)$ is a soft concept.

(4) 

X is a soft concept if and only if $X={\mathbf{F}}^{+}\left(B\right)$ for some $B\in P\left(A\right)$.

(5) 

$\mathbf{Im}\left({\mathbf{F}}^{+}\right)=sC(U,A,F)$.

In a soft context $(U,A,F)$, for $D\subseteq A$, consider a set-valued mapping ${F|}_D:D\to P\left(U\right)$ defined by ${F|}_D\left(d\right)=F\left(d\right)$ for all $d\in D$. Then, obviously, $(F{|}_D,D)$ is a soft set. Since $(F{|}_D,D)$ is a soft set, $(U,D,F{|}_D)$ is also a soft context. From now on, we consider only a subset $D\subseteq A$ satisfying the soft set $(F{|}_D,D)$ which is pure.

Then, naturally, the associated operation ${\mathsf{\Psi }|}_D$, associated mappings ${\mathbf{F}|}_{\mathbf{D}}^{+}$ and $\mathbf{F}|{\mathbf{D}}^{-}$ are induced by the soft set $\left(F\right|D,D)$ as follows:

• ${\mathbf{F}|}_{\mathbf{D}}^{+}:P\left(D\right)\to P\left(U\right) \mathrm{is} \mathrm{defined} \mathrm{by} {\mathbf{F}|}_{\mathbf{D}}^{+}\left(B\right)={\cap }_{b\in B}F\left(b\right)$ for each $B\in P\left(D\right)$.
• ${\mathbf{F}|}_{\mathbf{D}}^{-}:P\left(U\right)\to P\left(D\right) \mathrm{is} \mathrm{defined} \mathrm{by} {\mathbf{F}|}_{\mathbf{D}}^{-}\left(X\right)=\{a\in D:X\subseteq F\left(a\right)\}$ for each $X\in P\left(U\right)$.
• ${\mathsf{\Psi }|}_D:P\left(U\right)\to P\left(U\right) \mathrm{defined} \mathrm{as} \mathrm{for} \mathrm{each} X\in P\left(U\right),$

  $${\mathsf{\Psi }|}_D\left(X\right)={\mathbf{F}|}_{\mathbf{D}}^{+}{\mathbf{F}|}_{\mathbf{D}}^{-}\left(X\right).$$

Then, obviously, the following were shown in [17]:

Lemma 1.

([17]) Let $(U,A,F)$ be a soft context, $D\subseteq A$ and $X\subseteq U$. Then

(1) 

${\mathbf{F}|}_{\mathbf{D}}^{-}\left(X\right)\subseteq {\mathbf{F}}^{-}\left(X\right)$.

(2) 

${\mathbf{F}|}_{\mathbf{D}}^{-}\left(X\right)={\mathbf{F}}^{-}\left(X\right)\cap D$.

(3) 

$sC(U,D,F{|}_D)\subseteq sC(U,A,F)$.

Now, for $X\in sC(U,A,F)$,

(1)

X is said to be dependent [17] on $sC(U,A,F)$ if there exist $X_1,\cdots ,X_n\in sC(U,A,F)$ satisfying $X⊊X_i$ and $X=\cap X_i$, $i=1,\cdots ,n$ ($n\geqq 2$).

(2)

X is said to be independent of $sC(U,A,F)$ if X is not dependent.

We will denote:

• $sD=\{X\in sC(U,A,F)\mid X \mathrm{is} \mathrm{dependent} \mathrm{on} sC(U,A,F\left)\right\};$
• $sI=\{X\in sC(U,A,F)\mid X \mathrm{is} \mathrm{independent} \mathrm{of} sC(U,A,F\left)\right\}.$

The basic properties of such notions are as follows:

Theorem 3

([17]). Let $(U,A,F)$ be a soft context.

(1) 

Both ∅ and U are dependent.

(2) 

$sD\cap sI=\mathsf{\varnothing }$; $sD\cup sI=sC(U,A,F)$.

(3) 

For a non-empty set $X\in sD$, there exists $B\in P\left(A\right)$ such that ${\mathbf{F}}^{+}\left(B\right)=X⊊F\left(b\right)$ for $b\in B$.

(4) 

For $X\in sI$, there exists $b\in A$ satisfying $F\left(b\right)=X$.

3. Consistent Sets of Soft Contexts

We introduce the notion of consistent set on a given soft context, and investigate the characterizations of consistent sets. In general, in a formal context $(U,A,I)$, for $x\in U$, if $x^{*}=\mathsf{\varnothing }$ or $x^{*}=A$, then x could be omitted from $x\in U$, and the structure of concept lattice and reduction are not affected. Dually, for $a\in A$, if $a^{*}=\mathsf{\varnothing }$ or $a^{*}=U$, then a could be omitted from $a\in A$, and the structure of concept lattice and reduction is not affected.

Based on this fact, from now on, we assume that every soft set $(F,A)$ is pure [18], which is defined as: ${\cap }_{a\in A}F\left(a\right)=\mathsf{\varnothing }$, ${\cup }_{a\in A^{\prime }}F\left(a\right)=U^{\prime }$, $F\left(a\right)\ne U$ and $F\left(a\right)\ne \mathsf{\varnothing }$ for every $a\in A$.

Definition 1.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, C is called a consistent set of $(U,A,F)$ if $sC(U,A,F)=sC(U,C,F{|}_C)$.

We recall the notion of base for $sC(U,A,F)$ in a soft context $(U,A,F)$ defined in [17]: Let $(U,A,F)$ be a soft context. A subfamily $\mathcal{S}$ of $sC(U,A,F)$ is called a base for $sC(U,A,F)$ if it satisfies the following conditions:

(1)

$\mathcal{S}\subseteq sC(U,A,F)$;

(2)

For each $X\in sC(U,A,F)$, there exists ${\mathcal{S}}^{\prime }\subseteq \mathcal{S}$ such that $X=\cap {\mathcal{S}}^{\prime }$.

Theorem 4

([17]). For a soft context $(U,A,F)$, the family ${\mathcal{F}}_A=\{F\left(a\right)\mid a\in A\}$ is a base for $sC(U,A,F)$.

Example 1.

Let $U=\{1,2,3,4\}$ and $A=\{a,b,c,d,e,f\}$. Let us consider a soft context $(U,A,F)$ induced by a soft set $(F,A)$ where the set-valued mapping $F:A\to P\left(U\right)$ is defined by

$$F\left(a\right)=F\left(b\right)=\{1,2,4\};F\left(c\right)=\{2,3,4\};$$

$$F\left(d\right)=F\left(f\right)=F\left(g\right)=\{1,3\};F\left(e\right)=\{2,4\}.$$

Then, by Theorem 4,

$$sC(U,A,F)=\{\mathsf{\varnothing },\{1\},\{3\},\{1,3\},\{2,4\},\{1,2,4\},\{2,3,4\},U\}.$$

For $C=\{b,c,d,f\}\subseteq A$, ${F|}_C:C\to P\left(U\right)$ is a set-valued function defined as follows:

$$F\left(b\right)=\{1,2,4\};F\left(c\right)=\{2,3,4\};F\left(d\right)=F\left(f\right)=\{1,3\}.$$

Then $(F{|}_C,C)$ is a soft set and $(U,C,F{|}_C)$ is a soft context. Furthermore, by Theorem 4,

$$sC(U,C,F{|}_C)=\{\mathsf{\varnothing },\left\{1\right\},\left\{3\right\},\{1,3\},\{2,4\},\{1,2,4\},\{2,3,4\},U\}.$$

So, $sC(U,C,F{|}_C)=sC(U,A,F)$, and C is a consistent set of $(U,A,F)$.

Theorem 5.

Let $(U,A,F)$ be a soft context, $C\subseteq A$ and $C\ne \mathsf{\varnothing }$. Then, C is a consistent set of $(U,A,F)$ if and only if $\mathbf{Im}\left(\mathbf{F}{|}_{\mathbf{C}}^{+}\right)=\mathbf{Im}\left({\mathbf{F}}^{+}\right).$

Proof. 

Since $(U,A,F)$ and $(U,C,F{|}_C)$ are soft contexts over U, from (5) of Theorem 2, it is obviously obtained. □

Theorem 6.

Let $(U,A,F)$ be a soft context, $C\subseteq A$ and $C\ne \mathsf{\varnothing }$. Then, C is a consistent set of $(U,A,F)$ if and only if (1) $sD=s{D}_C$ and (2) $sI=s{I}_C$.

Proof. 

Let C be a consistent set of $(U,A,F)$. Then, by Theorem 3, $sI\cup sD=sC(U,A,F)=sC(U,C,F{|}_C)=s{I}_C\cup s{D}_C$ and in general, $s{D}_C\subseteq sD$, $s{I}_C\subseteq sI$, $s{D}_C\cap s{I}_C=\mathsf{\varnothing }$ and $sD\cap sI=\mathsf{\varnothing }$. So, $sD=s{D}_C$ and $sI=s{I}_C$.

The converse is obviously obtained. □

Theorem 7.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, the following are equivalent:

(1) 

C is a consistent set of $(U,A,F)$.

(2) 

$\mathcal{C}=\left\{F\right(d)\mid d\in C\}$ is a base of $sC(U,A,F)$.

Proof. 

(1) ⇒ (2) Let C be a consistent set of $(U,A,F)$. Then, $sC(U,A,F)=sC(U,C,F{|}_C)$ and by Theorem 4, $\mathcal{C}$ is a base of $sC(U,C,F{|}_C)$. So, $\mathcal{C}$ is also a base of $sC(U,A,F)$.

(2) ⇒ (1) For $C\subseteq A$, it is obviously $sC(U,C,F{|}_C)\subseteq sC(U,A,F)$. Now, for the proof of the inclusion relation $sC(U,A,F)\subseteq sC(U,C,F{|}_C)$, let $X\in sC(U,A,F)$. Then, by hypothesis, there exists $\mathcal{S}\subseteq \mathcal{C}$ such that $X=\cap \mathcal{S}$. Since $X=\cap \mathcal{S}=\cap \{F\left(d\right)\mid F\left(d\right)\in \mathcal{S}\subseteq \mathcal{C}\}={\mathbf{F}|}_{\mathbf{C}}^{+}\left(\{d\mid F\left(d\right)\in \mathcal{S}\}\right)\in \mathbf{Im}\left(\mathbf{F}{|}_{\mathbf{C}}^{+}\right)=sC(U,C,F{|}_C)$, $X\in sC(U,C,F{|}_C)$. Consequently, $sC(U,A,F)=sC(U,C,F{|}_C)$ and so, C is a consistent set of $(U,A,F)$. □

Corollary 1.

Let $(U,A,F)$ be a soft context. Then, A is the greatest consistent set of $(U,A,F)$.

Theorem 8 (Fundamental Theorem I of consistent sets).

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, C is a consistent set of $(U,A,F)$ if and only if for each $e\in A-C$, there exists a nonempty subset B of C such that ${\mathbf{F}}^{+}\left(B\right)={\cap }_{b\in B}F\left(b\right)=F\left(e\right)$.

Proof. 

Suppose that C is a consistent set of $(U,A,F)$. For the proof, let $e\in A-C$. Then, by (3) of Theorem 2, $F\left(e\right)\in sC(U,A,F)$. Since $\mathcal{C}=\left\{F\right(a)\mid a\in C\}$ is a base for $sC(U,A,F)$, there exists $\mathcal{S}\subseteq \mathcal{C}$ such that $F\left(e\right)=\cap \mathcal{S}$. Set $B=\{b\mid F(b)\in \mathcal{S}\subseteq \mathcal{C}\}$. Then, $B\subseteq C$ and ${\mathbf{F}}^{+}\left(B\right)=\cap \mathcal{B}={\cap }_{b\in B}F\left(b\right)=\cap \mathcal{S}=F\left(e\right)$. So, the condition is satisfied.

Conversely, suppose that for each $e\in A-C$, there exists $B\subseteq C$ such that ${\mathbf{F}}^{+}\left(B\right)=F\left(e\right)$. Now, we show that $\mathcal{C}=\left\{F\right(d)\mid d\in C\}$ is a base for $sC(U,A,F)$. It is sufficient to show that for each $X\in sC(U,A,F)$, there exists $\mathcal{S}\subseteq \mathcal{C}$ such that $X=\cap \mathcal{S}$. For the proof, let $X\in sC(U,A,F)$. First, since ${\mathcal{F}}_A=\{F\left(a\right)\mid a\in A\}$ is a base for $sC(U,A,F)$, we can take $\mathcal{E}\subseteq {\mathcal{F}}_A$ such that $X=\cap \mathcal{E}$. From $\mathcal{E}\subseteq {\mathcal{F}}_A$, it follows that there exists $E\subseteq A$ such that $\mathcal{E}=\left\{F\right(e)\mid e\in E\}$. Now, put $E_1=E\cap (A-C),E_2=E\cap C$, ${\mathcal{E}}_1=\{F\left(e\right)\mid e\in E_1\}$ and ${\mathcal{E}}_2=\{F\left(e\right)\mid e\in E_2\}$. Then, $E=E_1\cup E_2$, $\mathcal{E}={\mathcal{E}}_1\cup {\mathcal{E}}_2$ and $E_2\subseteq C$. For each $e\in E_1\subseteq A-C$, by hypothesis, there exists $B_e\subseteq C$ such that $F\left(e\right)={\mathbf{F}}^{+}\left(B_e\right)$. From Theorem 1, it follows that $X=\cap \mathcal{E}=(\cap {\mathcal{E}}_1)\cap (\cap {\mathcal{E}}_2)={\mathbf{F}}^{+}\left(E_1\right)\cap {\mathbf{F}}^{+}\left(E_2\right)=\left({\cap }_{e\in E_1}F\left(e\right)\right)\cap {\mathbf{F}}^{+}\left(E_2\right)=\left({\cap }_{e\in E_1}{\mathbf{F}}^{+}\left(B_e\right)\right)\cap {\mathbf{F}}^{+}\left(E_2\right)={\mathbf{F}}^{+}\left({\cup }_{e\in E_1}{B}_e\right)\cap {\mathbf{F}}^{+}\left(E_2\right)={\mathbf{F}}^{+}(\left({\cup }_{e\in E_1}{B}_e\right)\cup E_2)$. Consequently, put $\mathcal{S}=\{F\left(e\right)\mid e\in \left({\cup }_{e\in E_1}{B}_e\right)\cup E_2\}$; then, from ${\cup }_{e\in E_1}{B}_e\cup E_2\subseteq C$, it follows that $\mathcal{S}\subseteq \mathcal{C}$ and $X={\mathbf{F}}^{+}(\left({\cup }_{e\in E_1}{B}_e\right)\cup E_2)=\cap \mathcal{S}$. So, the proof is completed. □

Corollary 2.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, C is a consistent set of $(U,A,F)$ if and only if for every nonempty subset B of $A-C$, there exists a nonempty subset E of C such that ${\mathbf{F}}^{+}\left(E\right)={\mathbf{F}}^{+}\left(B\right)$.

Proof. 

Suppose that C is a consistent set. Let $B\subseteq A-C$. Then, for each $b\in B$, there exists $E_b\subseteq C$ such that $F\left(b\right)={\mathbf{F}}^{+}\left(E_b\right)$. So, ${\mathbf{F}}^{+}\left(B\right)={\mathbf{F}}^{+}\left({\cup }_{b\in B}\left\{b\right\}\right)={\cap }_{b\in B}{\mathbf{F}}^{+}\left(E_b\right)={\mathbf{F}}^{+}\left({\cup }_{b\in B}{E}_b\right)$ and ${\cup }_{b\in B}{E}_b\subseteq C$. So, the statement is obtained.

The converse is obvious. □

Theorem 9

([17]). Let $(U,A,F)$ be a soft context. For $D\subseteq A$, if a mapping $\phi :D\to sI$ defined by $\phi \left(d\right)=F\left(d\right)$ for $d\in D$ is surjective, then ${\mathcal{F}}_D=\{F\left(d\right)\mid d\in D\}$ is a base for $sC(U,A,F)$.

By the above theorem, we obtain the following useful theorem in finding consistent sets:

Theorem 10.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. If there exists a surjective mapping $\phi :C\to sI$, then C is a consistent set.

Remark 1.

In the above theorem, the converse is not always true as shown in the next example.

Example 2.

In Example 1, $s_I=\{\{1,3\},\{1,2,4\},\{2,3,4\}\}$. Consider a consistent set $C_1=\{b,c,d,e\}$. Then, since

$${\mathcal{F}}_{C_1}=\{F\left(d\right)\mid d\in C_1\}=\{\{2,4\},\{1,3\},\{1,2,4\},\{2,3,4\}\},$$

it is impossible that there is any surjective mapping $\phi :C_1\to s_I$ defined as follows $\phi \left(d\right)=F\left(d\right)$ for $d\in C_1$. So, in Theorem 10, the converse is not true.

Let $(U,A,F)$ be a soft context and $G_a=\{g\in A\mid F\left(a\right)⊊F\left(g\right)\}$.

For $d\in A$, d is said to be dependent on A if there exists $G_d\ne \mathsf{\varnothing }$ satisfying $F\left(d\right)={\mathbf{F}}^{+}\left(G_d\right)={\cap }_{g\in G_d}F\left(g\right)$: Otherwise, d is said to be independent on A.

We denote:

• $A_D=\{a\in A\mid a \mathrm{is} \mathrm{dependent} \mathrm{on} A\};$$A_I=\{a\in A\mid a \mathrm{is} \mathrm{independent} \mathrm{on} A\}.$

Example 3.

In Example 1, $G_a=G_b=G_c=\left\{e\right\}$, $G_d=G_f=G_g=\mathsf{\varnothing }$ and $G_e=\{a,b,c\}$. For $e\in A$, $F\left(e\right)=F\left(a\right)\cap F\left(b\right)\cap F\left(c\right)={\mathbf{F}}^{+}\left(G_e\right)$ and so, e is dependent. From $G_d=G_f=G_g=\mathsf{\varnothing }$, $d,f$ and g are obviously independent on A. a is also independent on A, since $G_a\ne \mathsf{\varnothing }$ but ${\mathbf{F}}^{+}\left(G_a\right)=F\left(e\right)\ne F\left(a\right)$. For the same reason, b and c are independent on A.

$$A_I=\{a,b,c,d,f,g\}; A_D=\left\{e\right\}.$$

Obviously, the following are obtained:

Lemma 2.

Let $(U,A,F)$ be a soft context. Then

(1) 

$A_I\cup A_D=A$ and $A_I\cap A_D=\mathsf{\varnothing }$;

(2) 

if a is dependent, then there exists $B\subseteq A$ such that ${\mathbf{F}}^{+}\left(B\right)={\cap }_{b\in B}F\left(b\right)=F\left(a\right)$ where $F\left(a\right)⊊F\left(b\right)$.

Theorem 11.

Let $(U,A,F)$ be a soft context. Then, $A_I\subseteq A$ is a consistent set of $(U,A,F)$.

Proof. 

First, we show that the mapping $\phi :A_I\to sI$ defined by $\phi \left(a\right)=F\left(a\right)$ for $a\in A_I$ is well-defined and surjective. For each $a\in A_I$, suppose that $F\left(a\right)\notin sI$ for $a\in A$. Then, $F\left(a\right)\in sD$, by (3) of Theorem 3, there exists $B\in P\left(A\right)$ such that $\left|B\right|\geqq 2$ and ${\mathbf{F}}^{+}\left(B\right)=F\left(a\right)⊊F\left(b\right)$. Then, $B\subseteq G_a=\{g\in A:F\left(a\right)⊊F\left(g\right)\}\ne \mathsf{\varnothing }$ and $F\left(a\right)\subseteq {\mathbf{F}}^{+}\left(G_a\right)\subseteq {\mathbf{F}}^{+}\left(B\right)=F\left(a\right)$. Thus, $G_a\ne \mathsf{\varnothing }$ and ${\mathbf{F}}^{+}\left(G_a\right)=F\left(a\right)$. This implies that $a\in A_D$, and it is a contradiction. So, the mapping $\phi :A_I\to sI$ is well defined.

For each $X\in sI$, by (4) of Theorem 3, there exists an element $a\in A$ such that $F\left(a\right)=X$. If $a\notin A_I$, then by Lemma 2, $a\in A_D$ and there exists $B\subseteq A$ such that ${\mathbf{F}}^{+}\left(B\right)={\cap }_{b\in B}F\left(b\right)=F\left(a\right)=X$ where $X=F\left(a\right)⊊F\left(b\right)$. Then, $X\in sD$, which contradicts $X\in sI$. From this fact, we can say that $a\in A_I$, and so $\phi$ is surjective.

Finally, by Theorem 10, $A_I$ is a consistent set of $(U,A,F)$. □

Definition 2.

For a soft context $(U,A,F)$, put $n\left(a\right)=\left|\right\{b\in A_I\mid F\left(a\right)=F\left(b\right)\left\}\right|$. Then,

$$1^{\circ }\left(A\right)=\{a\in A_I\mid n\left(a\right)=1\}; 2^{\circ }\left(A\right)=\{a\in A_I\mid n\left(a\right)>1\}.$$

Example 4.

In Example 3, for a soft context $(U,A,F)$ where $U=\{1,2,3,4\}$ and $A=\{a,b,c,d,e,f,g\}$, we showed that $A_I=\{a,b,c,d,f,g\}$ and $A_D=\left\{e\right\}.$

For $A_I=\{a,b,c,d,f,g\}$,

$F\left(a\right)=F\left(b\right)=\{1,2,4\}; F\left(c\right)=\{2,3,4\}; F\left(d\right)=F\left(f\right)=F\left(g\right)=\{1,3\}$;

and

from $\{x\in A_I\mid F\left(c\right)=F\left(x\right)\}=\left\{c\right\}$, $n\left(c\right)=1$;

from $F\left(a\right)=F\left(b\right)$, $n\left(a\right)=n\left(b\right)=2$;

from $F\left(d\right)=F\left(f\right)=F\left(g\right)$, $n\left(d\right)=n\left(f\right)=n\left(g\right)=3$.

Consequently, $1^{\circ }\left(A\right)=\left\{c\right\}; 2^{\circ }\left(A\right)=\{a,b,d,f,g\}.$

The following is directly obtained:

Lemma 3.

For a soft context $(U,A,F)$,

(1) 

$A_I=1^{\circ }\left(A\right)\cup 2^{\circ }\left(A\right)$;

(2) 

$a\in 1^{\circ }\left(A\right)$ if and only if $a\in A$ and $F\left(a\right)\ne F\left(e\right)$ for every $e\in A-\left\{a\right\}$.

Theorem 12.

Let $(U,A,F)$ be a soft context and $2^{\circ }\left(A\right)\ne \mathsf{\varnothing }$. Then, for $x\in 2^{\circ }\left(A\right)$, $A_I-\left\{x\right\}$ is a consistent set of $(U,A,F)$.

Proof. 

We showed that there exists a surjective mapping $\phi :A_I\to s_I$ defined by $\phi \left(a\right)=F\left(a\right)$ in the proof of Theorem 11. Now, for $x\in 2^{\circ }\left(A\right)$, let $\phi \left(x\right)=X\in sI$ and consider the inclusion map $i:A_I-\left\{x\right\}\to A_I$. Since $x\in 2^{\circ }\left(A\right)$, there is at least one element $z\in A_I$ such that $z\ne x$ and $F\left(z\right)=F\left(x\right)=X$. This implies that the composition map $\phi \circ i:A_I-\left\{x\right\}\to s_I$ is surjective, and by Theorem 10, $A_I-\left\{x\right\}$ is a consistent set of $(U,A,F)$. □

Theorem 13.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Let C be a consistent set of $(U,A,F)$. Then, for $e\in C$, $e\in 1^{\circ }\left(C\right)$ if and only if $C-\left\{e\right\}$ is not a consistent set of $(U,A,F)$.

Proof. 

Let $e\in 1^{\circ }\left(C\right)$ and suppose that $C-\left\{e\right\}$ is a consistent set of $(U,A,F)$. Then, $\mathcal{S}=\left\{F\right(d)\mid d\in C-\{e\left\}\right\}$ is a base for $sC(U,A,F)$. From this fact, for $F\left(e\right)\in sC(U,A,F)$, there exists a nonempty subset $D\subseteq C-\left\{e\right\}$ such that ${\mathbf{F}}^{+}\left(D\right)={\cap }_{d\in D}F\left(d\right)=F\left(e\right)$. This contradicts $e\in 1^{\circ }\left(C\right)$. So, $C-\left\{e\right\}$ is not a consistent set of $(U,A,F)$.

Conversely, for $e\in C$, assume that $e\notin 1^{\circ }\left(C\right)$. Then, from $C=C_I\cup C_D=1^{\circ }\left(C\right)\cup 2^{\circ }\left(C\right)\cup C_D$, $e\in 2^{\circ }\left(C\right)\cup C_D$. In case: $e\in 2^{\circ }\left(C\right)$. By Theorem 12, $C_I-\left\{e\right\}$ is a consistent set of $(U,C,F{|}_C)$, and since $C_I-\left\{e\right\}\subseteq C-\left\{e\right\}$, $C-\left\{e\right\}$ is a consistent set of $(U,C,F{|}_C)$. By hypothesis, since C is a consistent set of $(U,A,F)$, $C-\left\{e\right\}$ is also a consistent set of $(U,A,F)$.

In case: $e\in C_D$. Since $C_I$ is also a consistent set of $(U,A,F)$ and $C_I\subseteq C-\left\{e\right\}$, $C-\left\{e\right\}$ is a consistent set of $(U,A,F)$. □

Theorem 14.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. If C is a consistent set of $(U,A,F)$ and $2^{\circ }\left(A\right)\ne \mathsf{\varnothing }$, then (1) $1^{\circ }\left(A\right)\subseteq 1^{\circ }\left(C\right)$: (2) $2^{\circ }\left(A\right)\cap C\ne \mathsf{\varnothing }$.

Proof. 

(1) It is sufficient to show that $1^{\circ }\left(A\right)\subseteq 1^{\circ }\left(C\right)$. Suppose that for $x\in 1^{\circ }\left(A\right)$, $x\notin 1^{\circ }\left(C\right)$. Since $C=1^{\circ }\left(C\right)\cup 2^{\circ }\left(C\right)\cup C_D$, $x\in 2^{\circ }\left(C\right)\cup C_D\subseteq 2^{\circ }\left(A\right)\cup A_D$. So, $x\notin 1^{\circ }\left(A\right)$, which contradicts the assumption $x\in 1^{\circ }\left(A\right)$. Consequently, $1^{\circ }\left(A\right)\subseteq 1^{\circ }\left(C\right)$.

(2) Suppose that $2^{\circ }\left(A\right)\cap C=\mathsf{\varnothing }$. Then, for $x\in 2^{\circ }\left(A\right)$, since $x\in A_I$, there is no subset B of C such that ${\mathbf{F}}^{+}\left(B\right)=F\left(x\right)$ where $F\left(x\right)⊊F\left(b\right)$ for $b\in B$. So, $\mathcal{C}=\left\{F\right(c)\mid c\in C\}$ is not a base for $sC(U,A,F)$, that is, C is a consistent set of $(U,A,F)$. So, the proof is completed. □

The converse of Theorem 14 is not always true as shown in the next example:

Example 5.

Let $U=\{1,2,3,4\}$ and $A=\{a,b,c,d,e,f,g\}$. As in Example 1, consider a soft context $(U,A,F)$ and the set-valued mapping $F:A\to P\left(U\right)$ defined by

$$F\left(a\right)=F\left(b\right)=\{1,2,4\};F\left(c\right)=\{2,3,4\};F\left(d\right)=F\left(f\right)=F\left(g\right)=\{1,3\};F\left(e\right)=\{2,4\}.$$

Then, we showed $A_I=\{a,b,c,d,f,g\}$ in Example 3. For $A_I$, in Example 4, we found that $1^0\left(A\right)=\left\{c\right\}$ and $2^0\left(A\right)=\{a,b,d,f,g\}$.

Take $C=\{a,b,c,e\}\subseteq A$. Then, it is easily obtained:

$$C_I=\{a,b,c\}; C_D=\left\{e\right\}; 1^0\left(C\right)=\left\{c\right\}; 2^0\left(C\right)=\{a,b\}.$$

Clearly, $1^0\left(A\right)\subseteq 1^0\left(C\right)$ and $2^0\left(A\right)\cap C\ne \mathsf{\varnothing }$. However, for $d\in A-C$, there is no $B\subseteq C$ such that ${\mathbf{F}}^{+}\left(B\right)=F\left(d\right)$. So, by Theorem 8, C is not a consistent set of $(U,A,F)$.

Remark 2 (Essential Zone of consistent sets).

For a soft context $(U,A,F)$, from Theorems 13 and 14, we found that every consistent set has to contain the set $1^{\circ }\left(A\right)$. This result is very important information that we should consider when constructing a consistent set of a soft context $(U,A,F)$. Based on this fact, the following fundamental theorem of consistent sets is obtained.

Theorem 15 (Fundamental Theorem II of consistent sets).

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, C is a consistent set of $(U,A,F)$ if and only if C satisfies that

(1) 

$1^{\circ }\left(A\right)\subseteq C$:

(2) 

For each $a\in 2^{\circ }\left(A\right)$, $\{b\in A_I\mid F\left(b\right)=F\left(a\right)\}\cap C\ne \mathsf{\varnothing }$.

Proof. 

Let C be a consistent set of $(U,A,F)$. Then, obviously, (1) is satisfied by Theorem 14. For the proof of (2), suppose that there is some $a\in 2^{\circ }\left(A\right)$ such that $\{b\in A_I\mid F\left(b\right)=F\left(a\right)\}\cap C=\mathsf{\varnothing }$. For $a\in 2^{\circ }\left(A\right)$, let $F\left(a\right)=X$. Then, we know that $X\in sC(U,A,F)$ and $a\in A_I$. Now, for $a\in A_I$, there is no $G_a=\{g\in A\mid F\left(a\right)⊊F\left(g\right)\}$ such that ${\cap }_{g\in G_a}F\left(g\right)=F\left(a\right)=X$. This means that there is no $C_a\subseteq C\subseteq A$ such that ${\cap }_{c\in C_a}F\left(c\right)=X$. So, $\mathcal{C}=\left\{F\right(c)\mid c\in C\}$ is not a base for $sC(U,A,F)$, C is not a consistent set.

For the converse, assume that the two conditions (1) and (2) are satisfied. Put $B_a=\{b\in A_I\mid F\left(b\right)=F\left(a\right)\}$ for $a\in 2^{\circ }\left(A\right)$. Then, for each $a\in 2^{\circ }\left(A\right)$, since $B_a\cap C\ne \mathsf{\varnothing }$, $C_0=\cup (B_a\cap C)$ is a nonempty subset of C, and so $1^{\circ }\left(A\right)\cup C_0\subseteq C$. Now, we show that the mapping $\phi :1^{\circ }\left(A\right)\cup C_0\to sI$ defined by $\phi \left(d\right)=F\left(d\right)$ for $d\in 1^{\circ }\left(A\right)\cup C_0$ is surjective. For the proof of surjection, let $X\in sI$. Then, by Theorem 11, there is an element $e\in A_I$ such that $F\left(e\right)=X$. From $A_I=1^{\circ }\left(A\right)\cup 2^{\circ }\left(A\right)$, in case $e\in 1^{\circ }\left(A\right)$, it is obviously $e\in 1^{\circ }\left(A\right)\cup C_0$. In case $e\in 2^{\circ }\left(A\right)$, by the condition (2), there exists some $c\in C_0$ such that $F\left(c\right)=F\left(e\right)$. So, in any case, for $X\in sI$, there exists $c\in 1^{\circ }\left(A\right)\cup C_0$ satisfying $\phi \left(c\right)=X$. Consequently, $\phi$ is surjective and so $\mathcal{S}=\{F\left(c\right)\mid c\in 1^{\circ }\left(A\right)\cup C_0\subseteq C$ is a base for $sC(U,A,F)$, and so, $\mathcal{C}$ is also a base for $sC(U,A,F)$. Hence, C is a consistent set of $(U,A,F)$. □

Corollary 3.

Let $(U,A,F)$ be a soft context and $C\subseteq A$. Then, for each $e\in A-C$, there exists a nonempty subset B of C such that ${\mathbf{F}}^{+}\left(B\right)=F\left(e\right)$ if and only if C satisfies that

(1) 

$1^{\circ }\left(A\right)\subseteq C$;

(2) 

For each $a\in 2^{\circ }\left(A\right)$, $\{b\in A_I\mid F\left(b\right)=F\left(a\right)\}\cap C\ne \mathsf{\varnothing }$.

Proof. 

It follows from Theorems 8 and 15. □

Let $(U,A,F)$ be a soft context. In [17], we defined an order between $X_1,X_2\in sC(U,A,F)$ as follows: For $X_1,X_2\in sC(U,A,F)$,

$$X_1\precsim X_2 \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} X_1\subseteq X_2.$$

Then the infimum ⋏ and supremum ⋎ in the ordered set $\left(sC\right(U,A,F),⪯)$, are defined as follows:

$$X_1⋏X_2=X_1\cap X_2;\hspace{1em}{X}_1⋎X_2=\mathsf{\Psi }(X_1\cup X_2)=F^{+}{F}^{-}(X_1\cup X_2).$$

Then, we showed that $\left(sC\right(U,A,F),⪯,⋏,⋎)$ is a complete lattice. The complete lattice $\left(sC\right(U,A,F),\precsim ,⋏,⋎)$ is called the soft concept lattice and simply, denoted by $sL(U,A,F)$.

Let $sL(U,A_1,F_1)$ and $sL(U,A_2,F_2)$ be two soft concept lattices. $sL(U,A_1,F_1)$ is said to be finer than $sL(U,A_2,F_2)$, which is denoted by the following:

$$sL(U,A_1,F_1)\le sL(U,A_2,F_2)\iff sC(U,A_2,F_2)\subseteq sC(U,A_1,F_1)$$

If $sL(U,A_1,F_1)\le sL(U,A_2,F_2)$ and $sL(U,A_2,F_2)\le sL(U,A_1,F_1)$, then these two soft concept lattices are said to be isomorphic to each other, and denoted as follows

$$sL(U,A_1,F_1)\cong sL(U,A_2,F_2).$$

Theorem 16

([17]). Let $(U,A,F)$ be a soft context. Then, $sL(U,A_1,F_1)\cong sL(U,A_2,F_2)$ if and only if $\mathbf{Im}\left({\mathbf{F}}_{\mathbf{1}}^{+}\right)=\mathbf{Im}\left({\mathbf{F}}_{\mathbf{2}}^{+}\right)$.

Theorem 17.

Let $(U,A,F)$ be a soft context. If C is a consistent set of $(U,A,F)$, then $sL(U,A,F)\cong sL(U,C,F{|}_C)$.

Proof. 

For a consistent set $C\subseteq A$, by Theorem 5, $sC(U,A,F)=sC(U,C,F{|}_C)$ if and only if $\mathbf{Im}\left({\mathbf{F}}^{+}\right)=\mathbf{Im}\left(\mathbf{F}{|}_{\mathbf{C}}^{+}\right)$. So, $sL(U,A,F)\cong sL(U,C,F{|}_C)$. □

For a formal context $(U,A,I)$, let us define a soft set $F_I:A\to P\left(U\right)$ as follows $F_I\left(a\right)=\{x\in U:(x,a)\in I\}$. Then, $(U,A,F_I)$ is a soft context. Therefore, every formal context $(U,A,I)$ induces a soft context $(U,A,F_I)$. We call $(U,A,F_I)$ the associated soft context [17] induced by a formal context $(U,A,I)$. Furthermore, for $D\subseteq A$. Then, denote $I_D=I\cap (U\times D)$. Then, $(U,D,I_D)$ is a formal context and $(U,A,F_{I_D})$ is also the associated soft context induced by a formal context $(U,D,I_D)$.

Theorem 18

([17]). Let $(U,A,I)$ be a formal context. Then,

(1) 

the formal concept lattice $L(U,A,I)$ is order-isomorphic to $sL(U,A,F_I)$;

(2) 

for the formal concept lattice $L(U,A,I)$ of $(U,A,I)$,

$$L(U,A,I)=\left\{(X,{{\mathbf{F}}_I}^{-}\left(X\right))\right|X is any element of sL(U,A,F_I)\}.$$

Corollary 4.

Let $(U,A,I)$ be a formal context and $D\subseteq A$. Then,

(1) 

the formal concept lattice $L(U,D,I_D)$ is order-isomorphic to $sL(U,D,F_{I_D})$;

(2) 

$L(U,D,I_D)=\left\{(X,{{\mathbf{F}}_I}^{-}\left(X\right))\right|X is any element of sL(U,D,F_{I_D})\}.$

Proof. 

(1) For $D\subseteq A$, $(U,D,I_D)$ is a formal context and $(U,D,F_{I_D})$ is the associated soft context of $(U,D,I_D)$. By Theorem 18, the formal concept lattice $L(U,D,I_D)$ is order-isomorphic to $sL(U,D,F_{I_D})$.

(2) Since $(U,D,I_D)$ is a formal context and $L(U,D,I_D)$ is the formal concept lattice of $(U,D,I_D)$, it follows from (2) of Theorem 18. □

Let $(U,A,I)$ be a formal context. Then, D is called a consistent [7] of $(U,A,I)$ if there exists a set $D\subseteq A$ such that $L(U,D,I_D)\cong L(U,A,I)$.

Finally, we obtain the meaningful theorem for the consistent set of a given formal context:

Theorem 19.

Let $(U,A,I)$ be a formal context. Then, C is a consistent of $(U,A,I)$ if and only if C is a consistent set of the associated soft context $(U,A,F_I)$.

Proof. 

Let C be a consistent set of a formal context $(U,A,I)$. Then, by Theorem 18 and Corollary 4, $L(U,A,I)\cong L(U,C,I_C)$ if and only if $sL(U,A,F_I)\cong sL(U,C,F_{I_C})$ if and only if $sC(U,A,F_I)=sC(U,C,F_{I_C})$. Hence, C is also a consistent set of the associated soft context $(U,A,F_I)$. □

4. Application

In this section, we apply the Fundamental Theorem II of Consistent Sets (Theorem 15) to obtain a consistent set of a given formal context. We may write $xyz$ instead of a set $\{x,y,z\}$.

For $U=\{1,2,3,4,5\}$ and $A=\{a,b,c,d,e,f,g,h,i,j\}$, Table 1 shows a formal context $(U,A,I)$.

Table 1. A formal context.

-	a	b	c	d	e	f	g	h	i	j
1	1	1	0	1	1	1	0	1	0	0
2	0	1	1	0	0	0	1	0	1	1
3	1	0	0	1	1	0	0	0	0	0
4	0	1	1	0	0	0	1	0	0	1
5	1	1	0	1	0	1	0	0	0	0

From the formal context $(U,A,I)$, naturally, we can define a set-valued mapping $F_I:A\to P\left(U\right)$ as $F_I\left(a\right)=\{x\in U|xIa\}$, and from now on, the set-valued mapping $F_I$ is simply denoted by F. Then, $(F,A)$ is a soft set as follows:

$\hspace{1em}\hspace{1em}\hspace{1em}F\left(a\right)=F\left(d\right)=135; F\left(b\right)=1245; F\left(c\right)=F\left(g\right)=F\left(j\right)=24;$

$\hspace{1em}\hspace{1em}\hspace{1em}F\left(e\right)=13; F\left(f\right)=15; F\left(h\right)=1; F\left(i\right)=2.$

Therefore, we have the associated soft context $(U,A,F_I)$ (simply, $(U,A,F)$) induced by a formal context $(U,A,I)$. Then, by Theorem 4 and ${\mathcal{F}}_A=\left\{F\left(a\right)\right|a\in A\}$, we can find the family $sC(U,A,F)$ of all soft concepts as:

$$sC(U,A,F)=\{\cap \mathcal{S}|\mathcal{S}\subseteq {\mathcal{F}}_A\}=\{\mathsf{\varnothing },1,2,13,15,24,135,1245,U\}.$$

Consequently, by Theorem 18 and $sL(U,A,F)=\left(sC\right(U,A,F),⪯,⋏,⋎)$, the formal concept lattice $L(U,A,I)$ is easily obtained as the following diagram:

From now on, we will describe the process of obtaining a consistent set of $(U,A,I)$ by using Theorem 19.

First, we explain how to obtain a consistent set of the associated soft context $(U,A,F)$ through three steps by using Theorem 15.

Step 1: By using the soft set $(F,A)$ defined above, we obtain the independent set $A_I=\{a,b,c,d,e,g,i,j\}$ on A in the following way:

(1)

From $G_a=\{g\in A\mid F\left(a\right)⊊F\left(g\right)\}$,

$G_a=G_b=G_d=\mathsf{\varnothing }$; $G_c=G_g=G_j=\left\{b\right\}$; $G_e=\{a,d\}$;

$G_f=\{a,b,d\}$; $G_h=\{a,b,d,e,f\}$; $G_i=\{b,c,g\}$:

(2)

${\mathbf{F}}^{+}\left(G_f\right)=\cap \left\{F\left(a\right)\right|a\in G_f\}=F\left(a\right)\cap F\left(b\right)\cap F\left(d\right)=15=F\left(f\right)$;

${\mathbf{F}}^{+}\left(G_h\right)=F\left(a\right)\cap F\left(b\right)\cap F\left(d\right)\cap F\left(e\right)\cap F\left(f\right)=1=F\left(h\right)$;

${\mathbf{F}}^{+}\left(G_c\right)={\mathbf{F}}^{+}\left(G_g\right)={\mathbf{F}}^{+}\left(G_j\right)\ne F\left(c\right)(F\left(g\right),F\left(j\right))$;

${\mathbf{F}}^{+}\left(G_e\right)\ne F\left(e\right)$; ${\mathbf{F}}^{+}\left(G_i\right)\ne F\left(i\right)$.

From ${\mathbf{F}}^{+}\left(G_f\right)=F\left(f\right)$ and ${\mathbf{F}}^{+}\left(G_h\right)=F\left(h\right)$, it follows that $A_D=\{f,h\}$, and so,

$$A_I=A-A_D=\{a,b,c,d,e,g,i,j\}.$$

Step 2: We find two classes $1^{\circ }\left(A\right)=\{b,e,i\}$ and $2^{\circ }\left(A\right)=\{a,c,d,g,j\}$ of $A_I$ in the following way: For $A_I=\{a,b,c,d,e,g,i,j\}$,

$\hspace{1em}\hspace{1em}\{x\in A_I\mid F\left(a\right)=F\left(x\right)\}=\{a,d\}$; $\{x\in A_I\mid F\left(b\right)=F\left(x\right)\}=\left\{b\right\}$;

$\hspace{1em}\hspace{1em}\{x\in A_I\mid F\left(c\right)=F\left(x\right)\}=\{c,g,j\}$; $\{x\in A_I\mid F\left(e\right)=F\left(x\right)\}=\left\{e\right\}$;

$\hspace{1em}\hspace{1em}\{x\in A_I\mid F\left(i\right)=F\left(x\right)\}=\left\{i\right\}$.

So, $n\left(a\right)=n\left(d\right)=2$; $n\left(c\right)=n\left(g\right)=n\left(j\right)=3$; $n\left(b\right)=n\left(e\right)=n\left(i\right)=1$.

Hence, $1^{\circ }\left(A\right)=\{b,e,i\}; 2^{\circ }\left(A\right)=\{a,c,d,g,j\}.$

Step 3: By using Theorem 15, we construct a consistent set C of the associated soft context $(U,A,F)$ as follows:

$$C=1^{\circ }\left(A\right)\cup \{a,g\}=\{a,b,e,g,i\}.$$

So finally, we obtain a consistent set $C=\{a,b,e,g,i\}$ of the associated soft context $(U,A,F)$.

Furthermore, by Theorem 19, $C=\{a,b,e,g,i\}\subseteq A$ is also a consistent set of a formal context $(U,A,I)$ and $L(U,A,I)\cong L(U,C,I_C)$.

In fact, we can construct the formal concept lattice $L(U,C,I_C)$ by using the following facts: For a consistent set $C=\{a,b,e,g,i\}$ of the associated soft context $(U,A,F)$,

(1)

${F|}_C:C\to P\left(U\right)$ is a set-valued mapping defined as follows:

$${F|}_C\left(a\right)=135; {F|}_C\left(b\right)=1245; {F|}_C\left(g\right)=24; F{|}_C\left(e\right)=13; {F|}_C\left(i\right)=2.$$

(2)

$sC(U,C,F{|}_C)=sC(U,A,F)=\{\mathsf{\varnothing },1,2,13,15,24,135,1245,U\}$.

(3)

${{\mathbf{F}|}_C}^{-}:P\left(U\right)\to P\left(C\right)$ is a mapping defined as follows: For $X\in P\left(U\right),$

$${{\mathbf{F}|}_C}^{-}\left(X\right)=\{a\in C:X\subseteq F{|}_C\left(a\right)\}.$$

Finally, by Corollary 4 and $sL(U,C,F{|}_C)=(sC(U,C,F{|}_C),⪯,⋏,⋎)$,

$L(U,C,I_C)$

$\hspace{1em}\hspace{1em}=\left\{(X,{{\mathbf{F}|}_C}^{-}\left(X\right))\right| X \mathrm{is} \mathrm{any} \mathrm{element} \mathrm{of} sL(U,C,F{|}_C)\}$

$\hspace{1em}\hspace{1em}=\left\{\right(\mathsf{\varnothing },C),(1,abe),(2,bgi),(13,ae),(15,ab),(24,bg),(135,a),(1245,b),(U,\mathsf{\varnothing }\left)\right\}.$

where

$\hspace{1em}\hspace{1em}{{\mathbf{F}|}_C}^{-}\left(U\right)=\mathsf{\varnothing }; {{\mathbf{F}|}_C}^{-}\left(\mathsf{\varnothing }\right)=C; {{\mathbf{F}|}_C}^{-}\left(1\right)=abe; {{\mathbf{F}|}_C}^{-}\left(2\right)=bgi; {{\mathbf{F}|}_C}^{-}\left(13\right)=ae;$

$\hspace{1em}\hspace{1em}{{\mathbf{F}|}_C}^{-}\left(15\right)=ab; {{\mathbf{F}|}_C}^{-}\left(24\right)=bg; {{\mathbf{F}|}_C}^{-}\left(135\right)=a; {{\mathbf{F}|}_C}^{-}\left(1245\right)=b.$

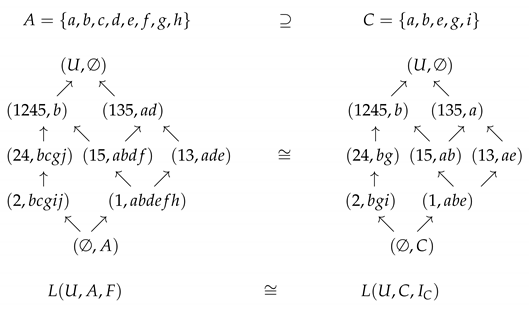
5. Conclusions

The soft context is a system proposed to study a more effective method of finding all formal concepts and reductions in a formal context, which is induced using a soft set instead of a binary relationship in formal contexts. In this paper, we investigated the notion of consistent sets of soft contexts as in the formal context. For the purpose of studying the characterizations of consistent sets, we introduced the notions of $1^0$ and $2^0$ classes of independent attributes, and determined that every consistent set has to contain the Essential Zone $1^0$ of consistent sets. Additionally, we studied the fundamental theorems necessary to construct the consistent sets of a given soft context. In particular, we have shown that the Fundamental Theorem II provides a more efficient way of constructing a consistent set of a formal context. In a subsequent study, we intend to obtain a more effective method of finding reducts in a formal context using associated soft contexts as in this study. So, we will investigate the notion of reducts of a soft context and a method of constructing reduction of a soft context. In particular, we will look for ways to construct reduction using independent soft concepts and subsets of independent attributes of a soft context. Finally, we will apply the reduction of a soft context to the reduction of a formal context.