On Wrapping of Quasi Lindley Distribution
Abstract
:1. Introduction
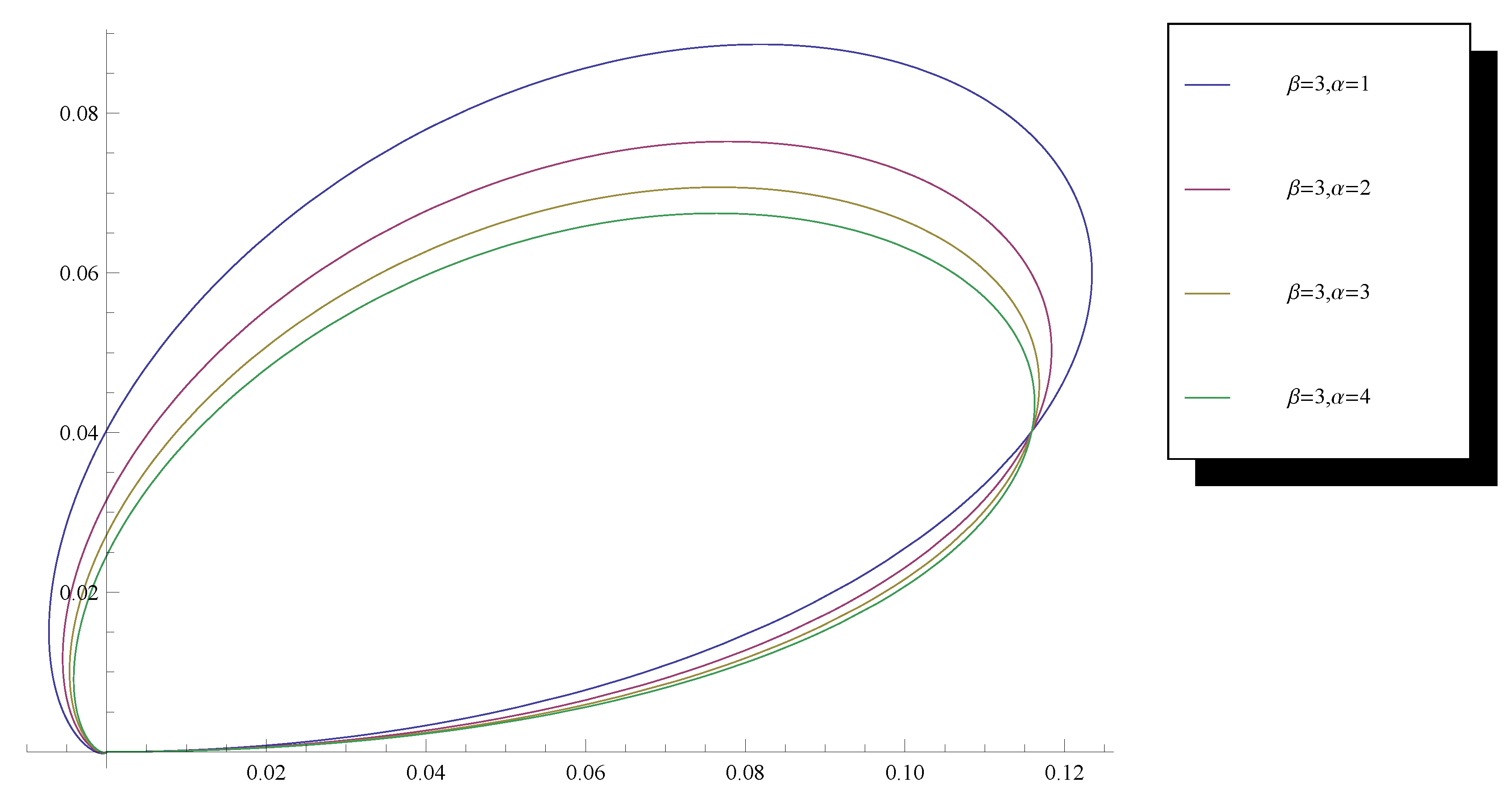
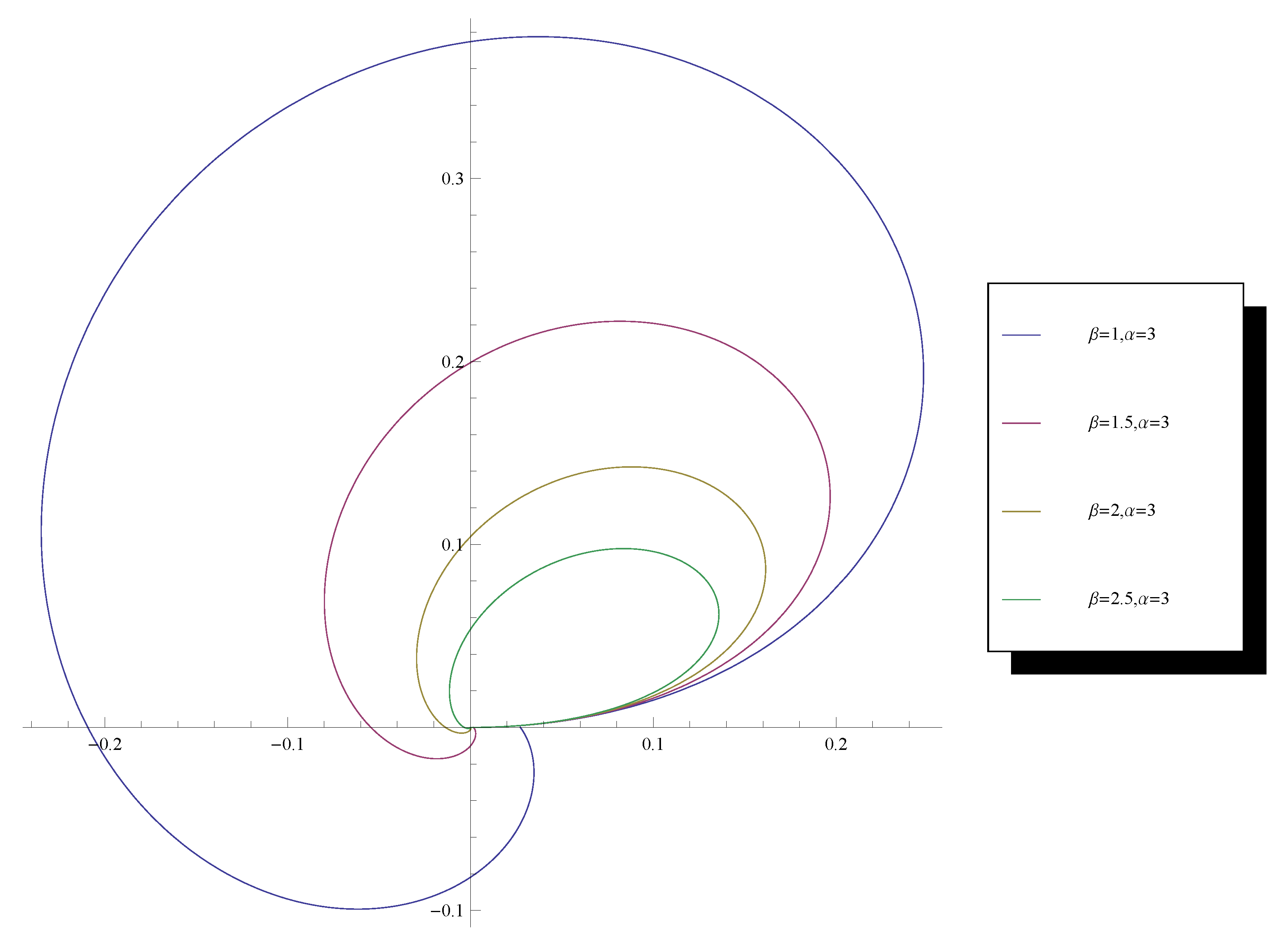
2. Circular Distribution
- 1.
- and
- 2.
- .
3. Characteristic Function of Wrapped Quasi Lindley Distribution
4. Maximum Likehood Estimations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mardia, K.V.; Jupp, P.E. Directional Statistics, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Lévy, P.L. Addition des variables alétoires définies sur une circonférence. Bull. Soc. Math. Franc. 1939, 67, 1–41. [Google Scholar]
- Rao, S.J.; Kozubowski, T.J. New families of wrapped distributions for modeling skew circular data. Commun. Stat.-Theory Methods 2004, 33, 2059–2074. [Google Scholar]
- Rao, A.V.D.; Sarma, I.R.; Girija, S.V.S. On wrapped version of some life testing models. Commun. Stat.-Theory Methods 2007, 36, 2027–2035. [Google Scholar]
- Roy, S.; Adnan, M.A.S. Wrapped weighted exponential distributions. Stat. Probab. Lett. 2012, 82, 77–83. [Google Scholar] [CrossRef]
- Rao, A.V.D.; Girija, S.V.S.; Devaraaj, V.J. On characteristics of wrapped gamma distribution. IRACST Eng. Sci. Technol. Int. J. (ESTIJ) 2013, 3, 228–232. [Google Scholar]
- Joshi, S.; Jose, K.K.; Bhati, D. Estimation of a change point in the hazard rate of Lindley model under right censoring. Commun. Stat. Simul. Comput. 2017, 46, 3563–3574. [Google Scholar] [CrossRef]
- Adnan, M.A.S.; Roy, S. Wrapped variance gamma distribution with an application to wind direction. J. Environ. Stat. 2014, 6, 1–10. [Google Scholar]
- Lindley, D. Fiducial distributions and Bayes’ theorem. J. R. Stat. Soc. 1958, 20, 102–107. [Google Scholar] [CrossRef]
- Lindley, D. Introduction to Probability and Statistics from a Bayesian Viewpoint; Cambridge University Press: New York, NY, USA, 1981. [Google Scholar]
- Joshi, S.; Jose, K.K. Wrapped Lindley distribution. Commun. Stat. Theory Methods 2018, 47, 1013–1021. [Google Scholar] [CrossRef]
- Shanker, R.; Mishra, A. A quasi Lindley distribution. Afr. J. Math. Comput. Sci. Res. 2013, 6, 64–71. [Google Scholar]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 87, 493–506. [Google Scholar] [CrossRef]
- Rao, S.J.; SenGupta, A. Topics in Circular Statistics; Series On Multivariate Analysis; World Scientific: New York, NY, USA, 2001; Volume 5. [Google Scholar] [CrossRef]
- Mardia, K.V. Statistics of Directional Data. J. R. Stat. Soc. 1975, 37, 349–393. [Google Scholar] [CrossRef]

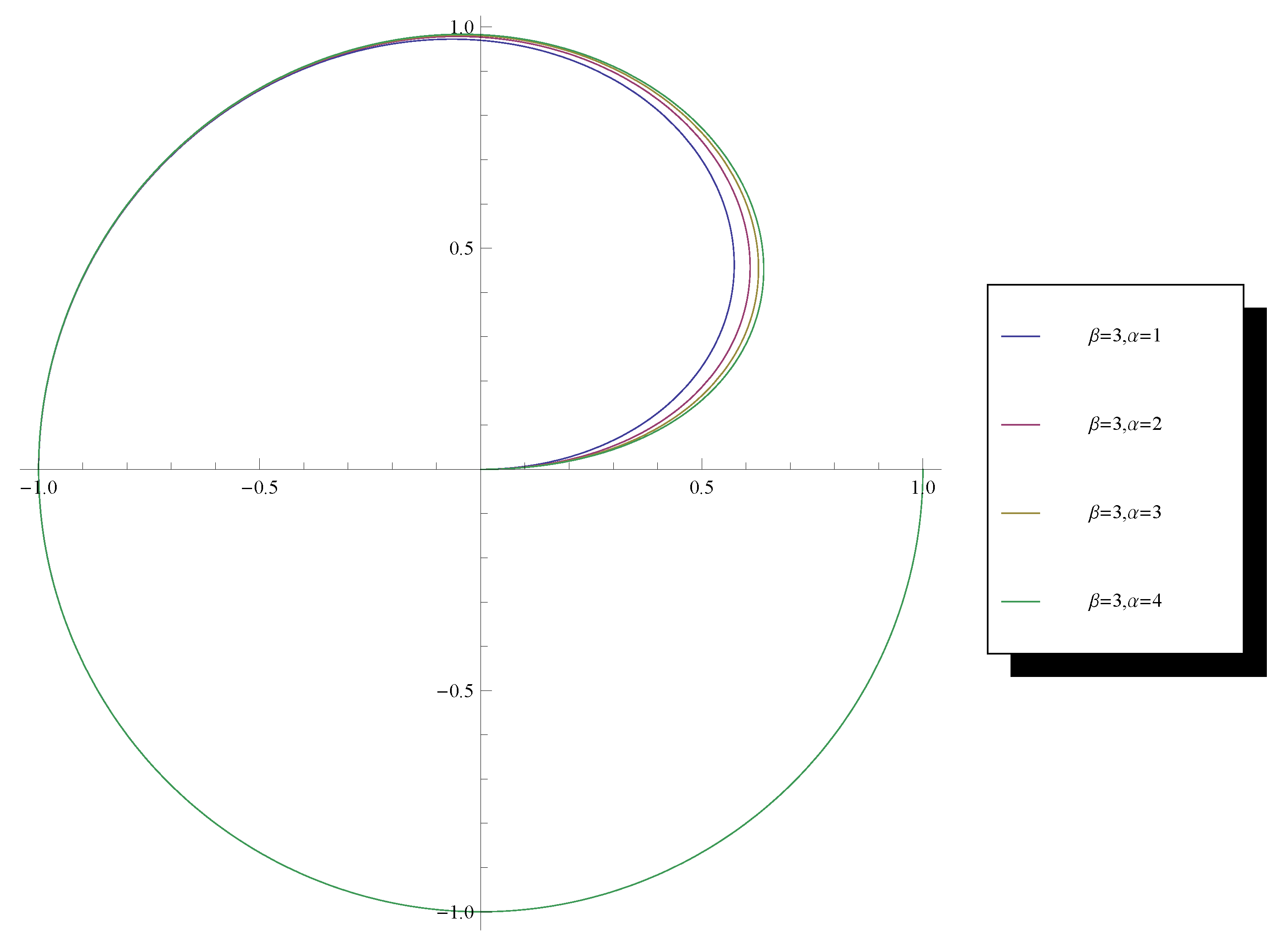
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-khazaleh, A.M.H.; Alkhazaleh, S. On Wrapping of Quasi Lindley Distribution. Mathematics 2019, 7, 930. https://doi.org/10.3390/math7100930
Al-khazaleh AMH, Alkhazaleh S. On Wrapping of Quasi Lindley Distribution. Mathematics. 2019; 7(10):930. https://doi.org/10.3390/math7100930
Chicago/Turabian StyleAl-khazaleh, Ahmad M. H., and Shawkat Alkhazaleh. 2019. "On Wrapping of Quasi Lindley Distribution" Mathematics 7, no. 10: 930. https://doi.org/10.3390/math7100930




