Using G-Functions to Investigate the Evolutionary Stability of Bacterial Quorum Sensing
Abstract
1. Introduction
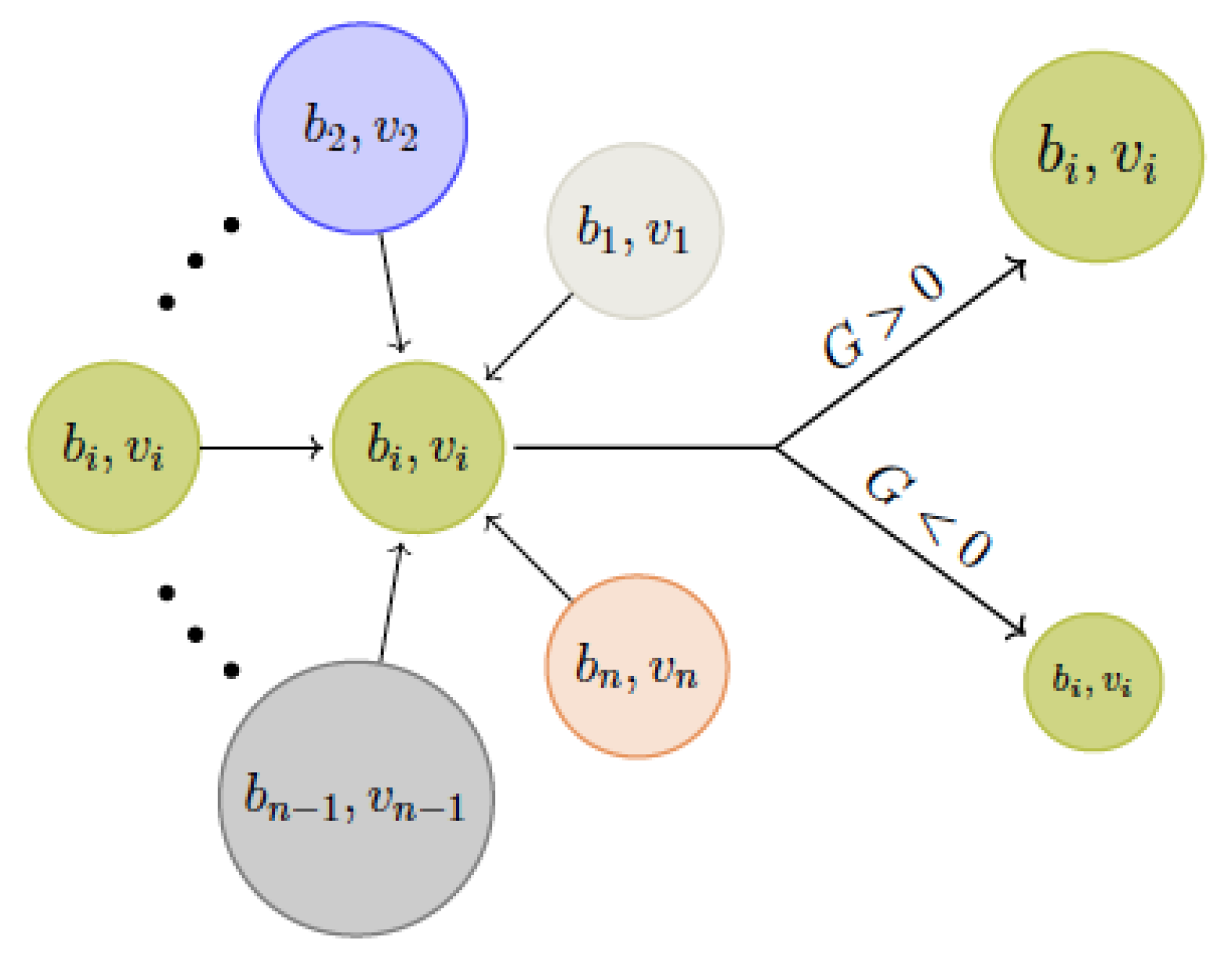
2. The Basic Model: Using the G-Function Approach
- (I)
- is Lipschitz continuous in all variables.
- (II)
- is Lipschitz continuous in ,where denotes transpose. Additionally, we make some assumptions on G from the biological background.
- (III)
- has a (direct or indirect) negative feedback loop in . The population number cannot go towards infinity.
- (IV)
- . From a certain threshold onwards, higher strategy values no longer not a higher net growth.
- (V)
- . Reducing the strategy further than the value provides no higher growth rate.
2.1. Cost and Benefit
- (VI)
- As public good production is costly, C is strictly monotonically decreasing for .
- (VII)
- When producing public goods, the growth rate is reduced by a certain factor:
- (VIII)
- There is a limit to how much benefit can be obtained,
- (IX)
- There is no benefit if no public goods are produced,
2.2. Analysis
3. Models with Private Benefit
3.1. First Type of Model Terms with Monotonicity Property
3.2. Second Type of Model Terms: Hill Equations
- .
- .
- , with if .
- has exactly one maximum, .
- for , with a function for which .
4. Numerical Simulations
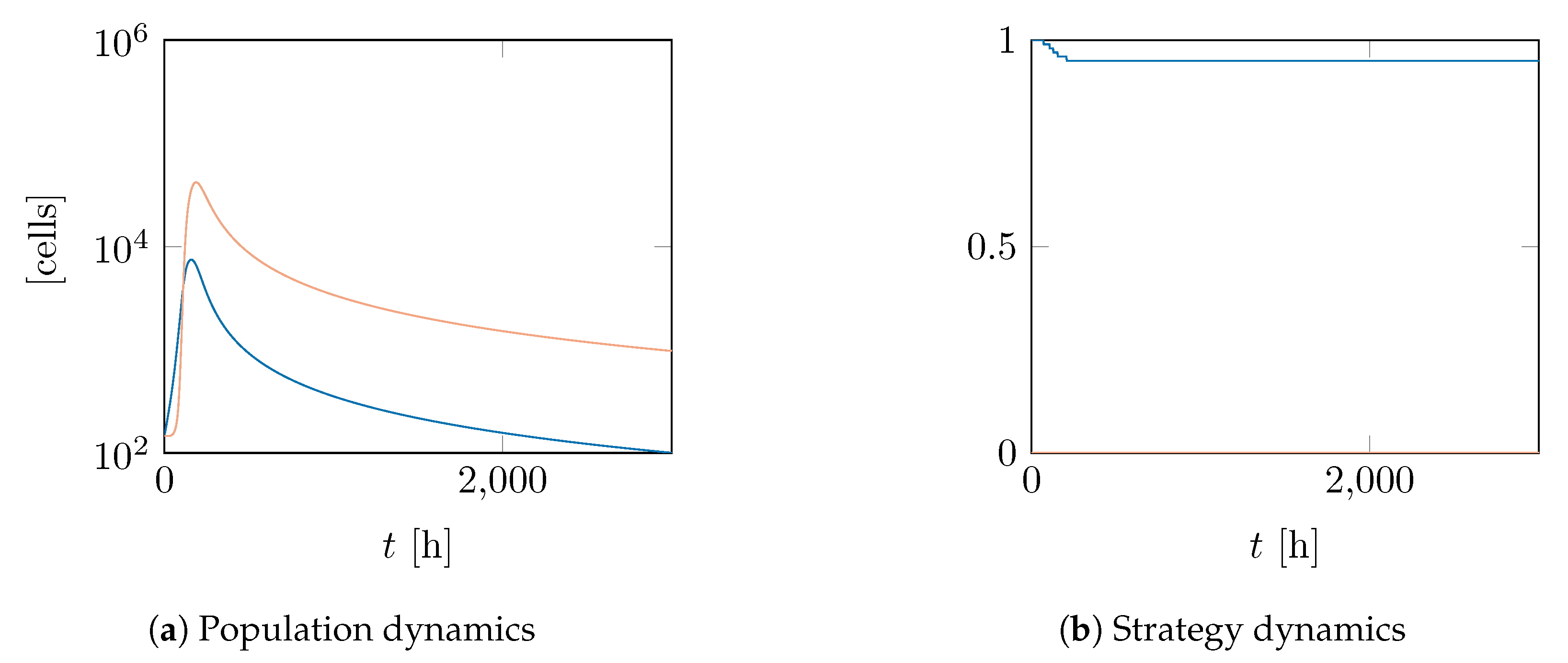
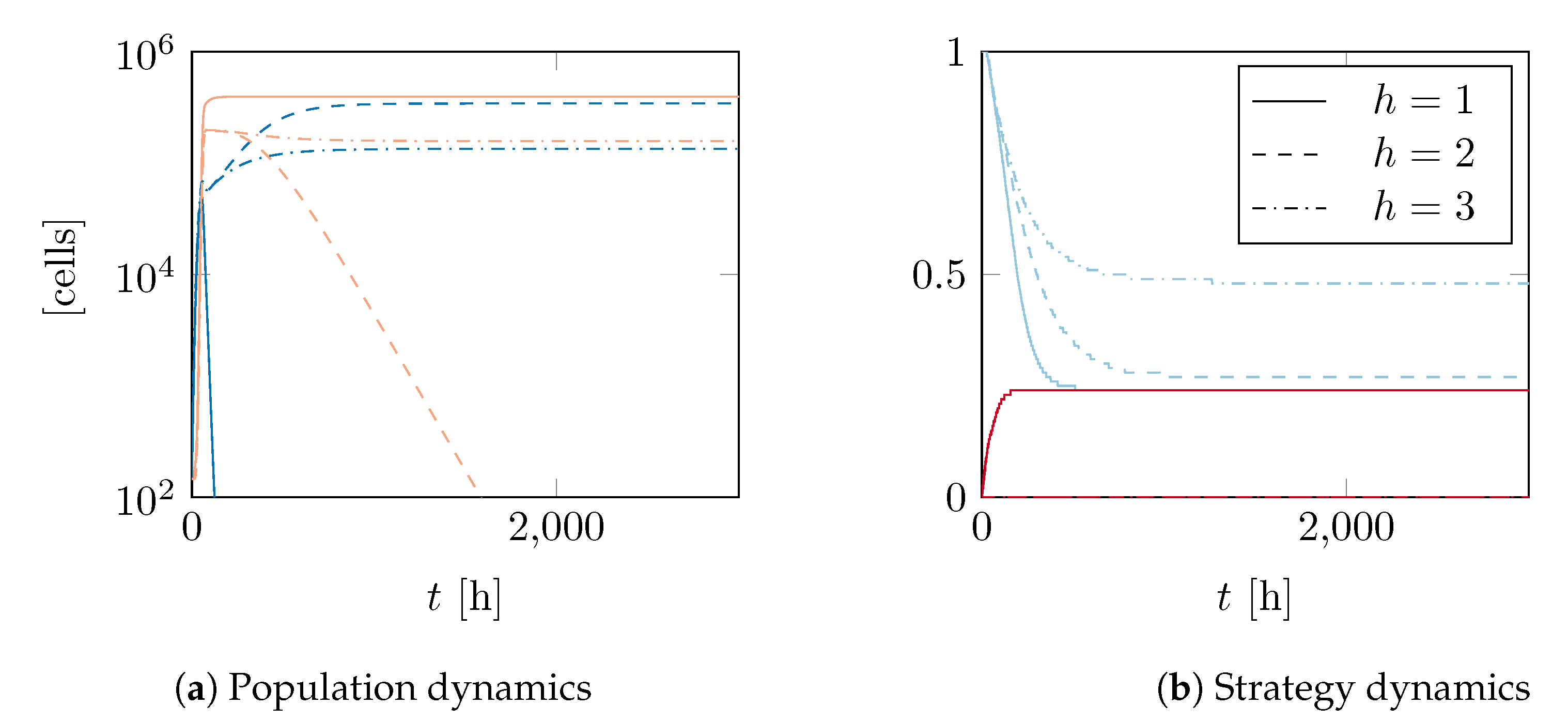
4.1. Basic Model
4.2. Models with Private Benefit
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. Variables and Parameters
| Name | Value | Stands for | |
|---|---|---|---|
| a | 7.186 × 10 | 1 | threshold value for private benefit |
| 0.30 | 1/ | maximal bacterial growth rate | |
| K | 2.459 | 1 | cost of participating in QS |
| 7.24 × 10 | 1/ | bacterial death rate | |
| 7.24 × 10 | 1/ | minimal bacterial death rate for strategy-dependent death rate | |
| 6.06 × 10 | cells | threshold value for public benefit | |
Appendix B. Proofs
Appendix B.1. Properties of R(Vi) for the Second Type of Model Terms
- base case
- We can derive from the definition of thatwhere and thus .
- inductive step
- Assuming that the statement holds for and that , we havewhereand thus since and .
Appendix B.2. Stability of
Appendix B.2.1. Models with Private Benefit
First Type of Model Terms
Second Type of Model Terms
Appendix C. Spatial Evolution of Two Populations with Different Start Strategies

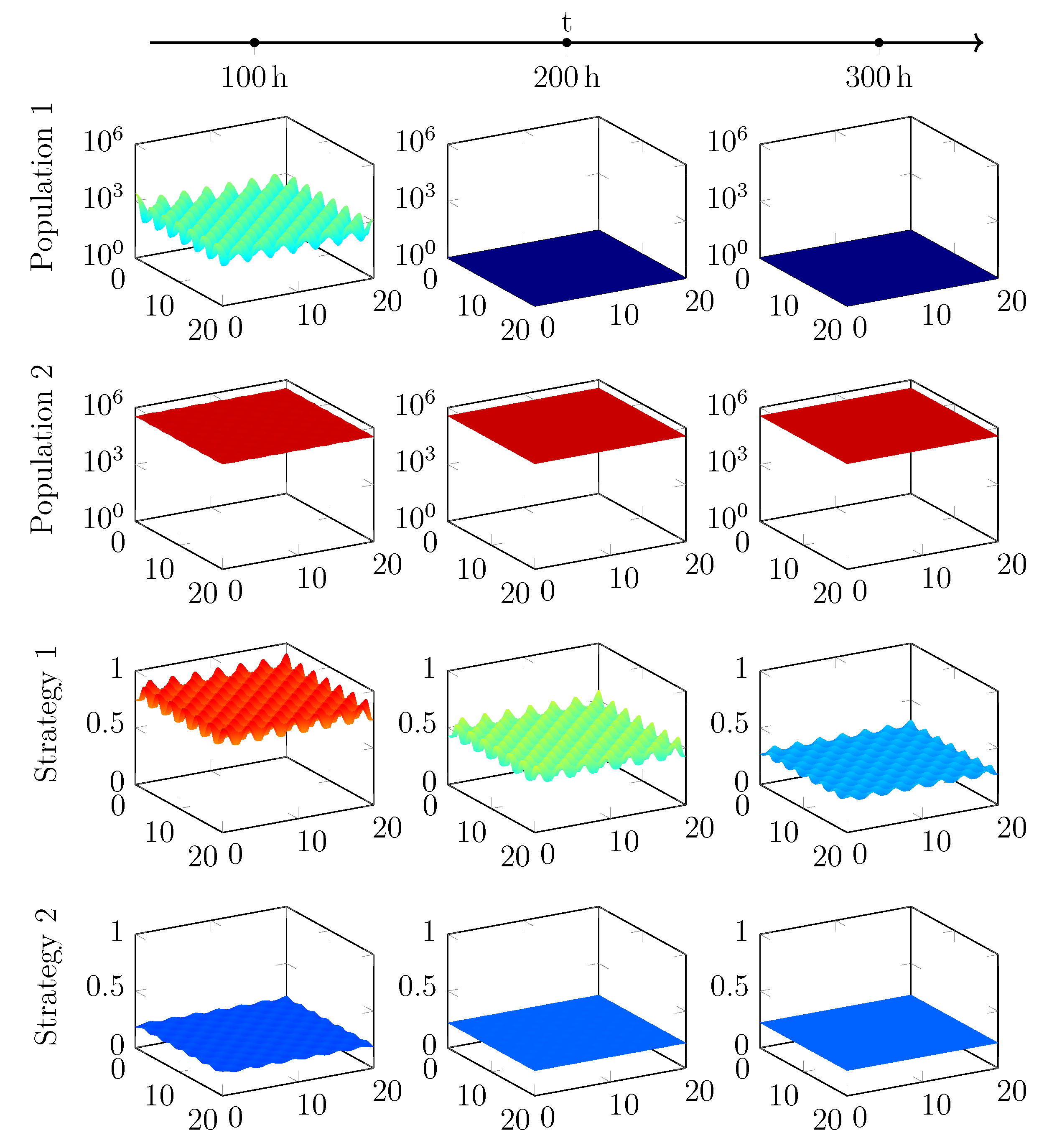
References
- Hastings, J.; Nealson, K. Bacterial bioluminescence. Annu. Rev. Microbiol. 1977, 31, 549–595. [Google Scholar] [CrossRef] [PubMed]
- Rutherford, S.T.; Bassler, B.L. Bacterial quorum sensing: Its role in virulence and possibilities for its control. Cold Spring Harbor Perspect. Med. 2012, 2, a012427. [Google Scholar] [CrossRef] [PubMed]
- Rumbaugh, K.P.; Diggle, S.P.; Watters, C.M.; Ross-Gillespie, A.; Griffin, A.S.; West, S.A. Quorum sensing and the social evolution of bacterial virulence. Curr. Biol. 2009, 19, 341–345. [Google Scholar] [CrossRef] [PubMed]
- West, S.A.; Griffin, A.S.; Gardner, A.; Diggle, S.P. Social evolution theory for microorganisms. Nat. Rev. Microbiol. 2006, 4, 597–609. [Google Scholar] [CrossRef] [PubMed]
- Diggle, S.P.; Griffin, A.S.; Campbell, G.S.; West, S.A. Cooperation and conflict in quorum-sensing bacterial populations. Nature 2007, 450, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.P.; Johnstone, R.A. Cooperation in the dark: Signalling and collective action in quorum-sensing bacteria. Proc. R. Soc. B 2001, 268, 961–965. [Google Scholar] [CrossRef] [PubMed]
- Bjarnsholt, T.; Jensen, P.; Jakobsen, T.H.; Phipps, R.; Nielsen, A.K.; Rybtke, M.T.; Tolker-Nielsen, T.; Givskov, M.; Høiby, N.; Ciofu, O.; et al. Quorum sensing and virulence of Pseudomonas aeruginosa during lung infection of cystic fibrosis patients. PLoS ONE 2010, 5, e10115. [Google Scholar] [CrossRef]
- Dénervaud, V.; TuQuoc, P.; Blanc, D.; Favre-Bonté, S.; Krishnapillai, V.; Reimmann, C.; Haas, D.; Delden, C.V. Characterization of cell-to-cell signaling-deficient Pseudomonas Aeruginosa Strains Colon. Intubated Patients. J. Clin. Microbiol. 2004, 42, 554–562. [Google Scholar] [CrossRef]
- Köhler, T.; Buckling, A.; van Delden, C. Cooperation and virulence of clinical Pseudomonas Aeruginosa Popul. Proc. Natl. Acad. Sci. USA 2009, 106, 6339–6344. [Google Scholar] [CrossRef]
- Schaber, J.A.; Carty, N.L.; McDonald, N.A.; Graham, E.D.; Cheluvappa, R.; Griswold, J.A.; Hamood, A.N. Analysis of quorum sensing-deficient clinical isolates of Pseudomonas Aeruginosa. J. Med. Microbiol. 2004, 53, 841–853. [Google Scholar] [CrossRef]
- Smith, E.E.; Buckley, D.G.; Wu, Z.; Saenphimmachak, C.; Hoffman, L.R.; D’Argenio, D.A.; Miller, S.I.; Ramsey, B.W.; Speert, D.P.; Moskowitz, S.M.; et al. Genetic adaptation by Pseudomonas Aeruginosa Airways Cyst. Fibros. Patients. Proc. Natl. Acad. Sci. USA 2006, 103, 8487–8492. [Google Scholar] [CrossRef] [PubMed]
- West, S.A.; Winzer, K.; Gardner, A.; Diggle, S.P. Quorum sensing and the confusion about diffusion. Trends Microbiol. 2012, 20, 586–594. [Google Scholar] [CrossRef] [PubMed]
- Wilder, C.N.; Allada, G.; Schuster, M. Instantaneous within-patient diversity of Pseudomonas Aeruginosa quorum-sensing populations from cystic fibrosis lung infections Lung Infect. Infec. Immun. 2009, 77, 5631–5639. [Google Scholar] [CrossRef] [PubMed]
- Popat, R.; Crusz, S.A.; Messina, M.; Williams, P.; West, S.A.; Diggle, S.P. Quorum-sensing and cheating in bacterial biofilms. Proc. R. Soc. Lond. B Biol. Sci. 2012, 479. [Google Scholar] [CrossRef]
- Wilder, C.N.; Diggle, S.P.; Schuster, M. Cooperation and cheating in Pseudomonas Aeruginosa: The roles of the las, rhl and pqs quorum-sensing systems. ISME J. 2011, 5, 1332–1343. [Google Scholar] [CrossRef]
- Pollitt, E.J.; West, S.A.; Crusz, S.A.; Burton-Chellew, M.N.; Diggle, S.P. Cooperation, quorum sensing, and evolution of virulence in Staphylococcus Aureus. Infection Immun. 2014, 82, 1045–1051. [Google Scholar] [CrossRef]
- Dandekar, A.A.; Chugani, S.; Greenberg, E.P. Bacterial quorum sensing and metabolic incentives to cooperate. Science 2012, 338, 264–266. [Google Scholar] [CrossRef]
- Schuster, M.; Sexton, D.J.; Hense, B.A. Why quorum sensing controls private goods. Front. Microbiol. 2017, 8, 885. [Google Scholar] [CrossRef]
- Kümmerli, R.; Schiessl, K.T.; Waldvogel, T.; McNeill, K.; Ackermann, M. Habitat structure and the evolution of diffusible siderophores in bacteria. Ecol. Lett. 2014, 17, 1536–1544. [Google Scholar] [CrossRef]
- Buckling, A.; Brockhurst, M.A. Kin selection and the evolution of virulence. Heredity 2008, 100, 484–488. [Google Scholar] [CrossRef]
- Wang, M.; Schaefer, A.L.; Dandekar, A.A.; Greenberg, E.P. Quorum sensing and policing of Pseudomonas Aeruginosa Soc. Cheaters. Proc. Natl. Acad. Sci. USA 2015, 112, 2187–2191. [Google Scholar] [CrossRef] [PubMed]
- Czárán, T.; Hoekstra, R.F. Microbial communication, cooperation and cheating: Quorum sensing drives the evolution of cooperation in bacteria. PLoS ONE 2009, 4, e6655. [Google Scholar] [CrossRef] [PubMed]
- Cremer, J.; Melbinger, A.; Frey, E. Growth dynamics and the evolution of cooperation in microbial populations. Sci. Rep. 2012, 2, 281. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Velázquez, J.; Hense, B.A. Differential Equations Models to Study Quorum Sensing; Springer: New York, NY, USA, 2018; pp. 253–271. ISBN 978-1-4939-7309-5. [Google Scholar] [CrossRef]
- Frank, S.A. Microbial secretor–cheater dynamics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 2515–2522. [Google Scholar] [CrossRef] [PubMed]
- Mund, A.; Kuttler, C.; Pérez-Velázquez, J.; Hense, B. An age-dependent model to analyse the evolutionary stability of bacterial quorum sensing. J. Theor. Biol. 2016, 405. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Y.; Vincent, T.; Brown, J. A G-function approach to fitness minima, fitness maxima, evolutionary stable strategies and adaptive landscapes. Evol. Ecol. Res. 1999, 1, 923–942. [Google Scholar]
- Apaloo, J.; Brown, J.S.; Vincent, T.L. Evolutionary game theory: ESS, convergence stability, and NIS. Evol. Ecol. Res. 2009, 11, 489–515. [Google Scholar]
- Brown, J.S.; Vincent, T.L. G-functions for the hermeneutic circle of evolution. Comput. Oper. Res. 2006, 33, 479–499. [Google Scholar] [CrossRef]
- Cohen, Y.; Pastor, J.; Vincent, T.L. Evolutionary strategies and nutrient cycling in ecosystems. Evol. Ecol. Res. 2000, 2, 719–743. [Google Scholar]
- Kronik, N.; Cohen, Y. Evolutionary games in space. Math. Model. Nat. Phenom. 2009, 4, 54–90. [Google Scholar] [CrossRef][Green Version]
- Müller, J.; Kuttler, C. Methods and Models in Mathematical Biology; Springer: Berlin, Germany, 2015; ISBN 978-3-642-27251-6. [Google Scholar]
- Kümmerli, R.; Griffin, A.S.; West, S.A.; Buckling, A.; Harrison, F. Viscous medium promotes cooperation in the pathogenic bacterium Pseudomonas Aeruginosa. Proc. R. Soc. Lond. B Biol. Sci. 2009, 276, 3531–3538. [Google Scholar] [CrossRef] [PubMed]
- Mund, A.; Diggle, S.P.; Harrison, F. The fitness of Pseudomonas aeruginosa quorum sensing signal cheats is influenced by the diffusivity of the environment. mBio 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Mund, A.; Kuttler, C.; Perez-Velazquez, J. Existence and uniqueness of solutions to a family of semi-linear parabolic systems using coupled upper-lower solutions. Discret. Contin. Dyn. Syst. B 2019, 24, 5695. [Google Scholar] [CrossRef]
- Dockery, J.D.; Keener, J.P. A mathematical model for quorum sensing in Pseudomonas Aeruginosa. Bull. Math. Biol. 2001, 63, 95–116. [Google Scholar] [CrossRef] [PubMed]
- Königsberger, K. Analysis 1; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-3-540-55116-4. [Google Scholar]
- Schiesser, W. The Numerical Method of Lines: Integration of Partial Differential Equation; Elsevier Science: Amsterdam, The Netherlands, 2012; ISBN 9780128015513. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mund, A.; Kuttler, C.; Pérez-Velázquez, J. Using G-Functions to Investigate the Evolutionary Stability of Bacterial Quorum Sensing. Mathematics 2019, 7, 1112. https://doi.org/10.3390/math7111112
Mund A, Kuttler C, Pérez-Velázquez J. Using G-Functions to Investigate the Evolutionary Stability of Bacterial Quorum Sensing. Mathematics. 2019; 7(11):1112. https://doi.org/10.3390/math7111112
Chicago/Turabian StyleMund, Anne, Christina Kuttler, and Judith Pérez-Velázquez. 2019. "Using G-Functions to Investigate the Evolutionary Stability of Bacterial Quorum Sensing" Mathematics 7, no. 11: 1112. https://doi.org/10.3390/math7111112
APA StyleMund, A., Kuttler, C., & Pérez-Velázquez, J. (2019). Using G-Functions to Investigate the Evolutionary Stability of Bacterial Quorum Sensing. Mathematics, 7(11), 1112. https://doi.org/10.3390/math7111112






