Pattern Formation and Bistability in a Generalist Predator-Prey Model
Abstract
1. Introduction
2. The Model
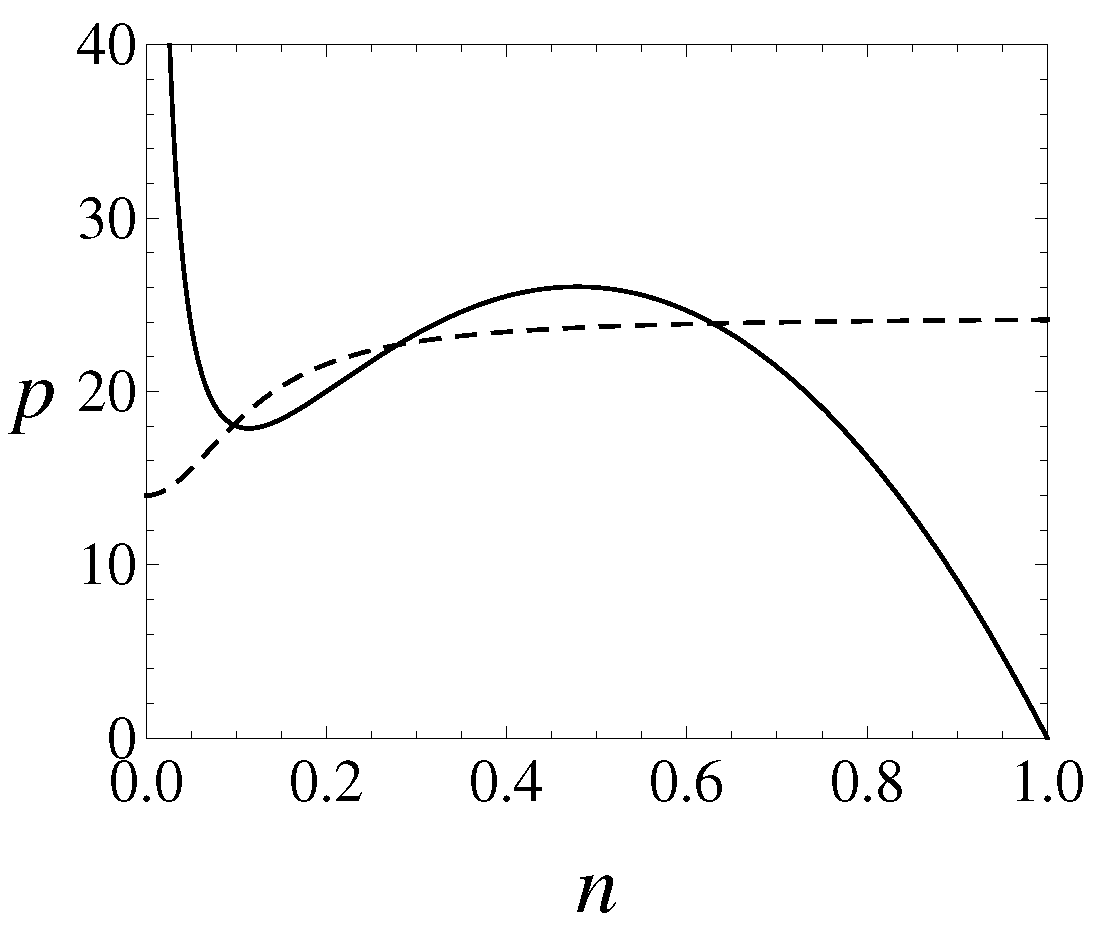
Local Stability
- (i)
- If , then the equilibrium is stable;
- (ii)
- The equilibrium is a saddle point if and only if .
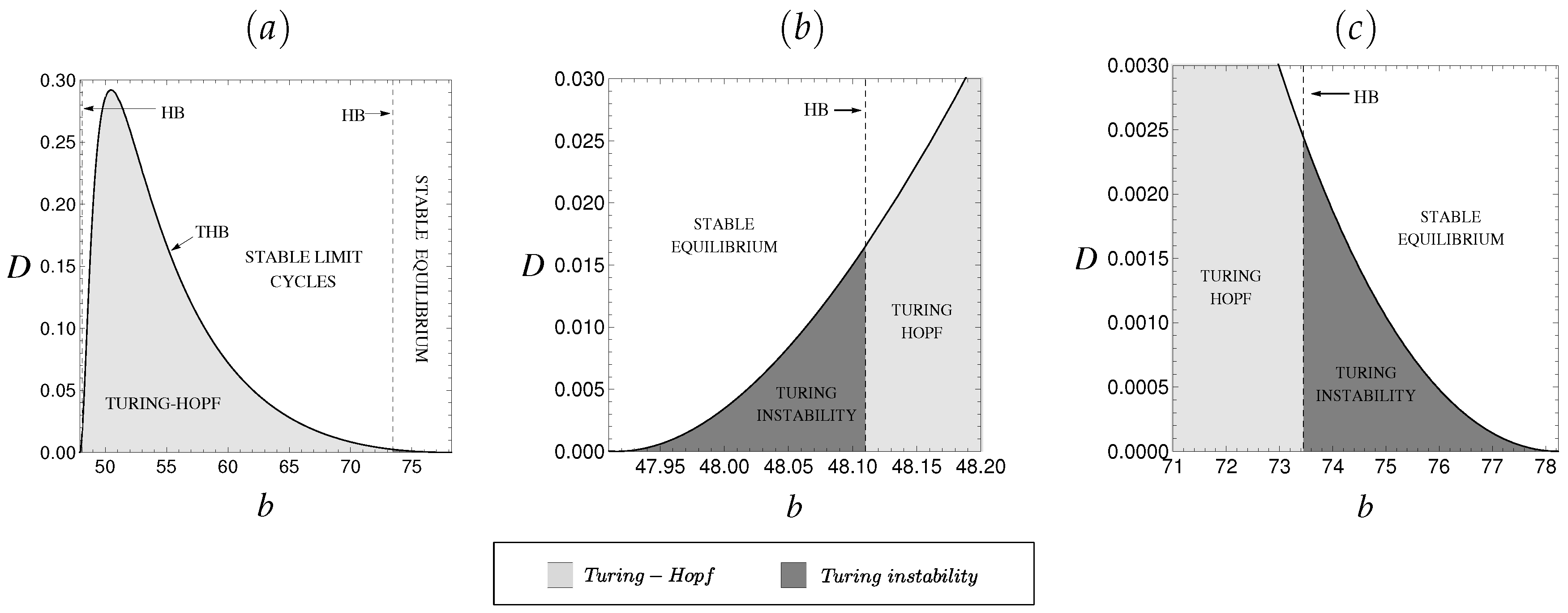
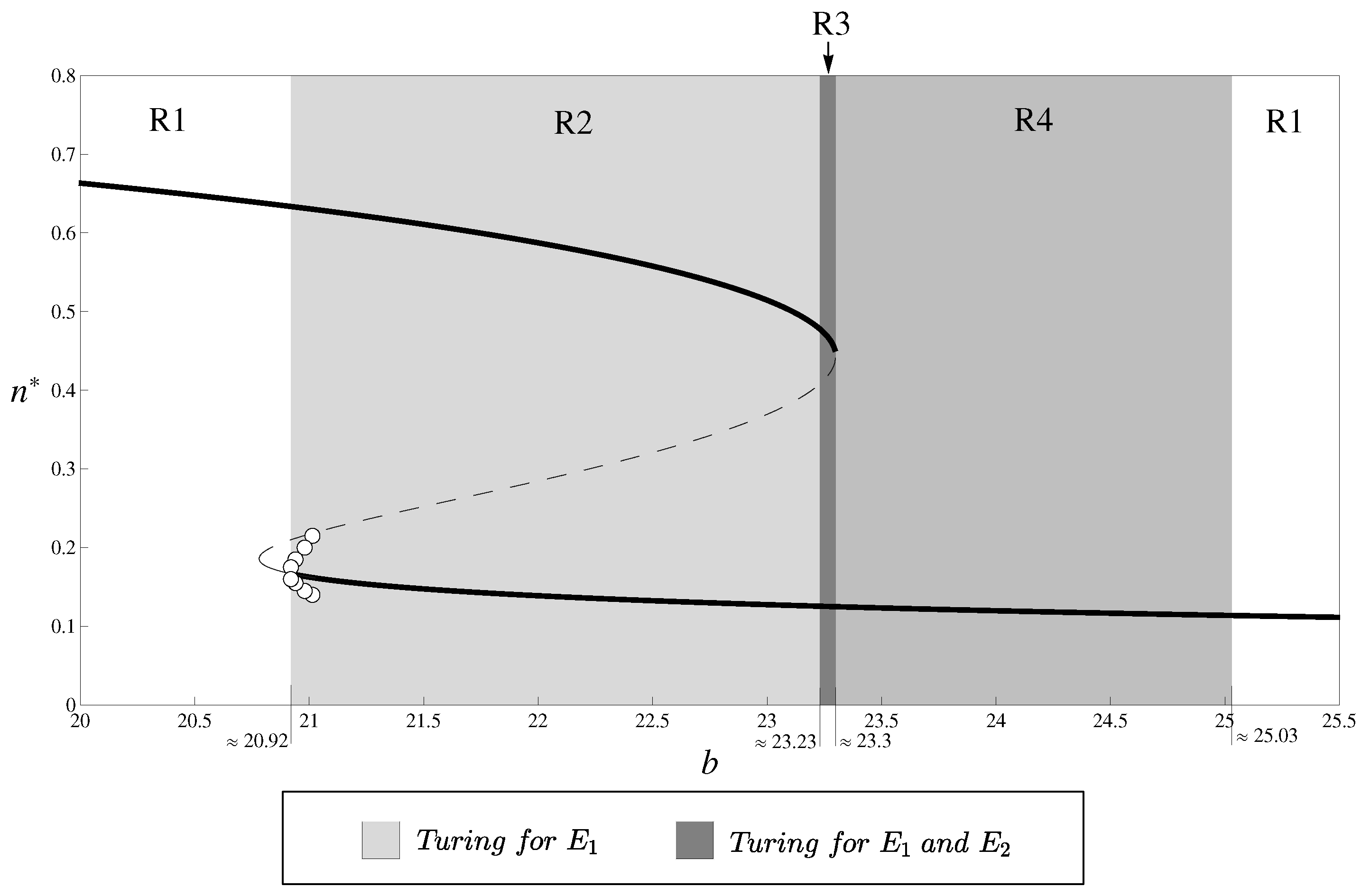
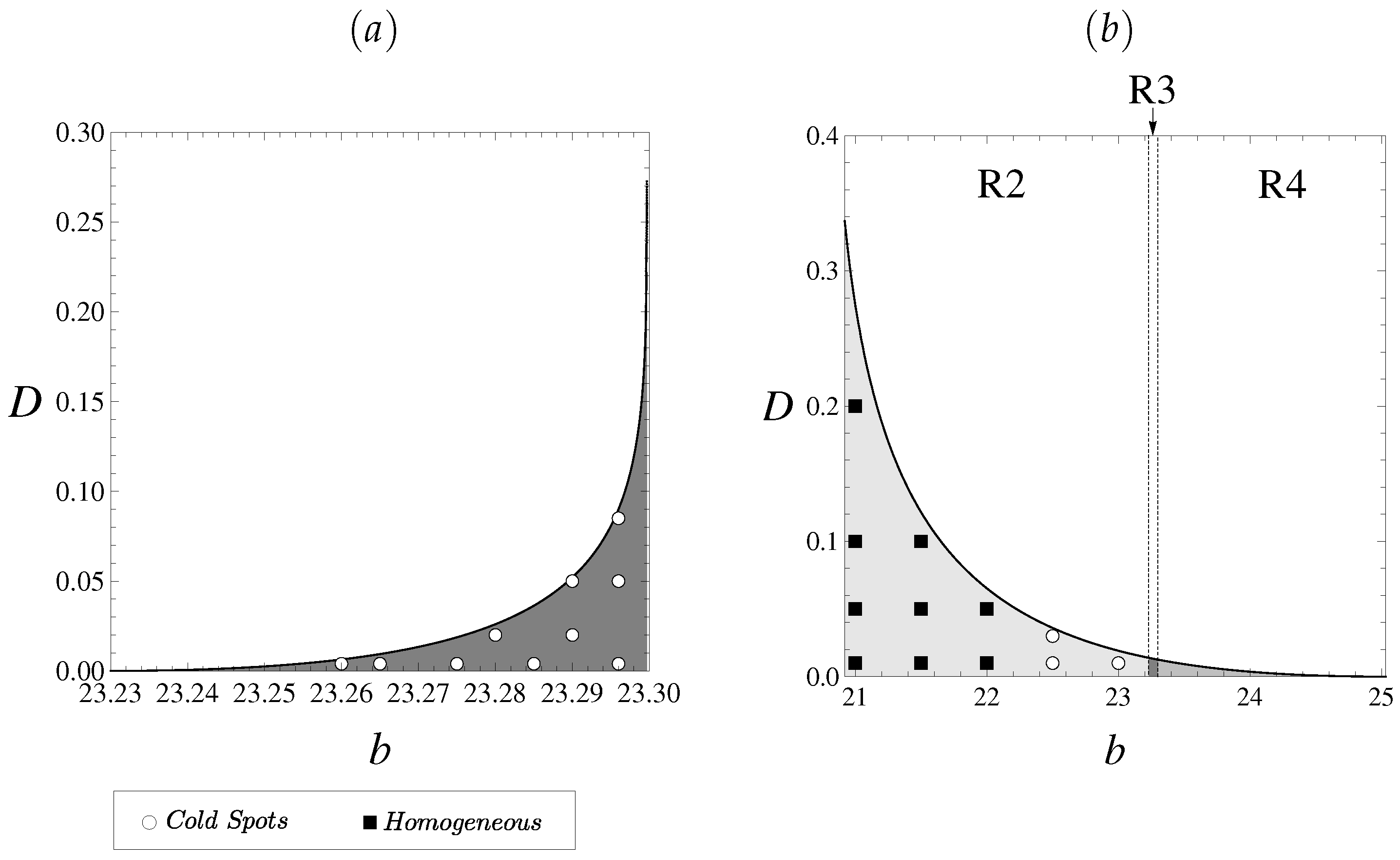
3. Turing Instability
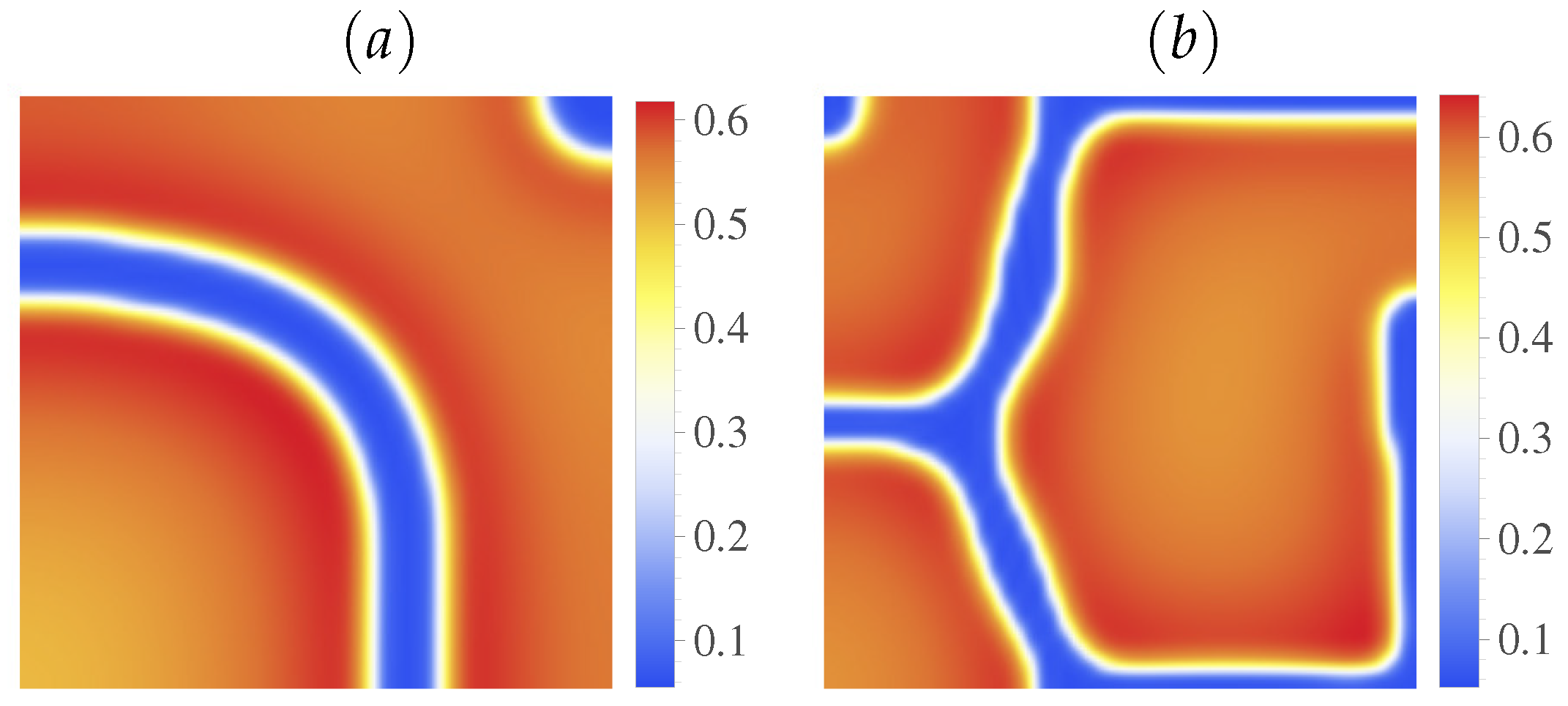
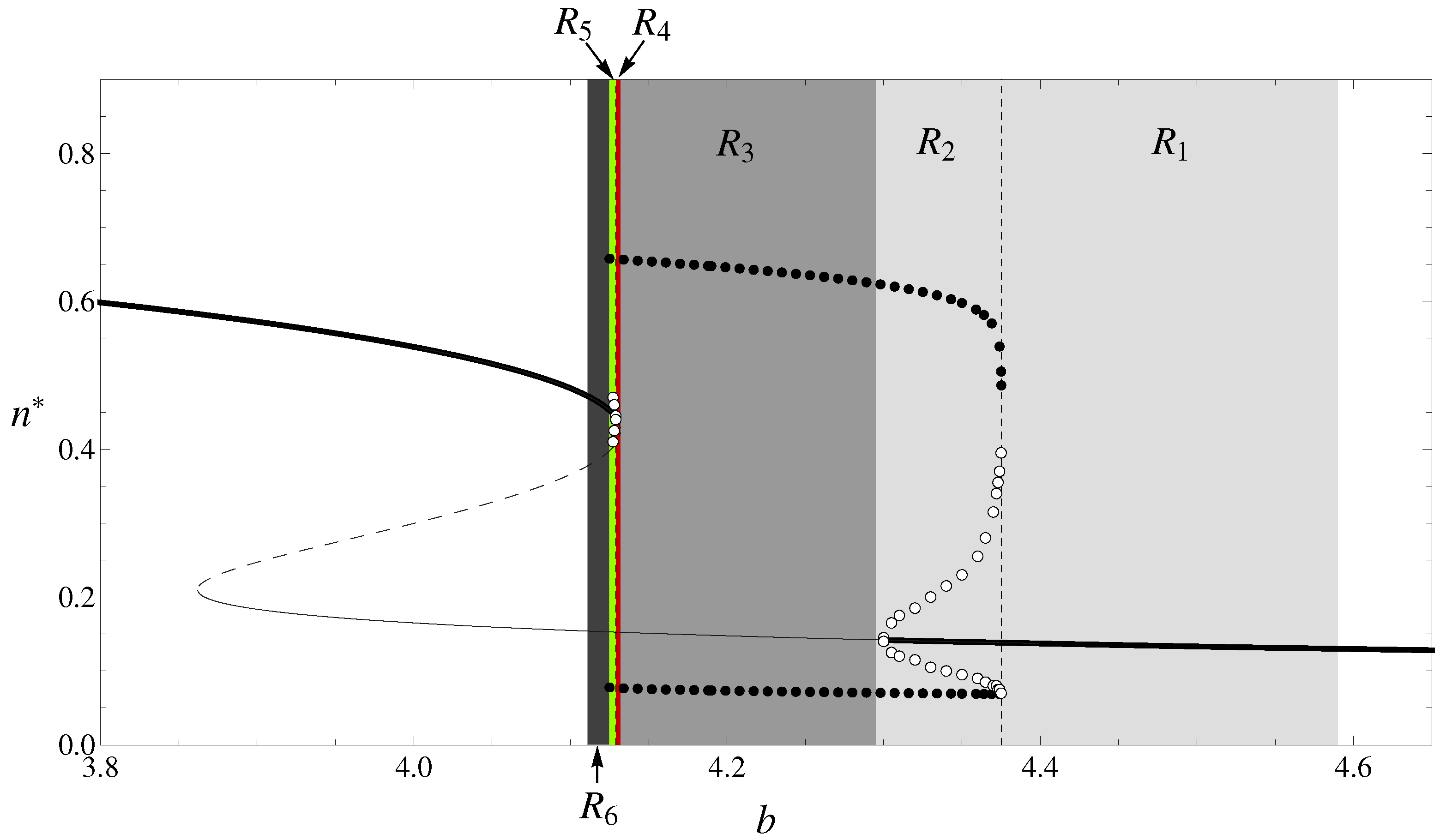
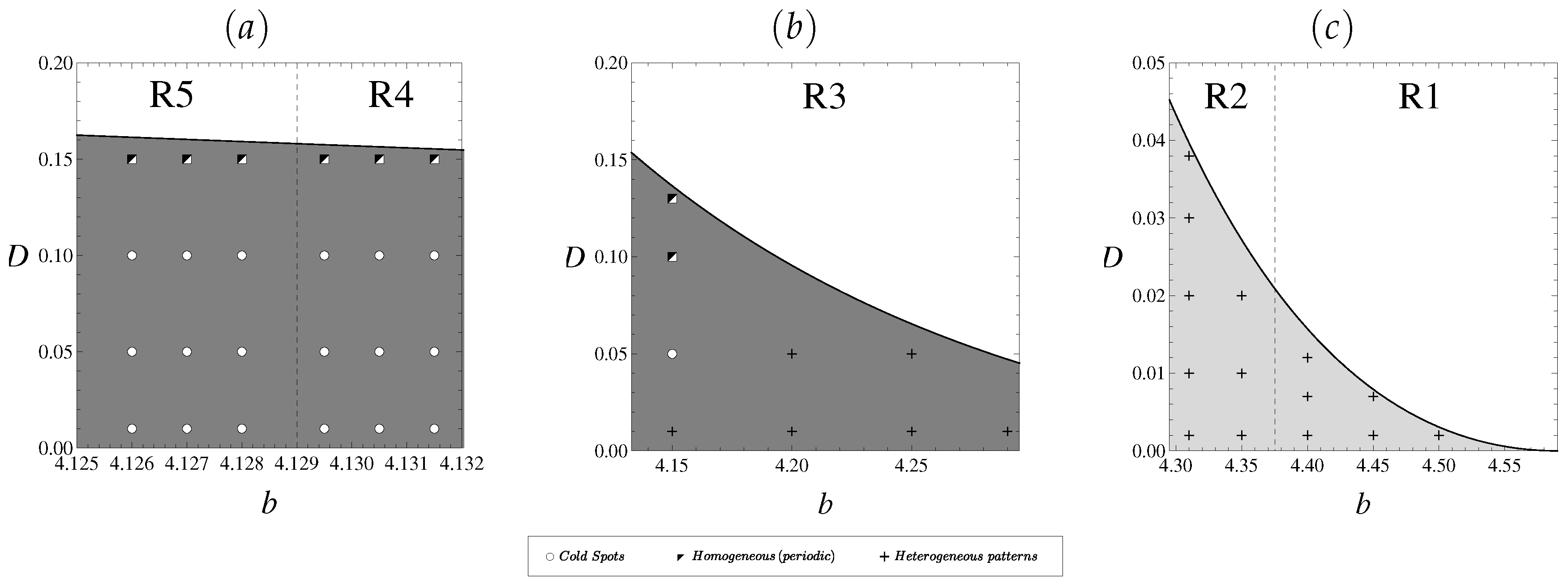
4. Numerical Simulations
- Set I: , , and ;
- Set II: , , and ;
- Set III: , , and .
5. Results
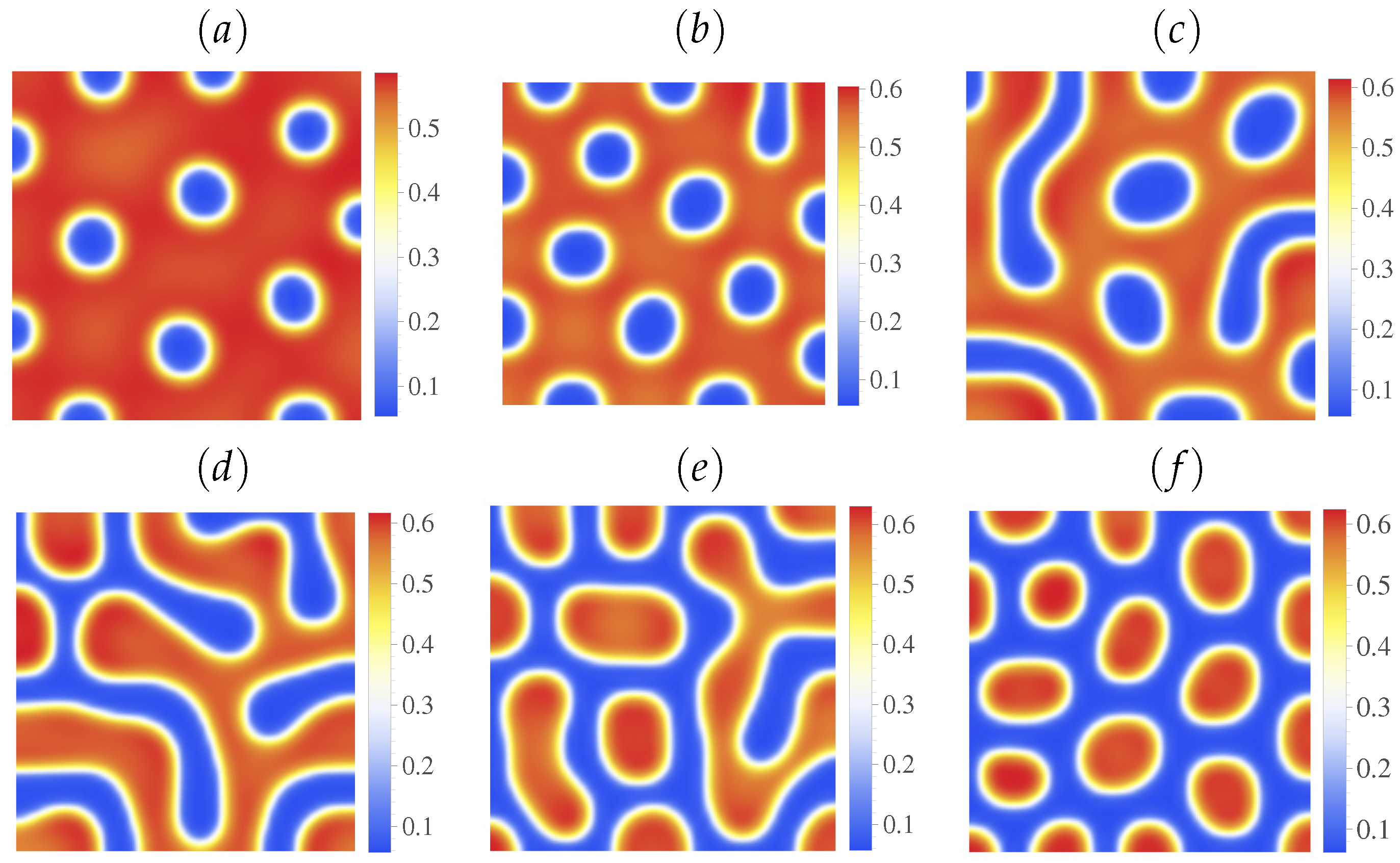
5.1. Set I
5.2. Set II
5.3. Set III
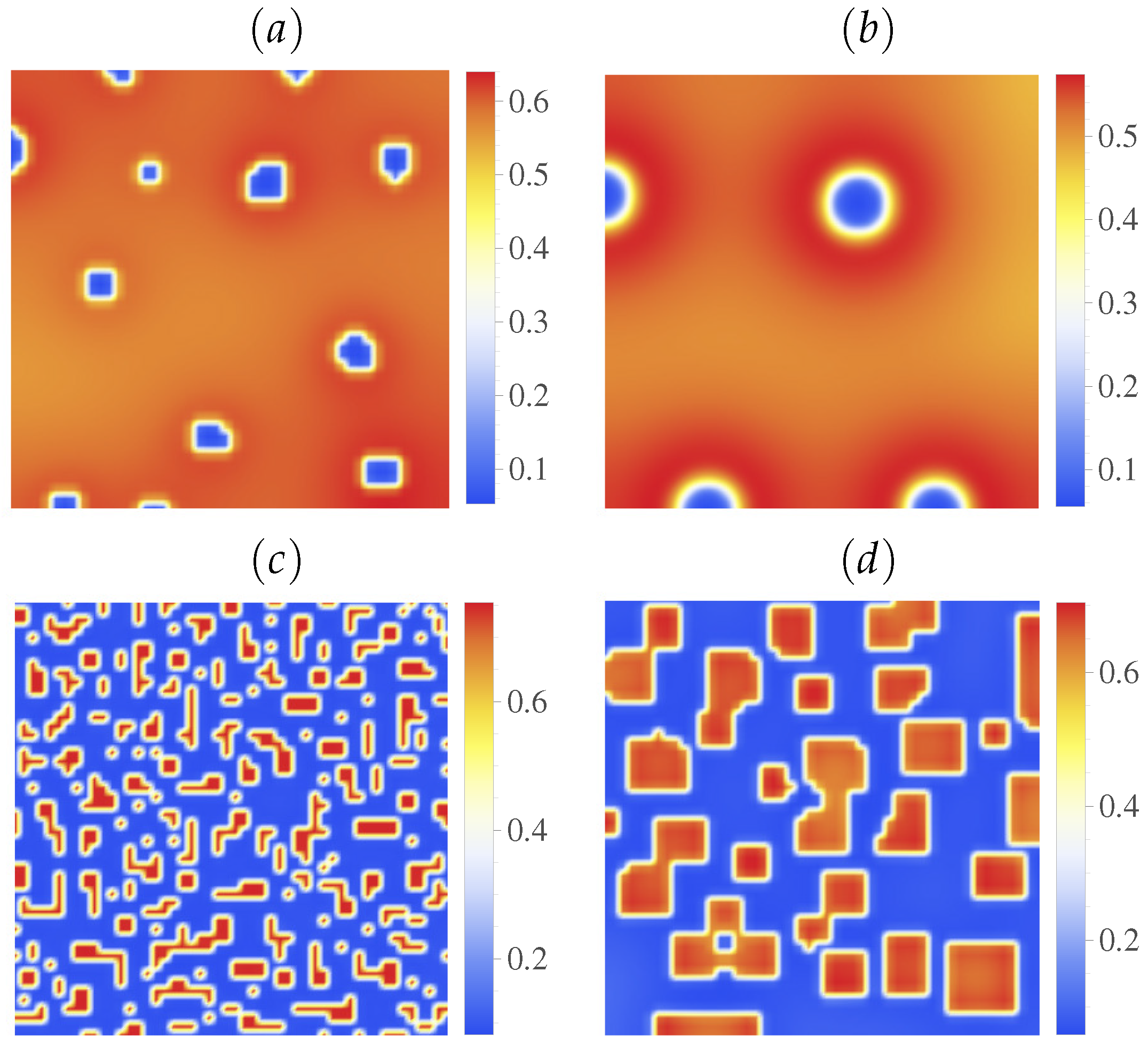
6. Discussion
6.1. Spatiotemporal Chaos
6.2. Bistability and Regime Shifts
Author Contributions
Funding
Conflicts of Interest
References
- Gibert, J.P.; Yeakel, J.D. Laplacian matrices and Turing bifurcations: Revisiting Levin 1974 and the consequences of spatial structure and movement for ecological dynamics. Theor. Ecol. 2019, 12, 265–281. [Google Scholar] [CrossRef]
- Nicholson, A.J.; Bailey, V.A. The balance of animal population. Part I. Proc. Zool. Soc. Lond. 1935, 3, 551–598. [Google Scholar] [CrossRef]
- Comins, H.N.; Hassell, M.P.; May, R.M. The spatial dynamics of host-parasitoid systems. J. Anim. Ecol. 1992, 61, 735–748. [Google Scholar] [CrossRef]
- Hassell, M.P.; Comins, H.N.; May, R.M. Spatial structure and chaos in insect population dynamics. Nature 1991, 353, 255–258. [Google Scholar] [CrossRef]
- Cantrell, R.S.; Cosner, C. Spatial Ecology via Reaction-Diffusion Equations; Wiley: London, UK, 2003. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; Random House: New York, NY, USA, 1988. [Google Scholar]
- Holmes, E.E.; Lewis, M.A.; Banks, J.E.; Veit, R.R. Partial differential equations in ecology: Spatial interactions and populations dynamics. Ecology 1994, 75, 17–29. [Google Scholar] [CrossRef]
- Okubo, A.O.; Levin, S.A. Diffusion and Ecological Problems. Modern Perspectives; Springer: New York, NY, USA, 2001. [Google Scholar]
- Lewis, M.A.; Kareiva, P. Allee dynamics and the spread of invading organisms. Theor. Pop. Biol. 1993, 43, 141–158. [Google Scholar] [CrossRef]
- Owen, M.; Lewis, M.A. How predation can stop, slow or reverse a prey invasion. Bull. Math. Biol. 2001, 63, 655–689. [Google Scholar] [CrossRef]
- Sherratt, J.A.; Lewis, M.A.; Fowler, A.C. Ecological chaos in invasion. Proc. Natl. Acad. Sci. USA 1995, 92, 2524–2528. [Google Scholar] [CrossRef]
- Shigesada, N.; Kawasaki, K. Biological Invasions: Theory and Practice; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Kierstead, H.; Slobodkin, L.B. The size of water masses containing plankton blooms. J. Mar. Res. 1953, 12, 141–147. [Google Scholar]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Ecoepidemiology: Theory, Models, and Simulations; Champman & and Hall: London, UK, 2008. [Google Scholar]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Segel, L.A.; Jackson, J.L. Dissipative structure: an explanation and an ecological example. J. Theor. Biol. 1972, 37, 545–559. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Gierer, A.; Meinhardt, H. A theory for biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Meinhardt, H. Models of Biological Pattern Formation; Academic Press: London, UK, 1982. [Google Scholar]
- Baurmann, M.; Gross, T.; Feudel, U. Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. J. Theor. Biol. 2007, 245, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Petrovskii, S. Self-organized spatial patterns and chaos in a ratio-dependent predator-prey system. Theor. Ecol. 2011, 4, 37–53. [Google Scholar] [CrossRef]
- Morozov, A.; Petrovskii, S. Excitable population dynamics, biological control failure, and spatiotemporal pattern formation in a model ecosystem. Bull. Math. Biol. 2009, 71, 863–887. [Google Scholar] [CrossRef]
- Kumari, N. Pattern formation in spatially extended tritrophic food chain model systems: Generalist versus specialist top predator. ISRN Biomath. 2013, 2013, 198185. [Google Scholar] [CrossRef]
- Magal, C.; Cosner, C.G.; Ruan, S.; Casas, J. Control of invasive hosts by generalist parasitoids. Math. Med. Biol. 2008, 25, 1–20. [Google Scholar] [CrossRef]
- Chakraborty, S. The influence of generalist predators in spatially extended predator-prey systems. Ecol. Complex. 2015, 23, 50–60. [Google Scholar] [CrossRef]
- Holling, C.S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 1959, 91, 385–398. [Google Scholar] [CrossRef]
- Erbach, A.; Lutscher, F.; Seo, G. Bistability and limit cycles in generalist predator-prey dynamics. Ecol. Complex. 2013, 14, 48–55. [Google Scholar] [CrossRef]
- Biggs, R.; Carpenter, S.R.; Brock, W.A. Turning back from the brink: Detecting an impeding regime shift in time to avert it. Proc. Natl. Acad. Sci. USA 2009, 106, 826–831. [Google Scholar] [CrossRef] [PubMed]
- Segel, L.A. Modeling Dynamic Phenomena in Molecular and Cellular Biology; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Jones, D.S.; Sleeman, B.D. Differential Equations and Mathematical Biology; Chapman & Hall/CRC: London, UK, 2003. [Google Scholar]
- Meixner, M.; De Wit, A.; Bose, S.; Scholl, E. Generic spatiotemporal dynamics near codimension-two Turing-Hopf bifurcations. Phys. Rev. E 1997, 55, 6690–6697. [Google Scholar] [CrossRef]
- Rodrigues, L.A.D.; Mistro, D.C.; Petrovskii, S. Pattern Formation, Long-Term Transients, and the Turing–Hopf Bifurcation in a Space- and Time-Discrete Predator–Prey System. Bull. Math. Biol. 2011, 73, 1812–1840. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Nonlinear Dynamics and Chaos. With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; Westview Press: Philadelphia, PA, USA, 2015. [Google Scholar]
- Kéfi, S.; Maarten, B.E.; de Ruiter, P.C.; Rietkerk, M. Bistability and regular patterns in arid systems. Theor. Ecol. 2010, 3, 257–269. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-Organized Patchiness and Catastrophic Shifts in Ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef] [PubMed]



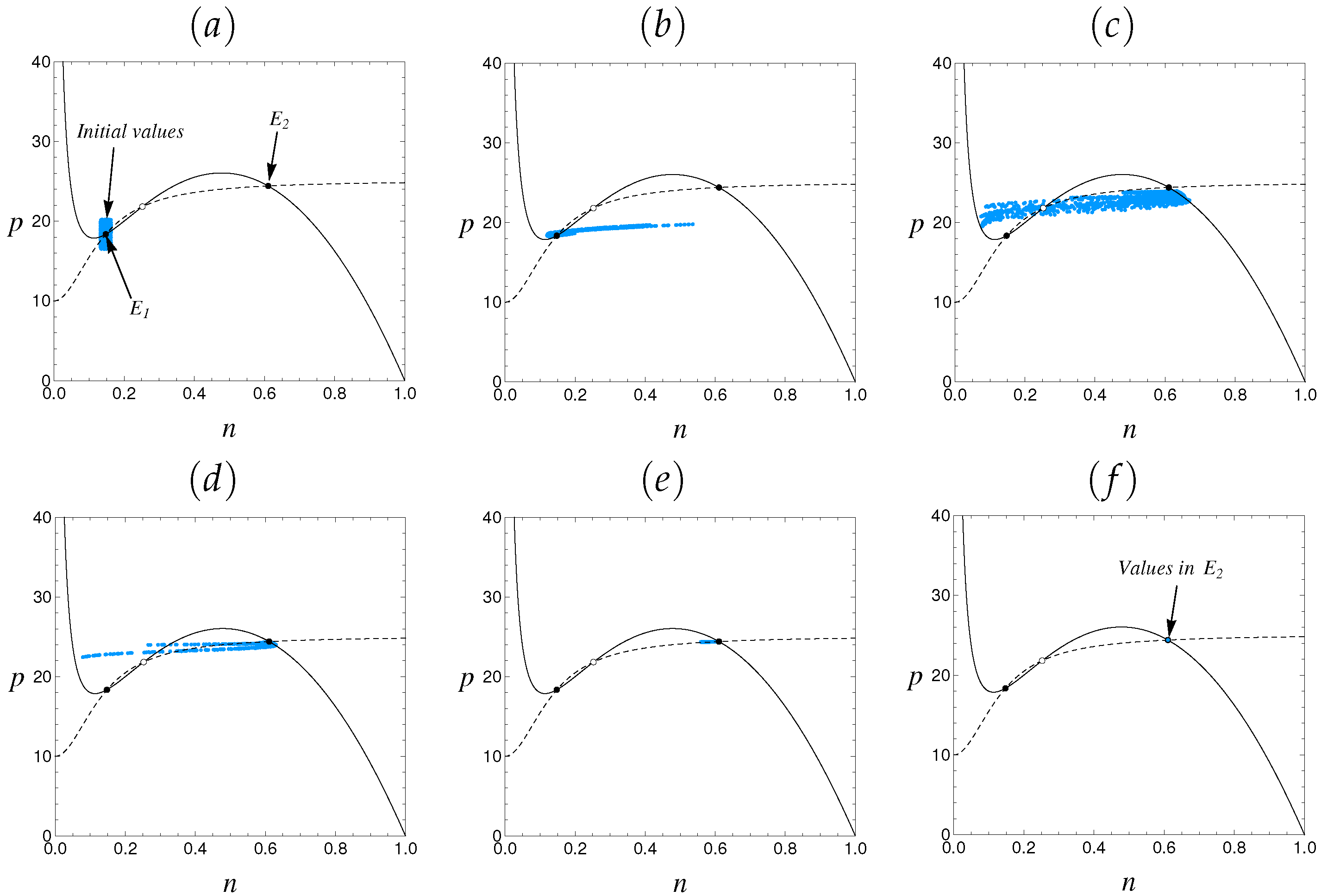

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weide Rodrigues, V.; Cristina Mistro, D.; Díaz Rodrigues, L.A. Pattern Formation and Bistability in a Generalist Predator-Prey Model. Mathematics 2020, 8, 20. https://doi.org/10.3390/math8010020
Weide Rodrigues V, Cristina Mistro D, Díaz Rodrigues LA. Pattern Formation and Bistability in a Generalist Predator-Prey Model. Mathematics. 2020; 8(1):20. https://doi.org/10.3390/math8010020
Chicago/Turabian StyleWeide Rodrigues, Vagner, Diomar Cristina Mistro, and Luiz Alberto Díaz Rodrigues. 2020. "Pattern Formation and Bistability in a Generalist Predator-Prey Model" Mathematics 8, no. 1: 20. https://doi.org/10.3390/math8010020
APA StyleWeide Rodrigues, V., Cristina Mistro, D., & Díaz Rodrigues, L. A. (2020). Pattern Formation and Bistability in a Generalist Predator-Prey Model. Mathematics, 8(1), 20. https://doi.org/10.3390/math8010020




