The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient
Abstract
:1. Introduction
2. The Ill-Posedness of the Backward Heat Conduction Problem
3. The Construction of Truncation Regularized Solution
4. The Improved Method of Fourth-Order Convergence for Choosing the Regularization Parameter
5. The Convergence Rate Analysis of Regularization Solution
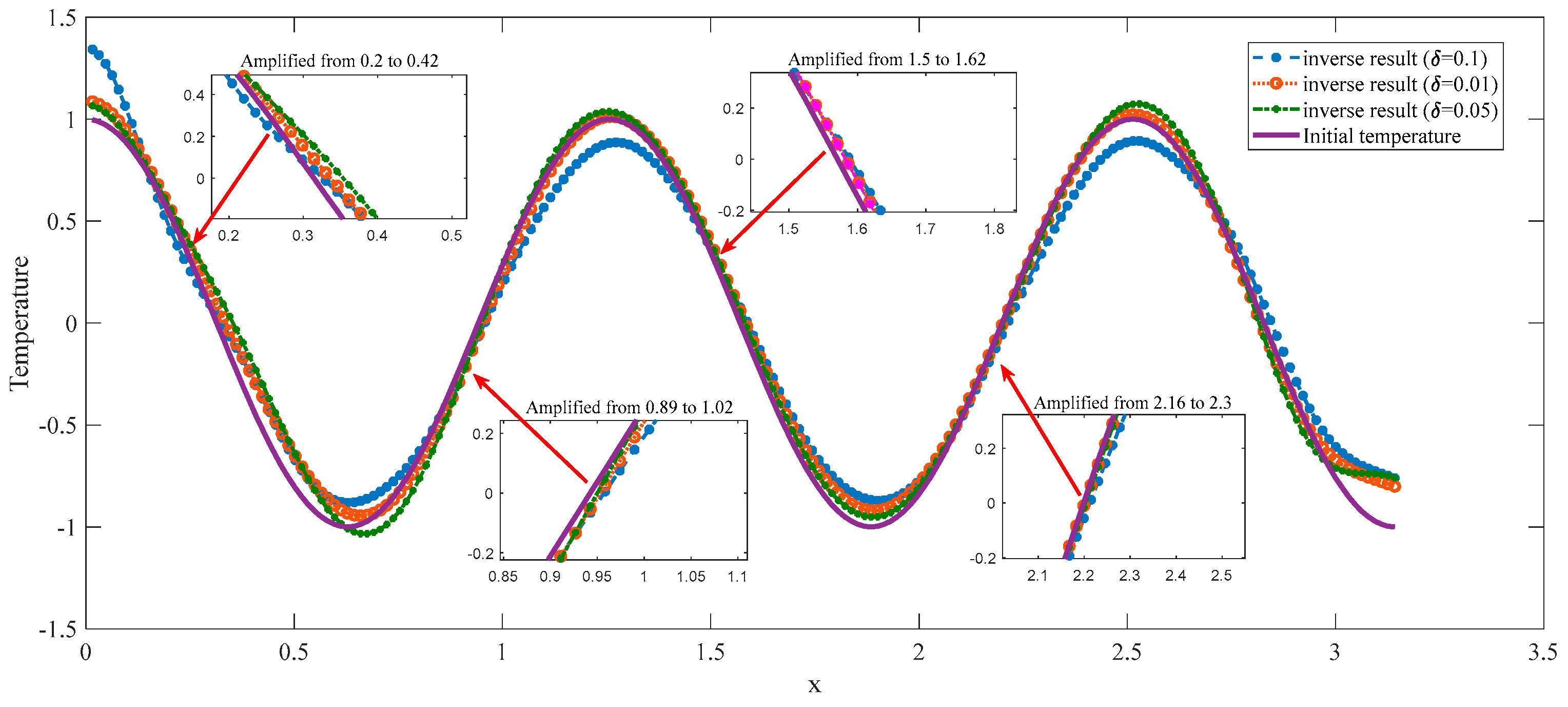
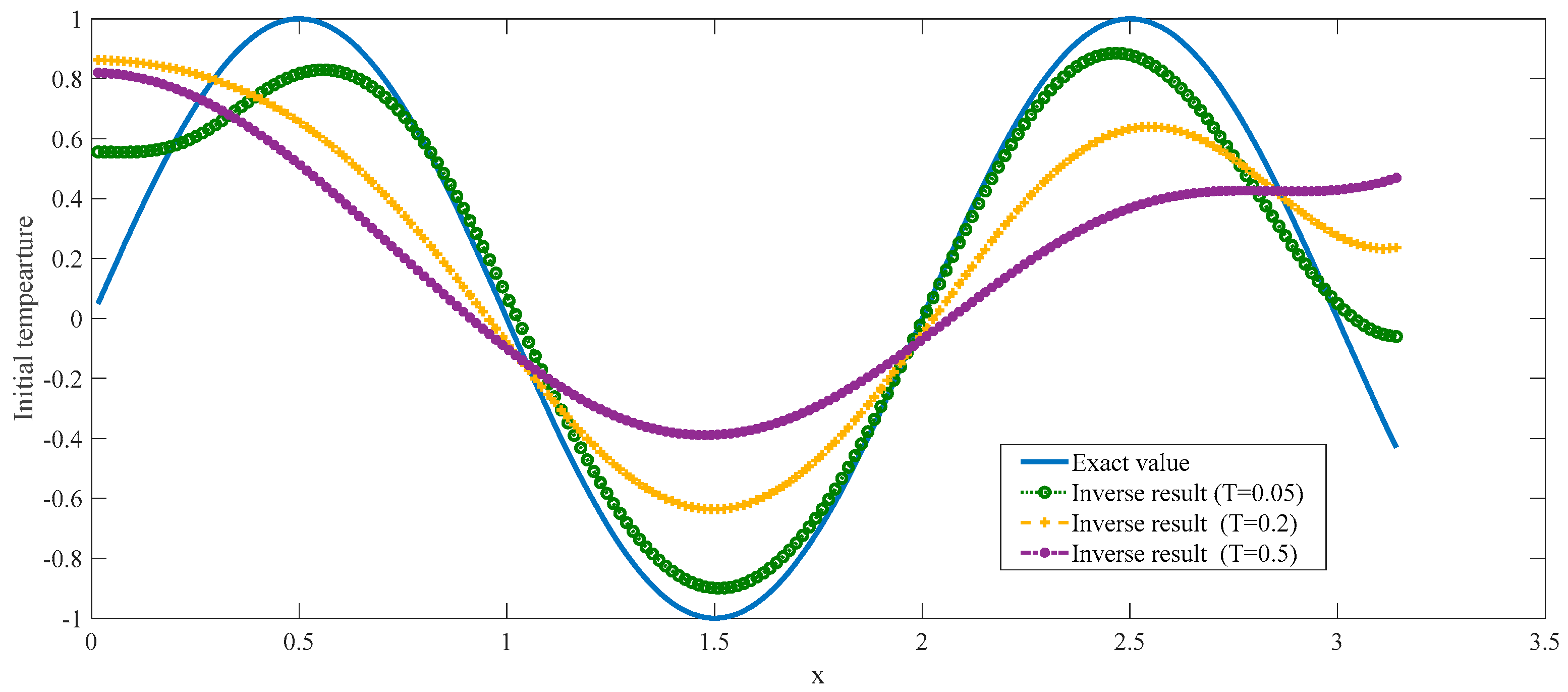
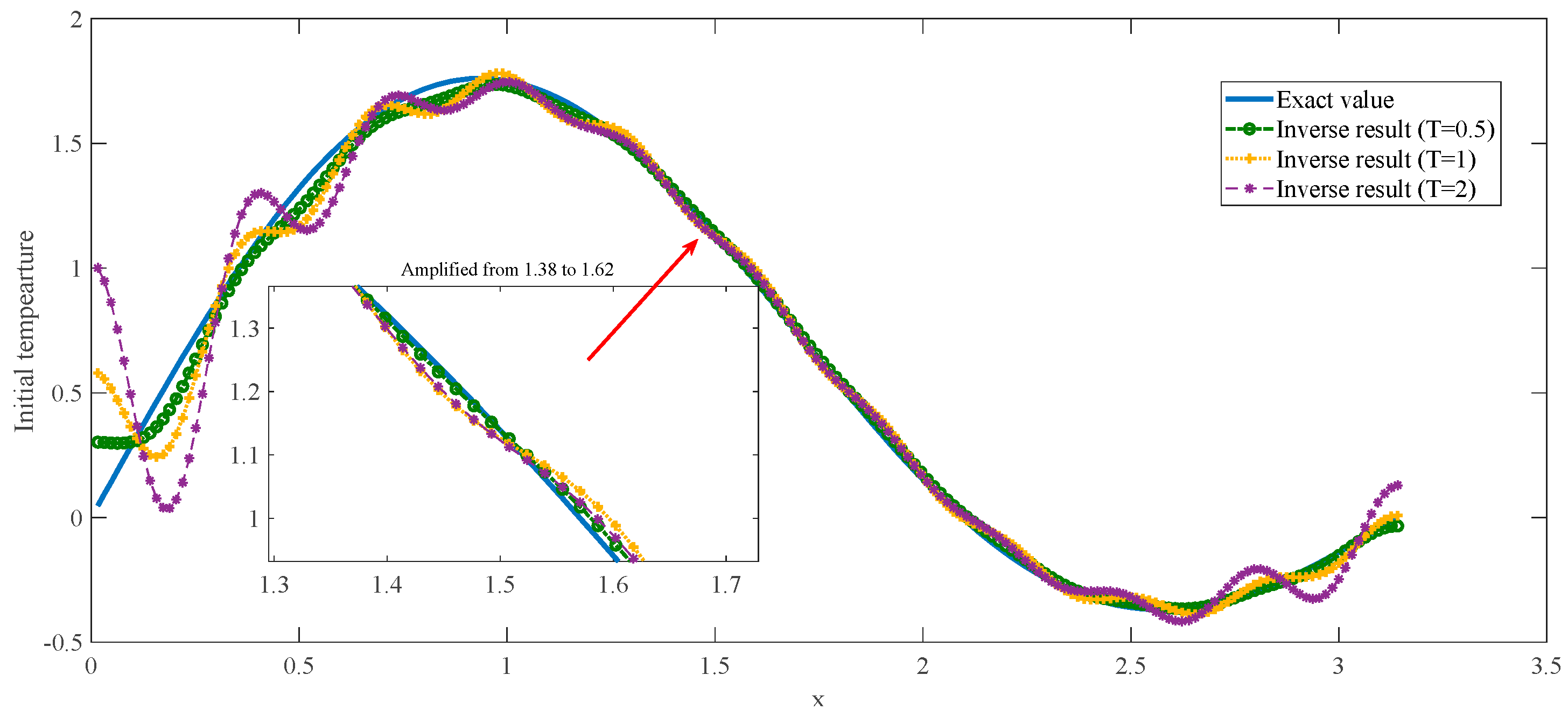
6. The Simulation Experiment
- Step 1: Choose the initial value , error level , stopping criterion , the maximum number and ;
- Step 2: Solve the Equations (73) and (74) with respect to and for ;
- Step 3: Compute , by Equations (71) and (72) respectively;
- Step 4: Obtain by Equation (80); if or iterative number reaches the maximum number , stop; else go back to step 2.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, J.G.; Wei, T.; Zhou, Y.B. Tikhonov Regularization Method for a Backward Problem for the Time-Fractional Diffusion Equation. Appl. Math. Model. 2013, 37, 8518–8532. [Google Scholar] [CrossRef]
- Liu, J.J.; Wang, B.X. Solving the Backward Heat Conduction Problem by Homotopy Analysis Method. Appl. Numer. Math. 2018, 128, 84–97. [Google Scholar] [CrossRef]
- Milad, K.; Fridoun, M.; Mojtaba, H. On Regularization and Error Estimates for the Backward Heat Conduction Problem with Time-Dependent Thermal Diffusivity Factor. Commun. Nonlinear Sci. 2018, 63, 21–37. [Google Scholar]
- Tuan, N.H.; Khoa, V.A.; Truong, M.T.N.; Hung, T.T.; Minh, M.N. Application of the Cut-off Projection to Solve a Backward Heat Conduction Problem in a Two-slab Composite System. Inverse Probl. Sci. 2019, 27, 460–483. [Google Scholar] [CrossRef]
- Tuan, N.H.; Huynh, L.N.; Ngoc, T.B.; Zhou, Y. On a Backward Problem for Nonlinear Fractional Diffusion Equations. Appl. Math. Lett. 2019, 92, 76–84. [Google Scholar] [CrossRef]
- Chen, Y.W. A Modified Lie-group Shooting Method for Multi-dimensional Backward Heat Conduction Problems under Long Time Span. Int. J. Heat Mass Tran. 2018, 127, 948–960. [Google Scholar] [CrossRef]
- Chen, Y.W. A Highly Accurate Backward-forward Algorithm for Multi-dimensional Backward Heat Conduction Problems in Fictitious Time Domains. Int. J. Heat Mass Tran. 2018, 120, 499–514. [Google Scholar] [CrossRef]
- Liu, X.; Qian, Z.M. Backward Problems for Stochastic Differential Equations on the Sierpinski Gasket. Stoch. Proc. Appl. 2018, 10, 3387–3418. [Google Scholar] [CrossRef]
- Cheng, W.; Ma, Y.J.; Fu, C.L. A Regularization Method for Solving the Radially Symmetric Backward Heat Conduction Problem. Appl. Math. Lett. 2014, 30, 38–43. [Google Scholar] [CrossRef]
- Su, L.D. A Radial Basis Function (RBF)-Finite Difference (FD) Method for the Backward Heat Conduction Problem. Appl. Math. Comput. 2019, 354, 232–247. [Google Scholar] [CrossRef]
- Vasil’ev, V.I.; Kardashevskii, A.M. Numerical Solution of the Retrospective Inverse Problem of Heat Conduction with the Help of the Poisson Integral. J. Appl. Ind. Math. 2018, 12, 577–586. [Google Scholar] [CrossRef]
- Beck, J.V.; Woodbury, K.A. Inverse Heat Conduction Problem: Sensitivity Coefficient Insights, Filter Coefficients, and Intrinsic Verification. Int. J. Heat Mass Tran. 2016, 97, 578–588. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.; Kasaeian, A. Flow and Heat Transfer in Non-Newtonian Nanofluids over Porous Surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Shahriyar, G.H.; Faramarz, T.; Masood, S. Analytical Solution of Steady State Heat Conduction Equations in Irregular Domains with Various BCs by Use of Schwarz-Christoffel Conformal Mapping. Thermal Sci. Eng. Progress 2019, 11, 8–18. [Google Scholar]
- Cheng, Y.K.; Chih, Y.L.; Wei, Y.; Chein, S.L.; Chia, M.F. A Novel Space–Time Meshless Method for Solving the Backward Heat Conduction Problem. Int. J. Heat Mass Tran. 2019, 130, 109–122. [Google Scholar]
- Chen, D.H.; Hofmann, B.; Zou, J. Regularization and Convergence for Ill-posed Backward Evolution Equations in Banach Spaces. J. Differ. Equat. 2018, 265, 3533–3566. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, X.C.; Liu, Q. Model Predictive Control of a Dynamic Nonlinear PDE System with Application to Continuous Casting. J. Process Contr. 2018, 65, 41–55. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, X.; Zhang, F.; Wang, S. GPU-based Model Predictive Control for Continuous Casting Spray Cooling Control System Using Particle Swarm Optimization. Control Eng. Pract. 2019, 84, 349–364. [Google Scholar] [CrossRef]
- Hou, R.R. Selection of Regularization Parameter for L1-regularized Damage Detection. J. Sound Vib. 2018, 423, 141–160. [Google Scholar] [CrossRef]
- Park, Y.; Reichel, L.; Rodriguez, G.; Yu, X. Parameter Determination for Tikhonov Regularization Problems in General Form. J. Comput. Appl. Math. 2018, 343, 12–25. [Google Scholar] [CrossRef]
- Reddy, G.D. A Class of Parameter Choice Rules for Stationary Iterated Weighted Tikhonov Regularization Scheme. Appl. Math. Comput. 2019, 347, 464–476. [Google Scholar] [CrossRef]
- Neggal, B.; Boussetila, N.; Rebbani, F. Projected Tikhonov Regularization Method for Fredholm Integral Equations of The First Kind. J. Inequal. Appl. 2016, 195, 1–21. [Google Scholar]
- Zou, Y.K.; Wang, L.J.; Zhang, R. Cubically Convergent Methods for Selecting the Regularization Parameters in Linear Inverse Problems. J. Math. Anal. Appl. 2009, 356, 355–362. [Google Scholar] [CrossRef]
- Chun, C.B. Some Fourth-order Iterative Method for Solving Nonlinear Equations. Appl. Math. Comput. 2008, 195, 454–459. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.J. Solution of Backward Heat Problem by Morozov Discrepancy Principle and Conditional Stability. Numer. Math. J. Chin. Univ. 2005, 14, 180–192. [Google Scholar]
| Algorithm | Iterative Number | ||
|---|---|---|---|
| Newton method [19] | 14 | 2.5396 × 10−4 | 2.812 × 10−4 |
| Cubic convergent method [22] | 12 | 2.5396 × 10−4 | 2.812 × 10−4 |
| Chebyshev method [23] | 13 | 2.5396 × 10−4 | 2.812 × 10−4 |
| Halley method [23] | 12 | 2.5396 × 10−4 | 2.812 × 10−4 |
| Super-Halley method [23] | 11 | 2.5396 × 10−4 | 2.812 × 10−4 |
| The improved method | 10 | 2.5396 × 10−4 | 2.812 × 10−4 |
| Algorithm | Iterative Number | ||
|---|---|---|---|
| Newton method [19] | 12 | 1.2618 × 10−3 | 1.4 × 10−3 |
| Cubic convergent method [22] | 11 | 1.2618 × 10−3 | 1.4 × 10−3 |
| Chebyshev method [23] | 11 | 1.2618 × 10−3 | 1.4 × 10−3 |
| Halley method [23] | 11 | 1.2618 × 10−3 | 1.4 × 10−3 |
| Super-Halley method [23] | 11 | 1.2618 × 10−3 | 1.4 × 10−3 |
| The improved method | 9 | 1.2618 × 10−3 | 1.4 × 10−3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Luo, X.; Zhang, H.; Zhang, Q. The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient. Mathematics 2019, 7, 388. https://doi.org/10.3390/math7050388
Yu Y, Luo X, Zhang H, Zhang Q. The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient. Mathematics. 2019; 7(5):388. https://doi.org/10.3390/math7050388
Chicago/Turabian StyleYu, Yang, Xiaochuan Luo, Huaxi (Yulin) Zhang, and Qingxin Zhang. 2019. "The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient" Mathematics 7, no. 5: 388. https://doi.org/10.3390/math7050388





