n₀-Order Weighted Pseudo Δ-Almost Automorphic Functions and Abstract Dynamic Equations

Abstract

In this paper, we introduce the concept of a $n_0$-order weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic function under the matched space for time scales and we present some properties. The results are valid for q-difference dynamic equations among others. Moreover, we obtain some sufficient conditions for the existence of weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic mild solutions to a class of semilinear dynamic equations under the matched space. Finally, we end the paper with a further discussion and some open problems of this topic.

1. Introduction

In 1962, Bochner introduced the concept of an almost automorphic function on the real numbers (see [1]) and such functions and applications were studied in [2,3,4,5]. In the literature [6,7,8,9,10,11], existence and uniqueness of pseudo almost automorphic solutions to semilinear abstract differential equations were studied. In [12], the authors proposed a concept of weighted pseudo almost automorphic functions (WPAA) and completeness and a composition theorem of the function space formed by WPAA were obtained (this generalizes weighted pseudo almost periodic functions [13,14,15,16]).

Almost periodic and almost automorphic problems of dynamic equations on time scales were studied in [17,18,19,20,21,22,23,24,25]. In 1988, Hilger [26] (see also the books [27,28]) initiated the theory of time scales. An arbitrary closed nonempty subset of the reals is called a time scale and it covers the theories of classical differential and of difference equations (see [29,30]). Based on the translation regularity of periodic time scales, the definition of almost automorphic functions on regular periodic time scales was successfully proposed because of the nice translation-closedness for all periodic time scales. However, for the translation irregularity of some basic time scales such as $\mathbb{T}=\overline{q^{{\mathbb{N}}_0}}:=\{q^t:t\in {\mathbb{N}}_0\mathrm{for}q>1\}\cup \{0\}$ or $\mathbb{T}=\overline{{(-q)}^{\mathbb{Z}}}:=\{{(-q)}^t:t\in \mathbb{Z}\mathrm{for}q>1\}\cup \{0\}$ (which is widely applied to quantum or quantum-like theory) and other types of time scales such as $\mathbb{T}=\pm {\mathbb{N}}^{\frac{1}{2}}:=\{\pm \sqrt{n}:n\in \mathbb{N}\}$ and $\mathbb{T}={\mathbb{T}}_n$ the space of the harmonic numbers, it is very difficult to introduce almost automorphic functions (note it is of interest to study almost automorphic dynamic behavior of solutions to quantum-like dynamic equations including q-difference dynamic equations and others). In the literature [31], the authors introduced and studied a new type of almost periodic functions and stochastic process in which the almost periodic functions and dynamic equations on quantum-like time scales was investigated for the first time.

In this paper, by employing the concept of matched spaces theory, the strict shift-closedness of time scales will be guaranteed under non-translational shift (see [32]), the concepts of $\delta$-almost automorphic functions and $n_0$-order weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions are introduced and their basic properties are obtained. Using this, we establish some sufficient conditions to obtain the existence of weighted pseudo $\delta$-almost automorphic mild solutions to a class of semilinear dynamic equations involving quantum-like dynamic equations like q-difference dynamic equations and others.

The organization of this paper is as follows: in Section 2, we introduce the concept of $\delta$-almost automorphic functions and $n_0$-order weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions under the matched space of time scales, and some properties are presented. In Section 3, the existence of weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic mild solutions is investigated for a type of abstract semilinear dynamic equations. In Section 4 and Section 5, an example is provided and a further discussion is conducted with some interesting open problems of this topic.

2. N₀-Order Weighted Pseudo Δ-Almost Automorphic Functions

In this part, first, we will recall some basic knowledge of matched spaces for time scales. For more details of dynamic equations on time scales and matched spaces, the reader may consult [26,27,28,32,33,34].

Definition 1

([32]). Let ${\Pi }^{*}$ be a subset of $\mathbb{R}$ together with an operation $\tilde{\delta }$ and the pair $({\Pi }^{*},\tilde{\delta })$ be an Abelian group, and $\tilde{\delta }$ be increasing with respect to its second argument, i.e., ${\Pi }^{*}$ and $\tilde{\delta }$ satisfy the following conditions:

(1)

${\Pi }^{*}$ is closed with respect to the operation $\tilde{\delta }$, i.e., for any ${\tau }_1,{\tau }_2\in {\Pi }^{*}$, we have $\tilde{\delta }({\tau }_1,{\tau }_2)\in {\Pi }^{*}$.

(2)

There exists an identity element $e_{{\Pi }^{*}}\in {\Pi }^{*}$ such that $\tilde{\delta }(e_{{\Pi }^{*}},\tau )=\tau$ for all $\tau \in {\Pi }^{*}$.

(3)

For all ${\tau }_1,{\tau }_2,{\tau }_3\in {\Pi }^{*}$, $\tilde{\delta }\left({\tau }_1,\tilde{\delta }({\tau }_2,{\tau }_3)\right)=\tilde{\delta }\left(\tilde{\delta }({\tau }_1,{\tau }_2),{\tau }_3\right)$ and $\tilde{\delta }({\tau }_1,{\tau }_2)=\tilde{\delta }({\tau }_2,{\tau }_1)$.

(4)

For each $\tau \in {\Pi }^{*}$, there exists an element ${\tau }^{-1}\in {\Pi }^{*}$ such that $\tilde{\delta }(\tau ,{\tau }^{-1})=\tilde{\delta }({\tau }^{-1},\tau )=e_{{\Pi }^{*}}$, where $e_{{\Pi }^{*}}$ is the identity element in ${\Pi }^{*}$.

(5)

If ${\tau }_1>{\tau }_2$, then $\tilde{\delta }(·,{\tau }_1)>\tilde{\delta }(·,{\tau }_2)$.

A subset S of $\mathbb{R}$ is called relatively dense with respect to the pair $({\Pi }^{*},\tilde{\delta })$ if there exists a number $L\in {\Pi }^{*}$ such that ${\left[a,\tilde{\delta }(a,L)\right]}_{{\Pi }^{*}}\cap S\ne \varnothing$ (or ${\left[\tilde{\delta }(a,L),a\right]}_{{\Pi }^{*}}\cap S\ne \varnothing$) for all $a\in {\Pi }^{*}$. The number $\left|L\right|$ is called the inclusion length with respect to the group $({\Pi }^{*},\tilde{\delta })$.

From Definition 1, for example, let ${\Pi }^{*}={\mathbb{N}}_{\pm }^{\frac{1}{2}}:=\left\{\pm \sqrt{n},n\in \mathbb{N}\right\}$. Then, $e_{{\Pi }^{*}}=0$ and

$$\tilde{\delta }({\tau }_1,{\tau }_2)=\sqrt{{\tau }_1^2+{\tau }_2^2},{\tau }_1,{\tau }_2\ge 0;\tilde{\delta }({\tau }_1,{\tau }_2)=-\sqrt{{\tau }_1^2+{\tau }_2^2},{\tau }_1,{\tau }_2\le 0;\tilde{\delta }({\tau }_1,{\tau }_2)=0,{\tau }_1>0,{\tau }_2<0.$$

We can obtain the following definition.

Definition 2

([32]). A subset S of $\mathbb{R}$ is called relatively dense with respect to the pair $({\mathbb{N}}_{\pm }^{\frac{1}{2}},\tilde{\delta })$ if there exists a number $L\in {(1,+\infty )}_{{\mathbb{N}}_{+}^{\frac{1}{2}}}$ such that ${[a,\sqrt{a^2+L^2}]}_{{\mathbb{N}}_{+}^{\frac{1}{2}}}\cap S\ne \varnothing$ for all $a\in {\mathbb{N}}_{+}^{\frac{1}{2}}$ and ${[-\sqrt{a^2+L^2},a]}_{{\mathbb{N}}_{-}^{\frac{1}{2}}}\cap S\ne \varnothing$ for all $a\in {\mathbb{N}}_{-}^{\frac{1}{2}}$. The number L is called the inclusion length with respect to the group $({\mathbb{N}}_{\pm }^{\frac{1}{2}},\tilde{\delta })$.

Definition 3

([32]). Let $\mathbb{T}$ and $\Pi$ be time scales, where $\mathbb{T}={\bigcup }_{i\in I_1}{A}_i$, $\Pi ={\bigcup }_{i\in I_2}{B}_i$ and $A_i$ is a sub-timescale of $\mathbb{T}$ for each $i\in I_1$. If ${\Pi }^{*}$ is the largest open subset of the time scale $\Pi$, i.e., $\overline{{\Pi }^{*}}=\Pi$, where $\overline{A}$ denote the closure of the set A, and $({\Pi }^{*},\tilde{\delta })$ is an Abelian group, $I_1,I_2$ are countable index sets; then, we say $\Pi$ is an adjoint set of $\mathbb{T}$ if there exists a bijective mapping:

$$\begin{array}{cc}\hfill F:& \mathbb{T}\to \Pi \hfill \\ & A\in \left\{A_i,i\in I_1\right\}\to B\in \left\{B_i,i\in I_2\right\},\hfill \end{array}$$

i.e., $F(A)=B$. Now, F is called the adjoint mapping between $\mathbb{T}$ and $\Pi$.

Remark 1.

A subset K of a time scale $\mathbb{T}$ is said to be a sub-timescale of $\mathbb{T}$ if and only if $K\subset \mathbb{T}$ is a time scale.

Remark 2.

Note that the largest open subset of a time scale (i.e., the topological interior of a time scale) is unique. For example, let ${\mathbb{T}}_1=\overline{q^{{\mathbb{N}}_0}}:=\{q^t:t\in {\mathbb{N}}_{0}forq>1\}\cup \{0\}$; then, ${\mathbb{T}}_1^{*}=q^{{\mathbb{N}}_0}$; let ${\mathbb{T}}_2=\overline{{(-q)}^{\mathbb{Z}}}:=\{{(-q)}^t:t\in \mathbb{Z}forq>1\}\cup \{0\}$; then, ${\mathbb{T}}_2^{*}={(-q)}^{\mathbb{Z}}$; let ${\mathbb{T}}_3=\pm {\mathbb{N}}^{\frac{1}{2}}:=\{\pm \sqrt{n}:n\in \mathbb{N}\}$; then, ${\mathbb{T}}_3^{*}=\pm {\mathbb{N}}^{\frac{1}{2}}={\mathbb{T}}_3$. For other classical cases, for instance, let ${\mathbb{T}}_4=\mathbb{R}$; then, ${\mathbb{T}}_4={\mathbb{T}}_4^{*}$; let ${\mathbb{T}}_5=h\mathbb{Z}$ ($h>0$); then, ${\mathbb{T}}_5={\mathbb{T}}_5^{*}$, etc.

Definition 4

([32]). Let the pair $({\Pi }^{*},\tilde{\delta })$ be an Abelian group and ${\Pi }^{*},{\mathbb{T}}^{*}$ be the largest open subsets of the time scales $\Pi$ and $\mathbb{T}$, respectively. Furthermore, let $\Pi$ be the adjoint set of $\mathbb{T}$ and F the adjoint mapping between $\mathbb{T}$ and $\Pi$. The operator $\delta :{\Pi }^{*}\times {\mathbb{T}}^{*}\to {\mathbb{T}}^{*}$ satisfies the following properties:

(P₁)

(Monotonicity) The function δ is strictly increasing with respect to all its arguments, i.e., if

$$(T_0,t),(T_0,u)\in {\mathcal{D}}_{\delta }:=\left\{(s,t)\in {\Pi }^{*}\times {\mathbb{T}}^{*}:\delta (s,t)\in {\mathbb{T}}^{*}\right\},$$

then, $t<u$ implies $\delta (T_0,t)<\delta (T_0,u)$; if $(T_1,u),(T_2,u)\in {\mathcal{D}}_{\delta }$ with $T_1<T_2$, then $\delta (T_1,u)<\delta (T_2,u)$.

(P₂)

(Existence of inverse elements) The operator δ has the inverse operator ${\delta }^{-1}:{\Pi }^{*}\times {\mathbb{T}}^{*}\to {\mathbb{T}}^{*}$ and ${\delta }^{-1}(\tau ,t)=\delta ({\tau }^{-1},t)$, where ${\tau }^{-1}\in {\Pi }^{*}$ is the inverse element of τ.

(P₃)

(Existence of identity element) $e_{{\Pi }^{*}}\in {\Pi }^{*}$ and $\delta (e_{{\Pi }^{*}},t)=t$ for any $t\in {\mathbb{T}}^{*}$, where $e_{{\Pi }^{*}}$ is the identity element in ${\Pi }^{*}$.

(P₄)

(Bridge condition) For any ${\tau }_1,{\tau }_2\in {\Pi }^{*}$ and $t\in {\mathbb{T}}^{*}$, $\delta \left(\tilde{\delta }({\tau }_1,{\tau }_2),t\right)=\delta \left({\tau }_1,\delta ({\tau }_2,t)\right)=\delta \left({\tau }_2,\delta ({\tau }_1,t)\right)$.

Then, the operator $\delta (s,t)$ associated with $e_{{\Pi }^{*}}\in {\Pi }^{*}$ is said to be a shift operator on the set ${\mathbb{T}}^{*}$. The variable $s\in {\Pi }^{*}$ in δ is called the shift size. The value $\delta (s,t)$ in ${\mathbb{T}}^{*}$ indicates s units shift of the term $t\in {\mathbb{T}}^{*}$. The set ${\mathcal{D}}_{\delta }$ is the domain of the shift operator δ.

Now, we present the concept of matched spaces for time scales.

Definition 5

([32]). Let the pair $({\Pi }^{*},\tilde{\delta })$ be an Abelian group, and ${\Pi }^{*},{\mathbb{T}}^{*}$ be the largest open subsets of the time scales $\Pi$ and $\mathbb{T}$, respectively. Furthermore, let $\Pi$ be an adjoint set of $\mathbb{T}$ and F the adjoint mapping between $\mathbb{T}$ and $\Pi$. If there exists the shift operator δ satisfying Definition 4, then we say the group $(\mathbb{T},\Pi ,F,\delta )$ is a matched space for the time scale $\mathbb{T}$.

Definition 6

([32]). A time scale $\mathbb{T}$ is called a periodic time scale under a matched space $(\mathbb{T},\Pi ,F,\delta )$ if

$$\tilde{\Pi }:=\left\{\tau \in {\Pi }^{*}:({\tau }^{\pm 1},t)\in {\mathcal{D}}_{\delta },\forall t\in {\mathbb{T}}^{*}\right\}\notin \left\{\{e_{{\Pi }^{*}}\},\varnothing \right\}.$$

(1)

In the following, we always assume that the group $(\mathbb{T},F,\Pi ,\delta )$ is a regular matched space of $\mathbb{T},$ which is a periodic time scale in the sense of Definition 6. For concise notation, we use the symbols $\tilde{\Pi }\cap (-\infty ,e_{{\Pi }^{*}}]:={\tilde{\Pi }}^{-}$ and $\tilde{\Pi }\cap [e_{{\Pi }^{*}},+\infty ):={\tilde{\Pi }}^{+}$. For convenience, we denote $\delta (\tau ,t):={\delta }_{\tau }(t)$ and $\mathbb{X}$ is a Banach space.

For a matched space $(\mathbb{T},F,\Pi ,\delta )$, we denote $A_{i_t}$ the sub-timescale which the argument t belongs to, and clearly, $i_t\in I_1$, where $I_1$ is an index set satisfying $\mathbb{T}={\bigcup }_{i\in I_1}{A}_i$.

Remark 3.

By Definition 6, we will demonstrate the following time scales are periodic under matched spaces:

(i)

$\mathbb{T}=\mathbb{R}$ is periodic since $\tilde{\Pi }:=\left\{\tau \in {\Pi }^{*}:({\tau }^{\pm 1},t)\in {\mathcal{D}}_{\delta },\forall t\in {\mathbb{T}}^{*}\right\}\notin \left\{0,\varnothing \right\}$, where $\tilde{\Pi }={\Pi }^{*}=\mathbb{R}$ and $\delta ({\tau }^{\pm 1},t)=t\pm \tau$.

(ii)

$\mathbb{T}=h\mathbb{Z}$ is periodic since $\tilde{\Pi }:=\left\{\tau \in {\Pi }^{*}:({\tau }^{\pm 1},t)\in {\mathcal{D}}_{\delta },\forall t\in {\mathbb{T}}^{*}\right\}\notin \left\{0,\varnothing \right\}$, where $\tilde{\Pi }={\Pi }^{*}=h\mathbb{Z}$ and $\delta ({\tau }^{\pm 1},t)=t\pm \tau$.

(iii)

$\mathbb{T}=\overline{{(-q)}^{\mathbb{Z}}}$ is periodic since $\tilde{\Pi }:=\left\{\tau \in {\Pi }^{*}:({\tau }^{\pm 1},t)\in {\mathcal{D}}_{\delta },\forall t\in {\mathbb{T}}^{*}\right\}\notin \left\{1,\varnothing \right\}$. In fact,

$$\delta (\tau ,t)=\left\{\begin{array}{c}t\tau ,t\in {\mathbb{T}}_1,\tau \in {\tilde{\Pi }}^{+},\hfill \\ t/\tau ,t\in {\mathbb{T}}_2,\tau \in {\tilde{\Pi }}^{-},\hfill \end{array}\right.{\delta }^{-1}(\tau ,t)=\left\{\begin{array}{c}t/\tau ,t\in {\mathbb{T}}_1,\tau \in {\tilde{\Pi }}^{+},\hfill \\ t\tau ,t\in {\mathbb{T}}_2,\tau \in {\tilde{\Pi }}^{-},\hfill \end{array}\right.$$

where ${\tilde{\Pi }}^{+}=\left\{q^{2n}:q>1,n\in {\mathbb{Z}}^{+}\right\}$, ${\tilde{\Pi }}^{-}=\left\{q^{2n}:q>1,n\in {\mathbb{Z}}^{-}\right\}$ and ${\mathbb{T}}_1=\left\{q^{2n}:q>1,n\in \mathbb{Z}\right\}\cup \{1\}$, ${\mathbb{T}}_2=\left\{-q^{2n-1}:q>1,n\in \mathbb{Z}\right\}\cup \{1\}$. Note that ${\mathbb{T}}_1\cup {\mathbb{T}}_2={\mathbb{T}}^{*}={(-q)}^{\mathbb{Z}}$.

Remark 4.

In Remark 3 $(iii)$, from the property of the operation δ (note that δ is discontinuous at $t=e_{{\Pi }^{*}}=1$), we can obtain the right shift closedness of ${\mathbb{T}}_1$ and the left shift closedness of ${\mathbb{T}}_2$, respectively.

Theorem 1.

If $\mathbb{T}$ is a periodic time scale under a matched space $(\mathbb{T},\Pi ,F,\delta )$ in the sense of Definition 6, then ${\mathbb{T}}^{\delta }=\mathbb{T}$, where ${\mathbb{T}}^{\delta }:=\left\{{\delta }_{\tau }(t):\forall t\in \mathbb{T},\tau \in \tilde{\Pi }\right\}$.

Proof. 

For any $t\in \mathbb{T}$, we have $t={\delta }_{e_{{\Pi }^{*}}}(t)\in {\mathbb{T}}^{\delta }$. Moreover, for any $s\in {\mathbb{T}}^{\delta }$, there exists some $t\in \mathbb{T}$ and $\tau \in \tilde{\Pi }$ such that $s={\delta }_{\tau }(t)\in \mathbb{T}$. This completes the proof. □

Let $\tau \in {\Pi }^{*}$, we introduce a function $A:{\Pi }^{*}\to {\Pi }^{*}$,

$$A(\tau )=\tilde{\delta }(\tau ,e_{{\Pi }^{*}}),\tau \ge e_{{\Pi }^{*}},A(\tau )=\tilde{\delta }({\tau }^{-1},e_{{\Pi }^{*}}),\tau <e_{{\Pi }^{*}}.$$

(2)

Let

$${\mathbb{T}}^{\mathfrak{D}}:=\left\{t\in {\mathbb{T}}^{*}:{\delta }_{\tau }(t)\mathrm{is}\mathsf{\Delta }-\mathrm{differentiable},\mathrm{where}\tau \in \tilde{\Pi }\backslash \{e_{{\Pi }^{*}}\}\right\},$$

$${\tilde{\Pi }}^{\mathfrak{D}}:=\left\{\tau \in \tilde{\Pi }:{\delta }_{\tau }(t)\in {\mathbb{T}}^{\mathfrak{D}},\forall t\in {\mathbb{T}}^{\mathfrak{D}}\right\},$$

and $C^{\delta }(\mathbb{T},\mathbb{X})\subseteq BC(\mathbb{T},\mathbb{X})$ denote a function space which has the property that $\forall \{f_n\}\subseteq C^{\delta }(\mathbb{T},\mathbb{X})$; if $f_n\to f$, then $f_n\left({\delta }_{\tau }(t)\right){\delta }_{\tau }^{\mathsf{\Delta }}(t)\to f\left({\delta }_{\tau }(t)\right){\delta }_{\tau }^{\mathsf{\Delta }}(t)$ for all $t\in {\mathbb{T}}^{\mathfrak{D}}$ and $\tau \in {\tilde{\Pi }}^{\mathfrak{D}}$, where $BC(\mathbb{T},\mathbb{X})$ denotes a bounded function space from $\mathbb{T}$ to $\mathbb{X}$.

Remark 5.

From definition of ${\mathbb{T}}^{\mathfrak{D}}$, if ${\delta }_{\tau }(t)$ is Δ-differentiable for all $t\in {\mathbb{T}}^{*}$, then ${\mathbb{T}}^{*}={\mathbb{T}}^{\mathfrak{D}}$.

Remark 6.

If $\mathbb{T}$ is a time scale which satisfies Definition 6 and ${\mathbb{T}}^{\mathfrak{D}}={\mathbb{T}}^{*}$, then it follows that ${\tilde{\Pi }}^{\mathfrak{D}}=\tilde{\Pi }$. In fact, from Definition 6, we can obtain that ${\tau }^{-1}\in {\tilde{\Pi }}^{\mathfrak{D}}$ and it implies that ${\tilde{\Pi }}^{\mathfrak{D}}=\tilde{\Pi }$.

Remark 7.

Let ${\mathbb{N}}_{\pm }^{\frac{1}{2}}=\left\{\pm \sqrt{n}:n\in \mathbb{N}\right\}$. Then, we can get ${\Pi }^{*}={\mathbb{N}}_{\pm }^{\frac{1}{2}}:=\left\{\pm \sqrt{n},n\in \mathbb{N}\right\}$. Hence,

$$\delta (\tau ,t)=\sqrt{t^2+{\tau }^2},t\ge 0,\tau \in {\tilde{\Pi }}^{+};\delta (\tau ,t)=-\sqrt{t^2+{\tau }^2},t\le 0,\tau \in {\tilde{\Pi }}^{-}$$

(3)

and, for $\left|t\right|\ge \left|\tau \right|$,

$${\delta }^{-1}(\tau ,t)=\sqrt{t^2-{\tau }^2},t\ge 0,\tau \in {\tilde{\Pi }}^{+};{\delta }^{-1}(\tau ,t)=-\sqrt{t^2-{\tau }^2},t\le 0,\tau \in {\tilde{\Pi }}^{-}.$$

(4)

Note that $\delta (\tau ,t)$ is continuous in $t=0$ if and only if $\tau =0$, which implies that, for any $\tau \in \tilde{\Pi }\backslash \{0\}$, $\delta (\tau ,t)$ is not continuous at $t=0=e_{{\Pi }^{*}}$, i.e., $\delta (\tau ,t)$ is not Δ-differentiable at $t=0$ for $\tau \in \tilde{\Pi }\backslash \{0\}$. Moreover, ${\mathbb{T}}^{*}$ has oriented shift closedness in parts by starting with $t=0$. In this example, the part ${[0,+\infty )}_{{\mathbb{T}}^{*}}$ has closedness during right shift and the other part ${(-\infty ,0]}_{{\mathbb{T}}^{*}}$ has closedness during left shift.

Definition 7

([32]). If the adjoint mapping $F:\mathbb{T}\to \Pi$ is continuous and satisfies

(1)

for any $\tau \in {\Pi }^{*},t_0\in \mathbb{T}$, $F\left({\delta }_{\tau }(A_{i_{t_0}})\right)=\tilde{\delta }\left(\tau ,F(A_{i_{t_0}})\right)$ holds;

(2)

if $t_1,t_2\in \mathbb{T}$ and $t_1\le t_2$, then $F(A_{i_{t_1}})\le F(A_{i_{t_2}})$,

we say $(\mathbb{T},F,\Pi ,\delta )$ is a regular matched space for the time scale $\mathbb{T}$.

Lemma 1.

If the time scale $\mathbb{T}$ is periodic in the sense of Definition 6 and $(\mathbb{T},F,\Pi ,\delta )$ is a regular matched space, then for any fixed point $t_0\in \mathbb{T}$, there exists a suitable adjoint mapping $\widehat{F}:\mathbb{T}\to \Pi$ such that $\widehat{F}(A_{i_{t_0}})=e_{{\Pi }^{*}}$.

Proof. 

Since the time scale $\mathbb{T}$ is periodic in the sense of Definition 6, then $e_{{\Pi }^{*}}$ is also the identity element in $\tilde{\Pi }$.

From Definition 6, there exists an inverse element ${[F(A_{i_{t_0}})]}^{-1}\in \tilde{\Pi }$ such that $\tilde{\delta }\left({[F(A_{i_{t_0}})]}^{-1},F(A_{i_{t_0}})\right)=e_{{\Pi }^{*}}$, so there exists a suitable constant $b\in {\Pi }^{*}$ such that $\tilde{\delta }\left(b,F(A_{i_{t_0}})\right)=(F\circ {\delta }_b)(A_{i_{t_0}}):=\widehat{F}(A_{i_{t_0}})=e_{{\Pi }^{*}}$. In fact, from condition $(1)$ of Definition 7, let $b={[F(A_{i_{t_0}})]}^{-1}\in \tilde{\Pi }$, we have $\tilde{\delta }\left(b,F(A_{i_{t_0}})\right)=F\left({\delta }_{{[F(A_{i_{t_0}})]}^{-1}}(A_{i_{t_0}})\right)=e_{{\Pi }^{*}}$. Thus, we have $\widehat{F}=F\circ {\delta }_{{[F(A_{i_{t_0}})]}^{-1}}$. This completes the proof. □

Remark 8.

From condition $(2)$ in Definition 7, if $F(A_{i_{t_0}})=e_{{\Pi }^{*}}$ for a fixed $t_0\in \mathbb{T}$, then it follows that $F(A_{i_t})\le e_{{\Pi }^{*}}$ for $t\le t_0$ and $F(A_{i_t})\ge e_{{\Pi }^{*}}$ for $t\ge t_0$.

Next, we will introduce the concepts of $\delta$-almost automorphic functions and $n_0$-order Δ-almost automorphic functions (i.e., ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions).

Definition 8

(δ-almost automorphic functions).

(i)

Let $f:\mathbb{T}\to \mathbb{X}$ be a bounded continuous function. f is said to be δ-almost automorphic under the matched space $(\mathbb{T},F,\Pi ,\delta )$ if for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset {\tilde{\Pi }}^{\mathfrak{D}},$ one can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }\subset {\tilde{\Pi }}^{\mathfrak{D}}$ such that:

$$g(t)=\underset{n\to \infty }{lim}f\left({\delta }_{{\tau }_n}(t)\right)$$

is well defined for each $t\in {\mathbb{T}}^{\mathfrak{D}}$ and a sequence $\{{\beta }_{{\tau }_n}\}\subset {\tilde{\Pi }}^{\mathfrak{D}}$ that is dependent on $\{{\tau }_n\}$ such that

$$\underset{n\to \infty }{lim}g\left({\delta }_{{\beta }_{{\tau }_n}}(t)\right)=f(t)$$

for each $t\in {\mathbb{T}}^{\mathfrak{D}}.$ Denote by $A{A}^{\delta }(\mathbb{T},\mathbb{X})$ the set of all such functions.

(ii)

A continuous function $f:\mathbb{T}\times \mathbb{X}\to \mathbb{X}$ is said to be δ-almost automorphic if $f(t,x)$ is δ-almost automorphic in $t\in \mathbb{T}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$ Denote by $A{A}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ the set of all such functions.

If there exists inverse element ${\tau }^{-1}$ in ${\tilde{\Pi }}^{\mathfrak{D}}$ for each $\tau \in {\tilde{\Pi }}^{\mathfrak{D}}$, then ${\tilde{\Pi }}^{\mathfrak{D}}=\tilde{\Pi }$ and Definition 8 can be written into the following form by taking ${\beta }_{{\tau }_n}={\tau }_n^{-1}$.

Definition 9.

(i)

Let $f:\mathbb{T}\to \mathbb{X}$ be a bounded continuous function and ${\delta }_{\tau }(·)$ is Δ-differentiable. f is said to be δ-almost automorphic under the matched space $(\mathbb{T},F,\Pi ,\delta )$ if for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset \tilde{\Pi },$ one can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }\subset \tilde{\Pi }$ such that:

$$g(t)=\underset{n\to \infty }{lim}f\left({\delta }_{{\tau }_n}(t)\right)$$

is well defined for each $t\in {\mathbb{T}}^{*}$ and

$$\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n^{-1}}(t)\right)=\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n}^{-1}(t)\right)=f(t)$$

for each $t\in {\mathbb{T}}^{*}.$ Denote by $A{A}^{\delta }(\mathbb{T},\mathbb{X})$ the set of all such functions.

(ii)

A continuous function $f:\mathbb{T}\times \mathbb{X}\to \mathbb{X}$ is said to be δ-almost automorphic if $f(t,x)$ is δ-almost automorphic in $t\in \mathbb{T}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$ Denote by $A{A}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ the set of all such functions.

As an extension of Definition 8, we can introduce the following concept.

Definition 10

(${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions).

(i)

Let $f\in C^{\delta }(\mathbb{T},\mathbb{X})$ be a bounded continuous function. f is said to be${\mathbf{n}}_{\mathbf{0}}$-order Δ-almost automorphic (${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic) under the matched space $(\mathbb{T},F,\Pi ,\delta )$ if there exists some $i_0\ge 1,n_i\in \mathbb{Z},i=1,2,\dots ,i_0$ such that, for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset {\tilde{\Pi }}^{\mathfrak{D}},$ we can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }\subset {\tilde{\Pi }}^{\mathfrak{D}}$ such that:

$$S_g^{\overline{n_1,n_{i_0}}}(t)=\underset{n\to \infty }{lim}f\left({\delta }_{{\tau }_n}(t)\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(t)\right)}^{n_0}$$

is well defined for each $t\in {\mathbb{T}}^{\mathfrak{D}}$ and a sequence $\{{\beta }_{{\tau }_n}\}$ that is dependent on $\{{\tau }_n\}$ such that

$$\underset{n\to \infty }{lim}g\left({\delta }_{{\beta }_{{\tau }_n}}(t)\right)\prod _{i=1}^{i_0}{\left({\delta }_{{\beta }_{{\tau }_n}}^{\mathsf{\Delta }}(t)\right)}^{n_i}=f(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}$$

for each $t\in {\mathbb{T}}^{\mathfrak{D}}$, where

$$S_g^{\overline{n_1,n_{i_0}}}(t)=g(t)\prod _{i=1}^{i_0}{\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_i}.$$

Denote by $A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ the set of all such functions.

(ii)

A continuous function $f\in C^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ is said to be $n_0$-order ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic if $f(t,x)$ is ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic in $t\in \mathbb{T}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$ Denote by $A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ the set of all such functions.

In fact, if there exists inverse element ${\tau }^{-1}$ in ${\tilde{\Pi }}^{\mathfrak{D}}$ for each $\tau \in {\tilde{\Pi }}^{\mathfrak{D}}$, then Definition 10 can also be written into the following form by taking ${\beta }_{{\tau }_n}={\tau }_n^{-1}$.

Definition 11.

(i)

Let $f\in C^{\delta }(\mathbb{T},\mathbb{X})$ be a bounded continuous function and ${\delta }_{\tau }(·)$ is Δ-differentiable. f is said to be ${\mathbf{n}}_{\mathbf{0}}$-order Δ-almost automorphic (${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic) under the matched space $(\mathbb{T},F,\Pi ,\delta )$ if there exists some $i_0\ge 1,n_i\in \mathbb{Z},i=1,2,\dots ,i_0$ such that for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset \tilde{\Pi },$ we can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }\subset \tilde{\Pi }$ such that:

$$S_g^{\overline{n_1,n_{i_0}}}(t)=\underset{n\to \infty }{lim}f\left({\delta }_{{\tau }_n}(t)\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(t)\right)}^{n_0}$$

is well defined for each $t\in {\mathbb{T}}^{*}$ and

$$\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n^{-1}}(t)\right)\prod _{i=1}^{i_0}{\left({\delta }_{{\tau }_n^{-1}}^{\mathsf{\Delta }}(t)\right)}^{n_i}=\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n}^{-1}(t)\right)\prod _{i=1}^{i_0}{\left({\left({\delta }_{{\tau }_n}^{-1}(t)\right)}^{\mathsf{\Delta }}\right)}^{n_i}=f(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}$$

for each $t\in {\mathbb{T}}^{*}$, where

$$S_g^{\overline{n_1,n_{i_0}}}(t)=g(t)\prod _{i=1}^{i_0}{\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_i}.$$

Denote by $A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ the set of all such functions.

(ii)

A continuous function $f\in C^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ is said to be $n_0$-order ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic if $f(t,x)$ is ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic in $t\in \mathbb{T}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$ Denote by $A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ the set of all such functions.

Remark 9.

Note that the condition “${\delta }_{\tau }(·)$ is Δ-differentiable” from Definitions 9 and 11, which implies ${\mathbb{T}}^{*}={\mathbb{T}}^{\mathfrak{D}}$ according to Remark 5.

Remark 10.

Let $i_0=1,n_1=n_0$, so

$$S_g^{\overline{n_1,n_{i_0}}}(t)=g(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}.$$

Then, f is said to be a standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic function.

Remark 11.

In Definition 10, let $i_0=1,n_1=n_0=1$ and ${\delta }_{{\tau }^{\pm 1}}(t)=t\pm \tau$; if $\mathbb{T}=\mathbb{R}$ or $\mathbb{T}=h\mathbb{Z},h>0$, then ${\delta }_{{\tau }^{\pm 1}}^{\mathsf{\Delta }}(t)=1$ and the following classical concepts can be obtained.

Definition 12

(Case I. $\mathbb{T}=\mathbb{R}$, [2]).

(i)

Let $f:\mathbb{R}\to \mathbb{X}$ be a bounded continuous function. f is said to be almost automorphic if for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }$, one can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }$ such that:

$$g(t)=\underset{n\to \infty }{lim}f(t+{\tau }_n)$$

is well defined for each $t\in \mathbb{R}$ and

$$\underset{n\to \infty }{lim}g(t-{\tau }_n)=f(t)$$

for each $t\in \mathbb{R}.$

(ii)

A continuous function $f:\mathbb{R}\times \mathbb{X}\to \mathbb{X}$ is said to be almost automorphic if $f(t,x)$ is almost automorphic in $t\in \mathbb{R}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$

Definition 13

(Case II. $\mathbb{T}=h\mathbb{Z}$, [2]).

(i)

Let $f:h\mathbb{Z}\to \mathbb{X}$ be a bounded continuous function. f is said to be almost automorphic if for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset h\mathbb{Z}$, one can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }$ such that:

$$g(n_0)=\underset{n\to \infty }{lim}f(n_0+{\tau }_n)$$

is well defined for each $n_0\in h\mathbb{Z}$ and

$$\underset{n\to \infty }{lim}g(n_0-{\tau }_n)=f(n_0)$$

for each $n_0\in h\mathbb{Z}.$

(ii)

A continuous function $f:h\mathbb{Z}\times \mathbb{X}\to \mathbb{X}$ is said to be almost automorphic if $f(t,x)$ is almost automorphic in $n_0\in h\mathbb{Z}$ uniformly for all $x\in B,$ where B is any bounded subset of $\mathbb{X}.$

Now, we construct an $\delta$-almost automorphic function through through the following steps.

Example 1.

Consider $\mathbb{T}=\mathbb{R}$ and $\Pi =[0,+\infty )$, we introduce the operators as follows:

$${\delta }_{\tau }(t)=\left\{\begin{array}{c}\tau t,ift\ge 0,\hfill \\ t/\tau ,ift<0,\hfill \end{array}\right.for\tau \in [1,+\infty )\cap {\Pi }^{*},$$

$${\delta }_{\tau }^{-1}(t)=\left\{\begin{array}{c}t/\tau ,ift\ge 0,\hfill \\ \tau t,ift<0,\hfill \end{array}\right.for\tau \in [1,+\infty )\cap {\Pi }^{*},$$

then it follows that $(\mathbb{T},\Pi ,F,\delta )$ is a matched space of the time scale $\mathbb{T}$, where $F(A)=\left|A\right|$ for all $A\in {\mathbb{T}}^{*}=\mathbb{R}\backslash \{0\}$, ${\Pi }^{*}=(0,+\infty )$. Note that $\tilde{\delta }({\tau }_1,{\tau }_2)={\tau }_1·{\tau }_2$, where ${\tau }_1,{\tau }_2\in {\Pi }^{*}$.

Step 1. Periodic function construction. Since $\mathbb{R}$ is periodic under the matched space $(\mathbb{T},\Pi ,F,\delta )$, we construct the following function

$$f_{\tau }(t)=cos\left(\frac{ln\left|t\right|}{ln(1/\sqrt{\tau })}\pi \right),\tau >1andt\in {\mathbb{T}}^{*}=\mathbb{R}\backslash \{0\}$$

under a matched space $(\mathbb{T},\Pi ,F,\delta )$, then it follows that the function is periodic with the period $\tau =P^2,P>1$. In fact,

$$\begin{array}{ccc}\hfill f_{\tau }\left({\delta }_{{\tau }^{\pm 1}}(t)\right)& =& \left\{\begin{array}{c}{f}_{\tau }(t{P}^{\pm 2}),ift\ge 0,\hfill \\ f_{\tau }(t/P^{\pm 2}),ift<0,\hfill \end{array}\right.=cos\left(\frac{ln\left|t\right|\pm 2ln(1/P)}{ln(1/P)}\pi \right)\hfill \\ & =& cos\left(\frac{ln\left|t\right|}{ln(1/P)}\pi \pm 2\pi \right)=cos\left(\frac{ln\left|t\right|}{ln(1/P)}\pi \right)=f_{\tau }(t).\hfill \end{array}$$

Step 2. Almost periodic function construction. Based on Step 1, consider the function

$$\tilde{F}(t)=cos\left(\frac{ln|\sqrt{2}t|}{ln(1/P_1)}\pi \right)+cos\left(\frac{ln|\sqrt{3}t|}{ln(1/P_2)}\pi \right),$$

where $P_1\ne P_2,P_1,P_2>1$ and $t\in {\mathbb{T}}^{*}=\mathbb{R}\backslash \{0\}$, then we obtain that $\tilde{F}(t)$ is almost periodic. From Step 1, let

$$f_{P_1^2}(\sqrt{2}t)=cos\left(\frac{ln|\sqrt{2}t|}{ln(1/P_1)}\pi \right),f_{P_2^2}(\sqrt{3}t)=cos\left(\frac{ln|\sqrt{3}t|}{ln(1/P_2)}\pi \right),$$

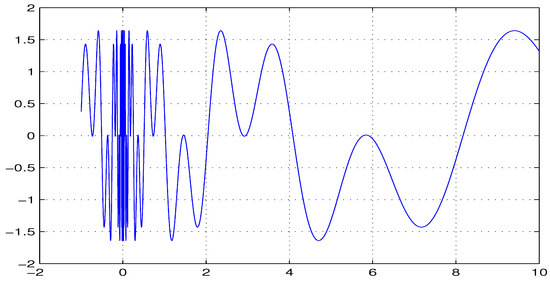
we obtain that $\tilde{F}(t)=f_{P_1^2}(\sqrt{2}t)+f_{P_2^2}(\sqrt{3}t)$. Note that $f_{P_1^2}$ and $f_{P_2^2}$ are periodic with different periods $P_1^2,P_2^2$, respectively (see Figure 1).

Figure 1. Graph of $\tilde{F}(t)=cos\left(\frac{ln|\sqrt{2}t|}{ln(1/P_1)}\pi \right)+cos\left(\frac{ln|\sqrt{3}t|}{ln(1/P_2)}\pi \right)$ with $P_1=2,P_2=\sqrt[3]{2}$.

Step 3. $\delta$-almost automorphic function construction. According to the above, we construct the following function:

$$\widehat{F}(t)=1/\left[cos\left(\frac{ln|\sqrt{2}t|}{ln(1/P_1)}\pi \right)+cos\left(\frac{ln|\sqrt{3}t|}{ln(1/P_2)}\pi \right)\right],$$

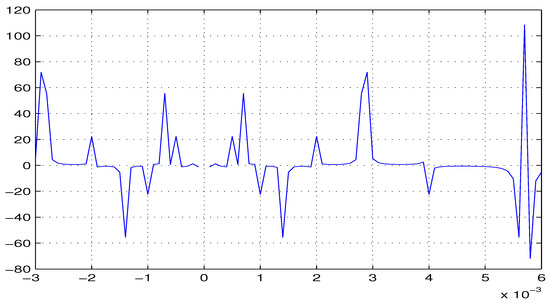
where $P_1\ne P_2,P_1,P_2>1$ and $t\in {\mathbb{T}}^{*}=\mathbb{R}\backslash \{0\}$, then $\widehat{F}(t)$ is almost automorphic under the matched space $(\mathbb{T},\Pi ,F,\delta )$. From Step 2, it follows that $\widehat{F}(t)=\frac{1}{f_{P_1^2}(\sqrt{2}t)+f_{P_2^2}(\sqrt{3}t)}$ (see Figure 2).

Figure 2. Graph of $\widehat{F}(t)=\frac{1}{cos\left(\frac{ln|\sqrt{2}t|}{ln(1/P_1)}\pi \right)+cos\left(\frac{ln|\sqrt{3}t|}{ln(1/P_2)}\pi \right)}$ with $P_1=2,P_2=\sqrt[3]{2}$.

Next, we construct an ${\mathsf{\Delta }}_1^{\delta }$-almost automorphic function through ${\mathsf{\Delta }}_1^{\delta }$-almost periodicity.

Example 2.

Step 1. ${\mathsf{\Delta }}_1^{\delta }$-periodic function construction. For any $a\in \mathbb{R}\backslash \{0\}$, consider the real valued function $f(t)=a/t$ whose domain is ${\mathbb{T}}^{*}={(\sqrt{5})}^{\mathbb{Z}}=\{{(\sqrt{5})}^n,n\in \mathbb{Z}\}$, then $f(t)$ is Δ-periodic with the period $\tau =\sqrt{5}$ under the matched space $(\mathbb{T},\Pi ,F,\delta )$. In fact,

$$f\left({\delta }_{{(\sqrt{5})}^{\pm 1}}(t)\right){\delta }_{{(\sqrt{5})}^{\pm 1}}^{\mathsf{\Delta }}(t)=\frac{a}{{(\sqrt{5})}^{\pm 1}t}{(\sqrt{5})}^{\pm 1}=\frac{a}{t}=f(t).$$

Step 2. ${\mathsf{\Delta }}_1^{\delta }$-almost periodic function construction. On $\mathbb{T}=\overline{{(\sqrt{5})}^{\mathbb{Z}}}=\{{(\sqrt{5})}^n,n\in \mathbb{Z}\}\cup \{0\}$, let $a,b\in \mathbb{R}\backslash \{0\},a\ne b$ and

$$g_1(t)=\frac{a}{t},g_2(t)=\frac{b}{{(-1)}^{{log}_{\sqrt{5}}t}t},\tilde{G}(t)=g_1(t)+g_2(t)=\frac{1}{t}+\frac{b}{{(-1)}^{{log}_{\sqrt{5}}t}t}.$$

From Step 1, we have $g_1\left({\delta }_{{(\sqrt{5})}^{\pm 1}}(t)\right){\delta }_{{(\sqrt{5})}^{\pm 1}}^{\mathsf{\Delta }}(t)=g_1(t)$. Note that

$$\begin{array}{ccc}\hfill g_2\left({\delta }_{{(\sqrt{5})}^{\pm 2}}(t)\right){({\delta }_{{(\sqrt{5})}^{\pm 2}})}^{\mathsf{\Delta }}(t)& =& \frac{b}{{(-1)}^{{log}_{\sqrt{5}}{(\sqrt{5})}^{\pm 2}t}·{(\sqrt{5})}^{\pm 2}t}·{(\sqrt{5})}^{\pm 2}=\frac{b}{{(-1)}^{\pm 2+{log}_{\sqrt{5}}t}·t}\hfill \\ & =& \frac{b}{{(-1)}^{{log}_{\sqrt{5}}t}t}=g_2(t).\hfill \end{array}$$

Hence, $\tilde{G}(t)$ is a ${\mathsf{\Delta }}_1^{\delta }$-almost periodic function under the matched space $(\mathbb{T},\Pi ,F,\delta )$ and $g_1(t)$ and $g_2(t)$ have completely different periods.

Step 3. ${\mathsf{\Delta }}_1^{\delta }$-almost automorphic function construction. According to Step 2, on $\mathbb{T}=\overline{{(\sqrt{5})}^{\mathbb{Z}}}=\{{(\sqrt{5})}^n,n\in \mathbb{Z}\}\cup \{0\}$, consider the following function on ${\mathbb{T}}^{*}$:

$$\widehat{G}(t)=1/\left[\frac{a}{t}+\frac{b}{{(-1)}^{{log}_{\sqrt{5}}t}t}\right],a,b\in \mathbb{R}\backslash \{0\},a\ne b,$$

then $\widehat{G}(t)$ is almost automorphic under the matched space $(\mathbb{T},\Pi ,F,\delta )$. From Step 2, it follows that $\widehat{G}(t)=\frac{1}{\tilde{G}(t)}$.

Remark 12.

From Examples 1–2, it demonstrates that Definitions 8 and 10 not only include the concepts of almost automorphic functions on periodic time scales under translations but also cover some new types of almost automorphic functions so almost automorphic problems for q-difference equations and others can be proposed and studied.

In what follows, for the convenience of our discussion, we always assume that ${\delta }_{\tau }(·)$ is $\mathsf{\Delta }$-differentiable and the time scale $\mathbb{T}$ satisfies Definition 6, i.e., ${\mathbb{T}}^{\mathfrak{D}}={\mathbb{T}}^{*}$ and ${\tilde{\Pi }}^{\mathfrak{D}}=\tilde{\Pi }$.

Let $\mathbb{X}$ be a Banach space endowed with the norm $\parallel ·\parallel$. Now $B(\mathbb{X},\mathbb{Y})$ denotes the Banach space of all bounded linear operators from $\mathbb{X}$ to $\mathbb{Y}$, $B(\mathbb{X},\mathbb{Y}):=B(\mathbb{X})$ if $\mathbb{X}=\mathbb{Y}$. Also $BC(\mathbb{T},\mathbb{X})$ is the space of bounded continuous function from $\mathbb{T}$ to $\mathbb{X}$ equipped with the supremum norm ${\parallel u\parallel }_{\infty }={sup}_{t\in \mathbb{T}}\parallel u(t)\parallel .$

Lemma 2.

If ${\delta }_{\tau }(·)$ is Δ-differentiable for $t\in {\mathbb{T}}^{*}$, then $A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ equipped with the norm ${\parallel ·\parallel }_{\infty }$ is a Banach space.

Proof. 

Let $\{f_n\}\subset A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ be a Cauchy sequence. Since $\mathbb{X}$ is a Banach space, we can obtain $f_n\to f,n\to \infty$. Hence, for any $\epsilon >0$, there is a ${\tilde{N}}_1>0$ so that $n>{\tilde{N}}_1$ implies

$$\parallel f_n\left({\delta }_{\tau }(t)\right){\left({\delta }_{\tau }^{\mathsf{\Delta }}(t)\right)}^{n_0}-f\left({\delta }_{\tau }(t)\right){\left({\delta }_{\tau }^{\mathsf{\Delta }}(t)\right)}^{n_0}{\parallel }_{\infty }<\epsilon \mathrm{for}\tau \in \tilde{\Pi }.$$

Because $\{f_n\}\subset A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$, for each $n\in \mathbb{N}$ and $\epsilon >0$, there exists a ${\tilde{N}}_2>0$ and $\{g_n\}$ so that $\tilde{n}>{\tilde{N}}_2$, for any sequence $\{{\tau }_k\}\subset \tilde{\Pi }$, there is a subsequence $\{{\tau }_{\tilde{n}}\}$ such that

$$\parallel f_n\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}-S_{g_n}^{\overline{n_1,n_{i_0}}}(t){\parallel }_{\infty }\le \epsilon .$$

(5)

Now, take ${\tilde{N}}_3=max\{{\tilde{N}}_1,{\tilde{N}}_2\}$, and when $n>{\tilde{N}}_3$, we obtain

$$\begin{array}{ccc}\hfill \parallel f\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}-S_{g_n}^{\overline{n_1,n_{i_0}}}(t){\parallel }_{\infty }& \le & \parallel f\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}-f_n\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}{\parallel }_{\infty }\hfill \\ & & +\parallel f_n\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}-S_{g_n}^{\overline{n_1,n_{i_0}}}(t){\parallel }_{\infty }\le 2\epsilon .\hfill \end{array}$$

We can take $n={\tilde{N}}_3+1$ such that

$$\underset{\tilde{n}\to \infty }{lim}{f}_{{\tilde{N}}_3+1}\left({\delta }_{{\tau }_{\tilde{n}}}(t)\right){\left({\delta }_{{\tau }_{\tilde{n}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}=S_{g_{{\tilde{N}}_3+1}}^{\overline{n_1,n_{i_0}}}(t),$$

which means that $f\in A{A}_{n_0}^{\delta }$. Hence, $A{A}_{n_0}^{\delta }$ is a Banach space equipped with the norm ${\parallel ·\parallel }_{\infty }$. □

Let U be the set of all functions $\rho :\mathbb{T}\to (0,\infty )$ which are positive and $\rho (t){\left({\delta }_{\tau }^{\mathsf{\Delta }}(t)\right)}^{n_0}$ be locally integrable over $\mathbb{T}$ for $\tau \in \tilde{\Pi }$ and $n_0\in \mathbb{N}$.

Remark 13.

Note that, if $\mathbb{T}=\mathbb{R}$ or $h\mathbb{Z},h>0$, then $\rho :\mathbb{T}\to (0,\infty )$ is positive and locally integrable over $\mathbb{T}$.

Remark 14.

Since ${\delta }_{\tau }^{\mathsf{\Delta }}(t)>0$ by $(P_1)$ from Definition 4, then $\rho (t){\delta }_{\tau }^{\mathsf{\Delta }}(t)>0$ for $\rho (t)>0$. Hence, if ${\delta }_{\tau }(·)$ is Δ-differentiable and $\rho (t)>0$, then $\rho (t){\delta }_{\tau }^{\mathsf{\Delta }}(t)$ is locally integrable over $\mathbb{T}$ is equivalent to the local integrability of $\rho (t)$ over $\mathbb{T}$.

For a given $r\in [e_{{\Pi }^{*}},+\infty )\cap \tilde{\Pi }:={\tilde{\Pi }}^{+},t_0\in \mathbb{T}$, set

$$m^{\delta }(t_0,r,\rho ):={\int }_{{\delta }_r^{-1}(t_0)}^{{\delta }_r(t_0)}\rho (s)\mathsf{\Delta }s,$$

(6)

for each $\rho \in U.$

Remark 15.

Under a regular matched space $(\mathbb{T},F,\Pi ,\delta )$, from Definition 7, we have $F\left({\left[{\delta }_{r^{-1}}(t_0),{\delta }_r(t_0)\right]}_{\mathbb{T}}\right)={\left[\tilde{\delta }(r^{-1},F(A_{i_{t_0}})),\tilde{\delta }(r,F(A_{i_{t_0}}))\right]}_{{\Pi }^{*}}$ i.e.,

$${\left[{\delta }_{r^{-1}}(t_0),{\delta }_r(t_0)\right]}_{\mathbb{T}}=F^{-1}\left({\left[\tilde{\delta }(r^{-1},F(A_{i_{t_0}})),\tilde{\delta }(r,F(A_{i_{t_0}}))\right]}_{{\Pi }^{*}}\right).$$

In particular, if $F(A_{i_{t_0}})=e_{{\Pi }^{*}}$, then ${\left[{\delta }_{r^{-1}}(t_0),{\delta }_r(t_0)\right]}_{\mathbb{T}}=F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})$, and, in this case, we say Label (6) is the standard weighted function and

$$m^{\delta }(t_0,r,\rho ):=m^{\delta }(r,\rho )={\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\rho (s)\mathsf{\Delta }s,$$

(7)

which is independent of $t_0$. Throughout the paper, we assume that $(\mathbb{T},F,\Pi ,\delta )$ is a regular matched space and employ the standard weighted function (7).

Remark 16.

For any fixed $t_0\in \mathbb{T}$ and $\tau \in \mathbb{R}$, if $r\to \infty$, then ${\delta }_r(t_0)\to \infty$ and $\tilde{\delta }(\tau ,r)\to \infty$. Hence, under a regular matched space $(\mathbb{T},F,\Pi ,\delta )$, we have $\mathrm{mes}\left(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})\right):={\mu }_{\mathsf{\Delta }}\left(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})\right)\to \infty$ if $r\to \infty$.

Let $B{C}^{\delta }(\mathbb{T},\mathbb{X}):=\{f:f\in C^{\delta }(\mathbb{T},\mathbb{X})\mathrm{is}\mathrm{bounded}\}$ and for any function $f\in B{C}^{\delta }(\mathbb{T},\mathbb{X})$, we use the notation $S_f^{n_0}:=f(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}$.

Define

$$U_{\infty }:=\{\rho \in U:\underset{r\to \infty }{lim}{m}^{\delta }(r,\rho )=\infty \}$$

and

$$U_B:=\left\{\rho \in U_{\infty }:\rho \mathrm{is}\mathrm{bounded}\mathrm{and}\underset{s\in \mathbb{T}}{inf}\rho (s)>0\right\}.$$

It is clear that $U_B\subset U_{\infty }\subset U.$

Now, for $\rho \in U_{\infty }$, define

$$\begin{array}{c}\hfill PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ):=\left\{f\in B{C}^{\delta }(\mathbb{T},\mathbb{X}):\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s=0,r\in {\tilde{\Pi }}^{+}\right\}.\end{array}$$

Similarly, we define $PA{A}_0^{\delta ,n_0}(\mathbb{T}\times \mathbb{X},\rho )$ as the collection of all functions $\tilde{F}:\mathbb{T}\times \mathbb{X}\to \mathbb{X}$ continuous with respect to its two arguments and $\tilde{F}(·,y)$ is bounded for each $y\in \mathbb{X},$ and

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\tilde{F}}^{n_0}(s,y)\parallel \rho (s)\mathsf{\Delta }s=0$$

uniformly for $y\in \mathbb{X},$ where $r\in {\tilde{\Pi }}^{+}$.

Lemma 3.

If ${\delta }_{\tau }(·)$ is Δ-differentiable for $t\in {\mathbb{T}}^{*}$, then $PA{A}_0^{\delta ,n_0}(\mathbb{T},\mathbb{X})$ equipped with the norm ${\parallel ·\parallel }_{\infty }$ is a Banach space.

Proof. 

Let $\{f_n\}$ be a Cauchy sequence in $PA{A}_0^{\delta ,n_0}(\mathbb{T},\mathbb{X})$. Then, for any $\epsilon >0$, there is a $N>0$ such that $n,m>N$ implies

$$\parallel S_{f_n}^{n_0}(t)-S_{f_m}^{n_0}(t)\parallel \le \parallel f_n(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}-f_m(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}\parallel \le \epsilon ,$$

which indicates that $\{S_{f_n}^{n_0}\}$ is also a Cauchy sequence. Since $\mathbb{X}$ is a Banach space, so we have $\parallel S_{f_n}^{n_0}(t)-S_f^{n_0}{(t)\parallel }_{\infty }\to 0$ as $n\to \infty .$ Therefore, from the definition of $PA{A}_0^{\delta ,n_0}$, we obtain $f\in PA{A}_0^{\delta ,n_0}$. This completes the proof. □

Definition 14.

The sets $WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )$ and $WPA{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\rho )$ of standard $n_0$-order weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions are introduced as follows:

$$WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )=\left\{f\in B{C}^{\delta }(\mathbb{T},\mathbb{X}):S_f^{n_0}=S_g^{n_0}+S_{\varphi }^{n_0},g\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})and\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )\right\};$$

$$\begin{array}{ccc}\hfill WPA{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\rho )& =& \{f\in B{C}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X}):S_f^{n_0}=S_g^{n_0}+S_{\varphi }^{n_0},g\in A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})\hfill \\ & & and\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T}\times \mathbb{X},\rho )\},\hfill \end{array}$$

and we say $S_f^{n_0}$ is the main part of f.

From the Definition of $WPA{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$, the following lemma is immediate:

Lemma 4.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and ${\delta }_{\tau }(·)$ is Δ-differentiable for all $t\in {\mathbb{T}}^{*}$. If $f=g+\varphi$ with a standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic function $g\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$, and $\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )$ where $\rho \in U_{\infty }$, then $S_g^{n_0}(\mathbb{T})\subset \overline{S_f^{n_0}(\mathbb{T})}.$

Proof. 

We prove it by contradiction. Assume that the claim does not hold. Then, there exist a $t_0\in \mathbb{T}$ and $\epsilon >0$ such that $\parallel S_g(t_0)-S_f(t)\parallel \ge 2\epsilon ,t\in \mathbb{T}.$ Since $g\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$, fix $t_0\in \mathbb{T}$ and $\epsilon >0$ and set $B_{\epsilon }:=\left\{\tau \in {\Pi }^{*}:\parallel g\left({\delta }_{\tau }(t_0)\right){\left({\delta }_{\tau }^{\mathsf{\Delta }}(t_0)\right)}^{n_0}-g(t_0){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t_0)\right)}^{n_0}\parallel <\epsilon \right\}$. According to Lemma 2.1.1 of [35], there exist $s_1,s_2,\dots ,s_m\in {\Pi }^{*}$ such that ${\bigcup }_{i=1}^m\tilde{\delta }\left(B_{\epsilon },s_i\right):={\bigcup }_{i=1}^m{\tilde{\delta }}_{B_{\epsilon }}(s_i)={\Pi }^{*}$. Without loss of generality, we assume that $s_1,s_2,\dots ,s_j\in {\tilde{\Pi }}^{-}$ and $s_{j+1},s_{j+2},\dots ,s_m\in {\tilde{\Pi }}^{+}$. Let

$${\widehat{s}}_i=\left\{\begin{array}{c}\tilde{\delta }\left(s_i,F(A_{i_{t_0}})\right),s_i\in {\tilde{\Pi }}^{-},\hfill \\ \tilde{\delta }\left(s_i^{-1},F(A_{i_{t_0}})\right),s_i\in {\tilde{\Pi }}^{+},\hfill \end{array}\right.$$

where $F(A_{i_{t_0}})=e_{{\Pi }^{*}}$, then ${\widehat{s}}_i\le e_{{\Pi }^{*}}$ and $\eta ={max}_{1\le i\le m}A({\widehat{s}}_i)>e_{{\Pi }^{*}}$. For $T\in {\Pi }^{*}$ with $A(T)>\eta$ and

$$B_{\epsilon ,T}^{(i)}={\left[\tilde{\delta }\left({\widehat{s}}_i^{-1},\tilde{\delta }(T^{-1},\eta )\right),\tilde{\delta }\left({\widehat{s}}_i^{-1},\tilde{\delta }(T,{\eta }^{-1}\right)\right]}_{{\Pi }^{*}}\cap \tilde{\delta }\left(F(A_{i_{t_0}}),B_{\epsilon }\right),1\le i\le m,$$

one has

$$\bigcup _{i=1}^m\tilde{\delta }({\widehat{s}}_i,B_{\epsilon ,T}^{(i)})\supseteq {\left[\tilde{\delta }(T^{-1},\eta ),\tilde{\delta }(T,{\eta }^{-1})\right]}_{{\Pi }^{*}}.$$

Thus, $F^{-1}\left({\bigcup }_{i=1}^m\tilde{\delta }({\widehat{s}}_i,B_{\epsilon ,T}^{(i)})\right)\supseteq F^{-1}\left({\left[\tilde{\delta }(T^{-1},\eta ),\tilde{\delta }(T,{\eta }^{-1})\right]}_{{\Pi }^{*}}\right).$

Using the fact that $B_{\epsilon ,T}^{(i)}\subset {[T^{-1},T]}_{{\Pi }^{*}}\cap \tilde{\delta }\left(F(A_{i_{t_0}}),B_{\epsilon }\right)$, $i=1,2,\dots ,m$, we obtain

$$\begin{array}{ccc}\hfill m^{\delta }\left(\tilde{\delta }(T,{\eta }^{-1}),\rho \right)& =& {\int }_{F^{-1}({[\tilde{\delta }(T^{-1},\eta ),\tilde{\delta }(T,{\eta }^{-1})]}_{{\Pi }^{*}})}\rho (t)\mathsf{\Delta }t\le {\int }_{F^{-1}({\cup }_{i=1}^m\tilde{\delta }({\widehat{s}}_i,B_{\epsilon ,T}^{(i)}))}\rho (t)\mathsf{\Delta }t\hfill \\ & \le & \sum _{i=1}^m{\int }_{F^{-1}(B_{\epsilon ,T}^{(i)})}\rho \left({\delta }_{{\widehat{s}}_i}(t)\right){\delta }_{{\widehat{s}}_i}^{\mathsf{\Delta }}(t)\mathsf{\Delta }t\le \sum _{i=1}^m{a}_i{\int }_{F^{-1}(B_{\epsilon ,T}^{(i)})}\rho (t)\mathsf{\Delta }t\hfill \\ & \le & \underset{1\le i\le m}{max}\{a_i\}\sum _{i=1}^m{\int }_{F^{-1}({[T^{-1},T]}_{{\Pi }^{*}}\cap \tilde{\delta }(F(A_{i_{t_0}}),B_{\epsilon }))}\rho (t)\mathsf{\Delta }t\hfill \\ & =& \underset{1\le i\le m}{max}\{a_i\}·m·{\int }_{F^{-1}({[T^{-1},T]}_{{\Pi }^{*}}\cap \tilde{\delta }(F(A_{i_{t_0}}),B_{\epsilon }))}\rho (t)\mathsf{\Delta }t,\hfill \end{array}$$

where $a_i={lim\; sup}_{t\to \infty }\frac{\rho ({\delta }_{{\widehat{s}}_i}(t)){\delta }_{{\widehat{s}}_i}^{\mathsf{\Delta }}(t)}{\rho (t)}<\infty$.

On the other hand, from the triangle inequality, for any $t\in \tilde{\delta }\left(F(A_{i_{t_0}}),B_{\epsilon }\right)$, one has

$$\parallel S_{\varphi }^{n_0}(t)\parallel =\parallel S_f^{n_0}(t)-S_g^{n_0}(t)\parallel \ge \parallel S_g^{n_0}(t_0)-S_f^{n_0}(t)\parallel +\parallel S_g^{n_0}(t)-S_g^{n_0}(t_0)\parallel >\epsilon .$$

Then,

$$\begin{array}{cc}& \frac{1}{m^{\delta }(T,\rho )}{\int }_{F^{-1}({[T^{-1},T]}_{{\Pi }^{*}})}\rho (t)\parallel S_{\varphi }^{n_0}(t)\parallel \mathsf{\Delta }t\hfill \\ \ge & \frac{1}{m^{\delta }(T,\rho )}{\int }_{F^{-1}({[T^{-1},T]}_{{\Pi }^{*}}\cap \tilde{\delta }(F(A_{i_{t_0}}),B_{\epsilon }))}\rho (t)\parallel S_{\varphi }^{n_0}(t)\parallel \mathsf{\Delta }t\hfill \\ \ge & \frac{\epsilon }{m^{\delta }(T,\rho )}{\int }_{F^{-1}({[T^{-1},T]}_{{\Pi }^{*}}\cap \tilde{\delta }(F(A_{i_{t_0}}),B_{\epsilon }))}\rho (t)\mathsf{\Delta }t\hfill \\ \ge & \frac{\epsilon }{m^{\delta }(T,\rho )}·\frac{m^{\delta }(\tilde{\delta }(T,{\eta }^{-1}),\rho )}{m·{max}_{1\le i\le m}\{a_i\}}\to \frac{b\epsilon }{m·{max}_{1\le i\le m}\{a_i\}}\mathrm{as}T\to \infty ,\hfill \end{array}$$

where $b={lim\; sup}_{t\to \infty }\frac{m^{\delta }(\tilde{\delta }(T,{\eta }^{-1}),\rho )}{m^{\delta }(T,\rho )}<\infty$ since $\rho \in U_{\infty }$. This is a contradiction since $\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T},\mathbb{X})$. Hence, the claim is true. This completes the proof. □

In the following, we introduce the following function space:

$$S_{A{A}_{n_0}^{\delta }}:=\left\{S_f^{n_0}=f(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}:f\in A{A}_{n_0}^{\delta }\right\},S_{PA{A}_0^{\delta ,n_0}}:=\left\{S_{\varphi }^{n_0}=\varphi (t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}:\varphi \in PA{A}_0^{\delta ,n_0}\right\},$$

$$S_{WPA{A}_{n_0}^{\delta }}:=\left\{S_f^{n_0}=f(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}:f\in WPA{A}_{n_0}^{\delta }\right\}.$$

Remark 17.

From Lemmas 2–3, we can easily obtain that $S_{A{A}_{n_0}^{\delta }}$ and $S_{PA{A}_0^{\delta ,n_0}}$ are also Banach spaces equipped with the norm ${\parallel ·\parallel }_{\infty }$.

Theorem 2.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space. Assume that $S_{PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )}$ is shift invariant under the matched space $(\mathbb{T},F,\Pi ,\delta )$. Then, the decomposition of a main part for a standard $n_0$-order weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic function as $S_{A{A}_{n_0}^{\delta }}\oplus S_{PA{A}_0^{\delta ,n_0}}$ is unique for any $\rho \in U_{\infty }$.

Proof. 

Assume that $S_f^{n_0}=S_{g_1}^{n_0}+S_{{\varphi }_1}^{n_0}$ and $S_f^{n_0}=S_{g_2}^{n_0}+S_{{\varphi }_2}^{n_0}.$ Then, $0=(S_{g_1}^{n_0}-S_{g_2}^{n_0})+(S_{{\varphi }_1}^{n_0}-S_{{\varphi }_2}^{n_0}).$ Since $S_{g_1}^{n_0}-S_{g_2}^{n_0}\in S_{A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})},$ and $S_{{\varphi }_1}^{n_0}-S_{{\varphi }_2}^{n_0}\in S_{PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )},$ and in view of Lemma 4, we deduce that $S_{g_1}^{n_0}-S_{g_2}^{n_0}=0.$ Consequently, $S_{{\varphi }_1}^{n_0}-S_{{\varphi }_2}^{n_0}=0,$ that is, $S_{{\varphi }_1}^{n_0}=S_{{\varphi }_2}^{n_0}.$ The proof is complete. □

Theorem 3.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space. Assume that $S_{PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )}$ is shift invariant and $\rho \in U_{\infty }$. Then, $(S_{WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )},\parallel ·{\parallel }_{\infty })$ is a Banach space.

Proof. 

Assume that ${\{S_{f_n}^{n_0}\}}_{n\in \mathbb{N}}$ is a Cauchy sequence in $S_{WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )}.$ We can write uniquely $S_{f_n}^{n_0}=S_{g_n}^{n_0}+S_{{\varphi }_n}^{n_0}$. Using Lemma 4, we see that: $\parallel S_{g_p}^{n_0}-S_{g_q}^{n_0}{\parallel }_{\infty }\le {\parallel S_{f_p}^{n_0}-S_{f_q}^{n_0}\parallel }_{\infty },$ from which we deduce that ${\{S_{g_n}^{n_0}\}}_{n\in \mathbb{N}}$ is a Cauchy sequence in the Banach space $S_{A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})}.$ Thus, $S_{{\varphi }_n}^{n_0}=S_{f_n}^{n_0}-S_{g_n}^{n_0}$ is also a Cauchy sequence in the Banach space $S_{PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )}.$ We deduce that $S_{g_n}^{n_0}\to S_g^{n_0}\in S_{A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})},$ $S_{{\varphi }_n}^{n_0}\to S_{\varphi }^{n_0}\in S_{PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )},$ and finally $S_{f_n}^{n_0}\to S_g^{n_0}+S_{\varphi }^{n_0}\in S_{WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )}.$ The proof is complete. □

Definition 15.

Let ${\rho }_1,{\rho }_2\in U_{\infty }.$ One says that ${\rho }_1$ equivalent to ${\rho }_2$, denoting this as ${\rho }_1\sim {\rho }_2$ if ${\displaystyle \frac{{\rho }_1}{{\rho }_2}}\in U_B.$

Let ${\rho }_1,{\rho }_2,{\rho }_3\in U_{\infty }.$ It is the fact that ${\rho }_1\prec {\rho }_1$ (reflexivity); if ${\rho }_1\prec {\rho }_2,$ then ${\rho }_2\prec {\rho }_1$ (symmetry), and if ${\rho }_1\prec {\rho }_2$ and ${\rho }_2\prec {\rho }_3,$ then ${\rho }_1\prec {\rho }_3$ (transitivity). Thus, ≺ is a binary equivalence relation on $U_{\infty }.$

Theorem 4.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and ${\rho }_1,{\rho }_2\in U_{\infty }.$ If ${\rho }_1\sim {\rho }_2$, then $S_{WPA{A}_{n_0}^{\delta }(\mathbb{T},{\rho }_1)}=S_{WPA{A}_{n_0}^{\delta }(\mathbb{T},{\rho }_2)}.$

Proof. 

Assume that ${\rho }_1\sim {\rho }_2.$ There exists $a>0,b>0$ such that $a{\rho }_1\le {\rho }_2\le b{\rho }_1.$ Thus,

$$a{m}^{\delta }(r,{\rho }_1)\le m^{\delta }(r,{\rho }_2)\le b{m}^{\delta }(r,{\rho }_1),$$

where $r\in {\tilde{\Pi }}^{+}$, and

$$\begin{array}{ccc}\hfill \frac{a}{b}\frac{1}{m^{\delta }(r,{\rho }_1)}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\varphi }^{n_0}(s)\parallel {\rho }_1(s)\mathsf{\Delta }s& \le & \frac{1}{m^{\delta }(r,{\rho }_2)}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\varphi }^{n_0}(s)\parallel {\rho }_2(s)\mathsf{\Delta }s\hfill \\ & \le & \frac{b}{a}\frac{1}{m^{\delta }(r,{\rho }_1)}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\varphi }^{n_0}(s)\parallel {\rho }_1(s)\mathsf{\Delta }s.\hfill \end{array}$$

The proof is complete. □

Lemma 5.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and $f\in B{C}^{\delta }(\mathbb{T},\mathbb{X}).$ Then, $f\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho )$ where $\rho \in U_B$ if and only if for every $\epsilon >0$,

$$\underset{r\to +\infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_f^{n_0}))=0,$$

where $r\in {\tilde{\Pi }}^{+}$ and $M_{r,\epsilon }^{\delta }(S_f^{n_0}):=\{t\in F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}):\parallel S_f^{n_0}(t)\parallel \ge \epsilon \}.$

Proof. 

(a)

Necessity. By contradiction, we suppose that there exists ${\epsilon }_0>0$ such that

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,{\epsilon }_0}^{\delta }(S_f^{n_0}))\ne 0.$$

Then, there exists ${\delta }^{*}>0$ such that, for every $n\in \mathbb{N},\frac{1}{m^{\delta }(r_n,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r_n,{\epsilon }_0}^{\delta }(S_f^{n_0}))\ge {\delta }^{*}$ for some $r_n>n$, where $r_n\in {\tilde{\Pi }}^{+}.$

As a result, we get

$$\begin{array}{cc}& \frac{1}{m^{\delta }(r_n,\rho )}{\int }_{F^{-1}({[r_n^{-1},r_n]}_{{\Pi }^{*}})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s=\frac{1}{m^{\delta }(r_n,\rho )}{\int }_{M_{r_n,{\epsilon }_0}^{\delta }(S_f)}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s\hfill \\ & +\frac{1}{m^{\delta }(r_n,\rho )}{\int }_{F^{-1}({[r_n^{-1},r_n]}_{{\Pi }^{*}}){]}_{\mathbb{T}})\backslash M_{r_n,{\epsilon }_0}^{\delta }(S_f^{n_0})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s\hfill \\ \ge & \frac{1}{m^{\delta }(r_n,\rho )}{\int }_{M_{r_n,{\epsilon }_0}^{\delta }(S_f^{n_0})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s\hfill \\ \ge & \frac{{\epsilon }_0}{m^{\delta }(r_n,\rho )}{\int }_{M_{r_n,{\epsilon }_0}^{\delta }(S_f^{n_0})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s\ge {\epsilon }_0{\delta }^{*}\gamma ,\hfill \end{array}$$

where $\gamma ={inf}_{s\in \mathbb{T}}\rho (s).$ This contradicts the assumption.

(b)

Sufficiency. Assume that $\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_f^{n_0}))=0.$ Then, for every $\epsilon >0,$ there exists $r_0>0$ such that for every $r>r_0$,

$$\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_f^{n_0}))<\frac{\epsilon }{KM},$$

where $M:=\underset{t\in \mathbb{T}}{sup}\parallel S_f^{n_0}(t)\parallel <\infty$ and $K:=\underset{t\in \mathbb{T}}{sup}\rho (t)<\infty .$

Now, we have

$$\begin{array}{ccc}\hfill \frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_f^{n_0}(s)\parallel \mathsf{\Delta }s& =& \frac{1}{m^{\delta }(r,\rho )}({\int }_{M_{r,\epsilon }^{\delta }(S_f^{n_0})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s\hfill \\ & & +{\int }_{(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}))\backslash M_{r,\epsilon }^{\delta }(S_f^{n_0})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s)\hfill \\ & \le & \frac{MK}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_f^{n_0}))\hfill \\ & & +\frac{\epsilon }{m^{\delta }(r,\rho )}{\int }_{(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}))\backslash M_{r,\epsilon }^{\delta }(S_f^{n_0})}\rho (s)\mathsf{\Delta }s\le 2\epsilon .\hfill \end{array}$$

Therefore, $\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_f^{n_0}(s)\parallel \rho (s)\mathsf{\Delta }s=0,$ that is $f\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ).$

The proof is complete. □

Lemma 6.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space. If $g\in A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ and $\alpha \in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ are standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions, then $G(·):=g\left(·,S_{\alpha }^{n_0}(·)\right)\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ is standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic.

Proof. 

From $g(t,x)\in A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$, then for every sequence of real numbers ${\{s_n\}}_{n=1}^{\infty }\subset \tilde{\Pi },$ we can extract a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }$ such that:

$$S_{g^{*}}^{n_0}(t,x):=\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n}(t),x\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(t)\right)}^{n_0}$$

is well defined for each $t\in {\mathbb{T}}^{*}$. In view of assumption $(i)$ in our definition and $\alpha \in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$, one can extract ${\{{\tau }_n^{{}^{\prime }}\}}_{n=1}^{\infty }\subset {\{{\tau }_n\}}_{n=1}^{\infty }$ such that

$$\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n^{{}^{\prime }}}(t),\alpha \left({\delta }_{{\tau }_n^{{}^{\prime }}}(t)\right){\left({\delta }_{{\tau }_n^{{}^{\prime }}}^{\mathsf{\Delta }}(t)\right)}^{n_0}\right){\left({\delta }_{{\tau }_n^{{}^{\prime }}}^{\mathsf{\Delta }}(t)\right)}^{n_0}=\underset{n\to \infty }{lim}g\left({\delta }_{{\tau }_n^{{}^{\prime }}}(t),S_{{\alpha }^{*}}^{n_0}(t)\right){\left({\delta }_{{\tau }_n^{{}^{\prime }}}^{\mathsf{\Delta }}(t)\right)}^{n_0}=S_{g^{*}}^{n_0}\left(t,S_{{\alpha }^{*}}^{n_0}(t)\right).$$

Hence, $G(·)\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ is standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic. The proof is complete. □

We introduce two hypotheses as follows:

(H1)

$S_f^{n_0}(t,x)$ is uniformly continuous in $t\in \mathbb{T}$ uniformly for any bounded subset $K\subset \mathbb{X}$.

(H2)

$S_g^{n_0}(t,x)$ is uniformly continuous in $t\in \mathbb{T}$ uniformly for any bounded subset $K\subset \mathbb{X}$.

Theorem 5.

Let $f=g+\varphi \in WPA{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\rho ),$ where $g\in A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ is standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic, $\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T}\times \mathbb{X},\rho ),\rho \in U_{\infty }$. Assume that $(\mathrm{H}1)$ and $(\mathrm{H}2)$ are satisfied. Then, the $L(·):=f\left(·,S_h^{n_0}(·)\right)\in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )$ if $h\in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )$, where $S_h^{n_0}(t)=h(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}$.

Proof. 

We have $S_f^{n_0}=S_g^{n_0}+S_{\varphi }^{n_0}$ where $g\in A{A}_{n_0}^{\delta }(\mathbb{T}\times \mathbb{X},\mathbb{X})$ and $\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T}\times \mathbb{X},\rho )$ and $S_h^{n_0}=S_{{\mu }_0}^{n_0}+S_{{\nu }_0}^{n_0}$ where ${\mu }_0\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ and ${\nu }_0\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ).$

Now, let us write

$$\begin{array}{ccc}\hfill S_L^{n_0}(·)& =& S_g^{n_0}(·,S_{{\mu }_0}^{n_0}(·))+S_f^{n_0}(·,S_h^{n_0}(·))-S_g^{n_0}(·,S_{{\mu }_0}^{n_0}(·))\hfill \\ & =& S_g^{n_0}(·,S_{{\mu }_0}^{n_0}(·))+S_f^{n_0}(·,S_h^{n_0}(·))-S_f^{n_0}(·,S_{{\mu }_0}^{n_0}(·))+S_{\varphi }^{n_0}(·,S_{{\mu }_0}^{n_0}(·)).\hfill \end{array}$$

From Lemma 6, $g\left(·,S_{{\mu }_0}^{n_0}(·)\right)\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X}).$ Consider now the function

$$S_{\mathsf{\Psi }}^{n_0}(·):=S_f^{n_0}(·,S_h^{n_0}(·))-S_f^{n_0}(·,S_{{\mu }_0}^{n_0}(·)).$$

Clearly $\mathsf{\Psi }(·)\in B{C}^{\delta }(\mathbb{T},\mathbb{X}).$ For $\mathsf{\Psi }$ to be in $PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ),$ it is sufficient to show that

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_{\mathsf{\Psi }}^{n_0}))=0.$$

From Lemma 4, $S_{\mu }^{n_0}(\mathbb{T})\subset \overline{S_h^{n_0}(\mathbb{T})}$ which is a bounded set. Using assumption $(\mathrm{H}1)$ with $K=\overline{S_h^{n_0}(\mathbb{T})},$ we say that for every $\epsilon >0$, there exists ${\delta }^{*}>0$ such that

$$x,y\in K,\parallel x-y\parallel <{\delta }^{*}\Rightarrow \parallel S_f^{n_0}(t,x)-S_f^{n_0}(t,y)\parallel <\epsilon ,t\in \mathbb{T}.$$

Thus, we obtain

$$\begin{array}{ccc}\hfill \frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}(M_{r,\epsilon }^{\delta }(S_{\mathsf{\Psi }}(t)))& =& \frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\epsilon }^{\delta }(S_f^{n_0}(t,S_h^{n_0}(t))-S_f^{n_0}(t,S_{{\mu }_0}^{n_0}(t)))\right)\hfill \\ & \le & \frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,{\delta }^{*}}^{\delta }(S_h^{n_0}(t)-S_{{\mu }_0}^{n_0}(t))\right)=\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,{\delta }^{*}}^{\delta }(S_{{\nu }_0}^{n_0}(t))\right).\hfill \end{array}$$

Now, since ${\nu }_0\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ),$ then, by Lemma 5, $\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\epsilon }^{\delta }(S_{{\nu }_0}(t))\right)=0.$ Consequently,

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\epsilon }^{\delta }(S_{\mathsf{\Psi }}^{n_0}(t))\right)=0.$$

Thus, $\mathsf{\Psi }\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\mathbb{X}).$

Finally, we need to show that $\varphi (·,S_{{\mu }_0}^{n_0}(·))\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ).$ Note that $S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t))$ is uniformly continuous on $F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}),$ and that $S_{{\mu }_0}^{n_0}(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}))$ is compact since ${\mu }_0$ is continuous on $\mathbb{T}$ as an almost automorphic function. Thus, given $\epsilon >0,$ there exists ${\delta }^{*}>0$ such that $S_{{\mu }_0}^{n_0}(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}))\subset {\displaystyle \bigcup _{k=1}^m}{B}_k,$ where $B_k=\{x\in \mathbb{X}:\parallel x-x_k\parallel <{\delta }^{*}\}$ for some $x_k\in S_{{\mu }_0}^{n_0}(F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})),$ and

$$\parallel S_{\varphi }^{n_0}(t,{\mu }_0(t))-S_{\varphi }^{n_0}(t,x_k)\parallel <\frac{\epsilon }{2},S_{{\mu }_0}^{n_0}(t)\in B_k,t\in F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}).$$

(8)

Note that the set $U_k:=\{t\in F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}):S_{{\mu }_0}^{n_0}(t)\in B_k\}$ is open in $F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})$ and that $F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})={\displaystyle \bigcup _{k=1}^m}{U}_k.$ Define $V_k$ by

$$V_1=U_1,V_k=U_k\backslash \bigcup _{i=1}^{k-1}{U}_i,2\le k\le m.$$

Then, $V_i\cap V_j=\varnothing$, if $i\ne j,$ $1\le i,j\le m.$ Thus, we get

$$\begin{array}{ccc}\hfill \mathrm{Y}& :=& \left\{t\in F^{-1}({[r^{-1},r]}_{{\Pi }^{*}}):\parallel S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t))\parallel \ge \frac{\epsilon }{2}\right\}\hfill \\ & \subset & \bigcup _{k=1}^m\left\{t\in V_k:\parallel S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t))-S_{\varphi }^{n_0}(t,x_k)\parallel +\parallel S_{\varphi }^{n_0}(t,x_k)\parallel \ge \epsilon \right\}\hfill \\ & \subset & \bigcup _{k=1}^m\left(\left\{t\in V_k:\parallel S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t))-S_{\varphi }^{n_0}(t,x_k)\parallel \ge \frac{\epsilon }{2}\right\}\bigcup \left\{t\in V_k:\parallel S_{\varphi }^{n_0}(t,x_k)\parallel \ge \frac{\epsilon }{2}\right\}\right).\hfill \end{array}$$

In view of Label (8), it follows that

$$\left\{t\in V_k:\parallel S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t))-S_{\varphi }^{n_0}(t,x_k)\parallel \ge \frac{\epsilon }{2}\right\}=\varnothing ,k=1,2,\dots ,m.$$

Thus, we get

$$\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\epsilon }^{\delta }(S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t)))\right)\le \sum _{k=1}^m\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\epsilon }^{\delta }(S_{\varphi }^{n_0}(t,x_k))\right).$$

Now, since $\varphi (·,x)\in PA{A}_0^{\delta ,n_0}(\mathbb{T}\times \mathbb{X},\rho )$ and $\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\frac{\epsilon }{2}}^{\delta }(S_{\varphi }^{n_0}(t,x_k))\right)=0,$ it follows that

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\mu }_{\mathsf{\Delta }}\left(M_{r,\frac{\epsilon }{2}}^{\delta }(S_{\varphi }^{n_0}(t,S_{{\mu }_0}^{n_0}(t)))\right)=0,$$

i.e., $\varphi \left(·,{\mu }_0(·)\right)\in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ).$ The proof is complete. □

From Theorem 5, we can establish the following consequence:

Corollary 1.

Let $f=g+\varphi \in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho ),$ where $\rho \in U_{\infty }$ and assume both $S_f$ and $S_g$ are Lipschitzian in $x\in \mathbb{X}$ uniformly in $t\in \mathbb{T}$. Then, $L(·):=f\left(·,S_h^{n_0}(·)\right)\in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )$ if $h\in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho ).$

3. Applications

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space for the time scale $\mathbb{T}$, and consider the following linear dynamic equation

$$x^{\mathsf{\Delta }}=S_A^{n_0}(t)x,$$

(9)

where $S_A^{n_0}(t)=A(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}(t\in \mathbb{T})$ is a linear operator in the Banach space $\mathbb{X}$.

Definition 16

([17]). $T(t,s):\mathbb{T}\times \mathbb{T}\to B(\mathbb{X})$ is called the linear evolution operator associated with (9) if $T(t,s)$ satisfies the following conditions:

(1)

$T(s,s)=\mathrm{Id}$,where $\mathrm{Id}$ denotes the identity operator in $\mathbb{X}$;

(2)

$T(t,s)T(s,r)=T(t,r);$

(3)

the mapping $(t,s)\to T(t,s)x$ is continuous for any fixed $x\in \mathbb{X}.$

To obtain our results, we will introduce the following concepts.

Definition 17.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a matched space. An evolution system $T(t,s)$ is called δ-exponentially stable if for any fixed $\tau \in \tilde{\Pi }$, there exists $K_0\ge 1$ and $\omega >0$ such that

$$\parallel T\left({\delta }_{\tau }(t),{\delta }_{\tau }(s)\right){\parallel }_{B(\mathbb{X})}\le K_0{e}_{\ominus \omega }\left(\sigma (t),s\right),t\ge s.$$

Remark 18.

From Definition 17, if an evolution system $T(t,s)$ is called exponentially stable, then there exist projections $P(t),Q(t):\mathbb{T}\to B(\mathbb{X})$ for each $t\in \mathbb{T}$ such that $P(t)+Q(t)=\mathrm{Id},$

$${\parallel Q(t)T(t,s)P(s)\parallel }_{B(\mathbb{X})}\le K_0{e}_{\ominus \omega }\left(\sigma (t),s\right),t\ge s$$

since

$$\parallel Q(t)T(t,s)P(s)\parallel \le {\parallel T(t,s)\parallel }_{B(\mathbb{X})}\le K_0{e}_{\ominus \omega }\left(\sigma (t),s\right),t\ge s.$$

Consider the abstract differential equation

$$x^{\mathsf{\Delta }}(t)=S_A^{n_0}(t)x(t)+S_f^{n_0}\left(t,x(t)\right),t\in \mathbb{T},$$

(10)

with the following assumptions:

(H₁)

The family $\{S_A^{n_0}(t):t\in \mathbb{T}\}$ of operators in $\mathbb{X}$ generates an $\delta$-exponentially stable evolution system $\{T(t,s):t\ge s\},$ i.e., for any fixed $\tau \in \tilde{\Pi }$, there exists $K_0(\tau )\ge 1$ and $\omega (\tau )>0$ such that

$$\parallel T\left({\delta }_{\tau }(t),{\delta }_{\tau }(s)\right){\parallel }_{B(\mathbb{X})}\le K_0{e}_{\ominus \omega }\left(\sigma (t),s\right),t\ge s,$$

and, for any sequence $\{{\tau }_n\}\subset \tilde{\Pi }$, there exists a subsequence $\{{\tau }_n^{{}^{\prime }}\}\subset \{{\tau }_n\}$ such that

$$\underset{n\to \infty }{lim}T\left({\delta }_{{\tau }_n^{{}^{\prime }}}(t),{\delta }_{{\tau }_n^{{}^{\prime }}}(s)\right)=T^{*}(t,s)\mathrm{is}\mathrm{well}\mathrm{defined}\mathrm{for}\mathrm{each}t,s\in \mathbb{T},t\ge s.$$

(H₂)

$f=g+\varphi \in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho ),$ where $\rho \in U_{\infty }.$

(H₃)

$\parallel S_f^{n_0-1}(t,x)-S_f^{n_0-1}(t,y)\parallel \le L_f\parallel x-y\parallel ,\forall x,y\in \mathbb{X}.$

(H₄)

$\parallel S_g^{n_0-1}(t,x)-S_g^{n_0-1}(t,y)\parallel \le L_g\parallel x-y\parallel ,\forall x,y\in \mathbb{X}.$

Definition 18.

A mild solution to (10) is a continuous function $x(t):\mathbb{T}\to \mathbb{X}$ satisfying

$$x(t)=T(t,c)x(c)+{\int }_c^{t}T(t,s)S_f^{n_0}\left(s,x(s)\right)\mathsf{\Delta }s$$

for all $t\ge c$ and for all $c\in \mathbb{T},$ where $S_f^{n_0}(t,x)=f(t,x){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0}:\mathbb{T}\times \mathbb{X}\to \mathbb{X}$.

Lemma 7.

$f\in PA{A}_0^{\delta ,n_0}$ if and only if $f\in PA{A}_0^{\delta ,n_0-1}$.

Proof. 

Assume that $f\in PA{A}_0^{\delta ,n_0-1}$. Then we obtain

$$\parallel S_f^{n_0-1}(t)\parallel \le \parallel S_f^{n_0}(t)\parallel =\parallel S_f^{n_0-1}(t)·{\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\parallel \le \parallel S_f^{n_0-1}(t)\parallel ,$$

so we get $f\in PA{A}_0^{\delta ,n_0}$.

On the other hand, if $f\in PA{A}_0^{\delta ,n_0}$, one can obtain

$$\parallel S_f^{n_0}(t)\parallel \le \parallel S_f^{n_0-1}(t)\parallel =\parallel S_f^{n_0}(t){[{\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)]}^{-1}\parallel \le \parallel S_f^{n_0}(t)\parallel .$$

Thus, we obtain $f\in PA{A}_0^{\delta ,n_0-1}$. This completes the proof. □

To investigate the existence and uniqueness of a weighted pseudo $\delta$-almost automorphic solution to (10), we need the following two lemmas:

Lemma 8.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and ${\delta }_{\tau }(·)$ be Δ-differentiable for all $t\in {\mathbb{T}}^{*}$. Assume $v\in A{A}_{n_0}^{\delta }(\mathbb{T},\mathbb{X})$ is a standard ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic function and $({\mathrm{H}}_1)$ is satisfied. If $S_u^{n_0-1}:\mathbb{T}\to \mathbb{X}$ is the function defined by

$$S_u^{n_0-1}(t)={\int }_{-\infty }^{t}T(t,s)S_v^{n_0-1}(s)\mathsf{\Delta }s,t\ge s,$$

then $u(·)\in A{A}_{n_0-1}^{\delta }(\mathbb{T},\mathbb{X})$ is a standard ${\mathsf{\Delta }}_{n_0-1}^{\delta }$-almost automorphic function.

Proof. 

Clearly, $u(t)$ is a continuous functions. Let ${\{s_n\}}_{n=1}^{\infty }\subset \tilde{\Pi }$ be an arbitrary sequence of real numbers. Since v is ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic, there exists a subsequence ${\{{\tau }_n\}}_{n=1}^{\infty }\subset {\{s_n\}}_{n=1}^{\infty }$ such that $S_h^{n_0}(t):=\underset{n\to \infty }{lim}v\left({\delta }_{{\tau }_n}(t)\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(t)\right)}^{n_0}$ is well defined for each $t\in {\mathbb{T}}^{*}$.

Now, we consider

$$\begin{array}{ccc}\hfill S_u^{n_0-1}\left({\delta }_{{\tau }_n}(t)\right)& =& {\int }_{-\infty }^{{\delta }_{{\tau }_n}(t)}T\left({\delta }_{{\tau }_n}(t),s\right)S_v^{n_0-1}(s)\mathsf{\Delta }s={\int }_{-\infty }^{t}T\left({\delta }_{{\tau }_n}(t),{\delta }_{{\tau }_n}(s)\right)S_v^{n_0-1}\left({\delta }_{{\tau }_n}(s)\right){\delta }_{{\tau }_n}^{\mathsf{\Delta }}(s)\mathsf{\Delta }s\hfill \\ & =& {\int }_{-\infty }^{t}T\left({\delta }_{{\tau }_n}(t),{\delta }_{{\tau }_n}(s)\right)v_n(s)\mathsf{\Delta }s,\hfill \end{array}$$

where $v_n(s)=S_v^{n_0-1}\left({\delta }_{{\tau }_n}(s)\right){\delta }_{{\tau }_n}^{\mathsf{\Delta }}(s)=v\left({\delta }_{{\tau }_n}(s)\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(s)\right)}^{n_0}=S_v^{n_0}\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(s)\right),n=1,2,\dots .$ In addition, we have

$$\begin{array}{ccc}\hfill \parallel S_u^{n_0-1}({\delta }_{{\tau }_n}(t))\parallel & \le & {\int }_{-\infty }^t\parallel T\left({\delta }_{{\tau }_n}(t),{\delta }_{{\tau }_n}(s)\right)v_n(s)\parallel \mathsf{\Delta }s\hfill \\ & \le & {\int }_{-\infty }^t{K}_0{e}_{\ominus \omega }(t,s)\parallel v_n(s)\parallel \mathsf{\Delta }s\hfill \\ & \le & K_0\parallel S_v^{n_0}\parallel {\int }_{-\infty }^t\ominus \omega e_{\ominus \omega }(t,\sigma (s))\mathsf{\Delta }s\hfill \\ & =& \frac{K_0\parallel S_v^{n_0}\parallel }{\omega }\left[e_{\ominus \omega }(t,t)-e_{\ominus \omega }(t,-\infty )\right]=\frac{K_0\parallel S_v^{n_0}\parallel }{\omega }.\hfill \end{array}$$

Note that

$$v_n(s)\to S_h^{n_0}(s),\mathrm{as}n\to \infty$$

for each $s\in \mathbb{T}$ fixed and any $t\ge s,$ and we get

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}u\left({\delta }_{{\tau }_n}(t)\right){\left({\delta }_{{\tau }_n}^{\mathsf{\Delta }}(t)\right)}^{n_0-1}& =& {\int }_{-\infty }^t{T}^{*}(t,s)S_h^{n_0}(s)\mathsf{\Delta }s\hfill \\ & =& \left({\int }_{-\infty }^t{T}^{*}(t,s)h(t){\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\mathsf{\Delta }s\right){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0-1}\hfill \\ & :=& \tilde{u}(t){\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0-1},\hfill \end{array}$$

by the Lebesgue’s dominated convergence theorem. Analogous to the above proof, we can obtain

$$\underset{n\to \infty }{lim}\tilde{u}\left({\delta }_{{{\tau }_n}^{-1}}(t)\right){\left({\delta }_{{\tau }_n^{-1}}^{\mathsf{\Delta }}(t)\right)}^{n_0-1}=\underset{n\to \infty }{lim}{\int }_{-\infty }^{{\delta }_{{\tau }_n^{-1}}(t)}{T}^{*}\left({\delta }_{{\tau }_n^{-1}}(t),s\right)S_h^{n_0}(s)\mathsf{\Delta }s=S_u^{n_0-1}(t).$$

This shows that $u(t)$ is a standard ${\mathsf{\Delta }}_{n_0-1}^{\delta }$-almost automorphic function. The proof is complete. □

Lemma 9.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and ${\delta }_{\tau }(·)$ be Δ-differentiable for fixed $t\in {\mathbb{T}}^{*}$. Let $f=g+\varphi \in WPA{A}_{n_0}^{\delta }(\mathbb{T},\rho )$, where $\rho \in U_{\infty }$. Furthermore, $(H_1)-(H_4)$ are satisfied and $\{T(t,s):t\ge s\}$ is exponentially stable. Then,

$$S_F^{n_0-1}(·):={\int }_{-\infty }^{·}T(·,s)S_f^{n_0-1}(s)\mathsf{\Delta }s\in S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}.$$

Proof. 

Let $S_F^{n_0-1}(t)=S_G^{n_0-1}(t)+S_{\mathsf{\Phi }}^{n_0-1}(t)$, where

$$S_G^{n_0-1}(t):={\int }_{-\infty }^{t}T(t,s)S_g^{n_0-1}(s)\mathsf{\Delta }s\mathrm{and}{S}_{\mathsf{\Phi }}^{n_0-1}(t):={\int }_{-\infty }^{t}T(t,s)S_{\varphi }^{n_0-1}(s)\mathsf{\Delta }s.$$

Then, by Lemma 8, $G(·)\in A{A}_{n_0-1}^{\delta }(\mathbb{T},\mathbb{X}).$ Now, we show that $\mathsf{\Phi }(·)\in PA{A}_0^{\delta ,n_0-1}(\mathbb{T},\rho ).$ First, take $t_0\in {\mathbb{T}}^{*}$ such that $F(A_{i_{t_0}})=e_{{\Pi }^{*}}$, and by Remark 15, we have ${\left[{\delta }_{r^{-1}}(t_0),{\delta }_r(t_0)\right]}_{\mathbb{T}}=F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})$, it follows from Theorem 2.15 in [34] that

$$\begin{array}{cc}& \frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\mathsf{\Phi }}^{n_0-1}(s)\parallel \mathsf{\Delta }s\hfill \\ =& \frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel {\int }_{-\infty }^{s}T(s,\theta )S_{\varphi }^{n_0-1}(\theta )\mathsf{\Delta }\theta \parallel \mathsf{\Delta }s\hfill \\ \le & \frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\mathsf{\Delta }s{\int }_{-\infty }^s{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta \hfill \\ =& \frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\mathsf{\Delta }s\left({\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}+{\int }_{{\delta }_{r^{-1}}(t_0)}^s{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \right)\mathsf{\Delta }\theta \hfill \\ =& \frac{1}{m^{\delta }(r,\rho )}{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s\hfill \\ & +\frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{\theta }^{{\delta }_r(t_0)}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s=I_1+I_2,\hfill \end{array}$$

where

$$I_1:=\frac{1}{m^{\delta }(r,\rho )}{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s$$

and

$$I_2:=\frac{1}{m^{\delta }(r,\rho )}{\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{\theta }^{{\delta }_r(t_0)}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s.$$

One can obtain

$$\begin{array}{ccc}\hfill I_1& =& \frac{1}{m^{\delta }(r,\rho )}{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s\hfill \\ & =& \frac{K_0}{\omega m^{\delta }(r,\rho )}{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{F^{-1}({[r^{-1},r]}_{{\Pi }^{*}})}\omega e_{\omega }(\theta ,\sigma (s))\mathsf{\Delta }s\hfill \\ & =& \frac{1}{m^{\delta }(r,\rho )}\frac{K_0}{\omega }{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel [e_{\omega }(\theta ,{\delta }_{r^{-1}}(t_0))-e_{\omega }(\theta ,{\delta }_r(t_0))]\mathsf{\Delta }\theta \hfill \\ & \le & \frac{1}{m^{\delta }(r,\rho )}\frac{K_0}{\omega }\parallel S_{\varphi }^{n_0-1}\parallel \left(\left|{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}{e}_{\ominus \omega }({\delta }_{r^{-1}}(t_0),\theta )\mathsf{\Delta }\theta \right|+\left|{\int }_{-\infty }^{{\delta }_{r^{-1}}(t_0)}{e}_{\ominus \omega }({\delta }_r(t_0),\theta )\mathsf{\Delta }\theta \right|\right)\hfill \\ & =& \frac{1}{m^{\delta }(r,\rho )}\frac{K_0}{{\omega }^2}\parallel S_{\varphi }^{n_0-1}\parallel (|e_{\ominus \omega }({\delta }_{r^{-1}}(t_0),-\infty )-e_{\ominus \omega }({\delta }_{r^{-1}}(t_0),{\delta }_{r^{-1}}(t_0))|+|e_{\ominus \omega }({\delta }_r(t_0),-\infty )\hfill \\ & & -e_{\ominus \omega }({\delta }_r(t_0),{\delta }_{r^{-1}}(t_0))|)\to 0\mathrm{as}r\to \infty ;\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_2& =& \frac{1}{m^{\delta }(r,\rho )}{\int }_{{\delta }_{r^{-1}}(t_0)}^{{\delta }_r(t_0)}\parallel S_{\varphi }^{n_0-1}\parallel (\theta )\parallel \mathsf{\Delta }\theta {\int }_{\theta }^{{\delta }_r(t_0)}{K}_0{e}_{\ominus \omega }(\sigma (s),\theta )\mathsf{\Delta }s\hfill \\ & =& \frac{K_0}{\omega m^{\delta }(r,\rho )}{\int }_{{\delta }_{r^{-1}}(t_0)}^{{\delta }_r(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta {\int }_{\theta }^{{\delta }_r(t_0)}\omega e_{\omega }(\theta ,\sigma (s))\mathsf{\Delta }s\hfill \\ & \le & \frac{1}{m^{\delta }(r,\rho )}\frac{K_0}{\omega }{\int }_{{\delta }_{r^{-1}}(t_0)}^{{\delta }_r(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \left[e_{\omega }(\theta ,\theta )-e_{\omega }(\theta ,{\delta }_r(t_0))\right]\mathsf{\Delta }\theta \hfill \\ & \le & \frac{1}{m^{\delta }(r,\rho )}\frac{K_0}{\omega }{\int }_{{\delta }_{r^{-1}}(t_0)}^{{\delta }_r(t_0)}\parallel S_{\varphi }^{n_0-1}(\theta )\parallel \mathsf{\Delta }\theta .\hfill \end{array}$$

Since $\varphi \in PA{A}_0^{\delta ,n_0}(\mathbb{T},\rho ),$ by Lemma 7, $\varphi \in PA{A}_0^{\delta ,n_0-1}(\mathbb{T},\rho ),$ then

$$\underset{r\to \infty }{lim}\frac{1}{m^{\delta }(r,\rho )}{\int }_{{\delta }_{r^{-1}}(t_0)}^{{\delta }_r(t_0)}\parallel S_{\varphi }^{n_0-1}(s)\parallel \mathsf{\Delta }s=0.$$

Hence, $\underset{r\to \infty }{lim}{I}_2=0$. The proof is complete. □

Theorem 6.

Let $(\mathbb{T},F,\Pi ,\delta )$ be a regular matched space and ${\delta }_{\tau }(·)$ be Δ-differentiable for $t\in {\mathbb{T}}^{*}$. Under assumptions $({\mathrm{H}}_1)-({\mathrm{H}}_4)$ above, (10) has a unique mild solution in $S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}$ provided $\frac{K_0{L}_f}{\omega }<1$.

Proof. 

Consider the nonlinear operator $\Gamma$ given by

$$(\Gamma x)(t):={\int }_{-\infty }^{t}T(t,s)S_f^{n_0-1}\left(s,x(s)\right)\mathsf{\Delta }s.$$

From Lemma 5, we see $\Gamma$ maps $S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}$ into $S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}$.

Now, if $x,y\in S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}$, we have

$$\begin{array}{ccc}\hfill \parallel (\Gamma x)(t)-(\Gamma y)(t)\parallel & =& \parallel {\int }_{-\infty }^{t}T(t,s)\left(S_f^{n_0-1}(s,x(s))-S_f^{n_0-1}(s,y(s))\right)\parallel \hfill \\ & \le & K_0{L}_f{\int }_{-\infty }^t{e}_{\ominus \omega }(t,s)\parallel x(s)-y(s)\parallel \mathsf{\Delta }s\hfill \\ & \le & \frac{K_0{L}_f}{\omega }{\parallel x-y\parallel }_{\infty }\le \frac{K_0{L}_f}{\omega }{\parallel x-y\parallel }_{\infty },\forall t\in \mathbb{T}.\hfill \end{array}$$

Thus,

$${\parallel \Gamma x-\Gamma y\parallel }_{\infty }\le \frac{K_0{L}_f}{\omega }{\parallel x-y\parallel }_{\infty }.$$

Hence, the conclusion follows from the contraction principle. The proof is complete. □

Corollary 2.

Suppose $(H_1)-(H_2)$ hold. Furthermore,

$$\parallel f(t,x)-f(t,y)\parallel \le l_f\parallel x-y\parallel ,\parallel g(t,x)-g(t,y)\parallel \le l_g\parallel x-y\parallel ,\forall x,y\in \mathbb{X}.$$

(11)

Then, (10) has a unique mild solution in $S_{WPA{A}_{n_0-1}^{\delta }(\mathbb{T},\rho )}$ provided $\frac{K_0{l}_f{({\delta }_{B_2}^{\mathsf{\Delta }})}^{n_0-1}}{\omega }<1$.

Proof. 

From (11), we can obtain

$$\parallel S_f^{n_0-1}(t,x)-S_f^{n_0-1}(t,y)\parallel \le \parallel f(t,x)-f(t,y)\parallel ·{\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0-1}\le l_f\parallel x-y\parallel ;$$

$$\parallel S_g^{n_0-1}(t,x)-S_g^{n_0-1}(t,y)\parallel \le \parallel g(t,x)-g(t,y)\parallel ·{\left({\delta }_{e_{{\Pi }^{*}}}^{\mathsf{\Delta }}(t)\right)}^{n_0-1}\le l_g\parallel x-y\parallel .$$

Let $L_f=l_f$, and according to Theorem 6, we obtain the desired result. The proof is complete. □

4. An Example

Let $({\mathbb{T}}_1,F,\Pi ,\delta )$ be a regular matched space and ${\mathbb{T}}_2$ be an arbitrary time scale with $0,\pi \in {\mathbb{T}}_2$ and $u:{\mathbb{T}}_1\times {\mathbb{T}}_2\to \mathbb{R}$, where ${\mathbb{T}}_1$ is the following time scale:

$${\mathbb{T}}_1=\overline{q^{\mathbb{Z}}}=\left\{q^n:q>1,n\in \mathbb{Z}\right\}\cup \{0\},\mathrm{where}q=\sqrt{3}.$$

Then, one will obtain that

$${\tilde{\Pi }}^{-}=\left\{q^n:q>1,n\in {\mathbb{Z}}^{-},t\in {\mathbb{T}}_1^{*}\right\},{\tilde{\Pi }}^{+}=\left\{q^n:q>1,n\in {\mathbb{Z}}^{+},t\in {\mathbb{T}}_1^{*}\right\},$$

where $\tilde{\delta }({\tau }_1,{\tau }_2)={\tau }_1{\tau }_2$ and $\delta (\tau ,t)=\tau t$, ${\tau }_1,{\tau }_2,\tau \in \tilde{\Pi }$. Consider the following partial dynamic equation:

$$\left\{\begin{array}{cc}& {\displaystyle \frac{\partial }{{\mathsf{\Delta }}_{1}t}}u(t,x)={\displaystyle \frac{{\partial }^2}{{\mathsf{\Delta }}_2{x}^2}}u\left(t,x\right)+{\displaystyle \frac{R(y)}{15}}\left(sint+cos\sqrt{2}t+g(t)\right)cosu(t,x),\hfill \\ & t\in {\mathbb{T}}_1,x\in {[0,\pi ]}_{{\mathbb{T}}_2},\hfill \\ & u(t,0)=u(t,\pi )=0,t\in {\mathbb{T}}_1,\hfill \end{array}\right.$$

(12)

where $g\in C(\mathbb{T},\mathbb{R})$ satisfies $\left|g(t)\right|\le 1,(t\in {\mathbb{T}}_1)$ and

$$\rho (t)=|sint|+1,R(y)=\frac{y}{1+y},y\in (0,1).$$

Define $\mathbb{X}=L^2{[0,\pi ]}_{{\mathbb{T}}_2}$, let $Au={\displaystyle \frac{{\partial }^2}{{\mathsf{\Delta }}_2{x}^2}}u(t,x),u\in D(A)=H_0^1{[0,\pi ]}_{{\mathbb{T}}_2}\cap H^2{[0,\pi ]}_{{\mathbb{T}}_2}.$ Clearly, it follows from the same discussion as Section 3.1. in [36], one can obtain that the evolution system $\{T(t,s):t\ge s\}$ satisfies $\parallel T(t,s)\parallel \le e_{\ominus \frac{1}{2}}(\sigma (t),s)(t\ge s)$. Then, for all $t\in {\mathbb{T}}_1$, by Lemma 3.3 from [21], we have

$$\begin{array}{ccc}\hfill \parallel T\left(\tau t,\tau s\right)\parallel & \le & {\left(e_{\ominus \frac{1}{2}}\left(\sigma (t),s\right)\right)}^{\tau }\le e^{-c\tau (\sigma (t)-s))}\hfill \\ & <& e_{\ominus c\tau }\left(\sigma (t),s\right),(t\ge s,\tau \in \tilde{\Pi },0<c<\frac{1}{2}).\hfill \end{array}$$

Let $K_0=1+c\tau ,\omega =c\tau$ and

$$f(t,u)=\frac{R(y)}{15}\left(sint+cos\sqrt{2}t+g(t)\right)cosu.$$

Clearly, for $y\in (0,c\tau )$, f satisfies the assumptions given in Theorem 6 with

$$L_f=\frac{y}{5(1+y)}\mathrm{and}\frac{K_0{L}_f}{\omega }<\frac{1+c\tau }{c\tau }·\frac{c\tau }{5(1+c\tau )}=\frac{1}{5}<1.$$

Therefore, (12) has the unique weighted pseudo $\delta$-almost automorphic mild solution for $y\in (0,c\tau )$.

5. Conclusions, Further Discussion and Open Problems

In this paper, using matched spaces for time scales, the properties of the complete-closed time scales under non-translational shift are established, and a wider range of irregular time scales turns into regular ones with “periodicity”. Then, the concepts of $n_0$-order $\mathsf{\Delta }$-almost automorphic functions and weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions are introduced, and some basic theorems are obtained for weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic functions and are then applied to investigate abstract dynamic equations. In addition, some sufficient conditions are derived to guarantee the existence of weighted pseudo ${\mathsf{\Delta }}_{n_0}^{\delta }$-almost automorphic solutions for a new type of abstract dynamic equations. The obtained results develop a new almost automorphic theory for abstract dynamic equations involving quantum-like dynamic equations like q-difference dynamic equations and others.

For the matched space $(\mathbb{T},\Pi ,\delta ,F)$, the shift operator ${\delta }_{\tau }(·)$ may have the discontinuous point at some $t_0\in {\mathbb{T}}^{*}$ for $\tau \in \tilde{\Pi }$ (we call it characteristic point of the time scale under this matched space), particularly, if $e_{{\Pi }^{*}}\in {\mathbb{T}}^{*}$, then $e_{{\Pi }^{*}}\in {\mathbb{T}}^{*}$ may be a characteristic point. For example, the time scales ${(-q)}^{\mathbb{Z}}$ and $\pm {\mathbb{N}}^{\frac{1}{2}}$ have the characteristic points $t=1$ and $t=0$ (see Figure 3 and Figure 4), repectively. The characteristic points will lead to splitting of time scales, for example, the time scales ${(-q)}^{\mathbb{Z}}$ and $\pm {\mathbb{N}}^{\frac{1}{2}}$ have the split point $t=0$. From Figure 3, one will see that the characteristic point is $t=1$, but the splitting point is $t=0$, which implies that the characteristic point and the splitting point may not be equivalent (they may equal to each other, see Figure 4). However, if ${\delta }_{\tau }(·)$ is continuous for all $\tau \in \tilde{\Pi }$, then ${\mathbb{T}}^{*}$ may have no characteristic point, it indicates that ${\mathbb{T}}^{*}$ will not split and have the bidirectional shift closedness, see Figure 5.

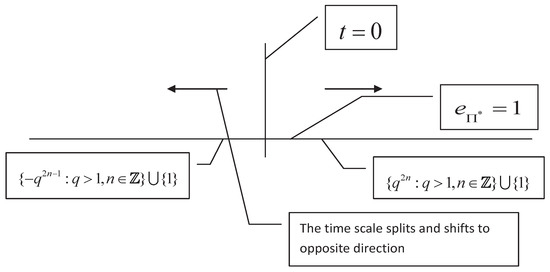
Figure 3. The time scale $\mathbb{T}=\overline{{(-q)}^{\mathbb{Z}}}$ has the characteristic point $e_{{\Pi }^{*}}=1$ at which the shift ${\delta }_{\tau }(·)$ is discontinuous. This time scale splits at $t=0$ and has the opposite shift closedness at the split point.

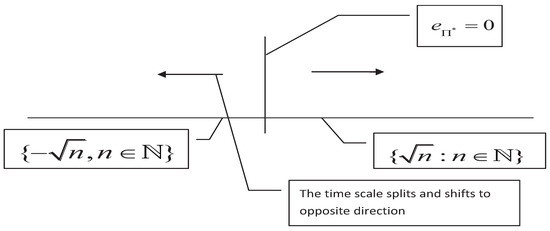
Figure 4. The time scale $\mathbb{T}=\pm {\mathbb{N}}^{\frac{1}{2}}$ has the characteristic point $e_{{\Pi }^{*}}=0$ at which the shift ${\delta }_{\tau }(·)$ is discontinuous. This time scale splits at $t=0$ and has the opposite shift closedness at the split point.

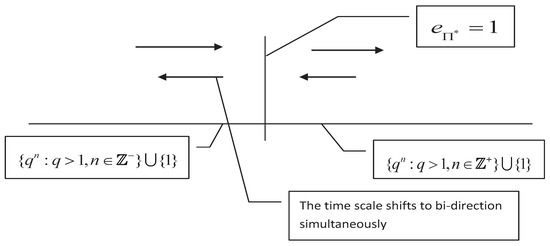
Figure 5. The time scale $\mathbb{T}=\overline{q^{\mathbb{Z}}}$ has the characteristic point $e_{{\Pi }^{*}}=1$ at which the shift ${\delta }_{\tau }(·)$ is continuous. This time scale has the bidirectional shift closedness.

For the above discussion, we propose the following open problems in a matched space $(\mathbb{T},\Pi ,\delta ,F)$.

(i)

What is the relationship between the characteristic points and the split points ?

(ii)

How many characteristic points and split points will a time scale have under a matched space?

(iii)

What is the relationship between the continuity of the shift operator ${\delta }_{\tau }(·)$ and the shift closedness of different parts of the time scale?