A Mathematical Model of Longitudinal Waves Incident at a Free Surface of a Pre-Stressed Dissipative Half-Space
Abstract
:1. Introduction
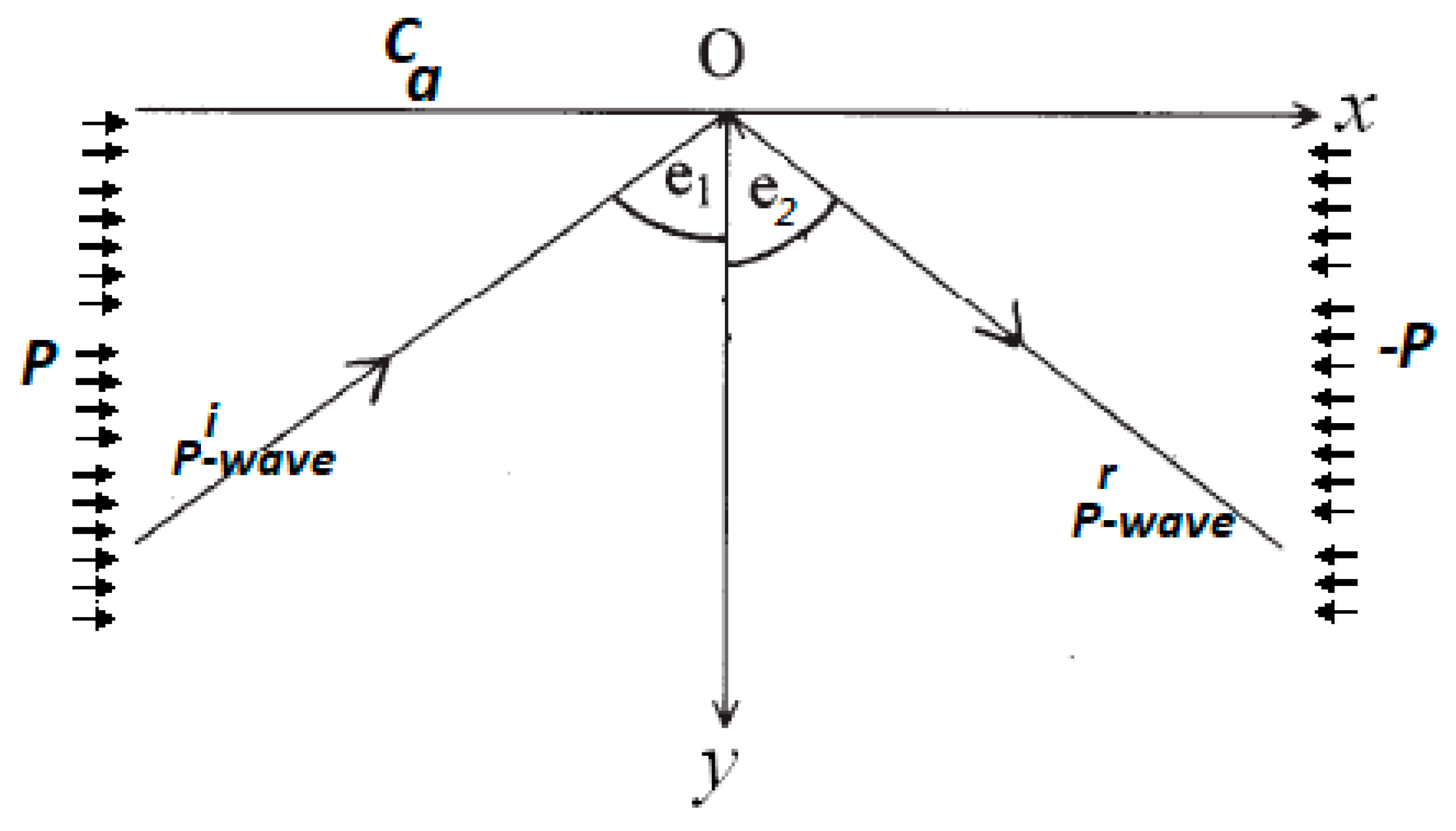
2. Model Establishment
3. Analytical Solution of the Model
3.1. Reflection of Longitudinal Waves
3.2. Boundary Conditions
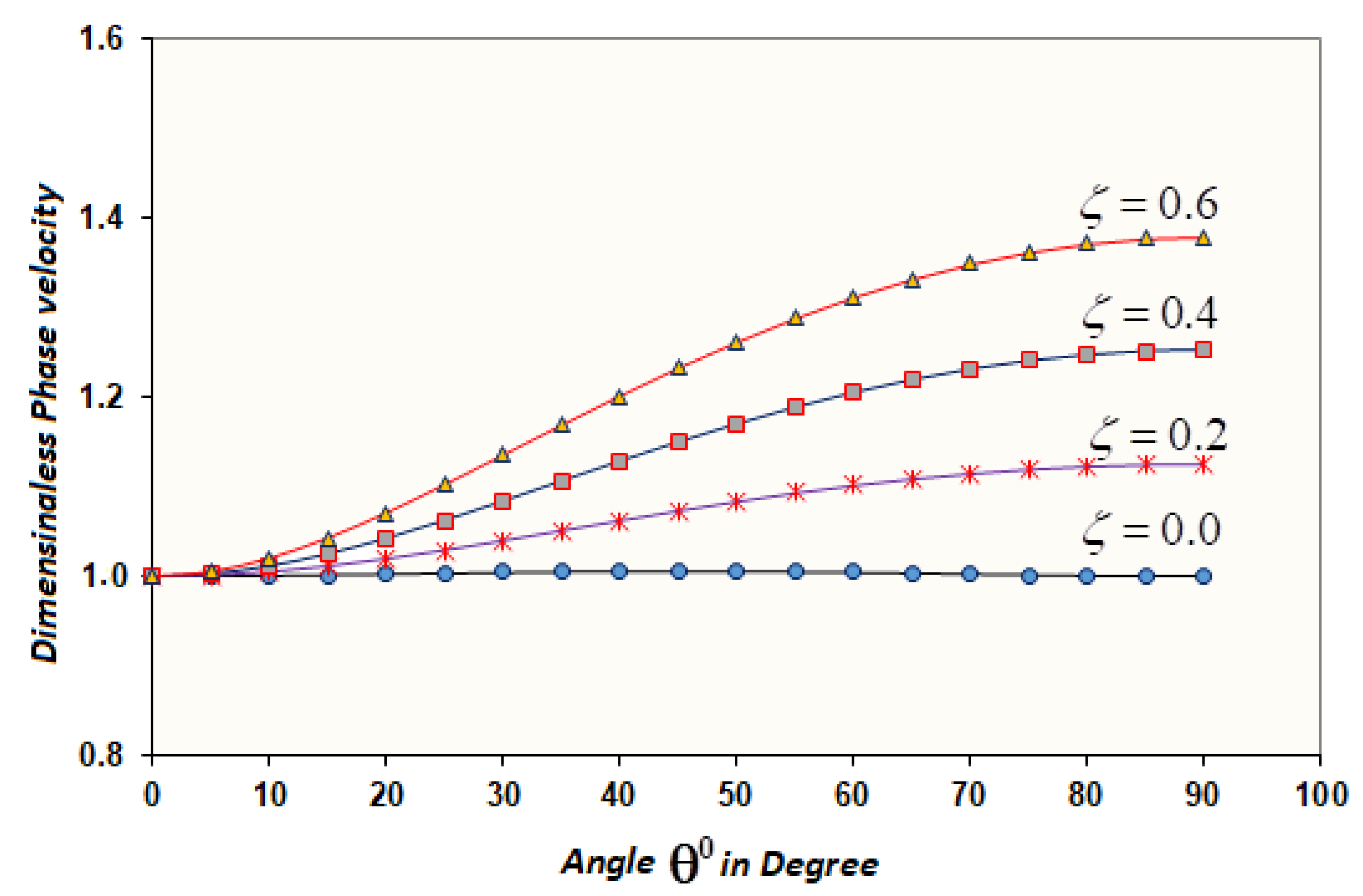
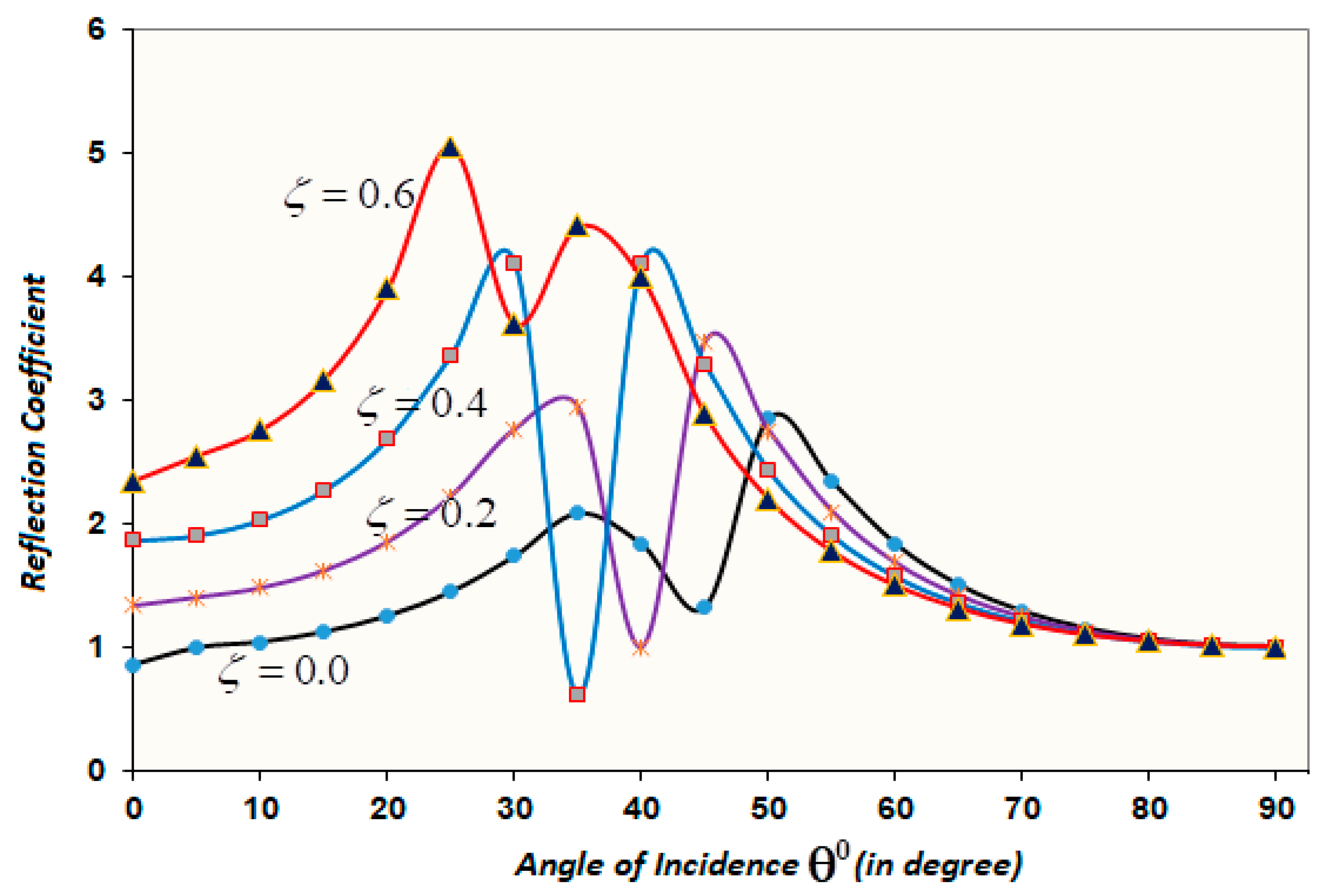
4. Numerical Calculation of the Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, B. Refection of plane waves from surface of a generalized thermo-viscoelastic porous solid half-space with impedance boundary conditions. Mech. Mech. Eng. 2018, 22, 1483–1496. [Google Scholar] [CrossRef]
- Polom, U.; Alrshdan, H.; Al-Halbouni, D.; Holohan, E.P.; Dahm, T.; Sawarieh, A.; Atallah, M.Y.; Krawczyk, C.M. Shear wave reflection seismic yields subsurface dissolution and subrosion patterns: Application to the Ghor Al-Haditha sinkhole site, Dead Sea, Jordan. Solid Earth 2018, 9, 1079–1098. [Google Scholar] [CrossRef] [Green Version]
- Legrand, F.; Gérardin, B.; Laurent, J.; Prada, C.; Aubry, A. Negative Reflection and Refraction of Guided Elastic Waves. In Proceedings of the 12th International Congress on Artificial Materials for Novel Wave Phenomena–Metamaterials, Espoo, Finland, 27 August–1 September 2018. [Google Scholar]
- Crespo, A.; García, J.; Manuel, F. Wave reflection at a stent. Proc. Inst. Mech. Eng. Part H 2013, 227, 72–77. [Google Scholar] [CrossRef]
- Liu, S.; Cui, T.J.; Noor, A.; Tao, Z.; Zhang, H.C.; Bai, G.D.; Yang, Y.; Zhou, X.Y. Negative reflection and negative surface wave conversion from obliquely incident electromagnetic waves. Light Sci. Appl. 2018, 7, 18008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manisty, C.; Mayet, J.; Tapp, R.J. Wave reflection predicts cardiovascular events in hypertensive individuals independent of blood pressure and other cardiovascular risk factors: An ASCOT (Anglo-Scandinavian Cardiac Outcome Trial) substudy. J. Am. Coll. Cardiol. 2010, 56, 24–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tooly, R.D.; Spencer, T.W.; Sagoci, H.F. Reflection and Transmission of plane compressional waves. Geophysics 1965, 30, 552–570. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.N. Reflection of plane waves from a linear transition layer in liquid media. Geophysics 1965, 30, 122–131. [Google Scholar] [CrossRef]
- Gupta, R.N. Reflection of elastic waves from a linear transition layer. Bull. Seism. Soc. Am. 1966, 56, 511–526. [Google Scholar]
- Gupta, R.N. Propagation of SH-waves in inhomogeneous media. J. Acoust. Soc. Am. 1967, 41, 1328–1329. [Google Scholar]
- Acharya, H.K. Reflection from the free surface of inhomogeneous media. Bull. Seism. Soc. Am. 1970, 60, 1101–1104. [Google Scholar]
- Cerveny, V. Reflection and Transmission coefficients for transition layers. Studia Geophys. Geod. 1974, 17, 59–68. [Google Scholar] [CrossRef]
- Singh, B.M.; Singh, S.J.; Chopra, S.D. Reflection and refraction of SH-waves and the plane boundary between two laterally and vertically heterogeneous solids. Acta Geophys. Pol. 1978, 26, 209–216. [Google Scholar]
- Singh, B.; Kumar, A.; Singh, J. Reflection of generalized thermos-elastic wave from a solid half-space under hydrostatic initial stress. Appl. Math. Comput. 2006, 177, 170–177. [Google Scholar]
- Saini, S.L. Reflection and Refraction of SH-Waves in Anisotropic Inhomogeneous Media. Ph.D. Thesis, Kurukshetra University, Kurukshetra City, India, 1979. [Google Scholar]
- Sinha, S.B. Transmission of elastic waves through a homogenous layer sandwiched in homogenous media. J. Phys. Earth 1999, 12, 1–4. [Google Scholar] [CrossRef]
- Tomar, S.K.; Singh, J. Transmission of longitudinal waves through a plane interface between two dissimilar porous elastic solid half-spaces. Appl. Math. Comput. 2005, 169, 671–688. [Google Scholar] [CrossRef]
- Sharma, M.D. Effect of initial stress on reflection at the free surfaces of anisotropic elastic medium. J. Earth Syst. Sci. 2007, 116, 537–551. [Google Scholar] [CrossRef]
- Singh, B.; Singh, L.; Deswal, D. Reflection of plane waves in thermo-diffusion elasticity without dissipation under the effect of rotation. Mech. Adv. Mater. Struct. 2016, 23, 74–79. [Google Scholar] [CrossRef]
- Biswas, S.; Sarkar, N. Fundamental solution of the steady oscillations equations in porous thermos-elastic medium with dual-phase-lag mode. J. Mech. Mater. 2018, 126, 140–147. [Google Scholar] [CrossRef]
- Li, Y.; Wei, P.; Wang, C. Propagation of thermos-elastic waves across an interface with consideration of couple stress and second sound. Math. Mech. Solids 2019, 24. [Google Scholar] [CrossRef]
- Saha, S.; Singh, A.K.; Chattopadhyay, A. Analysis of reflection and refraction of plane wave at the separating interface of two functionally graded incompressible monoclinic media under initial stress and gravity. Eur. Phys. J. Plus 2020, 135, 173. [Google Scholar] [CrossRef]
- Annand, K.Y. Effect of impedance on the reflection of plane waves in a rotating magneto-thermo-elastic solid half-space with diffusion. AIP Adv. 2020, 10, 075217. [Google Scholar] [CrossRef]
- Hacham, W.S.; Abdulla, N.N.; Al-Ammri, A.S. Wave Speed and Reflections Proximal to Aneurism and Stenosis of Flexible Tubes. In Proceedings of the 37th IEEE EMBS International Conference, Milan, Italy, 25–29 August 2015; pp. 1009–1012. [Google Scholar]
- Yao, Y.; Becker, J.M.; Ford, M.R.; Merrifield, M.A. Modeling wave processes over fringing reefs with an excavation pit. Coast. Eng. 2016, 109, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Parker, K.H.; Khir, A.W. Using wave intensity analysis to determine local reflection coefficient in flexible tubes. J. Biomech. 2016, 49, 2709–2717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Liu, Y.; Zhao, X. Numerical study of Bragg reflection of regular water waves over fringing reefs based on a Boussinesq model. Ocean Eng. 2019, 190, 106415. [Google Scholar] [CrossRef]
- Singh, B.; Sangwan, A.; Singh, J. Reflection and transmission of elastic waves at an interface between two micropolar piezoelectric half-spaces. J. Ocean Eng. Sci. 2019, 4, 227–237. [Google Scholar] [CrossRef]
- Hacham, W.S.; Khir, A.W. The speed, reflection and intensity of waves propagating in flexible tubes with aneurysm and stenosis: Experimental investigation. Proc. Mech. Part H J. Eng. Med. 2019, 233, 979–988. [Google Scholar] [CrossRef] [Green Version]
- Biot, M.A. Mechanics of Incremental Deformation; John Wiley and Sons Inc.: New York, NY, USA, 1965. [Google Scholar]
- Fung, Y.C. Foundation of Solid Mechanics; Prentice Hall of India: New Delhi, India, 1965. [Google Scholar]
- Selim, M.M.; Ahmed, M.K. Propagation and attenuation of seismic body waves in dissipative medium under initial and couple stresses. Appl. Math. Comput. 2006, 182, 1064–1074. [Google Scholar] [CrossRef]
- Kebeasy, R.M.; Bayoumy, A.I.; Gharib, A.A. Crustal structure modeling for the northern part of the Aswan Lake area using seismic waves generated by explosions and local earthquake. J. Geodyn. 1991, 14, 159–182. [Google Scholar] [CrossRef]
| 2.15 g/cm3 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selim, M.M.; Nofal, T.A. A Mathematical Model of Longitudinal Waves Incident at a Free Surface of a Pre-Stressed Dissipative Half-Space. Mathematics 2020, 8, 2011. https://doi.org/10.3390/math8112011
Selim MM, Nofal TA. A Mathematical Model of Longitudinal Waves Incident at a Free Surface of a Pre-Stressed Dissipative Half-Space. Mathematics. 2020; 8(11):2011. https://doi.org/10.3390/math8112011
Chicago/Turabian StyleSelim, Mahmoud M., and Taher A. Nofal. 2020. "A Mathematical Model of Longitudinal Waves Incident at a Free Surface of a Pre-Stressed Dissipative Half-Space" Mathematics 8, no. 11: 2011. https://doi.org/10.3390/math8112011
APA StyleSelim, M. M., & Nofal, T. A. (2020). A Mathematical Model of Longitudinal Waves Incident at a Free Surface of a Pre-Stressed Dissipative Half-Space. Mathematics, 8(11), 2011. https://doi.org/10.3390/math8112011





