Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach
Abstract
:1. Introduction
2. Model Statement
2.1. Wind Turbine Model
2.2. Doubly Fed Induction Generator Model
2.3. Grid-Side Converter and DC-Link Models
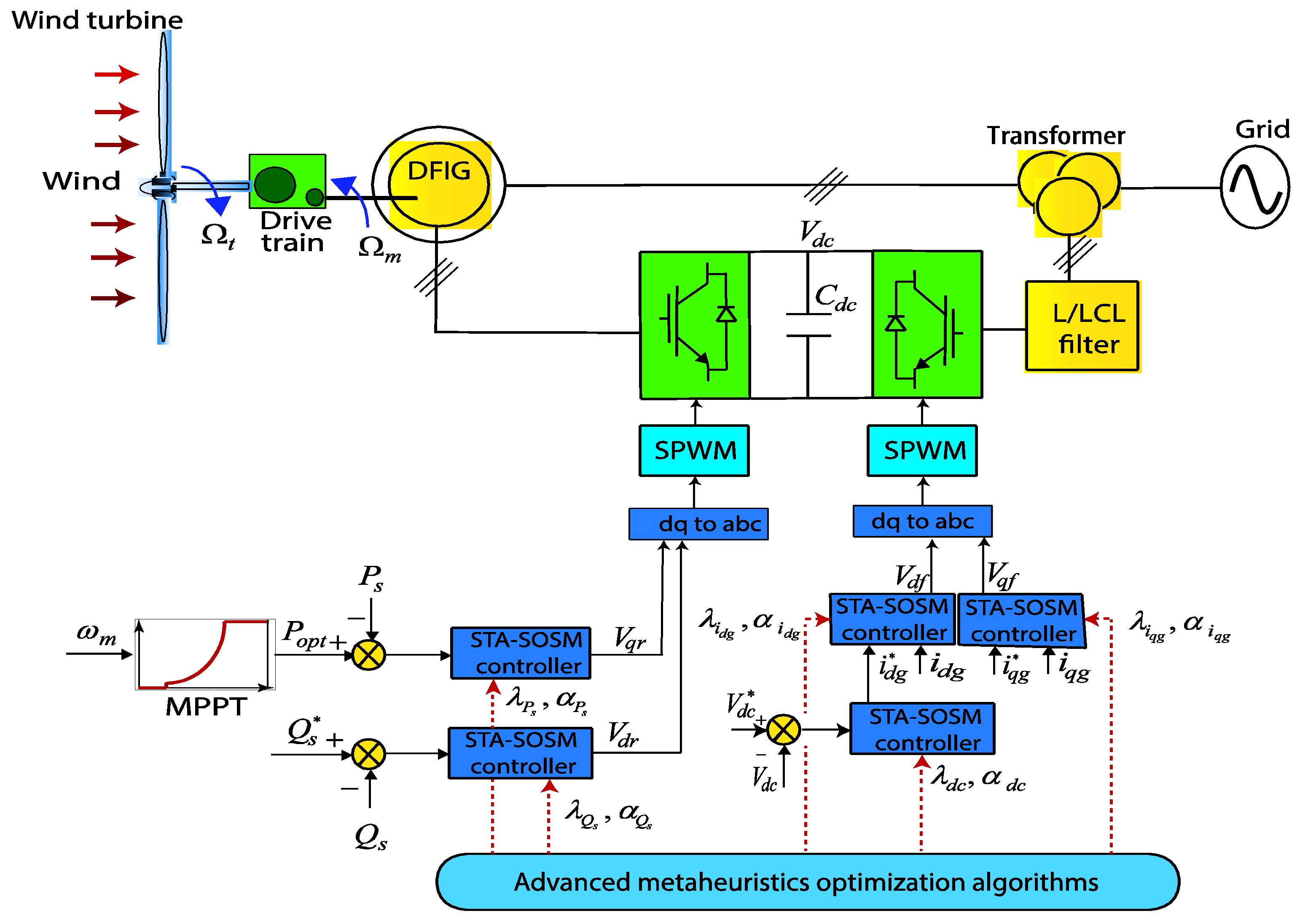
3. Metaheuristics-Based Integral Sliding Mode Control Strategy
3.1. Problem Statement
3.2. Robustness and Operational Constraints
3.3. Control Problem Formulation
3.4. Thermal Exchange Optimization Algorithm
4. Results and Discussion
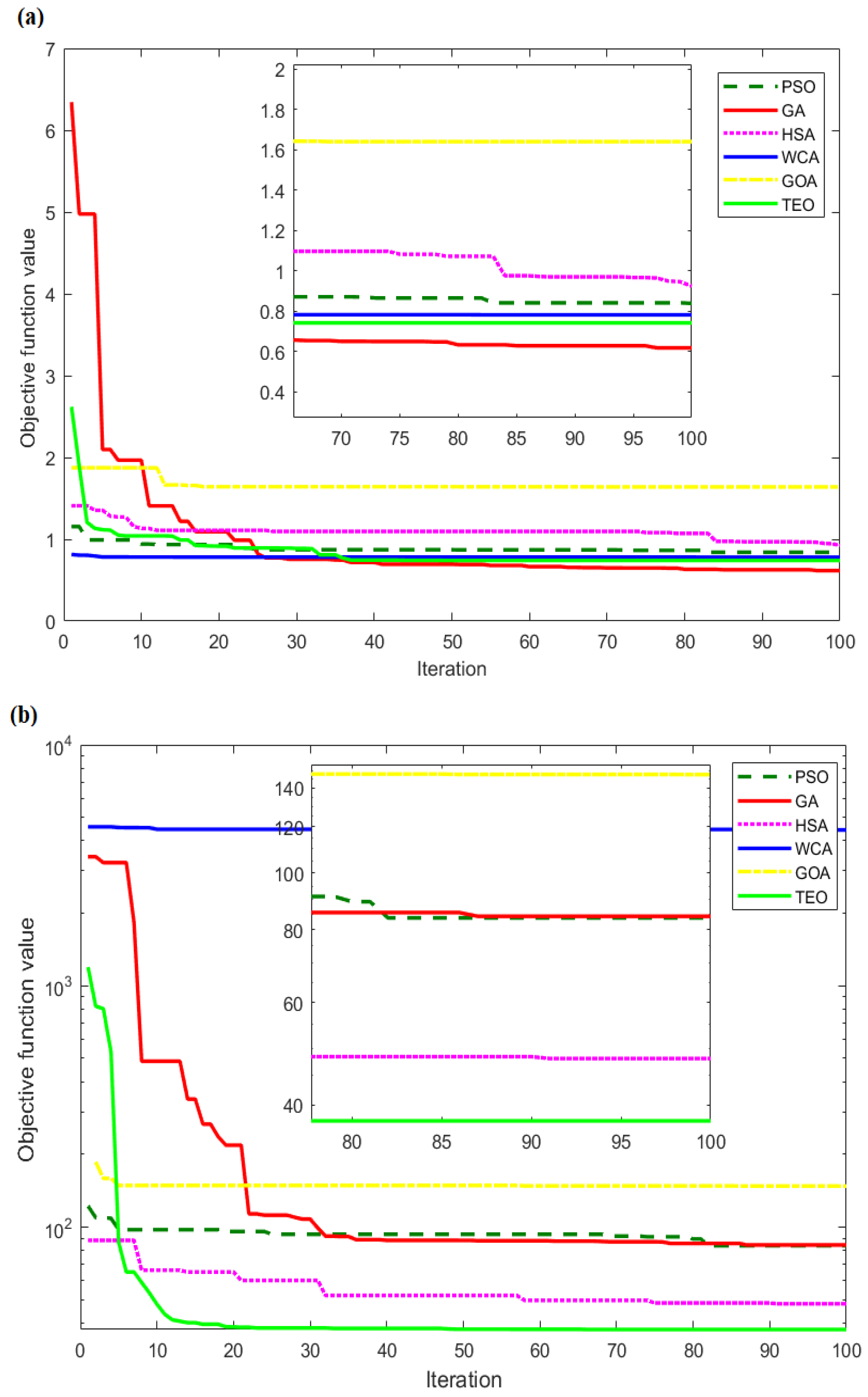
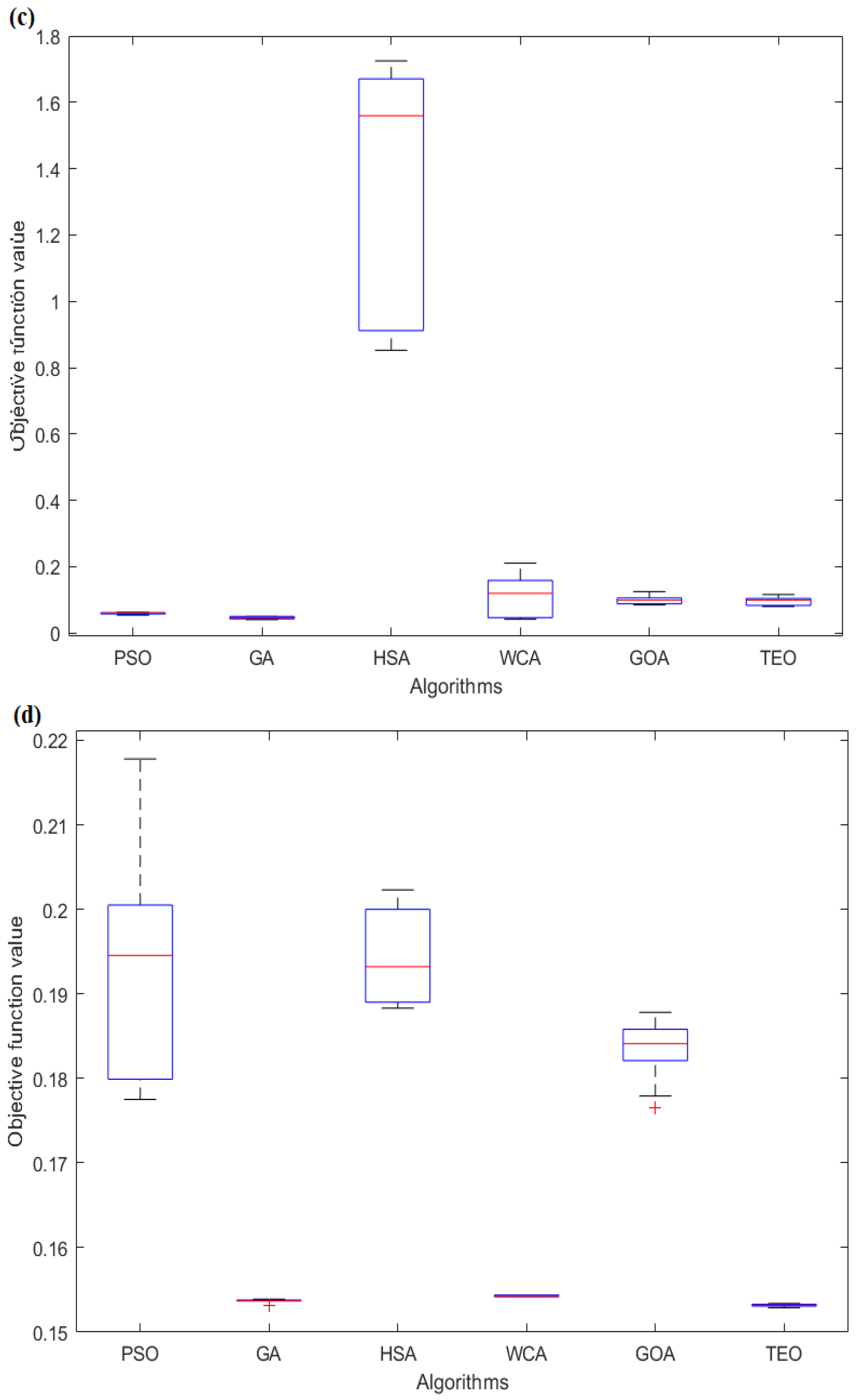
4.1. Convergence Rates
4.2. Statistical Analysis and Comparison
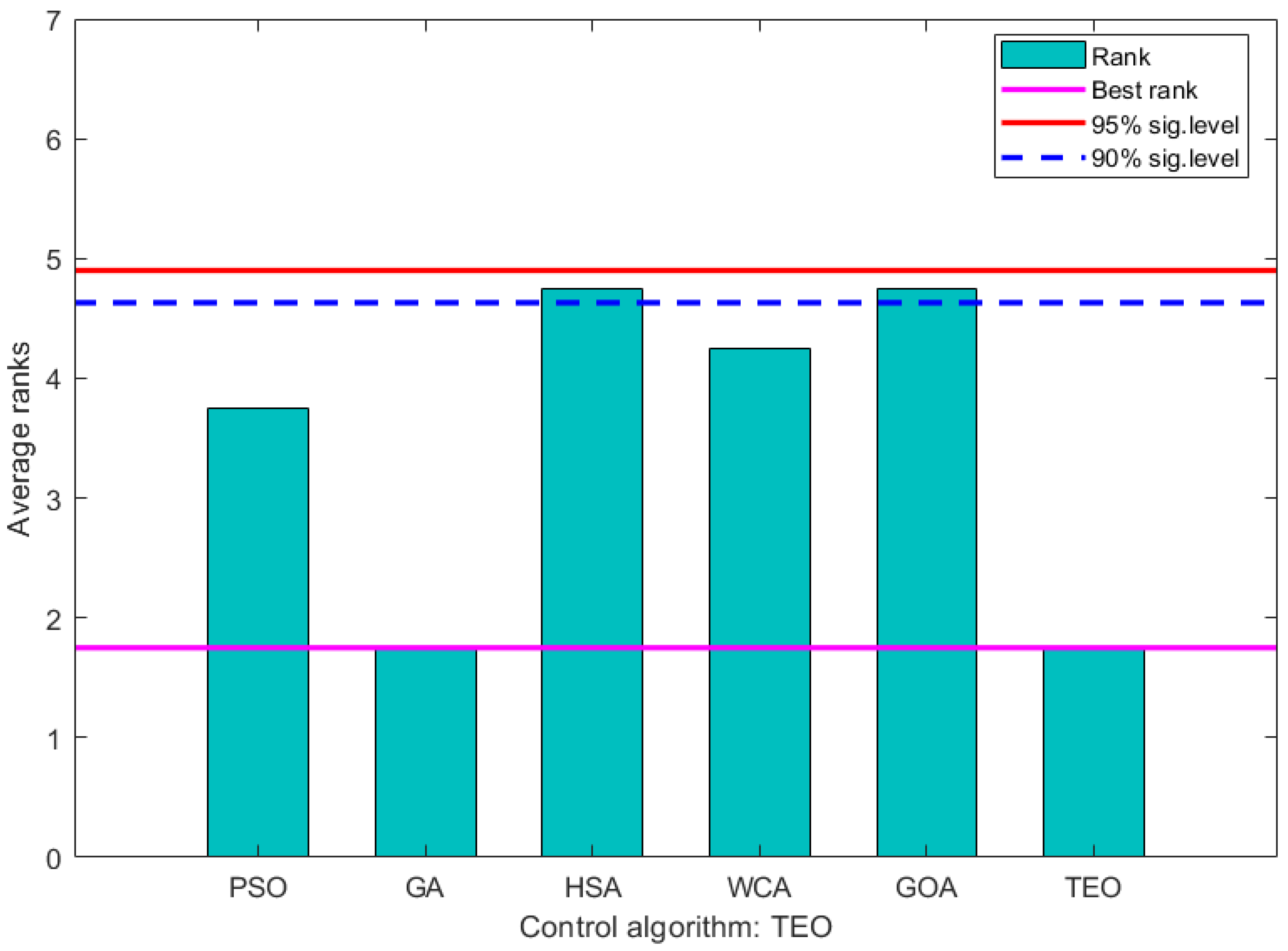
4.2.1. Friedman’s Test
4.2.2. Bonferroni–Dunn’s Test
4.2.3. Elapsed Time Efficiency
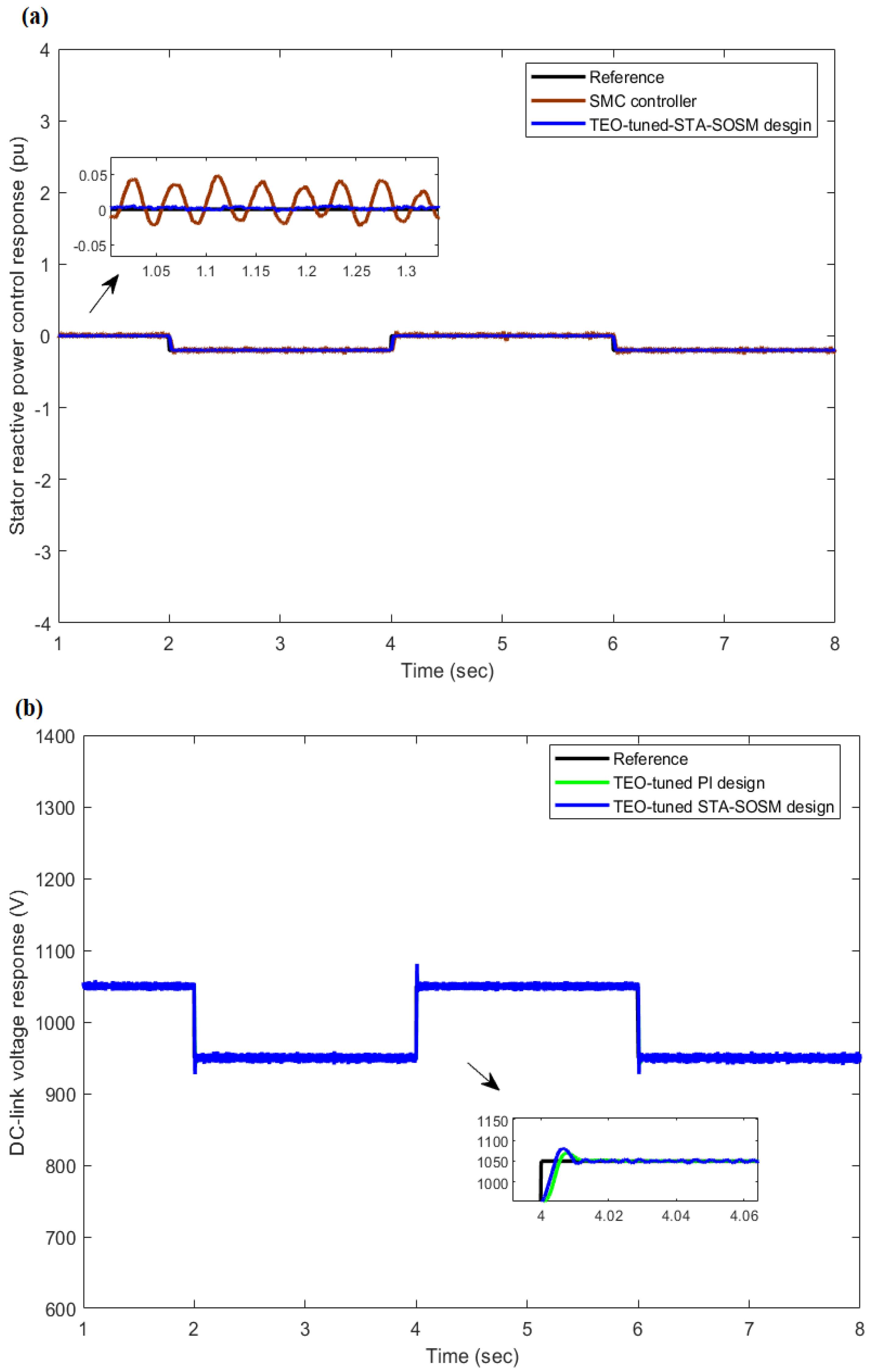
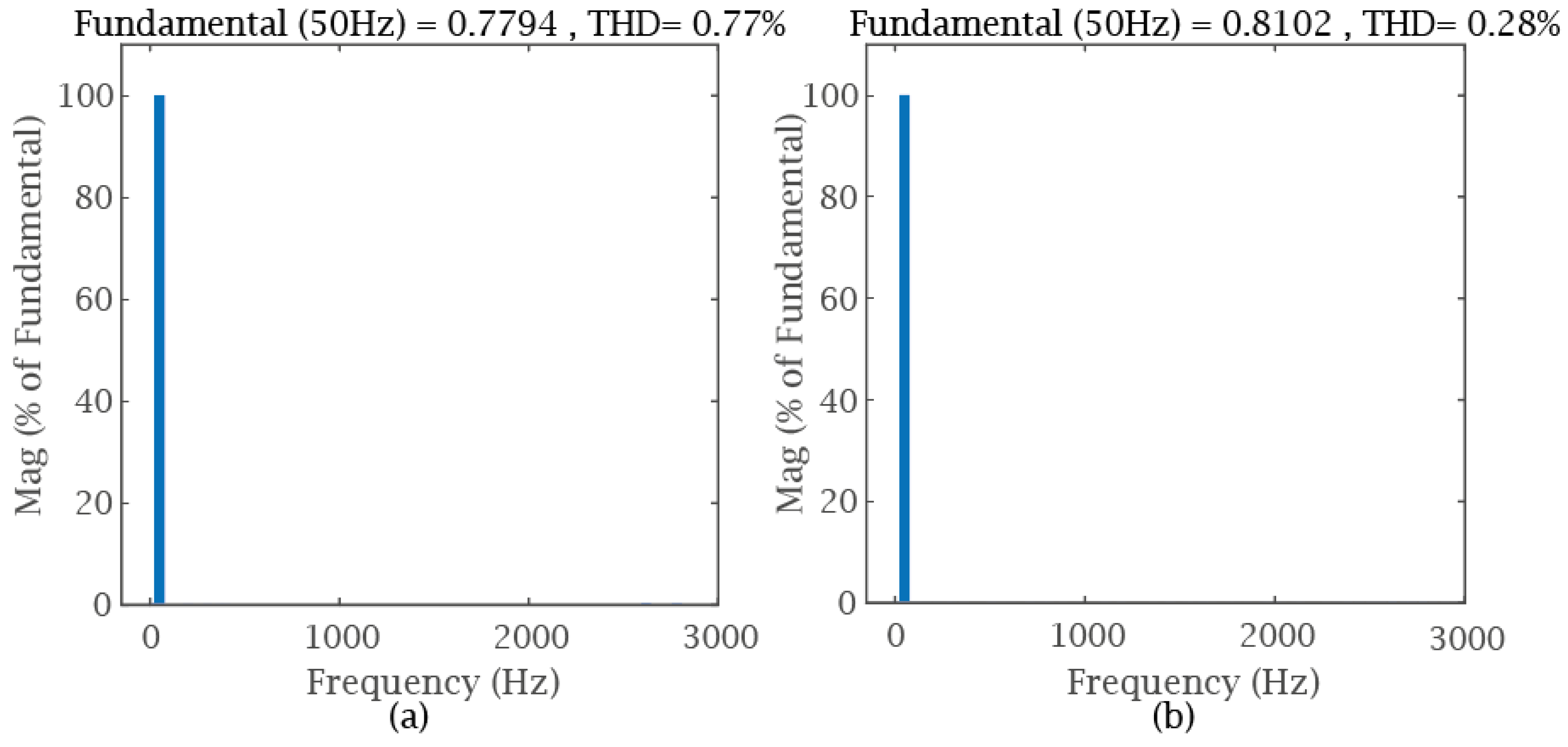
4.3. Reference Tracking Condition
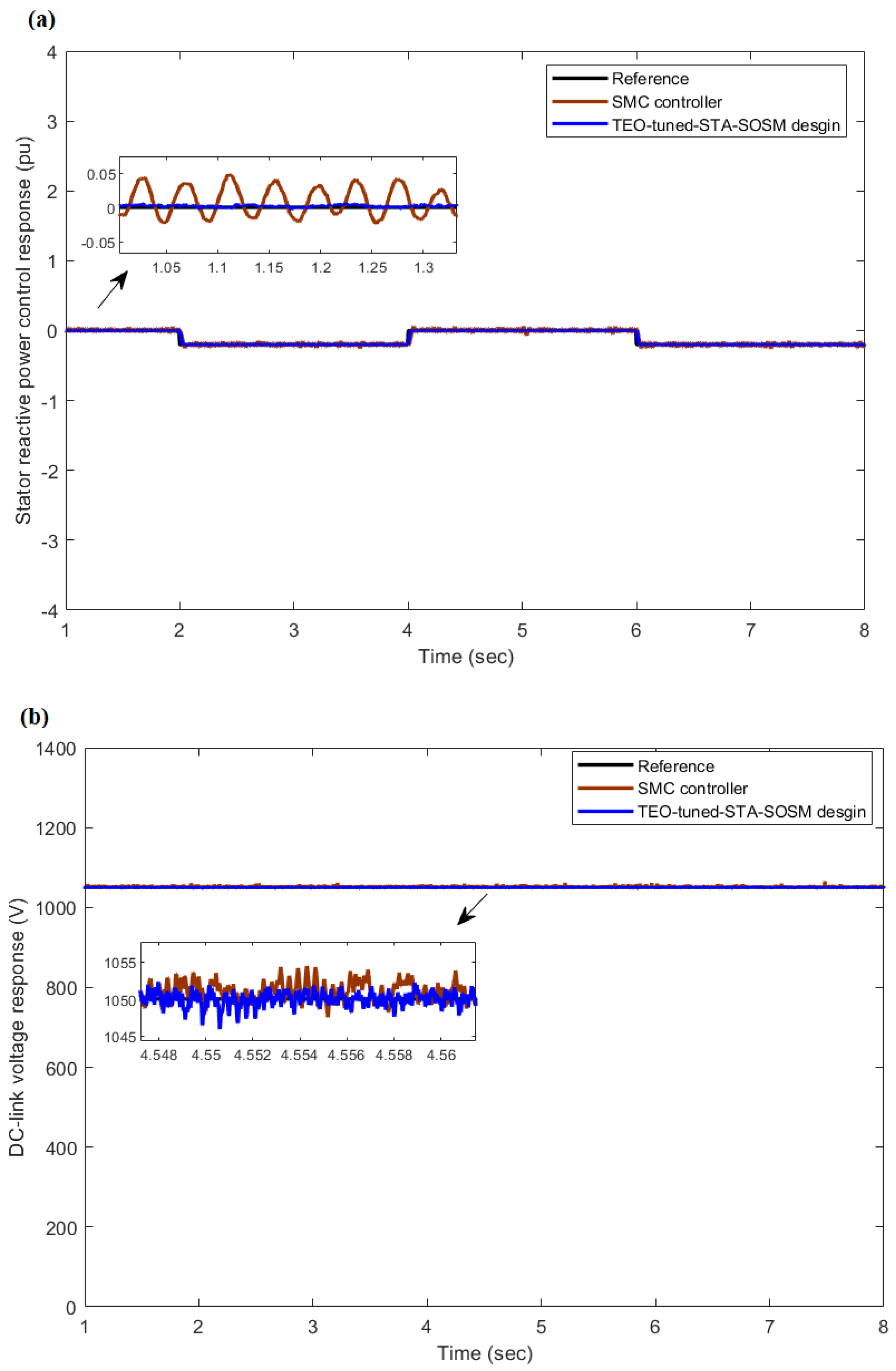
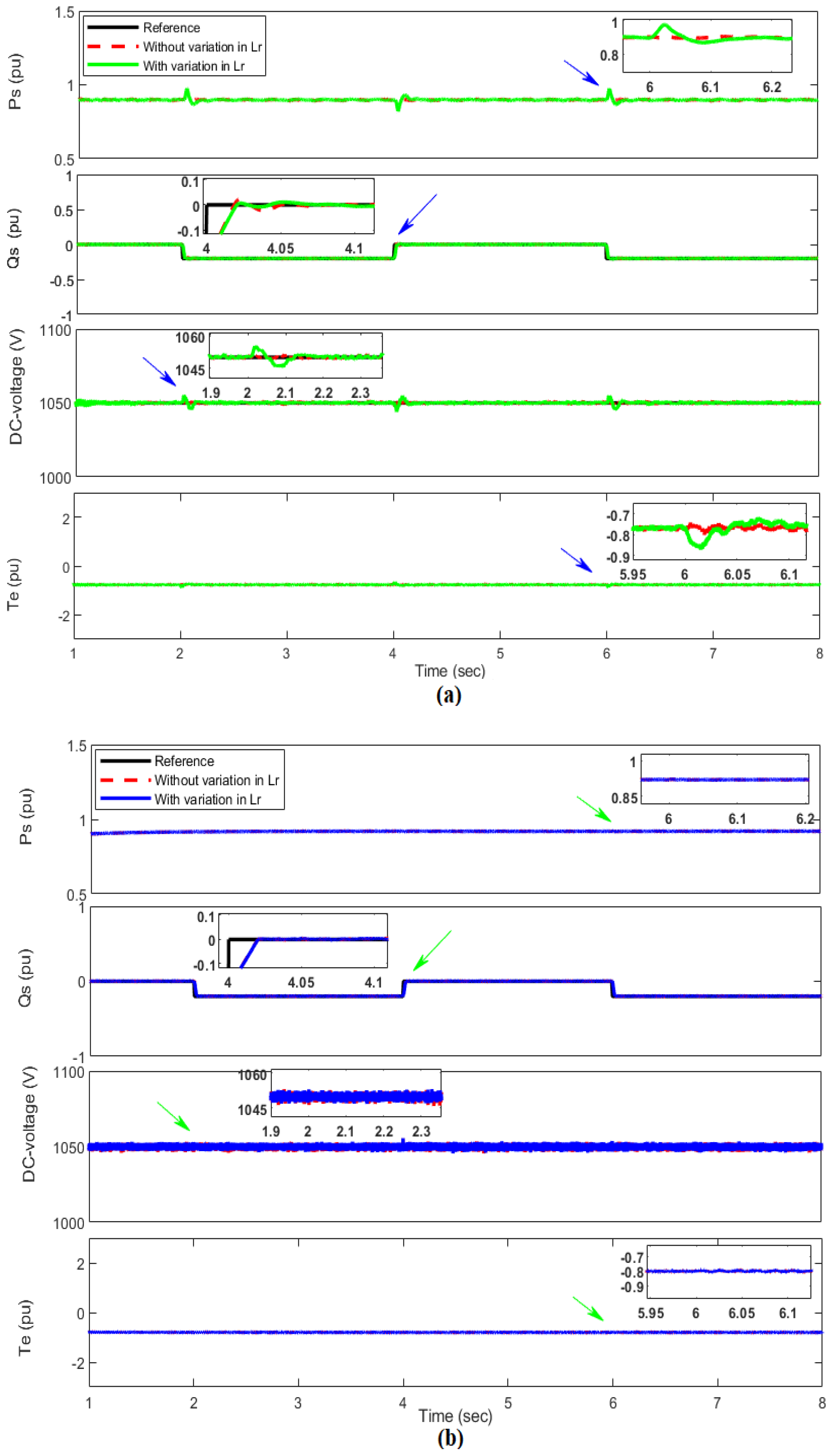
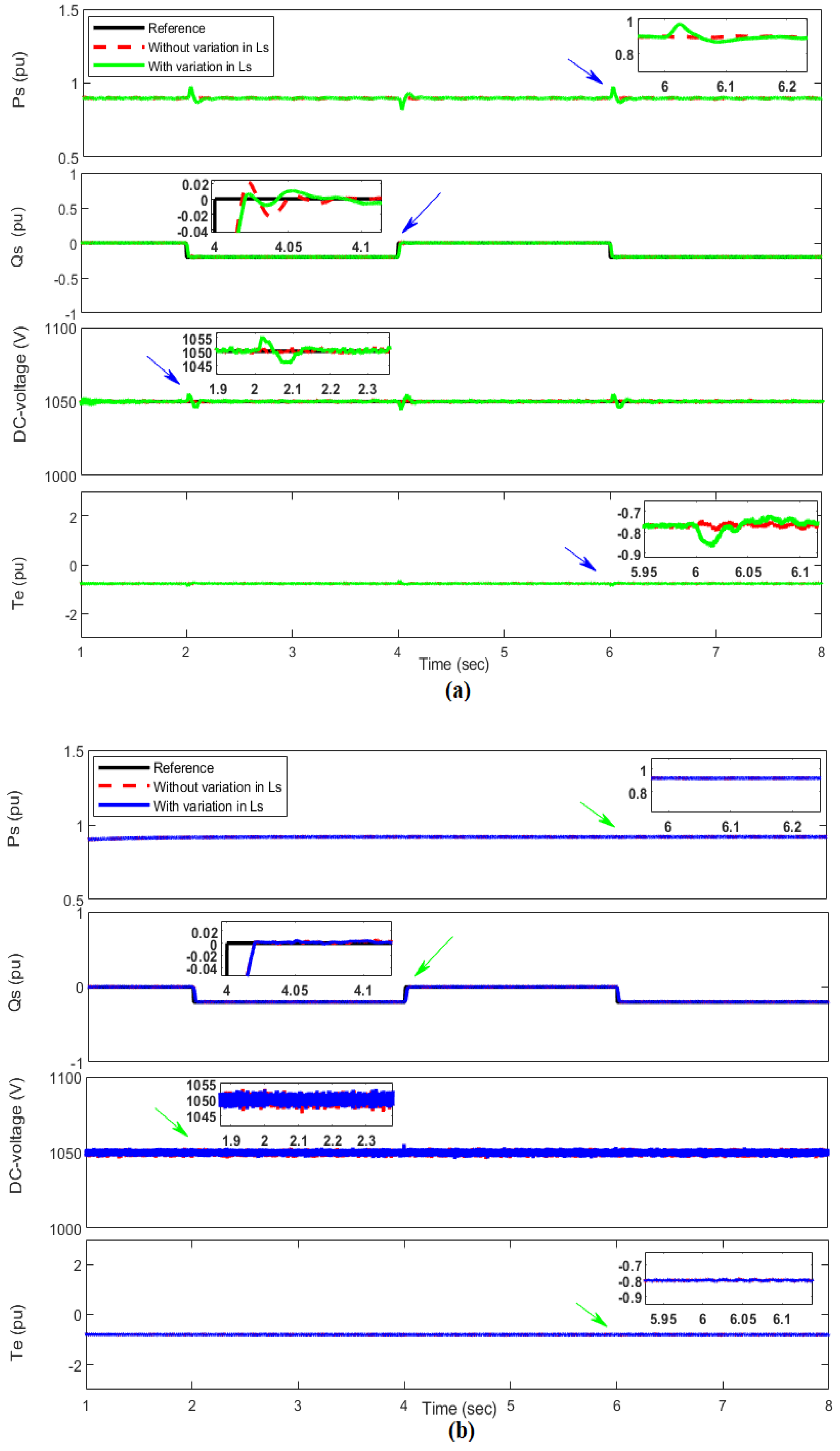
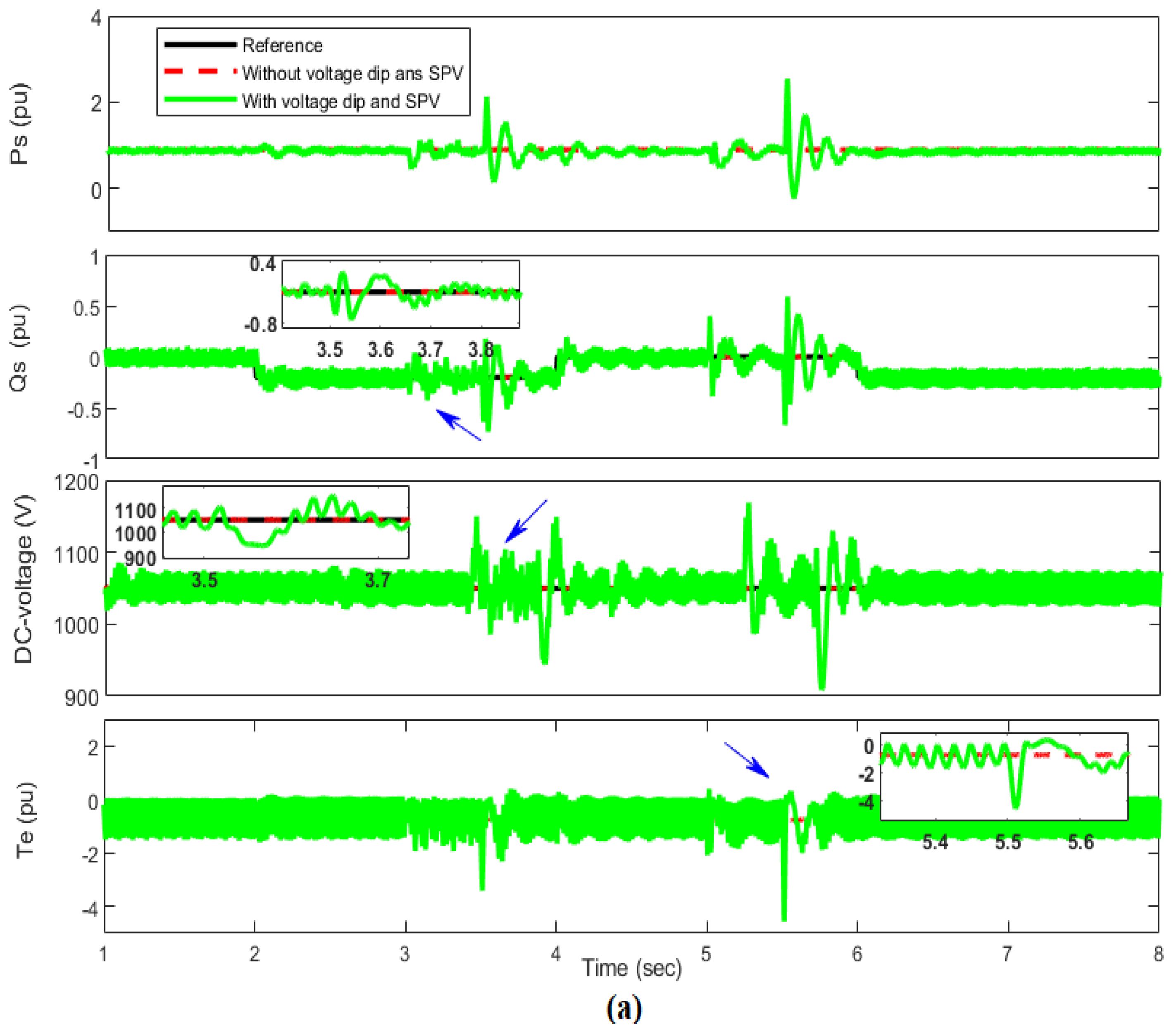
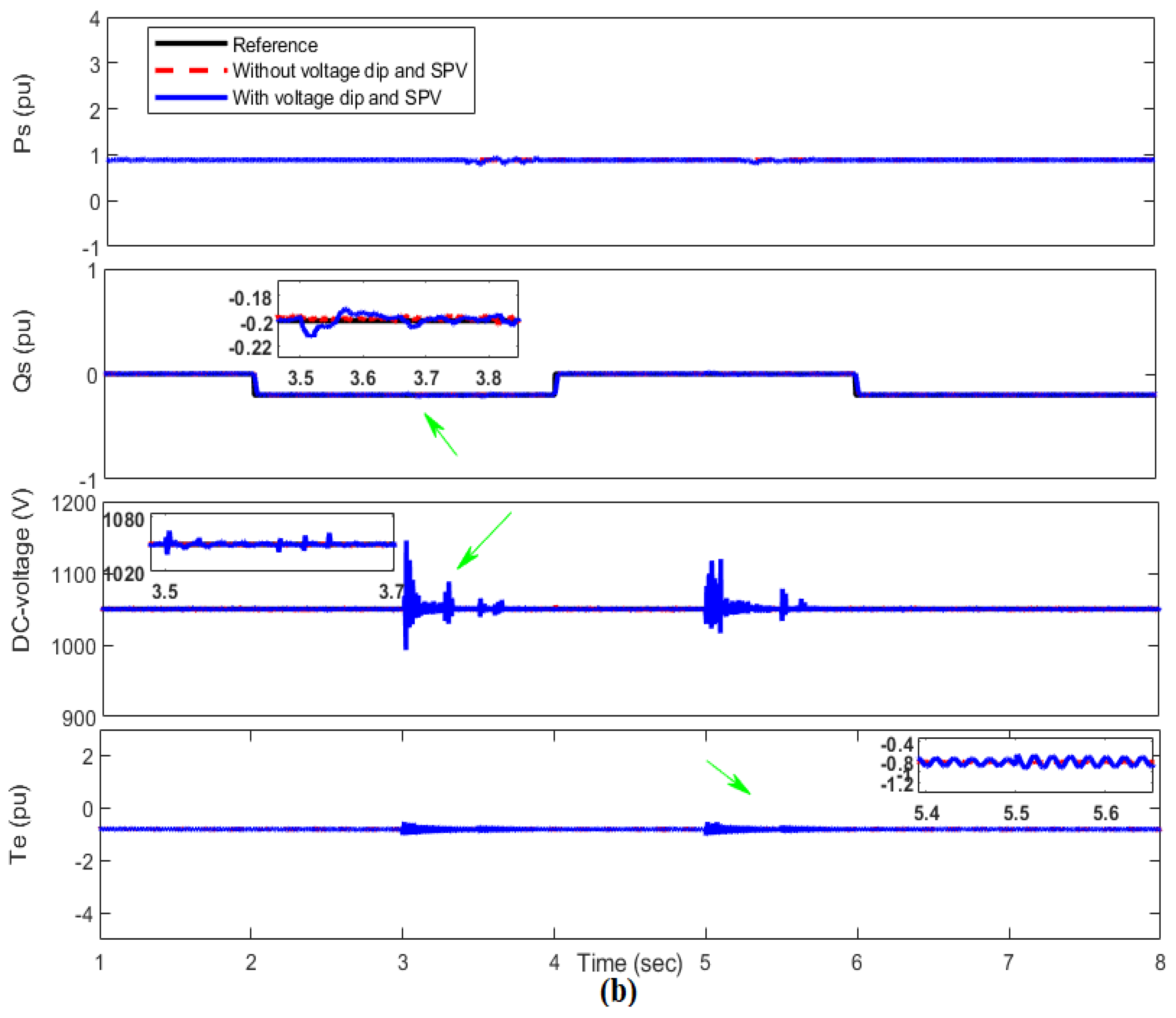
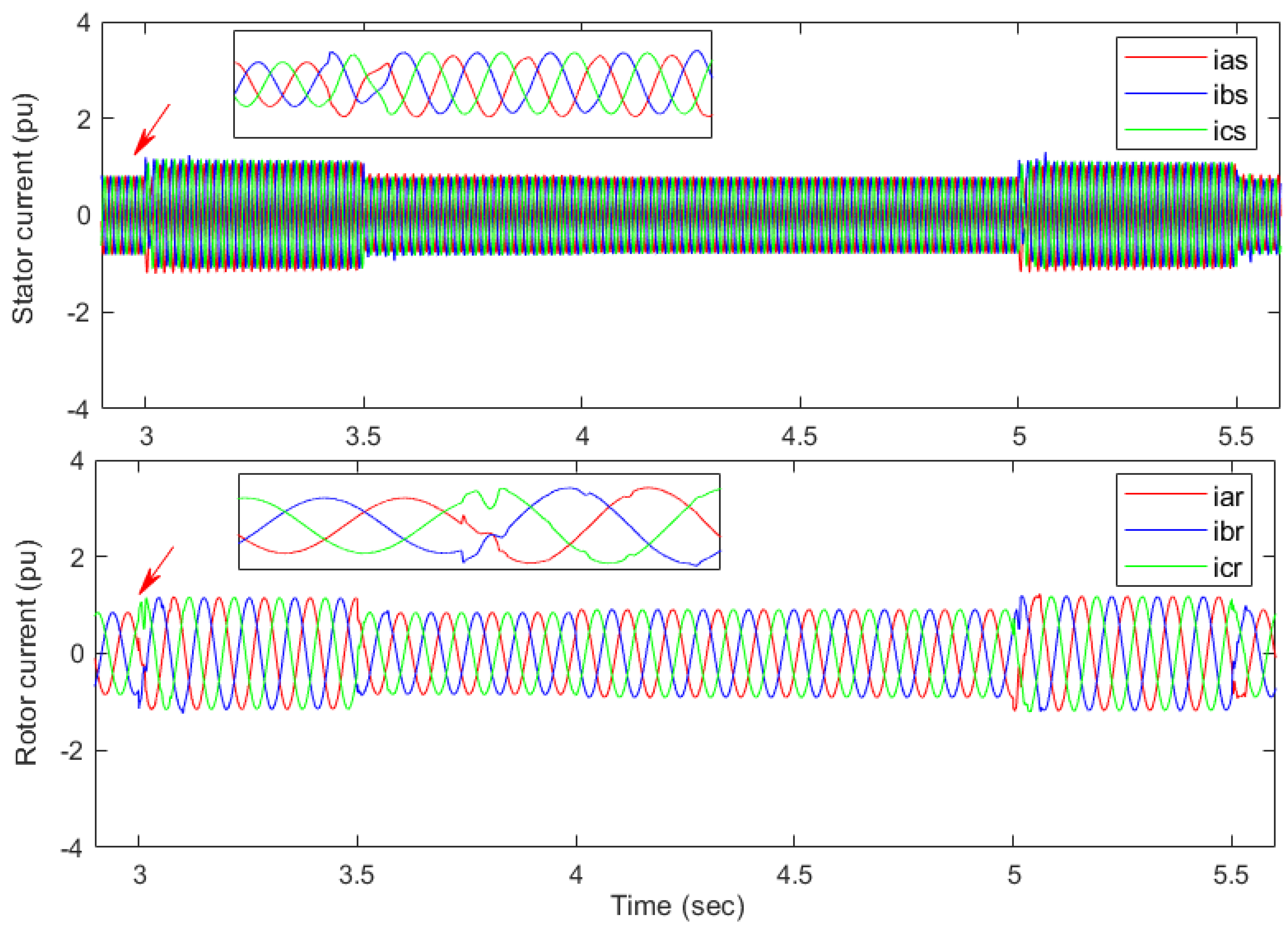
4.4. Robustness Analysis
4.4.1. Parametric Mismatch Condition
4.4.2. Grid Faults Condition
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| DC-link capacitor | |
| Grid voltages in dq reference frame | |
| Grid currents in dq reference frame | |
| Rotor currents in dq reference frame | |
| Stator currents in dq reference frame | |
| Mutual inductance | |
| Rotor and stator inductances | |
| Stator active power | |
| Stator reactive power | |
| Rotor and stator resistances | |
| DC-link voltage | |
| Grid converter voltage in dq reference frame | |
| Rotor converter voltage in dq reference frame | |
| RMS phase voltages for the stator | |
| Stator voltages in dq reference frame | |
| Angular grid frequency | |
| Rotor and stator angular frequencies | |
| Mechanical rotational speed | |
| Rotor fluxes in dq reference frame | |
| Stator fluxes in dq reference frame |
References
- Naik, K.A.; Gupta, C.P.; Fernandez, E. Design and implementation of interval type-2 fuzzy logic-PI based adaptive controller for DFIG based wind energy system. Int. J. Electr. Power Energy Syst. 2020, 115, 105468. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.; Asher, G. Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation. IEE Proc. Electr. Power Appl. 1996, 143, 231. [Google Scholar] [CrossRef] [Green Version]
- Poitiers, F.; Bouaouiche, T.; Machmoum, M. Advanced control of a doubly-fed induction generator for wind energy conversion. Electr. Power Syst. Res. 2009, 79, 1085–1096. [Google Scholar] [CrossRef]
- Djoudi, A.; Chekireb, H.; Berkouk, E.M.; Bacha, S. Low-cost sliding mode control of WECS based on DFIG with stability analysis. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1698–1714. [Google Scholar] [CrossRef]
- Merabet, A.; Eshaft, H.; Tanvir, A.A. Power-current controller based sliding mode control for DFIG-wind energy conversion system. IET Renew. Power Gener. 2018, 12, 1155–1163. [Google Scholar] [CrossRef]
- Hamane, B.; Doumbia, M.L.; Bouhamida, M.; Draou, A.; Chaoui, H.; Benghanem, M. Comparative study of PI, RST, sliding mode and fuzzy supervisory controllers for DFIG based wind energy conversion system. Int. J. Renew. Energy Res. 2015, 5, 1174–1185. [Google Scholar]
- Azzaoui, M.E.I.; Mahmoudi, H. Fuzzy-PI control of a doubly fed induction generator-based wind power system. Int. J. Autom. Control. 2017, 11, 54–66. [Google Scholar] [CrossRef]
- Zhi, D.; Xu, L.; Williams, B.W. Model-Based Predictive Direct Power Control of Doubly Fed Induction Generators. IEEE Trans. Power Electron. 2010, 25, 341–351. [Google Scholar] [CrossRef]
- Aidoud, M.; Sedraoui, M.; Lachouri, A.; Boualleg, A. A robustification of the two degree-of-freedom controller based upon multivariable generalized predictive control law and robust H∞ control for a doubly-fed induction generator. Trans. Inst. Meas. Control. 2018, 40, 1005–1017. [Google Scholar] [CrossRef]
- Douiri, M.R.; Essadki, A.; Cherkaoui, M. Neural Networks for Stable Control of Nonlinear DFIG in Wind Power Systems. Procedia Comput. Sci. 2018, 127, 454–463. [Google Scholar] [CrossRef]
- Hu, J.; Nian, H.; Hu, B.; He, Y.; Zhu, Z.Q. Direct Active and Reactive Power Regulation of DFIG Using Sliding-Mode Control Approach. IEEE Trans. Energy Convers. 2010, 25, 1028–1039. [Google Scholar] [CrossRef]
- Barambones, O.; Cortajarena, J.A.; Alkorta, P.; De Durana, J.M.G. A Real-Time Sliding Mode Control for a Wind Energy System Based on a Doubly Fed Induction Generator. Energies 2014, 7, 6412–6433. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Li, H.; Wang, J. Sliding Mode Control of DFIG Wind Turbines with a Fast Exponential Reaching Law. Energies 2017, 10, 1788. [Google Scholar] [CrossRef] [Green Version]
- Susperregui, A.; Martinez, M.; Zubia, I.; Tapia, G. Design and tuning of fixed-switching-frequency second-order sliding-mode controller for doubly fed induction generator power control. IET Electr. Power Appl. 2012, 6, 696. [Google Scholar] [CrossRef]
- Yaichi, I.; Semmah, A.; Wira, P.; Djeriri, Y. Super-twisting Sliding Mode Control of a Doubly-fed Induction Generator Based on the SVM Strategy. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 178–190. [Google Scholar] [CrossRef]
- Falehi, A.D. Optimal Power Tracking of DFIG-Based Wind Turbine Using MOGWO-Based Fractional-Order Sliding Mode Controller. J. Sol. Energy Eng. 2020, 142, 1–35. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Wang, C. Second-order sliding mode control for power optimisation of DFIG-based variable speed wind turbine. IET Renew. Power Gener. 2017, 11, 408–418. [Google Scholar] [CrossRef]
- Benamor, A.; Benchouia, M.; Srairi, K.; Benbouzid, M. A new rooted tree optimization algorithm for indirect power control of wind turbine based on a doubly-fed induction generator. ISA Trans. 2019, 88, 296–306. [Google Scholar] [CrossRef]
- Boubzizi, S.; Abid, H.; El Hajjaji, A.; Chaabane, M. Comparative study of three types of controllers for DFIG in wind energy conversion system. Prot. Control. Mod. Power Syst. 2018, 3, 21. [Google Scholar] [CrossRef]
- Alhato, M.M.; Bouallègue, S. Thermal exchange optimization based control of a doubly fed induction generator in wind energy conversion system. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1–8. [Google Scholar]
- Alhato, M.M.; Bouallègue, S. Direct Power Control Optimization for Doubly Fed Induction Generator Based Wind Turbine Systems. Math. Comput. Appl. 2019, 24, 77. [Google Scholar] [CrossRef] [Green Version]
- Djilali, L.; Sanchez, E.N.; Belkheiri, M. Real-time implementation of sliding-mode field-oriented control for a DFIG-based wind turbine. Int. Trans. Electr. Energy Syst. 2018, 28, e2539. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Moreno, J.A.; Plestan, F.; Fridman, L.M.; Poznyak, A.S. Super-twisting adaptive sliding mode control: A Lyapunov design. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 5109–5113. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control. 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Merabet, A.; Labib, L.; Ghias, A.M.; Al-Durra, A.; Debbouza, M. Dual-mode operation based second-order sliding mode control for grid-connected solar photovoltaic energy system. Int. J. Electr. Power Energy Syst. 2019, 111, 459–474. [Google Scholar] [CrossRef]
- Merabet, A.; Al-Durra, A.; Debouza, M.; Tanvir, A.A.; Eshaft, H. Integral sliding mode control for back-to-back converter of DFIG wind turbine system. J. Eng. 2020, 2020, 834–842. [Google Scholar] [CrossRef]
- Alhato, M.M.; Bouallègue, S.; Ayadi, M. Modeling and control of an AC-DC voltage source converter based on sliding mode and fuzzy gain scheduling approaches. In Proceedings of the 7th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications, Hammamet, Tunisia, 18–20 December 2016; pp. 332–337. [Google Scholar]
- Wang, J.-J.; Liu, G. Hierarchical sliding-mode control of spatial inverted pendulum with heterogeneous comprehensive learning particle swarm optimization. Inf. Sci. 2019, 495, 14–36. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Bouallègue, S.; Haggège, J.; Ayadi, M.; Benrejeb, M. PID-type fuzzy logic controller tuning based on particle swarm optimization. Eng. Appl. Artif. Intell. 2012, 25, 484–493. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 276, 66–72. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Diab, A.A.Z.; Rezk, H. Partial shading mitigation of PV systems via different meta-heuristic techniques. Renew. Energy 2019, 130, 1159–1175. [Google Scholar] [CrossRef]
- Abdalla, O.; Rezk, H.; Ahmed, E.M. Wind driven optimization algorithm based global MPPT for PV system under non-uniform solar irradiance. Sol. Energy 2019, 180, 429–444. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, W.; Zhang, S.; Zheng, N. Re-KISSME: A robust resampling scheme for distance metric learning in the presence of label noise. Neurocomputing 2019, 330, 138–150. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Guan, B.; Xu, P. Layout optimization of large-scale oil–gas gathering system based on combined optimization strategy. Neurocomputing 2019, 332, 159–183. [Google Scholar] [CrossRef]
- Sababha, M.; Zohdy, M.A.; Kafafy, M. The Enhanced Firefly Algorithm Based on Modified Exploitation and Exploration Mechanism. Electronics 2018, 7, 132. [Google Scholar] [CrossRef] [Green Version]







| Performance Criteria | PSO | GA | HSA | WCA | GOA | TEO | |
|---|---|---|---|---|---|---|---|
| IAE | Best | 0.838 | 0.617 | 0.883 | 0.672 | 1.27 | 0.724 |
| Mean | 0.880 | 0.649 | 0.915 | 0.861 | 1.42 | 0.778 | |
| Worst | 0.911 | 0.695 | 0.969 | 1.37 | 1.64 | 0.874 | |
| STD | 3 × 10−2 | 3.1 × 10−2 | 3.3 × 10−2 | 2.8 × 10−1 | 1.4 × 10−1 | 5.9 × 10−2 | |
| ET (s) | 10,822 | 13,722 | 9891 | 10,859 | 9576 | 9646 | |
| ISE | Best | 56.53 | 42.22 | 47.40 | 37.59 | 129.99 | 40.54 |
| Mean | 76.97 | 62.31 | 57.43 | 948.91 | 141.32 | 56.11 | |
| Worst | 94.42 | 86.93 | 73.40 | 4431.78 | 155.13 | 70.25 | |
| STD | 17.98 | 21.51 | 12.53 | 1947.20 | 10.75 | 11.97 | |
| ET (s) | 12,143 | 12,568 | 9274 | 11,761 | 9041 | 10,513 | |
| ITAE | Best | 0.054 | 0.040 | 0.852 | 0.041 | 0.084 | 0.079 |
| Mean | 0.059 | 0.046 | 1.34 | 0.112 | 0.099 | 0.096 | |
| Worst | 0.062 | 0.050 | 1.72 | 0.210 | 0.125 | 0.115 | |
| STD | 3 × 10−3 | 4 × 10−3 | 4.1 × 10−1 | 7 × 10−2 | 1.5 × 10−2 | 1.4 × 10−2 | |
| ET (s) | 13,380 | 11,665 | 9897 | 12,026 | 9841 | 10,271 | |
| ITSE | Best | 0.1775 | 0.1532 | 0.1883 | 0.1543 | 0.1765 | 0.1529 |
| Mean | 0.1941 | 0.1537 | 0.1944 | 0.1544 | 0.1832 | 0.1532 | |
| Worst | 0.2178 | 0.1539 | 0.2023 | 0.1545 | 0.1878 | 0.1534 | |
| STD | 1.5 × 10−2 | 1.8 × 10−4 | 3.9 × 10−3 | 8.6 × 10−5 | 3.6 × 10−3 | 1.6 × 10−4 | |
| ET (s) | 13,663 | 12,633 | 11,101 | 12,466 | 9850 | 9790 |
| Performance Criteria | Algorithms | STA-SOSM Controllers’ Gains | |||||
|---|---|---|---|---|---|---|---|
| IAE | PSO | 360.7 | 31.2 | 135.7 | 480.1 | 23.8 | 500 |
| GA | 5.6 | 595.2 | 7.7 | 211.2 | 58 | 355.9 | |
| HSA | 149.3 | 389.5 | 107.3 | 474.9 | 273.9 | 342.2 | |
| WCA | 7.3 | 34.5 | 52.4 | 391.7 | 8.9 | 404.9 | |
| GOA | 31.4 | 94.9 | 99.8 | 12.4 | 19.9 | 64.3 | |
| TEO | 1.5 | 33.1 | 26.1 | 14.5 | 32.4 | 5.2 | |
| ISE | PSO | 4 | 283.2 | 406.6 | 442.9 | 499.4 | 108.3 |
| GA | 7.9 | 303.6 | 83.1 | 305.2 | 9.6 | 138.4 | |
| HSA | 19.9 | 393.1 | 94.4 | 205.8 | 324.2 | 219.9 | |
| WCA | 9.7 | 336.4 | 14.7 | 227.8 | 3.2 | 386.7 | |
| GOA | 54.6 | 74.3 | 99.9 | 22.6 | 20 | 92.5 | |
| TEO | 28.9 | 13.2 | 17.4 | 93.6 | 5.7 | 93.2 | |
| ITAE | PSO | 348.2 | 31.9 | 77.3 | 377.8 | 10.4 | 432.1 |
| GA | 8.1 | 240.4 | 55.8 | 398.1 | 10.2 | 406.9 | |
| HSA | 61.5 | 157.6 | 56.1 | 339.5 | 279.8 | 276.1 | |
| WCA | 4.9 | 46.8 | 100.2 | 68.5 | 7.8 | 628.8 | |
| GOA | 63 | 93.6 | 62.9 | 95.1 | 35.1 | 22.6 | |
| TEO | 19.5 | 65.7 | 1.9 | 90.5 | 2.8 | 20 | |
| ITSE | PSO | 77.6 | 173.8 | 100.3 | 234.2 | 372.5 | 369.4 |
| GA | 9.8 | 335.2 | 98.5 | 146.5 | 7.82 | 670.4 | |
| HSA | 104.3 | 416 | 87.3 | 201.7 | 35 | 276.9 | |
| WCA | 10 | 650.5 | 91.9 | 182.3 | 6.9 | 124.6 | |
| GOA | 36.7 | 90.5 | 86.1 | 55.4 | 11.1 | 48.1 | |
| TEO | 63.7 | 57.2 | 12.3 | 53.9 | 42.5 | 5.8 | |
| Methods | Performance Criteria | Average Rank | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IAE | ISE | ITAE | ITSE | ||||||
| Score | Rank | Score | Rank | Score | Rank | Score | Rank | ||
| PSO | 0.880 | 4 | 76.97 | 4 | 0.059 | 2 | 0.1941 | 5 | 3.75 |
| GA | 0.649 | 1 | 62.31 | 3 | 0.046 | 1 | 0.1537 | 2 | 1.75 |
| HSA | 0.915 | 5 | 57.14 | 2 | 1.34 | 6 | 0.1944 | 6 | 4.75 |
| WCA | 0.861 | 3 | 948.91 | 6 | 0.112 | 5 | 0.1544 | 3 | 4.25 |
| GOA | 1.42 | 6 | 141.32 | 5 | 0.096 | 4 | 0.1832 | 4 | 4.75 |
| TEO | 0.778 | 2 | 57.11 | 1 | 0.099 | 3 | 0.1532 | 1 | 1.75 |
| Performance Criteria | Algorithms | |||||
|---|---|---|---|---|---|---|
| PSO | GA | HSA | WCA | GOA | TEO | |
| IAE | 16.77% | 21.26% | 15.33% | 16.83% | 14.84% | 14.95% |
| ISE | 18.59% | 19.24% | 14.20% | 18.01% | 13.84% | 16.09% |
| ITAE | 19.94% | 17.38% | 14.75% | 17.92% | 14.67% | 15.31% |
| ITSE | 19.65% | 18.17% | 15.97% | 17.93% | 14.17% | 14.08% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazen Alhato, M.; Bouallègue, S.; Rezk, H. Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics 2020, 8, 2012. https://doi.org/10.3390/math8112012
Mazen Alhato M, Bouallègue S, Rezk H. Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics. 2020; 8(11):2012. https://doi.org/10.3390/math8112012
Chicago/Turabian StyleMazen Alhato, Mohammed, Soufiene Bouallègue, and Hegazy Rezk. 2020. "Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach" Mathematics 8, no. 11: 2012. https://doi.org/10.3390/math8112012
APA StyleMazen Alhato, M., Bouallègue, S., & Rezk, H. (2020). Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics, 8(11), 2012. https://doi.org/10.3390/math8112012






