A Consensus Model for Extended Comparative Linguistic Expressions with Symbolic Translation

Abstract

Consensus Reaching Process (CRP) is a necessary process to achieve agreed solutions in group decision making (GDM) problems. Usually, these problems are defined in uncertain contexts, in which experts do not have a full and precise knowledge about all aspects of the problem. In real-world GDM problems under uncertainty, it is usual that experts express their preferences by using linguistic expressions. Consequently, different methodologies have modelled linguistic information, in which computing with words stands out and whose basis is the fuzzy linguistic approach and their extensions. Even though, multiple consensus approaches under fuzzy linguistic environments have been proposed in the specialized literature, there are still some areas where their performance must be improved because of several persistent drawbacks. The drawbacks include the use of single linguistic terms that are not always enough to model the uncertainty in experts’ knowledge or the oversimplification of fuzzy information during the computational processes by defuzzification processes into crisp values, which usually implies a loss of information and precision in the results and also a lack of interpretability. Therefore, to improving the effects of previous drawbacks, this paper aims at presenting a novel CRP for GDM problems dealing with Extended Comparative Linguistic Expressions with Symbolic Translation (ELICIT) for modelling experts’ linguistic preferences. Such a CRP will overcome previous limitations because ELICIT information allows both fuzzy modelling of the experts’ uncertainty including hesitancy and performs comprehensive fuzzy computations to, ultimately, obtain precise and understandable linguistic results. Additionally, the proposed CRP model is implemented and integrated into the CRP support system so-called A FRamework for the analYsis of Consensus Approaches (AFRYCA) 3.0 that facilitates the application of the proposed CRP and its comparison with previous models.

1. Introduction

Human beings are continuously facing decision making problems in their daily life, some of them so simple that we do not even notice their presence. However, not all decision problems are so easy to solve and the engagement of several people or experts with different knowledge may be necessary to reach the solution, giving rise to Group Decision Making (GDM) [1,2,3]. Obviously, the participation of several experts implies different points of view and consequently, conflicting opinions on the solution to the problem. A GDM classical resolution scheme ignores the latter aspect and usually computes the solution based on a simple aggregation of the initial experts’ preferences, disregarding the conflicts on the solution. It can result in several experts feeling that their opinions have been completely omitted [4], decreasing the support for the solution and the resolution scheme in this or future decisions.

To overcome the previous drawback of the GDM process, a Consensus Reaching Process (CRP) has been added to the GDM resolution scheme [5]. In brief, a CRP is a cyclical process in which the experts discuss with each other and modify their initial preferences in order to achieve a satisfactory and agreed solution. This process is usually guided by a moderator who identifies the experts whose opinions are furthest from the rest of the group and advises them with the aim of bringing their positions closer to the rest of the group. CRP has attracted the attention of many researchers and many consensus models that support CRPs have been developed [4,6,7].

Most real-world GDM problems and their correspondent CRPs deal with uncertain and vague information that should be properly modelled and managed to obtain reliable solutions. In such cases, experts usually elicit their information by means of linguistic values or expressions that make them more comfortable to represent their vague assessments. The inherent uncertainty of such linguistic values has been successfully modelled by the fuzzy linguistic approach [8,9,10,11] resulting in Linguistic Decision Making (LDM) [12,13]. Such a type of modelling implies processes of Computing with Words (CW) [14,15], which is one of the most used methodologies for operating with linguistic assessments (words in a natural or artificial language) and not numbers, thus emulating human cognitive processes [16]. The input in CW processes are represented by linguistic values that are manipulated to, finally, obtain results represented by linguistic information that is easy to understand [17]. Most classical LDM proposals in the literature model linguistic information by means of single linguistic terms [12], in which the linguistic 2-tuple model has a prominent position [18,19]. However, it provokes some limitations to experts during the elicitation of their knowledge [20]; thus, several proposals to model multiple linguistic terms for experts’ assessments have been proposed, with Hesitant Fuzzy Linguistic Term Sets standing out (HFLTSs) [21].

Accordingly, many consensus models that deal with LDM problems have been proposed in the specialized literature [6,22,23,24,25], but each presents significant, different drawbacks as follows:

• Limitation to model expert’s uncertain knowledge: some models use single linguistic terms to represent the experts’ preferences [22]. However, it is common that experts often have doubt among several linguistic terms when providing their opinions due to the complexity of the problem and such hesitancy cannot be modelled by using just a single linguistic term.
• Closeness to human reasoning: other models represent more complex linguistic assessments [6,26] but their preference modelling does not provide expressions close to humans’ way of thinking.
• CW integrity and Interpretability: in many linguistic CRPs, the fuzzy linguistic inputs are oversimplified, transforming fuzzy representation into interval or crisp values [27,28], which disrupts the CW process [16,17] suffering loss of information and lack of interpretability.

Even though, some recent improvements modeled linguistic expressions closer to human cognitive process, for instance, by means of the use of context-free grammars to generate richer and flexible comparative linguistic expressions (CLEs) based on HFLTSs [21,29]. This improves the interpretability and allows for the two previous drawbacks to be overcome but still, the consensus models for such a representation [26,30] cannot maintain an appropriate fuzzy representation during CW processes and they use linguistic discrete representation domains which produce bias during the CRP. Therefore, this paper takes advantage of a novel fuzzy linguistic modelling that hybridizes the main ideas of the linguistic 2-tuple model [18] and the HFLTSs [21] resulting in the Extended Comparative Linguistic Expressions with Symbolic Translation (ELICIT) information [31]. It provides the following advantages regarding the previous mentioned drawbacks: (i) their representation is based on the CLEs [21,29]; thus, they can model the experts’ hesitancy, (ii) the ELICIT information is transformed into fuzzy numbers with the premise of keeping as much information as possible by accomplishing fuzzy computations without loss of information and then, the fuzzy numbers are retranslated into linguistic expressions, which means the results are represented linguistically. Consequently, ELICIT information facilitates the representation of a continuous linguistic domain even in complex contexts with multiple linguistic-term-based expressions and provides a fuzzy operational computational approach to accomplish CW processes in a precise way, obtaining comprehensible results in decision making problems.

Therefore, the aim of this research is to introduce a new consensus model dealing with ELICIT that overcomes the previous limitations of an existing consensus model in LDM. This new consensus model presents a key novelty, the use of ELICIT information. As far as we know, there is no other proposal that uses this type of information in a CRP. Furthermore, the use of ELICIT provides relevant advantages related to CW processes, expressiveness, loss of information and interpretability. Then, contrary to other proposals, our consensus model performs precise fuzzy computations in a continuous domain thanks to the symbolic translation of the ELICIT information, avoiding the loss of information and, in turn, obtaining more accurate results that are easy to understand. In addition, the proposed consensus model is implemented and integrated in the consensus support software AFRYCA 3.0 (A FRamework for the analYsis of Consensus Approaches) [4,32,33] in order to simulate the performance of the CRP and solve real world LDM problems dealing with ELICIT information.

To sum up, this proposal aims to achieve the following goals:

• Define a new consensus model to deal with fuzzy linguistic information modelled by means of ELICIT information to overcome the limitations of the existing consensus model.
• Such a model will apply CW processes to ELICIT information that will obtain precise linguistic results that are easy to understand.
• Application of the ELICIT-based consensus model to a real-world GDM problem to show its performance validity and advantages in comparison with other approaches by its integration in the software AFRYCA 3.0 [32].

The remainder of this contribution is structured as follows: Section 2 reviews some basic concepts related to the proposal. Section 3 presents a novel consensus model based on ELICIT information. Section 4 introduces an LDM problem to show the performance of the proposal and includes a comparative analysis with another approach with similar characteristics. To conclude this work, Section 5 draws several conclusion and proposes future research directions.

2. Preliminaries

This section briefly revises the main concepts related to GDM, CRP and ELICIT information that are necessary to understand our proposal.

2.1. Group Decision Making

GDM consists of the participation of several experts in the resolution of a decision problem. By definition, a GDM problem is characterized by a finite set of experts, $E=\{e_1,e_2,\dots ,e_m\}$, who provide their opinions over a finite set of possible alternatives/solutions, $A=\{a_1,a_2,\dots ,a_n\}$ [1,5,34]. In GDM, each expert $e_i$ expresses her/his opinion by using a preference structure $P^k$, a $A\times A$ matrix so that

$$P^k=\left(\begin{array}{ccccc}& -& \cdots & p_{1n}^k& \\ & ⋮& \ddots & ⋮& \\ & p_{n1}^k& \cdots & -\end{array}\right)$$

where $p_{ij}^k$ represents the preference of the expert $e_k$ over the alternative $a_i$ regarding the alternative $a_j$.

The classical resolution scheme for this kind of problem is formed by two phases [35]: (i) aggregation: the experts’ preferences obtained are aggregated by using an aggregation operator and (ii) exploitation: one or several alternatives are selected as solutions to the problem (see Figure 1).

The definition of GDM problems under uncertainty is fairly common in real-world scenarios because of pressure to make quick decisions and the lack of information and knowledge about the problem. Therefore, the experts have to deal with incomplete and vague information and, as a result, expressing their knowledge may become an extremely complex task. Under these conditions, linguistic information and its modelling by linguistic variables [8,9,10] has obtained successful results [15] with the use of CW processes [14]. The resolution scheme for LDM problems varies slightly regarding the classical one shown in Figure 1—it includes, as the first step, the definition of the expression domain that experts use to provide their linguistic preferences [36] (see Figure 2).

The Figure 2 shows the need to accomplish computations with linguistic information to solve LDM problems. The CW methodology has been successfully applied to compute and reason by means of words, obtaining linguistic outputs from linguistic inputs [17,37]. Recently, CW has been intensively and comprehensively applied in decision making [15,38] and thus, multiple CW schemes have been proposed in the literature [39,40] to reinforce the need of easy computations to obtain accurate and understandable linguistic results. The CW scheme introduced by Yager in [17,40] includes two main processes in CW, translation and retranslation. The translation process transforms the linguistic assessments into a format based on fuzzy tools to accomplish the computations. Then, the retranslation process transforms the manipulated information into linguistic values that are easily to understand.

Multiple fuzzy-based linguistic modelling approaches together with their computational models have been developed for CW [41,42]. One of the most remarkable is the 2-tuple linguistic model proposed by Herrera and Martínez [18] due to its advantages in terms of interpretability and accuracy [43].

2.2. 2-Tuple Linguistic Model

The 2-tuple linguistic model [44] is one of the most widely used linguistic models thanks to its great qualities both in terms of interpretability and precision related to symbolic translation. This model represents the information by a 2-tuple $(s_p,\alpha )$ in which $s_p$ is a linguistic term belonging to a predefined linguistic term set $S=\{s_0,s_1,\dots ,s_g\}$ and $\alpha \in [-0.5,0.5)$ is so-called symbolic translation, a numerical value that represents the translation of the fuzzy membership function of $s_p$ in a continuous domain (see Figure 3).

$$\begin{array}{c}\hfill \alpha =\left\{\begin{array}{cc}[-0.5,0.5)\hfill & if{s}_p\in \{s_1,s_2,\dots ,s_{g-1}\}\hfill \\ [0,0.5)\hfill & if{s}_p=s_0\hfill \\ [-0.5,0]\hfill & if{s}_p=s_g\hfill \end{array}\right.\end{array}$$

Note that, the symbolic translation computation in linguistic terms in S provides a value $\beta \in [0,g]$. This value can be translated into its corresponding 2-tuple linguistic value, $(s_p,\alpha )$ using the function ${\Delta }_S$:

Definition 1.

[44] Let $S=\{s_0,\dots ,s_g\}$ be a set of linguistic terms and $\overline{S}$ the 2-tuple set associated with S defined as $\overline{S}=S\times [-0.5,0.5)$. The function ${\Delta }_S:[0,g]\to \overline{S}$ is given by:

$${\Delta }_S\left(\beta \right)=(s_p,\alpha ),with\left\{\begin{array}{c}p=round\left(\beta \right)\hfill \\ \alpha =\beta -p\hfill \end{array}\right.$$

with $round(·)$ being the function that assigns the closest integer number $i\in \{0,\dots ,g\}$ to β.

Therefore, a 2-tuple linguistic value $(s_p,\alpha )$ can be represented by its equivalent numerical value $\beta$ in the interval of granularity of S, $[0,g]$.

Proposition 1.

Let $S=\{s_0,\dots s_g\}$ be a linguistic term set and $(s_p,\alpha )\in \overline{S}$ be a 2-tuple linguistic value. There is a function, ${\Delta }^{-1}$:

$$\begin{array}{c}{\Delta }^{-1}:\overline{S}\to [0,g]\hfill \\ {\Delta }_S^{-1}(s_p,\alpha )=\alpha +p=\beta \hfill \end{array}$$

Remark 1.

Note that according to Definition 1 and Preposition 1, the transformation of a linguistic term $s_p\in S$ into a 2-tuple linguistic value in $\overline{S}$ is obtained by adding a zero as a symbolic translation to the linguistic term:

$$\begin{array}{c}\hfill s_p\in S\to (s_p,0)\in \overline{S}\end{array}$$

2.3. Consensus Reaching Process

The classical GDM resolution schemes shown in Figure 1 and Figure 2 directly aggregate the experts’ preferences and do not guarantee a solution that is accepted by all the experts because agreement on it is not considered. Therefore, some experts may disagree with the solution and feel that their opinions have not been sufficiently considered during the decision process, which can result in either a lack of support for the solution or lack of confidence in the GDM process. In such cases, to avoid such drawbacks, an additional CRP has been added to the GDM process [7].

A CRP is an iterative discussion process among experts involved in the GDM problem in which they discuss with each other, provide their different opinions and points of view and try to achieve a higher collective level of agreement by adjusting their initial preferences and seeking a common point of agreement [45]. A CRP is classically formed by four steps:

• Gathering preferences: the experts analyze the GDM problem and provide their opinions over the different alternatives by using preference relations.
• Consensus level: the level of agreement $\left(cl\right)$ within the group is computed.
• Consensus control: $cl$ is compared with a predefined consensus threshold ($\mu$), which represents the desired level of agreement to be achieved by the group. If the consensus threshold is reached, the CRP finishes and a selection process of the best alternative starts, otherwise a new consensus round begins. In order to avoid an endless CRP, the number of consensus rounds is limited with another threshold ($r_{max}$).
• Feedback generation: the moderator identifies the experts whose opinions are furthest from the rest of the group and advises them to change their preferences in order to reach a higher level of agreement.

CRPs have attracted great attention from many researchers in recent years and a large number of consensus models to support groups in CRPs have been presented in the specialized literature [7,23,46] and several metrics have been proposed to study their performance [31].

2.4. ELICIT Information

Labella et al. proposed in [31] a new fuzzy linguistic representation model so-called ELICIT with the aim of overcoming the drawbacks of existing linguistic representation models in terms of interpretability and precision. The ELICIT information has two main advantages:

• Interpretability: ELICIT information is generated by a context-free grammar [43]; thus, flexible and rich linguistic expressions are built that are able to model the experts’ hesitancy with expressions such as between, at least or at most. Furthermore, in spite of the ELICIT information being manipulated using fuzzy operations, the ELICIT computational model allows for the fuzzy numbers to be translated again into ELICIT information by obtaining interpretable linguistic results and following a CW approach [14].
• Accuracy: a key aspect in the ELICIT information is the representation in a continuous domain of the linguistic terms that compose the expressions, thanks to the symbolic translation value introduced in the 2-tuple linguistic model (see Section 2.2).

The different complex linguistic expressions that compose the ELICIT information are generated by means of the following context-free grammar:

Definition 2.

[31] Let $G_H$ be a context-free grammar and $S=\{s_0,\dots ,s_g\}$ a linguistic terms set. The elements of $G_H=(V_N,V_T,I,P)$ are defined as follows.

$$\begin{array}{cc}\hfill & V_N=\{\left(continuosprimaryterm\right),\left(compositeterm\right),\hfill \\ \hfill & \left(unaryrelation\right),\left(binaryrelation\right),\left(conjunction\right)\}\hfill \\ \hfill & V_T=\{atleast,atmost,between,and,{(s_0,\alpha )}^{\gamma },{(s_1,\alpha )}^{\gamma },\dots ,{(s_g,\alpha )}^{\gamma }\}\hfill \\ \hfill & I\in V_N\hfill \end{array}$$

The production rules defined in an extended Backus-Naur Form are:

$$\begin{array}{cc}\hfill & P=\{I::=(continuosprimaryterm\left)\right|\left(compositeterm\right)\hfill \\ \hfill & \left(compositeterm\right)::=\left(unaryrelation\right)\left(continuousprimaryterm\right)|\hfill \\ \hfill & \left(binaryrelation\right)\left(continuousprimaryterm\right)\left(conjunction\right)\left(continuousprimaryterm\right)\hfill \\ \hfill & \left(continuousprimaryterm\right)::={(s_0,\alpha )}^{\gamma }|{(s_1,\alpha )}^{\gamma }|\dots |{(s_g,\alpha )}^{\gamma }\hfill \\ \hfill & \left(unaryrelation\right)::=atleast|atmost\hfill \\ \hfill & \left(binaryrelation\right)::=between\hfill \\ \hfill & \left(conjunction\right)::=and\}\hfill \end{array}$$

Some examples of ELICIT information may be: “at least ${(s_p,\alpha )}^{\gamma }$", “at most ${(s_p,\alpha )}^{\gamma }$" and “between ${(s_p,{\alpha }_1)}^{{\gamma }_1}$ and ${(s_q,{\alpha }_2)}^{{\gamma }_2}$".

Remark 2.

Note that the parameter γ, so-called adjustment, preserves relevant information about the parametric form of the corresponding fuzzy number of a ELICIT and it is key to obtain results without loss of information [31,47].

The ELICIT representation model was proposed together with a CW approach based on the fuzzy linguistic approach. This approach allows for fuzzy information to be computed in a precise way and return linguistic and understandable results represented by ELICIT information. To carry out these fuzzy operations, first the initial linguistic assessments modelled by complex linguistic expressions are translated into trapezoidal fuzzy numbers (TrFNs) that represent their corresponding fuzzy envelopes [31]. Then, fuzzy arithmetic operations are applied to the fuzzy envelopes in order to preserve the fuzzy representation and guarantee that the new fuzzy numbers can be translated into ELICIT information.

The fuzzy arithmetic operations are based on the work introduced by Rezvani and Molani [48]. They proved that, by means of the fuzzy numbers shape function and $\alpha -cuts$, it is possible to accomplish arithmetic operations that preserve the fuzzy parametric representation. Here, we present the addition of the fuzzy operation because it will be used later in the contribution.

Definition 3.

Let $T_{\tilde{A}}(a_1,a_2,a_3,a_4)$ and $T_{\tilde{B}}(a_1^{\prime },a_2^{\prime },a_3^{\prime },a_4^{\prime })$ be two fuzzy envelopes modelled by two TrFNs. Suppose the normal shape functions of $\tilde{A}$, $\tilde{B}$ as follows:

$${\mu }_{\tilde{A}}=\left\{\begin{array}{cc}{\left({\displaystyle \frac{x-a_1}{a_2-a_1}}\right)}^n\hfill & \mathit{when}x\in [a_1,a_2),\hfill \\ 1\hfill & \mathit{when}x\in [a_2,a_3],\hfill \\ {\left({\displaystyle \frac{a_4-x}{a_4-a_3}}\right)}^n\hfill & \mathit{when}x\in (a_3,a_4],\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.{\mu }_{\tilde{B}}=\left\{\begin{array}{cc}{\left({\displaystyle \frac{x-a_1^{\prime }}{a_2^{\prime }-a_1^{\prime }}}\right)}^n\hfill & \mathit{when}x\in [a_1^{\prime },a_2^{\prime }),\hfill \\ 1\hfill & \mathit{when}x\in [a_2^{\prime },a_3^{\prime }],\hfill \\ {\left({\displaystyle \frac{a_4^{\prime }-x}{a_4^{\prime }-a_3^{\prime }}}\right)}^n\hfill & \mathit{when}x\in (a_3^{\prime },a_4^{\prime }],\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Supposing ${\tilde{A}}_{\overline{\alpha }}$, ${\tilde{B}}_{\overline{\alpha }}$ are the $\alpha -cuts$ of $\tilde{A}$ and $\tilde{B}$ [49], respectively:

$$\begin{array}{c}\hfill {\tilde{A}}_{\overline{\alpha }}=[a_1+{\overline{\alpha }}^{1/n}(a_2-a_1),a_4-{\overline{\alpha }}^{1/n}(a_4-a_3)]\\ \hfill {\tilde{B}}_{\overline{\alpha }}=[a_1^{\prime }+{\overline{\alpha }}^{1/n}(a_2^{\prime }-a_1^{\prime }),a_4^{\prime }-{\overline{\alpha }}^{1/n}(a_4^{\prime }-a_3^{\prime })]\end{array}$$

Definition 4.

[48] The addition of two fuzzy envelopes modelled by two TrFNs $\tilde{A}$, $\tilde{B}$ can be defined with a shape function ${\mu }_{\tilde{A}+\tilde{B}}$ as

$${\mu }_{\tilde{A}+\tilde{B}}=\left\{\begin{array}{cc}{\displaystyle \frac{{(x-(a_1+a_1^{\prime }))}^n}{(a_2+a_2^{\prime })-(a_1+a_1^{\prime })}}\hfill & a_1+a_1^{\prime }\le x\le a_2+a_2^{\prime },\hfill \\ 1\hfill & a_2+a_2^{\prime }\le x\le a_3+a_3^{\prime },\hfill \\ {\displaystyle \frac{{((a_4+a_4^{\prime })-x)}^n}{(a_4+a_4^{\prime })-(a_3+a_3^{\prime })}}\hfill & a_3+a_3^{\prime }\le x\le a_4+a_4^{\prime },\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The fuzzy arithmetic operations play a key role in the ELICIT computational model, since they allow for the retention of the fuzzy parametric form when the fuzzy envelopes are manipulated and make it possible to transform the fuzzy numbers back into linguistic information, fulfilling the basic premise of the CW approach. This retranslation process into linguistic information is accomplished by the function $\zeta$.

Definition 5.

[31] Let $S=\{s_0,\dots ,s_g\}$ be a set of linguistic terms and $\tilde{A}$ a fuzzy number. The function ζ is given by

$$\zeta \left(\tilde{A}\right)=x,where\left\{\begin{array}{c}x=atleast{(s_p,\alpha )}^{\gamma }if\tilde{A}=T(a_1,a_2,1,1)\hfill \\ x=atmost{(s_p,\alpha )}^{\gamma }if\tilde{A}=T(0,0,a_3,a_4)\hfill \\ x=between{(s_p,{\alpha }_1)}^{{\gamma }_1}and{(s_q,{\alpha }_2)}^{{\gamma }_2}if\tilde{A}=T(a_1,a_2,a_3,a_4)\hfill \end{array}\right.$$

(1)

Another key function in the ELICIT CW approach is ${\zeta }^{-1}$, which transforms the ELICIT information into TrFNs based on the fuzzy envelope computation:

Definition 6.

[31] Let x an ELICIT expression and $T(a_1,a_2,a_3,a_4)$ a TrFN. The function ${\zeta }^{-1}$ is defined as follows:

$${\zeta }^{-1}:x\to T(a_1,a_2,a_3,a_4)$$

(2)

such that, from an ELICIT expression, it returns its equivalent TrFN.

For the sake of clarity, the previous functions have not been fully described, see [31] for further details.

3. Consensus Model with ELICIT Information

The need for dealing with complex GDM problems defined under uncertainty in real-world scenarios demands new preference modelling that facilitates the flexible and correct elicitation of experts’ knowledge. We have pointed out that CLEs based on HFLTSs [43] provide such a flexibility and are similar to human cognitive processes. Different CRPs have been developed based on CLEs and HFLTSs [26,50,51]; however, as has been pointed out previously, the use of a discrete representation of the linguistic domain produces biases and problems in the evolution of the experts agreements across the CRP. Therefore, this section introduces a new CRP that is able to deal with ELICIT information that facilitates linguistic assessment elicitation, maintains the fuzzy representation across the CW processes, uses a continuous representation of the linguistic domain that results in a proper evolution of the agreement across the CRP and, finally, obtains precise and understandable results.

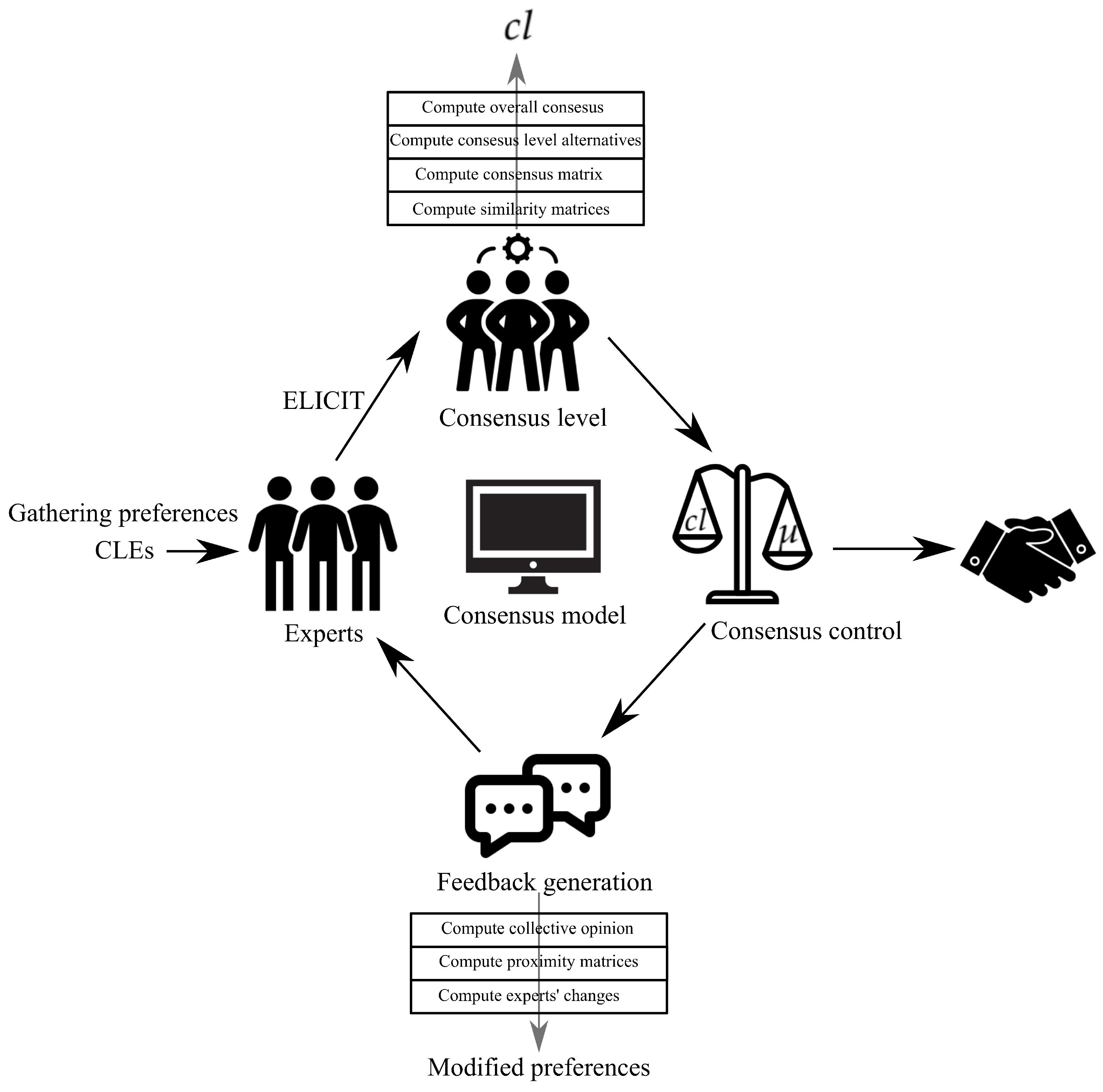
The ELICIT consensus model proposed follows the general scheme shown in Figure 4 but with additional tasks, which are highlighted in Figure 5.

The resolution scheme shown in Figure 5 includes additional steps regarding the classical CRP resolution scheme shown in Figure 4. First, the experts’ preferences are modelled by CLEs that are lately transformed into ELICIT information. Then, the consensus level is computed by the following four consecutive steps—(i) Compute similarity matrices; (ii) Compute consensus matrix; (iii) Compute consensus level of alternatives; (iv) Compute overall consensus. The overall consensus, $cl$, is compared with the predefined consensus threshold, $\mu$, in the consensus control step. Finally, if needed, a feedback process composed by three processes—(a) Compute collective opinion; (b) Compute proximity matrices; (c) Compute experts’ changes; will provide the modified preferences according to the suggestions provided by the consensus model. The previous steps and processes are described in further detail in the following subsections and summarized in Algorithm 1.

Algorithm 1: Proposal steps

3.1. Input Information

In this initial step of the proposed CRP, each expert $e_k$ can elicit their preferences into a linguistic preference relation whose values could be any of the generated ones for the context-free grammar introduced in Definition 2. Initially, it is reasonable that the elicited assessments by experts would be CLEs or linguistic terms to model her/his opinions in a matrix $P^k={\left(p_{ij}^k\right)}_{n\times n}$, where $p_{ij}^k$ is either a CLE or a linguistic term. Assuming the linguistic terms set, $S=\{veryweak,weak,fair,strong,verystrong\}$, an example of such an input matrix may be the following:

$$P^k=\left(\begin{array}{ccc}-\hfill & \mathit{\text{at most weak}}& \hfill \mathit{strong}\\ \mathit{\text{at least strong}}\hfill & -& \hfill \mathit{\text{between weak and fair}}\\ weak\hfill & \mathit{\text{between fair and strong}}& \hfill -\end{array}\right)$$

3.2. Transformation into ELICIT Information and Fuzzy Numbers

The initial CLEs expressions $p_{ij}^k$ provided by the experts are transformed into ELICIT information. Depending on the type of CLE, the corresponding ELICIT information is obtained according to Remark 1 as follows:

• single linguistic term: the CLE $s_p$ is transformed into ${(s_p,0)}^0$.
• at least expression: the CLE $atleast{s}_p$ is transformed into $atleast{(s_p,0)}^0$.
• at most expression: the CLE $atmost{s}_p$ is transformed into $atmost{(s_p,0)}^0$.
• between expression: the CLE $between{s}_{p}and{s}_q$ is transformed into $between{(s_p,0)}^{0}and{(s_q,0)}^0$.

Once the initial CLEs are transformed into ELICIT information, the fuzzy representation of the latter is obtained by the function ${\zeta }^{-1}$ (see Definition 6). The experts’ preferences transformed into TrFNs are noted as ${\tilde{p}}_{ij}^k$.

3.3. Compute Consensus Level

In this step, the current consensus level within the group is computed. This process is divided into several sub-steps:

3.3.1. Compute Similarity Matrices

A similarity matrix $S{M}^{kt}={\left(s{m}_{ij}^{kt}\right)}_{n\times n}$ for each pair of experts $(e_k,e_t)$ is computed:

$$s{m}_{ij}^{kt}=\sum _{k=1}^{m-1}\sum _{t=k+1}^m\sum _{i=1}^{n-1}\sum _{j=n+1}^{n}sim({\tilde{p}}_{ij}^k,{\tilde{p}}_{ij}^t)$$

(3)

where ${\tilde{p}}_{ij}^k$ and ${\tilde{p}}_{ij}^t$ represents the TrFNs of the preferences of the expert $e_k$ and $e_t$ over the pair of alternatives $(a_i,a_j)$ and $sim(·)$ computes the similarity between two TrFNs.

Definition 7.

Let $\tilde{A}=T(a_1,a_2,a_3,a_4)$ and $\tilde{B}=T(a_1^{\prime },a_2^{\prime },a_3^{\prime },a_4^{\prime })$ two fuzzy numbers, the similarity measure between them is computed as follows

$$sim(\tilde{A},\tilde{B})=1-dist(\tilde{A},\tilde{B})$$

(4)

where $dist(\tilde{A},\tilde{B})$ represents the distance between fuzzy numbers computed as follows

$$dist(\tilde{A},\tilde{B})=\frac{1}{4}\sum _{i=1}^4\left(\right|a_i-a_i^{\prime }\left|\right)$$

(5)

3.3.2. Compute Consensus Matrix

From the aggregation of the similarity values, a consensus matrix $CM={\left(c{m}_{ij}\right)}_{n\times n}$ is computed:

$$c{m}_{ij}=\sum _{i=1}^{n-1}\sum _{j=i+1}^n\frac{m(m-1)}{2}\sum _{k=1}^{m-1}\sum _{t=k+1}^{m}s{m}_{ij}^{kt}$$

(6)

3.3.3. Compute Consensus Level for Alternatives

The degree of consensus $c{a}_i$ for each alternative $a_i$ is computed:

$$c{a}_i=\frac{{\sum }_{j=1,j\ne i}^{n}c{m}_{ij}}{n-1}$$

(7)

3.3.4. Compute Overall Consensus

The overall consensus $cl$ is computed as:

$$cl=\frac{{\sum }_{i=1}^{n}c{a}_i}{n}$$

(8)

3.4. Consensus Control

The overall consensus degree $cl$ is compared with the predefined consensus threshold $\mu$. If the latter is achieved, a selection process of the best alternative starts, otherwise, the CRP requires another discussion round to increase the level of agreement.

3.5. Feedback Mechanism

The feedback mechanism requires the identification of the experts who are furthest from the rest of the group and the assessments over the alternatives to change.

3.5.1. Compute Collective Opinion

The collective opinion $C={\left(c_{ij}\right)}_{n\times n}$ of the experts’ group is obtained from:

$$c_{ij}=\sum _{i=1}^{n-1}\sum _{j=i+1}^n\overline{\psi }({\tilde{p}}_{ij}^1\dots ,{\tilde{p}}_{ij}^m)$$

(9)

where $\overline{\psi }$ represents the fuzzy arithmetic mean aggregation operator defined as follows (see Definition 4):

Definition 8.

[31] Let $\{{\tilde{A}}_1,\dots ,{\tilde{A}}_m\}$ be a set of fuzzy numbers, the fuzzy arithmetic mean $\overline{\psi }$ is computed as follows:

$$\begin{array}{c}\hfill \overline{\psi }\{{\tilde{A}}_1,\dots ,{\tilde{A}}_m\}={\displaystyle \frac{1}{m}}\left({\mu }_{{\tilde{A}}_1+{\tilde{A}}_2+\dots +{\tilde{A}}_m}\right)\end{array}$$

(10)

where the division between a TrFN, $\tilde{A}=T(a_1,a_2,a_3,a_4)$, and a scalar o is computed as follows:

$$\frac{\tilde{A}}{o}=T(\frac{a_1}{o},\frac{a_2}{o},\frac{a_3}{o},\frac{a_4}{o})$$

(11)

3.5.2. Compute Proximity Matrices

For each expert $e_k$ her/his proximity matrix $P{M}^k=\left(p{m}_{ij}^k\right)$ regarding the collective opinion is computed so:

$$p{m}_{ij}^k=\sum _{k=1}^m\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}sim({\tilde{p}}_{ij}^k,c_{ij})$$

(12)

3.5.3. Compute Experts’ Changes

To apply the changes to the experts’ preferences, it is necessary to identify the assessments of the pair of alternatives to change, and which experts have to modify such assessments.

• Identify alternatives: the pair of alternatives $(a_i,a_j)$ will be modified if $c{a}_i<\mu$ and $c{m}_{ij}<\mu$.
• Identify experts: the expert $e_k$ is candidate to modify their preferences if $p{m}_{ij}^k<{\overline{pm}}_{ij}$, where ${\overline{pm}}_{ij}$ is the average proximity value of all the experts for each pair of alternatives $(a_i,a_j)$ selected to be modified.

Once the alternatives and experts have been identified, the next step consists of defining the direction of change (increase/decrease). To determine the direction, an acceptability threshold of change, $\epsilon$, is introduced. According to this value, several direction rules are applied:

• RULE 1: If $\varphi \left({\tilde{p}}_{ij}^k\right)-\varphi \left(c_{ij}\right)<-\epsilon$ then $e_k$ should increase her/his assessments $p_{ij}^k$ on $(a_i,a_j)$.
• RULE 2: If $\varphi \left({\tilde{p}}_{ij}^k\right)-\varphi \left(c_{ij}\right)>\epsilon$ then $e_k$ should decrease her/his assessments $p_{ij}^k$ on $(a_i,a_j)$.

where $\varphi (·)$ denotes the defuzzified value of a TrFN $T(a_1,a_2,a_3,a_4)$ such that:

$$\varphi \left(T(a_1,a_2,a_3,a_4)\right)={\displaystyle \frac{(a_1+2a_2+2a_3+a_4)}{6}}$$

(13)

Finally, we define how the change in the preference will take place. The degree of change to apply is a very relevant aspect in a CRP, since an excessive/insignificant modification in the experts’ preferences could lengthen the CRP more than necessary.

Our proposal includes an adaptive process to deal with the latter issue so a greater or slighter change is applied depending on the distance between the expert’s preference to be modified and the collective opinion. This is a key aspect of our contribution since, contrary to other existing proposals, the ELICIT information allows for the modification of the experts’ preferences in a continuous domain. Whereas other consensus models that use HFLTSs or CLEs apply the change in the experts’ preferences by means of “jumps” between the linguistic terms belonging to a predefined linguistic term set and thus, in a discrete domain, our proposal can use the symbolic translation of the ELICIT information to apply the changes in intermediate continuous values between linguistic terms. This facilitates the reaching of a consensus since excessive modifications in the experts’ preferences that may provoke a deadlock in the consensus process are avoided, as it will be shown in the comparative analysis introduced in Section 4.3.

To identify the degree of change needed in the expert’s preferences, we use the concept of centroid of a fuzzy number [52]. If the distance between the centroid of the fuzzy number that represents the expert’s preferences, noted as $cen\left({\tilde{p}}_{ij}^k\right)$, and the fuzzy number that represents the collective opinion, $cen\left(c_{ij}\right)$, for the pair of alternatives $(a_i,a_j)$ is greater than a predefined closeness threshold $\theta$, the change to apply will be greater, otherwise, it will be less. This is summarized in two cases:

• CASE 1: If $|cen\left({\tilde{p}}_{ij}^k\right)-cen\left(c_{ij}\right)\left)\right|>\theta$ then a significant change is applied. This change will be applied directly over the linguistic terms that compose the ELICIT expression.
• CASE 2: If $|cen\left({\tilde{p}}_{ij}^k\right))-cen\left(c_{ij}\right)\left)\right|\le \theta$, then a slight change is applied. This change will be applied over the symbolic translation of the terms of the ELICIT expression.

Remark 3.

The function $cen(·)$ represents the coordinate x of the centroid of a fuzzy number and the parameter $\theta >0$ defined as a closeness threshold between the expert’s preference and the collective opinion.

Depending on the case, we studied two changes direction, increase and decrease:

• CASE 1

  -

  Increase assessment

  ∗

  If $p_{ij}^k=(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=(s_{p+{\theta }_1},\alpha )$, ${\theta }_1\in [1,g-1]$, $p+{\theta }_1\le g$. In case that $s_p=s_g$ no change will be applied.

  ∗

  If $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha )$ or $\mathit{\text{at most}}(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=\mathit{\text{at least}}(s_{p+{\theta }_1},\alpha )$ or $\mathit{\text{at most}}(s_{p+{\theta }_1},\alpha )$, respectively, ${\theta }_1\in [1,g-1]$, $p+{\theta }_1\le g$. In case that $s_p=s_g$ no change will be applied.

  ∗

  If $p_{ij}^k=between(s_p,{\alpha }_1)and(s_q,{\alpha }_2)$ then the advice for the expert is $p_{ij}^k=between(s_{p+{\theta }_1},{\alpha }_1)and(s_q,{\alpha }_2)$, ${\theta }_1\in [1,g-1]$, $p+{\theta }_1\le g$ and $p+{\theta }_1\le q$. In case that $s_{p+{\theta }_1}=s_q$ and ${\alpha }_1\ge {\alpha }_2$, the new assessment is $p_{ij}^k=(s_{p+{\theta }_1},{\alpha }_1)$.

  -

  Decrease assessment

  ∗

  If $p_{ij}^k=(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=(s_{p-{\theta }_1},\alpha )$, ${\theta }_1\in [1,g-1]$, $p-{\theta }_1\ge 0$. In case that $s_p=s_0$ no change will be applied.

  ∗

  If $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha )$ or $\mathit{\text{at most}}(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=\mathit{\text{at least}}(s_{p-{\theta }_1},\alpha )$ or $\mathit{\text{at most}}(s_{p-{\theta }_1},\alpha )$, respectively, ${\theta }_1\in [1,g-1]$, $p-{\theta }_1\ge 0$. In case that $s_p=s_0$, no change will be applied.

  ∗

  If $p_{ij}^k=between(s_p,{\alpha }_1)and(s_q,{\alpha }_2)$, then the advice for the expert is $p_{ij}^k=between(s_p,{\alpha }_1)and(s_{q-{\theta }_1},{\alpha }_2)$, ${\theta }_1\in [1,g-1]$, $q-{\theta }_1\ge 0$ and $q-\theta \ge p$. In case that $s_{q-{\theta }_1}=s_p$ and ${\alpha }_2\le {\alpha }_1$, the new assessment is $p_{ij}^k=(s_{q-{\theta }_1},{\alpha }_2)$.

• CASE 2

  -

  Increase assessment

  ∗

  If $p_{ij}^k=(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=(s_p,\alpha +{\theta }_2)$, ${\theta }_2\in [0,0.5]$.

  ∗

  If $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha )$ or $\mathit{\text{at most}}(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha +{\theta }_2)$ or $\mathit{\text{at most}}(s_p,\alpha +{\theta }_2)$, respectively, ${\theta }_2\in [0,0.5]$.

  ∗

  If $p_{ij}^k=between(s_p,{\alpha }_1)and(s_q,{\alpha }_2)$ then the advice for the expert is $p_{ij}^k=between(s_p,{\alpha }_1+{\theta }_2)and(s_q,{\alpha }_2)$, ${\theta }_2\in [0,0.5]$. In case that ($s_p,{\alpha }_1+{\theta }_2)\ge (s_q,{\alpha }_2)$, the new assessment is $p_{ij}^k=(s_p,{\alpha }_1+{\theta }_2)$.

  -

  Decrease assessment

  ∗

  If $p_{ij}^k=(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=(s_p,\alpha -{\theta }_2)$, ${\theta }_1\in [0,0.5]$.

  ∗

  If $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha )$ or $\mathit{\text{at most}}(s_p,\alpha )$, then the advice for the expert is $p_{ij}^k=\mathit{\text{at least}}(s_p,\alpha -{\theta }_2)$ or $\mathit{\text{at most}}(s_p,\alpha -{\theta }_2)$, respectively, ${\theta }_2\in [0,0.5]$.

  ∗

  If $p_{ij}^k=between(s_p,{\alpha }_1)and(s_q,{\alpha }_2)$, then the advice for the expert is $p_{ij}^k=between(s_p,{\alpha }_1)and(s_q,{\alpha }_2-{\theta }_2)$, ${\theta }_2\in [0,0.5]$. In case that ($s_q,{\alpha }_2-{\theta }_2)\le (s_p,{\alpha }_1)$, the new assessment is $p_{ij}^k=(s_q,{\alpha }_2-{\theta }_2)$.

Remark 4.

The adjustment parameters ${\theta }_1$ and ${\theta }_2$ represent the change degree to apply.

4. Case Study

This section introduces a real world GDM problem to show the performance of the proposed consensus model together with its advantages and novelties. Furthermore, a comparative performance analysis with another consensus approach is introduced. Note that both the GDM problem below and the consensus approaches have been integrated into the AFRYCA 3.0 software [4,32,33].

Let us suppose a panel of eight experts, $E=\{e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8\}$, who have to decide between three action plans to increase the flow of tourists in a given city. The three action plans are $A=\{a_1:TVadvertisement,a_2:sportevent,a_3:commercialproducts\}$. Due to the complexity of the the decision, the experts express their preferences by using the linguistic expression domain shown in Figure 6.

The adjustment parameters to solve this problem are as follows:

Remark 5.

Note that the values of the parameters (see

Table 1. Parameters.

Parameter	Value
$\mu$	0.9
$r_{max}$	5
$\epsilon$	0.05
$\theta$	1/g
${\theta }_1$	2
${\theta }_2$	0.2

) μ and $r_{max}$ have been assigned with the aim of showing clearly that our proposal is able to reach a high level of agreement in decision situations in which the time pressure is key. The parameters ε, ${\theta }_1$ and ${\theta }_2$ have been evaluated taking into account the multiple experiments that we have carried out using the AFRYCA software. Finally, the value for θ represents the distance between two consecutive linguistic labels in a linguistic term set. We consider that when the distance between the centroids of the expert’s preference and the collective opinion is greater than θ, we should apply a significant change. Otherwise, the distance would be smaller than the one between two consecutive linguistic labels and the change should be slighter.

Finally, a key aspect in any CRP is the experts’ behavior in the face of the changes advised by the model. AFRYCA 3.0 allows for the configuration and simulation of different experts’ behavior, which means experts may accept the recommendations provided for the consensus approach or refuse them. Keeping in mind our idea of doing a fair comparison between our proposal and another CRP model and showing the advantages of the former, we considered that experts always accept the recommendations provided by both models.

4.1. Resolution Scheme

In order to solve the GDM problem by using the CRP support system AFRYCA 3.0 and according to the resolution scheme introduced in Section 3:

• Input information: the experts provide their assessments by means of HLPR using the expression domain shown in Figure 6. These preferences are shown below:

  $$\begin{array}{cc}\hfill & e_1=\left(\begin{array}{ccc}-& verybad& good\\ verygood& -& atmostverybad\\ bad& atleastverygood& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_2=\left(\begin{array}{ccc}-& verygood& verybad\\ verybad& -& verygood\\ verygood& verybad& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_3=\left(\begin{array}{ccc}-& bthorribleandverybad& good\\ btverygoodandexcellent& -& verybad\\ bad& verygood& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_4=\left(\begin{array}{ccc}-& btmediumandgood& medium\\ btbadandmedium& -& verygood\\ bad& verybad& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_5=\left(\begin{array}{ccc}-& verygood& medium\\ verybad& -& bad\\ medium& good& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_6=\left(\begin{array}{ccc}-& good& horrible\\ bad& -& atmostverybad\\ excellent& atleastverygood& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_7=\left(\begin{array}{ccc}-& bad& horrible\\ good& -& btmediumandgood\\ excellent& btbadandmedium& -\end{array}\right)\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & e_8=\left(\begin{array}{ccc}-& medium& good\\ medium& -& atmostverybad\\ bad& atleastverygood& -\end{array}\right)\hfill \end{array}$$
• Transformation into ELICIT information and Fuzzy Numbers: the assessments modelled by CLEs are transformed into ELICIT information and, finally, into TrFN, ${\tilde{p}}_{ij}^k$.
• Compute the consensus level: initially, the level of agreement within the group is $cl=0.72$.
• Consensus control: taking into account that $\mu =0.9$, the desired level of consensus is not achieved thus, a consensus round is necessary.
• Feedback mechanism: the pair of alternatives to be changed and the expert candidates to modify their assessments are identified:
  • Pair of alternatives to change: $(a_1,a_2),(a_1,a_3),(a_2,a_3)$
  • Experts’ assessments to change: $e_1=\{(a_1,a_2),(a_1,a_3),(a_2,a_3)\}, e_2=\{(a_1,a_2),(a_2,a_3)\}, e_3=\{(a_1,a_2),(a_1,a_3)\}, e_4=\left\{(a_2,a_3)\right\}, e_5=\left\{(a_1,a_2)\right\}, e_6=\{(a_1,a_3),(a_2,a_3)\}, e_7=\left\{(a_1,a_3)\right\}, e_8=\{(a_1,a_3),(a_2,a_3)\}$
  Then, depending on the direction of change and the degree of change needed, the assessments are modified. Figure 7 represents the evolution of the experts’ preferences across the CRP by using the multi-dimensional scaling technique [53]. In the center of each plot, the collective opinion of the experts is represented and around it, the experts’ preferences. The closer the experts are to the collective opinion, the greater the level of agreement in the group.

After the first discussion round, the level of agreement achieved in the group is $cl=0.9$. Due to $cl\ge \mu$, the CRP finishes and the selection process of the best alternative starts. For this problem, the ranking of alternatives is $a_3\succ a_2\succ a_1$, thus $a_3$ is selected as the solution to the problem. The ranking of the alternatives is obtained from the collective opinion computed by Equation (9) and a dominance process [54].

4.2. Discussion

The results obtained in the previous section demonstrate the good performance of the proposed consensus model. Despite the desired level of consensus being high ($\mu =0.9$) and the initial consensus degree in the group being far from this value ($cl=0.72$), our consensus model needs only one discussion round to achieve the desired level of consensus. That means, that our consensus model is able to achieve a high level of agreement rapidly, thus, it can be applied perfectly both to LDM problems where a high level of consensus is required within the group and to problems where the time pressure is key, such as emergency decision situations. The ELICIT information and its modelling in a continuous domain are key to achieving these excellent results, since both precise fuzzy computations and changes in experts’ preferences can be carried out. The computations by means fuzzy operations avoid the loss of information in the resolution process by obtaining more reliable solutions and the experts’ preferences are modified in the right measure, discarding excessive changes that negatively influence the achievement of consensus. Furthermore, the initial preferences are represented linguistically as well as the final preferences, which facilitates the elicitation task and the understanding of the CRP. This is of great importance since experts should be able to understand the results that the consensus model provides, otherwise, it is meaningless. To further highlight the good performance of our proposal, in the following section, we will detail a comparative analysis with another model similar to ours.

Inevitably, our proposal presents some limitations that may be fixed in future works. For instance, the values for the parameters introduced in Table 1 have been assigned according to several experiments carried out with AFRYCA but, undoubtedly, on many occasions, these values will depend on the decision problem to deal with. Although many of the values have a good performance in any decision situation, it would be interesting to provide a formal methodology to set them accordingly. Additionally, we have focused our proposal on decision making problems with few experts but, today, decision problems with hundreds or thousands of experts are common too [7,23]. We should adapt our consensus model to deal with the challenges related to this kind of problems, such as scalability or polarized opinions.

4.3. Comparative Analysis

Despite the previous results that show a good performance according to our goals, it is key to perform comparisons with other CRP approaches with similar features. In our case, we compare with the CRP proposed in [55] because of its similarity with our proposal.

In the resolution of the previous GDM problem with the latter approach, we draw interesting conclusions. The model achieves the maximum number of rounds and does not reach the desired level of agreement (see Figure 8). There are two main reasons for this behavior. Firstly, the linguistic information is transformed into numerical values, losing information in the process. Secondly, when the experts express their preferences in a continuous domain, as in the ELICIT assessments case, the change can vary greatly but, in a discrete one, such change is less because it will not be greater than the granularity of the linguistic term set, which limits a lot the feedback process. The latter drawback can be also appreciated in

Table 2. Consensus level in different rounds.

Round	$\mathit{cl}$
1	0.77
2	0.86
3	0.82
4	0.71
5	0.82

. The consensus level achieved $cl=0.86$ in the second round but, in the third one, the level of agreement decreased. This means that the model accomplishes excessive changes in the experts’ preferences that decrease the level of agreement within the group.

This comparative analysis shows the importance of using ELICIT information in CRPs, since it allows for more accurate computations and precise changes in the experts’ preferences to be carried out, which helps a desired level of consensus to be acheived faster.

5. Conclusions and Future Works

This work has introduced a new consensus model under linguistic environments based on ELICIT information. This approach allows for modeling of the experts’ preferences by means of linguistic complex expressions to be closer to the experts’ way of thinking by facilitating the elicitation task. Furthermore, precise computations with fuzzy operations are carried out together with a linguistic representation of the result that facilitates their understanding by the experts. Finally, a case study has been presented in order to show the performance of the proposal together with a comparative analysis with another proposal to highlight its superior performance. The results obtained from the case study and the comparative analysis show the good performance of our proposal. It is able to achieve a high level of consensus with just a single consensus round. The use of ELICIT information and its modelling in a continuous domain allows for the application of more precise changes to the experts’ preferences and positively influences the achievement of the consensus within the group. The latter issue has been widely proved in the comparative analysis with another proposal with similar characteristics in which the desired level of consensus is never reached.

As future research, Large-Scale Group Decision Making (LSGDM) problems are becoming more common and they are drawing the attention of researchers. In this type of problem, it is even more necessary to apply CRP because of the large number of experts involved in the decision process. For this reason, we will study how to apply the proposed consensus approach to deal with LS-GDM problems.