1. Introduction
Precise modeling of electromagnetic devices helps us to develop energy-efficient devices. Modeling of modern electromagnetic devices is done mainly with the use of numerical models, such as the finite element model. To get a precise model that allows accurate modeling of electromagnetic devices, the description of the materials’ properties should be as good as possible. Often nonlinear magnetic material is described using a magnetization curve. To make a better material description and consider hysteresis losses, material hysteresis also has to be modeled. In the past, different hysteresis models were presented by different authors.
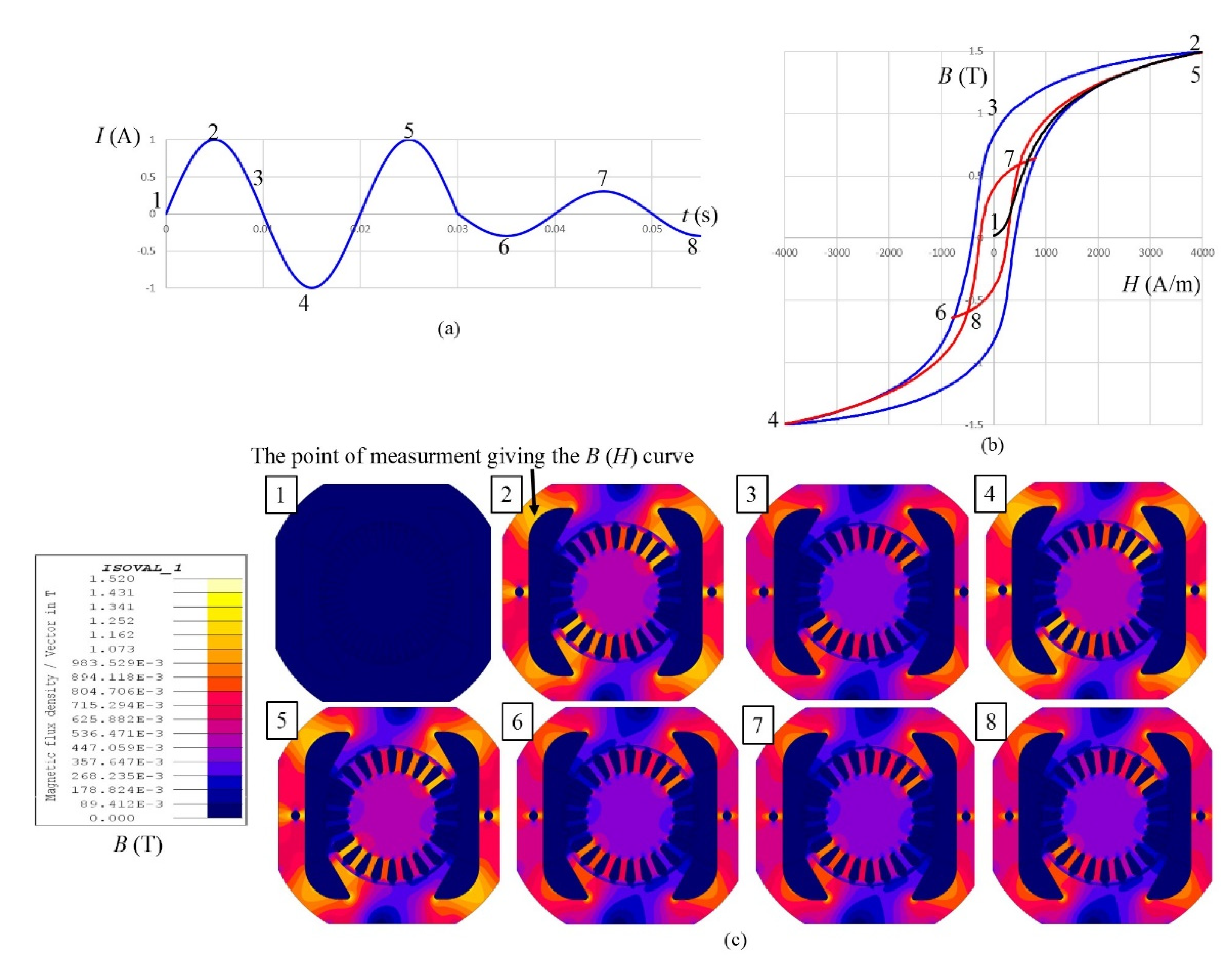
To understand the meaning of the hysteresis model better, the magnetization of the motor cross-section using hysteresis is presented schematically in
Figure 1. The value of the excitation current (
Figure 1a) changes from the value presented with point 1 to values in points 2, 3, … to point 8. Magnetization changes according to the curves presented between points marked at the hysteresis loop (
Figure 1b) and appropriate magnetic flux density
B at a cross-section of the motor for magnetization at each presented point (
Figure 1c).
The magnetization process starts with demagnetized material at point 1. Magnetization from zero to the maximum current, point 2, is made using the original magnetization curve. From point 2 to point 4, magnetization is made according to the left part of the major hysteresis loop. From point 4 to point 5, magnetization is made according to the right part of the major hysteresis loop. For smaller current at points 6, 7 and 8, the magnetization is made according to the first-order reversal magnetization curves. The current can have any value, so the magnetization can be anywhere inside the hysteresis loop. Some of the first-order curves inside the hysteresis loop are measured, but most of them should be obtained using a hysteresis model.
Mathematical models can be classified into two main categories: physical and phenomenological. The former (physical model) is created from the physics of a phenomenon, while the latter merely describes the end result with mathematical functions. Therefore, the latter is usually less complex, but it loses the connection to the physics of the material. Among the physical models is the Stoner–Wohlfarth model [
1], which is often used to describe events in ferromagnetic thin layers. The material is treated as a single magnetic domain. Jiles-Atherton [
2,
3,
4], on the other hand, also considers inter-domain interactions. Their main advantage is the connection with the physical parameters. More numerically oriented is the Preisach model of hysteresis [
5,
6,
7]. It enables the description of different forms of hysteresis loops that are constructed from the so-called hysterons. They can switch between −1 and 1, depending on whether the input data exceed the start-up or shut-off threshold. Other less known hysteresis models can be found, such as the Mayergoyz Vector Hysteresis model [
8], or Vector Magneto–Hysteretic H&S model [
9], and many modifications and corrections of existing models. The phenomenological, numerically oriented approach is presented in the paper.
The history of the magnetization process must also be known in the case of magnetic field calculation considering hysteresis. For the Finite Element Method (FEM) calculation [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20], the magnetization process could be different for almost every element. Due to this fact, it is favorable that the description of the magnetization history is as simple as possible. It is expected that the model is suitable for a wide range of different materials. It is a challenging problem to determine the parameters of the hysteresis models.
In our work, a phenomenological scalar hysteresis model is made, which offers a simple description of the magnetization process. Different mathematical expressions are tested to get the most appropriate.
This test is possible only if a reliable tool to determine the parameters is available. Different evolutionary optimization methods were used for the determination of the parameters, with the aim to determine the best for such a problem. The improper determination of model parameters due to the improper selection of the optimization method can lead to an incorrect evaluation of model quality. The used methods were genetic algorithm (GA) [
21,
22,
23,
24,
25,
26], differential evolution (DE) with three different strategies, which are DE/rand/1/exp, DE/rand/2/exp, DE/best/1/bin [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36], teaching–learning-based optimization (TLBO) [
37,
38,
39,
40,
41,
42,
43,
44,
45] and artificial bee colony (ABC) [
46,
47,
48,
49,
50,
51,
52,
53,
54,
55]. If an inappropriate solving method is used, the adequacy of the mathematical expression will not be determined correctly.
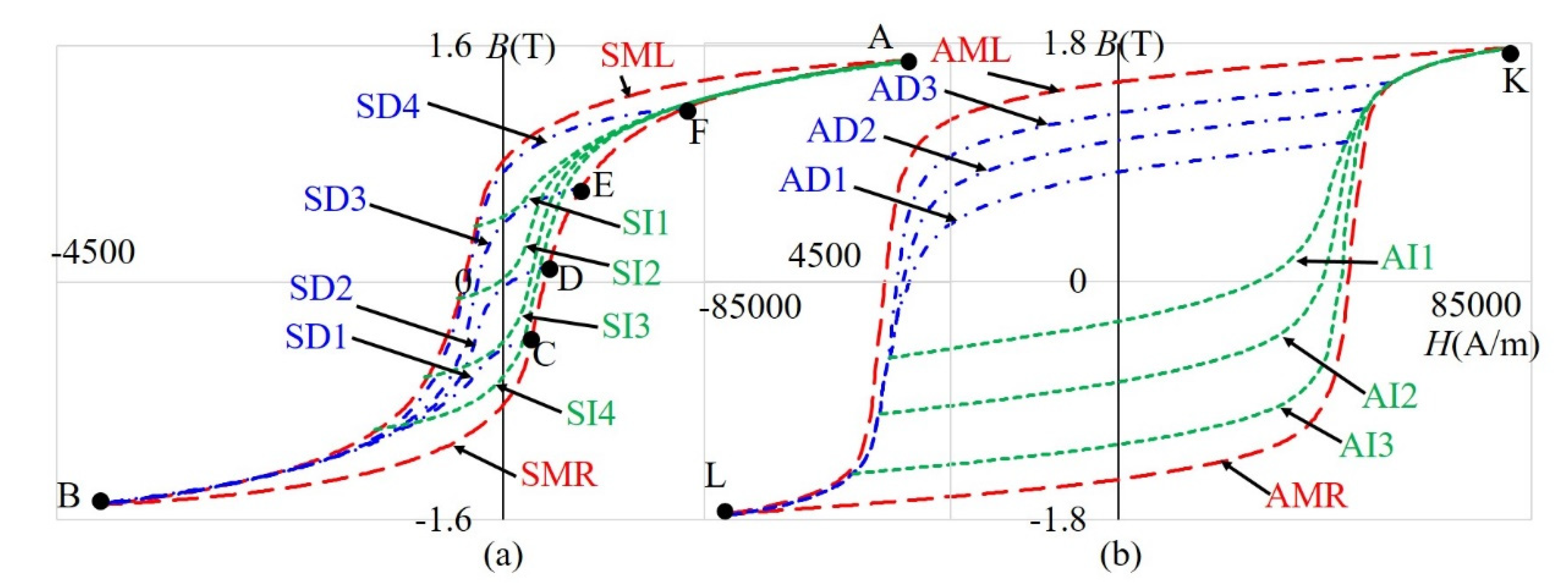
Two measured hystereses of materials 9S20 and Alnico with first-order reversal curves were used for the tests, and both are presented in
Figure 2. The materials 9S20 and Alnico are magnetic, with very different hysteresis curves.
For the material 9S20, the parts of major hysteresis are marked with the left/right part of the measured major hysteresis loop (SML/SMR), decreasing first-order reversal curves are marked as SD1–SD4, and increasing first-order reversal curves are marked with SI1–SI4. For the material Alnico, the parts of major hysteresis are marked with the left/right part of the Alnico measured major hysteresis loop (AML/ AMR), decreasing curves are marked as AD1–AD3, and increasing curves are marked with AI1–AI3. The measured major hysteresis curve and first-order reversal curves were used to determine the parameters of the model. After that, only two points, the point at which the excitation is changed (for example, C–F in
Figure 2) and the point at the ends of the hysteresis (for example, A and B in
Figure 2), were used to determine the magnetization process in the hysteresis area between the measured curves.
No comparison between different mathematical expressions and their use on cases of very different hysteresis have been found in the literature, to know which of them is the most appropriate for the hysteresis modeling. Our contributions in this work are:
Modification of the mathematical expressions from the literature, such as expressions from [
56], by adding additional terms, with the aim to get a more suitable expression.
Determination of a mathematical expression, selected between seven modified expressions, and determination of an appropriate method for the calculation of the parameters, selected between six methods (four methods and three different strategies of DE), to get the combination of expression and solving method which is suitable for a wide range of different materials. The appropriate method for the determination of the parameters is suggested, and tested by using it for the determination of parameters of a major hysteresis loop and more reversal curves inside the hysteresis loop for two very different materials.
An innovative description of the magnetization process inside the hysteresis areas between the measured curves is presented, which offers a fast determination of the magnetization process and, with that, is suitable for use in the scope of the FEM calculation. It is impossible to make so many measurements that the calculation of curves in the area between the measurements would not be necessary.
Other authors have tried to make models appropriate for FEM calculation. In [
7] M. Kuczmann developed an inverse vector Preisach hysteresis model, and it was inserted in the finite element procedure. Y. Zhang et al. in [
57] presented a novel hysteresis core loss model for magnetic laminations, which is used in the scope of the finite element model. Like us, L. Petreswcu et al. in [
56] also used Sigmoid’s functions in hysteresis phenomena modeling. The main difference between our model and other models is that, in our model, each measured curve, major and reversal, is described with different parameters, obtained using the optimization method, and the magnetization process between measured curves is described according to the nearest measured curve. In other models there is mainly only one curve, a major hysteresis or magnetization curve, used for the determination of the parameters, and all other curves are then dependent on this curve.
The paper consists of six Sections. In
Section 2, different mathematical expressions are tested using standard optimization methods and evolutionary methods, and the best combination is presented of expression and method for determination of the parameters. The use of the model for the material 9S20 is presented in
Section 3, and for the material Alnico in
Section 4. The limits of the parameters are presented in
Section 5 and the use of the model is presented in
Section 6. In the last,
Section 7, conclusions are given considering the proposed model.
2. Tested Mathematical Expressions and Solving Methods
Many engineering problems were solved using optimization methods. Sometimes the number of function evaluations is severely limited by time or cost. In [
58] Jones et al. presented a response surface methodology to address this challenge. These surfaces can then be used for visualization, tradeoff analysis, and optimization. We were dealing with a problem presented in [
59] by Jesenik et al., where the Newton–Raphson method was used to solve it. It is combined with approximation planes for a two-dimensional problem, obtained with the time consuming Finite Element Model. In the presented work, we are dealing with a curve-fitting problem, and function evaluations are not costly. Therefore, approaches for decreasing the number of fitness evaluations are not used, such as the approach with response surface methodology.
2.1. Tested Mathematical Expressions
Hysteresis occurs in various fields of engineering work [
60,
61,
62]. In the past, different mathematical expressions were used for hysteresis modeling. The magnetization curve, and also hysteresis, can be modeled in the easiest way by using a Sigmoid function. In the literature, different expressions of the Sigmoid function can be found [
56], and it plays a very important role in hysteresis modeling. A Sigmoid function is a mathematical function, which usually has an “S” shape. It is real-valued and differentiable. It is used in many fields, such as in the field of Neural Networks, to describe the processes in the human brain, in mathematical psychology, etc. We selected seven mathematical expressions of Sigmoid function from [
56]. The Langevin function is related to the Boltzmann law of magnetic moment distributions. Other functions are mathematical expressions in which parameters have less physical meaning. These are used to adjust mathematical expressions to hysteresis curves.
Seven mathematical expressions from [
56] are modified appropriately by adding additional terms into the expressions, and tested on the basis of two very different hystereses of a material named 9S20, with coercive magnetic field strength 4096 A/m, and a material named Alnico, with coercive magnetic field strength 47,289 A/m, and both materials are presented in
Figure 2. Measurements were made in our laboratory (the Laboratory of Applied Electromagnetics at the Faculty of Electrical Engineering and Computer Science, University of Maribor). Based on our experience in working with magnetic materials, we added the following parts in each used expression:
- -
After each H, a parameter was added in the form (H + Pa), which offers the possibility to move a curve with respect to the H axis.
- -
Parameter + Pb was added, which offers the possibility to move a curve with respect to the B axis.
- -
Part Pc∙μ0∙(H + Pa) was added for better adjustment of saturation.
The used modified expressions are:
Hyptan (Hyperbolic tangents):
2.2. Calculation of the Parameters Using Standard Optimization Methods
Standard optimization methods can be used for the determination of the parameters. We tested the Levenberg-Marquardt algorithm and nonlinear regression to determine their usefulness for solving the described problem.For the test of the standard optimization methods, we used Elliot’s expression (7) and SML of the material 9S20, presented in
Figure 2.
The Objective Function (OF) is written in (8).
where
n is the number of measured points,
Bmeasured are the measured points, and
Bcalculated are the calculated points.
An initial guess is needed to start standard optimization methods. The Levenberg-Marquardt (LM) algorithm is often used for solving curve-fitting problems, which is also evident from the literature [
63,
64]. A set of nonlinear equations was solved in the least-square sense. The minimization of a sum of squares of equation residuals was made using the LM algorithm.
Unfortunately, the local minima caused that different initial values led to different results. The lack of change of the parameters was the stopping condition of the algorithm (the maximum change must be less than 10
−12).
Figure 3 shows the tests for the SML curve, and the values of the parameters which were used for both the initial and final curves are presented in
Table 1.
The results presented in
Figure 3b,c are not correct (OF is 0.1548 and 0.1215). The OF for cases (a) and (d) is 6.342·10
−4. Based on the results presented as (b) and (c) in
Table 1 and
Figure 3, it can be seen that, for two initial curves, the obtained results are in two different local minima (the final curve is not similar to the measured values), and they are not the global minimum. The results presented in (a) and (d) are global minima.
LM is very fast. A very good result can be obtained by using appropriate initial values. Due to the fact that LM is not able to bypass the local minima, it is not suitable to be used as a stand-alone method. Also, NonLinear regression using the Matlab function “nlinfit” and using analytical derivatives were not suitable for the presented problem.
2.3. Calculation of the Parameters Using Evolutionary Methods
Evolutionary optimization methods [
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55] are population-based search algorithms, where the space of all possible solutions is searched through many solutions with various suitability (fitness). Better solutions have a higher probability to survive into the next generation, where they might be altered by mutation and/or crossover. Evolutionary optimization methods have a remarkable ability to balance exploration and exploitation [
25] and, as such, avoid local optima. They are often used for technical problems, and also to determine the parameters of different models [
65] describing real material properties or real devices. In this work, we used and compared GA [
21,
22,
23,
24,
25,
26], DE [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36], TLBO [
37,
38,
39,
40,
41,
42,
43,
44,
45] and ABC [
46,
47,
48,
49,
50,
51,
52,
53,
54,
55]. In GA 0.5 was used for the fraction of the kept population, and 0.2 was used for the mutation rate. For all three used DE strategies, which were DE/rand/1/exp (Algorithm 1), DE/rand/2/exp and DE/best/1/bin, 0.8 was used for the crossover probability, and 0.6 was used for the amplification of the differential variation. Different strategies are used, because it is known that the appropriateness of the strategy depends on the problem being addressed. The duplication elimination phase was omitted in the TLBO used in our work. Therefore, the number of Fitness Evaluations (FEs) which were consumed for the calculation was determined statically as FEs = 2 * population size * iterations. The limit value used in ABC was set at 100, and was used as a control parameter for the bee population. A scout bee might not be used for every iteration [
49], therefore the number of FE’s used in ABC cannot be determined statically.
| Algorithm 1. Pseudo-code for DE/rand/1/exp. |
| 1. Setting control parameters (maximum number of FEs, population size, F, Cr) |
| 2. Randomly generates the initial population of vectors in the D-dimensional search space |
| 3. repeat |
| 4. for each vector i in the population do |
| 5. select three mutually exclusive random vectors |
| 6. generate a donor vector according to (9) |
| 7. |
| 8. |
| 9. do |
| 10. |
| 11. while (rand(0,1) <= Cr AND L <= D) |
| 12. N = a random integer in the range of [1,D] |
| 13. generate a trial vector using exponential crossover by (10) |
| 14. |
| 15. evaluate the candidate vector using (8) |
| 16. replace with , if fitness of is better than fitness of |
| 17. end-for |
| 18. until a termination condition is met |
For all tests we used 83,160 FEs, which were appropriate in [
66] for nine parameters, and in this work we are dealing with five (
D = 5) or six parameters (
D = 6). The population size is ten times the number of parameters, fifty for five parameters and sixty for six parameters. The OF which was used for the analytical curves’ quality estimation was defined previously in (8).
To compare the ability of the presented expressions (1)–(7) to express hysteresis analytically, they were tested at the left part of the 9S20 measured major hysteresis loop (SML) and AML, which are presented in
Figure 2. The number of independent runs was 30 for each expression for GA, three DE strategies, (DE/rand/1/exp, DE/rand/2/exp and DE/best/1/bin), TLBO and ABC. The best (B), worst (W), mean (M) OF and standard deviation (SD) are written in
Table 2 for SML, and in
Table 3 for AML. In
Table 2 and
Table 3 the lowest best OF and the lowest mean OF are marked with bold, and the second-lowest best OF and the second-lowest mean OF are marked with italics.
For each combination of expression and method from
Table 2, appropriate parameters obtained using results with the best OF are shown in
Table 4. For each presented combination in
Table 3, appropriate parameters obtained using results with the best OF are shown in
Table 5.
The aim of the results presented in
Table 2,
Table 3,
Table 4 and
Table 5 is also to find out if different algorithms lead to different parameters. For Langevin, Grompertz, Hyptan and Elliot, it can be seen that, with methods that reached the same best OF, the calculated parameters are also the same. If the best OF is only a little different, the parameters are also just slightly different. In the case of algebraic, the parameters are different, although the best OF is the same. In the case of logistic and Sigmoid, the obtained best OF is different for almost every algorithm, and, consequently, the calculated parameters are also different. Although the same best OF is obtained using different methods, mean OF can be very different, which means that some methods occasionally give poor results on this problem, which is not desirable.
A comparison of different expressions is presented graphically in
Figure 4 for SML and in
Figure 5 for AML. Parameters used were obtained from the calculation with the best OF.
From
Table 2 it can be seen that the best results were obtained using the Elliot expression and methods DE/rand/1/exp, DE/rand/2/exp and TLBO. The second-best result was obtained using Langevin and methods DE/rand/1/exp, DE/rand/2/exp and TLBO. On the other hand, based on
Table 3, it can be observed that the best results were obtained using Langevin and methods DE/rand/1/exp and DE/rand/2/exp. The second-best result was obtained using Elliot and methods DE/rand/1/exp and DE/rand/2/exp. We can conclude that the best results were obtained using the Elliot and Langevin expressions and DE/rand/1/exp and DE/rand/2/exp solving methods. To select the best, additional tests were made based on all curves of the material 9S20 (SML, SMR, SD1–SD4, SI1–SI4) and Alnico (AML, AMR, AD1–AD3, AI1–AI3), presented in
Figure 2.
In
Table 6, the results of 30 independent runs are presented for all 9S20 curves from
Figure 2 using DE/rand/1/exp and DE/rand/2/exp for the Elliot and Langevin expressions. In
Table 7, the results of 30 independent runs are presented for all Alnico curves from
Figure 2 using DE/rand/1/exp and DE/rand/2/exp for the Elliot and Langevin expressions.
The numbers of best results achieved for the combination of expression and method presented in
Table 6 and
Table 7 are shown in
Table 8.
Based on
Table 8, it can be seen that the best results were obtained using a combination of the Elliot expression and DE/rand/1/exp for the determination of the parameters. Based on the presented results, we decided to use the Elliot expression, written in (7), to model the hysteresis curve, and to use DE/rand/1/exp for determination of the parameters. The meaning of parameters
P1,
P2 and
P3 are presented in
Figure 6, and the meaning of parameters
P4,
P5 and
P6 is presented in
Figure 7.
Parameter P3 moves the curve according to the H axis, P6 according to the B axis, and parameters P1, P2, P4 and P5 influence the shape and size of the curve.
In the continuation, the use of the Elliot expression is presented for materials 9S20 and Alnico.
2.4. Discussion of Calculated Values with Respect to Measurement Error
Measurements were made on the device for the characterization of semi and hard magnetic materials. A Magnet-Physic yoke MIR-5 was used for the measurements. A sample of massive material was made with a circular cross-section (diameter of the sample was 10 mm) was used and it was 80 mm long. A tangential Hall probe HS-TGB5-104005 with basic accuracy 0.25% (to 3T) was used for measurement of H. The Hall probe was connected with a Magnet-Physic TESLAMETER with basic accuracy 0.3% (without probe). So that the accuracy of the H measurement, considering the accuracy of the TESLAMETER and probe, was 0.55%. In the measurements we also have to consider that, between the probe which was placed fixed near the sample and the sample, a small air gap appears. The magnetic field in the cross-section of the tested material was not completely homogeneous. The real accuracy for the measurement of H was around 5%.
B was measured by induction in the measuring coil with 500 turns, coiled around the center of the sample and connected with a Fluxmeter. A Magnet-Physic Electronic Fluxmeter EF5 was used for the measurement of B. The basic accuracy of the Fluxmeter was 0.25%. The frequency of the measurement was 10 mHz. Although the measuring coil was coiled tightly around the sample, there was still some air between the coil and the sample. For the measurement of B, it should be considered that the magnetic field in the cross-section of the tested material was not completely homogeneous. Because of that, the real accuracy for the measurement of B was around 5%.
The measured and calculated values of
B in point A (presented in
Figure 5) for 9S20 material and point K (presented in
Figure 6) for Alnico, are presented in
Table 9.
From
Table 9 it can be seen that three calculated values at point A were inside of the measurement accuracy range, three vales were at the border, and one value was outside of the measurement accuracy range. It can also be seen that all calculated values at point K were inside of the measurement accuracy range. Points A and K are points where the deviation between the measured value and the calculation is higher, but they are important for Hysteresis modeling, as will be presented in
Section 3.2 and
Section 4.2. Taking into account the measurement accuracy and the results presented in
Table 9, we can conclude that it is reasonable to search for expressions and methods to match the measured and calculated curves best (some calculated values were at the border or outside of the measurement accuracy range).
7. Conclusions
Precise magnetic material hysteresis modeling is important for accurate dimensioning of electromagnetic devices using FEM. The aim of the paper was to find a mathematical expression that describes a wide range of different hystereses authentically. Seven different mathematical expressions were modified appropriately with added parts, and tested on two same test examples. The results presented in
Table 6,
Table 7 and
Table 8 show that the combination of the Elliot expression and DE/rand/1/exp method for the determination of the parameters is the best between the tested expressions and methods. Both the highest number of the lowest best OF and the highest number of the lowest mean OF were obtained using the Elliot expression combined with DE/rand/1/exp.
The idea of the model is that both major and first-order reversal measured curves could be modeled using the Elliot expression. For each measured curve, parameters were determined using DE/rand/1/exp, and, with that, the best match was achieved between measured and calculated curves. After that, a simple procedure is presented for the calculation of the curves in the area between the measured curves. Therefore, DE/rand/1/exp offers a reliable procedure for the precise determination of the parameters.
A large number of measured first-order reversal curves allow the model to function well. To simulate hysteresis, the closest curve should be selected, along with its set of six parameters. Therefore, it is impossible to simulate a curve if a similar experimental curve was not fitted previously. The model is, therefore, a fit of experimental data, and, consequently, it has no predictive ability, which is the limitation of the model.
Considering the measurement accuracy (5% for measurement of
H and 5% for measurement of
B) and results presented in
Table 9, it can be concluded that it is reasonable to search for expressions and methods to match best the measured and calculated curves.
It can also be concluded that different algorithms lead to the same results. For almost all expressions in the case of the same calculated OF, calculated parameters are also the same. Although the same best OF is obtained using different methods, mean OF can be very different, which means that some methods occasionally give poor results on this problem, which is not desirable. Because of this, we have identified the method that is best for the presented problem.
The presented model shows the successful use of the evolutionary method for the determination of a higher number of parameters and simple determination of further magnetization processes. Findings about the used evolutionary methods, which are presented in the paper, will be used in the future to get better solutions of the optimization problems in Electromagnetics. The integration of the presented model into the FEM software will also be one of the future studies.