2. Main Results
Throughout this section, we always assume that
D is an integral domain. It is well known that an ideal
I of
D is flat if and only if
is flat for all prime ideals
P of
D [
10] (Proposition 3.10); so a nonzero flat ideal is
w-flat. Additionally, it was shown that a nonzero flat ideal is a
t-ideal [
11] (Theorem 1.4). Hence we have the following lemma.
Lemma 1. A w-flat w-ideal is a t-ideal.
Proof. Let
I be a
w-flat
w-ideal of
D. Then
is a flat ideal of
for all maximal
t-ideals
M of
D; so we have
where the second equality follows from the fact that a nonzero flat ideal is a
t-ideal. Thus
I is a
t-ideal. □
Our next result is the
w-flat analogue of Zafrullah’s result which states that a
t-finite type
t-ideal is flat if and only if it is invertible [
12] (Proposition 1). This shows that if a
w-ideal
I is
w-invertible but not invertible, then
I is
w-flat (see Lemma 2) but not flat.
Lemma 2. Let I be a w-finite type w-ideal of D. Then I is w-flat if and only if I is w-invertible.
Proof. (⇒) Since
I is a
w-finite type
w-ideal of
D,
for some finitely generated ideal
J of
D. Let
M be any maximal
t-ideal of
D. Then
; so
is a finitely generated flat ideal of
because
I is
w-flat in
D. Hence
is invertible and so
is principal. Thus
I is
w-invertible [
8] (Corollary 2.7).
(⇐) Let M be a maximal t-ideal of D. Since I is w-invertible, is principal; so is flat. Thus I is w-flat. □
We define
D to be a
w-FF domain if every
w-flat
w-ideal of
D is of
w-finite type (equivalently,
w-invertible by Lemma 2). Clearly, if every nonzero ideal of
D is a
w-ideal, then
D is an FF domain if and only if
D is a
w-FF domain. A simple example of
w-FF domains is a Krull domain, because
D is a Krull domain if and only if every nonzero ideal of
D is
w-invertible [
13] (Theorem 3.6). (Recall that
D is a
Krull domain if there exists a family
of rank-one essential discrete valuation overrings of
D such that
and this intersection has finite character,
i.e., each nonzero nonunit in
D is a nonunit in only finitely many of valuation overrings
.) Additionally, we say that
D is
of finite t-character if every nonzero nonunit in
D is contained in only finitely many maximal
t-ideals of
D, and
D is a
Mori domain if it satisfies the ascending chain condition on integral
v-ideals. It is well known that in a Mori domain,
, so every
t-ideal of a Mori domain is of
t-finite type.
Proposition 1. The following assertions hold.
- (1)
A w-FF domain is an FF domain.
- (2)
D is a w-FF domain if and only if every nonzero w-flat ideal of D is w-invertible.
- (3)
A t-locally FF domain with finite t-character is a w-FF domain.
- (4)
A Mori domain is a w-FF domain.
Proof. (1) Recall that a nonzero flat ideal is a
t-ideal. Thus the assertion follows directly from [
12] (Proposition 1), because a flat ideal of a
w-FF domain is of
w-finite type.
(2) This is an immediate consequence of Lemma 2 and the fact that a nonzero ideal I is w-flat if and only if is w-flat.
(3) Let
I be a
w-flat
w-ideal of a
t-locally FF domain
D, and let
. Since
D has finite
t-character, there exist only finitely many maximal
t-ideals of
D containing
x, say
. Fix an index
. Then
is a flat ideal of
. Since
is an FF domain,
for some
. Let
J be the ideal of
D generated by
x and
and
. Then
. If
N is a maximal
t-ideal of
D which is distinct from
, then
. Therefore
for all maximal
t-ideals
M of
D, and hence
[
7] (Theorem 4.3) (or [
14] (Corollary 2.11)). Thus
D is a
w-FF domain.
(4) Let
I be a
w-flat
w-ideal of
D. Then
I is a
t-ideal by Lemma 1. Since
D is a Mori domain,
I is of
t-finite type. Let
M be a maximal
w-ideal of
D. Then
is a flat ideal of a Mori domain
[
15] (§2, Théorème 2); so
is invertible [
12] (Corollary 4). Therefore
is principal. Hence
I is
w-invertible [
8] (Corollary 2.7), which implies that
I is of
w-finite type. Thus
D is a
w-FF domain. □
Recall that
D is a
Prüfer domain (respectively,
Prüfer v-multiplication domain (P
vMD)) if every nonzero finitely generated ideal of
D is invertible (respectively,
t-invertible). It is well known that every ideal of
D is flat if and only if
D is a Prüfer domain [
16] (Theorem 4.2). We give the P
vMD version of this result.
Proposition 2. The following statements are equivalent.
- (1)
D is a PvMD.
- (2)
Every w-ideal of D is w-flat.
- (3)
Every nonzero finitely generated ideal of D is w-flat.
- (4)
Every w-finite type w-ideal of D is w-flat.
Proof. (1) ⇒ (2) Let
I be a
w-ideal of
D. Then
is a nonzero finitely generated subideal of
. Let
M be any maximal
t-ideal of
D. Then we have
Since
D is a P
vMD,
is
w-invertible; so
is
w-flat by Lemma 2. Therefore
is flat, and hence
is flat [
17] (Proposition 10.3). Thus
I is
w-flat.
(2) ⇒ (3) ⇒ (4) These implications follow because a nonzero ideal I is w-flat if and only if is w-flat.
(4) ⇒ (1) This is an immediate consequence of Lemma 2. □
It is well known that
D is a P
vMD if and only if
is a P
vMD [
8] (Theorem 3.7). Thus by Theorem 2, we obtain the following result.
Corollary 1. Every w-ideal of D is w-flat if and only if every w-ideal of is w-flat.
Recall that D is a Dedekind domain if every nonzero ideal of D is invertible. We give new characterizations of Krull domains and Dedekind domains via the (w-)FF property.
Corollary 2. The following assertions hold.
- (1)
D is a Krull domain if and only if D is both a PvMD and a w-FF domain.
- (2)
D is a Dedekind domain if and only if D is both a Prüfer domain and an FF domain.
- (3)
A valuation domain V is an FF domain if and only if V is a rank-one discrete valuation domain.
Proof. (1) The necessary condition follows because every nonzero ideal of a Krull domain is t-invertible. For the converse, assume that D is both a PvMD and a w-FF domain. Let I be a nonzero ideal of D. Then by Proposition 2, is w-flat and so is of w-finite type. Therefore by Lemma 2, , and hence, I, are w-invertible. Thus D is a Krull domain.
(2) This follows directly from (1) because D is a Dedekind domain (respectively, Prüfer domain) if and only if D is a Krull domain (respectively, PvMD) and each nonzero ideal of D is a w-ideal.
(3) Note that a valuation domain is a quasi-local Prüfer domain and that a quasi-local domain is a Dedekind domain if and only if it is a rank-one discrete valuation domain. Thus the result is an immediate consequence of (2). □
Let denote the polynomial ring over D. For an , the content of f, denoted by , is the ideal of D generated by the coefficients of f. Let . (If there is no confusion, we simply denote and by and , respectively.) Then is a (saturated) multiplicative subset of , and the quotient ring is called the t-Nagata ring of D. For the sake of convenience, we sometimes use the notation instead of .
Lemma 3. The following assertions hold.
- (1)
If A is a flat ideal of , then is a flat ideal of D.
- (2)
If I is a w-flat ideal of , then is a w-flat ideal of D.
Proof. (1) Assume that
A is a flat ideal of
. Since
, we can find an integer
such that
but
; therefore,
for some ideal
B of
with
. Hence we may assume that
by replacing
A with
B, because
. Note that for any integer
,
[
18] (Lemma 1.4). Therefore the natural homomorphism
is a monomorphism for any integer
. In particular,
is a monomorphism. Now the flatness follows from the facts that
and
for any
D-module
M.
(2) Note that if
I is a
w-flat ideal of
, then
for all integers
[
4] (Lemma 2.8), and a
D-module
M is a
w-flat
D-module if and only if
is a
w-flat
-module [
4] (Theorem 1.7). Thus the result follows by applying the same argument as in the proof of (1). □
Next, we study the w-FF property of polynomial rings and t-Nagata rings.
Theorem 1. The following statements are equivalent.
- (1)
D is a w-FF domain.
- (2)
is a w-FF domain.
- (3)
is a w-FF domain.
- (4)
is an FF domain.
Proof. (1) ⇒ (2) Let
I be a
w-flat
w-ideal of
. Then by Lemma 3(2),
is a
w-flat ideal of
D. Since
D is a
w-FF domain,
is a
w-finite type ideal of
D. Let
such that
, and let
M be a maximal
w-ideal of
D. Then
[
7] (Theorem 4.3) (or [
14] (Proposition 2.10)); so
for all integers
. Let
g be a nonzero element of
with degree
l. Then for any integer
, there exists an element
and
such that
. Hence
; so
. Therefore we have
Thus
I is of
w-finite type [
4] (Theorem 2.6).
(2) ⇒ (3) Let
M be a maximal
t-ideal of
and let
be a
w-flat
w-ideal of
, where
I is an ideal of
. If
, then
is a maximal
t-ideal of
D and
[
19] (Proposition 1.1). Since
is a maximal
t-ideal of
and
,
is a flat ideal. If
, then
is a local PID; so
is principal. Therefore
is flat. Hence
I is
w-flat in
. Since
is a
w-FF domain,
is a
w-finite type
w-ideal of
, and so
is of
w-finite type. Thus
is a
w-FF domain.
(3) ⇒ (4) Proposition 1(1).
(4) ⇒ (1) Let
I be a
w-flat
w-ideal of
D. Then
is a flat ideal of an FF domain
[
4] (Theorem 1.7); so
is invertible. Hence
I is
w-invertible [
8] (Corollary 2.5), and thus
D is a
w-FF domain. □
Let
S be a (not necessarily saturated) multiplicative subset of
D, and for set
the constant term of
f belongs to
. Then
, and
is both the symmetric algebra
of
considered as a
D-module and the direct limit of
, where
. This kind of ring is usually called the
composite polynomial ring and was first introduced by Costa, Mott and Zafrullah in [
20]. For more on this construction, the readers can refer to [
21,
22,
23,
24,
25,
26,
27].
Corollary 3. Let S be a (not necessarily saturated) multiplicative subset of D. Then the following assertions hold.
- (1)
is a w-FF domain if and only if D is a w-FF domain and S consists of units of D.
- (2)
(cf. [
25] (Corollary 1.7))
is a Krull domain if and only if
D is a Krull domain and
S consists of units of
D.
Proof. (1) (⇒) Assume that
is a
w-FF domain, and fix an
. Then
is an ascending chain of principal ideals of
, so
is flat [
17] (Proposition 10.3). Therefore
is a
w-flat
w-ideal of
. Since
is a
w-FF domain,
is of
w-finite type, so
for some
. Hence we can find a suitable integer
such that
. Therefore
, which implies that
s is a unit in
D. Thus
S consists of units of
D and
D is a
w-FF domain by Theorem 1.
(⇐) This implication was shown in Theorem 1.
(2) Recall that
D is a Krull domain if and only if
is a Krull domain [
28] (Theorem 43.11). Thus the equivalence follows directly from (1) and Corollary 2(1). □
Let
M denote a nonzero maximal ideal of an integral domain
T,
be the residue field,
be the natural projection and
D be a proper subring of
K. Assume that
. Then
, which is the integral domain arising from the following pullback
of canonical homomorphisms:
We next study the
w-FF property of
R when
T is
t-local. (Recall that an integral domain is
t-local if it is quasi-local whose maximal ideal is a
t-ideal.) To do this, we need a simple lemma whose proof is word for word that of [
2] (Lemma 3.5).
Lemma 4. Given a pullback diagram , if R is a w-FF domain, then D is a field.
Proof. Let d be a nonzero element of D and m be a nonzero element of M. Then for all positive integers n; so . Since forms an ascending chain of principal ideals, is a w-flat w-ideal of R. Since R is a w-FF domain, a simple modification of the proof of Corollary 3(1) shows that for some integer . Hence , which indicates that d is a unit in D. Thus D is a field. □
Let be an extension of integral domains. Recall that is a t-linked extension (or is t-linked over ) if for a nonzero finitely generated ideal I of implies .
Theorem 2. Consider a pullback diagram . If T is a w-FF domain and M is a t-ideal of T, then R is a w-FF domain if and only if D is a field.
Proof. (⇒) This was shown in Lemma 4.
(⇐) Assume that
D is a field. In order to avoid the trivial case, we assume that
K properly contains
D. Let
I be a
w-flat
w-ideal of
R. Note that
T is
t-linked over
R [
29] (Proposition 3.1), so
is a
w-flat ideal of
T [
4] (Lemma 1.5). Since
T is a
w-FF domain, there exists a finitely generated ideal
of
R such that
. Note that
M is a maximal
t-ideal of
R [
30] (Proposition 2.1), because
D is a field. Hence
is flat in
. If
is not principal, then
[
1] (Lemma 2.1); so
. Note that
M is a maximal
t-ideal of
T; so we obtain
,
which shows that
. By Nakayama’s lemma,
, a contradiction. Hence
for some
. Let
. Then
and
. Let
N be a maximal
t-ideal of
R with
. Then there exists the unique prime ideal
Q of
T with
and
[
31] (page 335). Note that
Q is a maximal
t-ideal of
T [
29] (Lemma 3.3). Therefore we have
Thus R is a w-FF domain. □
Corollary 4. With the notation as in , if T is t-local, then R is a w-FF domain if and only if D is a field and T is a -)FF domain.
Proof. By Lemma 4 and Theorem 2, it suffices to show that if
R is a
w-FF domain, then
T is a
w-FF domain. Since
T is
t-local,
T is a
w-FF domain if and only if
T is an FF domain. Thus the result is an immediate consequence of Proposition 1(1) and [
2] (Corollary 3.7). □
It is well known that
D is a UFD if and only if every
t-ideal of
D is principal [
13] (
Section 1). Additionally, it was shown that every nonzero flat ideal is a
t-ideal, and hence every flat ideal of a UFD is principal. We will say that
D is an
FP domain (respectively,
w-FP domain) if every flat ideal (respectively,
w-flat
w-ideal) of
D is principal. If every nonzero ideal is a
w-ideal, then the notion of FP domains coincides with that of
w-FP domains. Additionally, it is clear that an FP domain (respectively,
w-FP domain) is an FF domain (respectively,
w-FF domain).
Proposition 3. The following assertions hold.
- (1)
A w-FP domain is an FP domain.
- (2)
Every invertible ideal of an FP domain is principal.
- (3)
Every w-invertible w-ideal of a w-FP domain is principal.
Proof. (1) This follows directly from the fact that any nonzero flat ideal is a w-flat w-ideal.
For Propositions (2) and (3): these results come easily from the fact that an invertible (respectively, w-invertible) ideal is flat (respectively, w-flat). □
Corollary 5. Let be a valuation domain and set , where K is a field, D is a subring of K and M is the maximal ideal of V. Then the following conditions are equivalent.
- (1)
R is a w-FF domain.
- (2)
R is an FF domain.
- (3)
R is a w-FP domain.
- (4)
R is an FP domain.
- (5)
V is a rank-one discrete valuation domain and D is a field.
Proof. (1) ⇒ (2) This was already shown in Proposition 1(1).
(2) ⇒ (3) Assume that
R is an FF domain. Then
D is a field [
2] (Corollary 3.8); so
R is
t-local. Thus
R is a
w-FP domain.
(3) ⇒ (4) Proposition 3(1).
(4) ⇒ (5) Since
R is an FP domain,
D is a field [
2] (Corollary 3.8); so
R is
t-local. Hence
R is a (
w-)FF domain. Since
V is
t-local,
V is a rank-one discrete valuation domain by Corollaries 2(3) and 4.
(5) ⇒ (1) Note that V is a pullback as in (□) and is t-local. Thus the implication comes directly from Corollaries 2(3) and 4.
We give new characterizations of UFDs and PIDs in terms of the (w-)FP property. □
Proposition 4. The following statements hold.
- (1)
D is a UFD if and only if D is both a PvMD and a w-FP domain.
- (2)
D is a PID if and only if D is both a Prüfer domain and an FP domain.
Proof. (1) (⇒) This implication is an immediate consequence of Lemma 1 and Corollary 2(1).
(⇐) Let I be a nonzero ideal of D. Since D is a PvMD, is w-flat by Proposition 2; so is principal because D is a w-FP domain. Thus D is a UFD.
(2) Note that D is a PID (respectively, Prüfer domain) if and only if D is a UFD (respectively, PvMD) and each nonzero ideal of D is a w-ideal; and that if every nonzero ideal of D is a w-ideal, then D is a w-FP domain if and only if D is an FP domain. Thus the equivalence follows from (1).
We next show that the power series ring over an FP domain is an FP domain.
Theorem 3. If D is an FP domain, then the power series ring is an FP domain.
Proof. We adapt the proof of [
1] (Theorem 4.1). Let
I be a nonzero flat ideal of
. Since
, there exists a nonnegative integer
m such that
but
; so
for some ideal
J of
with
. Hence we may assume that
by replacing
I with
J, because
. Let
be the ideal of
D generated by constant terms of elements of
I. Then
and
is flat. Since
D is an FP domain,
is principal. Let
such that
. Then
for all positive integers
n. Thus
[
32] (Proposition 12, §2, Chapter III). □
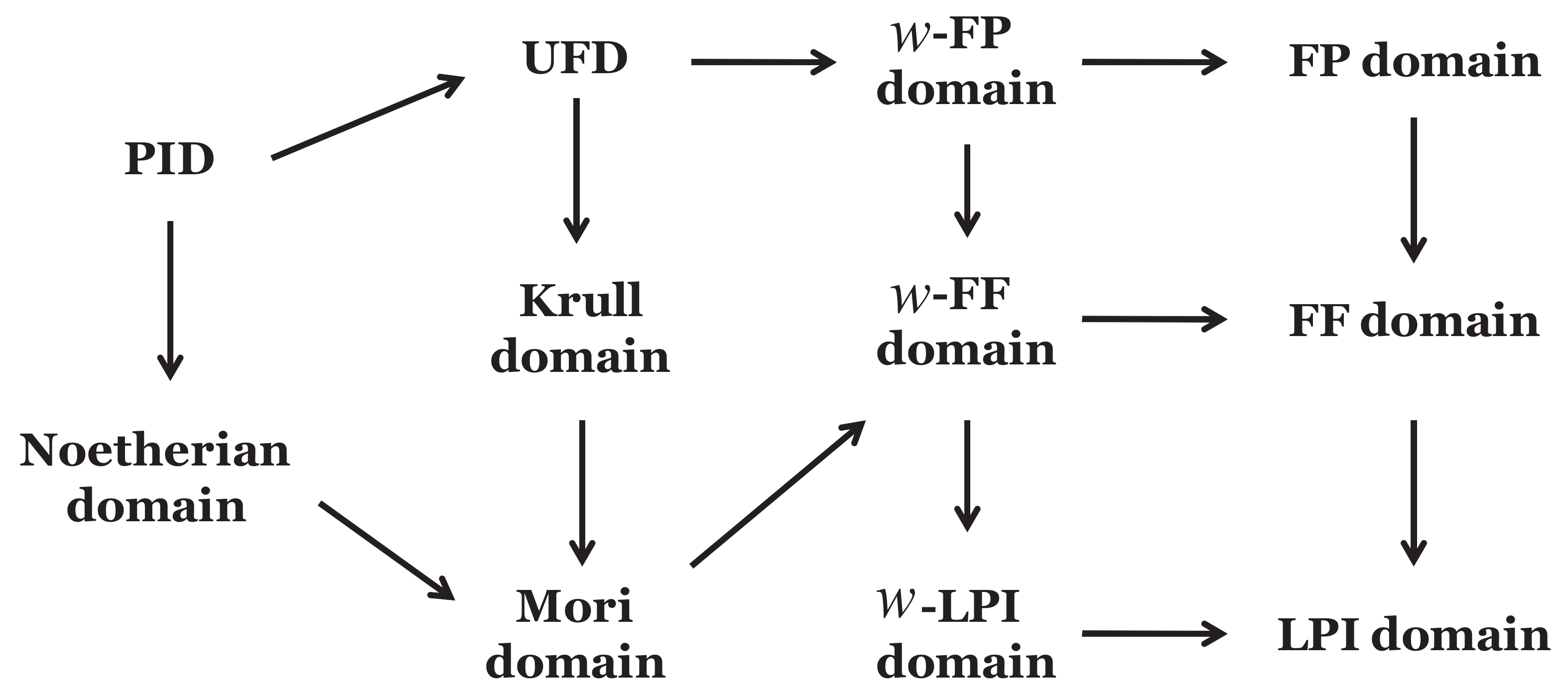
For the sake of the reader’s better understanding, we give a diagram of some integral domains related to w-FF domains.
The next examples show that any of the reverses in “UFD ⇒ FP domain ⇒ FF domain,” in “w-FP domain ⇒ FP domain,” in “w-FP domain ⇒w-FF domain” and “Mori domain ⇒w-FF domain” do not generally hold. We also give an example of a t-locally FF domain which is not a w-FF domain. (This shows that the hypothesis “finite t-character” in Proposition 1(3) is essential.). Furthermore, we construct an example of a PvMD that is not a w-FF domain. Finally, we give an example of a w-FP domain D such that is not a w-FP domain.
Example 1. - (1)
Let D be a Dedekind domain (respectively, Krull domain) which is not a PID (respectively, UFD). Then by Corollary 2 and Proposition 4, D is an FF domain (respectively, w-FF domain) that is not an FP domain (respectively, w-FP domain).
- (2)
Let D be a t-almost Dedekind domain which is not a Krull domain. (Recall that D is at-almost Dedekind domainif is a discrete valuation domain for each maximal t-ideal M of D.) Then D is both a PvMD and a t-locally (w-)FF domain (cf. Corollary 2(3)). Note that a t-almost Dedekind domain is a Krull domain if and only if it has finite t-character; and by Corollary 2(1), a t-almost Dedekind domain is a w-FF domain if and only if it is a Krull domain. Thus D is not a w-FF domain.
- (3)
This example is due to [33] (Section 4). Let , where L is a perfect field of characteristic 2 and satisfying . Then is not a UFD. Since D is a UFD, D is an FP domain by Propositions 3(1) and 4(1). Thus is an FP domain by Theorem 3. Note that D is a Krull domain; so is a Krull domain [28] (Corollary 44.11); so is a PvMD. Thus by Proposition 4(1), is not a w-FP domain. - (4)
Let (respectively, ) be the field of real (respectively, complex) numbers. Then is a t-local w-FF domain; so by Corollary 4, is also a w-FF domain.
- (5)
Let , where L is a field and are indeterminates over L. Let denote the images of , respectively, and let . Then is a two-dimensional integrally closed Noetherian domain that is not a UFD [34] (Example 7). Let I be a flat ideal of . Then I is finitely generated, and hence I is invertible. Therefore I is principal because is local. Thus is an FP domain. However, since is not a UFD, there exists a w-invertible ideal J of such that is not principal. Therefore is w-flat by Lemma 2 but not principal. Thus is not a w-FP domain. - (6)
Let D be a Mori domain such that is not a Mori domain. (The existence of such a domain D was shown in [35] (Proposition 8.3).) Then D is a w-FF domain; so by Theorem 1, is a w-FF domain. - (7)
Let be the ring of integers and let be the field of rational numbers. Then is a w-FF domain and is a (maximal) t-ideal of ; so is not a w-FF domain by Theorem 2 (or Corollary 3(1)). However, is a PvMD [20] (Theorem 4.43) (or [21] (Corollary 3.8)).
We end this paper with the following two questions.
Question 1. (1) Is an FF domain generally a w-FF domain?
(2) Can one characterize integral domains in which each
t-ideal is
w-flat? (Note that each
t-ideal of
D is flat if and only if
D is a generalized GCD-domain [
12] (Proposition 10). (Recall that
D is a
generalized GCD-domain if for every nonzero finitely generated ideal
I of
D,
is invertible.))