A Multilevel Iteration Method for Solving a Coupled Integral Equation Model in Image Restoration
Abstract
:1. Introduction
2. The Integral Equation Model for Image Restoration
2.1. System Overview
2.2. Model Definition
3. Fully Discrete Multiscale Collocation Method
3.1. Multiscale Collocation Method
3.2. Integral Approximation Strategy
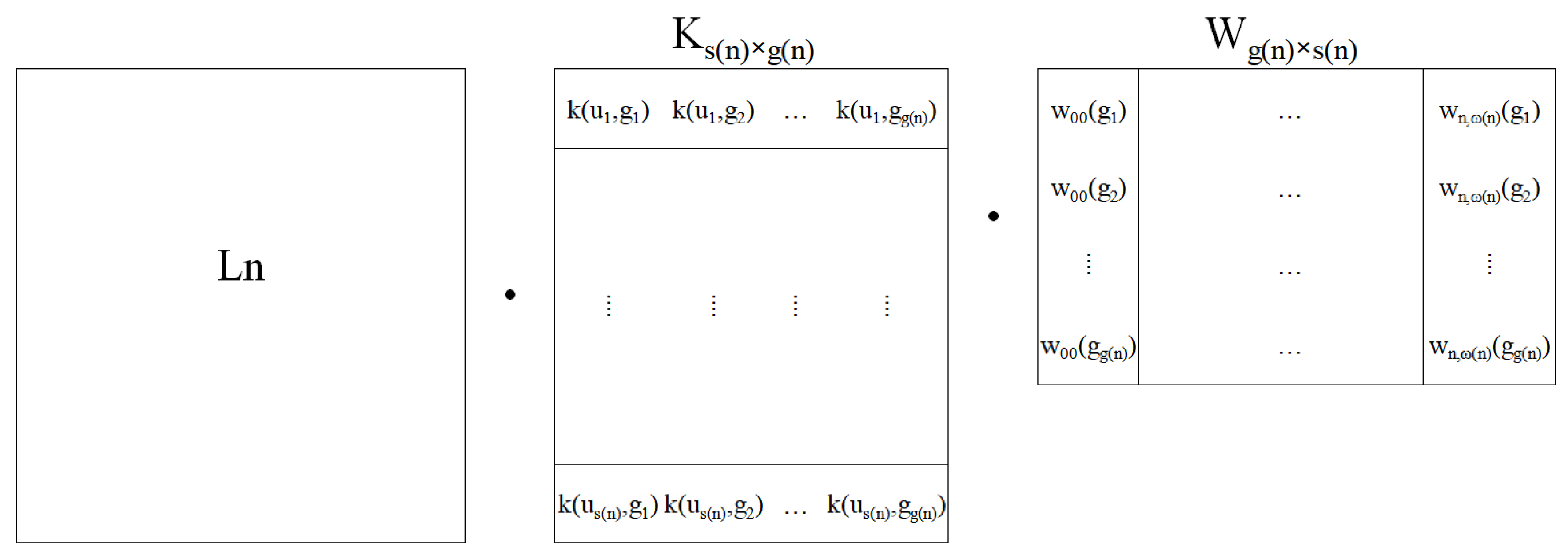
4. Multilevel Iteration Method
4.1. Multilevel Iteration Method
| Algorithm 1: Multilevel Iteration Method (MIM). | |
|
4.2. Computation Complexity
4.3. Error Estimation
5. Regularization Parameter Choice Strategies
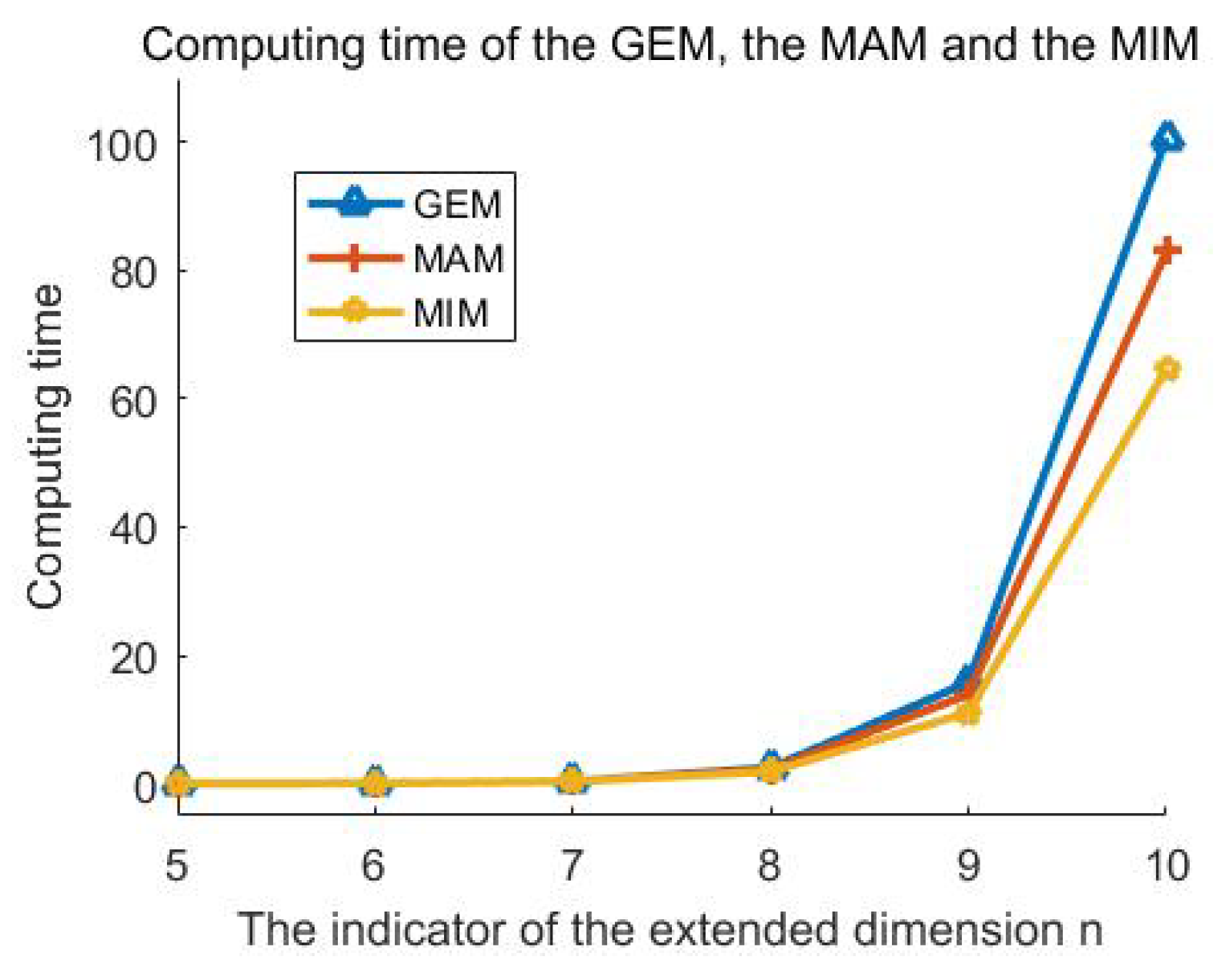
6. Numerical Experiments
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, Y.; Shen, L.; Xu, Y. Integral equation models for image restoration: High accuracy methods and fast algorithms. Inverse Probl. 2010, 26, 045006. [Google Scholar] [CrossRef]
- Chan, R.H.; Chan, T.F.; Shen, L.; Shen, Z. Wavelet algorithms for high-resolution image reconstruction. SIAM J. Sci. Comput. 2003, 24, 1408–1432. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, S.; Xu, Y. A Higher-Order Polynomial Method for SPECT Reconstruction. IEEE Trans. Med. Imaging 2019, 38, 1271–1283. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shen, L.; Xu, Y.; Yang, H. A collocation method solving integral equation models for image restoration. J. Integral Eq. Appl. 2016, 28, 263–307. [Google Scholar] [CrossRef]
- Groetsch, C.W. The Theory of Tikhonov Regularization for Fredholm Equations of the First Kind; Research Notes in Mathematics; Pitman (Advanced Publishing Program): Boston, MA, USA, 1984. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Mathematics and Its Applications; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Chen, Z.; Ding, S.; Xu, Y.; Yang, H. Multiscale collocation methods for ill-posed integral equations via a coupled system. Inverse Probl. 2012, 28, 025006. [Google Scholar] [CrossRef]
- Russell, R.D.; Shampine, L.F. A collocation method for boundary value problems. Numer. Math. 1972, 19, 1–28. [Google Scholar] [CrossRef]
- Krasnosel’skii, M.A.; Vainikko, G.M.; Zabreiko, P.P.; Rutitskii, Y.B.; Stetsenko, V.Y. Approximate Solution of Operator Equations; Wolters-Noordhoff Pub: Groningen, The Netherlands, 1972. [Google Scholar]
- Chen, Z.; Micchelli, C.A.; Xu, Y. Multiscale Methods for Fredholm Integral Equations; Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Micchelli, C.A.; Xu, Y.; Zhao, Y. Wavelet Galerkin methods for second-kind integral equations. J. Comput. Appl. Math. 1997, 86, 251–270. [Google Scholar] [CrossRef] [Green Version]
- Groetsch, C.W. Convergence analysis of a regularized degenerate kernel method for Fredholm integral equations of the first kind. Integral Eq. Oper. Theory 1990, 13, 67–75. [Google Scholar] [CrossRef]
- Hämarik, U.; Raus, T. About the balancing principle for choice of the regularization parameter. Numer. Funct. Anal. Optim. 2009, 30, 951–970. [Google Scholar] [CrossRef]
- Pereverzev, S.; Schock, E. On the adaptive selection of the parameter in regularization of ill-posed problems. SIAM J. Numer. Anal. 2005, 43, 2060–2076. [Google Scholar] [CrossRef]
- Bauer, F.; Kindermann, S. The quasi-optimality criterion for classical inverse problems. Inverse Probl. 2008, 24, 035002. [Google Scholar] [CrossRef]
- Jin, Q.; Wang, W. Analysis of the iteratively regularized Gauss-Newton method under a heuristic rule. Inverse Probl. 2018, 34, 035001. [Google Scholar] [CrossRef]
- Rajan, M.P. Convergence analysis of a regularized approximation for solving Fredholm integral equations of the first kind. J. Math. Anal. Appl. 2003, 279, 522–530. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Xu, Y. Computing integrals involved the Gaussian function with a small standard deviation. J. Sci. Comput. 2019, 78, 1744–1767. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Fan, L.; Wu, Y.; Li, F. Fast multi-level iteration methods with compression technique for solving ill-posed integral equations. J. Comput. Appl. Math. 2014, 256, 131–151. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Wintz, P. Digital Image Processing; Addison-Wesley Publishing Co.: Reading, MA, USA; London, UK; Amsterdam, The Netherlands, 1977. [Google Scholar]
- Chen, Z.; Micchelli, C.A.; Xu, Y. A construction of interpolating wavelets on invariant sets. Math. Comp. 1999, 68, 1569–1587. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xu, Y.; Yang, H. Fast collocation methods for solving ill-posed integral equations of the first kind. Inverse Probl. 2008, 24, 065007. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, Y.; Yang, H. A multilevel augmentation method for solving ill-posed operator equations. Inverse Probl. 2006, 22, 155–174. [Google Scholar] [CrossRef]
- Chen, Z.; Micchelli, C.A.; Xu, Y. Fast collocation methods for second kind integral equations. SIAM J. Numer. Anal. 2002, 40, 344–375. [Google Scholar] [CrossRef]
- Micchelli, C.A.; Xu, Y. Reconstruction and decomposition algorithms for biorthogonal multiwavelets. Multidimens. Syst. Signal Process. 1997, 8, 31–69. [Google Scholar] [CrossRef]
- Fang, W.; Lu, M. A fast collocation method for an inverse boundary value problem. Int. J. Numer. Methods Eng. 2004, 59, 1563–1585. [Google Scholar] [CrossRef]
- Groetsch, C.W. Uniform convergence of regularization methods for Fredholm equations of the first kind. J. Aust. Math. Soc. Ser. A 1985, 39, 282–286. [Google Scholar] [CrossRef] [Green Version]
- Kincaid, D.; Cheney, W. Numerical Analysis: Mathematics of Scientific Computing; Brooks/Cole Publishing Co.: Pacific Grove, CA, USA, 1991. [Google Scholar]
- Taylor, A.E.; Lay, D.C. Introduction to Functional Analysis, 2nd ed.; Robert, E., Ed.; Krieger Publishing Co., Inc.: Melbourne, FL, USA, 1986. [Google Scholar]



| n | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|
| 0.31 | 0.58 | 1.17 | 2.42 | 5.45 | 13.98 | |
| 0.002 | 0.004 | 0.013 | 0.047 | 0.190 | 2.14 |
| n | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|
| 0.0131 | 0.0645 | 0.3535 | 2.4250 | 15.8140 | 100.6399 | |
| 0.0103 | 0.0528 | 0.3454 | 2.2584 | 13.8898 | 82.9874 | |
| 0.0084 | 0.0500 | 0.3478 | 1.8875 | 11.0880 | 64.6845 |
| 0 | 0.01 | 0.03 | 0.05 | 0.10 | 0.15 | |
|---|---|---|---|---|---|---|
| 4.3980 × | 0.0067 | 0.0167 | 0.0256 | 0.04 | 0.05 | |
| 23.0173 | 22.9552 | 22.4792 | 21.6726 | 19.1102 | 16.7175 | |
| 31.9072 | 25.8306 | 24.5039 | 23.6348 | 21.9135 | 20.7536 |
| 0 | 0.01 | 0.03 | 0.05 | 0.10 | 0.15 | |
|---|---|---|---|---|---|---|
| 6.6570 × | 0.009 | 0.0199 | 0.0240 | 0.0394 | 0.0526 | |
| 23.0173 | 22.9528 | 22.4801 | 21.6692 | 19.1201 | 16.7044 | |
| 30.9030 | 25.9479 | 24.5537 | 23.6281 | 21.9105 | 20.7557 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zhou, B. A Multilevel Iteration Method for Solving a Coupled Integral Equation Model in Image Restoration. Mathematics 2020, 8, 346. https://doi.org/10.3390/math8030346
Yang H, Zhou B. A Multilevel Iteration Method for Solving a Coupled Integral Equation Model in Image Restoration. Mathematics. 2020; 8(3):346. https://doi.org/10.3390/math8030346
Chicago/Turabian StyleYang, Hongqi, and Bing Zhou. 2020. "A Multilevel Iteration Method for Solving a Coupled Integral Equation Model in Image Restoration" Mathematics 8, no. 3: 346. https://doi.org/10.3390/math8030346





