A Novel and Simple Mathematical Transform Improves the Perfomance of Lernmatrix in Pattern Classification

Abstract

The Lernmatrix is a classic associative memory model. The Lernmatrix is capable of executing the pattern classification task, but its performance is not competitive when compared to state-of-the-art classifiers. The main contribution of this paper consists of the proposal of a simple mathematical transform, whose application eliminates the subtractive alterations between patterns. As a consequence, the Lernmatrix performance is significantly improved. To perform the experiments, we selected 20 datasets that are challenging for any classifier, as they exhibit class imbalance. The effectiveness of our proposal was compared against seven supervised classifiers of the most important approaches (Bayes, nearest neighbors, decision trees, logistic function, support vector machines, and neural networks). By choosing balanced accuracy as a performance measure, our proposal obtained the best results in 10 datasets. The elimination of subtractive alterations makes the new model competitive against the best classifiers, and sometimes beats them. After applying the Friedman test and the Holm post hoc test, we can conclude that within a 95% confidence, our proposal competes successfully with the most effective classifiers of the state of the art.

1. Introduction

The human being possesses an ability that has been useful for his survival since his appearance on planet Earth. The recognition of everyday things, living things, events and chains of events, allows man to take actions that give him tools to successfully face daily existence. It is pertinent to note that this ability, which is so natural and evident in humans, can become a very complex problem for a computational algorithm. Computer sciences has a specific area, called pattern recognition, whose field of study is precisely this type of concepts [1]. One of the purposes of pattern recognition is to generate computational algorithms that are capable of recognizing the everyday things, living things, events and chains of events that man so easily recognizes. In the computational context, the entities to be recognized are represented by patterns, which can be vectors, tuples or data arrays. At the same time, there is a set of disciplines whose fields of study have important coincidences with pattern recognition, because they include modeling and automatic recognition of objects and actions from different perspectives. Among these disciplines, we can mention as the most relevant: machine learning [2], artificial intelligence [3], and data mining [4].

In pattern recognition and related areas, systematic exploration of human ability to recognize patterns leads to the scientific study of four basic tasks: classification, recalling, regression, and clustering. The first three tasks (classification, regression and recalling) correspond to the supervised learning paradigm [5], while clustering is the emblematic task of the paradigm known as unsupervised learning [6].

In this article, we will only deal with the first two tasks of the supervised paradigm: classification and recalling. Regarding the classification of patterns, it should be noted that the classification algorithms place patterns in the class that corresponds to them, in a specific problem. For example, a classification algorithm (a classifier) will be able to correctly decide, with a certain percentage of success, whether a chest radiograph corresponds to a patient suffering from pneumonia, or corresponds to a healthy person. In this hypothetical problem, there are two classes (“healthy” and “sick with pneumonia”) and the patterns are chest radiographs [7]. The hit rate depends on several factors, including the complexity of the dataset and the quality of the classification algorithm (how good it is).

Every pattern recognition scientist who designs and creates a new pattern classifier algorithm hopes that their model does not fail when classifying patterns. In the previous example, it is desirable that when presenting any chest radiograph to the classifier, the correct answer is obtained at the exit, without error. That is, in the ideal case, it is expected that in all cases the answer given by the classifier (sick or healthy) is always correct, indicating that there were zero errors, or equivalent, 100% performance.

However, this ideal situation is unattainable: the best classifier does not exist. This strong statement is scientifically based on the No-Free-Lunch theorem that was initially (more than half a century ago) stated for optimization problems [8]. However, this disruptive theorem was later adapted to the pattern recognition area, specifically to the pattern classification task. The No-Free-Lunch theorem governs the effectiveness of pattern classification algorithms, and it is true for all classifiers and datasets, without exception [9].

The existence of the No-Free-Lunch theorem has led scientists to conclude that it is useless to search for the best classifier, and it is also useless to pretend that a given classifier achieves zero errors when trying to classify all the patterns of a given dataset. An immediate consequence of the No-Free-Lunch theorem is that the perspectives of scientists investigating in the area of pattern recognition have changed. They are no longer looking for the ideal classifier, the perfect one without mistakes. Now, researchers are trying to design, implement and apply new pattern classification algorithms, always seeking to minimize classification errors, or equivalently, trying to maximize the performance. This search in performance improvement is carried out in several ways, among which the treatment of data [10] and the search for new effective algorithms [11] stand out.

In this order of ideas, let us now consider the second of the basic pattern recognition tasks that we will cover in this paper: pattern recalling. The algorithms that perform the recalling task execute the retrieval of a pattern (for example, a phone number) from a specified pattern at the algorithm input (for example, a person). Associative memories are algorithms specialized in the pattern recalling task [12].

The pioneering associative model is the Lernmatrix, which was created in Germany, in 1961, by Karl Steinbuch [13]. Due to the nature of the patterns it works with, this model behaves like a pattern classifier. However, as will be exemplified in this paper, the original Lernmatrix model is not competitive as a pattern classifier against the state-of-the-art classifier algorithms.

The main contribution of this paper consists of the proposal of a simple mathematical transform, whose application in the data significantly improves the performance of the Lernmatrix in the supervised classification of patterns. That is, the error in the classification of patterns decreases with the application of the improved model of the Lernmatrix, making the new model competitive against the classifier algorithms of the state of the art.

The rest of the article is structured as follows. To adequately contextualize the research question and hence clarify the contribution of this paper, Section 2 includes some materials and methods. Section 2 is made up of five subsections. Section 2.1 includes a brief summary of some conceptual elements related to the pattern classification task in pattern recognition, in addition to the approaches and theoretical bases of some of the state-of-the-art classifier algorithms. Section 2.2 describes the original model of the Lernmatrix and exemplifies how it performs the task of pattern classification. Section 2.3 is crucial to our proposal, given that it presents a summary of the milestones in the efforts that have been made to rescue the Lernmatrix and turn it into a contemporary competitive model. Based on the historical facts described, Section 2.4 presents some theoretical advances that have allowed the original model of the Lernmatrix to evolve, and includes some definitions and theorems. To conclude with Section 2, in Section 2.5 we present a method called the Johnson–Möbius code, which will be part of the proposed methodology. The content of Section 2.4 serves as a solid basis for Section 3, where the main contribution of this paper is presented, which is a new mathematical transform. In this section, the new transform is defined, a theorem is stated and proved, and simple examples of its meaning for performance improvement in the Lernmatrix are presented. Taking as a starting point the mathematical transform proposed in Section 3 and the Johnson–Möbius code, in Section 4 the complete methodology is presented. The experimental results accompanied by the analysis and discussion are presented in Section 5, while Section 6 contains the conclusions and future work. Finally, references are included.

2. Materials and Methods

In this section, some materials and methods related to the main proposal of this research work are presented. First, Section 2.1 includes a brief summary of some conceptual elements related to the pattern classification task in pattern recognition, in addition to the approaches and theoretical bases of some of the state-of-the-art classifier algorithms. Section 2.2 describes the original model of the Lernmatrix and exemplifies how it performs the task of pattern classification. Section 2.3 is crucial to our proposal, given that it presents a summary of the milestones in the efforts that have been made worldwide to rescue the Lernmatrix and turn it into a contemporary competitive model. Based on the historical facts described, Section 2.4 presents some theoretical advances that have allowed the original model of the Lernmatrix to evolve, and includes some definitions and theorems. Finally, in Section 2.5, we present a method called the Johnson–Möbius code, which will be part of the proposed methodology.

2.1. About Attributes, Patterns, Datasets, Validation, Performance, and Main Approaches to Pattern Classification

When working in pattern classification, the first step is to select and understand the tiny area of the universe it is desired to analyze. Once this selection has been made, it is important to identify the useful attributes (also called features) that describe the phenomenon under study.

The raw material to work in pattern recognition and related disciplines are the data, which have specific values of the attributes. For example, the attribute “number of children” could correspond to specific data, or values, such as: 0, 1, 3, 12, 20, while the values 1.78, 1.56, 2.08, measured in meters, could be data from an attribute called “height”. These two attributes are numerical. On the other hand, there are also categorical attributes and missing values. The data associated with the “sex” attribute could be F and M, and the “temperature” attribute could have the following data as specific values: hot, warm, cold.

The next step is to convert those features into something the computer can understand, and at the same time it is appropriate to be handy. The most common and easy thing to do is to use a vector which is composed of numbers that represent real-valued features. For instance, the color of a leaf can be represented by numbers that indicate the intensity of the color, size, morphology, smell, among others. For categorical or mixed attributes, it is possible to use arrays of values. Those representing arrays are known as patterns.

Patterns with common attributes form classes, and these sets representing various classes of a phenomenon under study, when joined, form datasets. For example, the vector [5.4, 3.7, 1.5, 0.2] represents a flower, and the four attributes (in cm) correspond to the sepal length, sepal width, petal length, and petal width, in that order. This flower is a pattern that belongs to one of the three classes (Iris Setosa) contained in the famous Iris Dataset (https://archive.ics.uci.edu/ml/datasets/iris).

Given a phenomenon under study, it is of vital importance to select properly the attributes and data, to form the patterns that correspond to each of the classes. Typically, the choice of attributes (how many and of what type), the formation of patterns and the design of datasets are all creative processes where the active participation of experts in the specific area of application is required. Experts in the areas of application (for example, physicians to classify diseases, or economists to classify financial risks) join with experts in pattern recognition, machine learning, artificial intelligence, and data mining to create useful datasets to solve problems in different application areas [1,2,3,4].

There are many pattern classifiers that only work with numerical attributes. In these cases, preprocessing has to be applied to the data in order to convert the categorical data to numerical ones and to impute the missing values [14]. After preprocessing, there will only be numerical values.

The patterns dimension can be from 3 or 4 attributes, up to hundreds, thousands or even millions, as it happens with the patterns of the datasets that contain bioinformatics data. For their part, datasets vary in size and can have millions of patterns in the field of big data [15].

A very important aspect related to classes is balance or imbalance. The ideal case is that in a dataset, all classes have the same size. However, the most interesting datasets are far from the ideal case. For example, in the datasets used for the classification of diseases, typically the class “sick” is the minority class (which is desirable). From the computational point of view, the imbalance has consequences related to the way of measuring the performance of the classifiers [1].

Given a dataset, the imbalance is measured using the imbalance ratio (IR), which is calculated as follows [16]:

$$IR=\frac{\left|majority\_class\right|}{\left|\min ority\_class\right|}$$

(1)

A dataset is considered imbalanced if it happens that $IR>1.5$.

There exist dataset repositories that have become important auxiliaries to those who develop algorithms and models in pattern recognition and related disciplines. Notable examples are the repositories powered by prestigious universities, of which two stand out. One of them is the repository http://archive.ics.uci.edu/ml/datasets.php, which was made available to research groups by the University of California Irvine, USA. The other repository is sponsored by the University of Granada in Spain: http://sci2s.ugr.es/keel/datasets.php. Recently, a dataset repository that runs contests has become very popular, where researchers test their pattern recognition algorithms on real-life datasets, with the chance to win cash prizes: https://www.kaggle.com/datasets.

The researchers in pattern recognition have certain software platforms at their disposal, where they can develop and test pattern classification algorithms. One of the most useful and famous platforms was developed by scientists from Waikato University in New Zealand: www.cs.waikato.ac.nz/ml/weka/. WEKA is an analysis environment platform written on Java. This platform contains a vast collection of algorithms for the analysis of data and predictive models that include methods that address problems of regression, classification, clustering, and feature selection. The software allows a dataset to be pre-processed, if required, and inserts it into a learning scheme in order to analyze the results and the performance of a selected classifier.

In the supervised paradigm, a classifier consists of two phases: learning and classification [17]. The classifier requires a training set to perform the learning. Already trained, the classifier runs the classification phase, where a class is assigned to testing pattern. A common practice is that given a dataset D, a partition is made into two subsets: L (learning or training) and T (test). The classifier learns with L and the patterns in T are used for testing (Figure 1).

Since it is a partition, the following must be true: $\mathrm{L}{{\displaystyle \cup }}^{}\mathrm{T}=\mathrm{D}$ and $\mathrm{L}{{\displaystyle \cap }}^{}\mathrm{T}=\varnothing$.

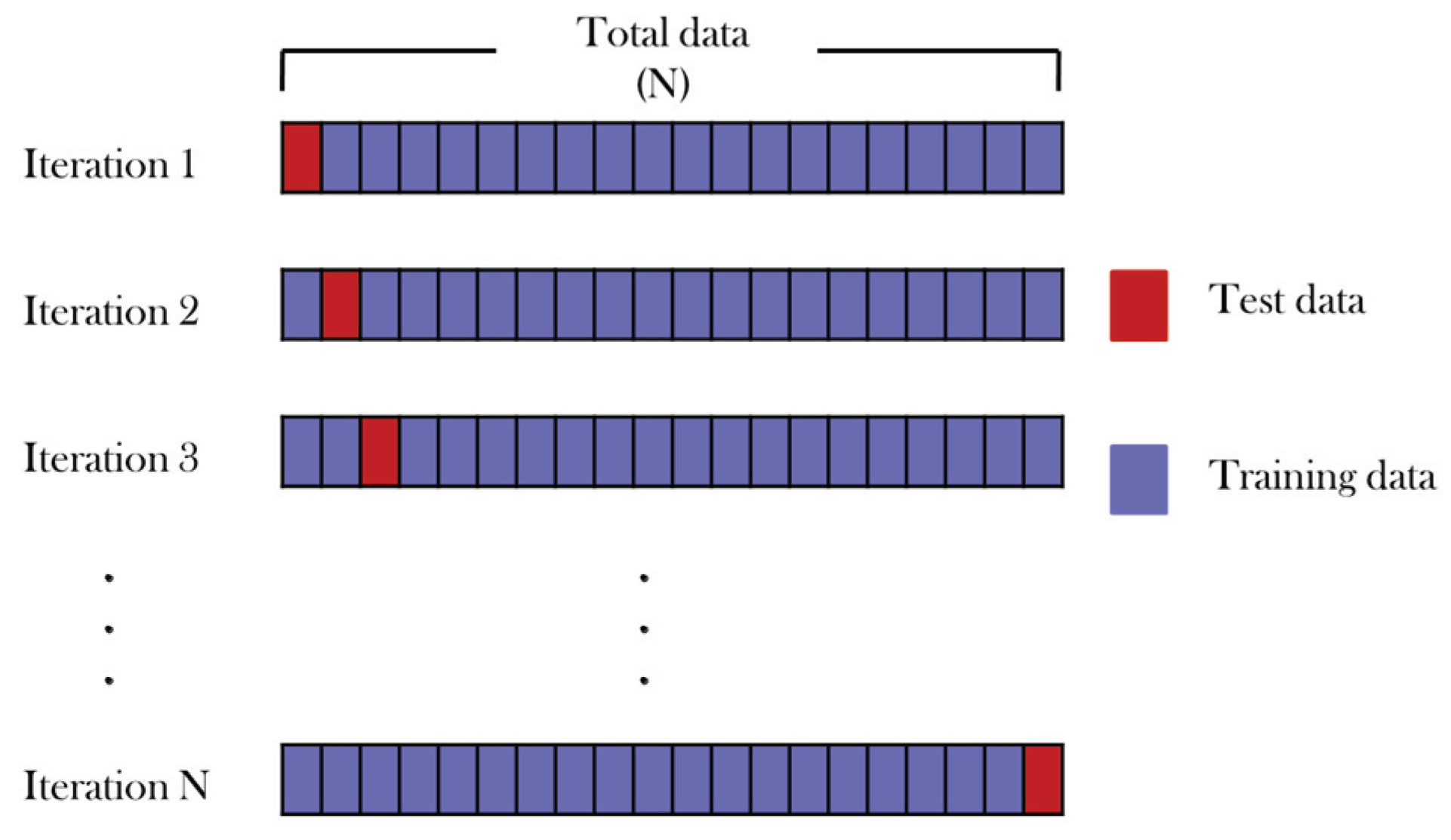
The partition is obtained through a validation method, among which the leave-one-out method stands out as one of the most used in the world of pattern recognition research [18]. As illustrated in Figure 2, in each iteration, a single testing pattern (in T) is left, and the model learns with the patterns in L, which are precisely the rest of the patterns in D.

Leave-one-out is a particular case of a more general cross-validation method called stratified k-fold cross-validation. It consists of partitioning the dataset into k folds, where k is a positive integer (k = 5 and k = 10 are the most popular values in the current specialized literature), ensuring that all classes are represented proportionally in each fold [19].

The operation of the k-fold cross-validation is very similar to the schematic diagram in Figure 2, except that instead of a pattern, one of the k folds is taken. Note that leave-one-out is a particular case of k-fold cross-validation with k = N, where N is the total number of patterns in the dataset.

In the experimental section of this article, we used the 5-fold cross-validation procedure. The reason is that some leading authors recommend this validation method especially for imbalanced datasets [20]. Figure 3 and Figure 4 show schematic diagrams of the 5-fold stratified cross-validation method for a 3-class dataset.

For datasets that return a value much greater than 1.5 when applying Equation (1), it is recommended to use a variant of cross-validation [21]. This is the 5 × 2 cross-validation method, which consists of partitioning the dataset into 2 stratified folds and performing 5 iterations. The process is illustrated in Figure 5.

After applying a validation method to the dataset under study, the researcher has at his disposal the partition of dataset D in sets L and T. Now a relevant question arises: how is the performance of a classification algorithm measured?

Common sense indicates that calculating accuracy is a good way to decide how good a classifier is. Accuracy is the ratio of the number of patterns classified correctly, among the total patterns contained in the testing set T, expressed as a percentage. If N is the total number of patterns in the testing set, T and C are the number of patterns correctly classified, the value of accuracy is calculated using Equation (2):

$$Accuracy=\frac{C}{N}\cdot 100\%$$

(2)

Obviously, it is true that $0\le C\le N$, so that $0\le Accuracy\le 100$.

For example, consider a study where dataset D is balanced and the testing set T contains patterns of 100 patients, 48 healthy and 52 sick. If an A1 classification algorithm learns with L and when testing it with T correctly classifies 95 of the patients, the accuracy of A1 in D is said to be 95%. In general, values above 90% for performance are considered to indicate that it is a good classifier. Accuracy is a very easy measure of performance for classifiers, but it has a huge disadvantage: it is only useful for datasets that give a value less than 1.5 when applying Equation (1).

Now, we will illustrate with a hypothetical example what might happen when using accuracy as a performance measure on a severely imbalanced dataset. To do this, consider again the study of the previous example, but now with D severely imbalanced (IR much greater than 1.5). When applying a stratified validation method, the testing set T also consists of 100 patients, with the difference that there are now 95 healthy and 5 sick.

To describe the hypothetical example, we are going to invent a very bad A2 classification algorithm. This A2 algorithm consists of assigning the “healthy” class to any testing pattern, whatever it may be. This classifier is very bad because the decision made is totally arbitrary, without even considering the values of the attributes in the patterns. When A2 is tested with the new T, the number of patterns classified “correctly” is 95, as in the previous example, and therefore the accuracy value is 95%, although we know that the A2 classifier is a fake one.

This example illustrates that using accuracy as a measure of classifier performance on an imbalanced dataset can privilege the majority class. What is surprising is that the behavior of the A2 classifier is replicated in many of the state-of-the-art classifiers. That is, many of the classifiers used by researchers in pattern recognition override the minority class in imbalanced datasets when accuracy is used as a performance measure. Typically, in pattern recognition, the jargon of the medical sciences is applied, and the minority class of a imbalanced dataset is called the “positive” class, while the majority class is the “negative” class.

The solution to the problem previously described is the use of the confusion matrix [22]. Without loss of generality, a schematic diagram of a confusion matrix for two classes (positive and negative) is included in Figure 6.

where:

• TP is the number of correct predictions that a pattern is positive.
• FN is the number of incorrect predictions that a positive pattern is negative.
• TN is the number of correct predictions that a pattern is negative.
• FP is the number of incorrect predictions that a negative pattern is positive.

If we note that the total of patterns correctly classified is TP + TN and that the total of patterns in the set T is TP + TN + FP + FN, Equation (3) is the way to express Equation (2) in terms of the elements of the confusion matrix:

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\cdot 100\%$$

(3)

A possible confusion matrix with which an accuracy value of 95% is obtained in the first example is shown in Figure 7. There we can see that of the 48 “sick” (positive class), 47 were correctly classified as “sick” (TP), and only one of the “sick” was incorrectly classified (FN) as healthy (negative class). Furthermore, of the 52 “healthy” (negative class), 48 were classified correctly as “healthy” (TN), and 4 of them were incorrectly (FP) classified as sick (positive class).

According to Equation (3), the 95% value for accuracy is obtained by dividing the sum of the correctly classified patterns (TP + TN = 47 + 48 = 95) by the total of the pattern in the set T (TP + TN + FP + FN = 47 + 48 + 4 + 1 = 100), and multiplying the result by 100.

For the hypothetical second example, the confusion matrix is illustrated in Figure 8. The A2 classification algorithm classifies all the patterns in T as if they were of the negative class (“healthy”). Indeed, the accuracy value appears to be good (95%), but in reality it is a useless result because the “classifier” A2 was not able to detect any pattern of the positive class (“sick”).

Of course, it is difficult to find in the specialized literature any classification algorithm as bad as the A2 algorithm. The possibility of any state-of-the-art classifier giving zero as a result in FP or FN is practically null. Most classifiers behave “well” against datasets with severe imbalances. The purpose of any state-of-the-art classifier is, then, to minimize the values of FP, FN, the sum of FP and FN, or some performance measures derived from the confusion matrix.

Here is precisely the alternative to the problems caused by using accuracy as a performance measure on imbalanced datasets. The alternative is to define new performance measures that are derived from the confusion matrix.

There are a very large number of different performance measures that are derived from the confusion matrix [23]. However, here we will only mention the definitions of three: sensitivity, specificity and balanced accuracy, because these three performance measures will be used in the experimental section of this document [22].

In the confusion matrix of Figure 6, it can be easily seen that the total of patterns of the positive class is obtained with this sum: TP + FN. Also, it is evident that the total of patterns of the negative class is obtained with this sum: TN + FP.

The fraction of the number of positive patterns correctly classified with respect to the total of positive patterns in T is called sensitivity:

$$Sensitivity=\frac{TP}{TP+FN}$$

(4)

As the value of TP approaches the total of correctly classified positive patterns, FN tends to zero, and the value of sensitivity tends to 1. The ideal case is when FN = 0, so sensitivity = 1.

The undesirable extreme case is when TP = 0 and this means that the classifier failed to detect any positive pattern, as in Figure 8. In this case, sensitivity = 0.

The fraction of the number of negative patterns correctly classified with respect to the total of positive patterns in T is called specificity:

$$Specificity=\frac{TN}{TN+FP}$$

(5)

As the value of TN approaches the total of correctly classified negative patterns, FP tends to zero, and the value of specificity tends to 1. The ideal case is when FP = 0, so specificity = 1.

The undesirable extreme case is when TN = 0 and this means that the classifier failed to detect any negative pattern. In this case, specificity = 0.

It is not difficult to imagine that there is some parallelism between accuracy, sensitivity, and specificity, because these last two measures can be thought of as a local accuracy, by class. Sensitivity is a kind of accuracy for the positive class, while specificity is a kind of accuracy for the negative class. Therefore, it should not be strange that based on both measures, sensitivity and specificity, a performance measure is defined for imbalanced datasets, which takes both classes into account separately. This is balanced accuracy (BA), a measure that is defined as the average of sensitivity and specificity:

$$BA=Balanced\hspace{0.17em}Accuracy=\frac{Sensitivity+Specificity}{2}$$

(6)

From the values of the confusion matrix in Figure 7, we can calculate the performance measures of Equations (4)–(6). Sensitivity = 0.98, specificity = 0.92, and BA = 0.95, a value close to the ideal case. On the other hand, when performing the same calculations with the data from the confusion matrix in Figure 8, we obtain the following results: sensitivity = 0, specificity = 1, and finally BA = 0.5. Note how BA punishes the value 0 in the sensitivity that was obtained with the “classifier” A2.

So far we have talked about classification algorithms without specifying how these algorithms perform the classification of patterns in the context of pattern recognition. The time has come to comment on the theoretical foundations on which classifiers rest, and the different approaches to pattern classification derived from these scientific concepts.

The most important state-of-the-art approaches will be mentioned in this brief summary of pattern classification algorithms. For each approach, the philosophy of the approach will be described very concisely, in addition to the scientific ideas on which it rests. In addition, one of the algorithms representing that approach will be mentioned, which will be tested for comparison in the experimental section of this paper.

It must be emphasized that all the pattern classification algorithms against which our proposal will be compared in the experimental section of this paper are part of the state of the art [24]. Additionally, it is necessary to point out something important that shows the relevance and validity of the pattern classification algorithms used in this paper: each and every one of these algorithms is included in the WEKA platform. This is relevant because WEKA has become an indispensable auxiliary, at the world level, for researchers dedicated to pattern recognition [25].

In the state of the art, it is possible to find a great variety of conceptual bases that give theoretical support to the task of intelligent classification of patterns. One of the most important and well-known theoretical bases is the theory of probability and statistics, which gives rise to the probabilistic-statistical approach to pattern classification. The Bayes theorem is the cornerstone on which this approach to minimize classification errors rests, hence the classifiers are called Bayes classifiers [26]. It is an open research topic and researchers continue to search for new modalities that improve the algorithms of the Bayes classifiers. [27].

Metrics and their properties cannot be missing as the conceptual basis of one of the most important approaches of pattern recognition. In 1967, scientific research into pattern classification was greatly enriched when Cover and Hart created the NN (nearest neighbor) classifier [28]. The idea is so simple, that at first glance it seems futile to take it into account. Given a testing pattern, the NN rule is to assign it the class of the pattern that is closest in the attribute space, according to a specified metric (or a dissimilarity function). But the authors of the NN classifier demonstrated their theoretical support. Furthermore, the large number and quality of applications throughout these years show the effectiveness of the NN classifier and its great validity as a research topic [29]. The extension of the NN model led to the creation of k-NN, where the NN rule is generalized to the k nearest neighbors. In the k-NN model, the class is assigned to the test pattern by majority of the k closest learning set patterns [30]. Nowadays, k-NN classifiers are considered among the most important and useful approaches in pattern classification [31].

On the other hand, tree-based classifiers use the advanced theory of graphs and trees to try to keep the number of errors to a minimum when solving a classification problem [32]. In a decision tree, each of the internal nodes represents an attribute, and final nodes (leaves) constitute the classification result. All nodes are connected by branches representing simple if-then-else rules which are inferred from the data [33]. Decision trees are simple to understand because they can be depicted visually, data require little or no preparation at all, and it is able to handle both numerical and categorical data. The study of decision trees is a current topic of scientific research [34].

It is common for the logistic function to be present in the experimental section of many articles of pattern classification. In the specialized literature, the logistic regression classifier is mentioned, because the logistics function was originally designed to perform the regression task. However, as the name implies, the algorithm is a classifier [35]. This function is sigmoid (due to the shape of its graph) and its expression involves the exponential function whose base is the Euler’s constant or number e [36]. The argument to the input of the logistic function is a real number and to the output a real value is obtained in the open interval (0,1). Therefore, the logistic regression function is useful for classifying patterns on datasets of two classes [37].

Before the scientific revolution generated by the arrival of deep learning in 2012, the “enemy to be defeated” in comparative studies of pattern classifiers was a model known as support vector machines (SVM). This model originates from the famous statistical learning theory [38], and was unveiled in a famous article published a quarter of a century ago [39]. The optimization of analytical functions serves as a theoretical basis in the design and operation of SVM models, which attempts to find the maximum margin hyperplane to separate the classes in the attribute space. Although it is true that deep learning-based models obtain impressive results in patterns represented by digital images, it is also a fact that SVMs continue to occupy the first places in performance in classification problems where patterns are not digital images [40].

The “scientific revolution generated by the arrival of Deep Learning in 2012” mentioned in the previous paragraph began many years ago, in 1943, when McCulloch and Pitts presented the first mathematical model of human neuron to the world [41]. With this model began the study of the neuronal classifiers, which acquired great force in 1985–1986. In those years, several versions of an algorithm that allows training successfully neural networks were published [42,43]. This algorithm is called backpropagation, and two of the most important pioneers of the “Deep Learning era” participated in its creation: LeCun and Hinton [44]. Among the most relevant neural models with applications in many areas of human activity, the multi-layer perceptron (MLP) is one of those rated as excellent by the scientific community [45]. Therefore we have included it in the comparative study presented in the experimental section of this paper.

The last classifier that we have selected to be included in the experimental section of this paper does not belong to a different approach from those previously described. Rather, it is a set of classifiers from some of the approaches mentioned, which are grouped into an ensemble, where the classifiers operate in a collaborative environment [46]. Ensemble classifiers are methods which aggregate the predictions of a number of diverse base classifiers in order to produce a more accurate predictor, with the idea being that “many heads think better than one”. The ability to combine the outputs of multiple classifiers to improve upon the individual accuracy of each one has prompted much research and innovative ensemble construction proposals, such as bagging [47] and boosting [48]. Ensemble models have positioned themselves as valuable tools in pattern classification, routinely achieving excellent results on complex tasks. In this paper, we selected a boosting ensemble, the AdaBoost algorithm [49], using C4.5 as base classifier.

2.2. Lernmatix: The Original Model

The Lernmatrix is an associative memory [13]. Therefore, since an associative memory performs the task of pattern recall in pattern recognition, in principle the Lernmatrix receives patterns at the input and delivers patterns at the output. However, if the output patterns are chosen properly, the Lernmatrix can act as a pattern classifier. The Lernmatrix is an input-output system that accepts a binary pattern at the input. If there is no saturation, the Lernmatrix generates a one-hot pattern at the output. The saturation phenomenon will be amply illustrated in this subsection. A schematic diagram of the original Lernmatrix model is shown in Figure 9.

If M is a Lernmatrix and $x^1$ is an input pattern, an example of a 5-dimensional input pattern is:

$$x^1=\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right)$$

(7)

In Expression (7) the superscript 1 indicates that this is the first input pattern. In general, if μ is a positive integer, the notation $x^{\mu }$ indicates the μ-th input pattern. The j-th component of a pattern $x^{\mu }$ is denoted as:$x_j^{\mu }$.

The key to a Lernmatrix acting as a pattern classifier is found in the representation of the output patterns as one-hot vectors. It is assumed that in a pattern classification problem, there are p different classes, where p is a positive integer greater than 1. For the particular case in which p = 3, class 1 is represented by this one-hot vector:

$$y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)$$

(8)

while the representations of classes 2 and 3 are:

$$y^2=\left(\begin{array}{l}0\\ 1\\ 0\end{array}\right)\hspace{1em}\mathrm{and}\hspace{1em}{y}^3=\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

(9)

In general, to represent the class $k\in \left\{1,2,\dots ,p\right\}$, $1\le k\le p$, the following values are assigned to the output binary pattern: $y_k^k=1$, and for $j=1,2,\dots ,k-1,k+1,\dots ,p$, this value is assigned $y_j^k=0$.

The expressions for the learning and recalling phases were adapted from two articles published by Steinbuch: the 1961 article where he released his original model [13], and an article he published in 1965, co-authored with Widrow [50], who is the creator of one of the first neuronal models called ADALINE.

Learning phase for the Lernmatrix.

To start the learning phase of a Lernmatrix of p classes and with n-dimensional input binary patterns, a $M_{p\times n}$ is created, with $m_{ij}=0$, $\forall i,j$.

$$M=\left(\begin{array}{ccc}{m}_{11}& \dots & m_{1n}\\ ⋮& \ddots & ⋮\\ m_{p1}& \cdots & m_{pn}\end{array}\right)$$

(10)

For each input pattern $x^{\mu }$ and its corresponding output pattern $y^{\mu }$, each component $m_{ij}$ is updated according to the following rule: $m_{ij}=m_{ij}+\Delta m_{ij}$, with $\epsilon >0$.

$$\Delta m_{ij}=\{\begin{array}{c}+\epsilon \\ -\epsilon \\ 0\end{array}\begin{array}{c}\mathrm{if}{y}_i^{\mu }=1=x_j^{\mu }\\ \mathrm{if}{y}_i^{\mu }=1\mathrm{and}{x}_j^{\mu }=0\\ \mathrm{otherwise}\end{array}$$

(11)

Remark 1. 

The only restriction for the value of$\epsilon$is that it be positive. Therefore, it is valid to choose the value of$\epsilon$as 1. In all the examples in this paper, we will use the value$\epsilon =1$.

Example 1.

Execute the learning phase of a Lernmatrix that has 3 classes, and 5-dimensional input patterns (one input pattern for each class):

$$x^1=\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right),y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right),x^2=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right),y^2=\left(\begin{array}{l}0\\ 1\\ 0\end{array}\right),x^3=\left(\begin{array}{l}1\\ 0\\ 1\\ 1\\ 0\end{array}\right),y^3=\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

(12)

Initially, a$3\times 5$matrix is created with all its inputs set to zero. Then, the transpose of the first input pattern is placed on top, and the first class pattern to the left of the matrix. Then, the learning rule of Equation (11) is applied to each of the components of both patterns:

	$x_1^1=1$	$x_2^1=0$	$x_3^1=1$	$x_4^1=0$	$x_5^1=1$
$y_1^1=1$	0+1	0−1	0+1	0−1	0+1
$y_2^1=0$	0+0	0+0	0+0	0+0	0+0
$y_3^1=0$	0+0	0+0	0+0	0+0	0+0

The Lernmatrix looks like this after learning the pattern association$(x^1,y^1)$:

	$x_1^1=1$	$x_2^1=0$	$x_3^1=1$	$x_4^1=0$	$x_5^1=1$
$y_1^1=1$	1	−1	1	−1	1
$y_2^1=0$	0	0	0	0	0
$y_3^1=0$	0	0	0	0	0

Now, the learning rule of Equation (11) is applied to each of the components of both patterns of the second association$(x^2,y^2)$:

	$x_1^2=1$	$x_2^2=1$	$x_3^2=0$	$x_4^2=0$	$x_5^2=1$
$y_1^2=0$	1	−1	1	−1	1
$y_2^2=1$	1	1	−1	−1	1
$y_3^2=0$	0	0	0	0	0

When applying the learning rule of Equation (11) to each of the components of both patterns of the third association$(x^3,y^3)$, the matrix becomes:

	$x_1^3=1$	$x_2^3=0$	$x_3^3=1$	$x_4^3=1$	$x_5^3=0$
$y_1^3=0$	1	−1	1	−1	1
$y_2^3=0$	1	1	−1	−1	1
$y_3^3=1$	1	−1	1	1	−1

Since the rule of Equation (11) has already been applied to all pattern associations, the learning phase has concluded, and finally the Lernmatrix is:

$$M=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)$$

(13)

Recalling phase for the Lernmatrix.

If $x^{\omega }$ is a n-dimensional input pattern whose class is unknown, the recalling phase consists of operating the Lernmatrix with that input pattern, trying to find the corresponding p-dimensional one-hot vector $y^{\omega }$ (i.e., the class). The i-th coordinate $y_i^{\omega }$ is obtained according to the next expression, where ∨ is the maximum operator:

$$y_i^{\omega }=\{\begin{array}{c}1\mathrm{if}{\displaystyle {\sum }_{j=1}^n{m}_{ij}{x}_j^{\omega }={\vee }_{h=1}^p\left[{\displaystyle {\sum }_{j=1}^n{m}_{hj}{x}_j^{\omega }}\right]}\\ 0\mathrm{otherwise}\end{array}$$

(14)

Example 2.

Now we are going to apply Equation (14) to each of the input patterns of Expression 12, with the Lernmatrix of Expression 13.

$$M{x}^1=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}3\\ 1\\ 1\end{array}\right)$$

For i = 1 we have:${\displaystyle {\sum }_{j=1}^5{m}_{1j}{x}_j^1=3}$; for i = 2: ${\displaystyle {\sum }_{j=1}^5{m}_{2j}{x}_j^1=1}$; and for i = 3: ${\displaystyle {\sum }_{j=1}^5{m}_{3j}{x}_j^1=1}$. According to Equation (14), the value 1 will be assigned to the coordinate that gives the greatest sum, and 0 to all the others.

$$y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)$$

This means that input pattern$x^1$will be assigned the class vector$y^1$, which is correct according to Expression 12. When doing the same with input vectors$x^2$and$x^3$, we have:

$$M{x}^2=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}1\\ 3\\ -1\end{array}\right)\to \left(\begin{array}{l}0\\ 1\\ 0\end{array}\right)=y^2$$

$$M{x}^3=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}1\\ 0\\ 1\\ 1\\ 0\end{array}\right)=\left(\begin{array}{l}1\\ -1\\ 3\end{array}\right)\to \left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)=y^3$$

Example 3.

In Example 2, all input patterns were correctly assigned the class in the recalling phase. That is true, but an interesting question arises: what will happen to the recalling phase if there are more input patterns than classes? To find out the answer, we are going to add a new input pattern to class 1 of the Lernmatrix of Expression 13:

$$x^4=\left(\begin{array}{l}0\\ 1\\ 0\\ 1\\ 1\end{array}\right),y^4=y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)$$

(15)

When applying the learning rule of Equation (11) to each of the components of both patterns of the association$(x^4,y^4)$, the matrix becomes:

	$x_1^4=0$	$x_2^4=1$	$x_3^4=0$	$x_4^4=1$	$x_5^4=1$
$y_1^4=1$	1−1	−1+1	1−1	−1+1	1+1
$y_2^4=0$	1	1	−1	−1	1
$y_3^4=0$	1	−1	1	1	−1

$$M_{4\hspace{0.17em}inputs}=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)$$

(16)

It can be easily verified that if we apply Equation (14) to each of the input patterns of Expression 12 with the Lernmatrix of Expression 16, all three classes are correctly assigned by the Lernmatrix. What will happen to input pattern$x^4$?

$$M_{4\hspace{0.17em}inputs}{x}^4=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}0\\ 1\\ 0\\ 1\\ 1\end{array}\right)=\left(\begin{array}{l}2\\ 1\\ -1\end{array}\right)\to \left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)=y^1$$

Again, all input patterns were correctly assigned the class in the recalling phase. Another interesting question arises: will the Lernmatrix correctly assign classes to all patterns every time a new input pattern is added? The answer is no. Example 4 will illustrate a disadvantage exhibited by the Lernmatrix: a phenomenon called saturation.

Example 4.

We are going to add a new input pattern to class 3 of the Lernmatrix of Expression 16:

$$x^5=\left(\begin{array}{l}0\\ 0\\ 1\\ 0\\ 1\end{array}\right),y^5=y^3=\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

When applying the learning rule of Equation (11) to each of the components of both patterns of the association$(x^5,y^5)$, the matrix becomes:

	$x_1^5=0$	$x_2^5=0$	$x_3^5=1$	$x_4^5=0$	$x_5^5=1$
$y_1^5=0$	0	0	0	0	2
$y_2^5=0$	1	1	−1	−1	1
$y_3^5=1$	1−1	−1−1	1+1	1−1	−1+1

$$M_{5\hspace{0.17em}inputs}=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)$$

(17)

It can be easily verified that if we apply Equation (14) to each of the input patterns$x^2$,$x^3$, and$x^4$with the Lernmatrix of Expression 17, all three classes are correctly assigned by the Lernmatrix. Now we are going to verify what happens with input pattern$x^1$.

$$M_{5\hspace{0.17em}inputs}{x}^1=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}2\\ 1\\ 2\end{array}\right)\to \left(\begin{array}{l}1\\ 0\\ 1\end{array}\right)$$

Here is the Lernmatrix saturation phenomenon, because the output pattern is not one-hot, so there is ambiguity: what class should we assign to input pattern$x^1$?, Should we assign$x^1$class 1 or class 3?

The reader could easily verify that something similar occurs with input pattern$x^5$, where the saturation phenomenon also occurs and consequently there is ambiguity.

It is worth noting something that happened in the previous 4 examples. The Lernmatrix learned with 5 input patterns, and each of those same input patters was used as a testing pattern. This is contrary to the concepts illustrated in Figure 1, regarding the partition to be made to dataset D in two sets, one set L for learning and the other set T for testing. However, in the four previous examples, the following occurs: D = L = T. This strange procedure exists and has a technical name: it is called resubstitution error [51]. It is not an authentic method of validation, and is only used when we want to know the trend of a new classifier.

In the 4 examples mentioned, we have used 5 patterns out of the 32 available, since with 5 bits it is possible to form $2^5=32$different binary patterns. We will take advantage of the results of the 4 previous examples in order to exemplify the behavior of the Lernmatrix when there is a dataset D which is partitioned into L and T, as illustrated in Figure 1. It must be taken into account that due to its nature as associative memory, in the case of the Lernmatrix, the dataset D is made up of associations of two patterns, an input pattern and an output pattern, which represents the class. The same goes for L and T.

Example 5.

Specifically, we will assume that dataset D contains 8 associations, of which the first 5 of the previous 4 examples form learning set L and there are 3 more that form testing set T. That is, the learning set$L=\left\{(x^1,y^1),(x^2,y^2),(x^3,y^3),(x^4,y^1),(x^5,y^3)\right\}$and the testing set is$T=\left\{(x^6,y^1),(x^7,y^2),(x^8,y^3)\right\}$, where:

$$x^6=\left(\begin{array}{l}0\\ 0\\ 0\\ 1\\ 1\end{array}\right),y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right),x^7=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 0\end{array}\right),y^2=\left(\begin{array}{l}0\\ 1\\ 0\end{array}\right),x^8=\left(\begin{array}{l}0\\ 1\\ 0\\ 0\\ 1\end{array}\right),y^3=\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

After the learning phase where Expressions 10 and 11 were applied to the 5 patterns in set L, the Lernmatix is precisely the matrix of Expression 17:

$$M_{5\hspace{0.17em}inputs}=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)$$

During the recalling phase, the operations of Expression 14 are performed with the Lernmatrix$M_{5\hspace{0.17em}inputs}$and each of one of the testing patterns$x^6$,$x^7$, and$x^8$.

$$M_{5\hspace{0.17em}inputs}{x}^6=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)\left(\begin{array}{l}0\\ 0\\ 0\\ 1\\ 1\end{array}\right)=\left(\begin{array}{l}2\\ 0\\ 0\end{array}\right)\to \left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)=y^1$$

$$M_{5\hspace{0.17em}inputs}{x}^7=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{l}0\\ 2\\ -2\end{array}\right)\to \left(\begin{array}{l}0\\ 1\\ 0\end{array}\right)=y^2$$

$$M_{5\hspace{0.17em}inputs}{x}^8=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 0& -2& 2& 0& 0\end{array}\right)\left(\begin{array}{l}0\\ 1\\ 0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}2\\ 2\\ -2\end{array}\right)\to \left(\begin{array}{l}1\\ 1\\ 0\end{array}\right)\ne y^3$$

Two of the three patterns of the testing set T were correctly classified, and the saturation appears in the testing pattern $x^8$. If we use Expression 2 to calculate accuracy, we have:

$$Accuracy=\frac{2}{3}\cdot 100=66.66\%$$

Now that we have illustrated both phases of the Lernmatrix with very simple examples, it is worth investigating how good the Lernmatrix is as a pattern classifier in real datasets. Also, and since most real-life datasets do not contain only binary data, we must be clear about what we must do to apply the Lernmatrix on those datasets.

To illustrate how good the Lernamtrix is as a pattern classifier in real datasets, we will take the first dataset that we have included in the experimental section of this paper as an example. This is the ecoli-0_vs_1 dataset, which contains 220 patterns of 7 numerical attributes, and which can be downloaded from the website: http://www.keel.es/. The objective of this problem is to predict the localization site of proteins by employing two measures about the cell: cytoplasm (class 0) and inner membrane (class 1).

To apply the Lernmatrix, we must binarize the patterns. Since each pattern has 7 numerical attributes and each attribute requires 8 bits to represent it, then each pattern in the dataset consists of 56 binary attributes. As previously discussed, we decided to use the stratified 5-fold cross-validation method, and balance accuracy as a performance measure.

After each of the 5 learning phases, a 56 × 2 Lermatrix resulted.

Table 1. Balanced accuracy of the Lernmatrix and 7 classifiers of the state of the art (ecoli-0_vs_1 dataset).

Dataset	Seven State-of-the-Art Pattern Classification Algorithms							Lernmatrix
ecoli-0_vs_1	0.97	0.94	0.97	0.98	0.97	0.97	0.97	0.81

includes the performance of the Lernamtrix and also presents the performance values of 7 state-of-the-art classifiers (the complete table is included in Section 5).

As can be seen, the Lernmatrix as a dataset classifier, is very far from the performance values given by the most important state of the art classifiers. However, the main contribution of this paper is the proposal of a novel and simple mathematical transform, which will make it possible to significantly increase the performance of the Lernmatrix, to the point of making this ancient and beautiful model a competitive classifier against the most relevant classifiers in the state of the art.

In the next subsection, we will explain the reasons why the authors of this paper have decided to try to rescue the Lernmatrix, despite the modest performance results in Table 1.

2.3. Milestones in the Rescue of the Lernmatix

The Lernmatrix constitutes a crucial antecedent in the development of the contemporary models of associative memories [13], and was one on the first successful attempts to codify information in grid arrangements known as crossbars [52].

Due to unclear reasons, the Lernmatrix was almost forgotten for more than four decades, with two honorable exceptions. First, the German academics Prinz and Hower proposed, in 1976, to use the Lernmatrix within a mathematical approach to the assessment of air pollution effects, with promising results [53]. However, it is pertinent to note that their work was harshly criticized [54], causing them to leave the topic, with a shy and fleeting return nine years later [55]. Thereafter, they no longer published anything related to the Lernmatrix.

The other notable exception involves the academic Robert Hecht-Nielsen, professor at the University of California, who investigates the subject of computational neurobiology. After thirty years of work, Hecht-Nielsen published his theory of cerebral cortex, at the ICONIP congress of 1998 [56]; there, he presented his cortronic neural network models of cortical function [57]. Based on the results of these two research papers, that same year Defense Advanced Research Projects Agency (DARPA) supported him with several million dollars for the development of cortronic neural networks. According to what Hecht-Nielsen declared at the press conference organized by DARPA, cortronic architectures consist of linked classical associative memory structures, and their theoretical foundation is found in the concepts of the original Lernmatrix model. He said: “Although Steinbuch’s ideas have never been fashionable, I’m pretty sure they’re not wrong” [58].

A year later, through his HNC company, Hecht-Nielsen obtained the 1999 United States Patent 6366897, whose title is: “Cortronic neural networks with distributed processing.” From there, the scientific community has made contributions to the theory and applications of the cortronic neural networks, and the topic is still developing [59].

In the Alpha-Beta research group (to which the authors of this article belong), Lernmatrix was known in 2000. The results found by Hecht-Nielsen serve as inspiration to work with the associative model called Lernmatrix. In addition, interest in the model grew by discovering a surprising fact: none of the researchers involved with the Lernmatrix, or even its author, attempted to develop the theoretical foundations of the model.

The year 2001 marked the beginning of the work of the Alpha-Beta group with the Lernmatrix. By merging this model with another well-known associative model, the linear associator, a new pattern classification algorithm was created: the CHAT (Clasificador Híbrido con Traslación, in Spanish) [60]. This algorithm is still in development and is currently the subject of publications in impact journals [61,62,63,64,65,66,67].

The simplicity, effectiveness and efficiency of the Lernmatrix prompted the members of the Alpha-Beta group to undertake the task of investigate about its theoretical foundations. The first results of these investigations (in Spanish) [68], and their advances [69], were published in a local journal in 2002 and 2004, respectively.

In 2005, two relevant publications on the theoretical framework for the Lernmatrix were generated [70,71]. Two years after this, a further step was taken, with a modification to the algorithm that caused a notable increase in the performance [72].

For several years, efforts to find interesting advances were unsuccessful. Until recently, after arduous work sessions, we found an idea that crystallized with the main contribution of the present paper. Based on previous results obtained by Alpha-Beta group, a new transform is proposed that allows us to increase the performance of the Lernmatrix.

2.4. Lernmatix: Theoretical Advances

One of the first research actions that the Alpha-Beta group undertook when the researchers decided to work with the Lernmatrix was to create a new framework. This new framework rests on two initial definitions.

These two initial definitions served as decisive support to facilitate the statement and demonstration of the lemmas and theorems that make up the theoretical foundation of the Lernmatrix [71].

Definition 1.

A Steinbuch function is any function$f:\mathrm{ℝ}\to \mathrm{ℝ}$with the property:

$$f(0)=-1\hspace{1em}\mathrm{and}\hspace{1em}f(1)=1$$

(18)

Example 6.

The function$f(x)=2x-1$is a Steinbuch function, because$f(0)=2(0)-1=-1$and$f(1)=2(1)-1=1$, according to Definition 1.

Definition 2.

Let$f:\mathrm{ℝ}\to \mathrm{ℝ}$be a Steinbuch function. A Steinbuch vectorial function for$f$is any function$F:{\mathrm{ℝ}}^n\to {\mathrm{ℝ}}^n$with the following property:

$$F(x)=\left(\begin{array}{c}f(x_1)\\ f(x_2)\\ \dots \\ f(x_n)\end{array}\right)$$

(19)

In this paper, we have described the Lernmatrix as a pattern classifier, where its recalling phase is actually a classification phase in the supervised pattern classification paradigm. For this reason, we take into account what is exposed in Figure 1.

When designing a Lernmatrix, we assume that there is a dataset D, from which a partition is made in two subsets: L (learning or training) and T (testing). The Lernmatrix learns with L and the patterns in T are used for testing. In the case of the Lernmatrix, the set L is made up of associations of two patterns, an input pattern and an output pattern, which represents the class.

If we denote by m the number of associations that the learning set L contains, we can represent it with the following expression:

$$L=\left\{(x^{\mu },y^{\mu })|\mu =1,2,\dots ,m\right\}$$

(20)

Learning phase for the Lernmatrix in the new framework.

Let $L$ be a learning set, let f be a Steinbuch function, and let $F$ be an Steinbuch vectorial function for $f$. The Lernmatrix M is built according to the next rule:

$$M=\epsilon {\displaystyle \sum _{\mu =1}^m{y}^{\mu }{(F(x^{\mu }))}^T}$$

(21)

As previously discussed, the only restriction for the value of $\epsilon$ is that it be positive. In the spirit of simplifying expressions, henceforth we will assume that $\epsilon =1.$

$$M={\displaystyle \sum _{\mu =1}^m{y}^{\mu }{(F(x^{\mu }))}^T}$$

(22)

It can easily be verified that Expression 22 is equivalent to Expressions 10 and 11, which define the learning phase of the original Lernmatrix model. To illustrate this equivalence we will replicate the Example 1 (Expression 12) in the new framework.

Example 7.

Making$\mu =1$in Expression 21, the first association in Example 1 generates this:

$$\begin{array}{l}F(x^1)=\left(\begin{array}{l}1\\ -1\\ 1\\ -1\\ 1\end{array}\right),\hspace{1em}{\left(F(x^1)\right)}^T=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\end{array}\right),\hspace{1em}\mathrm{and}\\ y^1{\left(F(x^1)\right)}^T=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)\left(\begin{array}{ccccc}1& -1& 1& -1& 1\end{array}\right)=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\end{array}$$

Performing similar operations for the other two associations in Example 1, and applying Expression 22:

$$\begin{array}{l}M={\displaystyle \sum _{\mu =1}^3{y}^{\mu }{(F(x^{\mu }))}^T}=y^1{\left(F(x^1)\right)}^T+y^2{\left(F(x^2)\right)}^T+y^3{\left(F(x^3)\right)}^T\\ =\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)+\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 1& 1& -1& -1& 1\\ 0& 0& 0& 0& 0\end{array}\right)+\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 1& -1& 1& 1& -1\end{array}\right)\\ =\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\end{array}$$

Note that this result coincides with Expression 13. We are going to perform the same operations for the fourth association $(x^4,y^4)$, to obtain the Lernmatrix$M_{4\hspace{0.17em}inputs}$(Expressions 15 and 16).

$$M_{4\hspace{0.17em}inputs}=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)+\left(\begin{array}{ccccc}-1& 1& -1& 1& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)=\left(\begin{array}{ccccc}0& 0& 0& 0& 2\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)$$

The reader can easily verify that the result for the Lernmatrix$M_{5\hspace{0.17em}inputs}$coincides with Expression 17.

Recalling phase for the Lernmatrix in the new framework.

Let M be a Lernmatrix built using Expression 22, and let $(x^{\omega },y^{\omega })$ be an association of patterns with attributes and dimensions as in Expression 20. The output pattern ${\tilde{y}}^{\omega }$ is obtained by operating the Lermatrix M and pattern $x^{\omega }$, according to the operations specified by Equation (23):

$$\begin{array}{l}{z}^{\omega }=M{x}^{\omega }\\ {\tilde{y}}_i^{\omega }=\{\begin{array}{l}1\hspace{1em}\mathrm{if}{z}_i^{\omega }={\vee }_{h=1}^m{z}_h^{\omega }\\ 0\hspace{1em}\mathrm{otherwise}\end{array}\end{array}$$

(23)

If there is saturation, the output pattern ${\tilde{y}}^{\omega }$ is not necessarily equal to $y^{\omega }$.

Definition 3.

If${\tilde{y}}^{\omega }=y^{\omega }$, then the recalling is correct.

Example 8.

It can easily be verified that Expression 23 is equivalent to Expression 14, both defining the recalling phase of the original Lernmatrix model. To illustrate this equivalence, we will replicate the first case of Example 2 in the new framework.

$$z^1=M{x}^1=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}3\\ 1\\ 1\end{array}\right)$$

$${\tilde{y}}^{\omega }=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)=y^{\omega }$$

Something similar occurs with the remaining cases in Example 2, and with all the cases in Examples 3, 4 and 5.

According to [68], the original model of the Lernmatrix suffers from a big problem: saturation, which has been one of the enemies to beat by the Alpha-Beta group since 2001. Saturation, as illustrated in Example 4, is considered as the overtraining of a memory, to the extent that it is not possible to remember or recall, correctly, the patterns learned. In other words, the class obtained is not one of those established in the learning set L.

This fact, visualized in the recalling phase, generates another problem known as ambiguity. This problem is the inability to determine the class associated with a certain input pattern, because the Lernmatrix output pattern is not a one-hot pattern. Ambiguity can be caused by two reasons that have been clearly identified by the Alpha-Beta group: (1) due to memory saturation or (2) due to the structure inherent to the patterns belonging to dataset D.

Ambiguity is another of the enemies to be defeated by the Alpha-Beta group since 2001. Over almost two decades of research, we have proposed several partial solutions to these two problems. Before presenting some of these partial solutions that the Alpha-Beta group has published, it is necessary to previously define the alteration between patterns, and the corresponding notation.

Definition 4.

Two n-dimensional binary patterns$x^{\alpha },x^{\beta }$are equal (denoted by$x^{\alpha }=x^{\beta }$) if and only if:

$$x_j^{\alpha }=x_j^{\beta },\forall j\in \left\{1,\dots ,n\right\}$$

(24)

Example 9.

In Example 8, the two 3-dimensional binary patterns${\tilde{y}}^{\omega }$and$y^{\omega }$are equal, because they satisfy the condition of Definition 4. However, patterns$x^6$and$x^7$in Example 5 are not equal because for j = 1, it happens that$x_j^6\ne x_j^7$.

Definition 5.

Let$x^{\alpha },x^{\beta }$be two n-dimensional binary patterns. The pattern$x^{\alpha }$in less than or equal to pattern$x^{\beta }$(denoted by$x^{\alpha }\le x^{\beta }$) if and only if:

$$\left(x_j^{\alpha }=1\right)\to \left(x_j^{\beta }=1\right),\forall j\in \left\{1,\dots ,n\right\}$$

(25)

Example 10.

The pattern$x^7$of Example 5 is less than or equal to pattern$x^2$of Example 1 ($x^7\le x^2$), because every time it happens that$x_j^7$(in indices j = 1 and j = 2), it is also true that$x_j^2$, according to Definition 5.

$$x^7=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 0\end{array}\right)\le x^2=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right)$$

Example 11.

When considering the pattern$x^7$of Example 5 and the pattern$x^3$of Example 1, the expression$x^7\le x^3$is false according to Definition 5. The reason is that$x_2^7=1$but$x_2^3=0$, which contradicts Definition 5, because the expression$(x_2^7=1)\to (x_2^3=1)$ is false.

$$\mathrm{If}\hspace{0.17em}{x}^7=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 0\end{array}\right)\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}{x}^3=\left(\begin{array}{l}1\\ 0\\ 1\\ 1\\ 0\end{array}\right),\hspace{0.17em}\mathrm{this}\hspace{0.17em}\mathrm{expression}\hspace{0.17em}\mathrm{is}\hspace{0.17em}\mathrm{false}:x^7\le x^3\hspace{1em}$$

Definition 6.

Let$x^{\alpha },x^{\beta }$be two n-dimensional binary patterns such that$x^{\alpha }\le x^{\beta }$from the Definition 5. If$\exists j\in \left\{1,\dots ,n\right\}$such that$x_j^{\alpha }<x_j^{\beta }$, then the pattern$x^{\alpha }$exhibits subtractive alteration with respect to the pattern$x^{\beta }$. This is denoted by$x^{\alpha }<x^{\beta }$.

Example 12.

From Example 10,$x^7\le x^2$. Also, the pattern$x^7$exhibits subtractive alteration with respect to the pattern$x^2$because$x_5^7<x_5^2$according to Definition 6. Thus, this expression is true:$x^7<x^2$.

Below is a brief anthology of the most important advances obtained by the Alpha-Beta group, in relation to the theoretical foundations of the Lernmatrix. These results serve as a solid basis for the proposal of the mathematical transform, which represents the main contribution of this paper. In turn, this novel and simple mathematical transform is the cornerstone of the methodology that gives rise to the new Lernmatrix, a model that is now competitive against the most important classifiers of the state of the art. All these results can be consulted in these papers: [68,69,70,71,73].

Definition 7.

Let$x^{\alpha }$be a n-dimensional binary pattern. The characteristic set of$x^{\alpha }$is defined by$H^{\alpha }=\left\{j|x_j^{\alpha }=1\right\}$. The cardinality of the characteristic set$\left|H^{\alpha }\right|$is the number of ones in the pattern$x^{\alpha }$.

Example 13.

From Examples 1 and 5, it is possible to verify the following expressions:$H^1=\left\{1,3,5\right\}$and$\left|H^1\right|=3$;$H^2=\left\{1,2,5\right\}$and$\left|H^2\right|=3$;$H^3=\left\{1,3,4\right\}$and$\left|H^3\right|=3$;$H^6=\left\{4,5\right\}$and$\left|H^6\right|=2$;$H^7=\left\{1,2\right\}$and$\left|H^7\right|=2$;$H^8=\left\{2,5\right\}$and$\left|H^8\right|=2$.

Lemma 1.

Let$x^{\alpha },x^{\beta }$be two n-dimensional binary patterns. Then$x^{\alpha }<x^{\beta }$if and only if$H^{\alpha }\subset H^{\beta }$.

Proof. 

By Definition 6,$x^{\alpha }<x^{\beta }$if and only$x^{\alpha }\le x^{\beta }$and$\exists j\in \left\{1,\dots ,n\right\}$such that$x_j^{\alpha }<x_j^{\beta }$; if and only if (Definition 5)$\left(x_j^{\alpha }=1\right)\to \left(x_j^{\beta }=1\right),\forall j\in \left\{1,\dots ,n\right\}$and$H^{\alpha }\ne H^{\beta }$; if and only if (Definition 7)$\left(j\in H^{\alpha }\right)\to \left(j\in H^{\beta }\right),\forall j\in \left\{1,\dots ,n\right\}$and$H^{\alpha }\ne H^{\beta }$; if and only if$H^{\alpha }\subseteq H^{\beta }$and$H^{\alpha }\ne H^{\beta }$; if and only if$H^{\alpha }\subset H^{\beta }$. □

Remark 2. 

Hereinafter, the symbol □ will indicate the end of a proof.

The importance of Lemma 1 lies in showing that an order relationship between patterns implies an order relationship between their characteristic sets and vice versa.

Example 14.

From Example 10$x^7\le x^2$, and from Example 13, we have$\left|H^7\right|\subseteq \left|H^2\right|$.

Lemma 2.

Let M be a Lernmatrix which was built from the learning set$L=\left\{(x^{\mu },y^{\mu })|\mu =1,2,\dots ,m\right\}$by applying Expression 22, fulfilling$y^{\alpha }=y^{\beta }$if and only if$\alpha =\beta$. Let $x^{\omega }$be a n-dimensional binary pattern and$z^{\omega }=M{x}^{\omega }$. Then the k-th component of$z^{\omega }$is obtained by the following expression:$z_k^{\omega }=2|H^k\cap H^{\omega }|-\left|H^{\omega }\right|$.

Proof. 

By Expression 22,$M={\displaystyle \sum _{\mu =1}^m{y}^{\mu }{(F(x^{\mu }))}^T}=y^1{(F(x^1))}^T+\dots +y^k{(F(x^k))}^T+\dots +y^m{(F(x^m))}^T.$Since the patterns$y^{\mu }$are one-hot, the Lernmatrix M can be written as follows:

$$\begin{array}{l}M=\left(\begin{array}{l}1\\ ⋮\\ 0\\ ⋮\\ 0\end{array}\right)(f(x_1^1)\cdots f(x_j^1)\cdots f(x_n^1))\hspace{0.17em}+\dots +\left(\begin{array}{l}0\\ ⋮\\ 1\\ ⋮\\ 0\end{array}\right)(f(x_1^k)\cdots f(x_j^k)\cdots f(x_n^k))+\dots \\ \dots +\left(\begin{array}{l}0\\ ⋮\\ 0\\ ⋮\\ 1\end{array}\right)(f(x_1^m)\cdots f(x_j^m)\cdots f(x_n^m))\end{array}$$

(26)

By performing the summation:

$$M=\left(\begin{array}{l}f(x_1^1)\cdots f(x_j^1)\cdots f(x_n^1)\\ ⋮\\ f(x_1^k)\cdots f(x_j^k)\cdots f(x_n^k)\\ ⋮\\ f(x_1^m)\cdots f(x_j^m)\cdots f(x_n^m)\end{array}\right)$$

(27)

By multiplying by $x^{\omega }$:

$$z^{\omega }=M{x}^{\omega }=\left(\begin{array}{l}f(x_1^1)\cdots f(x_j^1)\cdots f(x_n^1)\\ ⋮\\ f(x_1^k)\cdots f(x_j^k)\cdots f(x_n^k)\\ ⋮\\ f(x_1^m)\cdots f(x_j^m)\cdots f(x_n^m)\end{array}\right)x^{\omega }=\left(\begin{array}{l}f(x_1^1)\cdots f(x_j^1)\cdots f(x_n^1)\\ ⋮\\ f(x_1^k)\cdots f(x_j^k)\cdots f(x_n^k)\\ ⋮\\ f(x_1^m)\cdots f(x_j^m)\cdots f(x_n^m)\end{array}\right)\left(\begin{array}{l}{x}_1^{\omega }\\ ⋮\\ x_k^{\omega }\\ ⋮\\ x_n^{\omega }\end{array}\right)=\left(\begin{array}{l}{\displaystyle \sum _{j=1}^{n}f(x_j^1)x_j^{\omega }}\\ ⋮\\ {\displaystyle \sum _{j=1}^{n}f(x_j^k)x_j^{\omega }}\\ ⋮\\ {\displaystyle \sum _{j=1}^{n}f(x_j^m)x_j^{\omega }}\end{array}\right)$$

(28)

Hence, the k-th component is:

$$z_k^{\omega }={\displaystyle \sum _{j=1}^{n}f(x_j^k)x_j^{\omega }}$$

(29)

Only the components of $x^{\omega }$ that are equal to 1 contribute to the sum, and by Definition 7 we have:

$$z_k^{\omega }={\displaystyle \sum _{j\in H^{\omega }}f(x_j^k)}$$

(30)

This summation has exactly$\left|H^{\omega }\right|$terms, which may be 1 or −1 according to Definition 1.

If we know the number of terms with value 1 and the number of terms with value −1, the result of the summation 30 is calculated using elementary algebra. If we denote by$ones$the number of terms with value 1, and by$m\_ones$the number of terms with value −1, the result of the summation 30 is:

$$z_k^{\omega }={\displaystyle \sum _{j\in H^{\omega }}f(x_j^k)}=ones+(-1)m\_ones$$

(31)

Since the summation has exactly$\left|H^{\omega }\right|$terms, the number of terms with value −1 is:

$$m\_ones=\left|H^{\omega }\right|-ones$$

(32)

So Expression 31 becomes:

$$z_k^{\omega }={\displaystyle \sum _{j\in H^{\omega }}f(x_j^k)}=ones+(-1)(\left|H^{\omega }\right|-ones)=ones-(\left|H^{\omega }\right|-ones)=2ones-\left|H^{\omega }\right|$$

(33)

We are going to analyze the application of Definitions 1 and 7 in Expression 30, in order to elucidate the meaning of the quantity$ones$. According to Definition 1, positions with value 1 in pattern$x^k$remain in$f(x^k)$with value 1, if$f$is a Steinbuch function. That is, the characteristic set of$f(x^k)$is equal to$H^k$, according to Definition 7. However, according to Expression 30,$ones$does not count all the values 1 of pattern$x^k$, but is restricted to those positions of the characteristic set$H^{\omega }$, where pattern$x^{\omega }$has value 1 according to Definition 7. Thus,$ones$is equal to the cardinality of the intersection of both characteristic sets:

$$ones=|H^k\cap H^{\omega }|$$

(34)

So, by substituting 34 in Expression 33, we obtain the thesis: $z_k^{\omega }=2|H^k\cap H^{\omega }|-\left|H^{\omega }\right|$. □

Example 15.

When operating the Lernmatrix of Expression 13 with the second pattern of the learning set L, we have (Example 2)$x^{\omega }=x^2$,$H^{\omega }=\left\{1,2,5\right\}$and$\left|H^{\omega }\right|=3$:

$$z^{\omega }=M{x}^2=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{l}1\\ 3\\ -1\end{array}\right)$$

For k = 1,$H^1=\left|\left\{1,3,5\right\}\right|$, and$2|H^1\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{1,5\right\}\right|-3=4-3=1=z_1^{\omega }$.

For k = 2,$H^2=\left|\left\{1,2,5\right\}\right|$, and$2|H^2\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{1,2,5\right\}\right|-3=6-3=3=z_2^{\omega }$.

For k = 3,$H^3=\left|\left\{1,3,4\right\}\right|$, and $2|H^3\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{1\right\}\right|-3=2-3=-1=z_3^{\omega }$.

Example 16.

If we wanted to verify that Lemma 2 is fulfilled in the results of Example 3, it would not be possible, because the hypothesis is violated. In Example 3, there are two equal output patterns but whose indices are different:$y^4=y^1$.

Remark 3. 

By applying the methodology proposed in this paper, this problem disappears because in the associations of the learning set L all the output patterns are different. We have used this successful idea previously in [61].

Example 17.

A solution to the problem exposed in Example 16 is to modify the matrix of Expression 30, to create a new Lernmatrix by adding pattern 4. But the output pattern would no longer be$y^1$, but a four-bit one-hot pattern$y^4$, modifying the three output patterns of$x^1$,$x^2$, and$x^3$to four bits. The new Lernmatrix is converted as a$4\times 5$matrix and now we can verify that Lemma 2 is fulfilled, with$x^{\omega }=x^4$,$H^{\omega }=\left\{2,4,5\right\}$and $\left|H^{\omega }\right|=3$:

$$z^4=M{x}^4=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\\ -1& 1& -1& 1& 1\end{array}\right)\left(\begin{array}{l}0\\ 1\\ 0\\ 1\\ 1\end{array}\right)=\left(\begin{array}{l}-1\\ 1\\ -1\\ 3\end{array}\right)$$

For k = 1,$H^1=\left|\left\{1,3,5\right\}\right|$, and$2|H^1\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{5\right\}\right|-3=2-3=-1=z_1^{\omega }$.

For k = 2,$H^2=\left|\left\{1,2,5\right\}\right|$, and$2|H^2\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{2,5\right\}\right|-3=4-3=1=z_2^{\omega }$.

For k = 3,$H^3=\left|\left\{1,3,4\right\}\right|$, and$2|H^3\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{4\right\}\right|-3=2-3=-1=z_3^{\omega }$.

For k = 3,$H^4=\left|\left\{2,4,5\right\}\right|$, and$2|H^4\cap H^{\omega }|-\left|H^{\omega }\right|=2\left|\left\{2,4,5\right\}\right|-3=6-3=3=z_4^{\omega }$.

Lemma 3.

Let M be a Lernmatrix which was built from the learning set$L=\left\{(x^{\mu },y^{\mu })|\mu =1,2,\dots ,m\right\}$by applying Expression 22, fulfilling$y^{\alpha }=y^{\beta }$if and only if$\alpha =\beta$. Let$x^{\omega }$be a n-dimensional binary pattern. Then$y^{\alpha }$is the output pattern (for$x^{\omega }$) of the Lernmatrix recalling phase with$\alpha \in \left\{1,2,\dots ,m\right\}$, if and only if$|H^{\alpha }\cap H^{\omega }|>|H^{\beta }\cap H^{\omega }|$,$\forall \beta \in \left\{1,2,\dots ,m\right\}$,$\beta \ne \alpha$.

Proof. 

Since $y^{\alpha }$ is a one-hot pattern, its components fulfill the following condition:

$$y_{\alpha }^{\alpha }=1,\hspace{1em}{y}_{j\ne \alpha }^{\alpha }=0$$

(35)

By Expressions 23 and 35,$y^{\alpha }$is the output pattern for$x^{\omega }$if and only if:

$$z_{\alpha }^{\omega }={\vee }_{h=1}^m{z}_h^{\omega }$$

(36)

This occurs if and only if:

$$z_{\alpha }^{\omega }>z_{\beta }^{\omega }$$

(37)

for any arbitrary index$\beta$, such that$\beta \in \left\{1,2,\dots ,m\right\}$, $\beta \ne \alpha$.

By Lemma 2:

$$z_{\alpha }^{\omega }=2|H^{\alpha }\cap H^{\omega }|-\left|H^{\omega }\right|\mathrm{and}{z}_{\beta }^{\omega }=2|H^{\beta }\cap H^{\omega }|-\left|H^{\omega }\right|$$

(38)

So, by substituting 38 in Expression 37, we obtain the thesis:

$$|H^{\alpha }\cap H^{\omega }|>|H^{\beta }\cap H^{\omega }|,\forall \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha$$

 □

Example 18.

We will illustrate Lemma 3 with the patterns of the learning set L of Example 1 and the Lermatrix obtained in Expression 13. We will obtain the output pattern for a pattern that does not belong to L.

This is the learning set L of Example 1:

$$x^1=\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 1\end{array}\right),y^1=\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right),x^2=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right),y^2=\left(\begin{array}{l}0\\ 1\\ 0\end{array}\right),x^3=\left(\begin{array}{l}1\\ 0\\ 1\\ 1\\ 0\end{array}\right),y^3=\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

This is the Lermatrix obtained in Expression 13:

$$M=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)$$

We will choose the pattern$x^{\omega }$not belonging to L as the input pattern to this Lernmatrix.

$$z^{\omega }=M{x}^{\omega }=\left(\begin{array}{ccccc}1& -1& 1& -1& 1\\ 1& 1& -1& -1& 1\\ 1& -1& 1& 1& -1\end{array}\right)\left(\begin{array}{l}0\\ 1\\ 1\\ 1\\ 0\end{array}\right)=\left(\begin{array}{l}-1\\ -1\\ 2\end{array}\right)\to \left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)$$

In this example,$\alpha =3$, and we will verify the inequality of Lemma 2, with the values$\beta =1$and$\beta =2$. Also:$H^{\omega }=\left|\left\{2,3,4\right\}\right|$, and$H^{\alpha }=H^3=\left|\left\{1,3,4\right\}\right|$and$\left|H^{\alpha }\cap H^{\omega }\right|=\left|\left\{3,4\right\}\right|=2.$

For$\beta =1$,$\left|H^{\beta }\cap H^{\omega }\right|=\left|\left\{3\right\}\right|=1$. So that:$|H^{\alpha }\cap H^{\omega }|>|H^{\beta }\cap H^{\omega }|$.

For$\beta =2$,$\left|H^{\beta }\cap H^{\omega }\right|=\left|\left\{2\right\}\right|=1$. So that: $|H^{\alpha }\cap H^{\omega }|>|H^{\beta }\cap H^{\omega }|$.

Theorem 1.

Let M be a Lernmatrix which was built from the learning set$L=\left\{(x^{\mu },y^{\mu })|\mu =1,2,\dots ,m\right\}$by applying Expression 22, fulfilling$y^{\alpha }=y^{\beta }$if and only if$\alpha =\beta$. Let$x^{\omega }$be a n-dimensional binary pattern which exhibits subtractive alteration with respect to the pattern $x^{\alpha }$,for some$\alpha \in \left\{1,2,\dots ,m\right\}$. Then$y^{\alpha }$is the output pattern (for$x^{\omega }$) of the Lernmatrix recalling phase if and only if the expression$x^{\omega }<x^{\beta }$(according to Definition 6) is false$\forall \beta \in \left\{1,2,\dots ,m\right\}$,$\beta \ne \alpha$.

Proof. 

By Lemma 3,$y^{\alpha }$is the output pattern for$x^{\omega }$if and only if:

$$|H^{\alpha }\cap H^{\omega }|>|H^{\beta }\cap H^{\omega }|,\forall \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha$$

(39)

By Definition 6, given that$x^{\omega }$is a n-dimensional binary pattern which exhibits subtractive alteration with respect to the pattern $x^{\alpha }$, for some$\alpha \in \left\{1,2,\dots ,m\right\}$, we have$x^{\omega }<x^{\alpha }$, and by Lemma 1 this is true if and only if:

$$H^{\omega }\subset H^{\alpha }$$

(40)

By elementary set theory, Expression 40 is true if and only if:

$$H^{\alpha }\cap H^{\omega }=H^{\omega }$$

(41)

By substituting Expression 41 in Expression 39, we have:

$$\left|H^{\omega }\right|>|H^{\beta }\cap H^{\omega }|,\forall \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha$$

(42)

Expression 42 is equivalent to:

$$H^{\omega }\subset H^{\beta }\mathrm{is}\mathrm{false}\forall \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha$$

(43)

By contradiction, we suppose that the negation of the proposition 43 is true:

$$\exists \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha \mathrm{such}\mathrm{that}{H}^{\omega }\subset H^{\beta }$$

This proposition is equivalent to:

$$\exists \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha \mathrm{such}\mathrm{that}{H}^{\beta }\cap H^{\omega }=H^{\omega }$$

(44)

By Expressions 44, 41, and 39, we have:

$$\exists \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha \mathrm{such}\mathrm{that}\left|H^{\omega }\right|>\left|H^{\omega }\right|\mathrm{which}\mathrm{is}\mathrm{a}\mathrm{contradiction}$$

(45)

By Lemma 1, Expression 43 is true if and only if:

$$x^{\alpha }<x^{\beta }\left(\mathrm{according}\mathrm{to}\mathrm{Definition}6\right)\mathrm{is}\mathrm{false}\forall \beta \in \left\{1,2,\dots ,m\right\},\beta \ne \alpha$$

 □

What is expressed in Theorem 1 is very relevant for the state of the art in the topic of associative memories, when these models convert the task of pattern recalling into the task of pattern classification. The relevance lies in that Theorem 1 provides necessary and sufficient conditions for the Lernmatrix to correctly classify a pattern$x^{\omega }$that does not belong to learning set L. The pattern$x^{\omega }$belongs to testing set T, and is characterized by exhibit subtractive alteration with respect to some pattern belonging to the learning set L, say$x^{\alpha }$.

However, to achieve the correct classification of the$x^{\omega }$pattern, the condition included in Theorem 1 is very strong. Theorem 1 requires this condition to be fulfilled: there must be no subtractive alteration of testing pattern$x^{\omega }$with respect to any of the patterns in the learning set L, different from$x^{\alpha }$.

As mentioned previously, saturation and ambiguity are two problems that the Alpha-Beta group has faced since almost twenty years ago. It is now obvious that both problems appear as a direct consequence of the strong condition of Theorem 1 not being fulfilled. This is evidenced in the poor results that the Lernmatrix shows in the dataset of Table 1.

During a recent Alpha-Beta group work session, a disruptive idea suddenly emerged: what would happen if we do something to modify the pattern data so that the patterns fulfill the strong condition of Theorem 1? From that moment on, we worked hard in the search for some transform that is capable of eliminating the subtractive alteration$x^{\omega }<x^{\beta }$for all values of$\beta$different from$\alpha$, assuming that the test pattern$x^{\omega }$exhibits subtractive alteration with respect to$x^{\alpha }$.

This is precisely the achievement made in this research work. Finally we have found the long-awaited transform, which is proposed in Section 3. With this new representation of the data, the strong condition of Theorem 1 is fulfilled.

Section 5 of this article shows that with this new representation of the data, the performance of the Lernmatrix increases ostensibly, to the degree of competing with the supervised classifiers of the state of the art. The methodology proposed in this work includes, as one of the relevant methodological steps, the new transform.

2.5. The Johnson-Möbius Code

This subsection may seem out of place. However, the content is relevant to this article, because here a method that will be part of the methodology proposed in Section 4 is presented. The method consists of a binary data transformation code called the Johnson–Möbius code, which we proposed in the Alpha-Beta group nineteen years ago. The Johnson-Möbius code was used in a research work where we predicted levels of environmental pollutants [74]. Notice that here we are not working with the code previously introduced in [75].

The Johnson–Möbius code allows us to convert a set of real numbers into binary representations by following these three steps:

• Subtract the minimum (of the set of numbers) from each number, leaving only non-negative real numbers.
• Scale up the numbers (truncating the remaining decimals if necessary) by multiplying all numbers by an appropriate power of 10, in order to leave only non-negative integer numbers.
• Concatenate $e_m-e_j$ zeros with $e_j$ ones, where $e_m$ is the greatest non-negative integer number to be coded, and $e_j$ is the current non-negative integer number to be coded.

Example 19.

We will illustrate the Johnson–Möbius code with an example taken from [74].

We will use the Johnson–Möbius code to convert these 5 real numbers: 1.7, −0.1, 1.9, 0.2, and 0.6 into binary digit strings.

The first step is to subtract the minimum (which in this case is −0.1) from each number. The original 5 real numbers are transformed into 5 non-negative real numbers which are: 1.8, 0.0, 2.0, 0.3, and 0.7.

The second step is to multiply each number by 10, to get only non-negative integers: 18, 0, 20, 3, and 7. For this example $e_m=20$, because it is the greatest non-negative integer number to be coded. When performing the concatenations of zeros and ones, the final conversion is:

$$\begin{array}{l}\hspace{0.17em}\hspace{0.17em}1.7\to 00111111111111111111\\ -0.1\to 00000000000000000000\\ \hspace{0.17em}\hspace{0.17em}1.9\to 11111111111111111111\\ \hspace{0.17em}\hspace{0.17em}0.2\to 00000000000000000111\\ \hspace{0.17em}\hspace{0.17em}0.6\to 00000000000001111111\end{array}$$

(46)

3. Our Main Proposal: The ${\mathit{\tau }}^{[9]}$ Transform

The meaning of 9 in the transform symbol ${\tau }^{[9]}$ is related to the binary code of the decimal number 9 $[1001]$, which implicitly includes the two transformations: $1\to [10]$ and $0\to [01]$.

Definition 8.

The${\tau }^{[9]}$transform is defined in such a way that it has a binary digit as input and at the output it delivers a binary pattern of dimension 2, according to the following:

$$\begin{array}{l}{\tau }^{[9]}(1)=\left(\begin{array}{l}1\\ 0\end{array}\right)\\ {\tau }^{[9]}(0)=\left(\begin{array}{l}0\\ 1\end{array}\right)\end{array}$$

(47)

Notation 1.

The application of the novel${\tau }^{[9]}$transform to each and every component of a n-dimensional binary vector$x^{\omega }$, is denoted by${\mathsf{\Gamma }}^{[9]}(x^{\omega })$.

This novel transform looks very simple. However, it must be emphasized that${\tau }^{[9]}$is a powerful, yet simple, mathematical transform, as will be shown in Section 5 of this paper. This powerful simplicity goes hand in hand with the spirit that has guided the Alpha-Beta group in their scientific research activities. Since its creation in 2002, the Alpha-Beta research group has taken as inspiration ideas that highlight the simplicity of scientific or technological concepts. An example is the Ockham Razor (s. XIV), one of whose free interpretations reads as follows: “If you have two or more hypotheses for a fact, you should choose the simplest one” [76].

Theorem 2.

Let$x^{\alpha },x^{\beta }$be two n-dimensional binary patterns such thatthe pattern$x^{\alpha }$exhibits subtractive alteration with respect to the pattern$x^{\beta }$, i.e.,$x^{\alpha }<x^{\beta }$according the Definition 6. Then, by applying the${\tau }^{[9]}$transform to each and every one of the components of both vectors, the subtractive alteration is eliminated. That is, ${\mathsf{\Gamma }}^{[9]}(x^{\alpha })$does not exhibit subtractive alteration with respect to${\mathsf{\Gamma }}^{[9]}(x^{\beta })$, nor does${\mathsf{\Gamma }}^{[9]}(x^{\beta })$exhibit subtractive alteration with respect to${{\rm T}}^{[9]}(x^{\alpha })$.

Proof. 

By Definitions 5 and 6, the hypothesis$x^{\alpha }<x^{\beta }$is true if and only if the following two conditions are fulfilled simultaneously:

$$\exists j\in \left\{1,\dots ,n\right\}\mathrm{such}\mathrm{that}{x}_j^{\alpha }<x_j^{\beta }$$

(48)

$$\left(x_j^{\alpha }=1\right)\to \left(x_j^{\beta }=1\right),\forall j\in \left\{1,\dots ,n\right\}$$

(49)

Since by the hypothesis$x^{\alpha }$and$x^{\beta }$are binary patterns, the only possibility that the inequality 48 is true is that$x_j^{\alpha }=0$and$x_j^{\beta }=1$. By Definition 8, when applying the transform, the result is:

$${\tau }^{[9]}(x_j^{\alpha })={\tau }^{[9]}(0)=\left(\begin{array}{l}0\\ 1\end{array}\right)$$

(50)

$${\tau }^{[9]}(x_j^{\beta })={\tau }^{[9]}(1)=\left(\begin{array}{l}1\\ 0\end{array}\right)$$

(51)

while condition 48 persists in the first component of the new two-dimensional binary patterns, condition 49 has been eliminated. A brief analysis of the behavior of the second component in both two-dimensional binary patterns, allows us to conclude that condition 49 is false. This is easily evident because the antecedent of the conditional 49 is true, while the consequent is false. By elementary Boolean logic, this conditional is false. This short analysis is replicated for each index that originally fulfills condition 50. That is, ${\mathsf{\Gamma }}^{[9]}(x^{\alpha })$ does not exhibit subtractive alteration with respect to ${\mathsf{\Gamma }}^{[9]}(x^{\beta })$. By performing a similar analysis in reverse, we can see that condition 49 is eliminated in the first component of both two-dimensional binary patterns. Therefore, it is possible to conclude that ${\mathsf{\Gamma }}^{[9]}(x^{\beta })$ does not exhibit subtractive alteration with respect to ${\mathsf{\Gamma }}^{[9]}(x^{\alpha })$. □

Example 20.

We will illustrate Theorem 2 with the patterns from Examples 10 and 12.

$$x^7=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 0\end{array}\right),x^2=\left(\begin{array}{l}1\\ 1\\ 0\\ 0\\ 1\end{array}\right)$$

From Example 10,$x^7\le x^2$. Also, from Example 12, the pattern$x^7$exhibits subtractive alteration with respect to the pattern$x^2$because$x_5^7<x_5^2$according to Definition 6.

By applicating the${\tau }^{[9]}$transform to both patterns:

$${\mathsf{\Gamma }}^{[9]}(x^7)=\left(\begin{array}{l}{\tau }^{[9]}(1)\\ {\tau }^{[9]}(1)\\ {\tau }^{[9]}(0)\\ {\tau }^{[9]}(0)\\ {\tau }^{[9]}(0)\end{array}\right)=\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 0\\ 1\\ 0\\ 1\\ 0\\ 1\end{array}\right),{\mathsf{\Gamma }}^{[9]}(x^2)=\left(\begin{array}{l}{\tau }^{[9]}(1)\\ {\tau }^{[9]}(1)\\ {\tau }^{[9]}(0)\\ {\tau }^{[9]}(0)\\ {\tau }^{[9]}(1)\end{array}\right)=\left(\begin{array}{l}1\\ 0\\ 1\\ 0\\ 0\\ 1\\ 0\\ 1\\ 1\\ 0\end{array}\right),$$

By carrying out a brief analysis with the last two components of both binary patterns, it is possible to conclude that${\mathsf{\Gamma }}^{[9]}(x^7)$does not exhibit subtractive alteration with respect to${\mathsf{\Gamma }}^{[9]}(x^2)$. In addition,${\mathsf{\Gamma }}^{[9]}(x^2)$does not exhibit subtractive alteration with respect to${\mathsf{\Gamma }}^{[9]}(x^7)$.

Now we already have Theorem 2, which becomes a powerful tool that allows us to face the strong condition of Theorem 1.

4. Proposed Methodology

Although the new transform ${\tau }^{[9]}$ is crucial for the success of the proposed methodology, this methodology includes concepts and algorithms that the Alpha-Beta group has published over the years. In the description of the proposed model, the references containing those concepts and algorithms will be indicated.

Let D be a dataset which is partitioned into c different sets representing the classes $K_1,K_2,\dots ,K_c$ where c is a positive integer. These c sets fulfill the following conditions:

$$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{c}{\cup }}{K}_i}=D\\ K_i\cap K_j=\varnothing ,i,j\in \left\{1,2,\dots ,c\right\}\hspace{0.17em}\hspace{0.17em}\mathrm{such}\hspace{0.17em}\mathrm{that}\hspace{0.17em}\hspace{0.17em}i\ne j\end{array}$$

(52)

If necessary, preprocessing is applied to the data, in order to convert the categorical data to numerical ones and to impute the missing values.

When applying a stratified validation method, the dataset D is partitioned in two disjoint sets: the learning set L and testing set T. The sets L and T fulfill the following conditions:

$$\begin{array}{l}L\cup T=D\\ L\cap T=\varnothing \end{array}$$

(53)

In the learning set L, the proportion of the c classes $K_1,K_2,\dots ,K_c$ is maintained. The set of patterns in L that belong to class $K_i$ is denoted by $K_i^L$, and its cardinality is $\left|K_i^L\right|$. The c sets $K_i^L$ fulfill the following condition:

$${\displaystyle \sum _{i=1}^c\left|K_i^L\right|=\left|L\right|}$$

(54)

Each of the c classes $K_i^L$ contains $\left|K_i^L\right|$ learning patterns in L, which are located in different positions within the set L. Therefore, the patterns in $K_i^L$ correspond to $\left|K_i^L\right|$ values of the m indices $\mu \in \left\{1,2,\dots ,m\right\}$. We will denote the set of indices in L that correspond to the patterns belonging to class $K_i^L$, as follows:

$$I_i=\left\{j\in \left\{1,2,\dots ,m\right\}|x^j\in K_i^L\right\},i\in \left\{1,2,\dots ,c\right\}\hspace{0.17em}$$

(55)

Each element of the learning set L is an association of two patterns. The first component of the association is a pattern $x^{\mu }$ (input pattern) that belongs to D, and the second component is the corresponding class label $y^{\mu }$ (output pattern). Assuming that L contains m patterns:

$$L=\left\{(x^{\mu },y^{\mu })|\mu =1,2,\dots ,m\right\}$$

(56)

Taking into account that according to Expression 55 the cardinality of L is m, Expression 54 becomes:

$${\displaystyle \sum _{i=1}^c\left|K_i^L\right|=\left|L\right|}=m$$

(57)

The methodology for the proposed model, which we have named $LM({\tau }^{[9]})$, consists of two phases: learning phase and recalling phase.

The learning phase structure of the proposed model is outlined in the diagrams of Figure 10 and Figure 11, which were inspired by [77]. The diagram in Figure 10 includes a general outline for the learning phase of the proposed model.

The diagram in Figure 10 emphasizes a fact that is common to all associative memory models. In the learning phase, both input patterns $x^{\mu }$ and output patterns $y^{\mu }$ are used to create the model with specific operations described below, i.e., both types of patterns enter the diagram.

The diagram in Figure 11 is more detailed. Specific operations performed with input patterns $x^{\mu }$ and output patterns $y^{\mu }$ are included. The expressions of the description of the learning phase where the corresponding operations are explained in detail are specified.

Learning phase for the proposed model$LM({\tau }^{[9]})$.

• Apply the Johnson–Möbius code to each and every one of the input patterns $x^{\mu }$ of the learning set L [74], to obtain a p-dimensional binary pattern:

  $$\mathrm{JM}(x^{\mu }),\mu \in \left\{1,2,\dots ,m\right\}$$

  (58)
• Apply the proposed transform to each pattern $\mathrm{JM}(x^{\mu })$, to obtain a 2p-dimensional binary pattern:

  $${\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\mu })),\mu \in \left\{1,2,\dots ,m\right\}$$

  (59)
• For each input pattern $x^{\mu }$ of the learning set L, code the output pattern $y^{\mu }$ as an one-hot pattern [61]:

  $$y^{\mu }\to o{h}^{\mu },\mu \in \left\{1,2,\dots ,m\right\}$$

  (60)
  With this step, one of the conditions of the hypothesis of Theorem 1 is guaranteed: $y^{\alpha }=y^{\beta }$ if and only if $\alpha =\beta$.
• Build the new model $LM({\tau }^{[9]})$. This is achieved by training the Lernmatrix by applying Expression 22, using the new learning set $\left\{({\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\mu })),o{h}^{\mu })|\mu =1,2,\dots ,m\right\}$, which was obtained in the three previous steps.

  $$LM({\tau }^{[9]})={\displaystyle \sum _{\mu =1}^{m}o{h}^{\mu }{\left(F({\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\mu })))\right)}^T}$$

  (61)
  If $n=2p$, the new model $LM({\tau }^{[9]})$ is a $m\times n$ Lernmatrix.
  The recalling phase structure of the proposed model is outlined in the diagrams of Figure 12 and Figure 13, which were inspired by [77].

Note that the diagram in Figure 12 is different from the diagram in Figure 10. In the recalling phase, only the testing pattern $x^{\omega }\in \mathrm{T}$ enters the diagram. Inside the box that corresponds to the model, specific operations (which are described below) are performed that have as a result the generation of the class label for the testing pattern. Precisely the class label is located after the exit arrow.

The diagram in Figure 13 is more detailed. Specific operations performed with the testing pattern $x^{\omega }\in \mathrm{T}$ and the proposed model $LM({\tau }^{[9]})$ are included. The expressions of the description of the recalling phase where the corresponding operations are explained in detail are specified.

Recalling phase for the proposed model$LM({\tau }^{[9]})$.

• Let $x^{\omega }\in \mathrm{T}$ be a test pattern. Apply the Johnson–Möbius code to the pattern $x^{\omega }$, to obtain a p-dimensional binary pattern $\mathrm{JM}(x^{\omega })$.
• Apply the proposed transform to the pattern $\mathrm{JM}(x^{\omega })$, to obtain a n-dimensional binary pattern ${\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\omega }))$.
• Using the first part of Expression 23, obtain a m-dimensional binary pattern by the product of the $m\times n$ Lernmatrix $LM({\tau }^{[9]})$ and the n-dimensional binary pattern ${\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\omega }))$:

  $$z^{\omega }=\left(LM({\tau }^{[9]})\right)\left({\mathsf{\Gamma }}^{[9]}(\mathrm{JM}(x^{\omega }))\right)$$

  (62)
• This last step of the recalling phase is extremely relevant, since in this step the class is assigned to the testing pattern $x^{\omega }$. To achieve this, we must first consider that the pattern $z^{\omega }$ obtained in step 3 consists of m binary digits. Furthermore, it should be noted that in these m binary digits, all the c classes that were specified in Expressions 54 to 57 are represented. Due to its importance and the processes involved, this step consists of four sub-steps:

  4.1.

  Define the pattern of binary digits in the m-dimensional binary pattern $z^{\omega }$, which are found in positions corresponding to each class $K_i$, i.e., in the set $I_i$ from Expression 55:

  $$K_i^{z^{\omega }}=\left\{z_j^{\omega }\in z^{\omega }|j\in I_i\right\},i\in \left\{1,2,\dots ,c\right\}\hspace{0.17em}$$

  (63)

  4.2.

  From Definition 7 and Expression 63, we will generate the characteristic set $H_i^{z^{\omega }}$ of the pattern $K_i^{z^{\omega }}$. The characteristic set $H_i^{z^{\omega }}$ contains all the components of pattern $z^{\omega }$ with value 1, whose positions correspond to the class $K_i$:

  $$H_i^{z^{\omega }}=\left\{a\in K_i^{z^{\omega }}|a=1\right\},i\in \left\{1,2,\dots ,c\right\}\hspace{0.17em}$$

  (64)

  4.3.

  Now, for each $i\in \left\{1,2,\dots ,c\right\}$ we will calculate a positive real number $E_i$, which represents the weighted expression of the class $K_i$ in the pattern $z^{\omega }$:

  $$E_i=\frac{\left|H_i^{z^{\omega }}\right|}{\left|K_i^{z^{\omega }}\right|},i\in \left\{1,2,\dots ,c\right\}\hspace{0.17em}$$

  (65)

  4.4.

  If $E_i={\vee }_{k=1}^c{E}_k$, the class label of $K_i$ is assigned to pattern $z^{\omega }$.

The weighted expression of classes technique described in step 4.3 has previously been used by the Alpha-Beta group in various research papers, the summaries of which are included in [78].

5. Results and Discussion

In this section, we detail the experimental results carried out in order to compare the proposed model $LM({\tau }^{[9]})$ against the most important classifiers of the state of the art. We have been very careful in choosing datasets that reflect the different activities of the human being, and that are used by world scientists when trying new models of pattern classification. In Section 5.1, the 20 selected datasets will be described in detail. Regarding the classifiers, we selected in total seven algorithms: six supervised classifiers, from each family of algorithms detailed in Section 2.1, plus an algorithm that works with an ensemble of classifiers. Section 5.2 will describe the seven algorithms, their specifications and strengths. Section 5.3 is the culmination of the efforts described throughout the paper, because in this subsection the experimental results are presented, which show the competitiveness of the proposed model $LM({\tau }^{[9]})$. Firstly, the validation method used to partition the datasets is described. Then, the performance measure used and the reasons why we have chosen this performance measure are specified. Finally, the tables of results, the statistical tests of significance, and the discussion of these relevant results are presented.

5.1. Datasets

In Section 2.1, it was clearly specified that there exist dataset repositories that have become important auxiliaries to those who develop algorithms and models in pattern recognition and related disciplines. One of the best repositories is in the public domain, namely the KEEL repository, which is sponsored by the University of Granada in Spain [79]. This repository has been made available to researchers around the world: http://sci2s.ugr.es/keel/datasets.php.

We selected 20 datasets from the KEEL repository. The first criterion was to consider datasets whose patterns only contain numerical attributes. The number of attributes (all numerical) in the 20 selected datasets varies from four to 18, while the number of patterns ranges from 150 to 1484.

The second criterion that we took into account to carry out the selection was the number of classes [24]. As it is the most studied case, we have included in this selection datasets with only two classes, i.e., in Expression 52, c = 2 and in each dataset the only classes will be $K_1$ and $K_2$.

The most important criterion to consider was to make sure that our proposed model faced a challenging problem. The main purpose of this paper is to leave evidence that the proposed novel model $LM({\tau }^{[9]})$ is capable of contributing in a relevant way to the state of the art in pattern classification, by successfully facing a challenge.

We have found the challenge in the imbalance of classes [16,23]. In accordance with what was described in Section 2.1, the most interesting datasets are far from the ideal case, where the cardinalities of the classes are equal (or almost equal). The importance of datasets is normally reflected in their social impact, and the datasets used for the classification of diseases are a good example [7,34]. However, these are precisely the datasets that exhibit the challenge of imbalance. According to Expression 1, the imbalance ratio (IR) for the 20 selected datasets varies from 1.86 to 39.14.

Table 2. Datasets used in the experiments: number of attributes, number of patterns, and Imbalance Ratio.

Datasets	Attributes (All Numerical)	Patterns	IR
ecoli-0_vs_1	7	220	1.86
ecoli-0-1-3-7_vs_2-6	7	281	39.14
ecoli1	7	336	3.36
ecoli2	7	336	5.46
ecoli3	7	336	8.6
iris0	4	150	2
new-thyroid1	5	215	5.14
new-thyroid2	5	215	5.14
shuttle-c2-vs-c4	9	129	20.5
vehicle0	18	846	3.25
vehicle2	18	846	2.88
vowel0	13	988	9.98
wisconsin	9	683	1.86
yeast1	8	1484	2.46
yeast-1_vs_7	8	459	14.3
yeast-1-2-8-9_vs_7	8	947	30.57
yeast-1-4-5-8_vs_7	8	693	22.1
yeast-2_vs_4	8	514	9.08
yeast-2_vs_8	8	482	23.1
yeast4	8	1484	28.1

includes the specifications of the 20 selected datasets, in alphabetical order.

In addition to the criteria mentioned above, we have been very careful in choosing datasets that reflect the activities important to humans. The 20 selected datasets came from different scenarios (medical, agricultural, economical, speaking). Below are brief descriptions, which are adapted from http://sci2s.ugr.es/keel/datasets.php and http://archive.ics.uci.edu/ml/datasets.php:

(a)

Regarding the Ecoli dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original name of the dataset is “Protein Localization Sites”, and that it was created by Kenta Nakai from the Institute of Molecular and Cellular Biology, Osaka University. The patterns consist of seven numerical attributes: mcg: McGeoch’s method for signal sequence recognition; gvh: von Heijne’s method for signal sequence recognition; lip: von Heijne’s Signal Peptidase II consensus sequence score; chg: Presence of charge on N-terminus of predicted lipoproteins; aac: score of discriminant analysis of the amino acid content of outer membrane and periplasmic proteins; alm1: score of the ALOM membrane spanning region prediction program; and alm2: score of ALOM program after excluding putative cleavable signal regions from the sequence. Originally, there were eight classes: cp (cytoplasm), im (inner membrane without signal sequence), pp (perisplasm), imU (inner membrane, uncleavable signal sequence), om (outer membrane), omL (outer membrane lipoprotein), imL (inner membrane lipoprotein), and imS (inner membrane, cleavable signal sequence).

Using the Ecoli dataset as a base, the KEEL project generated the five imbalanced datasets of two classes that we included in our selection:

ecoli-0_vs_1: This dataset is an imbalanced version of the Ecoli dataset, where the positive examples belong to class im and the negative examples belong to the class cp.

ecoli-0-1-3-7_vs_2-6: This dataset is an imbalanced version of the Ecoli dataset, where the positive examples belong to classes pp and imL and the negative examples belong to classes cp, im, imU and imS.

ecoli1: This dataset is an imbalanced version of the Ecoli dataset, where the positive examples belong to class im and the negative examples belong to the rest.

ecoli2: This dataset is an imbalanced version of the Ecoli dataset, where the positive examples belong to class pp and the negative examples belong to the rest.

ecoli3: This dataset is an imbalanced version of the Ecoli dataset, where the positive examples belong to class imU and the negative examples belong to the rest.

(b)

The sixth selected dataset is an adaptation of the Iris Dataset, which originally consisted of three classes (https://archive.ics.uci.edu/ml/datasets/iris).

iris0: This is an imbalanced version of the well-known Iris data set. There are two classes defined: positive (the old iris-setosa class) and negative (the old iris-versicolor and iris-virginica classes).

(c)

Regarding the New Thyroid dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was donated by Stefan Aberhard from James Cook University, Australia. The dataset deals with diagnosing a patient thyroid function. It has 215 patterns which consist of five numerical attributes T3-resin uptake test, total serum thyroxin as measured by the isotopic displacement method, total serum tri-odothyronine as measured by radioimmuno assay, basal thyroid-stimulating hormone (TSH) as measured by radioimmuno assay, and maximal absolute difference of TSH value after injection of 200 μg of thyrotropin-releasing hormone as compared to the basal value. There are three classes of thyroid functions; normal, hyper and hypo functioning.

Using the New Thyroid dataset as a base, the KEEL project generated the two imbalanced datasets of two classes that we included in our selection:

new-thyroid1: This dataset is an imbalanced version of the New Thyroid dataset, where the positive examples belong to class 2 (hyperthyroidism) and the negative examples belong to the rest.

new-thyroid2: This dataset is an imbalanced version of the New Thyroid dataset, where the positive examples belong to class 3 (hypothyroidism) and the negative examples belong to the rest.

(d)

Regarding the Shuttle dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was donated by Jason Catlett from University of Sydney, Australia. This dataset was generated originally to extract comprehensible rules for determining the conditions under which an autolanding would be preferable to the manual control of a spacecraft. The patterns consist of nine numerical attributes and seven possible values for the class label: Rad Flow, Fpv Close, Fpv Open, High, Bypass, Bpv Close, and Bpv Open.

Using the Shuttle dataset as a base, the KEEL project generated the imbalanced dataset of two classes that we included in our selection:

shuttle-c2-vs-c4: This dataset is an imbalanced version of the Shuttle dataset, where the positive examples belong to class 2 (Fpv Close) and the negative examples belong to class 4 (High).

(e)

Regarding the Vehicle Silhouettes dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was donated by Pete Mowforth and Barry Shepherd from the Turing Institute, Glasgow, Scotland. The purpose is to classify a given silhouette as one of four types of vehicle, using a set of attributes extracted from the silhouette. The vehicle may be viewed from one of many different angles. The patterns consist of 18 numerical attributes and four possible values for the class label: van, saab, bus, opel.

Using the Vehicle Silhouettes dataset as a base, the KEEL project generated two imbalanced dataset of two classes that we included in our selection:

vehicle0: This dataset is an imbalanced version of the Vehicle Silhouettes dataset, where the positive examples belong to class 0 (van) and the negative examples belong to the rest.

vehicle2: This dataset is an imbalanced version of the Vehicle Silhouettes dataset, where the positive examples belong to class 2 (bus) and the negative examples belong to the rest.

(f)

Regarding the Vowel Recognition dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but was instead obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was donated by David Deterding, Mahesan Niranjan, and Tony Robinson from the University of Cambridge, UK. This dataset deals with speaker independent recognition of the eleven steady state vowels of British English. The patterns consist of 13 numerical attributes and 11 possible values for the class label.

Using the Vowel Recognition dataset as a base, the KEEL project generated the imbalanced dataset of two classes that we included in our selection:

vowel0: This dataset is an imbalanced version of the Vowel Recognition dataset, where the positive examples belong to class 0 and the negative examples belong to the rest.

(g)

Regarding the Wisconsin dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was donated by William H. Wolberg from the University of Wisconsin Hospitals, USA. The task is to determine if the detected tumor is benign or malignant. The patterns consist of 13 numerical attributes: Clump Thickness, Uniformity of Cell Size, Uniformity of Cell Shape, Marginal Adhesion, Single Epithelial Cell Size, Bare Nuclei, Bland Chromatin, Normal Nucleoli, and Mitoses. There are two possible values for the class label: benign and malignant.

Using the Wisconsin dataset as a base, the KEEL project generated the imbalanced dataset of two classes that we included in our selection:

wisconsin: This dataset is an imbalanced version of the Wisconsin dataset, where the classes have been renamed to positive and negative.

(h)

Regarding the Yeast dataset, the administrators of the KEEL repository note that this is not a native dataset from the KEEL project, but instead was obtained from the UCI machine learning repository: http://archive.ics.uci.edu/ml/datasets.php. In this website, it is specified that the original dataset was created by Kenta Nakai from the Institue of Molecular and Cellular Biology, Osaka University. This database contains information about a set of yeast cells. The patterns consist of eight numerical attributes: Mcg: McGeoch’s method for signal sequence recognition; Gvh: von Heijne’s method for signal sequence recognition; Alm: Score of the ALOM membrane spanning region prediction program; Mit: Score of discriminant analysis of the amino acid content of the N-terminal region (20 residues long) of mitochondrial and non-mitochondrial proteins; Erl: Presence of “HDEL” substring (thought to act as a signal for retention in the endoplasmic reticulum lumen); Pox: Peroxisomal targeting signal in the C-terminus; Vac: Score of discriminant analysis of the amino acid content of vacuolar and extracellular proteins, and Nuc: Score of discriminant analysis of nuclear localization signals of nuclear and non-nuclear proteins. The task is to determine the localization site of each cell among 10 possible alternatives: MIT, NUC, CYT, ME1, ME2, ME3, EXC, VAC, POX, ERL.

Using the Yeast dataset as a base, the KEEL project generated the seven imbalanced datasets of two classes that we included in our selection:

yeast1: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class NUC and the negative examples belong to the rest.

yeast-1_vs_7: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class VAC and the negative examples belong to the class NUC.

yeast-1-2-8-9_vs_7: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class VAC and the negative examples belong to classes NUC, CYT, POX, ERL.

yeast-1-4-5-8_vs_7: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class VAC and the negative examples belong to classes NUC, ME2, ME3, POX.

yeast-2_vs_4: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class CYT and the negative examples belong to the class ME2.

yeast-2_vs_8: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class CYT and the negative examples belong to the class POX.

Yeast4: This dataset is an imbalanced version of the Yeast dataset, where the positive examples belong to class ME2 and the negative examples belong to the rest.

5.2. Supervised Classification Algorithms under Comparison

We have taken special care in selecting the pattern classification algorithms against which we will compare the performance of the new model. After a serious analysis of the different approaches to the state of the art in pattern classification, we have chosen a representative algorithm of each approach, according to the detailed descriptions of the six approaches in Section 2.1. Additionally, we have chosen an ensemble of supervised classification algorithms [24].

All algorithms were executed using the WEKA platform [25]. With the exception of SVM, the default configuration was used in all other classifiers. We used a personal computer with Windows operating system, having Intel(R) Core (TM) 2 Duo CPU E6550 processor at 2.33GHz, with 2 Gb of RAM.

The first algorithm selected is a Bayes classifier. Although there are a large number of Bayes classifiers in the state of the art (in WEKA alone we can count almost ten of them) there is a model that stands out for its simplicity and effectiveness: it is the Naïve Bayes, which is currently applied in different areas of science and technology [80]. It is based on the Bayes theorem and assumes that attributes are independent given the value of the class label. This classifier is one of the simplest classification algorithms and has been selected for our experiments.

A glance at recent articles on pattern classification allows us to see that k-NN classifiers are always present in the experimental section. This occurs because the use of metrics and their properties provides conceptual support for k-NN classifiers, which are considered among the most important and useful approaches in pattern classification. [31]. For this reason, in this paper we have chosen 3-NN for the experimental section, because it was the one that yielded the best results of several k-NN that we tested.

The importance of the study of decision trees in contemporary specialized literature is undeniable [34]. However, there is an algorithm that cannot be missing in a pattern classification results table. This is the C4.5 algorithm, which is one of the most important classifiers of this approach [81]. That is the reason why we selected algorithm C4.5 to be included in the experimental section of this paper.

The algorithm based on the multinomial logistic regression function is very effective as a pattern classifier on datasets of two classes [35]. This efficient classifier with the popular name of logit was included in the experimental section of this paper [37].

In Section 2.1, the relevance of SVMs has been emphasized as one of the most appreciated classifiers by the international scientific community [40]. For this reason, we included a representative model of the SVM in the experimental section of this paper. The configuration in WEKA for the SVM that we have selected is: gamma = 1, Polinomial grade 3.

Due to its relevance and effectiveness, a neural network could not be missing. We included the MLP [45], with the default configuration in WEKA, as a representative of this approach. We also selected one of the most popular classifier assemblies. We included the AdaBoost algorithm [82], using the decision tree C4.5 as base classifier.

5.3. Tables of Results, Statistical Tests, and Discussion

In Section 5.1, we established three criteria that guided us in the selection of the 20 datasets. First, we decided that patterns only contain numerical attributes. This was done to avoid the imputation procedure and conversion of categorical to numerical attributes. The second criterion (only two classes) addresses the fact that pattern classification involving only two classes is the most studied case in contemporary literature.

The third criterion (imbalance of classes) is the most important in the context of this article, because it gives us the valuable opportunity to successfully face one of the great challenges of pattern classification. It allows our proposed model $LM({\tau }^{[9]})$ to contribute positively to the state of the art in pattern classification. Obviously, the challenge of dealing with class imbalance has been in the scientific arena for a long time. Therefore, it is a fact that all the algorithms for classifying patterns in the state of the art have had the opportunity to face it successfully. The experimental results of this research work show that our proposal is successful in facing the challenge.

However, working with imbalanced datasets requires us to make two very relevant decisions. First, we must choose the validation method because not all of them are useful to classify imbalanced datasets. We decided to use the five-fold stratified cross-validation method, because this validation method is widely recommended for imbalanced datasets by prestigious researchers [16,20,23,63].

The second decision we must make is regarding the performance measure. In Section 2.1, the reasons why accuracy is no longer useful as a performance measure when classifying imbalanced datasets are extensively detailed. However, as also mentioned, there are several alternative performance measures, which derive from the confusion matrix [23].

Due to the benefits it exhibits, we have decided to use balanced accuracy (BA) as a performance measure. BA is a measure that does not take bias towards the majority class into account. BA is calculated as the average between sensitivity and specificity, according to Expressions 4, 5, and 6, which we replicate in Expression 66:

$$\begin{array}{l}Sensitivity=\frac{TP}{TP+FN},\hspace{1em}Specificity=\frac{TN}{TN+FP}\\ BA=Balanced\hspace{0.17em}Accuracy=\frac{Sensitivity+Specificity}{2}\end{array}$$

(66)

We tested the seven supervised classifiers from the literature (Naïve Bayes, 3-NN, C4.5, Logit, SVM, MLP, and AdaBoost), as well as the proposed model $LM({\tau }^{[9]})$.

The results of the BA performance measure are shown in

Table 3. Results of the balanced accuracy (BA) measure for the 8 classifiers in the 20 datasets. The best results are highlighted in bold.

Datasets	NaïveBayes [80]	3-NN [31]	C4.5 [81]	Logit [37]	SVM [40]	MLP [45]	Ada Boost [82]	$\mathbf{LM}({\mathit{\tau }}^{[9]})$
ecoli-0_vs_1	0.97	0.94	0.98	0.97	0.97	0.97	0.97	0.97
ecoli-0-1-3-7_vs_2-6	0.78	0.84	0.74	0.84	0.78	0.84	0.74	0.84
ecoli1	0.86	0.88	0.86	0.84	0.85	0.86	0.87	0.82
ecoli2	0.90	0.93	0.86	0.78	0.80	0.89	0.87	0.89
ecoli3	0.86	0.70	0.72	0.73	0.77	0.79	0.73	0.77
iris0	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.00
new-thyroid1	0.98	0.96	0.94	0.96	0.96	0.95	1.00	1.00
new-thyroid2	0.98	0.92	0.94	0.98	0.98	0.95	0.97	1.00
shuttle-c2-vs-c4	0.90	0.95	1.00	0.94	1.00	0.94	0.95	1.00
vehicle0	0.73	0.89	0.92	0.95	0.96	0.95	0.81	0.94
vehicle2	0.72	0.94	0.94	0.95	0.96	0.97	0.90	0.95
vowel0	0.92	0.98	0.97	0.91	0.99	0.99	0.87	1.00
wisconsin	0.97	0.97	0.94	0.96	0.93	0.95	0.94	0.97
yeast1	0.68	0.63	0.66	0.63	0.59	0.68	0.67	0.65
yeast-1_vs_7	0.66	0.55	0.59	0.55	0.50	0.61	0.56	0.63
yeast-1-2-8-9_vs_7	0.61	0.51	0.61	0.54	0.50	0.53	0.57	0.55
yeast-1-4-5-8_vs_7	0.51	0.49	0.50	0.50	0.50	0.51	0.50	0.56
yeast-2_vs_4	0.88	0.84	0.83	0.80	0.83	0.85	0.75	0.84
yeast-2_vs_8	0.74	0.77	0.50	0.74	0.74	0.77	0.74	0.77
yeast4	0.68	0.59	0.59	0.56	0.50	0.66	0.60	0.68

. The best results are highlighted in bold.

As we have previously commented, these experimental results are the culmination of the efforts that led to the realization of the proposed model $LM({\tau }^{[9]})$. Analysis of Table 3 will show that the proposed model is competitive against the best classifiers in the state of the art.

The first important element in this analysis is to establish that the data in Table 3 provide evidence of the validity and certainty of No-Free-Lunch theorem [8,9], as previously described in the introduction to this paper. There it was made clear that the No-Free-Lunch theorem governs the effectiveness of pattern classification algorithms, and that it is useless to pretend that in all cases there are zero classification errors. In Table 3, there are very few cases (14 out of 160 cases) where a classifier obtained zero errors, which is equivalent to obtaining 1 in the BA value. None of the eight classifiers obtained zero errors in the 20 datasets, which is totally in accordance with the No-Free-Lunch theorem.

By counting the number of times that any of the classifiers obtained 1 in the balanced accuracy value, we realize that our proposed model $LM({\tau }^{[9]})$ did so with five of the 20 datasets: iris0, new-thyroid1, new-thyroid2, shuttle-c2-vs-c4, and vowel0. None of the other seven classifiers scored 1 five times in BA. The closest are SVM and AdaBoost, which have two each. On the other hand, it is curious to note that each of the classifiers achieved a value of 1 in BA in at least one of the 20 datasets, and here is a fact that is pertinent to emphasize in favor of our proposed model: in none of the 20 datasets did it happen that when some classifier achieved the value 1 in BA, the model $LM({\tau }^{[9]})$ had less than 1.

In the iris0 dataset, it happened that all the classifiers, with the exception of C4.5, achieved the value 1 in BA, which means that with this dataset, almost any classifier, no matter how bad it is, performs well. With the shuttle-c2-vs-c4 dataset, something similar happened, but to a lesser extent. Besides the model $LM({\tau }^{[9]})$, only two classifiers obtained the value 1 in BA: C4.5 and SVM. Note the contrast, because in this dataset the C4.5 beats five of the best classifiers, while in the iris0 dataset C4.5 was beaten by all the others. Furthermore, with the ecoli-0_vs_1 dataset, the C4.5 was the best of the eight algorithms, including the model $LM({\tau }^{[9]})$.

There are datasets that behave completely differently than the iris0 dataset, in which any classifier is successful. With the yeast-1-4-5-8_vs_7 dataset, all eight classifiers performed very poorly. Although the proposed model $LM({\tau }^{[9]})$ obtained the best result, this is not something to be proud of, because the performance barely reached 0.56, which is a value very close to throwing a toss. However, the other classifiers had worse performances. There is even one of them, the 3-NN, where the performance is 0.49, a value that is below what would result from tossing a coin. This is considering that the 3-NN classifier is one of the best in the world, such that in Table 3 it looks like the best of all in six of the 20 datasets. These are real manifestations of the No-Free-Lunch theorem.

In some of the 20 datasets, the difference in performance is overwhelming. In the ecoli3 dataset, the best is the Naïve Bayes, with 0.86, while the closest is the MLP with 0.79. However, almost all the other classifiers are more than a tenth of a point (a very big difference), with the exception of SVM and the proposed model $LM({\tau }^{[9]})$.

However, there are also datasets in which the difference in performance between the classifiers is minimal. The ecoli-0_vs_1 dataset is a good example to illustrate this concept. It happens that the best value of BA corresponds to C4.5, whose performance is 0.98. By taking a closer look at what happens to the other classifiers, we can see that all of them exhibit a BA value of 0.97, which is only one hundredth of the best value. The exception is 3-NN, which is four hundredths. Here a valid question arises: considering that the five-fold cross-validation method includes a random step, is it possible that this minimal difference is due to this random step and does not indicate any superiority of C4.5 compared to the other classifiers?

One of the questions whose answer might seem very relevant when making value judgments about the supremacy of any of the classifiers in these datasets is the following: in how many of the 20 datasets was a classifying algorithm the best? The answer is in

Table 4. Number of datasets from Table 3 in which each algorithm obtained the best result of BA.

	NaïveBayes	3-NN	C4.5	Logit	SVM	MLP	Ada Boost	$\mathbf{LM}({\mathit{\tau }}^{[9]})$
Number of datasets in which the algorithm obtained the best BA	8	6	3	2	3	5	2	10

, which contains the number of datasets from Table 3 in which each algorithm obtained the best result of BA.

A quick look at Table 4 allows us to see that the proposed model $LM({\tau }^{[9]})$ is the best in 10 of the 20 datasets, closely followed by the Naïve Bayes, which is the best in eight of the 20 datasets, and third is the MLP, which is the best in five of the 20 datasets. If we were forced to make a quick value judgment on the supremacy of any of the eight classifiers, perhaps we would be inclined to express that the proposed model $LM({\tau }^{[9]})$ is the best, and that the second and third places are occupied by the Naïve Bayes and the MLP, respectively.

However, as we have detailed in the analysis of the previous paragraphs, the relationships between the data that of the performance of the classifiers are very varied. If in a certain dataset some classifier is the best, it turns out that the performances of that same classifier in other datasets is really bad.

For example, although it is indisputable that the proposed model $LM({\tau }^{[9]})$ is the best in 10 of the 20 datasets, it is pertinent to ask: What are its BA values in the other datasets with respect to the best classifier? Looking at Table 3, we can verify that in most of the remaining 10 datasets, the proposed model $LM({\tau }^{[9]})$ is very close to the best. However, an argument against giving the proposed model first place, would be that in the ecoli1 dataset the BA value it displays is the last, and that in the ecoli1 dataset, its BA value is far from the best (Naïve Bayes).

We should not neglect a relevant fact: the purpose of this comparative analysis is to find elements to decide how good a classifier is compared to others. This information is very useful at the moment when a certain researcher will have to decide which classifier of which approach would be convenient to use in his experiments.

Fortunately, there is a way to make a decision from this comparative analysis. The answer is found in statistical tests, which have been used in other areas of science and technology for many years. Some notable researchers have recommended using statistical tests to express the results of comparative statistical analyzes of a certain set of classifiers in a set of datasets [83,84].

There are several types of statistical test, in the comparison of multiple classifiers over multiple dataset. We focus on non-parametric, multiple comparisons tests for related samples, among which the Friedman test stands out [85,86]. The application of the Friedman test implies the creation of a block for each one of the analyzed subjects in such a way that blocks (for instance, datasets) contains observations coming from the application the different contrasts or treatments (for instance, algorithms). In terms of matrices, the blocks correspond to rows and treatments to columns.

Like every other comparison statistical test, the Friedman test works with two hypotheses: the null hypothesis H1 and alternative hypothesis H2. The null hypothesis establishes that the performances obtained by different treatments are equivalent, while the alternative hypothesis proposes that there is a difference between these performances, which would imply differences in the central tendency.

Let k be the number of treatments. Then, for each block a rank between 1 and k is assigned: 1 to the best result and k to the worst. In case of ties, the average rank is assigned. Next, the sum of the ranks of treatment j is assigned to variable $R_j$, $j=1,\dots ,k$. If the performances obtained from different treatments are equivalent, then $R_i=R_j$ for $i\ne j$. Thus, following this process, it is possible to determine when an observed disparity between $R_j$ (for every j) is enough to reject the null hypothesis. Let n be the number of blocks, and k be the number of treatments. Then, the Friedman statistic (S) is given by:

$$S=\frac{12}{nk(k+1)}\left({\displaystyle \sum _{j=1}^k{R}_j^2}\right)-3n(k+1)$$

(67)

Statistical tests are subject to a certain predetermined number of blocks and treatments to have the adequate power. If the number of samples (blocks) used in the experiments is small, statistical tests lack of power to determine the existence of statistically significant differences between the performances of the algorithms (treatments) [85]. The required number of samples to obtain satisfactory results is given by the expression $n\ge 2k$.

In this research, 20 datasets were used, which means that at most ten algorithms can be compared through the Friedman test, without losing statistical power. The condition is fulfilled because in our experiments we compare eight classifiers.

Taking the data from Table 3 as a base, a statistical test that is applied correctly can tell us if there are significant statistical differences in these data. To determine the existence or not of significant differences, we use hypothesis tests: null hypothesis H1 and alternative hypothesis H2:

Hypothesis 1 (H1).

there are no differences in the performance of the compared algorithms.

Hypothesis 2 (H2).

the proposed model$LM({\tau }^{[9]})$exhibits a better performance than the other seven supervised classification algorithms.

Due to the relationship between the number of classifiers and the number of datasets, we decided to use the non-parametric Friedman test [85,86]. There are two results from this test: a probability value (p-value) and a ranking of the classifiers involved in the experiment, where the lowest value is the best. It is common in this type of tests to set the value of statistical significance to 95%, which gives a value $\alpha =0.05$.

If the result that the Friedman test gives us for the p-value is less than or equal to alpha, then the null hypothesis is rejected. The p-value obtained by the Friedman test in the data in Table 3 is 0.004989, which indicates that the Friedman test rejects the null hypothesis H1.

The results of the Friedman ranking are shown in

Table 5. Rankings obtained by the Friedman test.

Algorithm	Ranking
${\mathrm{LM}}_{({\tau }^{[9]})}$	3.000
MLP	3.550
Naïve Bayes	3.675
3-NN	4.925
AdaBoost	5.100
SVM	5.125
Logit	5.300
C4.5	5.325

. As shown, the proposed model $LM({\tau }^{[9]})$ was the best ranked algorithm, according to Friedman test.

Since the Friedman test determined the existence of significant differences between the performances of the algorithms, a post hoc test is highly recommended to find in which of the compared algorithms those differences exist. Among several post hoc tests suggested [83], we chose the Holm test [87]. The Holm test was designed to reduce the Type I error, which occurs when the null hypothesis is rejected even if it is true. It is usual to analyze phenomena that include several hypotheses. In these cases, we seek to adjust the rejection criteria for each of the hypotheses.

The process begins with an upward sorting of p-values of each hypothesis. Once sorted, each one of those p-values is compared with the ratio of the significance level divided by the total number of hypotheses of which the p-value has not been compared. When a p-value greater than the ratio is found, all the null hypotheses associated to the p-values that had been compared are rejected.

Thus, let $H_1,\dots H_k$ be k hypotheses and $p_1,\dots p_k$ the corresponding p-values. When sorting the p-values upward, we have a new notation: $p_{\left(1\right)},\dots p_{\left(k\right)}$ denote the sorted p-values and $H_{\left(1\right)},\dots H_{\left(k\right)}$ for the hypothesis associated. If α is the significance level and j is the minimum index for which $p_{\left(j\right)}>\frac{\alpha }{k-j+1}$ is true, then the null hypotheses $H_{\left(1\right)},\dots H_{\left(j-1\right)}$ are rejected.

To determine with respect to which algorithms the proposed model $LM({\tau }^{[9]})$ (best ranked) has significant differences in performance, we use the Holm post hoc test [87], as shown in

Table 6. Post hoc comparison table for Holm test.

I	Algorithm	Z	P (unadjusted)	Holm
7	C4.5	3.001562	0.002686	0.007143
6	Logit	2.969287	0.002985	0.008333
5	SVM	2.743363	0.006081	0.010000
4	AdaBoost	2.711088	0.006706	0.012500
3	3-NN	2.485164	0.012949	0.016667
2	Naïve Bayes	0.871421	0.383524	0.025000
1	MLP	0.710047	0.477675	0.050000

.

In this experiment, Holm’s procedure rejects those hypotheses that have an unadjusted p-value lower or equal than 0.025.

The Holm test rejects the null hypothesis for 3-NN, AdaBoost, SVM, Logit, and C4.5. In all cases, the unadjusted p-values were lower than 0.025. That is, we can assure that the proposed model $LM({\tau }^{[9]})$ has a performance significantly better than the aforementioned classifiers.

For the MLP and Naïve Bayes algorithm, the test did not reject the null hypothesis, due to 0.47 and 0.38 being greater than 0.025. For now, we can conclude that, within 95% confidence, the proposed model $LM({\tau }^{[9]})$ is better than the best state-of-the-art classifiers with which the comparison was made. This is in terms of the BA performance measure, and with the exception of these two classifiers: MLP and Naïve Bayes.

6. Conclusions and Future Work

The first conclusion that we will state is related to the way in which new ideas arise in science. Anecdotes abound in the history of science about the emergence of new ideas and concepts (Newton’s apple, Kekulé’s dream with snakes, among other interesting stories, which may or may not be real). In our case, keeping the proportions, the idea of the new transform emerged spontaneously in a daily work meeting with the Alpha-Beta group. For years, we had before us the overwhelming results of Theorem 1, which we arrived at thanks to the new framework that we created from 2001 onwards. There were many attempts by group members to improve the results of the Lernmatrix, but they were unsuccessful. Until that successful day when a disruptive idea emerged, the key question we asked ourselves was: what would happen if we do something to modify the pattern data so that the patterns fulfill the strong condition of Theorem 1? The point was to break the strong condition of Theorem 1, which marks the disruptive nature of the new investigation. From that moment on, we worked hard in the search for some transform that is capable of eliminating the subtractive alteration, until we found it. The rest is history: we recovered some concepts and algorithms from our work, and then we structured the proposed model described in detail in Section 4.

The second conclusion is related to the results of Table 3 and their interpretation. As discussed in Section 5, it is difficult from raw data to make decisions about classifier comparisons. From this reflection arises the need to make use of statistical tests, which give great support to decision-making. Our conclusion regarding this issue is that we must emphasize the importance of tests of statistical significance (like Friedman’s) and post hoc tests (like Holm’s). Table 5 and Table 6 are the clear result of the importance of this type of test in comparative experimental analyzes.

The experimental results allow us to conclude that the application of the new transform, together with the other concepts and included in the proposed model, result in a significant improvement in the performance of the Lernmatrix as a pattern classifier. This information is very useful at the moment when a certain researcher will have to decide which classifier of which approach would be convenient to use in his experiments. When reviewing the results in Table 3 and the corresponding statistical tests, some researchers will decide to use our proposed model. This is very useful for the Alpha-Beta group, because it gives us elements to continue with the research efforts, with the aim of increasing the performance of our models even more.

The relevant future work arises from a brief analysis of Theorem 1 and from a simple reflection. The theorem only considered patterns that exhibit subtractive alteration with respect to some pattern of the learning set. But what happens to the patterns that do not exhibit subtractive alteration but additive alterations with respect to some pattern of the learning set? The following case is even more interesting: what happens to patterns that exhibit mixed or mixed alterations with respect to some pattern of the learning set? These ideas are “like ground gold” for researchers who are interested in continuing this fruitful research work, in order to improve the performance of the Lernmatrix.