Multi-Stack Lifetime Improvement through Adapted Power Electronic Architecture in a Fuel Cell Hybrid System
Abstract
1. Introduction
2. Proposed System Configuration
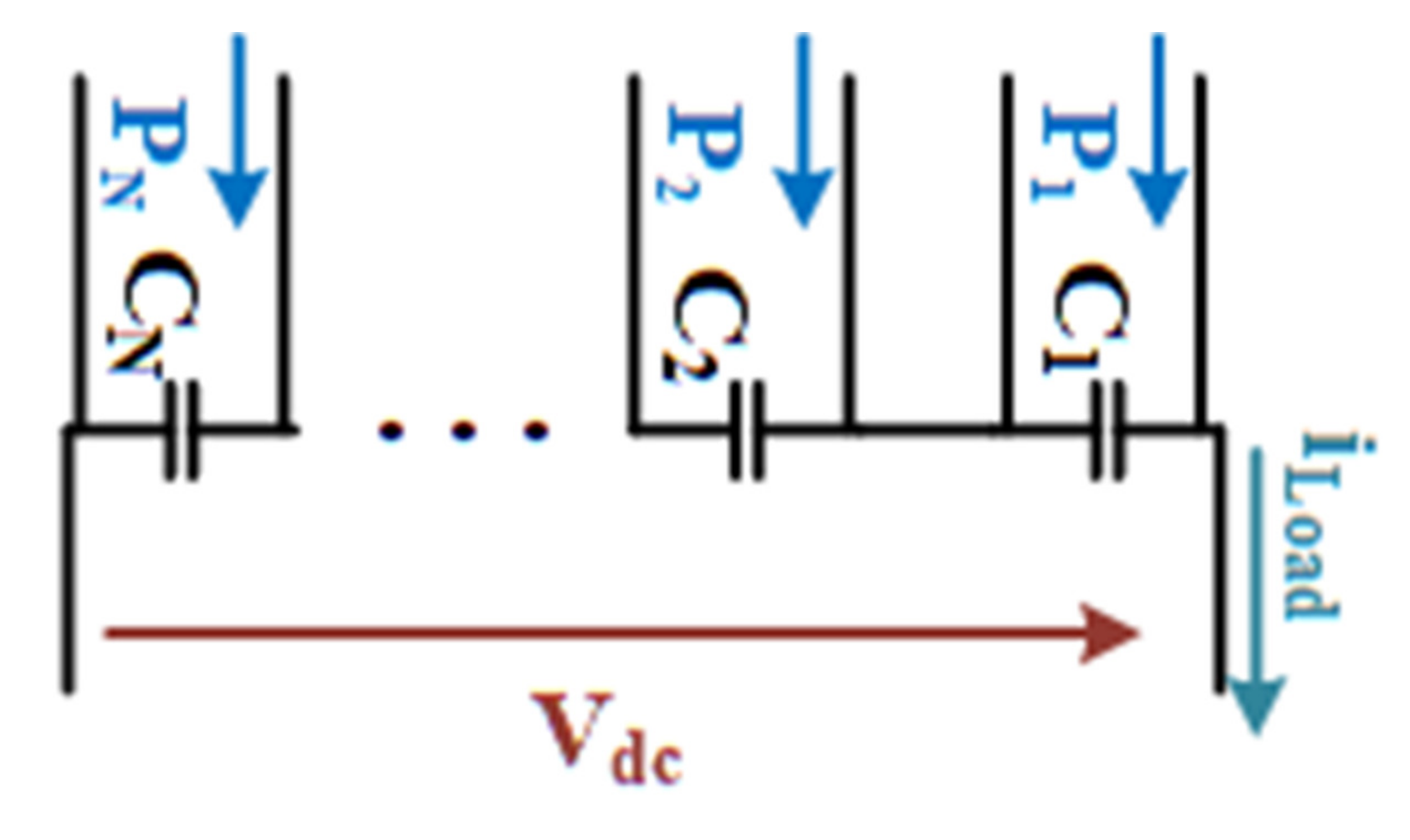
2.1. Model of the Equalizer
- (1)
- Turn ratio for all secondary windings are the same and equal to and k is the coupling coefficient.
- (2)
- The coupling coefficient between the primary and secondary windings are identical and equal to k.
- (3)
- The coupling coefficient between the secondary windings is unitary.
- (4)
- The DC bus voltage is controlled to a reference constant value.
- (5)
- The switches are considered as the ideal devices. The diode voltage drops are taken into account but their dynamical resistance is assumed zero.
- (1)
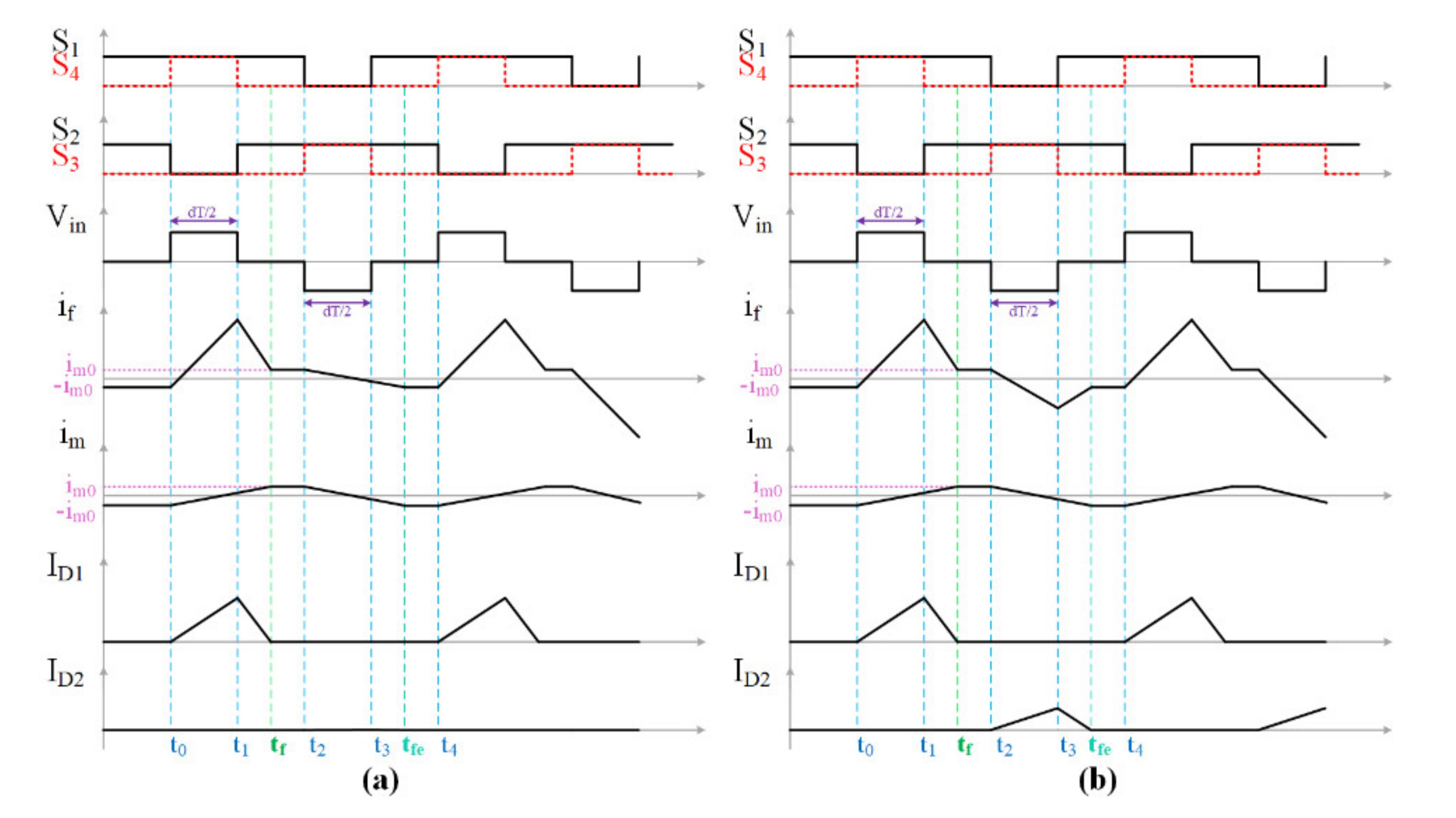
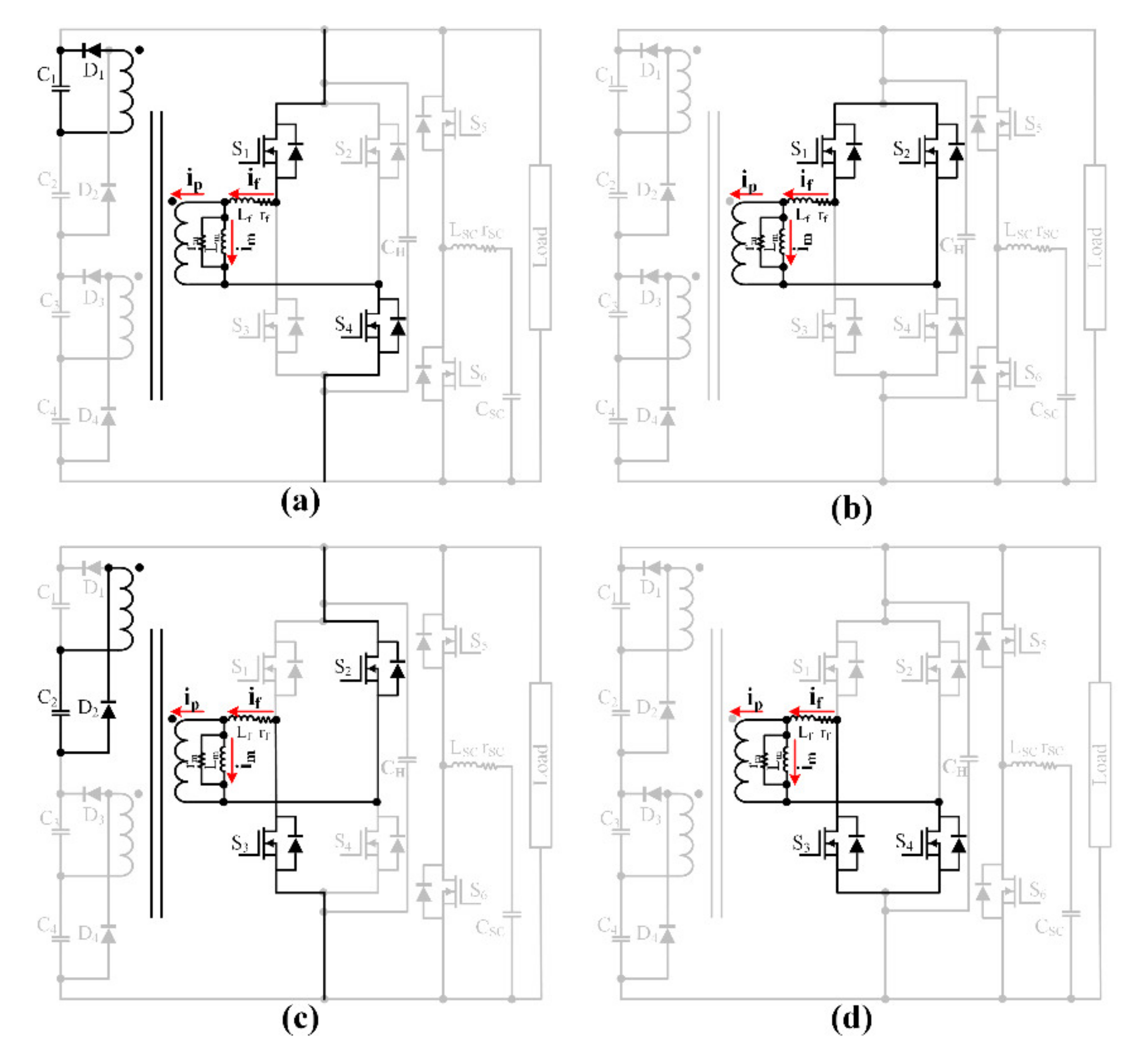
- Mode 1 [t0–t1: Figure 5a]: Based on the switching command of the H-bridge inverter, a positive voltage is imposed on the primary side of the transformer. Regarding the assumption that the first capacitor has the lower voltage between the odd-numbered capacitor, the first diode is turned on and the derivative equation of the system is as follows:where Lm and Lf are, respectively, the magnetic and leakage inductances, rm and rf are the magnetic and leakage resistances, im is the magnetizing current, if is the leakage current, Vd is the diode drop voltage, Vin is the input voltage at the primary side of the transformer, Vcj is the voltage of Cj, Pj is the injected power by the boost converter corresponding to the jth fuel cell, and iload is the load current.
- (2)
- Mode 2 [t1–t2: Figure 5b]: The input voltage of the HF transformer is equal to zero in this mode. D1 can continue to conduct during the interval of [t1,tf] and, as a result, the derivative equations of the system are as follows:The switching frequency of the H-bridge inverter is low enough that the diode can be turned off before the end of this mode. As a result, the derivative equations of the system during the interval of [tf,t2] are as following when the diode is off:
- (3)
- Mode 3 [t2–t3: Figure 5c]: A negative voltage is imposed on the primary side of the HF transformer in this mode. As a result, the second diode corresponding to the lower voltage capacitor among even-numbered capacitors starts to conduct. The derivative equations of the system are as follows:It can be noted that this mod does not exist for Figure 4a.
- (4)
- Mode 4 [t3–t4: Figure 5d]: This mode is similar to mode 2 but due to negative voltage imposed on the primary side of the HF transformer, the even-numbered diodes can be turned on. Since the second capacitor is assumed to be the lower voltage capacitor between the even-numbered capacitors, the second diode begins to conduct the current. The derivative equation of the system before the diode stops to conduct is as following during the interval of [t3,tfe]:
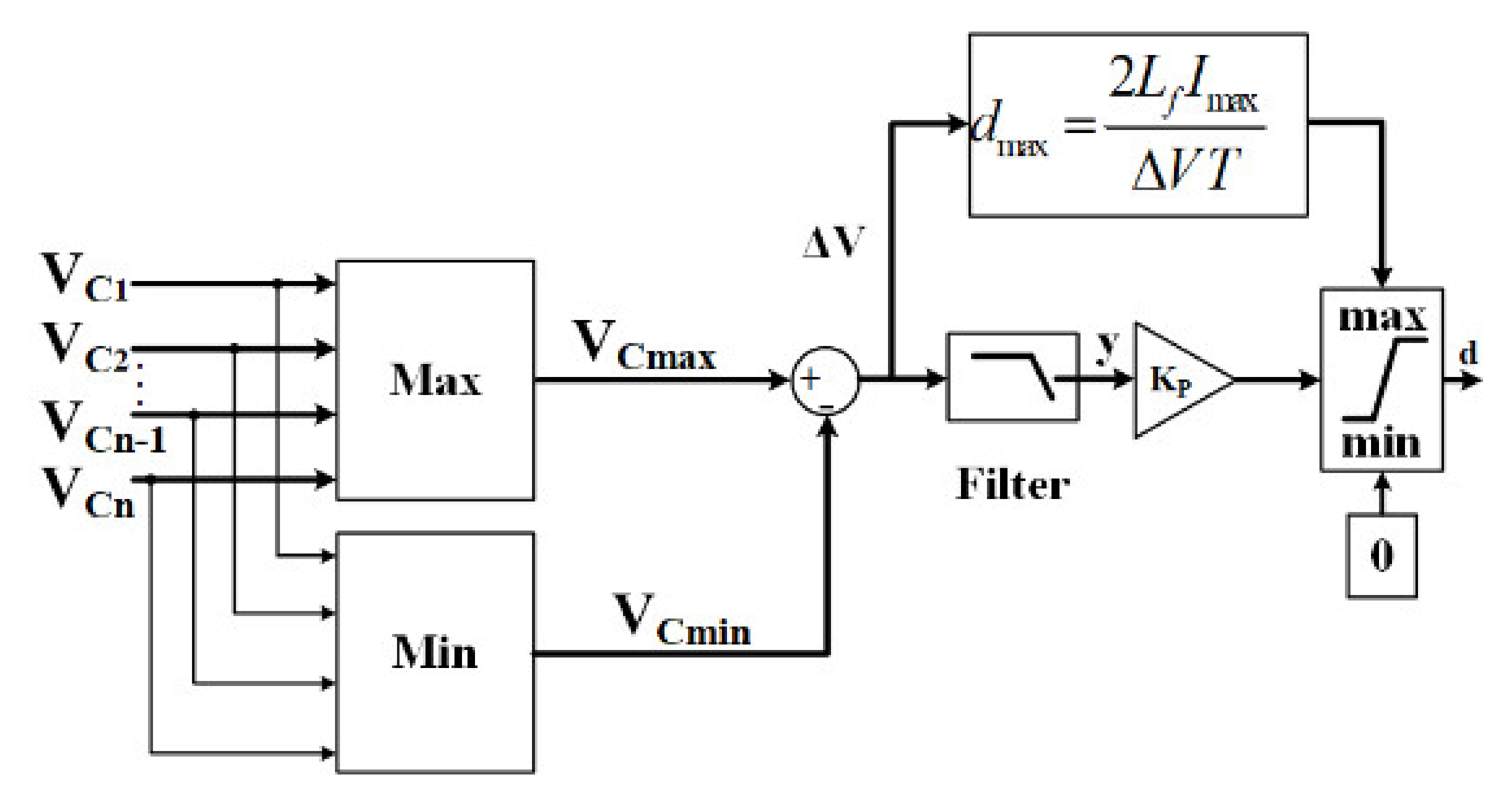
2.2. Improved Control Method for the Equalizer
2.3. Average Model
3. Hybridization
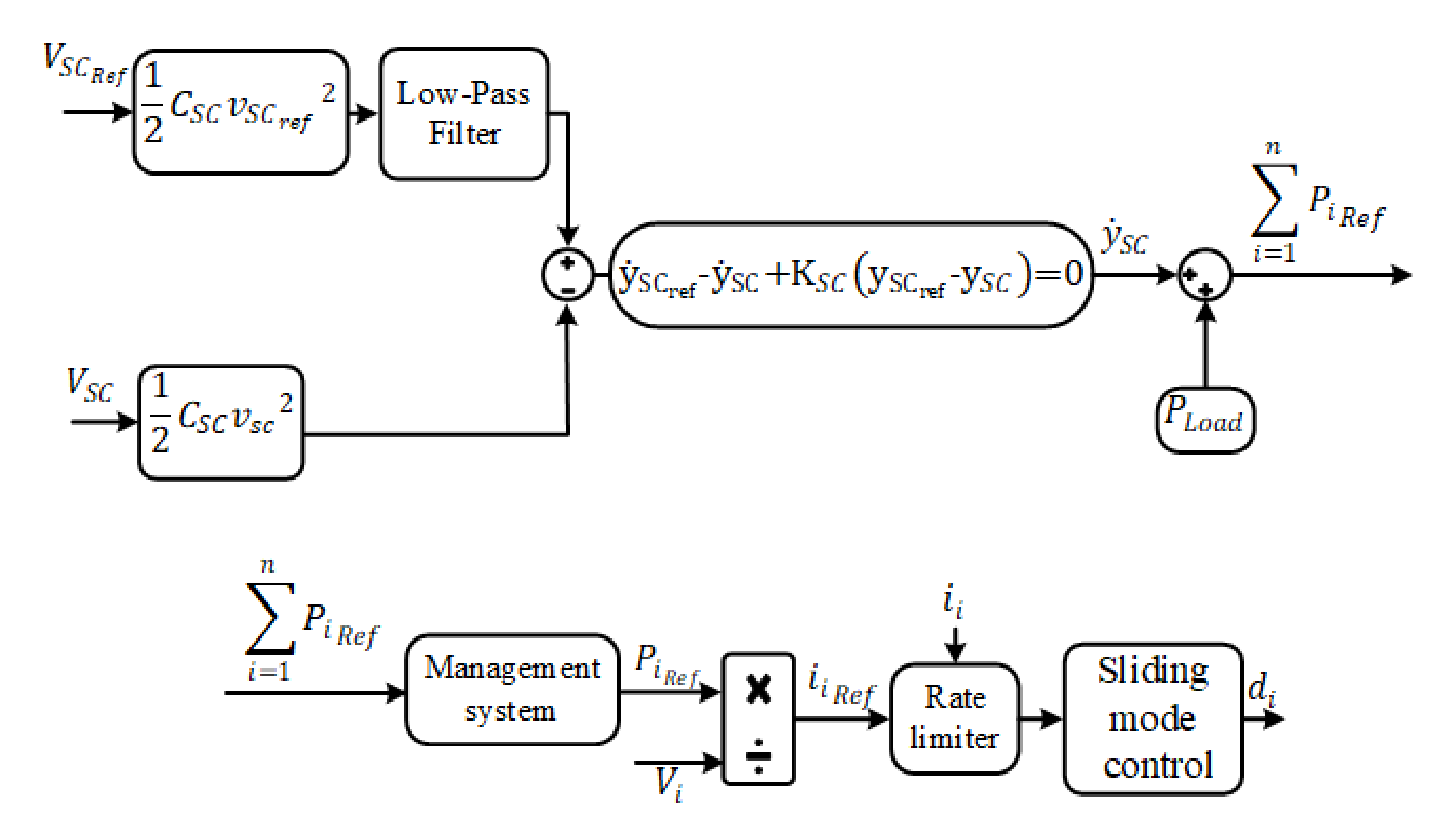
3.1. DC Bus Voltage Controller
3.2. SC Voltage Controller
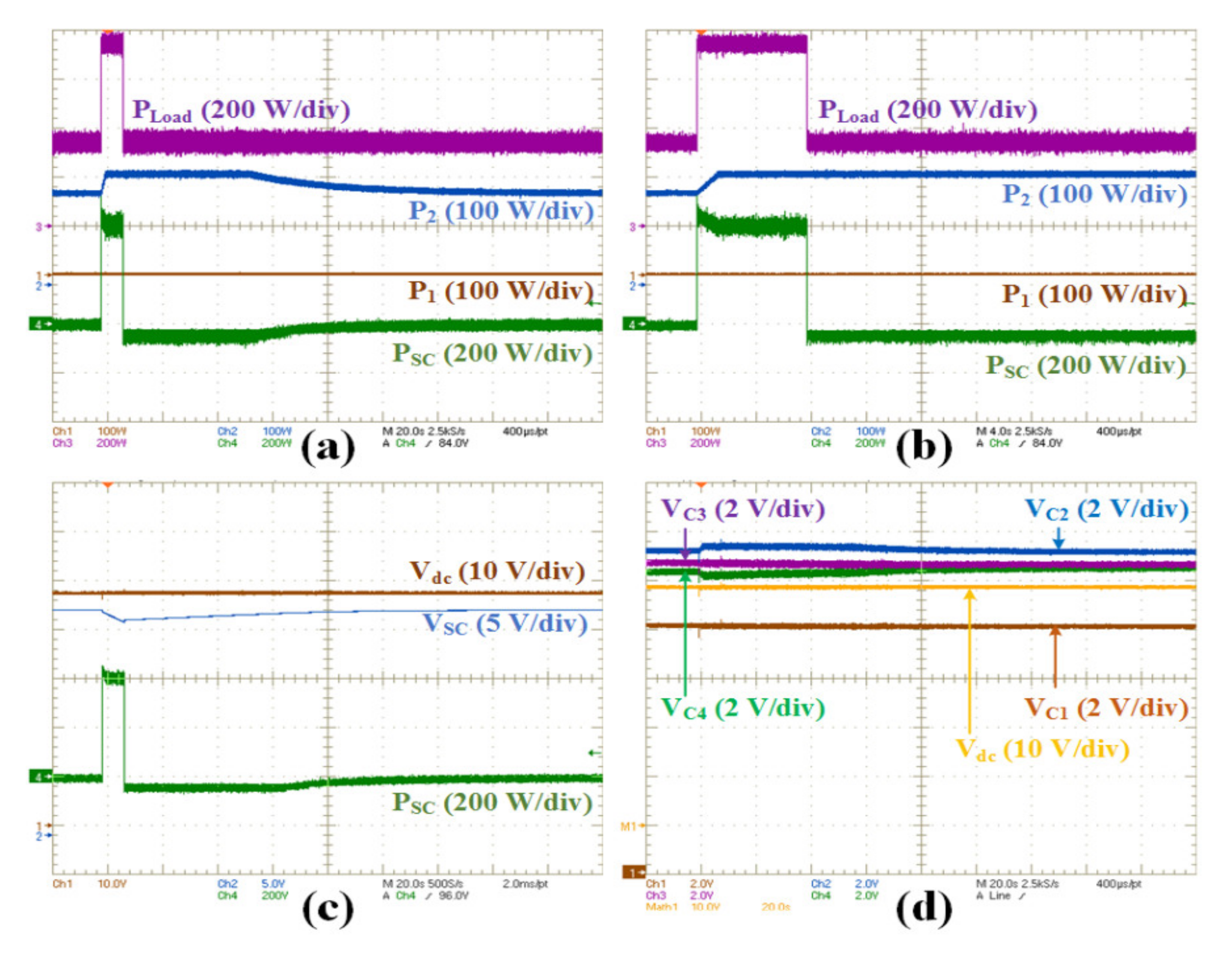
4. Simulation and Experimental Results
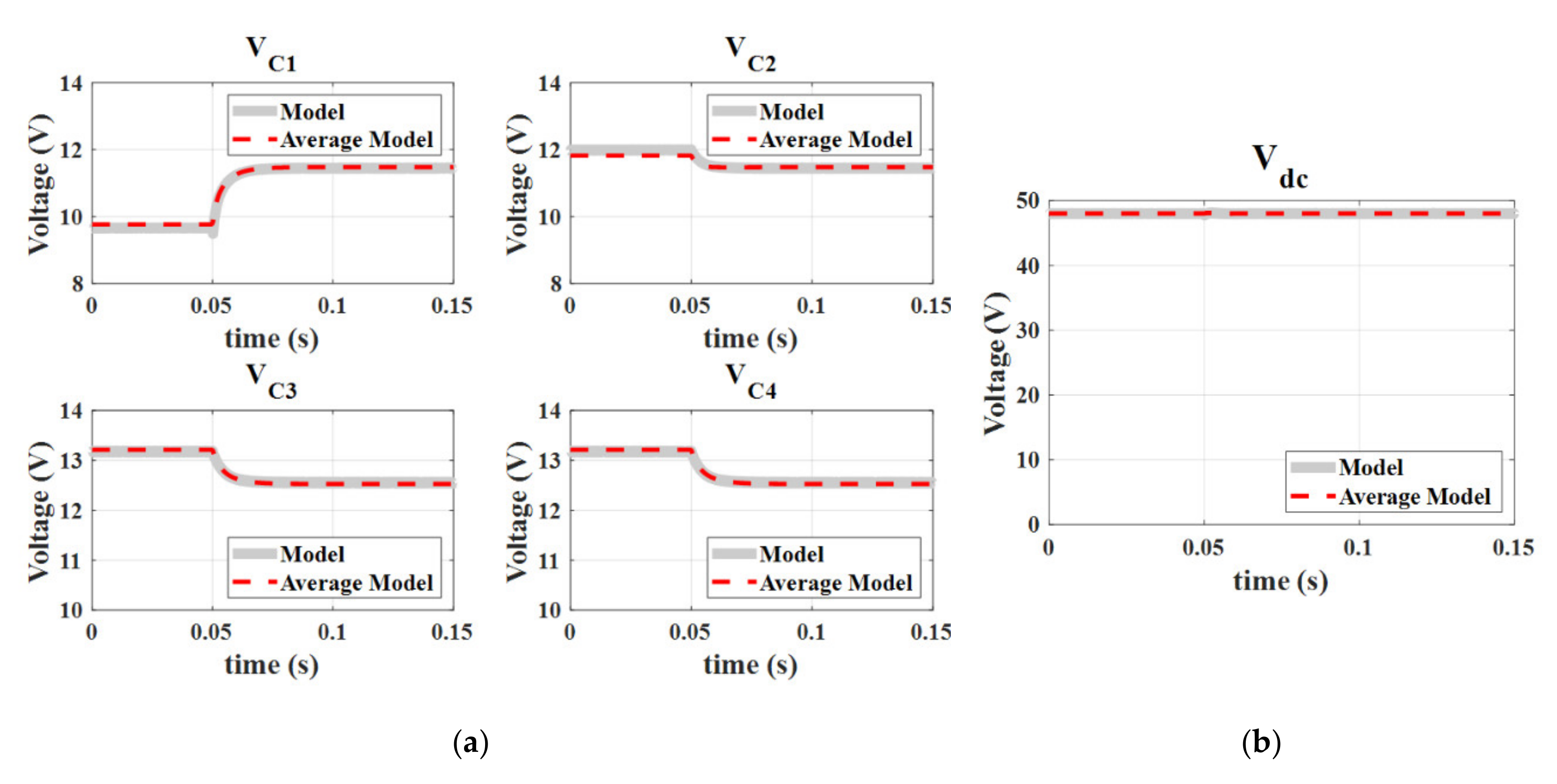
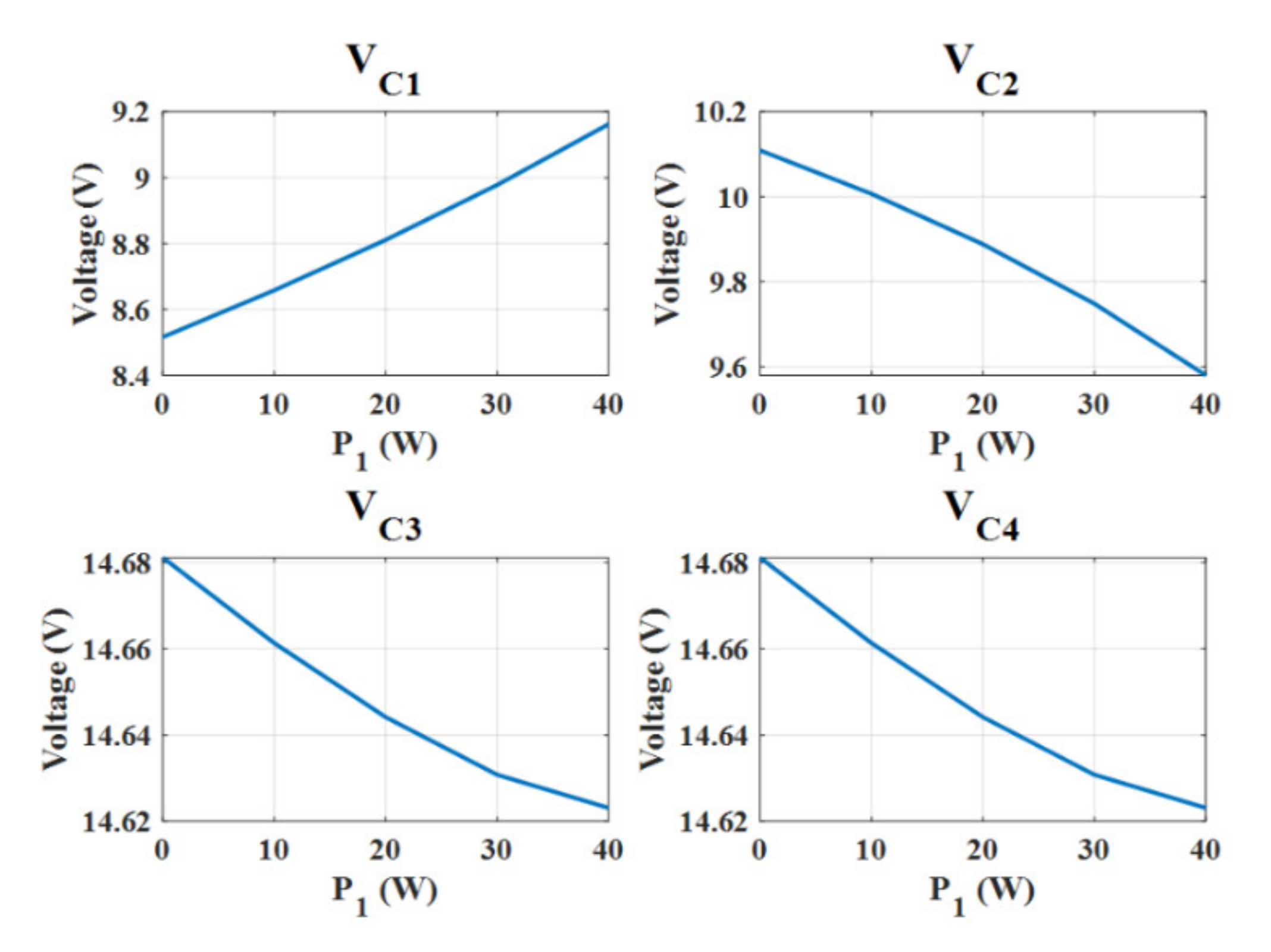
4.1. Simulation Results
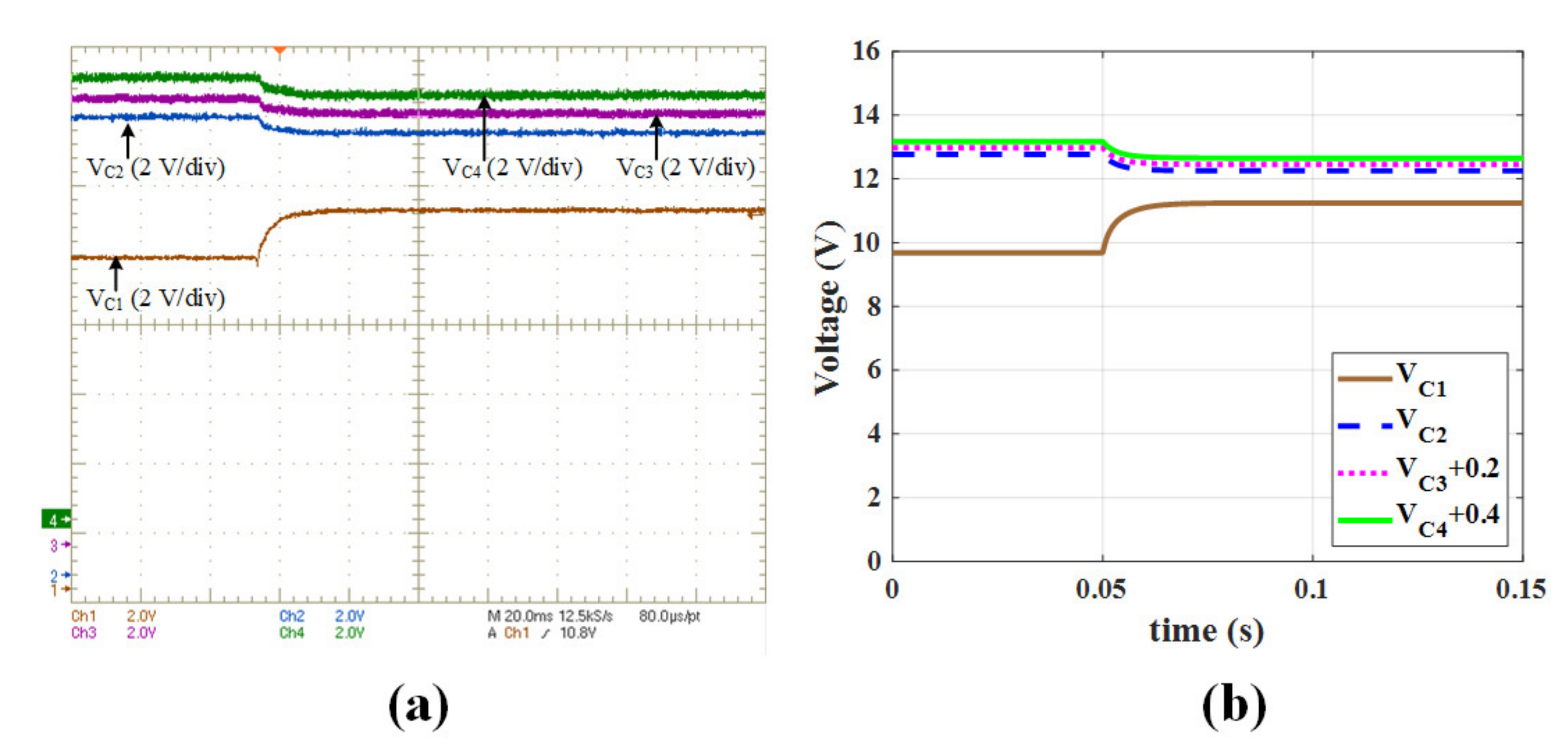
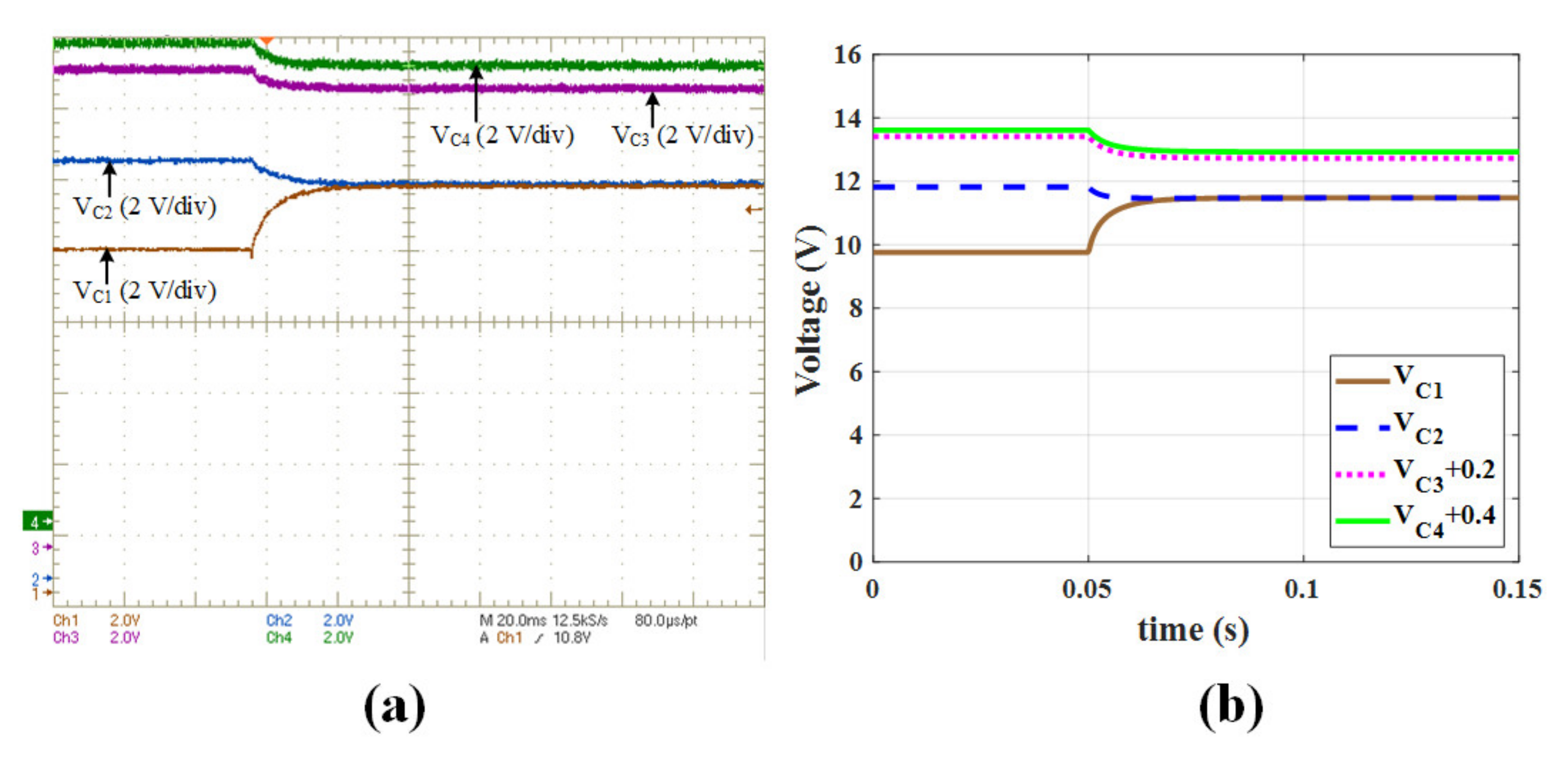
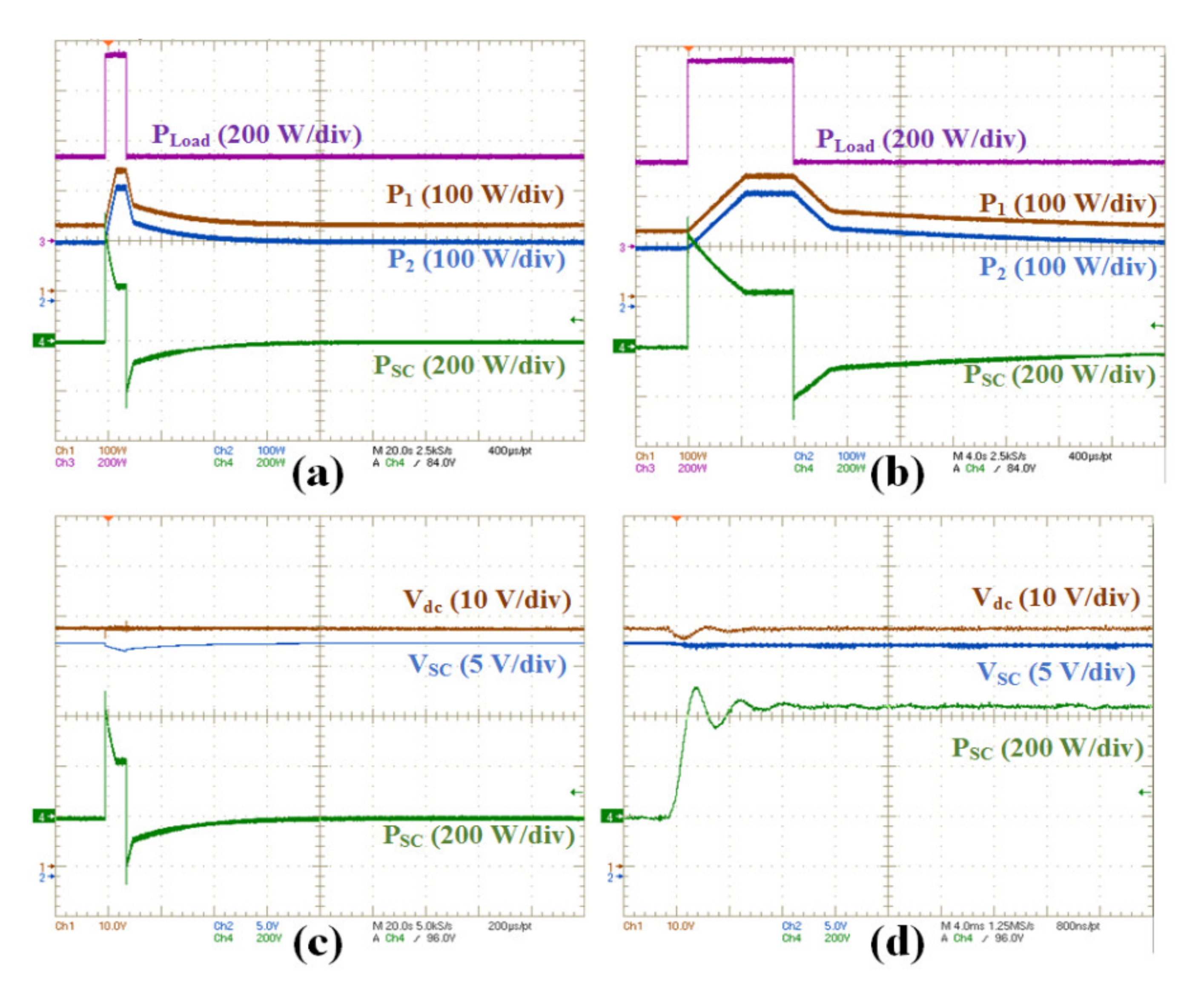
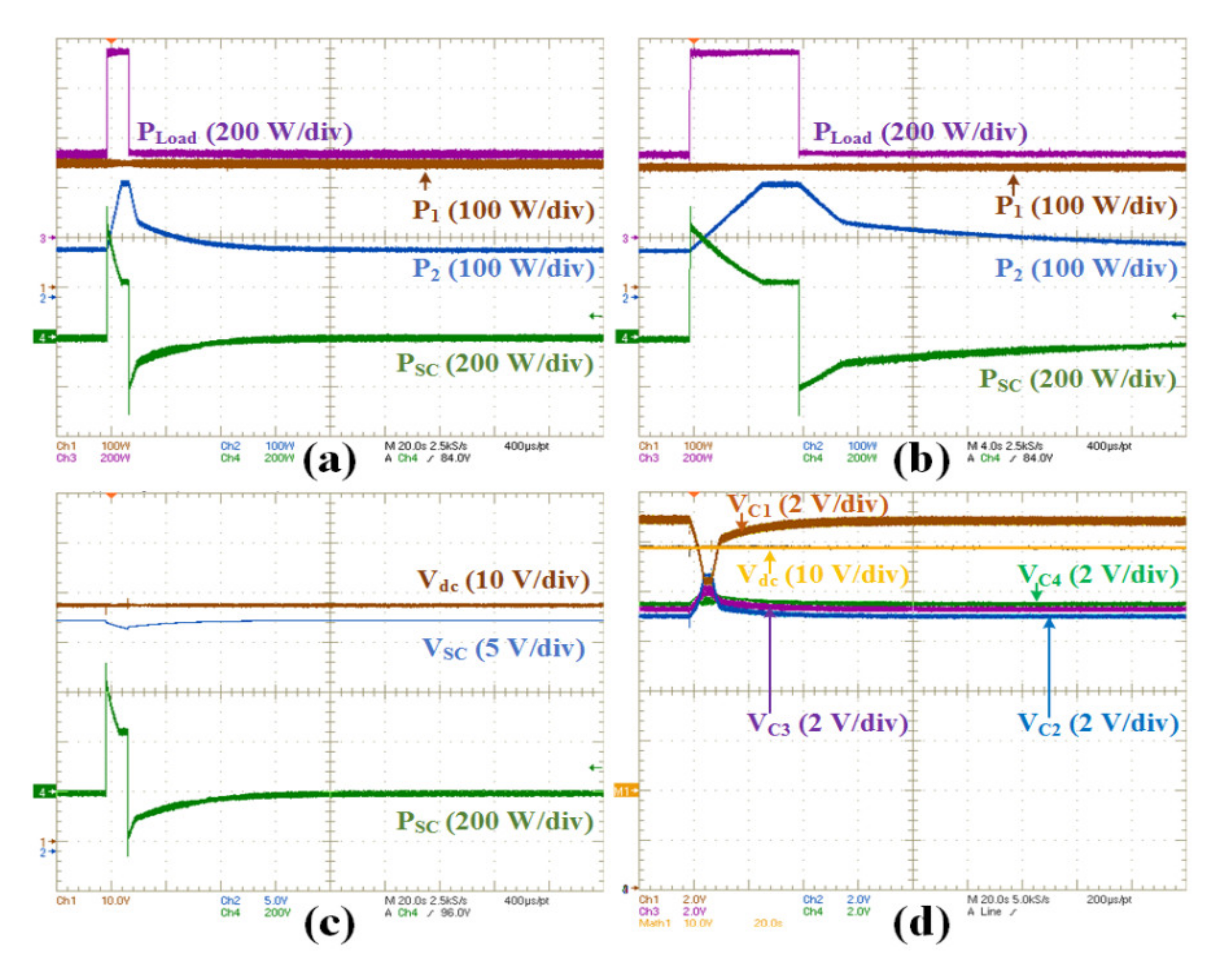
4.2. Experimental Results
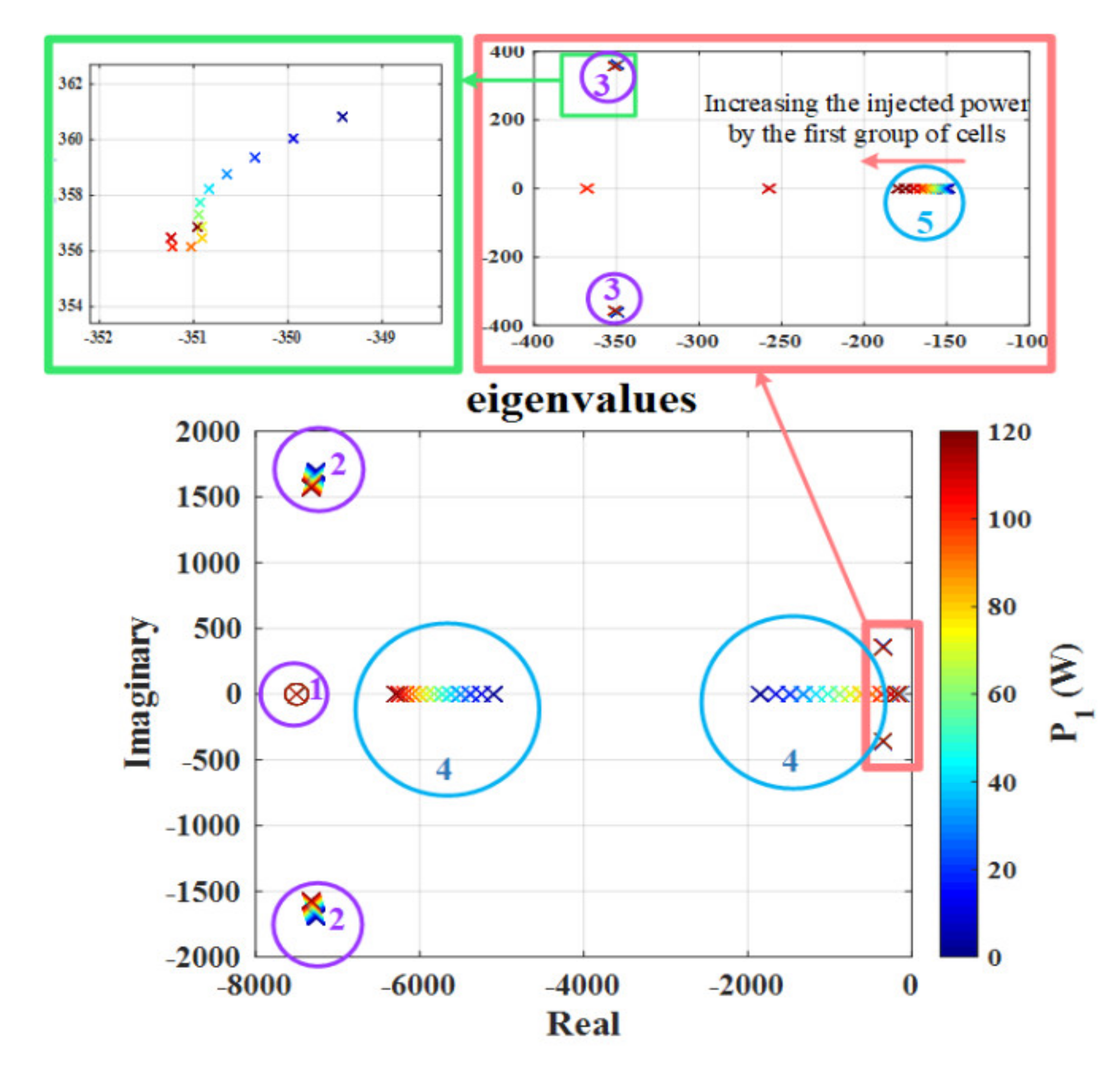
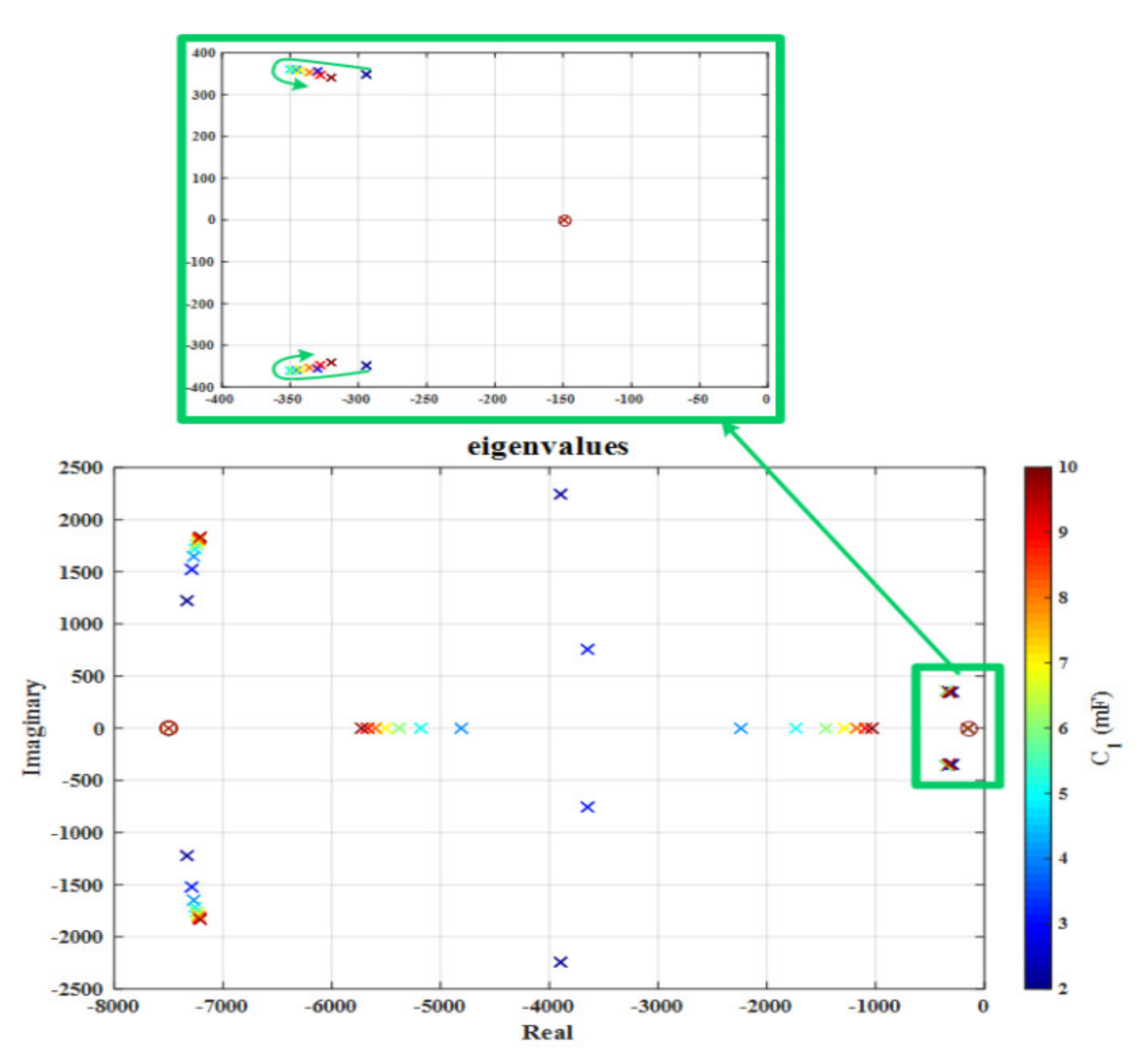
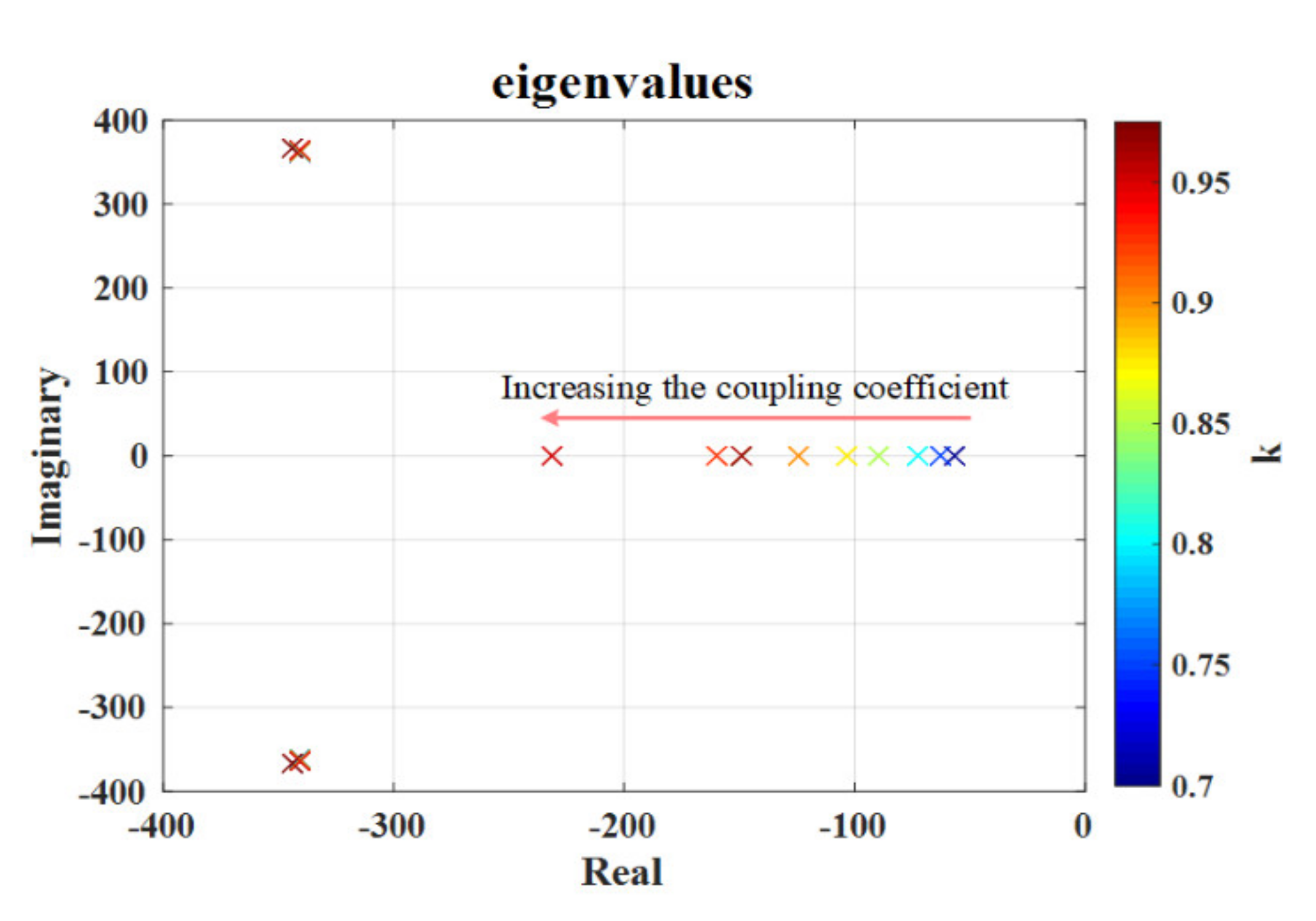
5. Stability Analysis and Energy Management
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bizon, N.; Thounthong, P. Energy efficiency and fuel economy of a fuel cell/renewable energy sources hybrid power system with the load-following control of the fueling regulators. Mathematics 2020, 8, 151. [Google Scholar] [CrossRef]
- Zandi, M.; Bahrami, M.; Eslami, S.; Gavagsaz-Ghoachani, R.; Payman, A.; Phattanasak, M.; Nahid-Mobarakeh, B.; Pierfederici, S. Evaluation and comparison of economic policies to increase distributed generation capacity in the Iranian household consumption sector using photovoltaic systems and RET Screen software. Renew. Energy 2017, 107, 215–222. [Google Scholar] [CrossRef]
- Bahrami, M.; Gavagsaz-Ghoachani, R.; Zandi, M.; Phattanasak, M.; Maranzanaa, G.; Nahid-Mobarakeh, B.; Pierfederici, S.; Meibody-Tabar, F. Hybrid maximum power point tracking algorithm with improved dynamic performance. Renew. Energy 2019, 130, 982–991. [Google Scholar] [CrossRef]
- El-fergany, A.A.; Hasanien, H.M.; Agwa, A.M. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 2019, 201, 112197. [Google Scholar] [CrossRef]
- Parol, M.; Wójtowicz, T.; Księżyk, K.; Wenge, C. Optimum management of power and energy in low voltage microgrids using evolutionary algorithms and energy storage. Int. J. Electr. Power Energy Syst. 2020, 119, 105886. [Google Scholar] [CrossRef]
- Lan, T.; Strunz, K. Modeling of multi-physics transients in PEM fuel cells using equivalent circuits for consistent representation of electric, pneumatic, and thermal quantities. Int. J. Electr. Power Energy Syst. 2020, 119, 105803. [Google Scholar] [CrossRef]
- Yoshida, T.; Kojima, K. Toyota MIRAI fuel cell vehicle and progress toward a future hydrogen society. Interface Mag. 2015, 24, 45–49. [Google Scholar] [CrossRef]
- Matsunaga, M.; Fukushima, T.; Ojima, K. Powertrain system of Honda FCX clarity fuel cell vehicle. World Electr. Veh. J. 2009, 3, 820–829. [Google Scholar] [CrossRef]
- Wang, J. System integration, durability and reliability of fuel cells: Challenges and solutions. Appl. Energy 2017, 189, 460–479. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Liu, X.; Yan, J. Enhancing fuel cell durability for fuel cell plug-in hybrid electric vehicles through strategic power management. Appl. Energy 2019, 241, 483–490. [Google Scholar] [CrossRef]
- Samavatian, V.; Radan, A. A novel low-ripple interleaved buck—Boost converter with high efficiency and low oscillation for fuel-cell applications. Int. J. Electr. Power Energy Syst. 2014, 63, 446–454. [Google Scholar] [CrossRef]
- Maranzana, G.; Didierjean, S.; Dillet, J.; Thomas, A.; Lottin, O. Improved Fuel Cell. U.S. Patent WO/2014/060198, 24 April 2014. [Google Scholar]
- Wang, T.; Li, Q.; Yin, L.; Chen, W. Hydrogen consumption minimization method based on the online identification for multi-stack PEMFCs system. Int. J. Hydrog. Energy 2019, 4, 5074–5081. [Google Scholar] [CrossRef]
- Ozpineci, B. Optimum fuel cell utilization with multilevel DC—DC converters. In Proceedings of the 19th Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004. [Google Scholar]
- Ozpineci, B.; Case, A.A. Multiple input converters for fuel cells. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004. [Google Scholar]
- Lopes, C.; Kelouwani, S.; Boulon, L.; Agbossou, K.; Marx, N.; Ettihir, K. Neural network modeling strategy applied to a multi-stack PEM fuel cell system. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–7. [Google Scholar]
- Ramadan, H.S.; de Bortoli, Q.; Becherif, M.; Claude, F. Multi-stack fuel cell efficiency enhancement based on thermal management. IET Electr. Syst. Transp. 2016, 7, 65–73. [Google Scholar]
- Marx, N.; Cardenas, D.C.T.; Boulon, L.; Gustin, F.; Hissel, D. Degraded mode operation of multi-stack fuel cell systems. IET Electr. Syst. Transp. 2016, 6, 3–11. [Google Scholar] [CrossRef]
- Cardenas, D.C.T.; Hissel, D.; Marx, N.; Boulon, L.; Gustin, F. Degraded mode operation of multi-stack fuel cell systems. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014. [Google Scholar]
- Garcia, J.E.; Herrera, D.F.; Boulon, L.; Sicard, P.; Hernandez, A. Power sharing for efficiency optimisation into a multi fuel cell system. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 218–223. [Google Scholar]
- Candusso, D.; De Bernardinis, A.; Peera, M.-C.; Harel, F.; Francois, X.; Hissel, D.; Coquery, G.; Kauffmann, J.-M. Fuel cell operation under degraded working modes and study of diode by-pass circuit dedicated to multi-stack association. Energy Convers. Manag. 2008, 49, 880–895. [Google Scholar] [CrossRef]
- Lape, N.; Dudfield, C.; Orsillo, A. Environmentally friendly power sources for aerospace applications. J. Power Sources 2008, 181, 353–362. [Google Scholar]
- Miller, A.R.; Hess, K.S.; Barnes, D.L.; Erickson, T.L. System design of a large fuel cell hybrid locomotive. J. Power Sources 2007, 173, 935–942. [Google Scholar] [CrossRef]
- Von Helmolt, R.; Eberle, U. Fuel cell vehicles: Status 2007. J. Power Sources 2007, 165, 833–843. [Google Scholar] [CrossRef]
- Hamad, K.B.; Taha, M.H.; Almaktoof, A.; Kahn, M.T.E. Modelling and analysis of a grid-connected megawatt fuel cell stack. In Proceedings of the 2019 International Conference on the Domestic Use of Energy (DUE), Wellington, South Africa, 25–27 March 2019; pp. 147–155. [Google Scholar]
- Cardozo, J.; Marx, N.; Hissel, D. Comparison of multi-stack fuel cell system architectures for residential power generation applications including electrical vehicle charging. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 2–7. [Google Scholar]
- Wang, C.; Nehrir, M.H.; Gao, H. Control of PEM fuel cell distributed generation systems. IEEE Trans. Energy Convers. 2006, 21, 586–595. [Google Scholar] [CrossRef]
- Marx, N.; Boulon, L.; Gustin, F.; Hissel, D.; Agbossou, K. A review of multi-stack and modular fuel cell systems: Interests, application areas and on-going research activities. Int. J. Hydrogen Energy 2014, 39, 12101–12111. [Google Scholar] [CrossRef]
- Arunkumari, T.; Indragandhi, V. An overview of high voltage conversion ratio DC-DC converter configurations used in DC micro-grid architectures. Renew. Sustain. Energy Rev. 2017, 77, 670–687. [Google Scholar] [CrossRef]
- Wu, Q.; Member, S.; Wang, Q.; Xu, J. A high efficiency step-up current-fed push-pull quasi-resonant converter with fewer components for fuel cell application. IEEE Trans. Ind. Electron. 2016, 64, 6639–6648. [Google Scholar] [CrossRef]
- Bahrami, M.; Martin, J.; Maranzana, G.; Pierfederici, S.; Weber, M.; Meibody-Tabar, F.; Zandi, M. Design and modeling of an equalizer for fuel cell energy management systems. IEEE Trans. Power Electron. 2019, 24, 10925–10935. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Cui, Y.; Zou, J.; Yang, S. A multi winding transformer cell-to-cell active equalization method for lithium-ion batteries with reduced number of driving circuits. IEEE Trans. Power Electron. 2016, 31, 4916–4929. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Ker, P.J.; Majlan, E.H.; Wan Daud, W.R. Optimization of energy management system for fuel-cell hybrid electric vehicles: Issues and recommendations. Appl. Energy 2018, 228, 2061–2079. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Marzougui, H.; Kadri, A.; Martin, J.; Amari, M.; Pierfederici, S. Implementation of energy management strategy of hybrid power source for electrical vehicle. Energy Convers. Manag. 2019, 195, 830–843. [Google Scholar] [CrossRef]
- Lü, X.; Qu, Y.; Wang, Y.; Qin, C.; Liu, G. A comprehensive review on hybrid power system for PEMFC-HEV: Issues and strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar] [CrossRef]
- Marx, N.; Hissel, D.; Gustin, F.; Boulon, L.; Agbossou, K. On the sizing and energy management of an hybrid multistack fuel cell e battery system for automotive applications. Int. J. Hydrog. Energy 2016, 42, 1518–1526. [Google Scholar] [CrossRef]
- Lü, X.; Wang, P.; Meng, L.; Chen, C. Energy optimization of logistics transport vehicle driven by fuel cell hybrid power system. Energy Convers. Manag. 2019, 199, 111887. [Google Scholar] [CrossRef]
- Zhan, Y.; Wang, H.; Zhu, J. Modelling and control of hybrid UPS system with backup PEM fuel cell/battery. Int. J. Electr. Power Energy Syst. 2012, 43, 1322–1331. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Ding, D. Predictive energy management of fuel cell supercapacitor hybrid construction equipment. Energy 2018, 149, 718–729. [Google Scholar] [CrossRef]
- Bizon, N.; Lopez-Guede, J.M.; Kurt, E.; Thounthong, P.; Gheorghita, A.; Mihai, L.; Iana, G. Hydrogen economy of the fuel cell hybrid power system optimized by air flow control to mitigate the effect of the uncertainty about available renewable power and load dynamics. Energy Convers. Manag. 2019, 179, 152–165. [Google Scholar] [CrossRef]
- Bizon, N.; Cristian, I. Hydrogen saving through optimized control of both fueling flows of the fuel cell hybrid power System under a variable load demand and an unknown renewable power profile. Energy Convers. Manag. 2019, 184, 1–14. [Google Scholar] [CrossRef]
- Phattanasak, M.; Martin, J.; Pierfederici, S.; Davat, B. Predicting the onset of bifurcation and stability study of a hybrid current controller for a boost converter. Math. Comput. Simul. 2013, 91, 262–273. [Google Scholar]
- Gavagsaz-ghoachani, R.; Phattanasak, M.; Zandi, M.; Martin, J.; Pierfederici, S.; Nahid-mobarakeh, B.; Davat, B. Estimation of the bifurcation point of a modulated-hysteresis current-controlled DC—DC boost converter: Stability analysis and experimental verification. IET Power Electron. 2015, 8, 2195–2203. [Google Scholar] [CrossRef]
- Saublet, L.; Gavagsaz-Ghoachani, R.; Martin, J.; Nahid-mobarakeh, B.; Member, S.; Pierfederici, S. Bifurcation analysis and stabilization of DC power systems for electrified transportation systems. IEEE Trans. Transp. Electrif. 2016, 2, 86–95. [Google Scholar] [CrossRef]
- Mira, M.C.; Zhang, Z.; Knott, A.; Andersen, M.A. Analysis, design, modeling, and control of an Interleaved-boost full-bridge three-port converter for hybrid renewable energy systems publication date: Analysis, design, modelling and control of an interleaved-boost full-bridge three-port converter f. IEEE Trans. Power Electron. 2017, 32, 1138–1155. [Google Scholar] [CrossRef]
- Wang, L.; Member, S.; Vo, Q.; Prokhorov, A. V Dynamic stability analysis of a hybrid wave and photovoltaic power generation system integrated into a distribution power grid. IEEE Trans. Sustain. Energy 2017, 8, 404–413. [Google Scholar] [CrossRef]
- Yuhimenko, V.; Member, S.; Geula, G.; Member, S.; Agranovich, G.; Averbukh, M.; Kuperman, A.; Member, S. Average modeling and performance analysis of voltage sensorless active supercapacitor balancer with peak current protection. IEEE Trans. Power Electron. 2017, 32, 1570–1578. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. Generalized average modeling of dual active. IEEE Trans. Power Electron. 2012, 27, 2078–2084. [Google Scholar] [CrossRef]
- Renaudineau, H.; Martin, J.; Nahid-Mobarakeh, B.; Member, S.; Pierfederici, S. DC—DC converters dynamic modeling with state observer-based parameter estimation. IEEE Trans. Power Electron. 2015, 30, 3356–3363. [Google Scholar] [CrossRef]
- Payman, A.; Pierfederici, S.; Meibody-Tabar, F.; Davat, B. An adapted control strategy to minimize DC—Bus capacitors of a parallel fuel cell/ultracapacitor hybrid system. IEEE Trans. Power Electron. 2011, 26, 3843–3852. [Google Scholar] [CrossRef]
- Payman, A.; Pierfederici, S.; Meibody-Tabar, F. Energy control of supercapacitor/fuel cell hybrid power source. Energy Convers. Manag. 2008, 49, 1637–1644. [Google Scholar] [CrossRef]
- Thounthong, P.; Pierfederici, S.; Davat, B. Analysis of differential flatness-based control for a fuel cell hybrid power source. IEEE Trans. Energy Convers. 2010, 25, 909–920. [Google Scholar] [CrossRef]
- Tabart, Q.; Vechiu, I.; Etxeberria, A.; Bacha, S. Hybrid energy storage system microgrids integration for power quality improvement using four leg three level NPC inverter and second order sliding mode control. IEEE Trans. Ind. Electron. 2018, 65, 424–435. [Google Scholar] [CrossRef]








| Symbol | Unit | Value | Description |
|---|---|---|---|
| C | 4700 | Electrochemical | |
| AL | nH/turns2 | 12,500 | Planar transformer core |
| N1 | turns | 1 | Primary winding turns |
| N2 | turns | 4 | Secondary winding turns |
| k | - | 0.98 | Coupling coefficient |
| F | kHz | 40 | Switching frequency of the H-bridge |
| Vbat | V | 48 | Nominal voltage of the battery |
| VC | V | 12 | Nominal output voltages of boosts |
| Vd | V | 0 | Drop voltage of diodes |
| PFC | W | 126 | Nominal injected power of different stacks |
| - | 1 | Efficiency of the equalizer system | |
| Rad/s | Cut-off radian frequency of the filter | ||
| Kp | - | 0.1 | Proportional gain of the controller |
| Rad/s | 7500 | ||
| ki | Rad/s | 7500 | |
| Fs | kHz | 29 | Switching frequency of the boost converters |
| KSC | - | 0.08 |
| Unit | Value | |
|---|---|---|
| FC | Power supply | TDK GENH 750 W |
| Boost converter | Inductance | (1 mH) |
| Switches | IGBT | |
| Capacitor | Electrochemical (4700 ) | |
| Equalizer | Diodes | DSS2x121-0045B |
| Magnetic core | B66295G Material N87 | |
| H-bridge switches | SiCMOSFET CCS050M12CM2 | |
| Capacitor | film (220 ) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahrami, M.; Martin, J.-P.; Maranzana, G.; Pierfederici, S.; Weber, M.; Meibody-Tabar, F.; Zandi, M. Multi-Stack Lifetime Improvement through Adapted Power Electronic Architecture in a Fuel Cell Hybrid System. Mathematics 2020, 8, 739. https://doi.org/10.3390/math8050739
Bahrami M, Martin J-P, Maranzana G, Pierfederici S, Weber M, Meibody-Tabar F, Zandi M. Multi-Stack Lifetime Improvement through Adapted Power Electronic Architecture in a Fuel Cell Hybrid System. Mathematics. 2020; 8(5):739. https://doi.org/10.3390/math8050739
Chicago/Turabian StyleBahrami, Milad, Jean-Philippe Martin, Gaël Maranzana, Serge Pierfederici, Mathieu Weber, Farid Meibody-Tabar, and Majid Zandi. 2020. "Multi-Stack Lifetime Improvement through Adapted Power Electronic Architecture in a Fuel Cell Hybrid System" Mathematics 8, no. 5: 739. https://doi.org/10.3390/math8050739
APA StyleBahrami, M., Martin, J.-P., Maranzana, G., Pierfederici, S., Weber, M., Meibody-Tabar, F., & Zandi, M. (2020). Multi-Stack Lifetime Improvement through Adapted Power Electronic Architecture in a Fuel Cell Hybrid System. Mathematics, 8(5), 739. https://doi.org/10.3390/math8050739





