Differential Flatness-Based Cascade Energy/Current Control of Battery/Supercapacitor Hybrid Source for Modern e–Vehicle Applications

Abstract

This article proposes a new control law for an embedded DC distributed network supplied by a supercapacitor module (as a supplementary source) and a battery module (as the main generator) for transportation applications. A novel control algorithm based on the nonlinear differential flatness approach is studied and implemented in the laboratory. Using the differential flatness theory, straightforward solutions to nonlinear system stability problems and energy management have been developed. To evaluate the performance of the studied control technique, a hardware power electronics system is designed and implemented with a fully digital calculation (real-time system) realized with a MicroLabBox dSPACE platform (dual-core processor and FPGA). Obtained test bench results with a small scale prototype platform (a supercapacitor module of 160 V, 6 F and a battery module of 120 V, 40 Ah) corroborate the excellent control structure during drive cycles: steady-state and dynamics.

1. Introduction

The crisis of continuously growing fossil fuel costs has provoked transportation industries to advance more efficient automobiles technology. Another solution is to transform technology into other sources including biodiesel or energy from ethanol, etc. Electric vehicles, or hybrid plug-in vehicles, or hybrid vehicles (which are mainly supplied by battery) are a promising solution. Therefore, the electric vehicles (e-vehicle, EVs) industries have designed and developed the technology to progress the extension of EVs [1,2,3]. A lot of research works have been conducted on future vehicle technology [1,2,3]. In EVs, the powertrains are composed of batteries, power converters, and AC electrical motors, such as permanent magnet synchronous motors due to their high energy efficiency, suitable torque-to-weight ratio, and long life span [4,5].

The request for power from battery during dynamic operations can decrease drastically its lifetime [6]. To cope with this challenging issue, the hybridization of batteries with supercapacitors (SC or “ultracapacitor” or “double-layer capacitor”) is an attractive solution. Indeed, SCs feature a high power density compared to batteries, which enables them to respond quickly to dynamic operations [7]. Besides, SCs are compact and have high energy efficiency, particularly fit for automotive applications. However, the combination of SC and battery requires a good control algorithm between these two sources, which is helpful in order to decrease the battery size and to enhance its life span [6,7].

The linear control is generally employed for energy management of the hybrid system. Generally, proportional–integral (PI) compensation is used for energy stability [8,9,10,11,12]. In [13], Marzouguia et al. have proposed a control technique of the hybrid network for a hydrogen electric vehicle (fuel cell car) based on three estimation approaches: first, “a fuzzy logic estimation”; second, “a differential flatness control approach” (model-based technique); third “rule-based algorithm”, making complex the energy management strategy. Indeed, the fuzzy logic controller is employed to manage the energy flows between the main source (i.e., fuel cell) and storage devices (i.e., battery, SC); whereas the flatness controller is used to regulating the DC bus voltage, allowing ensuring the stability of the microgrid. Finally, a rule-based algorithm enables controlling the state-of-charge of SC to keep a good operation of charge/discharge cycles. As a result, the three controllers must interact with each other and their implementations are more complex.

On the other side, batteries and SCs are interfaced with the DC bus through classic buck–boost converters, making them unavailable in case of power switch failures. These converters are controlled based on PI-current control laws. The parameters for PI controllers have been designed and tuned in agreement with the linear optimum technique, requiring classic linear approximations contingent on the defined equilibrium point. Hence, the performances can be guaranteed only for specific operating cases.

Since the hybrid system includes bidirectional DC–DC converters linked to storage devices, the power converter model is nonlinear behavior. Then, it is important to use a nonlinear model-based control approach to the balance of the nonlinearity of the power electronics network [13]. In [14], Song et al. have developed an energy management algorithm for an electric vehicle supplied by batteries and SCs. Two algorithms are used: one based on Lyapunov-function regulation to stabilize the DC bus, and another based on a sliding mode approach to regulate both classic 2-quadrant converters connected to power sources, making them less reliable in case of electrical failures. It has to be noted that availability and reliability are currently major concerns so that EVs must access the mass automotive market. On one hand, the use of sliding mode controllers allows ensuring excellent performances to control both the charge/discharge of batteries and SC. On the other hand, the development of the Lyapunov function to make it stable for any operating scenario is a challenging issue.

In [15], Zhang et al. have applied a real-time unified speed regulation and control technique of a hybrid car supplied by batteries and SCs. The developed strategy is based on the Lyapunov nonlinear control technique. However, only simulation results have been reported to validate the developed control strategy. Furthermore, compared to the work reported in [14], the Lyapunov-based controller has several objectives such as the speed control of the AC motor and the energy management of batteries and SC (i.e., reducing battery stress, and extending battery lifetime). Since the controller must meet both objectives, its stability must be analyzed thoroughly to ensure good dynamic performances.

Next, Fliess et al. [16] were the first to develop differential flatness estimation (nonlinear approach). This approach has enabled the system to be an alternative representative, of which motion planning and regulator tuning is clear-cut. This theory has lately been utilized in a variety of networks in different scientific domains [17,18,19,20,21,22,23]. Compared to the nonlinear algorithm (i.e., sliding mode, Lyapunov, fuzzy logic) reported in [13,14,15], nonlinear algorithms based on differential flatness require the use of trajectory planning to implement the control laws. This trajectory planning aims at controlling different variables (e.g., currents of converters, stored energy in the DC bus and SC) to manage the energy in an EV while optimizing the performance of the system for any operating point. The use of this algorithm allows ensuring the robustness of energy management to meet the requirements of EVs (e.g., dynamic performances, the extension of the lifetime of storage devices).

For clarity, Figure 1 presents experimental results from the laboratory comparing the nonlinear differential flatness estimation and the classic PI control law during the great changed current set-point [17] of 3-phase inverter control. From these test-bench results, the differential flatness-based estimation approach presents the excellent response of the current control to its set-point i_qREF from step 1 A to 6 A. For this reason, it can be concluded that differential flatness control offers better dynamics than the traditional PI regulator.

So far, algorithms based on differential flatness have been successfully applied to power converters (e.g., 3-phase inverter and rectifier, interleaved boost converter, modular multilevel converter) [17,18,20,21], permanent magnet synchronous motor and AC servomotor [19,22,23]. Based on these previous works, the purpose of this article is to extend the use of differential flatness algorithm in an embedded DC microgrid (i.e., EV powertrain) to manage optimally its operation during static and dynamic operations. It has to be noted that the implementation of this algorithm is challenging since several variables have to be controlled to meet some expectations from the dynamic performances and stability point of view.

In this work, following the introduction part in section 1, Section 2 is detailed on the presentation of the hybrid power source–Battery/SC devices: power converter circuits and system equations. Afterward, in Section 3, energy management strategy (inner current control loops and outer energy control loops) and control laws are provided. Finally, in Section 4, an experimental test bench results are given to corroborate the proposed control law.

2. Hybrid Power Source

2.1. Power Converter Structure

SC and Battery power modules are frequently combined with buck–boost DC–DC converters (or 2-quadrant converters) to allow the charge and discharge of the storage devices. However, these converter cells are restricted when increasing power scale or when a high voltage gain is requested. Besides, the availability and reliability of electric vehicles is an important issue, which cannot be met by using a classic buck–boost converter. Therefore, the parallel power converters (parallel multi-phase converters as shown in Figure 2) with the interleaved technique are particularly suitable to meet the abovementioned issues [24,25,26]. The load at the DC bus is a 3-phase inverter driving a three AC motor [induction motor or permanent magnet synchronous motor (PMSM)], as a vehicle traction drive.

2.2. Power Plant Modeling

The interleaved switching algorithm consists of the phase shift control signal of multiple converter modules (N) connecting in parallel [24,25,26]. In this article, two-phase interleaved buck–boost converters (N = 2) have been chosen to carry out this work. Indeed, by choosing only two phases, the shift control signal is equal to 180° and be easily achieved by using a prototyping dSPACE board (employed for experiment purposes). The differential equations of the two-phase buck–boost converters for SC and battery modules when the converter operates in continuous conduction mode may be expressed as [27]:

$$\frac{{\mathrm{di}}_{\mathrm{LB}1}}{\mathrm{dt}}=\frac{1}{{\mathrm{L}}_{\mathrm{LB}1}}\left[{\mathrm{v}}_{\mathrm{Bat}}-\left(1-{\mathrm{d}}_1\right)\times {\mathrm{v}}_{\mathrm{Bus}}-{\mathrm{r}}_{\mathrm{LB}1}\times {\mathrm{i}}_{\mathrm{LB}1}\right]$$

(1)

$$\frac{{\mathrm{di}}_{\mathrm{LB}2}}{\mathrm{dt}}=\frac{1}{{\mathrm{L}}_{\mathrm{LB}2}}\left[{\mathrm{v}}_{\mathrm{Bat}}-\left(1-{\mathrm{d}}_2\right)\times {\mathrm{v}}_{\mathrm{Bus}}-{\mathrm{r}}_{\mathrm{LB}2}\times {\mathrm{i}}_{\mathrm{LB}2}\right]$$

(2)

$$\frac{{\mathrm{di}}_{\mathrm{LC}1}}{\mathrm{dt}}=\frac{1}{{\mathrm{L}}_{\mathrm{LC}1}}\left[{\mathrm{v}}_{\mathrm{SC}}-\left(1-{\mathrm{d}}_3\right)\times {\mathrm{v}}_{\mathrm{Bus}}-{\mathrm{r}}_{\mathrm{LC}1}\times {\mathrm{i}}_{\mathrm{LC}1}\right]$$

(3)

$$\frac{{\mathrm{di}}_{\mathrm{LC}2}}{\mathrm{dt}}=\frac{1}{{\mathrm{L}}_{\mathrm{LC}2}}\left[{\mathrm{v}}_{\mathrm{SC}}-\left(1-{\mathrm{d}}_4\right)\times {\mathrm{v}}_{\mathrm{Bus}}-{\mathrm{r}}_{\mathrm{LC}2}\times {\mathrm{i}}_{\mathrm{LC}2}\right]$$

(4)

$$\frac{{\mathrm{dv}}_{\mathrm{Bus}}}{\mathrm{dt}}=\frac{1}{{\mathrm{C}}_{\mathrm{Bus}}}\left[\left(1-{\mathrm{d}}_1\right)\times {\mathrm{i}}_{\mathrm{LB}1}+\left(1-{\mathrm{d}}_2\right)\times {\mathrm{i}}_{\mathrm{LB}2}+\left(1-{\mathrm{d}}_3\right)\times {\mathrm{i}}_{\mathrm{LC}1}+\left(1-{\mathrm{d}}_4\right)\times {\mathrm{i}}_{\mathrm{LC}2}-{\mathrm{i}}_{\mathrm{Load}}\right]$$

(5)

where the subscripts B1, B2, C1, C2 are parameters of each cell connected to the battery (B) or SC (C); i_Load is the load current; v_SC is the SC voltage; v_Bat is the battery voltage; i_L is the inductor current; C_Bus is the total capacitance at the DC grid; L is the inductance, r_L is the parasitic resistor of the inductor; and d is the controlled duty cycle of the pulse width modulation (PWM) for power circuit. This model is simplified to carry out this work since it does not take into account some type of losses generally met in DC–DC converters (dynamics losses, switching dead-time, etc…) [28].

The SC and battery currents are assumed to follow their desired set-points completely. In consequence,

$${\mathrm{i}}_{\mathrm{Bat}}={\mathrm{i}}_{\mathrm{BatREF}}=\frac{{\mathrm{p}}_{\mathrm{Bat}}}{{\mathrm{v}}_{\mathrm{Bat}}}=\frac{{\mathrm{p}}_{\mathrm{BatREF}}}{{\mathrm{v}}_{\mathrm{Bat}}}$$

(6)

$${\mathrm{i}}_{\mathrm{SC}}={\mathrm{i}}_{\mathrm{SCREF}}=\frac{{\mathrm{p}}_{\mathrm{SC}}}{{\mathrm{v}}_{\mathrm{SC}}}=\frac{{\mathrm{p}}_{\mathrm{SCREF}}}{{\mathrm{v}}_{\mathrm{SC}}}$$

(7)

The DC grid electrostatic energy E_Bus and the SC electrostatic energy E_SC is given by [13]:

$${\mathrm{E}}_{\mathrm{Bus}}=\frac{1}{2}\times {\mathrm{C}}_{\mathrm{Bus}}\times {\mathrm{v}}^2{}_{\mathrm{Bus}}$$

(8)

$${\mathrm{E}}_{\mathrm{SC}}=\frac{1}{2}\times {\mathrm{C}}_{\mathrm{SC}}\times {\mathrm{v}}^2{}_{\mathrm{SC}}$$

(9)

The total stored energy E_T in the SC C_SC and in the DC bus capacitor C_Bus can be expressed by the following expression:

$${\mathrm{E}}_{\mathrm{T}}=\frac{1}{2}\times {\mathrm{C}}_{\mathrm{Bus}}\times {\mathrm{v}}^2{}_{\mathrm{Bus}}+\frac{1}{2}\times {\mathrm{C}}_{\mathrm{SC}}\times {\mathrm{v}}^2{}_{\mathrm{SC}}$$

(10)

Based on Figure 2, the differential equation of power balance is given as follows [6]:

$${\dot{\mathrm{E}}}_{\mathrm{Bus}}={\mathrm{p}}_{\mathrm{Bato}}+{\mathrm{p}}_{\mathrm{SCo}}-{\mathrm{p}}_{\mathrm{Load}}$$

(11)

where

$${\mathrm{p}}_{\mathrm{Bato}}={\mathrm{p}}_{\mathrm{Bat}}-{\mathrm{r}}_{\mathrm{Bat}}{\left(\frac{{\mathrm{p}}_{\mathrm{Bat}}}{{\mathrm{v}}_{\mathrm{Bat}}}\right)}^2$$

(12)

$${\mathrm{p}}_{\mathrm{SCo}}={\mathrm{p}}_{\mathrm{SC}}-{\mathrm{r}}_{\mathrm{SC}}{\left(\frac{{\mathrm{p}}_{\mathrm{SC}}}{{\mathrm{v}}_{\mathrm{SC}}}\right)}^2$$

(13)

$${\mathrm{p}}_{\mathrm{Load}}={\mathrm{v}}_{\mathrm{Bus}}\times {\mathrm{i}}_{\mathrm{Load}}=\sqrt{\frac{2{\mathrm{E}}_{\mathrm{Bus}}}{{\mathrm{C}}_{\mathrm{Bus}}}}\times {\mathrm{i}}_{\mathrm{Load}}$$

(14)

$${\mathrm{p}}_{\mathrm{SC}}={\mathrm{v}}_{\mathrm{SC}}\times {\mathrm{i}}_{\mathrm{SC}}=\sqrt{\frac{2{\mathrm{E}}_{\mathrm{SC}}}{{\mathrm{C}}_{\mathrm{SC}}}}\times {\mathrm{i}}_{\mathrm{SC}}$$

(15)

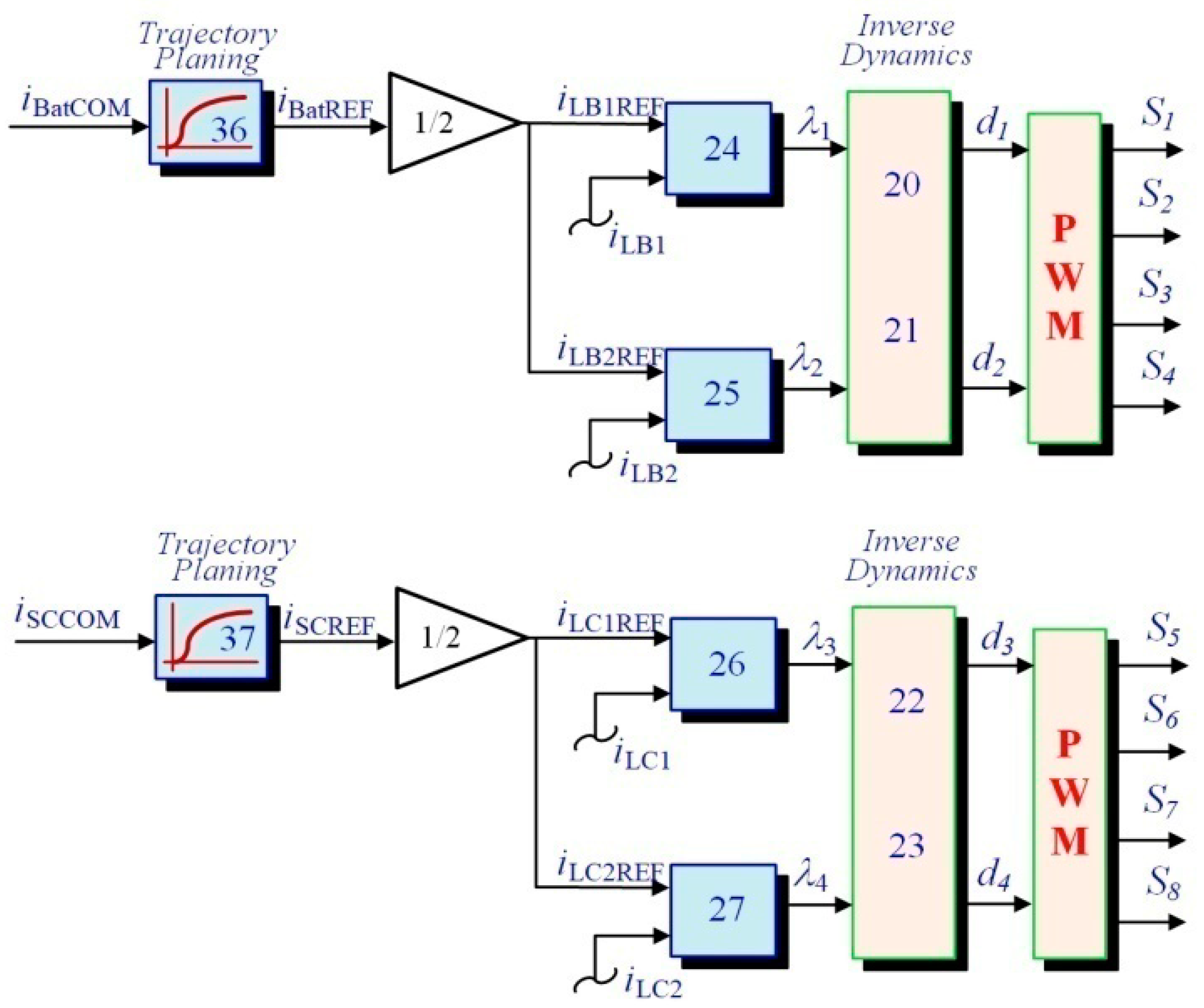
3. Control Structure and Control Laws

3.1. Inner Current Regulations

To evaluate if the studied network is flat [19,20], one defines the flat vector output variables: y₁, y₂, y₃, y₄; state vector variables: x₁, x₂, x₃, x₄; and control vector variables: u₁, u₂, u₃, u₄ as:

$${\mathrm{y}}_1={\mathrm{i}}_{\mathrm{LB}1};{\mathrm{y}}_2={\mathrm{i}}_{\mathrm{LB}2};{\mathrm{y}}_3={\mathrm{i}}_{\mathrm{LC}1};{\mathrm{y}}_4={\mathrm{i}}_{\mathrm{LC}2}$$

(16)

$${\mathrm{u}}_1={\mathrm{d}}_1;{\mathrm{u}}_2={\mathrm{d}}_2;{\mathrm{u}}_3={\mathrm{d}}_3;{\mathrm{u}}_4={\mathrm{d}}_4$$

(17)

$${\mathrm{x}}_1={\mathrm{i}}_{\mathrm{LB}1};{\mathrm{x}}_2={\mathrm{i}}_{\mathrm{LB}2};{\mathrm{x}}_3={\mathrm{i}}_{\mathrm{LC}1};{\mathrm{x}}_4={\mathrm{i}}_{\mathrm{LC}1}$$

(18)

Hence, the state vector variables: x₁, x₂, x₃, x₄ may be expressed as:

$${\mathrm{x}}_1={\mathsf{\phi }}_1\left({\mathrm{y}}_1\right);{\mathrm{x}}_2={\mathsf{\phi }}_2\left({\mathrm{y}}_2\right);{\mathrm{x}}_3={\mathsf{\phi }}_3\left({\mathrm{y}}_3\right);{\mathrm{x}}_4={\mathsf{\phi }}_4\left({\mathrm{y}}_4\right)$$

(19)

From (1) to (4) and (16) to (18), the control vector variables of u are assessed from the flat output variables y and its time derivative [19]:

$${\mathrm{u}}_1={\mathrm{d}}_1=1+\frac{1}{{\mathrm{v}}_{\mathrm{Bus}}}\left(\mathrm{L}{\dot{\mathrm{y}}}_1-{\mathrm{v}}_{\mathrm{Bat}}+{\mathrm{r}}_{\mathrm{LB}1}\times {\mathrm{y}}_1\right)={\mathsf{\psi }}_1\left({\mathrm{y}}_1,{\dot{\mathrm{y}}}_1\right)$$

(20)

$${\mathrm{u}}_2={\mathrm{d}}_2=1+\frac{1}{{\mathrm{v}}_{\mathrm{Bus}}}\left(\mathrm{L}{\dot{\mathrm{y}}}_2-{\mathrm{v}}_{\mathrm{Bat}}+{\mathrm{r}}_{\mathrm{LB}1}\times {\mathrm{y}}_2\right)={\mathsf{\psi }}_2\left({\mathrm{y}}_2,{\dot{\mathrm{y}}}_2\right)$$

(21)

$${\mathrm{u}}_3={\mathrm{d}}_3=1+\frac{1}{{\mathrm{v}}_{\mathrm{Bus}}}\left(\mathrm{L}{\dot{\mathrm{y}}}_3-{\mathrm{v}}_{\mathrm{SC}}+{\mathrm{r}}_{\mathrm{LC}1}\times {\mathrm{y}}_3\right)={\mathsf{\psi }}_3\left({\mathrm{y}}_3,{\dot{\mathrm{y}}}_3\right)$$

(22)

$${\mathrm{u}}_4={\mathrm{d}}_4=1+\frac{1}{{\mathrm{v}}_{\mathrm{Bus}}}\left(\mathrm{L}{\dot{\mathrm{y}}}_4-{\mathrm{v}}_{\mathrm{SC}}+{\mathrm{r}}_{\mathrm{LC}1}\times {\mathrm{y}}_4\right)={\mathsf{\psi }}_4\left({\mathrm{y}}_4,{\dot{\mathrm{y}}}_4\right)$$

(23)

The desired references of inductor current of each phase i_LB1, i_LB2, i_LC1, i_LC2 are defined by y_1REF (=i_LB1REF), y_2REF (=i_LB2REF), y_3REF (=i_LC1REF), y_4REF (=i_LC2REF). Control laws (feedback regulation) reaching an exponential following of the references are written as [19,29]:

$$\left({\dot{\mathrm{y}}}_1-{\dot{\mathrm{y}}}_{1\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}11}\left({\mathrm{y}}_1-{\mathrm{y}}_{1\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}12}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\left({\mathrm{y}}_1-{\mathrm{y}}_{1\mathrm{REF}}\right)}\mathrm{d}\mathsf{\tau }=0$$

(24)

$$\left({\dot{\mathrm{y}}}_2-{\dot{\mathrm{y}}}_{2\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}21}\left({\mathrm{y}}_2-{\mathrm{y}}_{2\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}22}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\left({\mathrm{y}}_2-{\mathrm{y}}_{2\mathrm{REF}}\right)}\mathrm{d}\mathsf{\tau }=0$$

(25)

$$\left({\dot{\mathrm{y}}}_3-{\dot{\mathrm{y}}}_{3\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}31}\left({\mathrm{y}}_3-{\mathrm{y}}_{3\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}32}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\left({\mathrm{y}}_3-{\mathrm{y}}_{3\mathrm{REF}}\right)}\mathrm{d}\mathsf{\tau }=0$$

(26)

$$\left({\dot{\mathrm{y}}}_4-{\dot{\mathrm{y}}}_{4\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}41}\left({\mathrm{y}}_4-{\mathrm{y}}_{4\mathrm{REF}}\right)+{\mathrm{K}}_{\mathrm{i}42}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\left({\mathrm{y}}_4-{\mathrm{y}}_{4\mathrm{REF}}\right)}\mathrm{d}\mathsf{\tau }=0$$

(27)

where K_i11, K_i12, K_i21, K_i22, K_i31, K_i32, K_i41, and K_i42, are the regulation parameters. A set dynamic polynomial can set the following as [30]:

$${\mathrm{p}}_1\left(\mathrm{s}\right)={\mathrm{s}}^2+2{\mathsf{\zeta }}_1{\mathsf{\omega }}_{\mathrm{n}1}\mathrm{s}+{\mathsf{\omega }}_{\mathrm{n}1}^2$$

(28)

$${\mathrm{p}}_2\left(\mathrm{s}\right)={\mathrm{s}}^2+2{\mathsf{\zeta }}_2{\mathsf{\omega }}_{\mathrm{n}2}\mathrm{s}+{\mathsf{\omega }}_{\mathrm{n}2}^2$$

(29)

$${\mathrm{p}}_3\left(\mathrm{s}\right)={\mathrm{s}}^2+2{\mathsf{\zeta }}_3{\mathsf{\omega }}_{\mathrm{n}3}\mathrm{s}+{\mathsf{\omega }}_{\mathrm{n}3}^2$$

(30)

$${\mathrm{p}}_4\left(\mathrm{s}\right)={\mathrm{s}}^2+2{\mathsf{\zeta }}_4{\mathsf{\omega }}_{\mathrm{n}4}\mathrm{s}+{\mathsf{\omega }}_{\mathrm{n}4}^2$$

(31)

$${\mathrm{K}}_{\mathrm{i}11}=2{\mathsf{\zeta }}_1{\mathsf{\omega }}_{\mathrm{n}1};{\mathrm{K}}_{\mathrm{i}12}={\mathsf{\omega }}_{\mathrm{n}1}^2$$

(32)

$${\mathrm{K}}_{\mathrm{i}21}=2{\mathsf{\zeta }}_2{\mathsf{\omega }}_{\mathrm{n}2};{\mathrm{K}}_{\mathrm{i}22}={\mathsf{\omega }}_{\mathrm{n}2}^2$$

(33)

$${\mathrm{K}}_{\mathrm{i}31}=2{\mathsf{\zeta }}_3{\mathsf{\omega }}_{\mathrm{n}3};{\mathrm{K}}_{\mathrm{i}32}={\mathsf{\omega }}_{\mathrm{n}3}^2$$

(34)

$${\mathrm{K}}_{\mathrm{i}41}=2{\mathsf{\zeta }}_4{\mathsf{\omega }}_{\mathrm{n}4};{\mathrm{K}}_{\mathrm{i}42}={\mathsf{\omega }}_{\mathrm{n}4}^2$$

(35)

where ζ₁, ζ₂, ζ₃, ζ₄, ω_n1, ω_n2, ω_n3, and ω_n4 are the chosen damping ratio and defined natural frequency. Therefore, new variables are determined${\mathsf{\lambda }}_1={\dot{\mathrm{y}}}_1$; ${\mathsf{\lambda }}_2={\dot{\mathrm{y}}}_2$; ${\mathsf{\lambda }}_3={\dot{\mathrm{y}}}_3$; ${\mathsf{\lambda }}_4={\dot{\mathrm{y}}}_4$.

The flatness-based control requires trajectory planning to implement the control law. Hence, a second-order filter has been chosen to set the battery and SC currents, dynamics commands i_BatCOM, i_SCCOM as the following equations [19]:

$$\frac{{\mathrm{i}}_{\mathrm{BatREF}}\left(\mathrm{s}\right)}{{\mathrm{i}}_{\mathrm{BatCCOM}}\left(\mathrm{s}\right)}=\frac{1}{{\left(\frac{\mathrm{s}}{{\mathsf{\omega }}_{\mathrm{nt}1}}\right)}^2+\frac{2{\mathsf{\zeta }}_{\mathrm{t}1}}{{\mathsf{\omega }}_{\mathrm{nt}1}}\mathrm{s}+1}$$

(36)

$$\frac{{\mathrm{i}}_{\mathrm{SCREF}}\left(\mathrm{s}\right)}{{\mathrm{i}}_{\mathrm{SCCCOM}}\left(\mathrm{s}\right)}=\frac{1}{{\left(\frac{\mathrm{s}}{{\mathsf{\omega }}_{\mathrm{nt}2}}\right)}^2+\frac{2{\mathsf{\zeta }}_{\mathrm{t}2}}{{\mathsf{\omega }}_{\mathrm{nt}2}}\mathrm{s}+1}$$

(37)

where ω_nt1, ω_nt2, ζ_t1, and ζ_t2, are again the desired natural frequency and dominant damping ratio, refer to Figure 3.

3.2. Outer Energy Controls

The energy control law for the studied system shown in Figure 2 consists of using two energy control laws which include DC link energy E_Bus and SC energy E_SC by two voltage variables to be regulated. Thus, based on the literature review [6,31,32], the first priority variable to be regulated is E_Bus and E_SC is a secondary variable. Given that the fastest dynamic power source of the studied system is the SC, it has been decided to use this device to supply energy to the DC link. On the other side, since the slowest dynamic power source is the battery, the latter has been chosen to provide the energy to both the SC C_SC and the DC bus capacitor C_Bus to store energy.

The flat output y₅, y₆, state variable x₅, x₆ and control variable u₅, u₆ can be expressed as follows [6]:

$${\mathrm{y}}_5={\mathrm{E}}_{\mathrm{Bus}};{\mathrm{y}}_6={\mathrm{E}}_{\mathrm{T}}$$

(38)

$${\mathrm{u}}_5={\mathrm{p}}_{\mathrm{SCREF}};{\mathrm{u}}_6={\mathrm{p}}_{\mathrm{SCREF}}$$

(39)

$${\mathrm{x}}_5={\mathrm{v}}_{\mathrm{Bus}};{\mathrm{x}}_6={\mathrm{i}}_{\mathrm{SC}}$$

(40)

$${\mathrm{x}}_5=\sqrt{\frac{2{\mathrm{y}}_5}{{\mathrm{C}}_{\mathrm{Bus}}}}={\mathsf{\phi }}_5\left({\mathrm{y}}_5\right)$$

(41)

$${\mathrm{x}}_6=\sqrt{\frac{\left(2{\mathrm{y}}_6-{\mathrm{y}}_5\right)}{{\mathrm{C}}_{\mathrm{SC}}}}={\mathsf{\phi }}_2\left({\mathrm{y}}_5,{\mathrm{y}}_6\right)$$

(42)

By using (8)–(15), the control input vector u may be computed from the flat output variable y and its time derivatives [6]:

$${\mathrm{u}}_5=2{\mathrm{p}}_{\mathrm{SC}\mathrm{Max}}\left[1-\sqrt{1-\frac{{\dot{\mathrm{y}}}_5+\sqrt{\frac{2{\mathrm{y}}_5}{{\mathrm{C}}_{\mathrm{Bus}}}}\times {\mathrm{i}}_{\mathrm{Load}}-{\mathrm{p}}_{\mathrm{Bato}}}{{\mathrm{p}}_{\mathrm{SCMax}}}}\right]={\mathsf{\psi }}_5\left({\mathrm{y}}_5,{\dot{\mathrm{y}}}_5\right)={\mathrm{p}}_{\mathrm{SCREF}}$$

(43)

$${\mathrm{u}}_6=2{\mathrm{p}}_{\mathrm{T}\mathrm{Max}}\left[1-\sqrt{1-\frac{{\dot{\mathrm{y}}}_6+\sqrt{\frac{2{\mathrm{y}}_6}{{\mathrm{C}}_{\mathrm{Bus}}}}\times {\mathrm{i}}_{\mathrm{Load}}}{{\mathrm{p}}_{\mathrm{TMax}}}}\right]={\mathsf{\psi }}_6\left({\mathrm{y}}_6,{\dot{\mathrm{y}}}_6\right)={\mathrm{p}}_{\mathrm{T}\mathrm{REF}}$$

(44)

where

$${\mathrm{p}}_{\mathrm{SCMax}}=\frac{{\mathrm{v}}^2{}_{\mathrm{SC}}}{4{\mathrm{r}}_{\mathrm{SC}}},{\mathrm{p}}_{\mathrm{TMax}}=\frac{{\mathrm{v}}^2{}_{\mathrm{T}}}{4{\mathrm{r}}_{\mathrm{T}}}$$

(45)

In this case, p_TMax and p_SCMax correspond to the set limited power of the SC and battery devices (maximum power), respectively.

In the first energy control law, the set-point for the DC link energy is defined by y_5REF. The closed-loop control law is written by the following expression:

$${\dot{y}}_5-{\dot{y}}_{5\mathrm{REF}}+K_{\mathrm{v}1}\left(y_5-y_{5\mathrm{REF}}\right)+K_{\mathrm{v}2}{\displaystyle \underset{0}{\overset{\mathrm{t}}{\int }}\left(y_5-y_{5\mathrm{REF}}\right)}dt=0$$

(46)

where K_v1 and K_v2 are the controller parameters. The suitable way to tune these parameters is achieved by corresponding the desired dynamic polynomial p(s), with set root positions. One can set the following equations:

$$p_5\left(s\right)=s^2+2{\mathsf{\zeta }}_5{\mathsf{\omega }}_{\mathrm{n}5}s+{\mathsf{\omega }}_{\mathrm{n}5}^2$$

(47)

$$K_{\mathrm{v}1}=2{\mathsf{\zeta }}_5{\mathsf{\omega }}_{\mathrm{n}5};K_{\mathrm{v}2}={\mathsf{\omega }}_{\mathrm{n}5}^2$$

(48)

where ω_n5 and ζ₅ are the chosen natural frequency and dominant damping ratio.

The control law of the DC link energy regulation detailed previously is displayed in Figure 4. The proposed control law generates an SC power desired variable p_SCREF. Next, this signal is divided by the SC voltage v_SC and restricted to keep the SC voltage within the gap [maximum V_SCMax, minimum V_SCMin] by limiting the SC module discharging current or charging current, as shown in the block “SuperC Current Limitation Function” [32]. Then, this becomes SC current command i_SCCOM.

Second, for the total energy control law (charging SC), the set-point is represented by y_6REF. Indeed, the SC energy has been set as slower dynamics than the DC link energy and the SC device features a high energy storage capacity. Again, the feedback control law is expressed as follows:

$${\dot{\mathrm{y}}}_6-{\dot{\mathrm{y}}}_{6\mathrm{REF}}+{\mathrm{K}}_{\mathrm{v}3}\left({\mathrm{y}}_6-{\mathrm{y}}_{6\mathrm{REF}}\right)=0$$

(49)

Refer to Figure 5, the proposed control law based on the differential flatness approach estimates the battery power set-point p_BatREF. Then, it is divided by the battery sensor voltage v_Bat and generates the battery current command i_BatCOM, limited within i_BatMax and i_BatMin (=0 A).

Finally, the soft-start system in the smooth transition point of view, the energy command has to be generated for the converter and restricted set-point profiles for smooth transforms between operating points. The trajectory motion planning for the reference signals E_BusREF and E_TREF are written as [19]:

$$\frac{{\mathrm{y}}_{\mathrm{BusREF}}\left(\mathrm{s}\right)}{{\mathrm{y}}_{\mathrm{BusCOM}}\left(\mathrm{s}\right)}=\frac{1}{{\left(\frac{\mathrm{s}}{{\mathsf{\omega }}_{\mathrm{nt}3}}\right)}^2+\frac{2{\mathsf{\zeta }}_{\mathrm{t}3}}{{\mathsf{\omega }}_{\mathrm{nt}3}}\mathrm{s}+1}$$

(50)

$$\frac{{\mathrm{y}}_{\mathrm{SCREF}}\left(\mathrm{s}\right)}{{\mathrm{y}}_{\mathrm{SCCOM}}\left(\mathrm{s}\right)}=\frac{1}{{\left(\frac{\mathrm{s}}{{\mathsf{\omega }}_{\mathrm{nt}4}}\right)}^2+\frac{2{\mathsf{\zeta }}_{\mathrm{t}4}}{{\mathsf{\omega }}_{\mathrm{nt}4}}\mathrm{s}+1}$$

(51)

where ω_n3, ω_n4, ζ_t3, and ζ_t4 are the chosen natural frequency and dominant damping ratio.

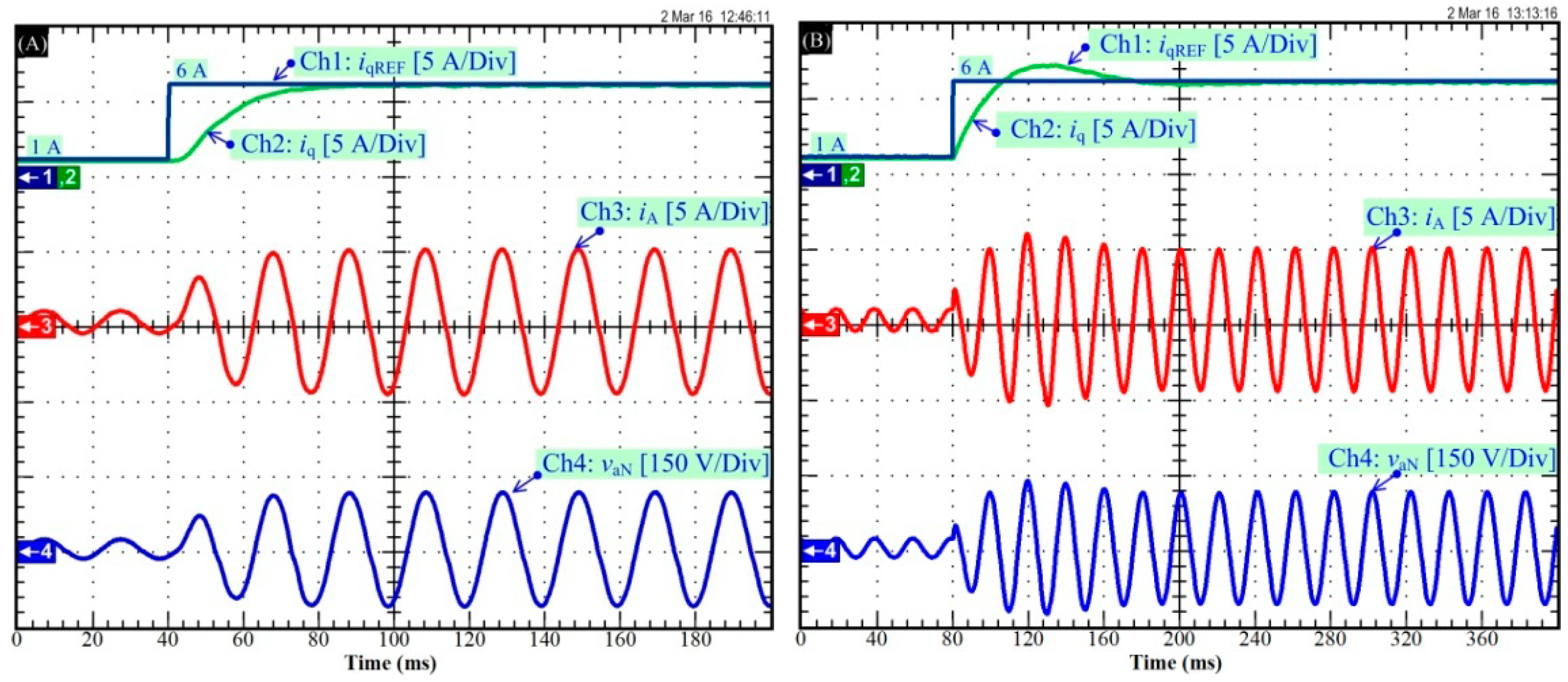
4. Performance Validation

4.1. Test Bench Setup and Flatness Control Parameters

To validate the effectiveness of the studied control algorithm for system management in an embedded DC microgrid, an experimental platform has been realized in the Renewable Energy Research Centre (RERC) at King Mongkut’s University of Technology North Bangkok, as presented in Figure 6. The DC–DC converter circuit parameters are provided in

Table 1. Converter parameters.

Parameters	Value
Rated DC grid voltage, vBus	310 V
Nominal battery voltage, vBat	120 V
Nominal SC voltage, vSC	140 V
Inductor LB1 = LB2 = LC1 = LC2	200 μH
Equivalent serial resistances RLB1 = RLB2 = RLC1 = RLC2	0.06 Ω
Total DC Bus Capacitors	2000 μF, 900 V
Power MOSFETs Switching Frequency, fS	25 kHz

. The SC module is 160 V, 6 F, (BMOD0006 E160 B02—Maxwell Technologies Company) and the battery module is 40 Ah, 120 V (Panasonic Technology). The studied DC link voltage is 310 V, meeting the high DC grid voltage requested for automotive applications. The inner current regulation parameters are given in

Table 2. Current control parameters.

Parameters	Value
ζ1 = ζ2 = ζ3 = ζ4	0.7
ωn1 = ωn2 = ωn3 = ωn4	8000
Ki11 =Ki21 = Ki31 = Ki41	11,200
Ki12 = Ki22 = Ki32 = Ki42	64,000,000

. Parameters related to the outer energy control parameters are shown in

Table 3. DC link energy regulation parameters.

Parameters	Value	Parameters	Value
vBusREF	310 V	pSCMax	+3600 W
ζ5	0.7	pSCMin	−3600 W
ωn5	80 rad·s−1	vSCMax	160 V
Kv1	112	VSCMin	70 V
Kv2	6400	iSCRated	30 A

and

Table 4. Total energy regulation parameters.

Parameters	Value	Parameters	Value
vSCREF	140 V	PBatMax	+2100 W
CSC	6 F	PBatMin	0 W
ζ6	1	IBatMax	+18 A
ωn6	0.8 rad·s−1	IBatMin	0 A
Kv3	0.1

, respectively. Additionally, the battery current slope control can be seen in Table 4. This number has been approved by experimental results to have the highest slope of the battery device. Besides, the proposed control algorithm (based on Figure 3, Figure 4 and Figure 5), which generates desired duty cycle signals d for both interleaved buck–boost converters, and regulates the total stored energy (including the DC bus and SC), has been realized in MATLAB^®—Simulink environment. Then, it has been implemented into the real-time board DS1202 dSPACE−MicroLabBox (2 GHz dual-core real-time microprocessor and user-programmable Field-Programmable Gate Array FPGA) with the sampling frequency (timer interrupt) of 25,000 Hz. This value is related to the high switching frequency of both interleaved buck–boost DC–DC converters.

Firstly, the oscilloscope waveforms in Figure 7 and Figure 8 show the steady-state switching behaviors of the studied interleaved 2-quadrant DC–DC converters for the battery and SC module at different current references. In Figure 7, the following signals are available:

• Ch1: the battery current set-point i_BatREF at +20 A (battery discharging mode);
• Ch2: the measured battery current i_Bat;
• Ch3: the 1st inductor current i_LB1;
• Ch4: the 2nd inductor current iLB2.

The obtained results show i_LB1 and i_LB2 where their average values are equal to i_BatREF/2 (i.e., 10 A). It can be observed that the current of the i_Bat battery is the sum of i_LB1 and i_LB2. It is equal to 20 A according to i_BatREF, but there is a small current ripple due to the use of an interleaved buck–boost converter.

Then, Figure 8 presents the experimental results in charge mode of the SC at 15 A or i_SCREF = −15 A. In Figure 8, the following measurements are available:

• Ch1: the SC current set-point i_SCREF;
• Ch2: the measured SC current i_SC;
• Ch3: the 1st inductor current i_LC1;
• Ch4: the 2nd inductor current i_LC2.

The current i_SC is equal to i_SCREF and is close to a pure DC current. The i_LC1 and i_LC2 have a very small ripple, with an average value of i_SCREF/2 equal to −7.5 A.

In Figure 9, it is shown the dynamics response when the battery reference i_BatREF increases instantaneously from initial +5 A to final +15 A. The following signals are available:

• Ch1: the battery reference i_BatREF;
• Ch2: the measured input battery current i_Bat;
• Ch3: the 1st inductor current i_LB1;
• Ch4: the 2nd inductor current i_LB2.

First of all, it can be seen that the current i_Bat follows perfectly the reference i_BatREF. As a result of the operating conditions change, the response of the current i_Bat is damped due to the use of a 2nd order filter equation. Like in the previous results, the battery current i_Bat (=i_BatREF) is the summation of i_LB1 and i_LB2.

Finally, Figure 10 shows the dynamics response by modifying the equilibrium points of the SC current from 5 A to −5 A. The following signals are available:

• Ch1: the SC current reference i_SCREF;
• Ch2: the measured SC current i_SC;
• Ch3: the 1st inductor current i_LC1;
• Ch4: the 2nd inductor current i_LC2.

It can be noted that the reference i_SCREF has a steep slope (2nd order filter characteristics) and the current i_SC follows i_SCREF completely, with a low settling time of 10 ms.

4.2. Hybrid Power Plant Load Cycles

To assess the performance of the differential flatness-based controller in regulating the DC bus energy by using SC, dynamic tests were carried out by modifying the load power from 0 W to 3 kW. The obtained results are shown in Figure 11, providing the DC bus voltage v_Bus, the SC voltage v_SC, the load power (disturbance) p_Load, and the SC power p_SC in transient and steady-state operation. Given that the first operating condition does not consider any load (i.e., from 0 to 120 ms), the storage device is full of charge (v_SCREF = v_SC = 140 V), and the DC link voltage is controlled at 310 V (v_BusREF = v_Bus = 310 V). Hence, the SC and battery powers are zero. Since the battery power is set to p_BatREF = 0 (see Figure 5), the role of SC module to maintain the DC bus voltage stability can be examined.

After that, at t = 120 ms, the load power (disturbance) instantly changes from 0 W to 3 kW (positive transition ↑). It can be observed that the SC module provides the steady-state and dynamics load power demand. The DC bus voltage is slightly influenced by the large load disturbance by utilizing the nonlinear differential flatness-based estimation for the proposed system.

Then, Figure 12 presents experimental results during a load drive cycle. Here, the electronic load has been changed to emulate the electric vehicle characteristics: overload, positive power (acceleration mode) or negative power (regenerative braking), and positive and negative transients. This Figure depicts the DC bus voltage v_Bus, the battery voltage v_Bat, the load power p_Load, the battery power p_Bat, the SC power p_SC, the battery current i_Bat, the SC current i_SC, and the SC voltage v_SC (represents the SC state-of-charge). Like in Figure 11, it can be noted that the DC bus voltage is not impacted by the large perturbation.

At the beginning, the load power = 600 W and the SC module is likewise full-of-charge (v_SC = v_SCREF = 140 V); consequently, the battery power is equal to 600 W for the load; while the SC is the second source, of which its power is equal to zero.

At t₁, the load power changes from 600 W to the 3600 W (overload, high energy requested by the load). The following explanation can be made:

1. The SC provides power most of the dynamic large load of 3600 W.

2. Concurrently, the battery power goes up to a limited level (maximum value setting) of 2100 W at t₂.

3. The SC device provides most of the power dynamics that are requested during the load step and continue in discharge mode.

After that at t₃, the load power demand decreases drastically from 3600 to 600 W; consequently, the SC module changes its operating mode from discharging to charging. It can be noted that:

1. The battery remains constant supplying its maximum power (limited power) of around 2100 W. It means the battery provides powers to load and charge the SC module.

2. At t₄ (v_SC = 130 V), the SC module is almost charged at 140 V, and afterward, the SC power decreases. Accordingly, the battery power is reduced gradually.

3. At t₅, the SC is full of charge at 140 V; after that, the SC current is zero. Synchronously, the battery main source provides only energy to the load 600 W.

Afterward, at t₆, the load power changes from 600 W to −600 W to emulate vehicle braking. The SC is extremely charged and recovers the energy at the DC bus; concurrently, the battery power declines (with a limited slope) to zero.

At t₇, the SC absorbs the negative power provided only by the load. Thus, the SC is in overcharged state, i.e., v_SC > v_SCREF = 140 V.

Subsequently, at t₈, the load power changes immediately from −600 W to +600 W, where v_SC = 155 V (overcharged); therefore, the SC modules changes its operating mode from charging to discharging and the battery remains in idle state (the current limitation at 0 A). Therefore, the requested load power is provided by only the SC source.

At t₉, when v_SC reaches v_SCREF equal to 140V, the SC power drops to 0 W; then, the battery current increases to provide the power for the load requested.

At t₁₀, the battery power remains at a constant level of 600 W.

Finally, at t₁₁, the load power changes from 600 W to zero (stop mode). The SC recovers the energy and the battery power decreases to zero. It can be concluded that the hybrid network enables keeping energy balance by using the proposed energy control law.

4.3. Comparison of the Performances Compared to the Previous Works

As highlighted in the introduction, the previous works reported in [13,14,15] have been focused on the energy management of electric vehicles based on various nonlinear algorithms (e.g., sliding mode, Lyapunov, fuzzy logic). However, only in [13,14], the developed control algorithms have been validated experimentally on load power profile. Both load power profiles present the same dynamic operations (i.e., three acceleration modes and one braking mode); whereas the chosen load power profile in this work includes one acceleration and braking operation as shown in Figure 12. The dynamic performances obtained both for batteries and SC are close to those obtained in [14]. In comparison, reported results in [13] show that the responses of sources (i.e., batteries, SC) to different dynamics are slower. Indeed, since PI current controllers are used to control both buck–boost converters connected to the sources, the required time to track the different references are longer. In conclusion, the algorithms based on Lyapunov-function and sliding mode controllers or differential flatness offer excellent dynamic performance while preserving the good operation of the storage devices against fast dynamics and keeping the stability of the DC bus. Besides, the use of interleaved buck–boost converters allows reducing the current ripple (as shown in Figure 9 and Figure 10) and ensuring the availability of both converters in case of power switch failures.

5. Conclusions

The key objective of this work is to study new energy management of supercapacitor/battery hybrid sources for modern electric transportation applications. The combination of battery and ultracapacitor is suitable for the hybridization network since it offers high power and high energy densities. The control law allows avoiding the fast dynamic current transient of battery and decreasing the battery stresses. For this reason, the proposed hybrid system allows optimizing its life span. However, this issue does not come within the scope of this article to reveal the battery’s lifetime.

The developed control strategy has been tested with an experimental prototype platform implemented in the laboratory, including a battery bank (120 V, 140 Ah—Panasonic) and a supercapacitor module (6 F, 160 V—Maxwell Technologies). The obtained experimental results have enabled validating the outstanding performances of the developed control strategy during the steady-state and dynamic state.

The differential flatness control theory is principally a model-based concept. It is mandatory to identify model parameters (such as r_LB1, r_LB2, etc.) to determine the flatness property, accurately [17]. To enhance the proposed control strategy, some parameter observers (or online state observers) will be studied in future works.