1. Introduction
Asynchronous computability, which means the solvability of tasks in asynchronous, failure-prone distributed systems, has been an active topic ever since 1985 when the well known FLP impossibility theorem was established [
1]. There is a long line of work that deals with this topic for numerous tasks in different systems under various failure models [
2,
3,
4,
5,
6,
7,
8,
9,
10]. However, only a pinch of results exist that characterize the asynchronous computability of general, rather than specific, tasks.
Such efforts date back to 1988, when Biran et al. [
11] established a graph-theoretical sufficient and necessary condition for the solvability of distributed tasks in message-passing systems. Their method applies only if there is at most one crash failure of the process. Breakthrough was made in 1993 by three independent teams [
5,
6,
12], among which Herlihy and Shavit [
6] presented a topological framework for studying the asynchronous computability of general tasks in share-memory or message-passing systems with
crash failures. This framework was then extended to a complete characterization of wait-free solvability of distributed tasks in shared-memory systems, namely, a task is solvable if and only if its specification is topologically compatible in some sense [
7]. The characterization was further generalized in two directions. One direction is generalization to systems with arbitrary communication objects (not just shared-memory of message passing) [
1,
13], to arbitrary resilience (rather than one or
n failures) [
6,
8,
14], to arbitrary synchrony [
15,
16], or to Byzantine failures that may do the most malicious harm on the system [
9,
17,
18]. The other direction is to characterize the relative hardness of distributed tasks in asynchronous shared-memory systems: two tasks are reducible to each other if and only if they are equivalent in a topological manner [
19,
20,
21,
22].
Closely related to computability is the concept of decidability, which means whether there is an efficient procedure to decide the solvability of a family of tasks in a system model. It was initiated by Herlihy and Rajsbaum in [
19] and continued in [
20,
23], where shared-memory and communication objects of consensus number more than one are considered.
The above-mentioned works mainly assume simple communication objects such as shared-memory and message passing. The two objects were generalized by Herlihy et al. in 2014 [
24] into a spectrum of
d-solo objects, where
d is a positive integer ranging over the set
and
n is the number of processes. Roughly speaking, a
d-solo communication object allows up to
d processes to run
solo, that is none of them gets information from any peer process. The
d-solo execution comes from a real-life distributed computing decision scenarios, the robot gathering problem [
25,
26,
27,
28]. A robot gathering problem of a set of
n asynchronous robots requires that robots can move to meet in a given area of some space (e.g., [
29,
30]) which depends on their initial positions. Since the initial position of a robot constitutes its input value and crash-prone robots may appear asynchronously in the space in the Look–Compute–Move model which corresponds to a wait-free snapshot shared-memory model [
31] where robots can take snapshots of the graph where they are located [
32], and a robot cannot view the positions of all other robots instantaneously in reality, for one robot looks in one direction, it could be that the other robot just moved out of the corresponding region, then it is possible that two robots don’t see each other during the execution of their Look–Compute–Move, which is a situation similar to d-solo executions.
It is not hard to see that shared-memory and message passing lie at the extremes of the spectrum with and , respectively. Then a question naturally arises: is it possible to generalize the asynchronous computability theory from the extremes to the whole spectrum?
To date, little has been known about the answer, except for the progress made by Herlihy et al. [
10]. However, Herlihy et al. [
10] only investigated the solvability of colorless tasks, which belong to a rather constrained class of distributed tasks introduced by Borowsky et al. in [
33]. The mission of our paper is to extend their work to general tasks, so as to completely answer the question.
Our contribution lies in three aspects. First, we fully characterize the asynchronous computability of distributed decision tasks on
d-solo systems for arbitrary
. The characterization is in terms of a topological property of the task’s specification, strengthening the bridge between topology and computing. Second, as an application, we derive a simple necessary and sufficient condition for the solvability of input-less tasks in
d-solo systems. input-less tasks were proposed by Gafni et al. in [
23]. They are among the simplest distributed tasks, and play a critical role in research on distributed computability and decidability. Third, we identify a hierarchy of input-less tasks, which exactly differentiates the computational power of
d-solo objects for different
d. This provides an alternative to the more sophisticated agreement-like tasks constructed by Herlihy et al. [
10].
2. Asynchronous Computability Theorem in d-Solo Models
2.1. Computational Model of Distributed Computing
In this subsection, we review briefly review some concepts of distributed computing. For details, please refer to [
6,
7,
13,
15,
19,
20,
23,
34].
A distributed system consists of sequential processes and some communication objects through which the processes communicate. Without loss of generality, assume that each process proceeds round by round. We further assume that the system is asynchronous and that up to n processes may fail by crashing. In any execution, each process starts with a private input value, and if non-faulty, ends with a private output value after a finite sequence of communications and local computations. A task is a specification of eligible outputs with regard to the inputs, which intuitively models a coordination problem.
Now, we recall the
d-solo communication object
proposed by Herlihy et al. [
24], where integers
and
stand for the solo-dimension and the round number, respectively. Roughly speaking,
only allows processes in round
r to communicate, and up to
d of the processes can run in solo, i.e., each gets no information from its peers. The behavior of
is depicted as follows. Let
be an ordered pairwise-disjoint partition of a non-empty subset
, such that
and
for any
. It represents the following communication result: each process
reaches round
r and invokes
on some value
, and the invocation returns
to
if
, while it returns
if
with
. Intuitively,
is the set of processes that run in solo in round
r. For more detail, refer to the literature [
10].
A protocol is a distributed program consisting of the processes. A protocol is said to solve a task if the outputs of each execution conform with the specification of the task. Full-information protocols are widely studied, where each process keeps communicating without local computation until it decides. Full-information protocols play a key role in distributed computing, because they are universal in the sense that a task is solvable if and only if it can be solved by a full-information protocol. When processes communicate via
d-solo object
, a full-information protocol has the form illustrated in
Table 1. Here,
is a boolean function indicating whether or not the process
can make a decision based on the local state
, and
returns
’s decision value. What we need to know is that
makes a decision and
returns just once if it can decide.
2.2. Topology Model of Distributed Computing
In this subsection, we review concepts of combinatorial topology briefly, and then we model distributed computing systems in terms of combinatorial topology. One can refer to [
34,
35,
36,
37] for further details.
2.2.1. Simplicial Complex and Simplicial Map
An , or complex for short, is a collection of non-empty subsets of a finite set. The complex is required to be closed under containment, meaning that if , then all non-empty subsets of are included in . A member of is called a simplex. Given two simplexes , we say that is a of if , and we say that is a proper of if . Define the dimension of a simplex to be , where stands for the cardinal number of the set . The dimension of a simplicial complex is the highest dimension among its simplexes. We simply call an n-dimensional simplex an n-simplex, and use the superscript form to indicate the dimension when needed. The notation is likewise defined on complexes. Any 0-simplex of a complex is called a vertex of , and we use to denote the set of vertices of . A n-complex is said to be pure, if any simplex is a face of some n-simplex . By default, we only consider pure complexes in this paper. Any complex is called a subcomplex of . Given a pure n-complex , any -simplex which is a face of a unique n-simplex is called a boundary simplex, and the subcomplex consisting of all boundary simplexes and their faces is called the boundary of , denoted by .
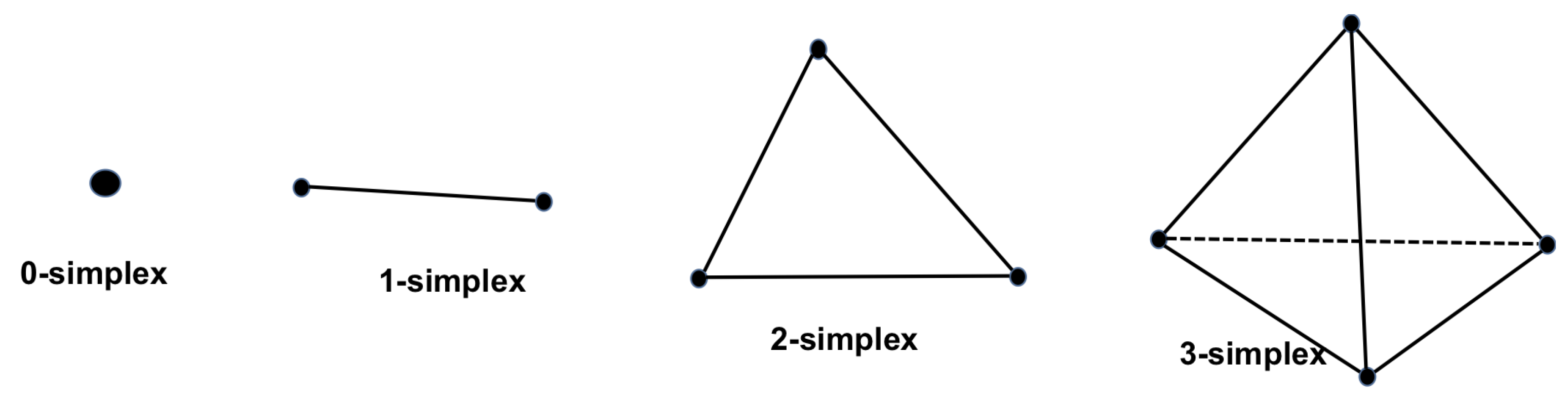
To ease understanding, one can equivalently view abstract simplicial complex
through the geometric lens which we call geometric simplicial complex. Bijectively map
to an arbitrary set of affinely independent points in an Euclidean space. Each simplex naturally corresponds to the convex hull spanned by the images of its vertices. Seeing
Figure 1, a vertex is 0-simplex, a line segment is a 1-simplex, a triangle is a 2-simplex and a tetrahedron is a 3-simplex. Putting the convex hulls together, we get a geometric realization
of
. Nevertheless, hereunder, we still adopt the definition of the abstract simplicial complex.
Given complexes and , a map is said to be a simplicial map from to if it map every simplex in to a simplex in . A map is called a carrier map from to . Given a simplicial map and a carrier map from to , we say that is carried by if for any simplex .
Let and be two complexes, we say that is isomorphic to if there exist simplicial maps and such that the compositions and are both identity maps.
Let be a simplicial complexes and be a finite set. We say is -chromatic if there is a map such that for any vertices of a common simplex. We call a -coloring of and use to denote the set of colors of the vertices of a simplex . Suppose complexes and have -colorings and , respectively. A map is called color-preserving if for any .
For any integer , we will use to stand for the set .
Let be an n-simplex and be a -coloring of . The standard chromatic subdivision of , denoted by , is the n-complex constructed as follows:
;
Any set of vertices is a simplex of if and only if both the following conditions are satisfied for any :
Note that has a natural -coloring: color any vertex in c. Hence is also -chromatic.
Figure 2 illustrates the barycenter subdivision which has a detailed description in [
37], and the standard chromatic subdivision of a 2-simplex, viewing through the geometric lens.
2.2.2. Task Formalization
Formally, a distributed task T on processes can be modeled as a triple , where and are pure n-complexes and is a carrier map from to . is dimension-preserving in the sense that for any , is a pure complex of dimension . The n-simplexes in the input complex are such where ranges over the input domain of process . Likewise for , except that the values range over the output domains. With any vertex colored by the color i, both and are -chromatic complexes. must satisfies that for any 0-simplex . Consider m-simplices and . Then, means when only processes participate in an execution, if each gets input , it is eligible that each ends with output for .
Example 1. As shown in Figure 3, it is a standard input-less 2-task , in which the left part of this Figure represents the input complex and the right part represents the output complex. The carrier map Δ is illustrated by the dash arrows. Specifically, it maps each vertex to , each 1-simplex to , and the 2-simplex to . Intuitively, this means that if some process does not participate, the participating ones have a unique output; otherwise, any outputs characterized by are eligible. 2.2.3. Protocol Complex
Consider a full-information protocol
as shown in
Table 1. Fix an input simplex
. In an execution, if each process
finishes round
k with local state
, the global state of
at the end of round
k in this execution is modeled as the simplex
. We say that
is reachable from
by
. All such simplexes, together with all their faces, constitute the
k-round protocol complex of
reachable from
, denoted by
. Let
k be the last round before making decision. Then complex
is called the protocol complex of
.
Example 2. Figure 4 illustrates the geometric view of the 1-round protocol complex of the full-information protocol on three processes. The dots are colored yellow, black and green to stand for the processes and . Consider the communication objects with , respectively. An arrow represents that the destination process has received the value communicated via by the source process. Each filled triangle represents a 2-simplex, modeling a reachable global state. The collection of all the 2-simplexes in the left part of the Figure 4 represents 1-round protocol complex when the communication object is 1-solo. The middle part of Figure 4 shows the extra 2-simplexes that appear when the communication object changes from 1-solo to 2-solo. Hence, the simplexes in the middle and those in the left part of this figure form the 1-round protocol complex when in . If we further increase d to 3, one more 2-simplex appears, as illustrated in the right part of Figure 4, which represents an execution in which all of the three processes run in solo. Putting all the simplexes together, we get the 1-round protocol complex when is used. 2.3. Chromatic Join
In this subsection, we mainly define a chromatic complex, a chromatic join, which can describe the execution of d-solo model accurately. Then we introduce a simple property of the complex.
Given two sets and with no intersection, call the join of and if .
Let be a chromatic simplex. Consider a non-empty set . Define the low-dimensional part , and the high-dimensional part . We say that S is compatible if both the following conditions hold:
For any , ;
is a simplex in for any .
Roughly speaking, S, if compatible, stands for the global state resulted from a 1-round execution of the full-information protocol, where processes in run in solo.
Definition 1. Given a chromatic simplex α and an integer , the chromatic d-join of α is defined to be Remark 1. We can regard S as a join of and that are subsets of for any element ;
In the definition of chromatic d-join, S can be such that . This implies that .
Now we extend the definition to complexes. Suppose is a chromatic n-complex. Its chromatic d-join is defined to be .
Lemma 1. is a chromatic simplicial complex.
Proof of Lemma 1. We first show that is closed under containment and intersection.
Let be any simplex in , then there is a simplex such that in which S is in . Suppose is any face of . There are three cases: or , or and . It is not hard to show that in each case of them, we can regard as a d-join of a subset of and a subset of . It follows that is in , and it is also in .
Let be any another simplex in . If the intersections of and is not empty set, then it must be a common face of them. By the upper argument, we know that it is also in .
Then label each vertex with c. From the definition of , it is obvious that this labeling is a coloring map of . □
Throughout this paper, whenever coloring of is mentioned, it always means the labeling in the proof.
Inductively, we define the s-fold chromatic d-join , for any positive integer s. Particularly, if , we set .
From Lemma 1, we note that is chromatic simplicial complex for any given chromatic simplex , then we can regard as a carrier map. On this ground, we define the of a simplex in .
Definition 2. Given a chromatic simplicial complex , consider an arbitrary simplex that . Let τ be the minimal simplex in such that . Then τ is called β’s carrier in under carrier map , denoted by . Inductively, we can define the carrier of , that is, .
Suppose , then if , otherwise, there must be a vertex such that for any vertex , , then .
The next lemma indicates that the d-join preserves some connectedness property.
Lemma 2. Let , be two -chromatic n-complexes. If there is a color-preserving simplicial map for non-negative integers k and d, there is a color-preserving simplicial map .
Proof of Lemma 2. Let
be any
n-simplex of
. Since
f is color-preserving simplicial map, then
is a chromatic
n-simplex of
with the same colors of
. Let
be a point-to-point map from
to
such that
for any
,
. We only need to check that
is simplicial map from
to
.
Let
is any
n-simplex of
, since
is chromatic complex by Lemma 1, then we can assume that
. It follows that
which is an
n-simplex in
. Since
is chosen arbitrarily, then
is a color-preserving simplicial map from
to
.
Assume
is another
n-simplex of
and
is the common face of
and
, then
It follows that
is equal to
by former argument. As a result, all such maps agree on their intersections. We just constructed
then
g is a color-preserving simplicial map such that for any simplex
of
,
is equal to
, where
is
. Note that
is arbitrary and
is
, it follows that
g is a color-preserving simplicial map from
to
. □
Remark 2. Let us explain the relation of maps and g. Since we have shown that is a simplicial map for any α in , then it is a “linear” map [38], which makes that the images of the intersection under and are the same if α has an intersection with β. Then we can regard g as an attaching map of all pieces . By this lemma, we know that if there is a color-preserving simplicial map from to , then there also exists a color-preserving simplicial map from to for any integer .
2.4. Main Theorem
In this subsection, we first show the connection between protocol complex and chromatic d-join of the input complex, and then we prove one of main theorems.
Lemma 3. When the input complex is , the protocol complex of any 1-round full-information protocol in d-solo model is exactly the chromatic d-join .
Proof of Lemma 3. The basic strategy of the proof is to show that there exists a one-to-one correspondence between the set of protocol complexes on of any protocol with 1-round and the once chromatic d-join of in Definition 1, where is the input complex colored by with colors . Roughly speaking, we firstly show that given an input simplex of and an execution of the protocol arbitrarily, the output complex is a subcomplex of . Secondly, we need to show that given any simplex O of , there must exist an execution and an input simplex such that there is a possible output which corresponds to O.
Consider any maximal input
n-simplex
in
as an initial global state, where
,
in which
i and
stand for the
and the input value of a participating process
. Let
be the set of processes that are coming from
I. Consider any execution
of protocol
with 1-round in
d-solo object
. From the behavior of object
,
factly gives a sequence of all processes along the order that run
, denoted by
, where
. That is if
then process
runs object
before
or both of them run concurrently. Define an ordered partition of
by this sequence, denoted by
, such that all processes in
run object
concurrently and processes in
run object
before processes in
for
. It follows that processes that executing solo appear only in
. Let
be an empty set if there is no process that runs solo. Note that at most
d processes run solo, then
. Assume that all processes of
finishing
have returns, denoted by
Note that if
, process
only see itself then
which is a 0-dimensional face of
I, and if
,
, process
will see all processes that run before and concurrently, then
is a non-zero dimensional face of
I. By the definition of standard chromatic subdivision,
for any
, then
.
Let
be equal to
and let
be complementary set of
in
S, then for any
and any
, we have
It follows that S is compatible. Note that , then S is a d-join and in by Definition 1. If not all processes have returns, that is, some processes may be faulty, then the returns is a subset of S, for all processes participate and deposit their initial local state in object . Then is also a d-join and in . Since I and are arbitrary, then .
On the contrary, given any m-simplex of . Suppose , then is a face of for any . Let , then . Let and let , then .
Since is a d-join, then it is compatible and it has form with , where and are the low-dimensional part and the high-dimensional part of . And then for any vertex , is a face of . It follows that we can give a partition of the set of classes over all processes of , denoted , such that, if then we put into ; and for any two processes , if then we put them in a same class with , and if we put and into and such that .
Next, we will give an ordered partition of
by
. Step 1. For any one
, check
, if
do nothing; if
that is, there exists at least one process that is in
but not in
, then put
together as a new class
between
and
. Step 2. For any one
,
, check
, if
then do nothing; if
that is, there exists at least one process that is in
but not in
, then put
together as a new class
between
and
. After checking all elements of this partition of
, we will get a new partition
. It is easy to show that this is a partition of
, because
is the carrier of
and there must be a vertex
in
Q such that
by Definitions 1 and 2.
By this ordered partition, we can construct an execution
such that when all processes finish the execution, the reachable simplex is
. Without loss of generality, we assume
. Step 1. Let all the processes in
access object
firstly such that all processes have returns and return their inputs, denoted this collection of executions by
; Step 2. Let all the processes in
access object
concurrently after
, such that none of them has return, which represents that all of them are crash, denoted this collection of executions by
; Step 3. Along with this ordered partition, do the similar steps as step 1 and step 2, denoted these ordered collections of executions by
,
for
. Let
be the composite of all executions, such that for each process in execution
there is no return, and for each process in execution
there must be a return. If for some
or
is an empty set, it needs just omit the corresponding executions in
. As a result,
is a reachable simplex under execution
.
For any face of , we just take the composite of the subset of corresponding executions. Since is arbitrary, it follows that is a subset of . From upper arguments, we can see that is equal to . □
Corollary 1. When the input complex is , the protocol complex of any s-round full-information protocol in d-solo model is exactly the s-fold chromatic d-join .
Proof of Corollary 1. Given arbitrary execution of protocol with s rounds, we can model as a sequence of executions, such that each process runs a protocol with at most one round in execution . Then each return of a process after executing is an input value of this process in execution , by Lemma 3 and Definition 1, is equal to the s-fold chromatic d-join . □
Theorem 1. A decision n-task has a wait-free protocol in d-solo model if and only if there is an integer and a color-preserving simplicial map such that for any simplex and , .
Proof of Theorem 1. From the
Figure 5, we know that the protocol
solves the task
iff there exists a simplicial color-preserving decision map
such that for every simplex
, and every simplex
,
,
.
Suppose there exists a protocol that solves task T. By Corollary 1, the protocol complex is equal to . Let , which shows the necessity of the theorem.
For sufficiency, suppose
is any
r-simplex in
, apply algorithm as
Table 1 in
d-solo model and after
k-round, any output simplex will agree on a simplex in
. By hypothesis, there exists a simplicial map
. Then a process that chooses vertex
v in
then chooses as its output the value labeling
. That is to say, this algorithm can solve this task. □
Remark 3. This theorem gives the topological characterization, he that is a pair of a chromatic join and a color-preserving simplicial map, of the wait-free solvability of a given decision task in d-solo systems, which we can use to give us theoretical help in hardware design or early warning.
Corollary 2. Let be a decidsion n-task, if T is not solvable in -solo model then it is also unsolvable in -solo model for .
Proof of Corollary 2. Suppose T is solvable in -solo model, then there is a color-preserving simplicial map from to for some integer k by Theorem 1. Note that is a subcomplex of for , then the restriction of on is a carrier and color preserving simplicial map from to , by Theorem 1, T is solvable in -solo model, which is a contradiction. □
3. Application
A standard input-less
n-task
is a task of
processes. Specifically,
is a pure complex having only one
n-simplex, implying that each process has no input;
has a subcomplex
L which is isomorphic to the boundary of an
n-simplex. If less than
processes participate in an execution, the output simplices must lie in
L, otherwise, any simplex in
is eligible. For simplicity, we can use
to stand for
. A standard input-less 2-task can be seen in
Figure 3.
By Gafni and Koutsoupias in [
23], we know that 2-task
T is solvable in wait-free iterated immediately snapshot model if and only if
L is contractible (i.e., there exists a continuous map from a 2-dimensional disk to
such that it maps the boundary of this disk to
) in
whose
-dimensional homotopy group can be represented. However, we will see that it is not true in
d-solo model, that is to say, it is too weak to derive the solvability of task
T from the condition in which
L is just contractible in
.
In this subsection, we mainly investigate the solvability of any standard input-less task, that is giving the necessary and sufficient conditions of solvability to these tasks, which also implies the classification of these tasks along their solvability in d-solo model. But before this, we need introduce the other topology space.
Intuitively, the standard chromatic subdivision of an n-simplex is an evolution of its barycentric subdivision, in which we need add the least new vertices in all but 0-dimensional faces of , such that each face is divided into more than one small pieces and each one is a chromatic simplex with the same colors and dimension of that face. However, in the next definition, we introduce a special chromatic subdivision in which the added vertices only appears in a face with its dimension at least k.
Definition 3. Let α be an -chromatic simplex and k be a non-negative integer. The k-type chromatic subdivision of α, denoted by , is a complex obtained from by removing simplices having any vertex with .
Remark 4. If , then , that is, there is no any operation on α. If then is equal to that is standard chromatic subdivision of α.
We can inductively define the
s-fold
k-type chromatic subdivision
of
with that
for any positive integer
s. Similarily, if
X is an
-chromatic
n-complex, we can get the
s-fold
k-type chromatic subdivision of
X, denoted by
. In addition, if
, set
. The
Figure 6 is an example that shows 1- type and 2-type chromatic subdivisions of a 2-simplex.
By definition, is a subcomplex of . Hence, if there is a simplicial map from to some chromatic complexes Y, there is a simplicial map from to Y for a given chromatic complexes Y. The next lemma implies the situation vice versa, which is usually not right for a pair of general simplicial complexes.
Lemma 4. Let X and Y be -chromatic n-simplexes. For any integers and , there exists a color-preserving simplicial map from to .
Proof of Lemma 4. We will show that by induction. Suppose
and
. When
,
and
, let
that takes
to
. When
, assume
and
,
. Let
be a point-to-point map from
to
such that
We will show that is a color-preserving simplicial map. Suppose is an arbitrary n-simplex in , then it is a k-join, that is, it is compatible and , then there are at most k vertices in such that for each vertex of them. By former Equation, . Note that is color-preserving and there are at most k vertices in such that for each vertex of them, then is compatible and , and then . Since each vertex of has form with , or with , then there is no vertex in such that , and then . Since is arbitrary, it follows that is a color-preserving simplicial map.
Suppose that for there is a color-preserving simplicial map . Consider . Let be arbitrary n-simplex of , where . By assumption, there exists a color-preserving simplicial map from to , then the restriction of on is also a color-preserving simplicial map from to .
Since
X and
Y are arbitrary, set
,
, by the former argument, we know that there is a color-preserving simplicial map
from
to
. As all such maps agree on their intersections, then we just constructed
It follows that g is a color-preserving simplicial map from to .
Note that
is a subset of
, then
is a subset of
. Let
be an inclusion map from
to
, then it is a color-preserving simplicial map. Let
be the composite of
and
g, then
is the color-preserving simplicial map from
to
. By now, we complete the induction. □
Remark 5. Let us explain what is the construction map . Since X and Y are chromtatic n-simplexes, then is isomorphic to . In other words, they are the same in topology. Because is a subcomplex of , then can be regarded as a collapse map from to its subcomplex essentially. That is to say map a simplex to itself if the simplex is in both and , otherwise collapses the simplex to one of its vertices.
Corollary 3. Let X and Y be two arbitrary -chromatic n-simplexes. If there is a color-preserving simplicial map from to Y for some non-negative integer s, there exists a color-preserving simplicial map from to Y.
Proof of Corollary 3. Assume
is the color-preserving simplicial map from
to
Y. By Lemma 4, there is a color-preserving simplicial map
from
to
. Let
be the composite of
and
, then
h is a color-preserving simplicial map from
to
Y. □
Suppose be a -chromatic simplex with . Let be the collection of all color-preserving simplicial maps that are from to any -chromatic complex with a subcomplex which is isomorphic to , such that for any .
Definition 4. is called s-length k-nest, while is called the k-nest.
Intuitively, the k-nest is a space of images of all color-preserving simplicial maps that are from s-fold k-type chromatic subdivision of a chromatic n-simplex to any chromatic n-complex for all non-negative integer s.
We say that a chromatic n-complex K holds k-nest structure which is bounded by a subcomplex means that there exists a subcomplex of K with boundary , such that is isomorphic to an element .
Observation For the spectral sequence about nests , if , is than , that is, there is at least one element in but not in .
In fact, we can always construct an element that is in
but not in
for
. A simple example shows that the left complex of the
Figure 7 is in
but not in
.
Example 3. There are two chromatic 2-complexes in Figure 7 with color . The left one denoted by F, and the right one denoted by . Each vertex has form , where C and t stand for color and some state of that vertex. The boundaries of them are the outer bold and black segments, denoted by L. There is no difficulty to show that holds 2-nest structure, because we only take , which is a chromatic 2-simplex with color , then there is a natural color-preserving simplicial from to . However, for F, we can never find an integer s such that there is a color-preserving simplicial from to F. But they all hold 1-nest structure, because, L is always contractible and is the standard chromatic subdivision operation. Then there always exists a large enough integer s such that there is a color-preserving simplicial from to F and by Lemma 2 of [23]. Theorem 2. Let be a standard input-less n-task. Then it is solvable in d-solo model if and only if holds d-nest structure that is bounded by L.
Proof of Theorem 2. For necessity. Assume T is solvable and is an input n-simplex, then there is a color-preserving simplicial map , which maps to L for some non-negative integer s by Theorem 1. Note that is a chromatic subcomplex of , then the restriction of on , denoted , is also a color-preserving simplicial map from to , which takes to L. It follows that , which implies that holds d-nest structure.
For sufficiency. Suppose holds d-nest structure which is bounded by L, then there exists an integer s and a subcomplex with boundary complex L, such that there is a color-preserving simplicial map f from to , which takes to L. By Corollary 3, there is a color-preserving simplicial map from to , which takes to L. It follows that T is solvable by Theorem 1. □
Remark 6. Even though Theorem 1 can be used to characterize the solvability of an input-less n-task in d-solo model, we find that it is difficult to describe the protocol complex and to find out the map δ. While, sometimes, we can check whether the output complex of the task holds d-nest structure or not easily. As a result, theorem 2 is an effective way to the characterization of solvability of tasks (at least for standard input-less task) in d-solo model.
Corollary 4. The power of computability of d-solo wait-free model is strictly getting weaker when d becomes bigger.
Proof of Corollary. Consider standard input-less n-task . Let be two positive integers and . Note that -nest structure does indeed a proper subset of -nest structure , then there does exist an element that is in but not in . Assume is that element, then holds -nest structure that is bounded by L but not holds -nest structure. It follows that T is solvable in -solo model but is not solvable in -solo model by Theorem 2. As a result, the power of computation of -solo is strictly weaker than the power of the computation of -solo. □
4. Discussion
It seems that our result, Theorem 1, is just some minor improvements of previous studies of Herlihy M. et al. [
6,
7,
13,
24] when someone catches a glimpse of them. Actually, that is not the case. In [
6,
7], the Asynchronous Computability Theorem (ACT) characterizes the tasks that can be solved in share-memory models, that is to say, it is the case when
. While in [
13,
24] ACT characterizes the tasks that can be solved in message-passing models, which is the case when
.
d-solo models, as a bridge that links share-memory models with message-passing models, which is introduced by Herlihy M. et al. [
24], where they just characterized a kind of special tasks, colorless tasks, that can be wait-free solvable. However, all the previous results are based on one of the central results of topology which is the Simplicial Approximation Theorem [
37]. That theorem establishes what is a “discrete version” of a continuous map. What a pity, this theorem cannot be used in a
d-solo model when
, because it is no longer the case that the diameter of the simplices in a subdivision is reduced. Our results bypass the Simplicial Approximation Theorem, and the span that is a pair of a protocol complex and a simplicial map
is constructed based on the topological structure of the protocol complex itself. At the same times, our ACT will be appropriate not just for colorless tasks but for arbitrary decision tasks. From these views, our result is a great improvement.
In addition, the topological framework itself holds the potential applications in real life, such as the information safety [
39,
40], the public safety networks [
41,
42], the big data analytics [
43,
44] and so on. Let us take the information safety as an example. Consider the realistic scenario [
45] of communication of information among a Trade Associations that consists of thousands of trading partners. The information, which is asynchronous, must be transmitted and delivered timely in an exchange process. One practical problem is that how can we use it to design an information exchange system which is as safe and efficient as possible [
39,
45]. Since we have obtained the computability of the
d-solo models, we can choose the corresponding
d according to the actual demand. The other is that how to do application development of a given information exchange system. Such as how to detect the defects of the system and make early warning [
46]. Some traditional ways may cost large mount of time or money and sometimes a result hardly convinces many people. Luckily, it seems to be easy, at least on a theoretical level, if we use the topological framework to construct a mechanism and then to analyze it. From this point, our framework has a far-reaching impact on the production and living. Furthermore, there should be more and more researchers who take part in the research that how to apply topological framework to real-life better.
Lastly, the chromatic join of a given chromatic complex itself is very interesting and it provides a way to generate a new chromatic complex from the original complex. Though the geometrical properties of the generated chromatic complex look more complicated than the original, their topological properties are similar. Roughly, if an input complex is isomorphic to an n-sphere, then the chromatic join of an input complex is isomorphic to a wedge sum of n-spheres, and the bigger d the more number of n-spheres in the wedge sum. So our research has a potential value to the studies of topology itself, especially in simplicial homotopy theory.