The SOS Platform: Designing, Tuning and Statistically Benchmarking Optimisation Algorithms
Abstract
:1. Introduction
- result visualisation methods (in both tabular and graphical formats).
- a vast and heterogeneous number of benchmark functions and real-world testbed problems;
- several state-of-the-art algorithms to be used for comparisons with newly-designed algorithms;
- libraries with implementations of the most popular algorithmic operators such as mutation methods, crossover methods, parent and survivor selection mechanisms, heuristics selection methods for memetic computing (MC) and hyperheuristic approaches, etc.;
- a system to spread the runs over multiple cores and threads, thus speeding up the data generation process, and automatically collecting and processing raw data into meaningful information.
- open source software, so that researchers can freely use it and build upon it;
- a simple and flexible structure so that new problems and algorithms can be easily added.
- Section 2 presents the SOS software platform and provides detailed descriptions of its features;
- Section 3 focuses on benchmarking optimisation algorithms with SOS and lists the available benchmark suites, including established benchmarks and one customised benchmark;
- Section 4 first provides a literature review on statistical methods for comparing stochastic optimisation algorithms, then describes the implementation and working mechanisms of three statistical analyses available in SOS;
- Section 5 reports on the result visualisation capabilities of SOS and provides “how-to” examples based on studies from the current literature in metaheuristic optimisation;
- Section 6 summarises the key points of this article and remarks on the novel aspects of SOS;
- Appendix A gives additional details on the routine used to produce average fitness trend graphs.
2. The SOS Platform
2.1. Functional Overview
- execute a list of experiments having different budgets, number of runs, problems and algorithms, or the same experiments repeated for different dimensionalities (if the problems are scalable);
- generate log files describing the performed experiments (i.e., the list of problems and their corresponding details, e.g., dimensionality, as well as the parameter setting, number of runs, etc.);
- store raw data and process them into results tables and plottable formats, as shown in Section 5.
- the execution of statistical tests for comparing optimisation algorithms, described in Section 4, including the advanced statistical analysis (ASA) presented in Section 4.3;
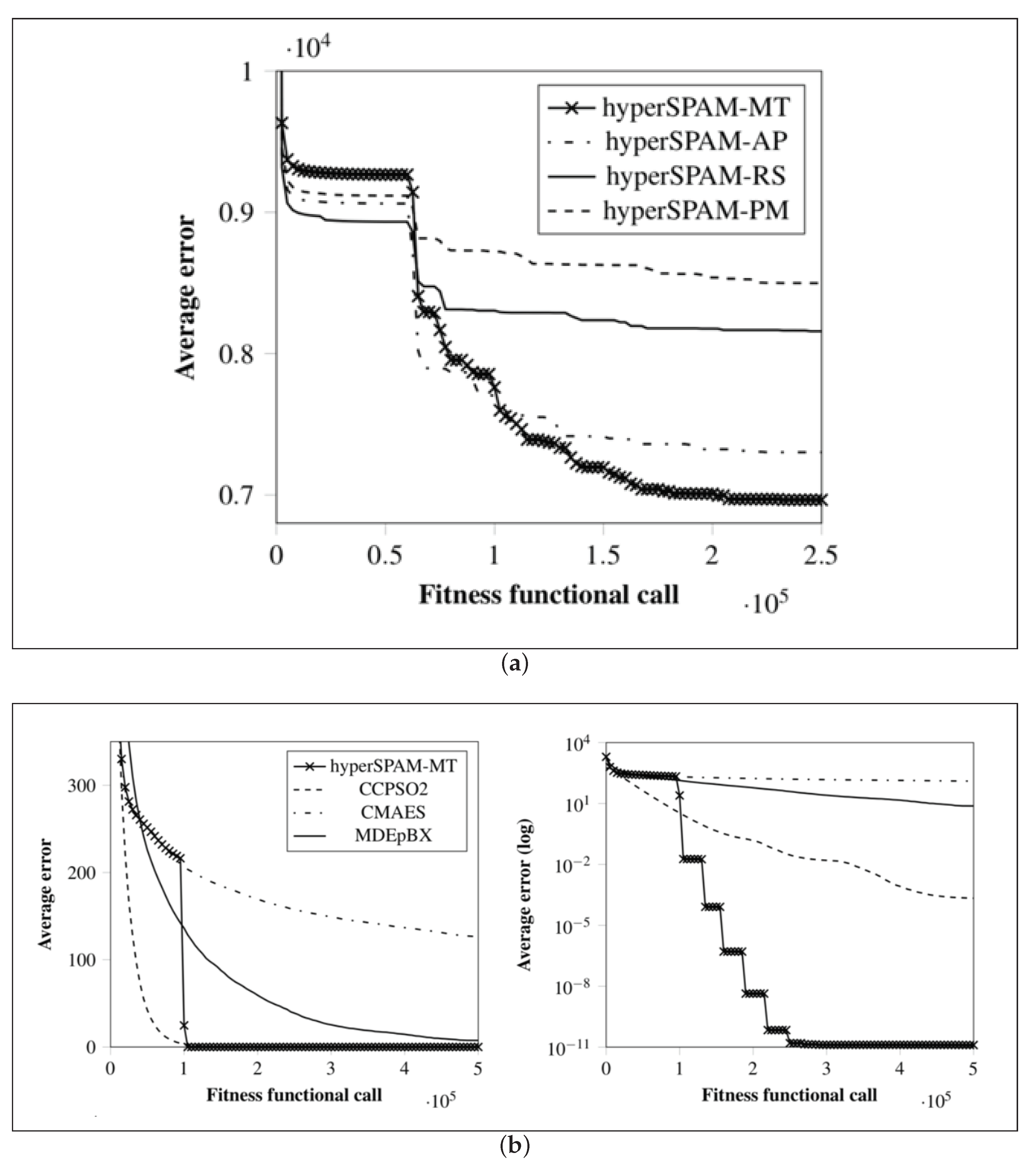
- the generation of plottable files suitable for Tikz, Matplotlib, Gnuplot or MATLAB scripts for displaying best/median/worse/average fitness trends, as shown in Section 5 and Appendix A;
- the generation of
tables (both source code and PDF files are produced) showing results in terms the average fitness value (or average error w.r.t. the known optimum, if available) with the corresponding standard deviation and further statistical evidence, as explained in Section 4 and graphically shown in Section 5.
 source of the comparative tables is generated without any user intervention, together with the corresponding PDF files.
source of the comparative tables is generated without any user intervention, together with the corresponding PDF files.2.2. Parameters’ Fine-Tuning
2.3. Adding New Algorithms and Problems
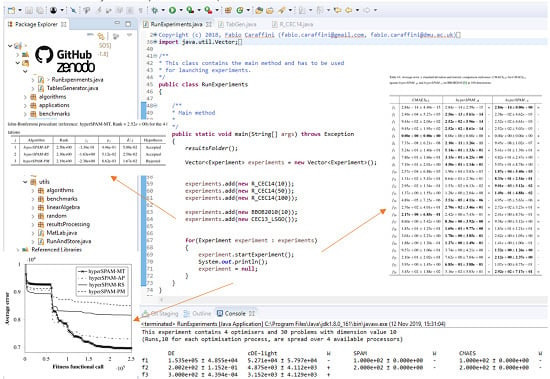
- RunAndStore: This class contains the implementation of all methods involved in executing an algorithm in single or multi-thread mode, collecting the results, displaying them on a console (unless differently specified) and saving them into text files.
- RunAndStore.FTrend: This class instantiates auxiliary objects storing information collected during the optimisation process and that must be returned by all the algorithms implemented in SOS. As shown in Figure 3b, the primary purpose of these objects is to store the fitness function evaluation counter and the corresponding fitness value in order to be able to retrieve the best (max or min according to the specific optimisation problem) and plot the so-called fitness trend graphs like those in Figure 1 and in Figure 8 of Section 5. The class provides numerous auxiliary methods to return the initial guess, the best fitness value, the median value, and so on. Obviously, the near-optimal solution must be also stored, and if needed, several other extra pieces of information can be added in the form of strings, integer or double values. As an example, in [11], population and fitness diversity measures were collected during the optimisation process.
- MatLab: This class provides several methods to initialise and manipulate matrices quickly. These methods include binary operations on matrices and, most importantly, auxiliary methods for generating matrices of indices, for making copies of other matrices and decomposing them.
- Counter: This is an auxiliary class to handle counters when several of them are required to, e.g., count fitness evaluations, count successful and unsuccessfully steps, etc. In [1,16], this class was used to keep track of the number of generated infeasible solutions and of how many times the pseudo-random number generator was called in a single run. It must be remarked that for obtaining this information in a facilitated way, it is necessary to extend the abstract class algorithmsISB rather than algorithms [17].
- the random utilities, which provide methods for generating random numbers from different distributions, initialising random (integer and real-valued) arrays, permuting the components of an array passed as input, changing the pseudo-random number generator, changing seed, etc.;
- a vast number of algorithmic operators (sub-package operators) implementing simple local search routines, restart mechanisms and most importantly:
- −
- the class GAOp, which provides numerous mutation, parent selection, survivor selection and crossover operators from the GA literature;
- −
- the class DEOp, which provides all the established DE mutation and crossover strategies, plus several others from the recent literature;
- −
- the classes in aos, which implements adaptive heuristic/operator selection mechanisms from the hyperheuristic field [24].
3. Benchmarking with SOS
- significantly reduce the optimisation time;
- investigate algorithmic behaviours over problems with known or partially known properties;
- be able to study the scalability of optimisation algorithms empirically.
- several complete benchmark suites amongst those released over the years for competitions on real-parameter optimisation at the IEEE Congress on Evolutionary Computation (CEC), namely:
- the fully-scalable test suite for the Special Issue of Soft Computing on scalability of evolutionary algorithms and other metaheuristics for large scale continuous optimisation problems [82];
- a novel variant of the CEC 2014 benchmark, named “R-CEC14” (the “R” indicates a rotation flag used to activate or deactivate rotation operators), presented in Section 3.
The R-CEC14 Benchmark Suite
- the efficacy of the so-called rotation-invariant operators in optimising rotated and unrotated landscapes, as done for DE in [4,53], where it was unveiled no difference in the performances of such operators over the two classes of problems (indeed, from the point of view of the algorithm, these are just different problems) thus arguing the need for rotating benchmark functions, if not for transforming separable functions into non-separable ones;
- separability and degrees of separability, measured, e.g., with the separability index proposed in [3], as well as on the suitability of certain algorithms and algorithmic operators for addressing separable and non-separable problems.
- the last 28 functions are their rotated versions.
4. Statistical Analysis with SOS
- a comparison test based on the Wilcoxon rank-sum test, described in Section 4.1
- a comparison test based on the Holm–Bonferroni test, described in Section 4.2;
- the advanced statistical analysis (ASA) test, described in Section 4.3.
4.1. The Wilcoxon Rank-Sum Test
4.1.1. Reference and Comparison Algorithms
4.1.2. Assigning Ranks
4.1.3. The Rank Distributions
4.1.4. Wilcoxon Rank-Sum Statistic and p-Value
4.1.5. Decision-Making
- if , the test fails at rejecting , i.e., the two algorithms are equivalent on P;
- if , the test rejects , and one can be confident that a significant difference does exist between A and B on P.
4.2. The Holm–Bonferroni Test
4.2.1. Choosing the Reference Algorithm
4.2.2. Assigning Ranks
- for each problem in E, a score equal to NA is assigned to the algorithm displaying the best average performance in terms of fitness function value, i.e., the greatest if it is a maximisation problem or the smallest if it is a minimisation one, while a score equal to is assigned to the second-best algorithm, a score equal to to the third-best algorithm, and so on. The algorithm with the worst final average fitness value gets a score equal to one;
- for each algorithm in E, the scores assigned over the NP problems are collected and averaged:
- −
- the average score of the reference algorithm is referred to as rank ;
- −
- the remaining average scores are used to sort the corresponding algorithms in descending order and constitute their ranks, which are indicated with (). These ranks provide a first indication of the global performance of the algorithms on E, and their order will be automatically displayed in the form of a “league” table.
4.2.3. Z-Statistics and p-Values
4.2.4. Sequential Decision-Making
- if , the test fails at rejecting the null-hypothesis ;
- if , the null-hypothesis is rejected, and the rank can be used as an indicator to establish which algorithm displayed a better performance on E.
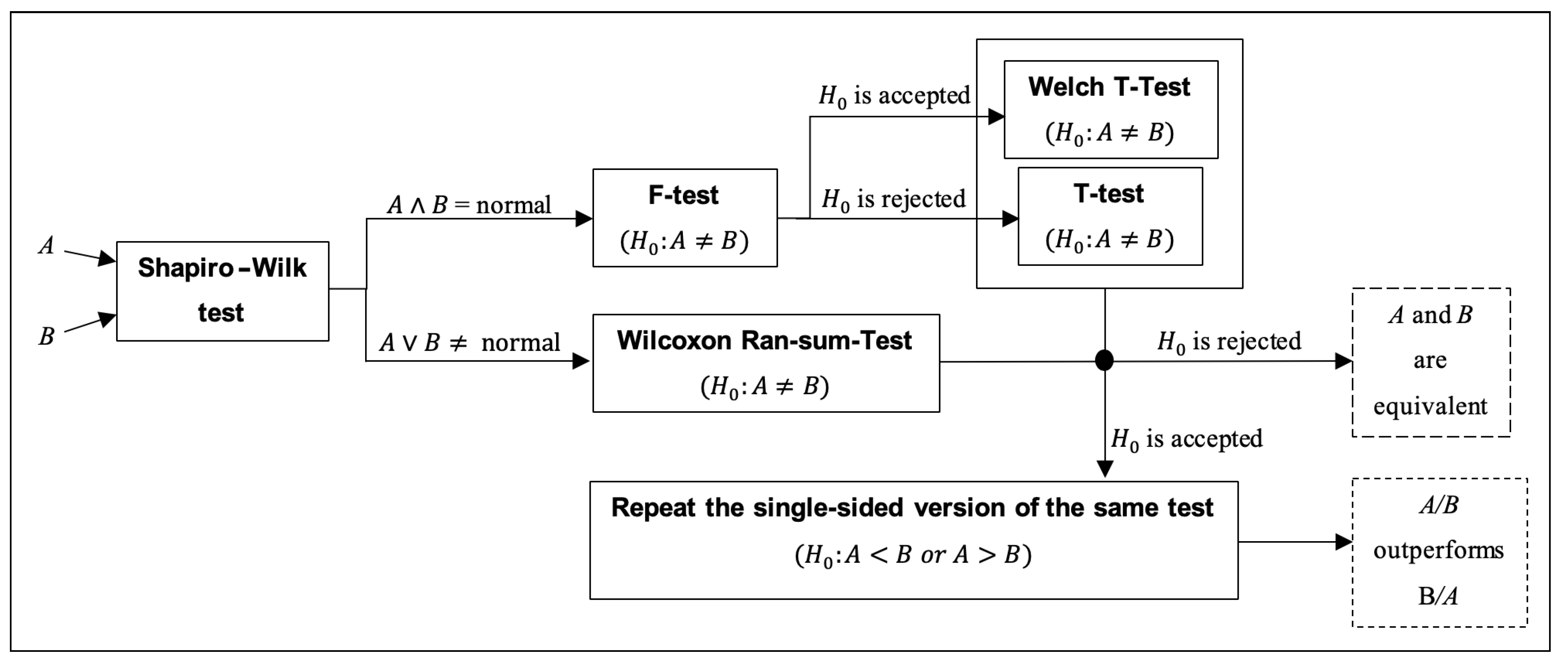
4.3. Advanced Statistical Analysis
- the Shapiro–Wilk test [92] is performed on the reference algorithm A and subsequently on the comparison algorithm B with null-hypothesis : “results are normally distributed”;
- if both A and B are normally distributed (i.e., the Shapiro–Wilk test fails at rejecting on both algorithms), the homoscedasticity of the two distributions (i.e., homogeneity of variances) is tested with the F-test [93], in order to check whether the normal distributions have identical variances and:
- if at least one between A and B is not normally distributed (i.e., the Shapiro–Wilk test rejects on at least one algorithm), a non-parametric test is necessary, and a two-sided Wilcoxon rank-sum test is performed to test and:
- ∘
- if the null-hypothesis is rejected, A and B are two equivalent stochastic processes. The test terminates.
- ∘
- if the test fails at rejecting , a one-sided Wilcoxon rank-sum test is performed to test if A outperforms B, i.e., is rejected, or B outperforms A, i.e., is rejected. The test terminates.
5. Visual Representation of Results
 source code formats. To structure compact, but highly informative tables, SOS provides specific classes. Let us keep following the example in Figure 7. One can see that four classes are used to produce tables for the experiment object passed as an argument to the constructor. These classes are:
source code formats. To structure compact, but highly informative tables, SOS provides specific classes. Let us keep following the example in Figure 7. One can see that four classes are used to produce tables for the experiment object passed as an argument to the constructor. These classes are:- TableCEC2013Competition, which produces tables displaying results according to the guidelines of the CEC 2013 competition [79];
- TableBestWorstMedAvgStd, which produces tables displaying the worst, the best, the median, and the average fitness value over the performed runs;
- TableHolmBonferroni, which produces tables displaying the “league table”, as shown in the examples of Figure 9, obtained with the Holm–Bonferroni test explained in Section 4.2;
- TableAvgStdStat, which produces tables displaying the average fitness value ± standard deviation and the results of the statistical analysis in terms of Wilcoxon rank-sum test, described in Section 4.1, or the ASA procedure, described in Section 4.3. Examples are given in Figure 10.
- if the reference algorithm A (i.e., the first one in the table) is statistically equivalent to a comparison algorithm B (i.e., cannot be rejected), the symbol “=” is placed in the corresponding column next to the average ± std. dev. fitness/error values of B;
- if A statistically outperforms B, the symbol “+” is placed in the corresponding column next to the average ± std. dev. fitness/error values of B;
- if A is statistically outperformed by B, the symbol “−” is placed in the corresponding column next to the average ± std. dev. fitness/error values of B;
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Terminology
| Computational budget | Maximum allowed number of fitness evaluations for an optimisation process |
| Fitness function | The objective function (from the EA jargon; usually, it refers to a scalar function) |
| Fitness | The value returned by the fitness function |
| Fitness landscape | Refers to the topology of the fitness function co-domain |
| Basin of attraction | A set of solutions from which the search moves to a particular attractor |
| Run | An optimisation process during which one algorithm optimises one problem |
| Initial guess | Initial (random/passed) solution of an algorithm |
| Population-based | A metaheuristic algorithm requiring a set of candidate solutions to function |
| Individual | In the EA jargon, a candidate solution to a given problem |
| Population | A set of individuals (i.e., candidate solutions) |
| Population size | Number of solutions processed by a population-based algorithm |
| Variation operators | Perturbation operators typical of EAs, e.g., recombination and mutation |
| Recombination | Operator producing a new solution from two or more individuals |
| Mutation | Operator perturbing a single solution |
| Parent selection | Method to select candidate solutions to perform recombination |
| Survivor selection | Method to form a new population from existing individuals |
| Local searcher | Operator suitable for refining a solution rather than exploring the search space |
| Non-parametric test | A statistical test that does not require any assumption on how data are distributed |
| Null-hypothesis | In statistics, it is the hypothesis of a lack of significant difference between two distributions |
Abbreviations
| CEC | Congress on Evolutionary Computation |
| CMA | Covariance matrix adaptation |
| DE | Differential evolution |
| EA | Evolutionary algorithm |
| EC | Evolutionary computation |
| ES | Evolution strategy |
| FWER | Family-wise error rate |
| GA | Genetic algorithm |
| IEEE | Institute of Electrical and Electronics Engineers |
| NFLT | No free lunch theorem |
| PSO | Particle swarm optimisation |
| SI | Swarm intelligence |
| SOS | Stochastic optimisation software |
Appendix A. Producing the Fitness Trend
References
- Caraffini, F.; Kononova, A.V.; Corne, D. Infeasibility and structural bias in differential evolution. Inf. Sci. 2019, 496, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Caraffini, F.; Neri, F.; Picinali, L. An analysis on separability for Memetic Computing automatic design. Inf. Sci. 2014, 265, 1–22. [Google Scholar] [CrossRef]
- Caraffini, F.; Neri, F. A study on rotation invariance in differential evolution. Swarm Evol. Comput. 2019, 50, 100436. [Google Scholar] [CrossRef]
- Mittelmann, H.D.; Spellucci, P. Decision Tree for Optimization Software. 2005. Available online: http://plato.asu.edu/guide.html (accessed on 31 March 2020).
- Hansen, N.; Auger, A.; Mersmann, O.; Tusar, T.; Brockhoff, D. COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting. arXiv 2016, arXiv:1603.08785. [Google Scholar]
- Doerr, C.; Ye, F.; Horesh, N.; Wang, H.; Shir, O.M.; Bäck, T. Benchmarking discrete optimization heuristics with IOHprofiler. Appl. Soft Comput. 2020, 88, 106027. [Google Scholar] [CrossRef]
- Durillo, J.J.; Nebro, A.J. jMetal: A Java framework for multi-objective optimization. Adv. Eng. Softw. 2011, 42, 760–771. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Reed, D.H.; Frankham, R. Correlation between fitness and genetic diversity. Conserv. Biol. 2003, 17, 230–237. [Google Scholar] [CrossRef]
- Yaman, A.; Iacca, G.; Caraffini, F. A comparison of three differential evolution strategies in terms of early convergence with different population sizes. AIP Conf. Proc. 2019, 2070, 020002. [Google Scholar] [CrossRef]
- Kononova, A.; Corne, D.; De Wilde, P.; Shneer, V.; Caraffini, F. Structural bias in population-based algorithms. Inf. Sci. 2015, 298. [Google Scholar] [CrossRef] [Green Version]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. A study of statistical techniques and performance measures for genetics-based machine learning: Accuracy and interpretability. Soft Comput. 2009, 13, 959–977. [Google Scholar] [CrossRef]
- Del Ser, J.; Osaba, E.; Molina, D.; Yang, X.S.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.N.; Coello Coello, C.A.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019, 48, 220–250. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Kononova, A.V.; Caraffini, F.; Wang, H.; Bäck, T. Can Single Solution Optimisation Methods Be Structurally Biased? Preprints 2020. [Google Scholar] [CrossRef] [Green Version]
- Caraffini, F. The Stochastic Optimisation Software (SOS) platform. Zenodo 2019. [Google Scholar] [CrossRef]
- Caraffini, F. Algorithmic Issues in Computational Intelligence Optimization: From Design to Implementation, from Implementation to Design; Number 243 in Jyväskylä studies in computing; University of Jyväskylä: Jyväskylä, Finland, 2016. [Google Scholar]
- Eiben, A.; Smith, J. Introduction to Evolutionary Computing; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2015; Volume 53. [Google Scholar] [CrossRef]
- Kennedy, J.; Shi, Y.; Eberhart, R.C. Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2001; p. 512. [Google Scholar]
- Burke, E.K.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A Classification of Hyper-heuristic Approaches. In Handbook of Metaheuristics; Springer: Boston, MA, USA, 2010; pp. 449–468. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef] [Green Version]
- Caraffini, F.; Neri, F.; Iacca, G.; Mol, A. Parallel memetic structures. Inf. Sci. 2013, 227, 60–82. [Google Scholar] [CrossRef]
- Caraffini, F.; Neri, F.; Epitropakis, M. HyperSPAM: A study on hyper-heuristic coordination strategies in the continuous domain. Inf. Sci. 2019, 477, 186–202. [Google Scholar] [CrossRef]
- Kenneth, V.P.; Rainer, M.S.; Jouni, A.L. Differential Evolution; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Xinchao, Z. Simulated annealing algorithm with adaptive neighborhood. Appl. Soft Comput. 2011, 11, 1827–1836. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Auger, A. Benchmarking the (1+1) evolution strategy with one-fifth success rule on the BBOB-2009 function testbed. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference—GECCO ’09; ACM Press: New York, NY, USA, 2009; p. 2447. [Google Scholar] [CrossRef] [Green Version]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Hansen, N. The CMA Evolution Strategy: A Comparing Review. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar] [CrossRef]
- Iacca, G.; Caraffini, F.; Neri, F.; Mininno, E. Single particle algorithms for continuous optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1610–1617. [Google Scholar]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Li, X.; Yao, X. Cooperatively Coevolving Particle Swarms for Large Scale Optimization. Evol. Comput. IEEE Trans. 2012, 16, 210–224. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Brest, J.; Maucec, M.S. Self-adaptive differential evolution algorithm using population size reduction and three strategies. Soft Comput. 2011, 15, 2157–2174. [Google Scholar] [CrossRef]
- Alic, A.; Berkovic, K.; Boskovic, B.; Brest, J. Population Size in Differential Evolution. In Swarm, Evolutionary, and Memetic Computing and Fuzzy and Neural Computing, Proceedings of the 7th International Conference, SEMCCO 2019, and 5th International Conference, FANCCO 2019, Maribor, Slovenia, July 10–12, 2019; Revised Selected Papers; Communications in Computer and Information Science Book Series; Zamuda, A., Das, S., Suganthan, P.N., Panigrahi, B.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1092, pp. 21–30. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A. JADE: Adaptive Differential Evolution With Optional External Archive. Evol. Comput. IEEE Trans. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Islam, S.M.; Das, S.; Ghosh, S.; Roy, S.; Suganthan, P.N. An Adaptive Differential Evolution Algorithm With Novel Mutation and Crossover Strategies for Global Numerical Optimization. IEEE Trans. Syst. Man, Cybern. Part B (Cybernetics) 2012, 42, 482–500. [Google Scholar] [CrossRef]
- Iacca, G.; Neri, F.; Mininno, E.; Ong, Y.S.; Lim, M.H. Ockham’s razor in memetic computing: Three stage optimal memetic exploration. Inf. Sci. 2012, 188, 17–43. [Google Scholar] [CrossRef] [Green Version]
- Molina, D.; Lozano, M.; Herrera, F. MA-SW-Chains: Memetic algorithm based on local search chains for large scale continuous global optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Epitropakis, M.G.; Caraffini, F.; Neri, F.; Burke, E.K. A Separability Prototype for Automatic Memes with Adaptive Operator Selection. In IEEE SSCI 2014—2014 IEEE Symposium Series on Computational Intelligence, Proceedings of the FOCI 2014: 2014 IEEE Symposium on Foundations of Computational Intelligence, Orlando, FL, USA, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 70–77. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Technical Report; Jadavpur University: Kolkata, India; Nanyang Technological University: Singapore, 2010. [Google Scholar]
- Caraffini, F.; Kononova, A.V. Structural bias in differential evolution: A preliminary study. AIP Conf. Proc. 2019, 2070, 020005. [Google Scholar] [CrossRef] [Green Version]
- Kononova, A.V.; Caraffini, F.; Bäck, T. Differential evolution outside the box. arXiv 2020, arXiv:2004.10489. [Google Scholar]
- Structural Bias in Optimisation Algorithms: Extended Results. Mendeley Data 2020. [CrossRef]
- Caraffini, F.; Kononova, A.V. Differential evolution outside the box—Extended results. Mendeley Data 2020. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Ho, Y.C.; Pepyne, D.L. Simple Explanation of the No Free Lunch Theorem of Optimization. Cybern. Syst. Anal. 2002, 38, 292–298. [Google Scholar] [CrossRef]
- Mason, K.; Duggan, J.; Howley, E. A meta optimisation analysis of particle swarm optimisation velocity update equations for watershed management learning. Appl. Soft Comput. 2018, 62, 148–161. [Google Scholar] [CrossRef]
- Neumüller, C.; Wagner, S.; Kronberger, G.; Affenzeller, M. Parameter Meta-optimization of Metaheuristic Optimization Algorithms. In Computer Aided Systems Theory—EUROCAST 2011; Moreno-Díaz, R., Pichler, F., Quesada-Arencibia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 367–374. [Google Scholar] [CrossRef]
- Andre, J.; Siarry, P.; Dognon, T. An improvement of the standard genetic algorithm fighting premature convergence in continuous optimization. Adv. Eng. Softw. 2001, 32, 49–60. [Google Scholar] [CrossRef]
- Lampinen, J.; Zelinka, I. On stagnation of the differential evolution algorithm. In Proceedings of the MENDEL, Brno, Czech Republic, 7–9 June 2000; pp. 76–83. [Google Scholar]
- Caraffini, F.; Neri, F. Rotation Invariance and Rotated Problems: An Experimental Study on Differential Evolution. In Applications of Evolutionary Computation; Sim, K., Kaufmann, P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 597–614. [Google Scholar] [CrossRef]
- Sang, H.Y.; Pan, Q.K.; Duan, P.y. Self-adaptive fruit fly optimizer for global optimization. Nat. Comput. 2019, 18, 785–813. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Chu, S.C.; Tsai, P.W.; Pan, J.S. Cat Swarm Optimization. In PRICAI 2006: Trends in Artificial Intelligence; Yang, Q., Webb, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 854–858. [Google Scholar] [CrossRef]
- Meng, X.B.; Gao, X.; Lu, L.; Liu, Y.; Zhang, H. A new bio-inspired optimisation algorithm: Bird Swarm Algorithm. J. Exp. Theor. Artif. Intell. 2016, 28, 673–687. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization. Eng. Opt. 2006, 38:2, 129–154. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Wang, Y.; Du, T. An Improved Squirrel Search Algorithm for Global Function Optimization. Algorithms 2019, 12, 80. [Google Scholar] [CrossRef] [Green Version]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles Mating Optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar] [CrossRef]
- Rao, R.; Savsani, V.; Vakharia, D. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Bidar, M.; Kanan, H.R.; Mouhoub, M.; Sadaoui, S. Mushroom Reproduction Optimization (MRO): A Novel Nature-Inspired Evolutionary Algorithm. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184, Including Special Section on New Trends in Ambient Intelligence and Bio-inspired Systems. [Google Scholar] [CrossRef]
- Taradeh, M.; Mafarja, M.; Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An evolutionary gravitational search-based feature selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Iacca, G.; Caraffini, F.; Neri, F. Compact Differential Evolution Light: High Performance Despite Limited Memory Requirement and Modest Computational Overhead. J. Comput. Sci. Technol. 2012, 27, 1056–1076. [Google Scholar] [CrossRef]
- Neri, F.; Mininno, E.; Iacca, G. Compact Particle Swarm Optimization. Inf. Sci. 2013, 239, 96–121. [Google Scholar] [CrossRef]
- Iacca, G.; Caraffini, F. Compact Optimization Algorithms with Re-Sampled Inheritance. In Applications of Evolutionary Computation; Kaufmann, P., Castillo, P.A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 523–534. [Google Scholar] [CrossRef] [Green Version]
- Takahama, T.; Sakai, S. Solving nonlinear optimization problems by Differential Evolution with a rotation-invariant crossover operation using Gram-Schmidt process. In Proceedings of the 2010 Second World Congress on Nature and Biologically Inspired Computing (NaBIC), Kitakyushu, Japan, 15–17 December 2010; pp. 526–533. [Google Scholar] [CrossRef]
- Guo, S.; Yang, C. Enhancing Differential Evolution Utilizing Eigenvector-Based Crossover Operator. IEEE Trans. Evol. Comput. 2015, 19, 31–49. [Google Scholar] [CrossRef]
- Caraffini, F.; Iacca, G.; Yaman, A. Improving (1+1) covariance matrix adaptation evolution strategy: A simple yet efficient approach. AIP Conf. Proc. 2019, 2070, 020004. [Google Scholar] [CrossRef] [Green Version]
- Igel, C.; Suttorp, T.; Hansen, N. A Computational Efficient Covariance Matrix Update and a (1+1)-CMA for Evolution Strategies. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, GECCO ’06, Seattle, WA, USA, 8–12 July 2006; Association for Computing Machinery: New York, NY, USA, 2006; pp. 453–460. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef] [Green Version]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report 201212; Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2005. [Google Scholar]
- Tang, K.; Yao, X.; Suganthan, P.N.; MacNish, C.; Chen, Y.P.; Chen, C.M.; Yang, Z. Benchmark Functions for the CEC 2008 Special Session and Competition on Large Scale Global Optimization. Technical Report; Nature Inspired Computation and Applications Laboratory, {USTC}: Hefei, China, 2007. [Google Scholar]
- Tang, K.; Li, X.; Suganthan, P.N.; Yang, Z.; Weise, T. Benchmark Functions for the CEC 2010 Special Session and Competition on Large-Scale Global Optimization; Technical Report 1, Technical Report; University of Science and Technology of China: Hefei, China, 2010. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report 201212; Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Li, X.; Tang, K.; Omidvar, M.N.; Yang, Z.; Qin, K. Benchmark Functions for the CEC’2013 Special Session and Competition on Large-Scale Global Optimization; Technical Report; RMIT University: Melbourne, Australia; University of Science and Technology of China: Hefei, China; National University of Defense Technology: Changsha, China, 2013. [Google Scholar]
- Li, X.; Tang, K.; Omidvar, M.N.; Yang, Z.; Qin, K. Benchmark Functions for the CEC’2015 Special Session and Competition on Large Scale Global Optimization; Technical Report; University of Science and Technology of China: Hefei, China, 2015. [Google Scholar]
- Herrera, F.; Lozano, M.; Molina, D. Test Suite for the Special Issue of Soft Computing on Scalability of Evolutionary Algorithms and other Metaheuristics for Large Scale Continuous Optimization Problems; Technical Report; University of Granada: Granada, Spain, 2010. [Google Scholar]
- Hansen, N.; Auger, A.; Finck, S.; Ros, R.; Hansen, N.; Auger, A.; Finck, S.; Optimiza, R.R.R.p.B.b. Real-Parameter Black-Box Optimization Benchmarking 2010: Experimental Setup; Technical Report; INRIA: Paris, France, 2010. [Google Scholar]
- Holm, S. A simple sequentially rejective multiple test approach. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Rey, D.; Neuhäuser, M. Wilcoxon-Signed-Rank Test. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1658–1659. [Google Scholar] [CrossRef]
- Iacca, G.; Caraffini, F.; Neri, F. Multi-Strategy Coevolving Aging Particle Optimization. Int. J. Neural Syst. 2013, 24, 1450008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- WILCOXON, F. Individual comparisons of grouped data by ranking methods. J. Econ. Entomol. 1946, 39, 269. [Google Scholar] [CrossRef] [PubMed]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Middleton, D.; Rice, J.A. Mathematical Statistics and Data Analysis. Math. Gaz. 1988, 72, 330. [Google Scholar] [CrossRef]
- Tango, T. 100 Statistical Tests. Stat. Med. 2000, 19, 3018. [Google Scholar] [CrossRef]
- Frey, B.B. Holm’s Sequential Bonferroni Procedure. In The SAGE Encyclopedia of Educational Research, Measurement, and Evaluation; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Thomas Lin, C. Some p-variate adaptations of the shapiro-wilk test of normality. Commun. Stat. Theory Methods 1995, 24, 953–985. [Google Scholar] [CrossRef]
- Cacoullos, T. The F-test of homoscedasticity for correlated normal variables. Stat. Probab. Lett. 2001, 54, 1–3. [Google Scholar] [CrossRef]
- Kim, T.K. T test as a parametric statistic. Korean J. Anesthesiol. 2015, 68, 540. [Google Scholar] [CrossRef] [Green Version]
- Cressie, N.A.C.; Whitford, H.J. How to Use the Two Samplet-Test. Biom. J. 1986, 28, 131–148. [Google Scholar] [CrossRef]
- Zimmerman, D.W.; Zumbo, B.D. Rank transformations and the power of the Student t test and Welch t’ test for non-normal populations with unequal variances. Can. J. Exp. Psychol. Can. Psychol. Exp. 1993, 47, 523–539. [Google Scholar] [CrossRef]
- Zimmerman, D.W. A note on preliminary tests of equality of variances. Br. J. Math. Stat. Psychol. 2004, 57, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Caraffini, F. Novel Memetic Structures (raw data & extended results). Mendeley Data 2020. [Google Scholar] [CrossRef]
- Caraffini, F.; Neri, F. Raw data & extended results for: A study on rotation invariance in differential evolution. Mendeley Data 2019. [Google Scholar] [CrossRef]








| Description | Content | Link |
|---|---|---|
| SOS web page | software documentation | https://tinyurl.com/FabioCaraffini-SOS |
| GitHub repository | source code | https://github.com/facaraff/SOS |
| Zenodo repository [17] | SOS releases | https://doi.org/10.5281/ZENODO.3237023 |
| f Class | f Number | Function Name and Description | |
|---|---|---|---|
| Unimodal | 1 | High Conditioned Elliptic Function | 100 |
| 2 | Bent Cigar Function | 200 | |
| 3 | Discus function | 300 | |
| Multimodal | 4 | Shifted Ackley’s Function | 400 |
| 5 | Shifted Rosenbrock’s | 500 | |
| 6 | Shifted Griewank’s Function | 600 | |
| 7 | Shifted Weierstrass Function | 700 | |
| 8 | Shifted Rastrigin’s | 900 | |
| 9 | Shifted Schwefel’s | 1100 | |
| 10 | Shifted Katsuura | 1200 | |
| 11 | Shifted HappyCat | 1300 | |
| 12 | Shifted HGBat | 1400 | |
| 13 | Shifted Expanded Griewank’s plus Rosenbrock’s | 1500 | |
| 14 | Shifted and Expanded Scaffer’s F6 Function | 1600 | |
| Hybrid | 15 | Hybrid Function 1 | 1700 |
| 16 | Hybrid Function 2 | 1800 | |
| 17 | Hybrid Function 3 | 1900 | |
| 18 | Hybrid Function 4 | 2000 | |
| 19 | Hybrid Function 5 | 2100 | |
| 20 | Hybrid Function 6 | 2200 | |
| Hybrid | 21 | Composition Function 1 | 2300 |
| 22 | Composition Function 2 | 2400 | |
| 23 | Composition Function 3 | 2500 | |
| 24 | Composition Function 4 | 2600 | |
| 25 | Composition Function 5 | 2700 | |
| 26 | Composition Function 6 | 2800 | |
| 27 | Composition Function 7 | 2900 | |
| 28 | Composition Function 8 | 3000 |
| Is True | Is False | |
|---|---|---|
| Test rejects | Type I error | Correct inference |
| (False Positive) | (True Positive) | |
| Test fails to rejects | Correct inference | Type II error |
| (False Negative) | (True Negative) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caraffini, F.; Iacca, G. The SOS Platform: Designing, Tuning and Statistically Benchmarking Optimisation Algorithms. Mathematics 2020, 8, 785. https://doi.org/10.3390/math8050785
Caraffini F, Iacca G. The SOS Platform: Designing, Tuning and Statistically Benchmarking Optimisation Algorithms. Mathematics. 2020; 8(5):785. https://doi.org/10.3390/math8050785
Chicago/Turabian StyleCaraffini, Fabio, and Giovanni Iacca. 2020. "The SOS Platform: Designing, Tuning and Statistically Benchmarking Optimisation Algorithms" Mathematics 8, no. 5: 785. https://doi.org/10.3390/math8050785
APA StyleCaraffini, F., & Iacca, G. (2020). The SOS Platform: Designing, Tuning and Statistically Benchmarking Optimisation Algorithms. Mathematics, 8(5), 785. https://doi.org/10.3390/math8050785