Periodic Intermediate β-Expansions of Pisot Numbers

Abstract

The subshift of finite type property (also known as the Markov property) is ubiquitous in dynamical systems and the simplest and most widely studied class of dynamical systems are $\beta$-shifts, namely transformations of the form $T_{\beta ,\alpha }:x\mapsto \beta x+\alpha mod1$ acting on $[-\alpha /(\beta -1),(1-\alpha )/(\beta -1)]$, where $(\beta ,\alpha )\in \Delta$ is fixed and where $\Delta ≔\{(\beta ,\alpha )\in {\mathbb{R}}^2:\beta \in (1,2)\mathrm{and}0\le \alpha \le 2-\beta \}$. Recently, it was shown, by Li et al. (Proc. Amer. Math. Soc. 147(5): 2045–2055, 2019), that the set of $(\beta ,\alpha )$ such that $T_{\beta ,\alpha }$ has the subshift of finite type property is dense in the parameter space $\Delta$. Here, they proposed the following question. Given a fixed $\beta \in (1,2)$ which is the n-th root of a Perron number, does there exists a dense set of $\alpha$ in the fiber $\left\{\beta \right\}\times (0,2-\beta )$, so that $T_{\beta ,\alpha }$ has the subshift of finite type property? We answer this question in the positive for a class of Pisot numbers. Further, we investigate if this question holds true when replacing the subshift of finite type property by the sofic property (that is a factor of a subshift of finite type). In doing so we generalise, a classical result of Schmidt (Bull. London Math. Soc., 12(4): 269–278, 1980) from the case when $\alpha =0$ to the case when $\alpha \in (0,2-\beta )$. That is, we examine the structure of the set of eventually periodic points of $T_{\beta ,\alpha }$ when $\beta$ is a Pisot number and when $\beta$ is the n-th root of a Pisot number.

1. Introduction, Motivation and Main Results

1.1. Introduction and Motivation

The pioneering work of Rényi [1] and Parry [2] on $\beta$-shifts and expansions have motivated a wealth of results providing practical solutions to a variety of problems. For instance, they arise as Poincaré maps of the geometric model of Lorenz differential equations [3], and Daubechies et al. [4] proposed a new approach to analog-to-digital conversion using $\beta$-expansion. A summary of some further applications can be found in [5]. Through their study, many new phenomena have appeared, revealing a rich combinatorial and topological structure, and unexpected connections to probability theory, ergodic theory, number theory and aperiodic order [6,7,8]. Additionally, through understanding $\beta$-shifts and expansions, advances have been made in the theory of Bernoulli convolutions [9,10].

For $\beta >1$ and $x\in [0,1/(\beta -1)]$, an infinite word ${({\omega }_n)}_{n\in \mathbb{N}}$ over the alphabet $\{0,1\}$ is said to be a $\beta$-expansion of x if

$$\begin{array}{c}\hfill x=\sum _{k=0}^{\infty }{\omega }_{k+1}{\beta }^{-k}.\end{array}$$

When $\beta \in \mathbb{N}$, all except a countable set of real numbers have a unique $\beta$-expansion. On the other hand, Erdös, Joó and Komornik [11] showed, if $\beta$ is less than the golden mean, then for every $x\in (0,1/(\beta -1))$, the set of $\beta$-expansions of x has cardinality equal to the cardinality of the continuum. Siderov [12] extended this result by showing, if $\beta$ is strictly less than two, then for Lebesgue almost all $x\in [0,1/(\beta -1)]$, the cardinality of the set of $\beta$-expansions of x is that of the continuum.

Through iterating the interval maps $G_{\beta }:[0,1/(\beta -1)]⥀$ and $L_{\beta }:[(\beta -2)/(\beta -1),1]⥀$ defined by

$$\begin{array}{c}\hfill G_{\beta }(x)≔\left\{\begin{array}{cc}\beta x\hfill & \mathrm{if}x<1/\beta ,\hfill \\ \beta x-1\hfill & \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{L}_{\beta }(x)≔\left\{\begin{array}{cc}\beta x+2-\beta \hfill & \mathrm{if}x\le 1-1/\beta ,\hfill \\ \beta x+1-\beta \hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

one obtains subsets of ${\{0,1\}}^{\mathbb{N}}$ known as the greedy and lazy $\beta$-shifts, respectively. Each point ${\omega }^{+}$ of the greedy $\beta$-shift and each point ${\omega }^{-}$ of the lazy $\beta$-shift corresponds to a $\beta$-expansion of a unique point in $[0,1/(\beta -1)]$. Note, if ${\omega }^{+}$ and ${\omega }^{-}$ are $\beta$-expansions of the same point, then ${\omega }^{+}$ and ${\omega }^{-}$ are not necessarily equal, see Example 1 and [6,13,14].

There are several ways in which one may generate $\beta$-expansions of real numbers, other than using the greedy and lazy $\beta$-shifts. For example, via intermediate $\beta$-shifts ${\mathsf{\Omega }}_{\beta ,\alpha }^{\pm }$. These symbolic spaces are coding spaces associated with intermediate $\beta$-transformations $T_{\beta ,\alpha }^{\pm }:[-\alpha /(\beta -1),(1-\alpha )/(\beta -1)]⥀$, where $(\beta ,\alpha )\in \Delta ≔\{(b,a)\in {\mathbb{R}}^2:b\in (1,2)\mathrm{and}a\in [0,2-\beta ]\}$ and where the interval maps $T_{\beta ,\alpha }^{\pm }$ are defined as follows. For $p=p_{\beta ,\alpha }≔(1-\alpha )/\beta$, set

$$\begin{array}{c}\hfill T_{\beta ,\alpha }^{+}(x)≔\left\{\begin{array}{cc}\beta x+\alpha \hfill & \mathrm{if}x<p,\hfill \\ \beta x+\alpha -1\hfill & \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{T}_{\beta ,\alpha }^{-}(x)≔\left\{\begin{array}{cc}\beta x+\alpha \hfill & \mathrm{if}x\le p,\hfill \\ \beta x+\alpha -1\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

Observe that $T_{\beta ,\alpha }^{-}(x)=1-T_{\beta ,2-\beta -\alpha }^{+}(1-x)$, and if $\alpha =0$, then $G_{\beta }=T_{\beta ,\alpha }^{+}$; and if $\alpha =2-\beta$, then $L_{\beta }=T_{\beta ,\alpha }^{-}$. Further, $-\alpha /(\beta -1)$ and $(1-\alpha )/(\beta -1)$ are fixed points for $T_{\beta ,\alpha }^{\pm }$ and the unit interval $[0,1]$ is a trapping region for $T_{\beta ,\alpha }^{\pm }$, that is if $x\in [0,1]$, then ${(T_{\beta ,\alpha }^{\pm })}^n(x)\in [0,1]$, for all $n\in \mathbb{N}$; and if $x\in (-\alpha /(\beta -1),0)\cup (1,(1-\alpha )/(\beta -1))$, then there exists an $m\in \mathbb{N}$ such that ${(T_{\beta ,\alpha }^{\pm })}^m(x)\in [0,1]$.

Every element of ${\mathsf{\Omega }}_{\beta ,\alpha }^{\pm }$ is a $\beta$-expansion of a unique point in the interval $[0,1/(\beta -1)]$, see (3), and ${\mathsf{\Omega }}_{\beta ,\alpha }≔{\mathsf{\Omega }}_{\beta ,\alpha }^{+}\cup {\mathsf{\Omega }}_{\beta ,\alpha }^{-}$ is invariant under the (left) shift map $\sigma$ and closed in ${\{0,1\}}^{\mathbb{N}}$; namely ${\mathsf{\Omega }}_{\beta ,\alpha }$ is a subshift. Here $\{0,1\}$ is equipped with the discrete topology and ${\{0,1\}}^{\mathbb{N}}$ is endowed with the product topology. Further, the dynamical systems $({\mathsf{\Omega }}_{\beta ,\alpha }^{\pm },\sigma )$ and $([0,1],T_{\beta ,\alpha }^{\pm })$ are topologically conjugate, that is they have ‘the same’ dynamical properties.

Subshifts of finite type play an essential rôle in the study of dynamical systems, and can be completely described by a finite set of forbidden words (see Section 2.1). They also have a simple representation as a finite directed graph, and thus, dynamical and combinatorial questions concerning subshifts of finite type can be phrased in terms of an adjacency matrix, making them much more tractable. Hence, it is of interest to classify the points $(\beta ,\alpha )\in \Delta$ for which ${\mathsf{\Omega }}_{\beta ,\alpha }$ a subshift of finite type. One of our aims is to give new insights towards such a classification.

Given $(\beta ,\alpha )\in \Delta$, the unique points in ${\mathsf{\Omega }}_{\beta ,\alpha }^{+}$ and ${\mathsf{\Omega }}_{\beta ,\alpha }^{-}$ that yield a $\beta$-expansion of p are called the kneading invariants of ${\mathsf{\Omega }}_{\beta ,\alpha }$. These invariants are extremely useful since they completely determine ${\mathsf{\Omega }}_{\beta ,\alpha }$, see Theorem 3 due to [15,16,17]. Moreover, the $\beta$-shift ${\mathsf{\Omega }}_{\beta ,\alpha }$ is a subshift of finite type if and only if the left shift of the kneading invariants are periodic, see Theorem 4 due to Ito and Takahashi [18], and Parry [19], for the case $\alpha \in \{0,2-\beta \}$, and Li et al. [20], for the case that $\alpha \in (0,2-\beta )$. These results immediately give us that the set of parameters in $\Delta$ which give rise to $\beta$-shifts of finite type is countable. In a second article [5] by Li et al., it was shown that this set of parameters is in fact dense in $\Delta$. In contrast, the structure of the set of $(\beta ,\alpha )$ in $\Delta$ for which ${\mathsf{\Omega }}_{\beta ,\alpha }$ is topologically transitive, with respect to the (left) shift map, is notably different to the set of $(\beta ,\alpha )$ in $\Delta$ for which ${\mathsf{\Omega }}_{\beta ,\alpha }$ is a subshift of finite type. It is worth noting that the former of these two sets has positive Lebesgue measure and is far from being dense in $\Delta$, see Theorem 6 due to Palmer [21] and Glendinning [22].

The results of [23,24] in tandem with those discussed above, yield the following.

(i)

If the $\beta$-shift ${\mathsf{\Omega }}_{\beta ,\alpha }$ is a subshift of finite type, then $\alpha \in \mathbb{Q}(\beta )$.

(ii)

If $\beta$ is not the positive nth-root of a Perron number, for some $n\in \mathbb{N}$, then the set of $\alpha$ with ${\mathsf{\Omega }}_{\beta ,\alpha }$ a subshift of finite type is empty.

Indeed, we require $\beta \in (1,2)$ to be a maximal root of a polynomial with coefficients in $\{-1,0,1\}$, and $\alpha \in \mathbb{Q}(\beta )$, for ${\mathsf{\Omega }}_{\beta ,\alpha }$ to be a subshift of finite type. This leads to the following natural question, to which we give a partial answer to in Theorem 1.

Question A. 

Let $\beta \in (1,2)$ denote the positive $n^{\mathrm{th}}$-root of a Perron number, for some $n\in \mathbb{N}$. Is the set of α with ${\mathsf{\Omega }}_{\beta ,\alpha }$ a subshift of finite type dense in $(0,2-\beta )$?

Another class of subshifts which is of interest here are those which are factors of a subshift of finite type. Such subshifts are called sofic; indeed, every subshift of finite type is sofic, but not vise versa. Kalle and Steiner [25] proved that a $\beta$-shift ${\mathsf{\Omega }}_{\beta ,\alpha }$ is sofic if and only if its kneading invariants are eventually periodic. Combining this result with those of Li et al. [5], one obtains that the set of $(\beta ,\alpha )\in \Delta$ with ${\mathsf{\Omega }}_{\beta ,\alpha }$ sofic is dense in $\Delta$. This naturally leads to the study of (eventually) periodic points.

Bertrand [26] and Schmidt [27], and subsequently Boyd [28,29,30] and Maia [31], addressed the following question. For a fixed $\beta$, what are the values of $x\in [0,1]$ which are eventually periodic under $G_{\beta }$? Recall, a point x is eventually periodic under $G_{\beta }$ if and only if the cardinality of $\{G_{\beta }^n(x):n\in \mathbb{N}\}$ is finite. Letting $Preper(\beta )$ denote the set of x which are eventually periodic under $G_{\beta }$, Schmidt points out that if $x,y\in Preper(\beta )\cap [0,1]$, then there is no obvious reason why $x+ymod1$ should also be an element of $Preper(\beta )\cap [0,1]$. In light of this, it is surprising that certain $\beta >1$ have the same behaviour as integers, in the sense that if $\beta$ is a Pisot number, then $Preper(\beta )\cap [0,1]=\mathbb{Q}(\beta )\cap [0,1]$. A natural question to ask here is:

Question B. 

What is the structure of the set ${Preper}^{\pm }(\beta ,\alpha )$ of eventually periodic points under $T_{\beta ,\alpha }^{\pm }$?

In Theorem 2, we show that, if $\beta \in (1,2)$ is a Pisot number and if $\alpha \in \mathbb{Q}(\beta )\cap (0,2-\beta )$, then ${Preper}^{\pm }(\beta ,\alpha )=\mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$, where $J_{\beta ,\alpha }$ denotes the domain of $T_{\beta ,\alpha }^{\pm }$. We also obtain a partial converse and in Corollary 1, we relate these results back to Question A.

1.2. Statement of Main Results

Our main contributions in this article and to the story of periodic $\beta$-expansions, is to show the following results, namely Theorems 1 and 2, and Corollaries 1 to 3.

For $\beta \in (1,2)$ set $\Delta (\beta )≔\{(\beta ,\alpha )\in {\mathbb{R}}^2:0\le \alpha \le 2-\beta \}$ and recall that the multinacci number ${\beta }_m$ of order $m\ge 2$ is the unique real solution to the equation $x^m=x^{m-1}+\cdots +x+1$ in the interval $(1,2)$. Note, the sequence ${({\beta }_m)}_{m=2}^{\infty }$ is strictly increasing and converges to 2, and that ${\beta }_2$ is the golden mean.

Theorem 1. 

Fix an integer $m\ge 2$. The set of $({\beta }_m,\alpha )$ in $\Delta ({\beta }_m)$ with ${\mathsf{\Omega }}_{{\beta }_m,\alpha }$ a subshift of finite type is dense in the fiber $\Delta ({\beta }_m)$.

The main difficulty in proving Theorem 1 was in finding a way to compare the space ${\mathsf{\Omega }}_{{\beta }_m,\alpha }$ and ${\mathsf{\Omega }}_{{\beta }_m,{\alpha }^{\prime }}$, for a fixed m and $\alpha \ne {\alpha }^{\prime }$. We achieved this by embedding all ${\beta }_m$-transformations into a single (multi-valued) dynamical system and carrying out our analysis in this larger system.

This result answers Question A for the class of multinacci number which belong to the wider class of algebraic numbers known as Pisôt numbers. Although many parts of our proof generalise from the class of multinacci numbers to the class of Pisot numbers, a central result (Proposition 1) which states that the upper kneading invariant is periodic if and only if the lower kneading invariant is periodic does not easily generalise, see Example 2 for examples of $(\beta ,\alpha )\in \Delta$ where this is not the case.

In the hope of circumventing this we turn our attention to Question B and examine the set of eventually periodic points under $T_{\beta ,\alpha }^{\pm }$.

Theorem 2. 

Let $\beta \in (1,2)$ and $\alpha \in \mathbb{Q}(\beta )\cap (0,2-\beta )$ be fixed, and let $J_{\beta ,\alpha }$ denote the domain of $T_{\beta ,\alpha }^{\pm }$.

(i) 

If $\mathbb{Q}\cap J_{\beta ,\alpha }\subseteq {Preper}^{\pm }(\beta ,\alpha )$, then β is either a Pisot or a Salem number.

(ii) 

If β is a Pisot number, then ${Preper}^{\pm }(\beta ,\alpha )=\mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$.

Theorem 2(i) also hold when $J_{\beta ,\alpha }$ is replaced by $[0,1]$, since $[0,1]$ is a trapping region for $T_{\beta ,\alpha }$.

As indicated above, Theorem 2 generalises the results of Schmidt [27]. Indeed, our proof is motivated by that of [27], with the following crucial difference. In the setting of [27], namely when $\alpha =0$, a key fact that is used is to any point x there exists a point y arbitrarily close to x and integers m and n, such that $G_{\beta }^{n+k}(y)$ is arbitrarily close to zero for all $k\in \{0,1,\dots ,m\}$. However, this is not the case, when $\alpha >0$. To circumvent this, we appeal to the kneading theory of Milnor and Thurston discussed in Section 2.2. We also remark that a similar question to Question B was considered by Baker [32]; via different methods to ours, and also Schmidt’s, Theorem 2(i) may be concluded from the work of Baker and Theorem 2(ii) can be seen as a strengthening of Baker’s results.

Further, as a consequence of Theorem 2(ii) and a result of [25], see Theorem 5, we obtain the following partial solution to Question A.

Corollary 1. 

Let $\beta \in (1,2)$ be a Pisot number. The set of $(\beta ,\alpha )$ in $\Delta (\beta )$ for which ${\mathsf{\Omega }}_{\beta ,\alpha }$ is sofic is dense in the fiber $\Delta (\beta )$.

In addition to this, combining the results of Palmer [21] and Glendinning [22] as well as Parry [21,33] with Theorems 1 and 2, we may

(i)

determine a set of $\alpha$ which lie dense in a subset of positive Lebesgue measure of the fibre $\Delta ({\beta }_m^{1/n})$, for all integers m and $n\ge 2$, and

(ii)

classify the set $Preper(\beta ,\alpha )$, in the case that $\beta$ is the n-th root of a Pisot number and $T_{\beta ,\alpha }$ is non-transitive.

In order to state these results we require a few preliminaries.

Let n and $k\in \mathbb{N}$ with $k<n$ and $gcd(n,k)=1$ be given, and let $s\in \{0,1,\dots ,k-1\}$ be such that $n=smodk$. For $j\in \{1,2,\dots ,s\}$, define $V_j$ and $r_j$ by $jk=V_{j}s+r_j$, where $r_j\in \{0,1,\dots ,s-1\}$, and $h_j$ by $V_j=h_1+h_2+\cdots +h_j$. For $\beta \in (1,2^{1/n}]$ set

$$\begin{array}{cc}\hfill I_{n,1}(\beta )≔& \left[\frac{1}{\beta ({\beta }^{n-1}+\cdots +1)},\frac{-{\beta }^{n+1}+{\beta }^n+2\beta -1}{\beta ({\beta }^{n-1}+\cdots +1)}\right],\mathrm{and}\hfill \\ \hfill I_{n,k}(\beta )≔& \left[\frac{1+\beta ({\sum }_{j=1}^s{W}_j-1)}{\beta ({\beta }^{n-1}+\cdots +1)},\frac{\beta ({\sum }_{j=1}^s{W}_j)-{\beta }^{n+1}+{\beta }^n+\beta -1}{\beta ({\beta }^{n-1}+\cdots +1)}\right],\hfill \end{array}$$

(1)

where, for $2\le j\le s$,

$$\begin{array}{c}\hfill W_j≔\sum _{i=1}^{h_j}{\beta }^{(V_s-V_{j-1}-i)m+s-j}\mathrm{and}{W}_1≔\sum _{i=1}^{V_1}{\beta }^{(V_s-i)m+s-1}\end{array}$$

(2)

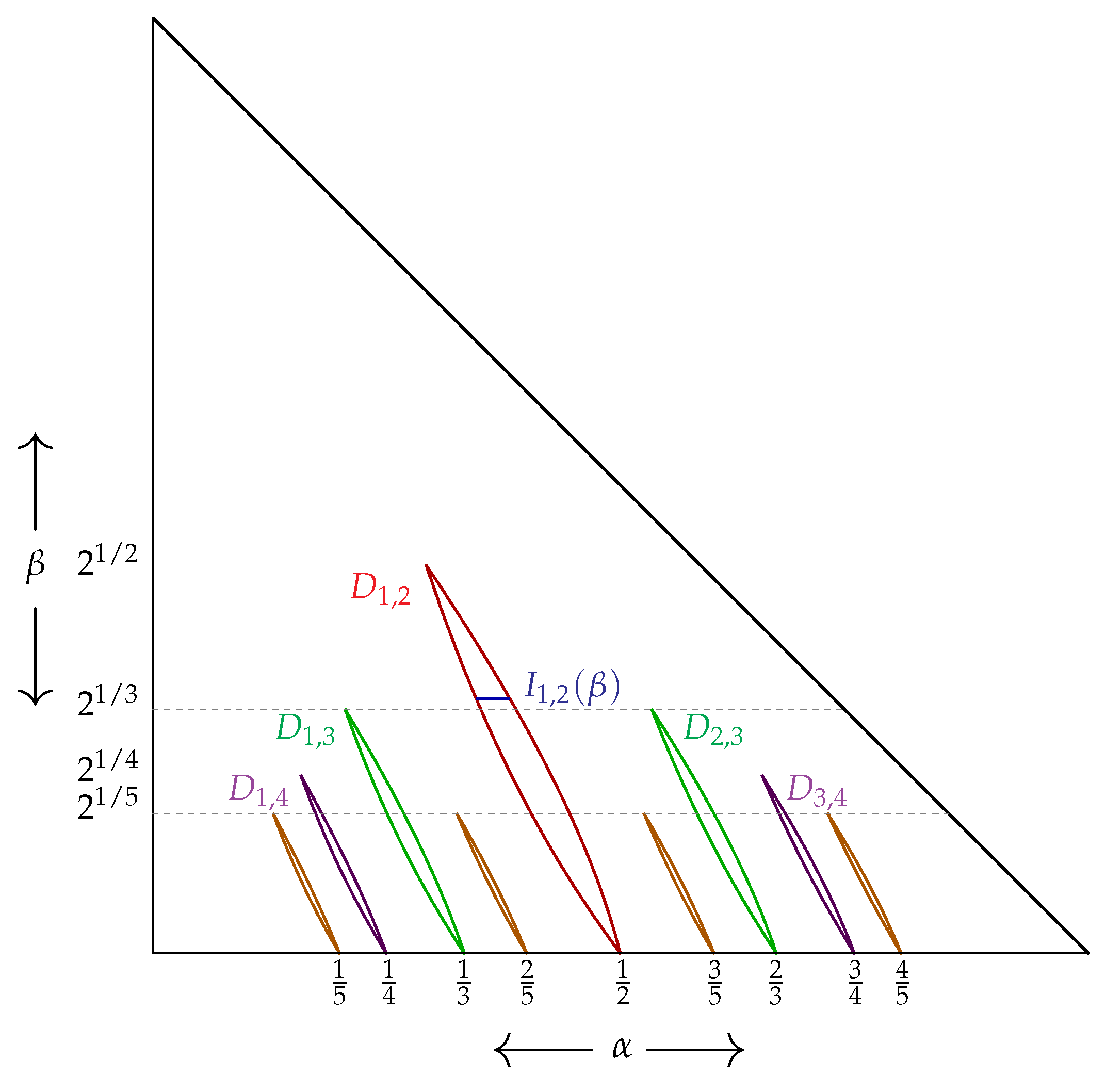
see Figure 1 for a sketch of the intervals $I_{n,k}(\beta )$. If $\beta =2^{1/n}$, then $I_{n,k}(\beta )$ is a single point and, if $\beta \in (0,2^{1/n})$, then $I_{n,k}(\beta )$ is an interval of positive Lebesgue measure. Further, for a fixed $\beta \in (1,2)$, in [22], it was shown that the Lebesgue measure of

$$\begin{array}{c}\hfill \left\{\alpha \in (0,2-\sqrt[l]{\beta }):k\in \{1,\dots ,l\}\mathrm{with}gcd(l,k)=1\mathrm{and}\alpha \in I_{l,k}(\sqrt[l]{\beta })\right\}\end{array}$$

remains bounded away from zero as $l\in \mathbb{N}$ tends to infinity.

Corollary 2. 

Let m and $n\ge 2$ denote two integers, and let $k\in \mathbb{N}$ be such that $k<n$ and $gcd(n,k)=1$. There exists a dense set of α in $I_{n,k}(\sqrt[n]{{\beta }_m})$ with ${\mathsf{\Omega }}_{\sqrt[n]{{\beta }_m},\alpha }$ a subshift of finite type. Moreover, if β is a Pisot number, then there exists a dense set of α in $I_{n,k}(\sqrt[n]{\beta })$ with ${\mathsf{\Omega }}_{\sqrt[n]{\beta },\alpha }$ sofic.

Before stating our final corollary we require one last preliminary. For $(\beta ,\alpha )\in \Delta$, Parry [33] constructed an absolutely continuous $T_{\beta ,\alpha }$-invariant probability measure, which we denote by ${\nu }_{\beta ,\alpha }$. Halfin [34] verified that the density $h_{\beta ,\alpha }$ is non-negative and Hofbauer [16,35,36] proved that ${\nu }_{\beta ,\alpha }$ is ergodic and maximal. Further, the results of Palmer [21] and Glendinning [22] give us that ${\nu }_{\beta ,\alpha }$ has support equal to $[0,1]$ if and only if $T_{\beta ,\alpha }$ is topologically transitive.

Corollary 3. 

Let n and $k\in \mathbb{N}$, let β denote a Pisot number and let $\alpha \in \mathbb{Q}(\beta )\cap [0,2-\beta ]$. Defining ${\alpha }_{n,k}={\alpha }_{n,k}(\beta ,\alpha )\in I_{n,k}(\sqrt[n]{\beta })$ by

$$\begin{array}{c}\hfill {\alpha }_{n,1}≔\frac{((1-\alpha )(1-\sqrt[n]{{\beta }^{-1}})-1)(1-\sqrt[n]{\beta })}{\beta -1}and{\alpha }_{n,k}≔\frac{((1-\alpha )(1-\sqrt[n]{{\beta }^{-1}})-{\sum }_{j=1}^s{W}_j)(1-\sqrt[n]{\beta })}{\beta -1},\end{array}$$

where $s\in \{0,1,\dots ,k-1\}$ satisfies $n=smodk$ and $W_j$ is as in (2), and setting $\mathsf{\Phi }(x)≔(\sqrt[n]{\beta }-1)x+{\alpha }_{n,k}$, we have

$$\begin{array}{c}\hfill {Preper}^{\pm }(\sqrt[n]{\beta },{\alpha }_{n,k})\cap supp({\nu }_{\sqrt[n]{\beta },{\alpha }_{n,k}})=\bigcup _{i=0}^{n-1}{(T_{\sqrt[n]{\beta },{\alpha }_{n,k}}^{\pm })}^i(\mathsf{\Phi }(\mathbb{Q}(\beta )\cap [0,1])).\end{array}$$

1.3. Outline

In Section 2 we give necessary definitions and results we require in our proofs of Theorems 1 and 2. Section 3 and Section 4 are dedicated to proving Theorems 1 and 2, respectively. We conclude with Section 5. The aim of this final section is to provide an overview of the results of [19,21,22,33] which in combination with our results (Theorems 1 and 2) yields Corollaries 2 and 3.

2. Preliminaries

We divide this section into three parts: Section 2.1 and Section 2.2 in which we discuss aspects of symbolic dynamics and $\beta$-shifts; and Section 2.3 where we review results concerning a related class of interval maps, namely uniform Lorenz maps, which are in essence scaled versions of $\beta$-transformations.

2.1. Subshifts

Let ${\{0,1\}}^{\mathbb{N}}$ denote the set infinite words over the alphabet $\{0,1\}$. We endow ${\{0,1\}}^{\mathbb{N}}$ with the topology induced by the (ultra) metric $\mathcal{D}:{\{0,1\}}^{\mathbb{N}}\times {\{0,1\}}^{\mathbb{N}}\to \mathbb{R}$ defined by

$$\begin{array}{c}\hfill \mathcal{D}(\omega ,\nu )=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\omega =\nu ,\hfill \\ 2^{-|\omega \wedge \nu |+1}\hfill & \mathrm{if}\omega \ne \nu ,\hfill \end{array}\right.\end{array}$$

where $|\omega \wedge \nu |≔min\{i\in \mathbb{N}:{\omega }_i\ne {\nu }_i\}$, for $\omega =({\omega }_1,{\omega }_2,\dots )$ and $\nu =({\nu }_1,{\nu }_2,\dots )$. This topology coincides with the product topology on ${\{0,1\}}^{\mathbb{N}}$, where $\{0,1\}$ is equipped with the discrete topology. For $n\in \mathbb{N}$ and $\omega \in {\{0,1\}}^{\mathbb{N}}$, we set ${\omega |}_n=({\omega }_1,\dots ,{\omega }_n)$ and call n the length of ${\omega |}_n$ denoted by $|\omega {|}_n|$. We define the (left) shift $\sigma$ on ${\{0,1\}}^{\mathbb{N}}$ by $\sigma ({\omega }_1,{\omega }_2,\dots )≔({\omega }_2,{\omega }_3,\dots )$. A closed subspace $\mathsf{\Omega }$ of ${\{0,1\}}^{\mathbb{N}}$ is a subshift if $\sigma (\mathsf{\Omega })\subseteq \mathsf{\Omega }$, namely if $\mathsf{\Omega }$ is invariant under $\sigma$. Given a subshift $\mathsf{\Omega }$ and $n\in \mathbb{N}$, we set

$$\begin{array}{c}\hfill {\mathsf{\Omega }|}_n≔\{({\xi }_1,{\xi }_2,\dots ,{\xi }_n)\in {\{0,1\}}^n:\mathrm{there}\mathrm{exists}\omega \in \mathsf{\Omega }\mathrm{with}\omega {|}_n=({\xi }_1,{\xi }_2,\dots ,{\xi }_n)\}\end{array}$$

and denote by ${\mathsf{\Omega }}^{*}≔{\bigcup }_{n\in \mathbb{N}}{\mathsf{\Omega }|}_n$ the collection of all finite words. A subshift $\mathsf{\Omega }$ is said to be of finite type if there exists a finite set F of finite words with

(i)

${\nu |}_n\notin F$ for all $\nu \in \mathsf{\Omega }$ and $n\in \mathbb{N}$;

(ii)

if $\nu \in {\{0,1\}}^{\mathbb{N}}\backslash \mathsf{\Omega }$, then there exist integers $n>0$ and $m\ge 0$ such that ${\sigma }^m{(\nu )|}_n\in F$.

The set F is often referred to as the set of forbidden words of $\mathsf{\Omega }$. If $\mathsf{\Omega }\subseteq {\{0,1\}}^{\mathbb{N}}$ is a factor of a subshift of finite type, then it is called sofic.

We call a word $\omega \in {\{0,1\}}^{\mathbb{N}}$ periodic with period $n\in \mathbb{N}$, if $({\omega }_1,\dots ,{\omega }_n)=({\omega }_{(m-1)n+1},\dots ,{\omega }_{mn})$ for all $m\in \mathbb{N}$, and write $\omega =(\overline{{\omega }_1,\dots ,{\omega }_n})$. The smallest such n is called the period of $\omega$. Similarly, a word $\omega \in {\{0,1\}}^{\mathbb{N}}$ is said to be pre-periodic with period $n\in \mathbb{N}$, if there exists $k\in \mathbb{N}$ with $({\omega }_{k+1},\dots ,{\omega }_{k+n})=({\omega }_{k+(m-1)n+1},\dots ,{\omega }_{k+mn})$ for all $m\in \mathbb{N}$, and write $\omega =({\omega }_1,\dots ,{\omega }_k,\overline{{\omega }_{k+1},\dots ,{\omega }_{k+n}})$. The smallest such n is called the period of $\omega$.

2.2. Intermediate $\beta$-Shifts and Expansions

Let $(\beta ,\alpha )\in \Delta$ be fixed and set $p=p_{\beta ,\alpha }≔(1-\alpha )/\beta$. Let ${\tau }_{\beta ,\alpha }^{\pm }:J_{\beta ,\alpha }\to {\{0,1\}}^{\mathbb{N}}$ be defined by

$$\begin{array}{c}\hfill {\tau }_{\beta ,\alpha }^{\pm }(x)≔({\omega }_1^{\pm }(x),{\omega }_2^{\pm }(x),\dots ),\end{array}$$

where, for $n\in \mathbb{N}$,

$$\begin{array}{c}\hfill {\omega }_n^{+}(x)≔\left\{\begin{array}{cc}0\hfill & \mathrm{if}{(T_{\beta ,\alpha }^{+})}^{n-1}(x)<p,\hfill \\ 1\hfill & \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{\omega }_n^{-}(x)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{(T_{\beta ,\alpha }^{-})}^{n-1}(x)\le p,\hfill \\ 1\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

We refer to ${\tau }_{\beta ,\alpha }^{\pm }$ as expansion maps. The image of $J_{\beta ,\alpha }$ under ${\tau }_{\beta ,\alpha }^{\pm }$ is denoted by ${\mathsf{\Omega }}_{\beta ,\alpha }^{\pm }$, and we set ${\mathsf{\Omega }}_{\beta ,\alpha }≔{\mathsf{\Omega }}_{\beta ,\alpha }^{+}\bigcup {\mathsf{\Omega }}_{\beta ,\alpha }^{-}$. We call ${\tau }_{\beta ,\alpha }^{+}(p)$ the upper and ${\tau }_{\beta ,\alpha }^{-}(p)$ the lower kneading invariant of ${\mathsf{\Omega }}_{\beta ,\alpha }$.

Remark 1. 

Let $\omega =({\omega }_1,{\omega }_2,\dots )$ and $\nu =({\nu }_1,{\nu }_2,\dots )$ respectively denote the upper and the lower kneading invariant of ${\mathsf{\Omega }}_{\beta ,\alpha }$. By definition, ${\omega }_1={\nu }_2=0$ and ${\omega }_2={\nu }_1=1$. It can also be shown, for $k\ge 2$ an integer, that $({\omega }_k,{\omega }_{k+1},\dots )=(\overline{1})$ if and only if $\alpha =2-\beta$, and that $({\nu }_k,{\nu }_{k+1},\dots )=(\overline{0})$ if and only if $\alpha =0$.

The inverse map ${\pi }_{\beta ,\alpha }:{\{0,1\}}^{\mathbb{N}}\to J_{\beta ,\alpha }$ of ${\tau }_{\beta ,\alpha }^{\pm }$ is called the projection map and defined by

$$\begin{array}{c}\hfill {\pi }_{\beta ,\alpha }({\omega }_1,{\omega }_2,\dots )≔\alpha {(1-\beta )}^{-1}+\sum _{i=1}^{\infty }{\omega }_i{\beta }^{-i}.\end{array}$$

An important property of ${\tau }_{\beta ,\alpha }^{\pm }$ and ${\pi }_{\beta ,\alpha }$ is that the following diagram commutes.

(3)

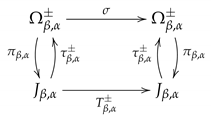
This result is verifiable from the definitions of the involved maps, see [15]. From this, one may deduce, for $x\in [0,1+1/(\beta -1)]$, that the words ${\tau }_{\beta ,\alpha }^{\pm }(x-\alpha /(\beta -1))$ are $\beta$-expansions of x. It is worth noting that the expansion of a point x given by ${\tau }_{\beta ,0}^{+}(x)$, namely the greedy $\beta$-expansion of x, is lexicographically the largest $\beta$-expansion of x, and the expansion given by ${\tau }_{\beta ,2-\beta }^{-}(x-(2-\beta )/(\beta -1))$, namely the lazy $\beta$-expansion of x, is lexicographically the smallest $\beta$-expansion of x, see [11]. Further, for Lebesgue all most all x, the expansion ${\tau }_{\beta ,\alpha }^{\pm }(x-\alpha /(\beta -1))$ lie in between the greedy and the lazy $\beta$-expansions of x, with respect to the lexicographic ordering, see [37]. There also exist $\beta$ such that the only $\beta$-expansion of one is the greedy $\beta$-expansion, such $\beta$ are called univoque, see [14].

Example 1. 

For $\beta =(1+\sqrt{5})/2$ and $x=1$, we have the following.

$$\begin{array}{cc}{\tau }_{\beta ,0}^{+}(x)=(1,1,\overline{0})\hfill & greedygoldenmean-expansionof1\hfill \\ {\tau }_{\beta ,1-\beta /2}^{\pm }(x-(1-\beta /2)/(\beta -1))=(\overline{1,0})\hfill & symmetricgoldenmean-expansion\mathrm{of}1\hfill \\ {\tau }_{\beta ,2-\beta }^{-}(x-(2-\beta )/(\beta -1))=(0,\overline{1})\hfill & lazygoldenmean-expansion\mathrm{of}1\hfill \end{array}$$

For β the largest positive real root of $z^{14}-2z^{13}+z^{11}-z^{10}-z^7+z^6-z^4+z^3-z+1$, and $x=1$,

$$\begin{array}{c}\hfill {\tau }_{\beta ,\alpha }^{\pm }(x-\alpha /(\beta -1))=(1,1,1,0,0,1,0,1,1,\overline{1,0,0,1,0,1,0}),\end{array}$$

for all $\alpha \in [0,2-\beta ]$. In [13], it was shown, in this latter case, that β is the smallest univoque Pisot number.

Next, we recall a result which shows that ${\mathsf{\Omega }}_{\beta ,\alpha }^{\pm }$ is completely determined its kneading invariants.

Theorem 3. 

[15,16,17] Letting $\prec ,⪯,\succ ,⪰$ denote the lexicographic orderings on ${\{0,1\}}^{\mathbb{N}}$, we have that

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_{\beta ,\alpha }^{+}& =\left\{\omega \in {\{0,1\}}^{\mathbb{N}}:foralln\in {\mathbb{N}}_0,{\sigma }^n(\omega )\prec {\tau }_{\beta ,\alpha }^{-}(p)or{\tau }_{\beta ,\alpha }^{+}(p)⪯{\sigma }^n(\omega )\right\},\hfill \\ \hfill {\mathsf{\Omega }}_{\beta ,\alpha }^{-}& =\left\{\omega \in {\{0,1\}}^{\mathbb{N}}:foralln\in {\mathbb{N}}_0,{\sigma }^n(\omega )⪯{\tau }_{\beta ,\alpha }^{-}(p)or{\tau }_{\beta ,\alpha }^{+}(p)\prec {\sigma }^n(\omega )\right\}.\hfill \end{array}$$

A necessary and sufficient condition on the kneading invariants of an intermediate $\beta$-shift for determining when it is a subshift of finite type is as follows.

Theorem 4 

([2,18,20]). For $(\beta ,\alpha )\in \Delta$, the intermediate shift ${\mathsf{\Omega }}_{\beta ,\alpha }$ is a subshift of finite type if and only if $\sigma ({\tau }_{\beta ,\alpha }^{\pm }(p))$ are both periodic.

With the above at hand, it is natural to ask if $\beta \in (1,2)$ and $\alpha \in (0,2-\beta )$, then is true that ${\tau }_{\beta ,\alpha }^{+}(p)$ is periodic if and only if ${\tau }_{\beta ,\alpha }^{-}(p)$ is periodic and vice versa? In Proposition 1 we show that this is indeed the case when $\beta$ is a multinacci number. However, there exist values of $\beta \in (1,2)$ for which this does not hold, as the following counterexample demonstrates. Thus, it would be interesting to investigate if there exists other values of $\beta \in (1,2)$, for which ${\tau }_{\beta ,\alpha }^{+}(p)$ is periodic if and only if ${\tau }_{\beta ,\alpha }^{-}(p)$. In fact this idea is very closely linked to the concept of matching which has recently attracted much attention, see for instance [38,39].

Example 2. 

Letting $\beta =\sqrt{{\beta }_2}$ and $\alpha =2-{\beta }_2$, we have that ${\tau }_{\beta ,\alpha }^{+}(p)=(\overline{1,0,0,1})$ and ${\tau }_{\beta ,\alpha }^{-}(p)=(0,1,\overline{1,0})$. Recall, ${\beta }_2$ denotes the second multinacci number, namely the golden mean.

Kalle and Steiner [25] developed an analogous result to Theorem 4 for determining when a $\beta$-shift is sofic; this allows us to conclude Corollary 1 from Theorem 2. Their result states the following.

Theorem 5 

([25]). The subshift ${\mathsf{\Omega }}_{\beta ,\alpha }$ is sofic if and only if ${\tau }_{\beta ,\alpha }^{\pm }(p)$ are both pre-periodic.

Our next proposition (Proposition 1) plays a key rôle in the proof of Theorem 1. We note that after the writing of this paper we became aware of [38] in which a proof of this result also appears. However, for completeness we include a short justification for which we require an auxiliary lemma (Lemma 1).

Proposition 1. 

Fix an integer $m\ge 2$ and let $\alpha \in \Delta ({\beta }_m)\backslash \{0,2-{\beta }_n\}$. The kneading invariant ${\tau }_{{\beta }_m,\alpha }^{-}(p)$ is periodic if and only if the kneading invariant ${\tau }_{{\beta }_m,\alpha }^{+}(p)$ is periodic.

Lemma 1. 

Under the assumptions of Proposition 1, we have

$$\begin{array}{c}\hfill {\tau }_{{\beta }_m,\alpha }^{+}(p){|}_{m+1}=(1\underset{m-times}{\underbrace{0,0,\dots ,0,0}})and{\tau }_{{\beta }_m,\alpha }^{-}(p)|{}_{m+1}=(0\underset{m-times}{\underbrace{1,1,\dots ,1,1}}).\end{array}$$

Proof. 

We present the proof for ${\tau }_{{\beta }_m,\alpha }^{-}(p)$; the proof for ${\tau }_{{\beta }_m,\alpha }^{+}(p)$ follows analogously. From Remark 1 we know ${\tau }_{\beta ,\alpha }^{-}{(p)|}_2=(0,1)$, and, since ${\beta }_m\ge {\beta }_2$, by definition ${(T_{{\beta }_m,\alpha }^{-})}^2(p)={\beta }_m+\alpha -1>p$. Suppose, for some $j\in \{1,2,\dots m-1\}$, that

$$\begin{array}{c}\hfill {\tau }_{{\beta }_m,\alpha }^{-}{(p)|}_{j+1}=(0\underset{j-times}{\underbrace{1,1,\dots ,1,1}}).\end{array}$$

Let $S_0(x)≔{\beta }_{m}x+\alpha$ and $S_1(x)≔{\beta }_{m}x+\alpha -1$. It suffices to show that

$$\begin{array}{c}\hfill \beta {(T_{\beta ,\alpha }^{-})}^{j+1}(p)+\alpha =\beta ({S_1}^j\circ S_0(p))+\alpha >1.\end{array}$$

To this end, observe that

$$\begin{array}{cc}\hfill \beta (S_1^j\circ S_0(p))+\alpha & ={\beta }_m^{j+1}+\alpha ({\beta }_m^j+{\beta }_m^{j-1}+\cdots +{\beta }_m+1)-{\beta }_m^j-{\beta }_m^{j-1}-\cdots -{\beta }_m\hfill \\ \hfill & >{\beta }_m^{j+1}-{\beta }_m^j-{\beta }_m^{j-1}-\cdots -{\beta }_m\ge {\beta }_{j+1}^{j+1}-{\beta }_{j+1}^j-{\beta }_{j+1}^{j-1}-\cdots -{\beta }_{j+1}=1.\hfill \end{array}$$

The first line follows from an elementary induction argument and the definition of $S_0^{-}$ and $S_1^{-}$; the second line holds since $\alpha >0$; the last and penultimate lines are a consequence of the facts ${({\beta }_k)}_{k\in \mathbb{N}}$ is an increasing sequence and ${\beta }_{j+1}$ is the unique real zero of the polynomial $x^{j+1}-x^j-\cdots -x-1$ in $(1,2)$. □

Proof of Proposition 1. 

By Lemma 1, we have

$$\begin{array}{c}\hfill {\tau }_{{\beta }_m,\alpha }^{+}(p){|}_{m+1}=(1,\underset{m-times}{\underbrace{0,0,\dots ,0,0}})and{\tau }_{{\beta }_m,\alpha }^{-}(p)|{}_{m+1}=(0,\underset{m-times}{\underbrace{1,1,\dots ,1,1}}).\end{array}$$

Letting $S_0$ and $S_1$ be as in the proof of Lemma 1, an elementary calculation yields the following.

$$\begin{array}{cc}\hfill {(T_{{\beta }_m,\alpha }^{+})}^{m+1}(p)& =S_0^m\circ S_1(p)=\alpha ({\beta }_m^{m-1}+{\beta }_m^{m-2}+\cdots +{\beta }_m+1)=\alpha {\beta }_m^m\hfill \\ \hfill {(T_{{\beta }_m,\alpha }^{-})}^{m+1}(p)& =\begin{array}{cc}\hfill S_1^m\circ S_0(p)& =\alpha ({\beta }_m^{m-1}+{\beta }_m^{m-2}+\cdots +{\beta }_m+1)+({\beta }_m^m-{\beta }_m^{m-1}-{\beta }_m^{m-2}-\cdots -{\beta }_m-1)\hfill \\ \hfill & =\alpha ({\beta }_m^{m-1}+{\beta }_m^{m-2}+\cdots +{\beta }_m+1)=\alpha {\beta }_m^m\hfill \end{array}\hfill \end{array}$$

Thus, ${\tau }_{{\beta }_m,\alpha }^{-}(p)$ is periodic if and only if ${\tau }_{{\beta }_m,\alpha }^{+}(p)$ is periodic. □

2.3. Uniform Lorenz Maps

A class of interval maps closely related to intermediate $\beta$-transformations, and which have been well studied, are Lorenz maps. They are expanding maps with a single discontinuity. Here, we consider the sub-class of uniform Lorenz maps $U_{\beta ,p}^{\pm }:[0,1]⥀$ defined, for $\beta \in (1,2)$ and $q\in [1-1/\beta ,1/\beta ]$, by

$$\begin{array}{c}\hfill U_{\beta ,q}^{+}(x)≔\left\{\begin{array}{cc}\beta x\hfill & \mathrm{if}x<q,\hfill \\ \beta x+1-\beta \hfill & \mathrm{if}x\ge q.\hfill \end{array}\right.\mathrm{and}{U}_{\beta ,q}^{-}(x)≔\left\{\begin{array}{cc}\beta x\hfill & \mathrm{if}x\le q,\hfill \\ \beta x+1-\beta \hfill & \mathrm{if}x>q,\hfill \end{array}\right.\end{array}$$

Let us now describe the relation between uniform Lorenz maps and $\beta$-transformations. For this we require the following concept, which determines when two dynamical systems are ‘the same’. Let X and Y denote two topological spaces and let $f:X⥀$ and $g:Y⥀$. We call f and g topologically conjugate if there exists a homeomorphism $h:X\to Y$ with $h\circ f=g\circ h$. The maps f and g are called topologically semi-conjugate if h is a continuous surjection.

An elementary calculation shows that $T_{\beta ,\alpha }^{\pm }$ and $U_{\beta ,1+(\alpha -1)/\beta }^{\pm }$ are topologically conjugate, where the conjugating homeomorphism is given by $x\mapsto (\beta -1)(x+\alpha /(\beta -1))$.

Similar to $\beta$-transformations, Lorenz maps have associated expansion maps ${\mu }_{\beta ,q}^{\pm }:[0,1]\to {\{0,1\}}^{\mathbb{N}}$ defined by ${\mu }_{\beta ,q}^{\pm }(x)≔({\nu }_1^{\pm }(x),{\nu }_2^{\pm }(x),\dots )$, where, for $n\in \mathbb{N}$,

$$\begin{array}{c}\hfill {\nu }_n^{+}(x)≔\left\{\begin{array}{cc}0\hfill & \mathrm{if}{(U_{\beta ,q}^{+})}^{n-1}(x)<q,\hfill \\ 1\hfill & \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{\nu }_n^{-}(x)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{(U_{\beta ,q}^{-})}^{n-1}(x)\le q,\hfill \\ 1\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

and an associated projection map ${\rho }_{\beta }:{\{0,1\}}^{\mathbb{N}}\to [0,1]$ given by ${\rho }_{\beta }({\omega }_1,{\omega }_2,\dots )≔(\beta -1){\sum }_{i=1}^{\infty }{\omega }_i{\beta }^{-i}$. As in the setting of Section 2.2 we have that the following diagram commutes.

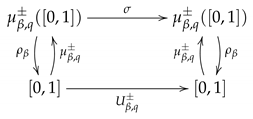
Additionally, we have the following monotonicity result.

Proposition 2. 

[15,40] Let $\beta \in (1,2)$ be fixed. The map $x\mapsto {\mu }_{\beta ,x}^{+}(x)$ is right-continuous and strictly increasing. Similarly, $x\mapsto {\mu }_{\beta ,x}^{-}(x)$ is left-continuous and strictly increasing. Moreover, points of discontinuity, for both maps, only occur at periodic points.

The main benefit of using uniform Lorenz maps stems from the idea that every $\beta$-trnasformation has a realisation as a uniform Lorenz map, as discussed above, and that every uniform Lorenz map is defined on $[0,1]$ and has the same fixed points. Thus, it allows one to easily compare the kneading invariants of systems with the same expansion rate, namely $\beta$, but with different translates, namely $\alpha$.

3. Fiber Denseness of Intermediate $\mathbf{\beta }$-Shifts of Finite Type: Proof of Theorem 1

The aim of this section is to prove Theorem 1. We divide the proof into two parts. We show that the sets ${Per}^{\pm }(\beta )≔\{\alpha \in \Delta (\beta ):{\tau }_{\beta ,\alpha }^{\pm }(p)\mathrm{is}\mathrm{periodic}\}$, for a given $\beta \in (1,2)$, are dense in $\Delta (\beta )$ with respect to the Euclidean norm, and with the help of Proposition 1, we have that ${\tau }_{{\beta }_k,\alpha }^{+}$ is periodic if and only if ${\tau }_{{\beta }_k,\alpha }^{-}$ is periodic. Theorem 1 follows by combining these two results together with Theorem 4.

Proof of Theorem 1. 

Fix $(\beta ,\alpha )\in \Delta$ with $\alpha \notin \{0,2-\beta \}$. Let $q=1+(\alpha -1)/\beta$, so that $U_{\beta ,q}^{\pm }$ is topologically conjugate to $T_{\beta ,\alpha }^{\pm }$. It is sufficient to show that there exists $q_s^{\pm }$ sufficiently close to q in $((\beta -1)/\beta ,1/\beta )$ with ${\mu }_{\beta ,q_s^{\pm }}^{\pm }(q_s^{\pm })$ periodic. We present the proof for ${\mu }_{\beta ,q_s^{-}}^{-}(q_s^{-})$; the proof for ${\mu }_{\beta ,q_s^{+}}^{+}(q_s^{+})$ follows analogously. To this end, suppose ${\mu }_{\beta ,q}^{-}(q)$ is not periodic, otherwise set $q_s^{-}=q$. Fix $k\in \mathbb{N}$ and set

$$\begin{array}{c}\hfill {\delta }_k^{(q)}≔min\{{\beta }^{-k}|{(U_{\beta ,q}^{-})}^l(q)-q|:l\in \{1,2,\dots ,k\}\}.\end{array}$$

Observe ${\mu }_{\beta ,q^{\prime }}^{-}(q^{\prime }){{|}_{k+1}={\mu }_{\beta ,q}^{-}(q)|}_{k+1}$, for all $q^{\prime }\in [q-{\delta }_k^{(q)},q)$. Let $j>k$ be the maximal integer such that

$$\begin{array}{c}\hfill {\mu }_{\beta ,q-{\delta }_k^{(q)}}^{-}(q-{\delta }_k^{(q)}){{|}_j={\mu }_{\beta ,q}^{-}(q)|}_j,{({\mu }_{\beta ,q-{\delta }_k^{(q)}}^{-}(q-{\delta }_k^{(q)}))}_{j+1}=0\mathrm{and}{({\mu }_{\beta ,q}^{-}(q))}_{j+1}=1.\end{array}$$

The existence of j is given by Proposition 2. Let $A\subseteq [q-{\delta }_k,q)$ be defined by

$$\begin{array}{c}\hfill A≔\{x\in [q-{\delta }_k^{(q)},q):{\mu }_{\beta ,x}^{-}(x){|}_j={\mu }_{\beta ,q}^{-}(q){|}_j\mathrm{and}{({\mu }_{\beta ,x}^{-}(x))}_{j+1}=0\}.\end{array}$$

Proposition 2 ensures that A is a non-empty, connected and closed, in particular that $q_s^{-}≔sup(A)\in A$. By way of contradiction, suppose that ${\mu }_{\beta ,q_s^{-}}^{-}(q_s^{-})$ is not periodic, in which case,

$$\begin{array}{c}\hfill {(U_{\beta ,q_s^{-}}^{-})}^j(q_s^{-})<q_s^{-}.\end{array}$$

By Proposition 2, there exists ${\delta }_{j+1}^{(q_s)}>0$ so that, if $q^{\prime }\in (q_s,q_s+{\delta }_{j+1}^{(q_s)})$, then ${\mu }_{\beta ,q_s^{-}}^{-}(q_s^{-}){{|}_{j+1}={\mu }_{\beta ,q^{\prime }}^{-}(q^{\prime })|}_{j+1}$. This implies $q^{\prime }\in A$; contradicting the fact $q_s^{-}$ is the supremum of A. Therefore, since ${\delta }_k^{(q)}<{\beta }^{-k}$, given $q\in (1-1/\beta ,1/\beta )$ and $ϵ>0$, there exist $q_s^{-}\in (1-1/\beta ,q)$ and $k\in \mathbb{N}$ with $q-q_s^{-}\le {\delta }_k^{(q)}<ϵ$ and ${\mu }_{\beta ,q_s^{-}}^{\pm }(q_s^{-})$ periodic.

Proposition 1 implies that ${Per}^{+}({\beta }_n)={Per}^{-}({\beta }_n)$, for all integers $n\ge 2$. Thus, we have that the set $\{\alpha \in \Delta (\beta ):{\tau }_{\beta ,\alpha }^{+}(p)\mathrm{and}{\tau }_{\beta ,\alpha }^{-}(p)\mathrm{are}\mathrm{periodic}\}$ is dense in $\Delta (\beta )$ with respect to the Euclidean norm. With this at hand, an application of Theorem 4 completes the proof. □

4. Periodic Expansions of Pisot and Salem Numbers: Proof of Theorem 2

Throughout this section, let $\beta \in (1,2)$ denote an algebraic integer with minimal polynomial

$$\begin{array}{c}\hfill P(z)≔\sum _{i=0}^{d-1}{a}_i{z}^i+z^d,\end{array}$$

where $z\in \mathbb{C}$, $d\in \mathbb{N}$ and $a_1,a_2,\dots ,a_d\in \mathbb{Z}$. In which case, $x\in \mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$ can be written in the form

$$\begin{array}{c}\hfill x=q^{-1}\sum _{i=0}^{d-1}{p}_i{\beta }^i,\end{array}$$

(4)

where $p_1,p_2,\dots ,p_{d-1}\in \mathbb{Z}$ and $q\in \mathbb{N}$. We assume that the integer q in (4) is as small as possible yielding a unique representation for x. Let ${\widehat{p}}_1,{\widehat{p}}_2,\dots ,{\widehat{p}}_{d-1}\in \mathbb{Z}$ and and $\widehat{q}\in \mathbb{N}$ denote the corresponding terms for $\alpha \in \mathbb{Q}(\beta )$:

$$\begin{array}{c}\hfill \alpha ={\widehat{q}}^{-1}\sum _{i=0}^{d-1}{\widehat{p}}_i{\beta }^i.\end{array}$$

(5)

Fix $\alpha \in \mathbb{Q}(\beta )\cap (0,2-\beta )$ and $x\in \mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$ with the forms given in (4) and (5). For $i\in \mathbb{N}$, let ${\omega }_i^{\pm }(x)$ respectively denote the i-th letter of ${\tau }_{\beta ,\alpha }^{\pm }(x)$. From the commutative diagram given in (3), we have, for n a non-negative integer, that

$$\begin{array}{c}\hfill {\rho }^{(n,\pm )}(x)≔{\beta }^n\left(x-\sum _{i=1}^n{\omega }_i^{\pm }(x){\beta }^{-i}+\alpha \sum _{i=1}^n{\beta }^{-i}\right)={(T_{\beta ,\alpha }^{\pm })}^n(x).\end{array}$$

(6)

Lemma 2. 

For $x\in \mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$ and $n\in {\mathbb{N}}_0$, there exists a unique vector $(r_1^{(n,\pm )}(x),\dots ,r_d^{(n,\pm )}(x))$ in ${\mathbb{Z}}^d$ with

$$\begin{array}{c}\hfill {\rho }^{(n,\pm )}(x)={(\widehat{q}q)}^{-1}\sum _{i=1}^d{r}_i^{(n,\pm )}(x){\beta }^{-i}.\end{array}$$

(7)

For ease of notation, and when the dependency on x is clear, we write ${\mathbf{r}}^{(n,\pm )}=(r_1^{(n,\pm )},\dots ,r_d^{(n,\pm )})$ in replace of ${\mathbf{r}}^{(n,\pm )}(x)=(r_1^{(n,\pm )}(x),\dots ,r_d^{(n,\pm )}(x))$.

Proof. 

By (4)–(6) we have that

$$\begin{array}{c}\hfill {\rho }^{(1,\pm )}(x)=q^{-1}\sum _{i=1}^d{p}_{i-1}{\beta }^i-{\omega }_1^{\pm }(x)+\alpha ={(\widehat{q}q)}^{-1}\left(\widehat{q}\sum _{i=1}^d{p}_{i-1}{\beta }^i-\widehat{q}q{\omega }_1^{\pm }(x)+q\sum _{i=0}^{d-1}{\widehat{p}}_i{\beta }^i\right).\end{array}$$

The result for $n=1$ follows from the fact that q and $\widehat{q}$ are fixed and that $B≔\{\beta ,{\beta }^2,\dots ,{\beta }^d\}$ is a basis for $\mathbb{Q}(\beta )$. An inductive argument yields the general result.  □

Lemma 3. 

For $x\in \mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$, $n\in {\mathbb{N}}_0$ and γ a Galois conjugate of β,

$$\begin{array}{c}\hfill {\gamma }^n\left(q^{-1}\sum _{i=0}^{d-1}{p}_i{\gamma }^i-\sum _{i=1}^n{\omega }_i^{\pm }(x){\gamma }^{-i}+\widehat{\alpha }\sum _{i=1}^n{\gamma }^{-i}\right)={(\widehat{q}q)}^{-1}\sum _{i=1}^d{r}_i^{(n,\pm )}{\gamma }^{-i},\end{array}$$

(8)

where $\widehat{\alpha }={\widehat{q}}^{-1}{\sum }_{i=0}^{d-1}{\widehat{p}}_i{\gamma }^i$. Moreover, if $|\gamma |>1$ and if $x\in {Preper}^{\pm }(\beta ,\alpha )\cap \mathbb{Q}(\beta )$, then

$$\begin{array}{c}\hfill q^{-1}\sum _{i=0}^{d-1}{p}_i{\gamma }^i=\frac{\widehat{\alpha }}{1-\gamma }+\sum _{i=1}^{\infty }{\omega }_i^{\pm }(x){\gamma }^{-i}.\end{array}$$

(9)

Proof. 

Combining (4), (6) and (7), we obtain that $\beta$ satisfies the polynomial equation

$$\begin{array}{c}\hfill z^{n+d}\left(\widehat{q}\sum _{i=0}^{d-1}{p}_i{z}^i-\widehat{q}q\sum _{i=1}^n{\omega }_i^{\pm }(x)z^{-i}+q\left(\sum _{j=0}^{d-1}{\widehat{p}}_j{z}^i\right)\left(\sum _{i=1}^n{z}^{-i}\right)\right)=\sum _{i=1}^d{r}_i^{(n,\pm )}{z}^{d-i}\end{array}$$

(10)

for all $n\ge 0$. Since $\gamma$ is a Galois conjugate of $\beta$, it is also a solution to (10), which proves (8). If $|\gamma |>1$ and if $x\in {Preper}^{\pm }(\beta ,\alpha )$, then the cardinality of the set $\{{\mathbf{r}}^{(n,\pm )}:n\in {\mathbb{N}}_0\}$ is finite, and thus

$$\begin{array}{c}\hfill c^{\pm }≔sup\{max\{|r_k^{(n,\pm )}|:k\in \{1,\dots ,d\}\}:n\in \mathbb{N}\}<\infty .\end{array}$$

(11)

Combining this with (8) we obtain

$$\begin{array}{c}\hfill \left|q^{-1}\sum _{i=0}^{d-1}{p}_i{\gamma }^i-\sum _{i=1}^n{\omega }_i^{\pm }(x){\gamma }^{-i}+\widehat{\alpha }\sum _{i=1}^n{\gamma }^{-i}\right|\le {(\widehat{q}q)}^{-1}{c}^{\pm }d{|\gamma |}^{-n}.\end{array}$$

Letting n tend to infinity in the above equation yields (9). □

With the above two lemmas at hand we are ready to prove Theorem 2(i).

Proof of Theorem 2(i). 

We show the result for $T_{\beta ,\alpha }^{+}$ noting that the proof is analogous for $T_{\beta ,\alpha }^{-}$. By way of contradiction, suppose there exists a Galois conjugate $\gamma \ne \beta$ of $\beta$ with $|\gamma |>1$. Let $x\in [\alpha ,\beta +\alpha -1]$ and let $a,b\in J_{\beta ,\alpha }$ be such that $a<b$ and $T_{\beta ,\alpha }^{+}(a)=T_{\beta ,\alpha }^{+}(b)=x$. Set $\delta ≔|{\beta }^{-1}-{\gamma }^{-1}|$ and let $\eta ≔max\{{\beta }^{-1},{|\gamma |}^{-1}\}$. Choose $m\in \mathbb{N}$ with ${\eta }^{m+1}/(1-\eta )<\delta /2$.

Let $a^{\prime },b^{\prime }\in \mathbb{Q}\cap J_{\beta ,\alpha }$ with ${\tau }_{\beta ,\alpha }^{+}(a){{|}_m={\tau }_{\beta ,\alpha }^{+}(a^{\prime })|}_m$ and ${\tau }_{\beta ,\alpha }^{+}(b){{|}_m={\tau }_{\beta ,\alpha }^{+}(b^{\prime })|}_m$; the existence of $a^{\prime }$ and $b^{\prime }$ is guaranteed by Proposition 2. By (3) and how $a^{\prime }$ and $b^{\prime }$ have been chosen, we have that $({\omega }_2^{+}(a^{\prime }),...,{\omega }_m^{+}(a^{\prime }))=({\omega }_2^{+}(b^{\prime }),...,{\omega }_m^{+}(b^{\prime }))$, ${\omega }_1^{+}(a^{\prime })=0$ and ${\omega }_1^{+}(b^{\prime })=1$. An application of Lemma 3 in tandem with (4), our hypothesis and the fact that $\gamma$ is a Galois conjugate of $\beta$, yields the following.

$$\begin{array}{cc}\hfill a^{\prime }& =\frac{\alpha }{1-\beta }+\sum _{i=1}^{\infty }{\omega }_i^{+}(a^{\prime }){\beta }^{-i}=\frac{\widehat{\alpha }}{1-\gamma }+\sum _{i=1}^{\infty }{\omega }_i^{+}(a^{\prime }){\gamma }^{-i}\hfill \\ \hfill b^{\prime }& =\frac{\alpha }{1-\beta }+\sum _{i=1}^{\infty }{\omega }_i^{+}(b^{\prime }){\beta }^{-i}=\frac{\widehat{\alpha }}{1-\gamma }+\sum _{i=1}^{\infty }{\omega }_i^{+}(b^{\prime }){\gamma }^{-i}\hfill \end{array}$$

From this we obtain the following chain of inequalities.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \delta =|{\beta }^{-1}-{\gamma }^{-1}|& =\left|\frac{\alpha }{1-\beta }+\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\beta }^{-i}-\frac{\widehat{\alpha }}{1-\gamma }-\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\gamma }^{-i}\right|\hfill \\ \hfill & \le \left|\frac{\alpha }{1-\beta }+\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\beta }^{-i}-a^{\prime }\right|+\left|a^{\prime }-\frac{\widehat{\alpha }}{1-\gamma }-\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\gamma }^{-i}\right|\hfill \\ \hfill & \le \left|\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\beta }^{-i}-\sum _{i=1}^{\infty }{\omega }_i^{+}(a^{\prime }){\beta }^{-i}\right|+\left|\sum _{i=1}^{\infty }{\omega }_i^{+}(a^{\prime }){\gamma }^{-i}-\sum _{i=2}^{\infty }{\omega }_i^{+}(b^{\prime }){\gamma }^{-i}\right|\hfill \\ \hfill & \le \sum _{i=m+1}^{\infty }|{\omega }_i^{+}(b^{\prime })-{\omega }_i^{+}(a^{\prime })|{\beta }^{-i}+\sum _{i=m+1}^{\infty }|{\omega }_i^{+}(b^{\prime })-{\omega }_i^{+}(a^{\prime })|{|\gamma |}^{-i}\le 2{\eta }^{m+1}{(1-\eta )}^{-1}<\delta \hfill \end{array}\end{array}$$

This yields a contradiction, and concludes the proof.  □

For the proof of Theorem 2(ii) we require an additional lemma.

Lemma 4. 

Set $\beta ={\gamma }_1$ and let ${\gamma }_2,\dots ,{\gamma }_d$ denote the Galois conjugates of β. For $x\in \mathbb{Q}(\beta )\cap J_{\beta ,\alpha }$, $n\in {\mathbb{N}}_0$ and $i\in \{1,2,\dots ,d\}$ set

$$\begin{array}{c}\hfill {\rho }_i^{(n,\pm )}(x)≔q^{-1}\sum _{k=1}^d{r}_k^{(n,\pm )}(x){\gamma }_i^{-k}.\end{array}$$

(12)

The following are equivalent.

(i) 

$x\in {Preper}^{\pm }(\beta ,\alpha )$

(ii) 

${\displaystyle max\{sup\{|{\rho }_i^{(n,\pm )}(x)|:n\in {\mathbb{N}}_0\}:i\in \{1,\dots ,d\}\}<\infty }$

(iii) 

${\displaystyle sup\{max\{|r_k^{(n,\pm )}(x)|:k\in \{1,\dots ,d\}\}:n\in {\mathbb{N}}_0\}<\infty }$

Proof. 

A similar argument to that given in the proof of Lemma 3, where we obtained (11), shows (i) implies (iii). That (iii) implies (ii) follows from (12). To complete the proof we show (ii) implies (i). To this end, assume (ii) and set

$$\begin{array}{c}\hfill {\mathbf{v}}^{(n,\pm )}(x)≔q\left(\begin{array}{c}{\rho }_1^{(n,\pm )}(x)\\ ⋮\\ {\rho }_d^{(n,\pm )}(x)\end{array}\right)=\underset{{\displaystyle ≕M_{\beta }}}{\underbrace{\left(\begin{array}{cccc}{\gamma }_1^{-1}& {\gamma }_1^{-2}& \dots & {\gamma }_1^{-d}\\ ⋮& ⋮& \ddots & ⋮\\ {\gamma }_d^{-1}& {\gamma }_d^{-2}& \dots & {\gamma }_d^{-d}\end{array}\right)}}\left(\begin{array}{c}{r}_1^{(n,\pm )}(x)\\ ⋮\\ r_d^{(n,\pm )}(x)\end{array}\right).\end{array}$$

(13)

By assumption, there exists $c^{\pm }\in \mathbb{R}$ with $\parallel {\mathbf{v}}^{(n,\pm )}(x)\parallel \le c^{\pm }$, for all $n\in {\mathbb{N}}_0$. Since the Galois group of a finite Galois extension acts transitively on the roots of any minimal polynomial, $M_{\beta }$ is a non-singular matrix. This implies there exists $k^{\pm }\in \mathbb{Z}$ with $\parallel {\mathbf{r}}^{(n,\pm )}(x)\parallel \le k^{\pm }$, for all $n\in {\mathbb{N}}_0$. Hence, as ${\mathbf{r}}^{(n,\pm )}(x)\in {\mathbb{Z}}^d$ it follows that ${\mathbf{r}}^{(m,\pm )}(x)={\mathbf{r}}^{(n,\pm )}(x)$, and therefore ${\rho }_i^{(m,\pm )}(x)={\rho }_i^{(n,\pm )}(x)$, for some $m,n\in {\mathbb{N}}_0$ with $m\ne n$ and all $i\in \{1,\dots ,d\}$. An application of Lemma 2 and (6) yields the required result. □

Proof of Theorem 2(ii). 

Fix $x\in \mathbb{Q}(\beta )\cap [0,1]$ with the form given in (4). As in Lemma 4, set ${\gamma }_1=\beta$ and let ${\gamma }_2,\dots ,{\gamma }_d$ denote the Galois conjugates of $\beta$. Since, by assumption, $\beta$ is a Pisot number, it follows ${\displaystyle \eta ≔max\{|{\gamma }_j|:j\in \{2,\dots ,d\}\}<1}$. For $j\in \{2,3,\dots ,d\}$, let

$$\begin{array}{c}\hfill {\widehat{\alpha }}_j≔{\widehat{q}}^{-1}\sum _{i=0}^{d-1}{\widehat{p}}_i{\gamma }_j{}^i,\end{array}$$

and set $\tilde{\alpha }≔max\{|{\widehat{\alpha }}_j|:j\in \{2,3,\dots ,d\}\}$. By (10) and (12) we have

$$\begin{array}{c}\hfill |{\rho }_i^{(n,\pm )}(x)|\le q^{-1}\sum _{j=0}^{d-1}|p_j|{\eta }^{n+j}+\sum _{i=0}^{n-1}(1+\tilde{\alpha }){\eta }^{n+i}\end{array}$$

for all $n\in {\mathbb{N}}_0$ and $i\in \{2,\dots ,d\}$. This in combination with (6) yields that Lemma 4(ii) is satisfied, and thus $x\in {Preper}^{\pm }(\beta ,\alpha )$. □

5. Periodic Expansions of Pisot and Salem Numbers: Proof of Corollaries 1 and 2

The aim of this final section is to provide an overview of the results of [19,21,22,33] which in combination with our results (Theorems 1 and 2) yield Corollaries 2 and 3.

An interval map $T:[a,b]⥀$ is called topologically transitive if for all open subintervals J there exists $m\in \mathbb{N}$ with

$$\begin{array}{c}\hfill \bigcup _{k=0}^m{T}^k(J)\supseteq (a,b).\end{array}$$

For $\beta \in (1,2)$, Parry [19] showed $T_{\beta ,1-\beta /2}^{\pm }$ is topologically transitive if and only if $\beta >\sqrt{2}$. This result was later generalised by Palmer [21] and Glendinning [22] who classified the set of points $(\beta ,\alpha )\in \Delta$ with $T_{\beta ,\alpha }^{\pm }$ is topologically transitive.

In order to state the results of Parry, Palmer and Glendinning we require the following. Let $n,k\in \mathbb{N}$ with $1\le k<n$ and $gcd(n,k)=1$, and let $I_{n,k}(\beta )$ be as in (1). Define $D_{n,k}$ to be the set

$$\begin{array}{c}\hfill \{(\beta ,\alpha )\in \Delta :\beta \in (1,2^{1/n}]\mathrm{and}\alpha \in I_{n,k}(\beta )\},\end{array}$$

see Figure 1 for an illustration of the intervals $I_{n,k}$ and the regions $D_{k,n}$.

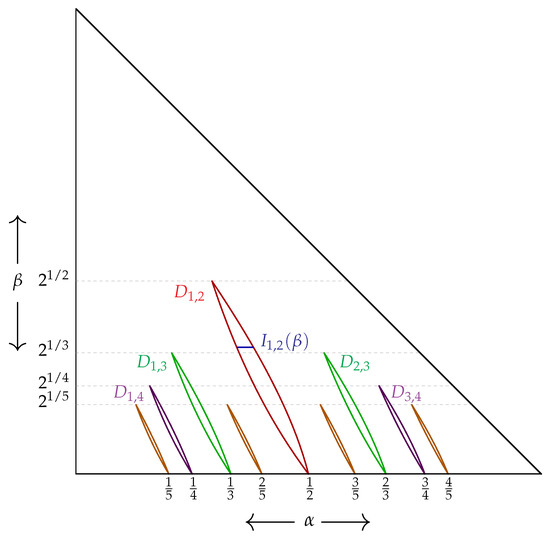
Figure 1. Plot of the parameter space $\Delta$, together with boundary of the regions $D_{1,2}$, $D_{1,3}$, $D_{2,3}$, $D_{1,4}$, $D_{3,4}$, $D_{1,5}$, $D_{2,5}$, $D_{3,5}$, $D_{4,5}$, $D_{1,6}$ and $D_{5,6}$. Further, in blue, a sketch of the interval $I_{1,2}(\beta )$, where $\beta$ is the square root of the golden mean, is given.

Theorem 6 

([19,21,22]). Let $(\beta ,\alpha )\in \Delta$. The tuple $(\beta ,\alpha )\in D_{k,n}$, for some $n,k\in \mathbb{N}$ with $1\le k<n$ and $\gcd (k,n)=1$, if and only if $T_{\beta ,\alpha }^{\pm }$ is not topologically transitive.

A main ingredient in the proof of this result is to show that for given $n,k\in \mathbb{N}$ with $1\le k<n$ and $gcd(n,k)=1$, there exists a one-to-one correspondence between points in $\Delta$ and points in $D_{n,k}$. More precisely, on the one hand, given $(\beta ,\alpha )\in \Delta$, there exists a unique $a\in I_{n,k}(\sqrt[n]{\beta })$, namely $a={\alpha }_{n,k}(\beta ,\alpha )$, see Corollary 3, such that, $T_{\beta ,\alpha }^{\pm }{|}_{[0,1]}$ and ${(T_{\sqrt[n]{\beta },a}^{\pm })}^n{|}_{[a,\sqrt[n]{\beta }+a-1]}$ are topologically conjugate with conjugating map $\mathsf{\Phi }(x)≔(\sqrt[n]{\beta }-1)x+a$; on the other hand, given $(\beta ,\alpha )\in D_{n,k}$, there exists $a\in [0,2-{\beta }^n]$, namely

$$\begin{array}{c}\hfill a=\left\{\begin{array}{cc}{\displaystyle 1-\frac{-\alpha ({\beta }^n-1)+\beta -1}{(\beta -1)(1-{\beta }^{-1})}}\hfill & \mathrm{if}k=1,\hfill \\ {\displaystyle 1-\frac{-\alpha ({\beta }^n-1)+(\beta -1){\sum }_{j=1}^s{W}_j}{(\beta -1)(1-{\beta }^{-1})}}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

such that ${(T_{\beta ,\alpha }^{\pm })}^n{|}_{[\alpha ,\beta +\alpha -1]}$ and $T_{{\beta }^n,a}^{\pm }$ are topologically conjugate, where the conjugating map is given by $x\mapsto {(\beta -1)}^{-1}(x-\alpha )$ and where $s\in \{0,1,\dots ,k-1\}$ satisfies $n=smodk$ and $W_j$ is as defined in (2). Moreover, in the case that $\beta \ne 2^{1/n}$ and $(\beta ,\alpha )\in D_{n,k}$

$$\begin{array}{c}\hfill \overline{{(T_{\beta ,\alpha }^{\pm })}^i([0,1])}\cap \overline{{(T_{\beta ,\alpha }^{\pm })}^j([0,1])}=\varnothing ,\end{array}$$

(14)

for all $i,j\in \{1,2,\dots ,n\}$ with $i\ne j$; in the case that $\beta \ne 2^{1/n}$ and $\alpha$ is the singleton in $I_{n,k}(\beta )$ the intersection in (14) is a singleton when $n\ne 2$ and a two point set when $n=2$. These observations in tandem with Theorem 1 and Corollary 1 directly yield Corollary 2. In order to prove Corollary 3, we require one final result.

Theorem 7 

([21,33]). Let $(\beta ,\alpha )\in \Delta$ be fixed. The absolutely continuous measure ${\nu }_{\beta ,\alpha }$ with density

$$\begin{array}{c}\hfill h_{\beta ,\alpha }≔\sum _{n=0}^{\infty }{\beta }^{-n}\left({𝟙}_{[0,{(T_{\beta ,\alpha }^{+})}^n(1))}-{𝟙}_{[0,{(T_{\beta ,\alpha }^{+})}^n(0))}\right)\end{array}$$

is invariant under $T^{\pm }$. Moreover, the support of ${\nu }_{\beta ,\alpha }$ equals $[0,1]$ and only if $(\beta ,\alpha )\notin D_{n,k}$ or if $\beta =2^{1/n}$ and α is the single point of $I_{n,k}(2^{1/n})$, for some $n,k\in \mathbb{N}$ with $k<n$ and $\gcd (k,n)=1$. Further, in the case that $\beta \ne 2^{1/n}$ and $(\beta ,\alpha )\in D_{n,k}$, the support of ${\nu }_{\beta ,\alpha }$ is contained in the disjoint union of intervals,

$$\begin{array}{c}\hfill \bigcup _{i=1}^n\overline{{(T_{\beta ,\alpha }^{\pm })}^i([0,1])}.\end{array}$$

Corollary 3 follows from this result in tandem with the observations directly proceeding it together with Theorem 2.