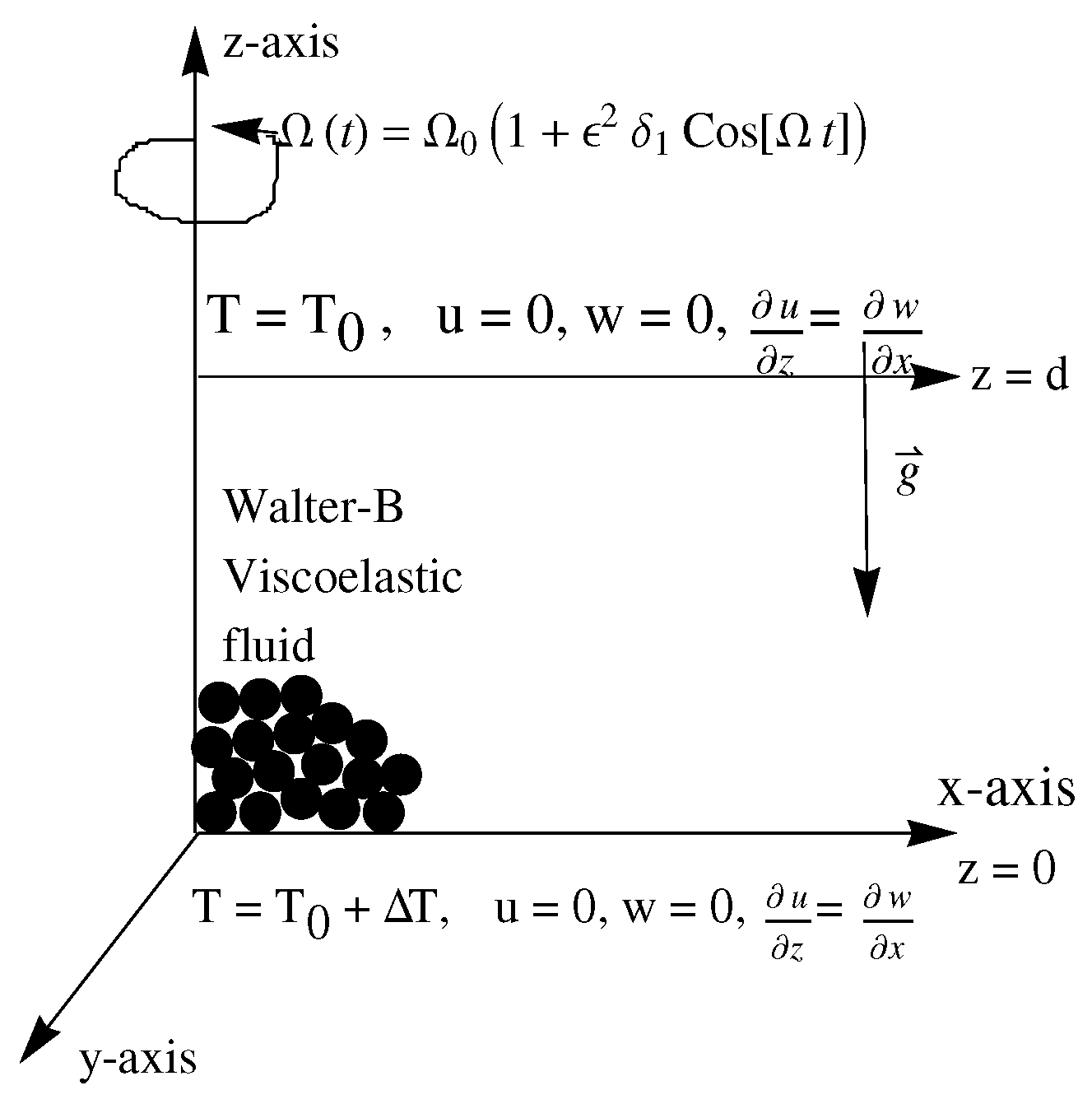Abstract
In this article, a study on the stability of Walter-B viscoelastic fluid in the highly permeable porous medium under the rotational speed modulation is presented. The impact of rotational modulation on heat transport is performed through a weakly nonlinear analysis. A perturbation procedure based on the small amplitude of the perturbing parameter is used to study the combined effect of rotation and permeability on the stability through a porous medium. Rayleigh–Bénard convection with the Coriolis expression has been examined to explain the impact of rotation on the convective flow. The graphical result of different parameters like modified Prandtl number, Darcy number, Rayleigh number, and Taylor number on heat transfer have discussed. Furthermore, it is found that the modified Prandtl number decelerates the heat transport which may be due to the combined effect of elastic parameter and Taylor number.
1. Introduction
The natural convection through porous media has numerous applications in real-life problems. The utilization of porous media is in the oil reservoir, geophysics, and solidification of binary alloys. The comprehensive study on investigations on porous media and its applications are compiled very nicely in the excellent books of Ingham and Pop [1,2], Vafai [3,4], Straughan (2004), and Nield and Bejan [5]. Bég and Makinde [6] considered the upper convected Maxwell model on the viscoelastic fluid to examine the species transfer in high permeability porous media. They have reported that the Darcy number and Deborah number have a negligible effect on species diffusion.
Furthermore, many more articles are found based on the flow through porous media, some of them are: Malashetty and Basavaraja [7] studied the onset of convection in a horizontal anisotropic porous layer under thermal/gravity modulation. They have found that the temperature modulation gives rise to both sub-critical and super-critical motion, whereas gravity modulation always leads to the sub-critical motion. Shivakumara et al. [8] investigated an interesting practical problem based on the Darcy–Bénard–Marangoni convection with high permeability. They have considered the effective viscosity and fluid viscosity are different and found that the permeability constant stabilizing the onset convection. In addition, Shivakumara et al. [9], Postelnicu [10], Shivakumara and Sureshkumar [11], and Malashetty et al. [12] studied about the saturated porous medium.
Most of the engineering applications in fluid mechanics are restricted to a system in which externally imposed forces played an important role. These forces may be considered as temperature modulation, concentration modulation, rotational speed modulation, and others. The influence of external rotation is widely known due to significantly altering the nature of fluid flow by the Coriolis force. The investigation on convective heat transfer together with the rotational process in Newtonian fluids have practical importance. Research on rotational speed modulation is essential because this problem has been used in many branches of modern science such as enlarged production from petroleum reservoirs, geothermal energy utilization, atomic scraps repository rotating, insulation engineering, turbo-machinery, and bio-mechanics. The investigations on the effect of externally rotating force on thermal convection are initiated by Bénard [13] and Taylor [14,15,16] in the form of theoretical and experimental studies. The thermal and gravity modulations were initially generated by the rotational speed modulation from the original work of Donnelly [17]. Donnelly [17] analyzed the influence of rotational speed modulation on the thermal convection between two cylinders. Rauscher and Kelly [18] examined the effects of thermal and rotation modulation on the onset of convection.
In addition, the theoretical and experimental literature for rotational speed modulation was reported by Ahlers et al. [19], Niemela and Donnelly [20], and Walsh and Donnelly [21]. Bhadauria and Kiran [22] presented Rayleigh–Bénard convection of temperature-dependent viscosity of the fluid in the presence of internal heat source and rotational speed modulation. Gupta et al. [23] studied the effect of concentration/gravity modulation on mass transport in a rotating fluid layer. They have observed that the mass transport can govern the proper changes in amplitude and frequency of the modulation. Gupta [24] analyzed the effect of concentration modulation under the effect of applied magnetic field in a rotating fluid layer. Drury et al. [25] analyzed the impact of rotational speed modulation on Kepler AP star KIC2569073. Bowman et al. [26] observed the influence of rotational speed modulation to be chemically peculiar on stars by the photometry method. Recently, some articles have been published which use different types of modulation, for example, Keshri et al. [27,28,29], Kumar et al. [30], Jeong et al. [31], Tahir et al. [32], Saravanan and Kousalya [33], Roth et al. [34], Bhattacharya et al. [35], and Tayebi and Chamkha [36].
Since viscoelastic fluids are in demand nowadays due to their wide range of applications in modern technology and industries, such as petroleum engineering, reservoir engineering, material processing, biorheology, geophysics, and chemical engineering, so the studies on thermal instabilities on viscoelastic fluids are needed. Viscoelastic fluids have some silent features of instabilities like over-stability, which is not reflected in Newtonian fluids. Herbert [37] documented a report on the effect of elasticity on Couette flow. He performed a linear stability analysis and found that elasticity has a destabilizing effect on fluid flow. Furthermore, Vest [38] envisaged the natural convection in Maxwell fluid and obtained that the elasticity destabilizes the convection. He also reported that the convection could be slightly stabilized by considering rigid-rigid boundaries. Later on, Bhatnagar [39] used the approximation method to examine the stability in viscoelastic fluids. He observed that the neutral stability curves are more complicated in nature, as reported by Herbert [37] in the case of Couette flow. Several authors made reports on viscoelastic fluid-saturated porous media in the recent past. A few of them are: Postelnieu [10], Comissiong [40], Shivkumara et al. [41], Sheu [42], Rajib and Layek [43], Bhadauria and Kiran [44,45,46], Bhadauria and Kiran [47], and Bhadauria [48].
Landau [49] proposed an equation for evolution of magnitude of disturbance, which is reducible to a linear differential equation and is now called the Landau equation, in order to explain the transition to turbulence without providing valid proof. It is assumed that the foundation of nonlinear instability was laid by Landau (Drazin and Reid [50]). Later on, Stuart [51] has derived the equations claimed by Landau from hydrodynamic equations for Poiseuille flow. A detailed discussion on Ginzburg–Landau equations are documented in the Statistical Physics (Landau and Lifshitz [52]). They derived a Ginzburg–Landau equation to analyze the behavior of semiconductor in a magnetic field. They have used the general Landau theory of phase transition of the second kind which states that the difference between the symmetrical and unsymmetrical phase is described by the order of parameter, which will be zero at transition point.
The above discussions show that investigation of rotational speed modulation on Walter-B viscoelastic fluids saturated in highly permeable porous media is required. Authors ensure that there is no document available that describes the impact of time-varying rotation on Walter-B viscoelastic fluids saturated in highly permeable porous media. With these motives, we have carried out a weakly nonlinear analysis of Walter-B viscoelastic fluids saturated in highly permeable porous media under a rotational speed modulation effect. A real Ginzburg–Landau equation has been obtained to depict the role of dimensionless parameters on heat transport.
2. Mathematical Formulation
In the present article, a Walter-B viscoelastic fluid enclosed within two parallel infinite flat plates saturated in highly permeable porous media is considered for the investigation. A Cartesian frame has been taken in such a way that the x-axis is along the lower plate and has an origin on it. The z-axis is taken perpendicular to the lower plate. For sustaining the fluid flow, an adverse temperature gradient is required; therefore, the upper plate is cooled and lower plate is heated. With a variable rotational speed , the fluid layer is rotating about the z-axis (see Figure 1). The centrifugal force term has been neglected because the impact of rotation is limited to the Coriolis term. The Boussinesq approximation is employed which assumes that the density varies linearly with temperature. In view of the assumptions above, the basic governing model is given by:
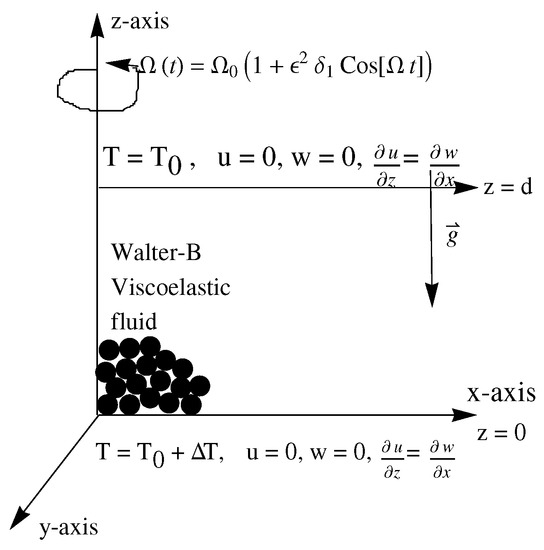
Figure 1.
Schematic diagram of the problem geometry.
The examined temperature boundary situation at the plates is:
where the variables have their usual meaning and are defined in the nomenclature section.
The present article focuses on the time-varying rotational speed modulation which alters the stability conditions and is defined as:
where is a very small quantity and is known as the amplitude of rotational speed modulation.
3. Basic State
The quantities at equilibrium position are defined as:
Substituting Equation (7) into Equations (2)–(4), we get the following relation which helps us to define the basic state of pressure and temperature
where subscript b refers to the basic state. The solution of Equation (9) with Equation (5) is given by
To perform the stability analysis, an infinitesimal disturbance is created in the variables defined at the equilibrium position and then we will observe the effect of these small disturbances on the system. Let us define the variables at a perturbed state as
where shows the amount of the small deviation in the variables at basic state.
Now, we have taken the curl for eliminating the pressure term from Equation (13). In addition, we have considered all physical quantities to be independent of the y-coordinate as their axis. For two-dimensional convection, the stream function was introduced as , . Furthermore, we write the resulting equations in dimensionless form by using the following transformation of variables:
The dimensionless form of governing equations (after dropping the asterisks) is
where and the dimensionless constants in the above equations are defined as: , is the modified Prandtl number, , is the modified Taylor number, , is the Darcy number, , is the elastic parameter, , is the Rayleigh number, is the modified thermal capacity ratio, and we have assumed .
Similarly, the expression of which arrives in Equation (18) can be collected through Equation (10) as
Since stability analysis is performed for a short time, the time variation is rescaled as . Thus, Equations (16)–(18) can be obtained as
The dimensionless thermal boundary conditions are given by
From the Equations (20)–(22), one can recover the equations for uniform rotation reported by Vadasz [53] and Gupta et al. [54] for .
4. Finite Amplitude Equation and Heat Transfer
To perform weakly nonlinear stability analysis, the asymptotic expansions method has been adopted. Thus, stream function , rotational velocity , temperature , and Rayleigh number are expanded in the power series of a small perturbation parameter . Accordingly, quantities are defined as
where denotes the critical value of the Rayleigh number at which starting convection take place. Now, the above system of equation will be solved for different powers of by equating the similar terms of on both the sides, we get a series of partial differential equations at different orders of a perturbation parameter.
4.1. First-Order System: Linear Stability Analysis
For the first-order problem, we have:
Here, and are independent of so and . Thus, the solutions of Equations (25)–(27) satisfying the boundary conditions are obtained as:
where and the value of amplitude has to determine what is not possible here. It will be determined by applying the solvability condition at the third-order solution.
The expressions for the critical value of Rayleigh number and corresponding wave number are obtained as
When , the expression for critical Rayleigh number and wave number, which, given by Equations (29) and (30), reduces to
The expressions in Equations (31) and (32) coincide with the classical result reported by Lapwood [55] for isotropic porous media.
4.2. Second-Order System
For the second-order problem, we have:
where , and are obtained as follows:
At this stage, the stream function, rotational velocity, and temperature profiles are independent of scaled time . Thus, these profiles for the second-order system, subject to boundary conditions, can be obtained as:
The local Nusselt number, , for the stationary mode of convection is determined by:
Now, putting the values of and into Equation (38), we get
4.3. Third-Order System
Equate the coefficient of from Equations (20)–(22) to determine the solution at third order. After putting the expansions of , v, and T, the following equations can be obtained:
where
Concerning the occurrence of the solution of the third-order arrangement, a solvability condition has been imposed that results in terms of the time-periodic coefficients known as the real Landau equation for stationary convection in the form:
where is the unmodulated amplitude of heat convection. The coefficients are given by
Equation (46) is reducible to the linear differential equation with the time-dependent coefficients; thus, determining its analytical solution is a difficult task. Therefore, a numerical solution has been obtained by using the in-built function NDSolve of Mathematica 11, subject to a suitable initial condition . In our calculations, assume that to keep the parameters to the minimum.
5. Results and Discussion
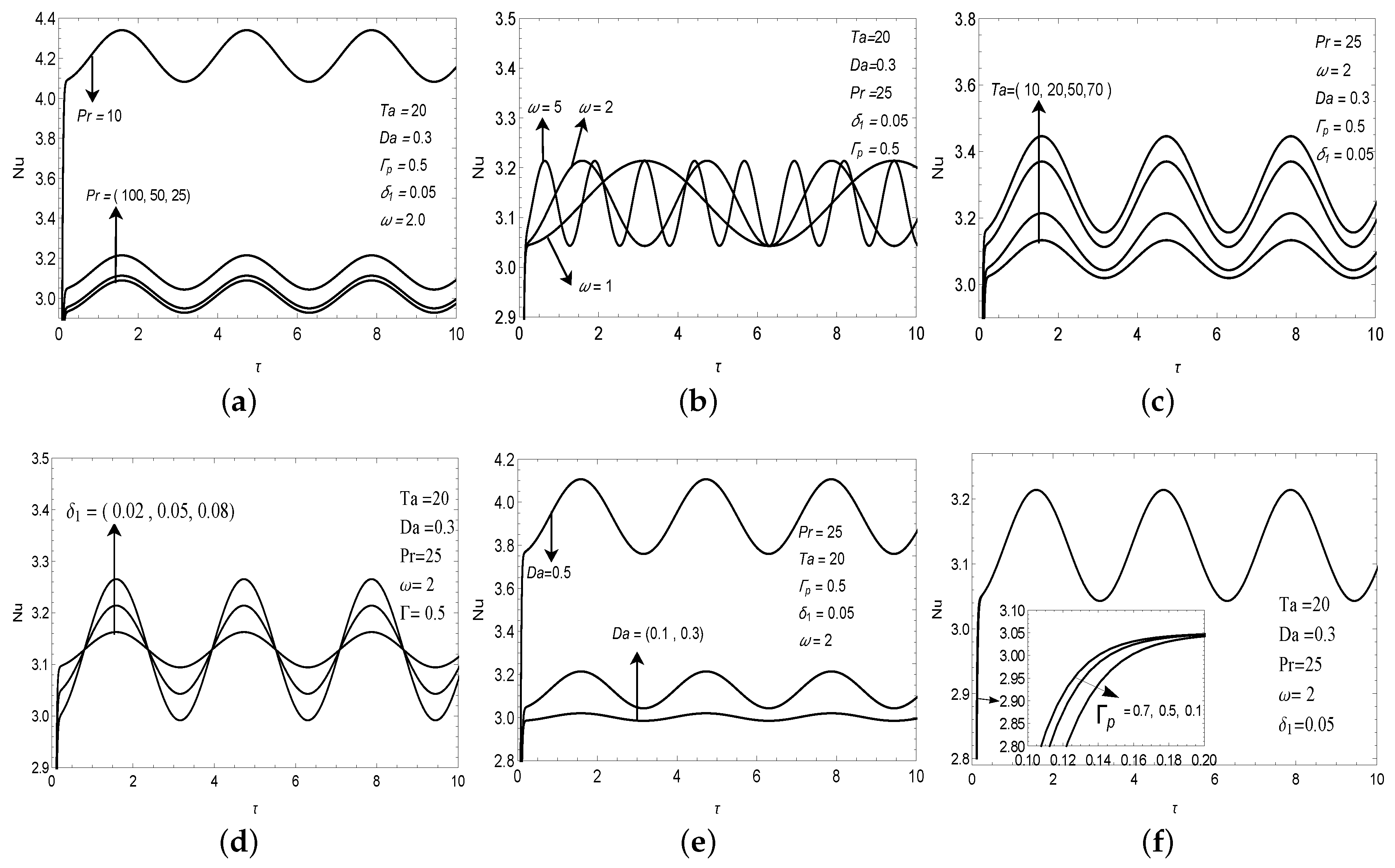
In this section, we have discussed the graphical representation of numerical outcomes in terms of heat transport versus slow time under rotational speed modulation of Walter-B viscoelastic fluid in highly permeable porous media. The study is performed under the weakly nonlinear stability theory, which indicates that the stability is possible by a certain choice of physical parameters. As we have known that many real-life applications complying with thermal convection under external regulatory forces are used for enhancing or inhibiting the heat transport in engineering and science, industry, food process, turbo-machinery, and chemical industry. Consequently, the rotational speed modulation as an external regulatory mechanism has been considered for the study of Walter-B viscoelastic fluid. The non-dimensional parameters that arise in the problem are , , , , , , and . These parameters influence the convective heat transfer. For the range of the considered parameters, we have followed the articles of Shivkumara et al. [41], Beg and Makinde [6], and Kumar et al. [30]. Furthermore, as the Darcy number increases, the flow profile decreases due to the Darcian force decrease (Beg and Makinde [6]). Thus, a higher Darcy number has been considered to accelerate the flow formation. The common values of the parameters are taken as = 25, = 0.3, = 2, = 0.05, = 0.5, and = 20 (unless otherwise stated). In all figures, the Nusselt number ()) concerning slow time under rotational speed modulation has been plotted for Walter-B viscoelastic fluid from Figure 2a–f.
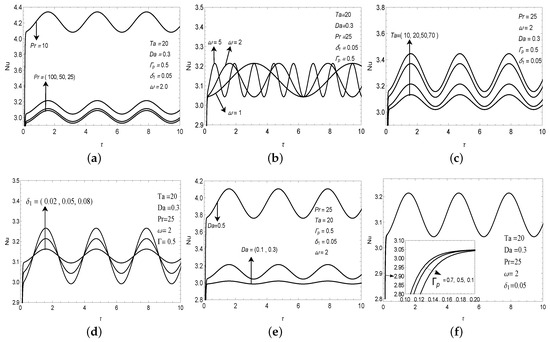
Figure 2.
Variation of Nusselt number () with slow time () for different values of parameters (a) , (b) , (c) , (d) , (e) , (f) .
In Figure 2a, the effect of Prandtl number on Nusselt number over slow time is depicted. As enlarges, the Nusselt number decreases by considering other parameters at their common values. This is due to the momentum diffusivity dominating and, consequently, the temperature gradient decreasing. In addition, at a low value of , the heat transfer rate is higher and, at higher values of , the heat transfer is slow. Thus, Prandtl number stabilizes the system. This character opposes the result produced Bhadauria and Kiran [44] under gravity modulation. This is due to the combined effect of elastic parameter and rotational speed modulation. Figure 2b illustrates the effect of frequency of Modulation on heat transport. Figure 2b shows that, for a small value of , the heat transfer is higher, while, at a large value of , the heat transfer is less. As increases, the amplitude of modulation increases and consequently decreases the value of heat transfer. Therefore, the frequency of modulation stabilizes the system. The effect of modified Taylor number () on the rate of heat transfer is depicted by Figure 2c. As increases, increases by considering the other parameter at their common value. When rotation increases, then temperature gradient increases and therefore heat transfer increases. Figure 2d scrutinizes the impact of amplitude of modulation () on Nusselt number for the common value of other parameters. The heat transport increases by increasing the value of . Thus, we can find that is an external controlling mechanism of convection. Hence, the system becomes destabilized as increases. Figure 2e shows the variation of for different values of Darcy number (). When increases, the fluid particle moves easier in the progressively less fibrous porous region because the Darcian force resists the fluid flow and is inversely proportional to the Darcy number. Actually, this indicates that the Darcian force will decline for a larger permeability (higher values). Thus, as permeability increases ( increases), the heat transport increases so the Darcy number has a destabilizing effect on the system as the rate of heat transfer increases. Figure 2f displays the variation of versus for different values of elastic parameter (). We found that an increase in the value of increases the value of Nusselt number () for a very short time. Thus, heat transport increases. At the same time, we also observe that the effect of the elastic parameter on the rate of heat transport diminishes as time passes.
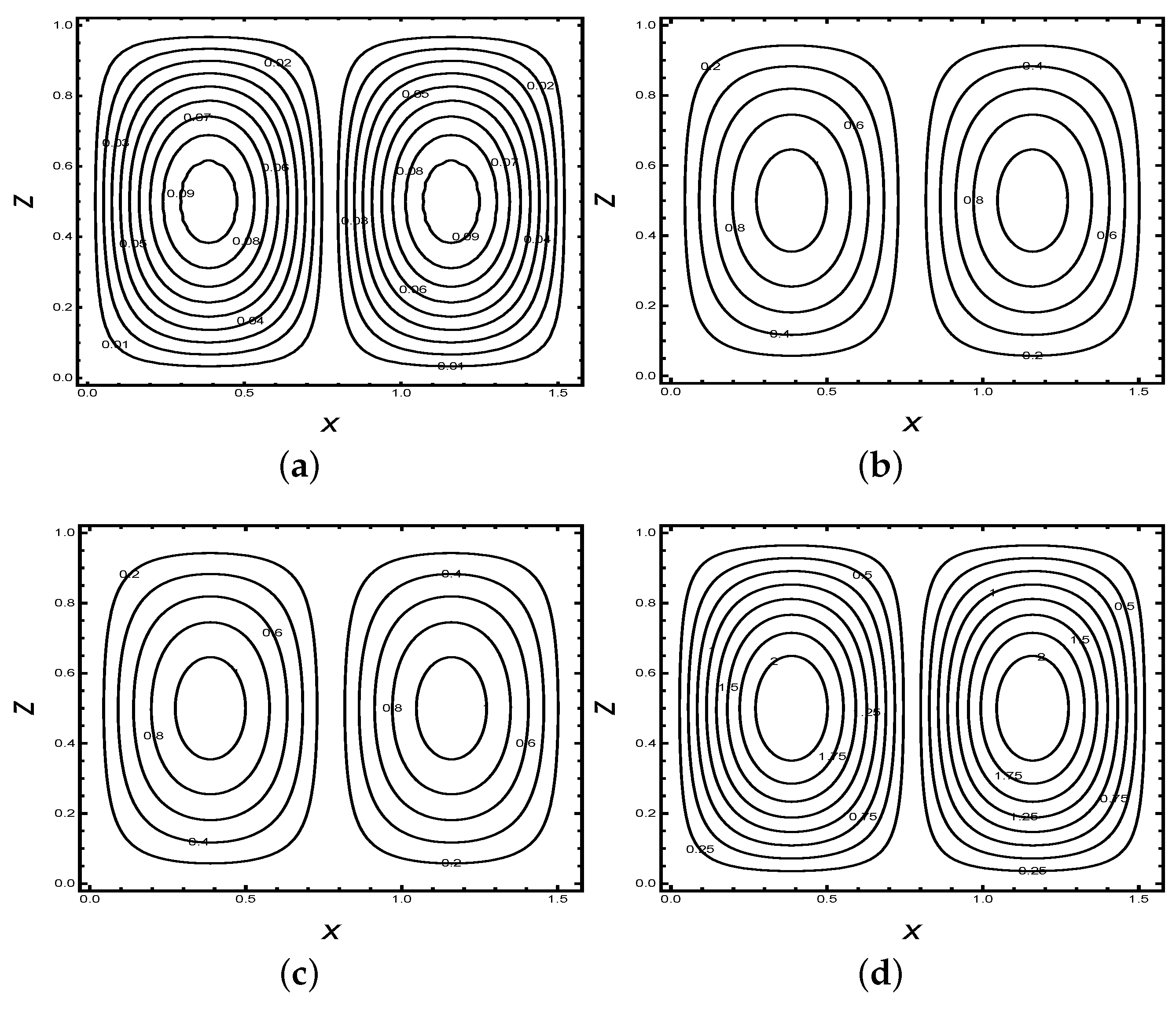
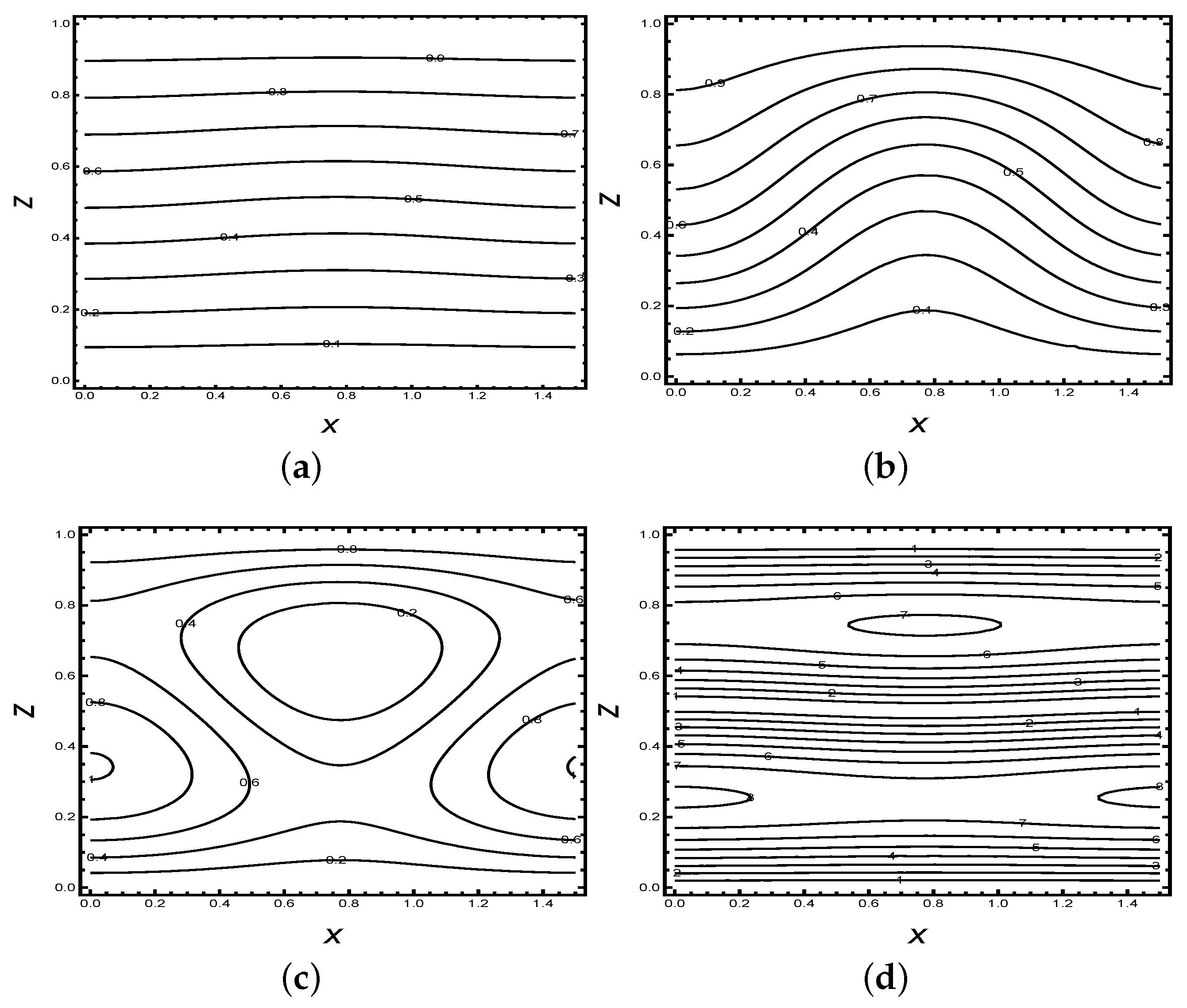
Figure 3 and Figure 4 are plotted for the streamlines and corresponding isotherms respectively at different values of and 2.5 for the fixed value of other parameters. The figures show that, initially, heat transport is in the conduction state because of the small magnitude of streamlines and flat nature of isotherms. As the value of increases, we observe that the magnitude of streamlines increases and isotherms have more contour which confirms that the heat transfer is due to convection. Furthermore, we examine that the convection takes place more rapidly as time () increases. From Figure 2d, we observe that contours are shifted towards the wall, which indicates that the system is approaching steady state. Figure 3d shows that the contours become flat at , which validates the results predicated by Figure 2d.
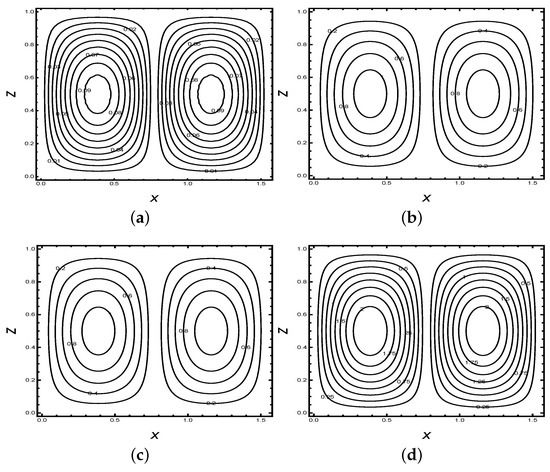
Figure 3.
Streamlines for the fixed values of parameters at different scaled time (a) , (b) , (c) , (d) for the fixed values of = 25, = 0.3, = 2, = 0.05, = 0.5 and = 20.
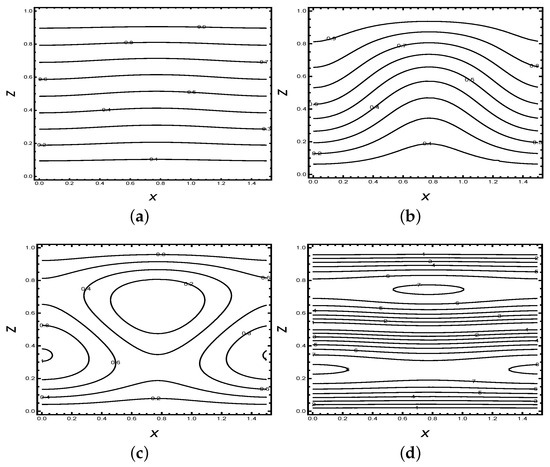
Figure 4.
Isotherms for the fixed values of parameters at different scaled time (a) , (b) , (c) , (d) for the fixed values of = 25, = 0.3, = 2, = 0.05, = 0.5 and = 20.
6. Conclusions
The present article displays the effect of modulated rotational speed in a highly permeable porous media saturated Walter-B viscoelastic fluid on Rayleigh–Bénard convection. In this study, an incompressible fluid saturated between two infinite parallel plates cooled from above and heated from below is considered. Here, a weekly nonlinear stability analysis has been presented by using a real Landau model in terms of the amplitude of convection. The impact of different dimensionless parameters is analyzed on the convective system, and we have drawn the following conclusions:
- The effect of the modified Prandtl number is to stabilize the convective system as decreases with . This is the combined effect of elastic parameter and Taylor number.
- The effect of the increasing modified Taylor number () is to increase the heat transfer rate, and thus destabilizes the system.
- The frequency of modulation stabilizes the system while the amplitude of modulation has the opposite effect.
- The heat transport can be accelerated with an increase in the Darcy number (i.e., rise in permeability) and hence the Darcy number destabilizes the convective system.
- Nusselt number increases with an increase in for an initial short period. After that, its effect is negligible on heat transport.
- At initially (), the heat transport is in a conduction mode and, when time () increases, the conduction mode is switched into convection mode. Thus, at moderate values of time (), heat transport is carried due to convection. After , we observe that the system arrives at a steady state.
We can summarize the above results as:
Author Contributions
Conceptualization, A.K., V.K.G. and N.M.; methodology, A.K., V.K.G. and N.M.; software, A.K., V.K.G. and N.M.; validation, A.K., V.K.G., N.M. and I.H.; formal analysis, A.K., V.K.G., N.M. and I.H.; investigation, A.K., V.K.G. and N.M.; resources, A.K., V.K.G. and N.M.; data curation, X.X.; writing—original draft preparation, A.K., V.K.G. and N.M.; writing—review and editing, A.K., V.K.G., N.M. and I.H.; funding acquisition, I.H. All authors have read and agreed to the published version of the manuscript.
Funding
We are grateful for the financial support received from the Universiti Kebangsaan Malaysia under the research grant GP-2019-K006388.
Acknowledgments
The authors are grateful to the referees for their most useful comments that helped refine the paper to the present form.
Conflicts of Interest
Authors declare no conflict of interest.
Nomenclature
| Latin Symbols | |
| A | Amplitude of convection |
| Amplitude of modulation | |
| Gravitational acceleration, (0, 0,) | |
| k | Wave number |
| Velocity Vector | |
| d | Depth between plates |
| Nusselt Number | |
| p | Pressure |
| Thermal Rayleigh Number | |
| Modified Taylor Number | |
| Modified Pradtl Number | |
| T | Temperature |
| Temperature Difference across the layer | |
| Darcy number | |
| M | Modified thermal capacity ratio, |
| Effective thermal diffusivity | |
| t | Time |
| Horizontal and Vertical co-ordinates | |
| Ratio of heat capacities | |
| Greek Symbols | |
| Coefficients of Thermal expansions | |
| k | Horizontal Wave Number |
| Perturbation Parameter | |
| Effective Thermal Diffusivity | |
| Frequency of Modulation | |
| Rotational Speed Vector (0,0,) | |
| Dynamic Viscosity of the Fluid | |
| Kinetic Viscosity | |
| Fluid Density | |
| Stream Function | |
| Scaled time | |
| porosity | |
| Heat capacity ratio | |
| Viscoelastic constant of Walter B liquid | |
| Elastic parameter, | |
| Subscripts | |
| b | Basic state |
| 0 | Critical |
| * | Non-dimensional value |
| Superscripts | |
| perturbed quantity | |
References
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media, 1st ed.; Pergamon: Oxford, UK, 1998. [Google Scholar]
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media, 3rd ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Vafai, K. (Ed.) Handbook of Porous Media; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Vafai, K. (Ed.) Handbook of Porous Media, 2nd ed.; Taylor and Francis (CRC): Boca Raton, FL, USA, 2005. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Beg, O.A.; Makinde, O.D. Viscoelastic flow and species transfer in a Darcian high-permeability channel. J. Pet. Sci. Eng. 2011, 76, 93–99. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Basavaraja, D. The effect of thermal/gravity modulation on the onset of convection in a horizontal anisotropic porous layer. Int. J. Appl. Mech. Eng. 2003, 8, 425–439. [Google Scholar]
- Shivakumara, I.S.; Nanjundappa, C.E.; Chavaraddi, K.B. Darcy-Benard-Marangoni convection in porous media. Int. J. Heat Mass Transf. 2009, 52, 2815–2823. [Google Scholar] [CrossRef]
- Shivakumara, I.S.; Malashetty, M.S.; Chavaraddi, K.B. Onset of convection in a viscoelastic-fluid-saturated sparsely packed porous layer using a thermal nonequilibrium model. Can. J. Phys. 2006, 84, 973–990. [Google Scholar] [CrossRef]
- Postelnicu, A. Thermal Hydrodynamic Instability of a Walters B Viscoelastic Fluid in a Fluid-Saturated Anisotropic Porous Medium with Fast Chemical Reaction; Eurotherm Seminar Reactive Heat Transfer in Porous Media: Ecole des Mines d’Albi, France, 2007; pp. 1–8. [Google Scholar]
- Shivakumara, I.S.; Sureshkumar, S. Convective instabilities in a viscoelastic-fluid-saturated porous medium with throughflow. J. Geophys. Eng. 2007, 4, 104–115. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Swamy, M.S.; Sidram, W. Thermal convection in a rotating viscoelastic fluid saturated porous layer. Int. J. Heat Mass Transf. 2010, 53, 5747–5756. [Google Scholar] [CrossRef]
- Bénard, H. Les tourbillions cellulaires dans une nappe liquide transportant de la chaleur par convection en régime permanent. Annal. Chim. Phys. 1901, 23, 62–144. [Google Scholar]
- Taylor, G.I. Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 1917, 93, 99–113. [Google Scholar]
- Taylor, G.I. Experiments with rotating fluids. Proc. R. Soc. Lond. A 1921, 100, 114–121. [Google Scholar]
- Taylor, G.I. The motion of a sphere in a rotating liquid. Proc. R. Soc. Lond. A 1922, 102, 180–189. [Google Scholar]
- Donnelly, R.J. Experiments on the stability of viscous flow between rotating cylinders enhancement of stability by modulation. Proc. R. Soc. Lond. A 1964, 281, 130–139. [Google Scholar]
- Rauscher, J.W.; Kelly, R.E. Effect of modulation on the onset of thermal convection in a rotating fluid. Int. J. Heat Mass Transf. 1975, 18, 1216–1217. [Google Scholar] [CrossRef]
- Ahlers, G.; Hohenberg, P.C.; Lucke, M. Thermal convection under external modulation of the driving force. I. The Lorenz model. Phys. Rev. A 1985, 32, 3493–3518. [Google Scholar] [CrossRef] [PubMed]
- Niemela, J.J.; Donnelly, R.J. Direct transition to turbulence in rotating Bénard convection. Phys. Rev. Lett. 1986, 57, 2524–2527. [Google Scholar] [CrossRef] [PubMed]
- Walsh, T.J.; Donnelly, R.J. Taylor-Couette flow with periodically corotated and counterrotated cylinders. Phys. Rev. Let. 1988, 60, 700–703. [Google Scholar] [CrossRef] [PubMed]
- Bhadauria, B.S.; Kiran, P. Effect of rotational speed modulation on heat transport in a fluid layer with temperature dependent viscosity and internal heat source. J. Ain Shams Eng. 2014, 5, 1287–1297. [Google Scholar] [CrossRef]
- Gupta, V.K.; Kumar, A.; Singh, A.K. Analytical study of weakly nonlinear mass transfer in rotating fluid layer under time-periodic concentration/gravity modulation. Int. J. Non-Linear Mech. 2017, 97, 22–29. [Google Scholar] [CrossRef]
- Gupta, V.K. Study of mass transport in rotating couple stress liquid under concentration modulation. Chin. J. Phys. 2018, 56, 911–921. [Google Scholar] [CrossRef]
- Drury, J.A.; Murphy, S.J.; Derekas, A.; Sódor, A.; Stello, D.; Kuehn, C.A.; Bedding, T.R.; Bognár, Z.; Szigetr, L.; Szakáts, R.; et al. Large amplitude change in spot-induced rotational modulation of the kepler ap star kic2569073. Mon. Not. R. Astron. Soc. Sol. Stellar Astrophys. 2017, 471, 3193–3199. [Google Scholar] [CrossRef]
- Bowman, D.M.; Buysschaert, B.; Neiner, C.; Pápics, P.I.; Oksala, M.E.; Aerts, C. K2 space photometry reveals rotational modulation and stellar pulsations in chemically peculiar a and b stars. Astron. Astrophys. 2018, 616, 1–40. [Google Scholar] [CrossRef]
- Keshri, O.P.; Kumar, A.; Gupta, V.K. Magento-solutal convection in Newtonian fluid layer with solutal modulated boundaries. Int. J. Non-Linear Mech. 2018, 107, 86–93. [Google Scholar] [CrossRef]
- Keshri, O.P.; Kumar, A.; Gupta, V.K. Effect of internal heat Source on magnetostationary convection of couple stress fluid under magnetic field modulation. Chin. J. Phys. 2019, 57, 105–115. [Google Scholar] [CrossRef]
- Keshri, O.P.; Gupta, V.K.; Kumar, A. Study of weakly nonlinear mass transport in Newtonian fluid with applied magnetic field under concentration/gravity modulation. Nonlinear Engg. 2019, 8, 513–522. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, V.K. Study of heat and mass transport in couple stress liquid under G-gitter effect. Ain Shams Eng. J. 2018, 9, 973–984. [Google Scholar] [CrossRef]
- Jeong, H.G.; Joon, K.B.; Sukyoon, L.; Bin, K.S.; Tackeun, K.; Hee-Joon, B.; Seung, B.J.; O-Ki, K.; Wan, O.C.; MOON-KU, H. Therapeutic temperature modulation against penumbral tissue loss in ischemic stroke. Crit. Care Med. 2020, 48, 353. [Google Scholar] [CrossRef]
- Tahir, M.; Riaz, S.; Hussain, S.S.; Awan, A.; Xu, Y.B.; Naseem, S. Solvent mediated phase stability and temperature dependent magnetic modulation in BiFeO3 nanoparticles. J. Magn. Magn. Mater. 2020, 503, 166563. [Google Scholar] [CrossRef]
- Saravanan, S.; Kousalya, M. On the onset of gravity modulated filtration convection in grade fluids via Mathieu functions. ASME J. Heat Transf. 2020, 142, 092701. [Google Scholar] [CrossRef]
- Roth, S.; Zander, I.; Michelson, Y.; Ben-David, Y.; Banin, E.; Danielli, A. Identification of protein-protein interactions using a magnetic modulation biosensing system. Sens. Actuators B Chem. 2020, 303, 127228. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Seth, G.S.; Kumar, R.; Chamkha, A.J. Simulation of Cattaneo—Christov heat flux on the flow of single and multi-walled carbon nanotubes between two stretchable coaxial rotating disks. J. Therm. Anal. Calorim. 2020, 139, 1655–1670. [Google Scholar] [CrossRef]
- Tayebi, T.; Chamkha, A.J. Entropy generation analysis during MHD natural convection flow of hybrid nanofluid in a square cavity containing a corrugated conducting block. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1115–1136. [Google Scholar] [CrossRef]
- Herbert, D.M. On the stability of viscoelastic liquids in heated plane Couette flow. J. Fluid Mech. 1963, 17, 353–359. [Google Scholar] [CrossRef]
- Vest, C.M.; Arpaci, V.S. Overstability of a viscoelastic fluid layer heated from below. J. Fluid Mech. 1969, 36, 613–623. [Google Scholar] [CrossRef]
- Bhatnagar, K.; Giesekus, H. On the stability of viscoelastic fluid flow—II. Rheol. Acta 1970, 9, 53–60. [Google Scholar] [CrossRef]
- Comissiong, D.M.G.; Dass, T.D.; Ramkissoon, H.; Sankar, A.R. On thermal instabilities in a viscoelastic fluid subject to internal heat generation. Int. J. Math. Comput. Sci. 2011, 56, 826–833. [Google Scholar]
- Shivakumara, S.; Lee, J.; Malashetty, M.S.; Sureshkumar, S. Effect of thermal modulation on the onset of convection in walters-B viscoelastic fluid-saturated porous medium. Trans. Porous Media 2011, 87, 291–307. [Google Scholar] [CrossRef]
- Sheu, L.J. Linear stability of convection in a viscoelastic nanofluid layer, World Academy of Science. Eng. Technol. 2011, 58, 10–22. [Google Scholar]
- Rajib, B.; Layek, G.C. The onset of thermo convection in a horizontal viscoelastic fluid layer heated underneath. Therm. Energy Power Eng. 2012, 1, 1–9. [Google Scholar]
- Bhadauria, B.S.; Kiran, P. Weak nonlinear oscillatory convection in a viscoelastic fluid layer under gravity modulation. Int. J. Nonlinear Mech. 2014, 65, 133–140. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Kiran, P. Weakly nonlinear oscillatory convection in a viscoelastic fluid saturating porous medium under temperature modulation. Int. J. Heat Mass Transf. 2014, 77, 843–851. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Kiran, P. Weak nonlinear oscillatory convection in a viscoelastic fluid-saturated porous medium under gravity modulation. Trans. Porous Media 2014, 104, 451–467. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Kiran, P. Chaotic and oscillatory magneto-convection in a binary viscoelastic fluid under G-jitter. Int. J. Heat Mass Transf. 2015, 84, 610–624. [Google Scholar] [CrossRef]
- Bhadauria, B.S. Chaotic convection in a viscoelastic fluid saturated porous medium with a heat source. J. Appl. Math. 2016, 1487616. [Google Scholar] [CrossRef]
- Landau, L.D. On the problem of turbulence. Dokl. Akad. Nauk SSSR 1944, 44, 339–349. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Stuart, J.T. On the nonlinear mechanics of hydrodynamic stability. J. Fluid Mech. 1958, 4, 1–21. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics-Part (2); Pergamon Press Ltd.: Oxford, UK, 1969. [Google Scholar]
- Vadasz, P. Heat transfer and fluid flow in rotating porous media. Dev. Water Sci. 2002, 47, 469–476. [Google Scholar]
- Gupta, V.K.; Bhadauria, B.S.; Hashim, I.; Jawdat, J.; Singh, A.K. Chaotic convection in rotating fluid layer. Alex. Eng. J. 2015, 54, 981–992. [Google Scholar] [CrossRef]
- Lapwood, E.R. Convection of a fluid in a porous medium. Mathe. Proc. Camb. Philos. Soc. 1948, 44, 508–521. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).