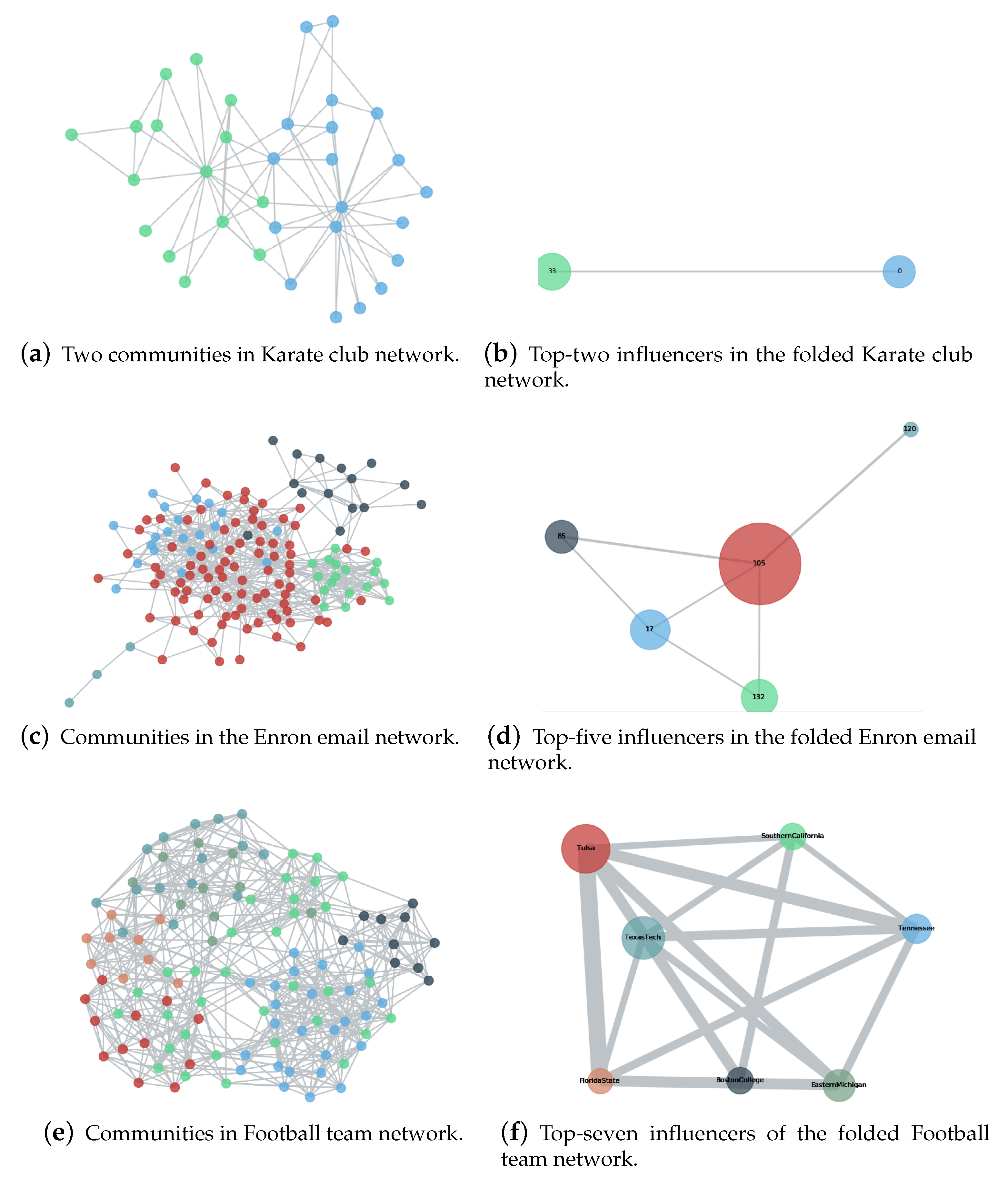
Figure 1.
Illustration of the proposed Maximum Influential Neighbors Expansion (MINE) algorithm. Communities in three real-world networks (i.e., Karate Club network [
62], Enron email network [
63] and College Football Team network [
64]) are presented in the left three panels the and top-ranking nodes are highlighted in the right three panels, which suggests that the MINE algorithm aims to identifying vital nodes hierarchically.
Figure 1.
Illustration of the proposed Maximum Influential Neighbors Expansion (MINE) algorithm. Communities in three real-world networks (i.e., Karate Club network [
62], Enron email network [
63] and College Football Team network [
64]) are presented in the left three panels the and top-ranking nodes are highlighted in the right three panels, which suggests that the MINE algorithm aims to identifying vital nodes hierarchically.
Figure 2.
The comparison of varying subgraphs with the removal of the most influential nodes repeatedly with each centrality method on 16 monolayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the BC and LGR methods by obtaining more subgraphs in the removal process.
Figure 2.
The comparison of varying subgraphs with the removal of the most influential nodes repeatedly with each centrality method on 16 monolayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the BC and LGR methods by obtaining more subgraphs in the removal process.
Figure 3.
The comparison of varying subgraphs with the removal of the most influential nodes repeatedly with each centrality method on 16 multilayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the BC and LGR methods on the majority of datasets except for HepatitusCVirus, while it is close to the performance of the LGR method (marked with green squares).
Figure 3.
The comparison of varying subgraphs with the removal of the most influential nodes repeatedly with each centrality method on 16 multilayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the BC and LGR methods on the majority of datasets except for HepatitusCVirus, while it is close to the performance of the LGR method (marked with green squares).
Figure 4.
The comparison of recovered nodes with varying k (from 0 to 20 percent of total nodes) on 16 monolayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the competitors on Polbooks, Enron, NS, DMLC, Game of Thrones and Power datasets. While on the Jazz dataset, the MINE algorithm is second to BC (marked with orange circles) when k is in the range of , while MINE achieves more recovered nodes (averaged 52.9888) than that of BC (averaged 52.5331) when k is set as 38 (i.e., twenty percent of the number of nodes in the Jazz dataset).
Figure 4.
The comparison of recovered nodes with varying k (from 0 to 20 percent of total nodes) on 16 monolayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the competitors on Polbooks, Enron, NS, DMLC, Game of Thrones and Power datasets. While on the Jazz dataset, the MINE algorithm is second to BC (marked with orange circles) when k is in the range of , while MINE achieves more recovered nodes (averaged 52.9888) than that of BC (averaged 52.5331) when k is set as 38 (i.e., twenty percent of the number of nodes in the Jazz dataset).
Figure 5.
The comparison of recovered nodes with varying k (from 0 to 20 percent of total nodes) on 16 multilayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the competitors on BOS, Candida, C.Elegans, DanioRerio, Gallus, HumanHerpes4, LondonTransport, Oryctolagus, Plasmodium, PierreAuger, Rattus and Xenopus datasets, while on the EUAirTransportation dataset, the MINE algorithm is second to INF (marked with purple diamonds).
Figure 5.
The comparison of recovered nodes with varying k (from 0 to 20 percent of total nodes) on 16 multilayer networks. The proposed MINE algorithm (marked with blue triangles) shows superiority to the competitors on BOS, Candida, C.Elegans, DanioRerio, Gallus, HumanHerpes4, LondonTransport, Oryctolagus, Plasmodium, PierreAuger, Rattus and Xenopus datasets, while on the EUAirTransportation dataset, the MINE algorithm is second to INF (marked with purple diamonds).
Figure 6.
Comparisons of accumulated execution time by performing the competitive measures on the grouped datasets.
Figure 6.
Comparisons of accumulated execution time by performing the competitive measures on the grouped datasets.
Figure 7.
The vital provinces of China measured by the proposed MINE algorithm, where Inner Mongolia, Sichuan, Zhejiang and Guangdong hold more importance in the graph of the adjacencies (formed by 34 vertices and 73 edges). By performing with the proposed MINE algorithm, we can find that Inner Mongolia holds the maximum importance in the derived network model, which may result from its huge span in longitude () and adjacencies to eight other provinces, i.e., Gansu, Ningxia, Shaanxi, Shanxi, Hebei, Liaoning, Jilin and Heilongjiang. Zhejiang is the second influential province measured by the MINE algorithm, which suggests its vital position in the southeast of China.
Figure 7.
The vital provinces of China measured by the proposed MINE algorithm, where Inner Mongolia, Sichuan, Zhejiang and Guangdong hold more importance in the graph of the adjacencies (formed by 34 vertices and 73 edges). By performing with the proposed MINE algorithm, we can find that Inner Mongolia holds the maximum importance in the derived network model, which may result from its huge span in longitude () and adjacencies to eight other provinces, i.e., Gansu, Ningxia, Shaanxi, Shanxi, Hebei, Liaoning, Jilin and Heilongjiang. Zhejiang is the second influential province measured by the MINE algorithm, which suggests its vital position in the southeast of China.
Figure 8.
The influence of the lower 48 United States is measured by the proposed MINE algorithm based on the graph of adjacencies (formed by 48 vertices and 104 edges). By performing with MINE algorithm, Missouri (with maximum importance which is same to the conclusion of Meghanathan’s research), following by Massachusetts and Idaho (also pointed out by Meghanathan as a vital state) are identified as the top-3 vital states, which are respectively located in the middle, east and west of the lower 48 United States. By activating the top-3 nodes and their neighbors in the graph of adjacencies, we are able to get a maximum collection of activated states that covers the majority of the United States, which are probably to exert strong influence.
Figure 8.
The influence of the lower 48 United States is measured by the proposed MINE algorithm based on the graph of adjacencies (formed by 48 vertices and 104 edges). By performing with MINE algorithm, Missouri (with maximum importance which is same to the conclusion of Meghanathan’s research), following by Massachusetts and Idaho (also pointed out by Meghanathan as a vital state) are identified as the top-3 vital states, which are respectively located in the middle, east and west of the lower 48 United States. By activating the top-3 nodes and their neighbors in the graph of adjacencies, we are able to get a maximum collection of activated states that covers the majority of the United States, which are probably to exert strong influence.
Table 1.
A brief comparison of node centrality measures.
Table 1.
A brief comparison of node centrality measures.
| Metric | Equation | Topology | Complexity |
|---|
| DC [22] | | Local | |
| BC [23] | | Global | |
| CC [24] | | Global | |
| EC [25] | | Global | |
| PR [26] | | Global | |
| H-index [27] | | Semi-local | |
| k-core [28] | s.t. | Global | |
| LR [34] | | Global | |
| GR, GR+ [29] | , | Global | |
| LGR [30] | | Semi-local | |
| INF [33] | | Local | |
Table 2.
Statistics of 16 monolayer network datasets that are utilized in this paper.
Table 2.
Statistics of 16 monolayer network datasets that are utilized in this paper.
| Dataset Name | | |E| | <k> | <d> | <C> | r | |H| | |
|---|
| Club [62] | 34 | 78 | 4.5882 | 2.4082 | 0.5706 | –0.4756 | 1.6933 | 0.1477 |
| Dolphins [65] | 62 | 159 | 5.1290 | 3.3570 | 0.2590 | –0.0436 | 1.3268 | 0.1723 |
| 911 [66] | 69 | 159 | 4.6087 | 2.4672 | 0.4698 | –0.0380 | 1.7304 | 0.1434 |
| Lesmis [67] | 77 | 254 | 6.5974 | 2.6411 | 0.5731 | –0.1652 | 1.8273 | 0.0905 |
| Voles [63] | 89 | 143 | 3.2135 | 0.5610 | 0.6083 | 0.2877 | 1.3340 | 0.3043 |
| Escherichia [68] | 97 | 212 | 4.3711 | 5.5369 | 0.3675 | 0.4116 | 1.2367 | 0.2270 |
| Polbooks [69] | 105 | 441 | 8.4000 | 3.0788 | 0.4875 | –0.1279 | 1.4207 | 0.0915 |
| Football [64] | 115 | 613 | 10.6609 | 2.5082 | 0.4032 | 0.1624 | 1.0069 | 0.1027 |
| Enron [63] | 143 | 623 | 8.7133 | 2.9670 | 0.4339 | –0.0195 | 1.4829 | 0.0839 |
| NEUSNCP [70] | 167 | 465 | 5.5689 | 2.8810 | 0.3122 | –0.3619 | 3.3624 | 0.0564 |
| Jazz [71] | 198 | 2742 | 27.6970 | 2.2350 | 0.6175 | 0.0202 | 1.3951 | 0.0266 |
| USAir [72] | 332 | 2126 | 12.8072 | 2.7381 | 0.6252 | –0.2079 | 3.4639 | 0.0231 |
| NS [73] | 379 | 914 | 4.8232 | 6.0419 | 0.7412 | –0.0817 | 1.6630 | 0.1424 |
| DMLC [74] | 659 | 1570 | 4.7648 | 2.6370 | 0.3279 | –0.1914 | 14.8897 | 0.0143 |
| Game of Thrones [75] | 796 | 2823 | 7.0930 | 3.4162 | 0.4859 | –0.1154 | 4.1941 | 0.0348 |
| Power [69] | 4941 | 6594 | 2.6691 | 18.9892 | 0.0801 | 0.0035 | 1.4504 | 0.3483 |
Table 3.
Statistics of 16 multilayer datasets that are utilized in this paper.
Table 3.
Statistics of 16 multilayer datasets that are utilized in this paper.
| Dataset Name | | | |E| | || | || | <k> | <d> | <C> | |
|---|
| Padgett [76] | 2 | 26 | 46 | 35 | 11 | 3.5385 | 2.6923 | 1.1550 | 0.3239 |
| HepatitusCVirus [77] | 3 | 129 | 152 | 125 | 27 | 2.3566 | 2.3582 | 12.4008 | 0.0354 |
| Oryctolagus [77] | 3 | 151 | 145 | 138 | 7 | 1.9205 | 0.5642 | 11.7317 | 0.0464 |
| LondonTransport [78] | 3 | 399 | 472 | 441 | 31 | 2.3659 | 14.2989 | 1.1597 | 0.5735 |
| CKM [79] | 3 | 674 | 2005 | 1370 | 635 | 5.9496 | 1.1677 | 1.1879 | 0.1648 |
| C.Elegans [80] | 3 | 791 | 3857 | 3108 | 749 | 9.7522 | 3.5346 | 1.6895 | 0.0646 |
| Plasmodium [81] | 3 | 1206 | 2489 | 2486 | 3 | 4.1277 | 3.9403 | 2.9832 | 0.0884 |
| HumanHerpes4 [77] | 4 | 261 | 299 | 241 | 58 | 2.2912 | 2.9561 | 18.5515 | 0.0241 |
| BOS [81] | 4 | 369 | 360 | 311 | 49 | 1.9512 | 0.4116 | 2.0429 | 0.3349 |
| DanioRerio [77] | 5 | 180 | 206 | 173 | 33 | 2.2889 | 0.3325 | 1.6161 | 0.3705 |
| Xenopus [77] | 5 | 582 | 710 | 568 | 142 | 2.4399 | 2.8018 | 2.0464 | 0.2504 |
| Gallus [81] | 6 | 367 | 411 | 348 | 63 | 2.2398 | 1.277 | 12.5034 | 0.0370 |
| Rattus [81] | 6 | 3263 | 4670 | 3956 | 714 | 2.8624 | 3.9011 | 30.0001 | 0.0118 |
| Candida [81] | 7 | 418 | 446 | 386 | 60 | 2.1340 | 2.1034 | 28.0935 | 0.0170 |
| PierreAuger [82] | 16 | 965 | 8022 | 7153 | 869 | 16.6259 | 4.8105 | 2.8617 | 0.0215 |
| EUAirTransportation [83] | 37 | 2034 | 15199 | 3588 | 11611 | 14.9449 | 3.5087 | 1.6187 | 0.0431 |
Table 4.
Runtime comparison of DC, BC, CC, LGR, INF and MINE on 32 real-world datasets.
Table 4.
Runtime comparison of DC, BC, CC, LGR, INF and MINE on 32 real-world datasets.
| Network | DC | BC | CC | LGR | INF | MINE |
|---|
| Club | < | < | < | < | < | < |
| Dolphins | < | < | 0.0156 | 0.0156 | < | 0.0156 |
| 911 | < | 0.0156 | < | < | < | 0.0156 |
| Lesmis | < | 0.0156 | 0.0156 | < | < | 0.0156 |
| Voles | < | < | < | < | 0.0156 | 0.0156 |
| Escherichia | < | 0.0312 | 0.0156 | < | < | 0.0156 |
| Polbooks | < | 0.0469 | 0.0312 | < | 0.0156 | 0.0156 |
| Football | < | 0.0469 | 0.0469 | < | 0.0312 | 0.0312 |
| Enron | < | 0.0625 | 0.0469 | < | 0.0156 | 0.0312 |
| NEUSNCP | < | 0.0938 | 0.0625 | < | 0.0312 | 0.0156 |
| Jazz | < | 0.1719 | 0.2188 | < | 0.0781 | 0.3750 |
| USAir | < | 0.3594 | 0.4531 | 0.0156 | 0.0938 | 0.2188 |
| NS | < | 0.3438 | 0.3438 | 0.0156 | 0.0156 | 0.0625 |
| DMLC | < | 1.0312 | 0.9219 | < | 0.4219 | 0.7656 |
| Game of Thrones | < | 1.8750 | 1.5312 | 0.0156 | 0.2344 | 0.4219 |
| Power | < | 73.8594 | 48.2344 | 0.0156 | 0.1562 | 21.9531 |
| Padgett | < | < | < | < | < | < |
| HepatitusCVirus | < | 0.0312 | 0.0312 | < | 0.0156 | 0.0156 |
| Oryctolagus | < | 0.0156 | < | < | 0.0156 | 0.0156 |
| LondonTransport | < | 0.4219 | 0.2969 | < | < | 0.2031 |
| CKM | < | 0.4844 | 0.3281 | < | 0.0469 | 0.4219 |
| C.Elegans | < | 2.0000 | 1.9219 | 0.0156 | 0.1406 | 0.7500 |
| Plasmodium | < | 3.8281 | 2.7812 | < | 0.1562 | 1.5625 |
| HumanHerpes4 | < | 0.0938 | 0.0781 | < | 0.0469 | 0.0312 |
| BOS | < | 0.0469 | 0.0156 | < | 0.0156 | 0.1094 |
| DanioRerio | < | 0.0156 | 0.0156 | < | < | 0.0312 |
| Xenopus | < | 0.3750 | 0.2969 | < | 0.0156 | 0.4375 |
| Gallus | < | 0.1094 | 0.0938 | < | 0.0469 | 0.1094 |
| Rattus | 0.0156 | 24.4375 | 17.9062 | < | 1.5000 | 9.8750 |
| Candida | < | 0.2500 | 0.1719 | < | 0.0938 | 0.1250 |
| PierreAuger | < | 3.0312 | 3.3438 | 0.0156 | 0.1719 | 0.9375 |
| EUAirTransportation | < | 19.7656 | 18.7344 | 0.0312 | 0.7500 | 3.4062 |
Table 5.
Comparison of provinces of China, measured by DC, BC, CC, LGR, INF and MINE.
Table 5.
Comparison of provinces of China, measured by DC, BC, CC, LGR, INF and MINE.
| Province | DC | BC | CC | LGR | INF | MINE |
|---|
| Inner Mongolia | 0.2424 | 0.1823 | 0.3793 | 366.0000 | 2.1845 | 11.2417 |
| Shaanxi | 0.2424 | 0.2438 | 0.4400 | 474.0000 | 1.5512 | 1.5512 |
| Hebei | 0.2121 | 0.1733 | 0.3626 | 269.5000 | 2.1250 | 2.1250 |
| Sichuan | 0.2121 | 0.1170 | 0.3708 | 322.0000 | 1.4417 | 7.8988 |
| Guangdong | 0.2121 | 0.2065 | 0.3474 | 231.0000 | 2.8333 | 4.2619 |
| Gansu | 0.1818 | 0.0914 | 0.3667 | 271.5000 | 1.3095 | 1.3095 |
| Henan | 0.1818 | 0.1291 | 0.4177 | 295.5000 | 1.1012 | 1.1012 |
| Hubei | 0.1818 | 0.1856 | 0.4459 | 324.0000 | 0.9917 | 0.9917 |
| Anhui | 0.1818 | 0.1112 | 0.3882 | 250.5000 | 1.2000 | 1.2000 |
| Jiangxi | 0.1818 | 0.1658 | 0.3976 | 270.0000 | 1.0929 | 1.0929 |
| Hunan | 0.1818 | 0.1204 | 0.3976 | 265.5000 | 1.1262 | 1.1262 |
| Chongqing | 0.1515 | 0.0611 | 0.4074 | 237.5000 | 0.8012 | 0.8012 |
| Guizhou | 0.1515 | 0.0326 | 0.3511 | 181.2500 | 1.0095 | 1.0095 |
| Zhejiang | 0.1515 | 0.0589 | 0.3267 | 147.5000 | 1.3333 | 10.5976 |
| Shanxi | 0.1212 | 0.0119 | 0.3626 | 165.0000 | 0.5595 | 0.5595 |
| Shandong | 0.1212 | 0.0665 | 0.3626 | 138.0000 | 0.7262 | 0.7262 |
| Qinghai | 0.1212 | 0.0059 | 0.3028 | 113.0000 | 0.8929 | 0.8929 |
| Jiangsu | 0.1212 | 0.0342 | 0.3173 | 97.0000 | 1.1167 | 1.1167 |
| Yunnan | 0.1212 | 0.0431 | 0.3300 | 119.0000 | 0.8429 | 0.8429 |
| Tibet | 0.1212 | 0.0195 | 0.3000 | 100.0000 | 0.9762 | 0.9762 |
| Fujian | 0.1212 | 0.0737 | 0.3204 | 109.0000 | 1.5095 | 1.5095 |
| Guangxi | 0.1212 | 0.0588 | 0.3333 | 125.0000 | 0.7595 | 0.7595 |
| Jilin | 0.0909 | 0.0009 | 0.2821 | 60.0000 | 0.9583 | 0.9583 |
| Liaoning | 0.0909 | 0.0073 | 0.3028 | 81.7500 | 0.6012 | 0.6012 |
| Ningxia | 0.0909 | 0.0000 | 0.3402 | 103.5000 | 0.4167 | 0.4167 |
| Xinjiang | 0.0909 | 0.0039 | 0.2920 | 64.5000 | 0.6667 | 0.6667 |
| Heilongjiang | 0.0606 | 0.0000 | 0.2797 | 37.5000 | 0.4583 | 0.4583 |
| Beijing | 0.0606 | 0.0000 | 0.2705 | 30.5000 | 0.6429 | 0.6429 |
| Tianjin | 0.0606 | 0.0000 | 0.2705 | 30.5000 | 0.6429 | 0.6429 |
| Shanghai | 0.0606 | 0.0000 | 0.2661 | 28.0000 | 0.4500 | 0.4500 |
| Hangkong | 0.0606 | 0.0000 | 0.2619 | 28.5000 | 0.6429 | 0.6429 |
| Macao | 0.0606 | 0.0000 | 0.2619 | 28.5000 | 0.6429 | 0.6429 |
| Taiwan | 0.0303 | 0.0000 | 0.2444 | 8.5000 | 0.2500 | 0.2500 |
| Hainan | 0.0303 | 0.0000 | 0.2598 | 13.0000 | 0.1429 | 0.1429 |
Table 6.
Comparison of the lower 48 United States, measured by DC, BC, CC, LGR, INF and MINE.
Table 6.
Comparison of the lower 48 United States, measured by DC, BC, CC, LGR, INF and MINE.
| State | DC | BC | CC | LGR | INF | MINE |
|---|
| Missouri | 0.1702 | 0.3703 | 0.3561 | 520.0000 | 1.4024 | 24.9286 |
| Kentucky | 0.1489 | 0.3437 | 0.3431 | 374.5000 | 1.3679 | 1.3679 |
| Tennessee | 0.1489 | 0.1862 | 0.3219 | 364.0000 | 1.3845 | 1.3845 |
| Idaho | 0.1277 | 0.0886 | 0.2271 | 198.0000 | 1.5667 | 7.0167 |
| Wyoming | 0.1277 | 0.1268 | 0.2717 | 273.0000 | 1.1167 | 1.1167 |
| Colorado | 0.1277 | 0.0658 | 0.2717 | 259.5000 | 1.2000 | 1.2000 |
| Nebraska | 0.1277 | 0.1606 | 0.3133 | 307.5000 | 1.0417 | 1.0417 |
| South Dakota | 0.1277 | 0.0590 | 0.2655 | 231.0000 | 1.3333 | 1.3333 |
| Oklahoma | 0.1277 | 0.1147 | 0.3032 | 271.5000 | 1.2083 | 1.2083 |
| Iowa | 0.1277 | 0.0820 | 0.3013 | 282.0000 | 1.1583 | 1.1583 |
| Arkansas | 0.1277 | 0.0733 | 0.2956 | 268.5000 | 1.2679 | 1.2679 |
| Pennsylvania | 0.1277 | 0.3018 | 0.2655 | 193.5000 | 1.5167 | 5.7690 |
| Nevada | 0.1064 | 0.0119 | 0.1992 | 137.5000 | 1.2000 | 1.2000 |
| Utah | 0.1064 | 0.0385 | 0.2327 | 183.7500 | 0.9500 | 0.9500 |
| Illinois | 0.1064 | 0.0451 | 0.3092 | 215.0000 | 0.9345 | 0.9345 |
| Ohio | 0.1064 | 0.1772 | 0.3032 | 178.7500 | 1.0929 | 1.0929 |
| West Virginia | 0.1064 | 0.1446 | 0.3013 | 182.5000 | 1.0095 | 1.0095 |
| Georgia | 0.1064 | 0.0380 | 0.2568 | 131.2500 | 1.6429 | 3.1857 |
| New York | 0.1064 | 0.2280 | 0.2238 | 127.5000 | 1.3667 | 1.3667 |
| Massachusetts | 0.1064 | 0.0634 | 0.1895 | 92.5000 | 1.7000 | 7.1000 |
| Oregon | 0.0851 | 0.0056 | 0.1918 | 83.0000 | 1.2000 | 1.2000 |
| Montana | 0.0851 | 0.0184 | 0.2293 | 122.0000 | 0.8333 | 0.8333 |
| Arizona | 0.0851 | 0.0481 | 0.2227 | 100.0000 | 0.9833 | 0.9833 |
| Kansas | 0.0851 | 0.0160 | 0.2956 | 160.0000 | 0.6250 | 0.6250 |
| New Mexico | 0.0851 | 0.0752 | 0.2582 | 126.0000 | 0.8333 | 0.8333 |
| Minnesota | 0.0851 | 0.0296 | 0.2655 | 108.0000 | 0.9167 | 0.9167 |
| Texas | 0.0851 | 0.0205 | 0.2527 | 109.0000 | 0.9167 | 0.9167 |
| Wisconsin | 0.0851 | 0.0475 | 0.2765 | 111.0000 | 0.9500 | 0.9500 |
| Mississippi | 0.0851 | 0.0148 | 0.2626 | 116.0000 | 0.8929 | 0.8929 |
| Indiana | 0.0851 | 0.0142 | 0.2883 | 120.0000 | 0.8762 | 0.8762 |
| Virginia | 0.0851 | 0.0581 | 0.2883 | 125.0000 | 0.8429 | 0.8429 |
| Alabama | 0.0851 | 0.0202 | 0.2527 | 102.0000 | 1.0929 | 1.0929 |
| North Carolina | 0.0851 | 0.0451 | 0.2733 | 112.0000 | 1.0929 | 1.0929 |
| Maryland | 0.0851 | 0.0334 | 0.2527 | 96.0000 | 0.9500 | 0.9500 |
| California | 0.0638 | 0.0031 | 0.1888 | 51.7500 | 0.7000 | 0.7000 |
| North Dakota | 0.0638 | 0.0046 | 0.2315 | 63.0000 | 0.6667 | 0.6667 |
| Louisiana | 0.0638 | 0.0032 | 0.2398 | 63.7500 | 0.6667 | 0.6667 |
| Michigan | 0.0638 | 0.0397 | 0.2626 | 63.7500 | 0.7000 | 0.7000 |
| Delaware | 0.0638 | 0.0017 | 0.2176 | 53.2500 | 0.7500 | 0.7500 |
| New Jersey | 0.0638 | 0.0032 | 0.2186 | 60.7500 | 0.7000 | 0.7000 |
| Vermont | 0.0638 | 0.0389 | 0.1880 | 50.2500 | 0.7333 | 0.7333 |
| Connecticut | 0.0638 | 0.0194 | 0.1873 | 47.2500 | 0.9000 | 0.9000 |
| New Hampshire | 0.0638 | 0.0426 | 0.1615 | 34.5000 | 1.5333 | 1.5333 |
| Washington | 0.0426 | 0.0000 | 0.1873 | 31.5000 | 0.4167 | 0.4167 |
| Florida | 0.0426 | 0.0000 | 0.2080 | 26.5000 | 0.4500 | 0.4500 |
| South Carolina | 0.0426 | 0.0000 | 0.2186 | 26.5000 | 0.4500 | 0.4500 |
| Rhode Island | 0.0426 | 0.0000 | 0.1604 | 21.5000 | 0.5333 | 0.5333 |
| Maine | 0.0213 | 0.0000 | 0.1395 | 5.0000 | 0.3333 | 0.3333 |