On S-Evolution Algebras and Their Enveloping Algebras
Abstract
1. Introduction
2. S-Evolution Algebras and Their Graphs
- (i)
- for all
- (ii)
- if and only if .
- 1.
- Assume that B is a symmetric matrix such that and for all . In this setting, one can see that ;
- 2.
- Assume that C is a skew-symmetric matrix such that , for all . It is clear that ;
- 3.
- Assume that M is a matrix such that , for all . In this setting, we have .
 |
- (i)
- solvable if there exists such that and the minimal such number is called index of solvability;
- (ii)
- right nilpotent if there exists such that and the minimal such number is called index of right nilpotency;
- (iii)
- nilpotent if there exists such that and the minimal such number is called index of nilpotency.
- (i)
- A graph , with and , is called the graph attached to the evolution algebra relative to the natural basis B.
- (ii)
- The triple , with and where ω is the map given by , is called the weighted graph attached to the S-evolution algebra relative to the natural basis B.
- (i)
- is simple.
- (ii)
- satisfies the following properties:
- (a)
- is non-degenerate.
- (b)
- .
- (c)
- is a non-zero ideal of A for a non-empty then
3. Some Properties of S-Evolution Algebras
 |
4. Enveloping Algebras Generated by S-Evolution Algebras
- (1)
- if is simple then for each
- (2)
- if is not simple then for each
- (3)
- if the sets contain linearly independent vectors then contains linearly independent vectors for any
- (i)
- vectors of are linearly independent;
- (ii)
- if is simple then for each the set is linearly independent;
- (iii)
- if is not simple then for each the set is linearly dependent.
- (i)
- if is simple then
- (ii)
- if is not simple and Thenwhere
- (i)
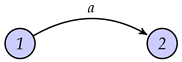
- If is simple then where is the number of edges in .
- (ii)
- If is not simple and Then
 |
 |
5. -Linear Derivation of Enveloping Algebras Generated by S-Evolution Algebras
- (i)
- If then
- (ii)
- If then , i.e., any -derivation is trivial.
6. -Linear Derivation of Enveloping Algebras Generated by Three Dimensional S-Evolution Algebras
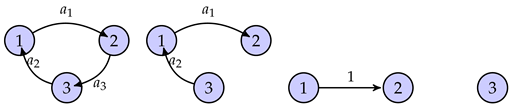 |
- (i)
- If the attached graph is a complete, then any -linear derivation is trivial.
- (ii)
- If the attached graph is disconnected, then any -linear derivation has the following form
- (iii)
- If the attached graph is connected, but not complete, then any -linear derivation has the following form
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Etherington, I.H. Genetic algebras. Proc. R. Soc. Edinb. 1940, 59, 242–258. [Google Scholar] [CrossRef]
- Reed, M. Algebraic structure of genetic inheritance. Bull. Am. Math. Soc. 1997, 34, 107–130. [Google Scholar] [CrossRef]
- Wörz-Busekros, A. Algebras in genetics. In Algebras in Genetics; Springer: Berlin/Heidelberg, Germany, 1980; pp. 5–16. [Google Scholar]
- Bernstein, S. Principe de stationnarité et géneralisation de la loi de Mendel. CR Acad. Sci. Paris 1923, 177, 581–584. [Google Scholar]
- Lyubich, Y.I. Mathematical Structures in Population Genetics; Biomathematics; Spinger: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Tian, J.; Li, B.-L. Coalgebraic structure of genetic inheritance. Math. Biosci. Eng. 2004, 1, 243. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.-P.; Vojtĕchovskỳ, P. Mathematical concepts of evolution algebras in non-mendelian genetics. Quasigroups Relat. Syst. 2006, 14, 111–122. [Google Scholar]
- Tian, J.P. Evolution Algebras and Their Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Becerra, J.; Beltrán, M.; Velasco, M.V. Pulse Processes in Networks and Evolution Algebras. Mathematics 2020, 8, 387. [Google Scholar] [CrossRef]
- Birky, C.W., Jr. The inheritance of genes in mitochondria and chloroplasts: Laws, mechanisms, and models. Annu. Rev. Genet. 2001, 35, 125–148. [Google Scholar] [CrossRef]
- Falcon, O.J.; Falcon, R.M.; Nunez, J. Classification of asexual diploid organisms by means of strongly isotopic evolution algebras defined over any field. J. Algebra 2017, 472, 573–593. [Google Scholar] [CrossRef]
- Ling, F.; Shibata, T. Mhr1p-dependent concatemeric mitochondrial dna formation for generating yeast mitochondrial homoplasmic cells. Mol. Biol. Cell 2004, 15, 310–322. [Google Scholar] [CrossRef]
- Rozikov, U.A.; Velasco, M.V. Discrete-time dynamical system and an evolution algebra of mosquito population. J. Math. Biol. 2019, 78, 1225–1244. [Google Scholar] [CrossRef]
- Bustamante, M.D.; Mellon, P.; Velasco, M.V. Determining when an algebra is an evolution algebra. Mathematics 2020, 8, 1349. [Google Scholar] [CrossRef]
- Cadavid, P.; Rodino Montoya, M.L.; Rodriguez, P.M. The connection between evolution algebras, random walks and graphs. J. Alg. Appl. 2020, 19, 2050023. [Google Scholar] [CrossRef]
- Cadavid, P.; Rodino Montoya, M.L.; Rodriguez, P.M. Characterization theorems for the spaces of derivations of evolution algebras associated to graphs. Linear Multilinear Algebra 2020, 68, 1340–1354. [Google Scholar] [CrossRef]
- Ceballos, M.; Nunez, J.; Tenorio, Á.F. Finite dimensional evolution algebras and (pseudo)digraphs. Math. Meth. Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Dzhumadil’daev, A.; Omirov, B.A.; Rozikov, U.A. Constrained evolution algebras and dynamical systems of a bisexual population. Linear Algebra Its Appl. 2016, 496, 351–380. [Google Scholar] [CrossRef]
- Elduque, A.; Labra, A. Evolution algebras and graphs. J. Algebra Appl. 2015, 14, 1550103. [Google Scholar] [CrossRef]
- Camacho, L.M.; Goméz, J.R.; Omirov, B.A.; Turdibaev, R.M. The derivations of some evolution algebras. Linear Multilinear Algebra 2013, 61, 309–322. [Google Scholar] [CrossRef]
- Casas, J.M.; Ladra, M.; Omirov, B.A.; Rozikov, U.A. On evolution algebras. Algebra Colloq. 2014, 21, 331–342. [Google Scholar] [CrossRef]
- Hegazi, A.S.; Abdelwahab, H. Nilpotent evolution algebras over arbitrary fields. Linear Algebra Appl. 2015, 486, 345–360. [Google Scholar] [CrossRef]
- Ladra, M.; Rozikov, U.A. Evolution algebra of a bisexual population. J. Algebra 2013, 378, 153–172. [Google Scholar] [CrossRef][Green Version]
- Omirov, B.; Rozikov, U.; Velasco, M.V. A class of nilpotent evolution algebras. Commun. Algebra 2019, 47, 1556–1567. [Google Scholar] [CrossRef]
- Casado, Y.C.; Molina, M.S.; Velasco, M.V. Evolution algebras of arbitrary dimension and their decompositions. Linear Algebra Appl. 2016, 495, 122–162. [Google Scholar] [CrossRef]
- Celorrio, M.E.; Velasco, M.V. Classifying evolution algebras of dimensions two and three. Mathematics 2019, 7, 1236. [Google Scholar] [CrossRef]
- Velasco, M.V. The Jacobson radical of an evolution algebra. J. Spectr. Theory 2019, 9, 601–634. [Google Scholar] [CrossRef]
- Gutierrez, J.C.; Garcia, C.I. On Lotka—Volterra algebras. J. Algebra Appl. 2019, 18, 1950187. [Google Scholar]
- Itoh, Y. Nonassociative algebra and Lotka—Volterra equation with ternary interaction. Nonlinear Anal. 1981, 5, 53–56. [Google Scholar] [CrossRef]
- Qaralleh, I.; Mukhamedov, F. Volterra evolution algebras and their graphs. Linear Multilinear Algebra 2019. [Google Scholar] [CrossRef]
- Ganikhodzhaev, R.; Mukhamedov, F.; Pirnapasov, A.; Qaralleh, I. On genetic Volterra algebras and their derivations. Commun. Algebra 2018, 46, 1353–1366. [Google Scholar] [CrossRef]
- Zhevlakov, K.A.; Slin’ko, A.M.; Shestakov, I.P.; Shirshov, A.I. Rings That Are Nearly Associative; Academic Press: London, UK, 1982. [Google Scholar]
- Mukhamedov, F.; Khakimov, O.; Qaralleh, I. Classification of nilpotent evolution algebras and extensions of their derivations. Commun. Algebra 2020, 48, 4155–4169. [Google Scholar] [CrossRef]
- Solan, E.; Vieille, N. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar]
- Casado, Y.C.; Cadavid, P.; Rodino Montoya, M.L.; Rodriguez, P.M. On the characterization of the space of derivations in evolution algebras. Ann. Mat. Pura Appl. 2021, 200, 737–755. [Google Scholar] [CrossRef]
- Desamparados, F.T.; Gómez-Sousa, V.M.; Núñez-Valdés, J. The evolution operator of evolution algebras. Linear Multilinear Algebra 2021. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Khakimov, F.; Omirov, B.; Qaralleh, I. Derivations and automorphisms of nilpotent evolution algebras with maximal nilindex. J. Algebra Appl. 2019, 18, 1950233. [Google Scholar] [CrossRef]
- Reis, T.; Cadavid, P. Derivations of evolution algebras associated to graphs over a field of any characteristic. Linear Multilinear Algebra 2020. [Google Scholar] [CrossRef]
- Arenasa, M.; Labra, A.; Paniello, I. Lotka—Volterra coalgebras. Linear Multilin. Alg. 2020. [Google Scholar] [CrossRef]
- Akin, E.; Losert, V. Evolutionary dynamics of zero-sum game. J. Math. Biol. 1984, 20, 231–258. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ganikhodzhaev, N.; Pah, C.H. Rock-Paper-Scissors lattice model. Malays. J. Fund. Appl. Sci. 2020, 16, 400–402. [Google Scholar] [CrossRef]
- Mukhamedov, F. On factor associated with the disordered phase of λ-model on a Cayley tree. Rep. Math. Phys. 2004, 53, 1–18. [Google Scholar] [CrossRef]
- Rozikov, U.A.; Tian, J.P. Evolution algebras generated by Gibbs measures. Lobachevskii J. Math. 2011, 32, 270–277. [Google Scholar] [CrossRef]
- Paniello, I. Markov evolution algebras. Linear Multilinear Algebra 2021. [Google Scholar] [CrossRef]
- Casado, Y.C.; Kanuni, M.; Molina, M.S. Basic ideals in evolution algebras. Linear Algebra Appl. 2019, 570, 148–180. [Google Scholar] [CrossRef]
- Drozd, Y.A.; Kirichenko, V.V. Finite Dimensional Algebras; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhamedov, F.; Qaralleh, I. On S-Evolution Algebras and Their Enveloping Algebras. Mathematics 2021, 9, 1195. https://doi.org/10.3390/math9111195
Mukhamedov F, Qaralleh I. On S-Evolution Algebras and Their Enveloping Algebras. Mathematics. 2021; 9(11):1195. https://doi.org/10.3390/math9111195
Chicago/Turabian StyleMukhamedov, Farrukh, and Izzat Qaralleh. 2021. "On S-Evolution Algebras and Their Enveloping Algebras" Mathematics 9, no. 11: 1195. https://doi.org/10.3390/math9111195
APA StyleMukhamedov, F., & Qaralleh, I. (2021). On S-Evolution Algebras and Their Enveloping Algebras. Mathematics, 9(11), 1195. https://doi.org/10.3390/math9111195






