The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five
Abstract
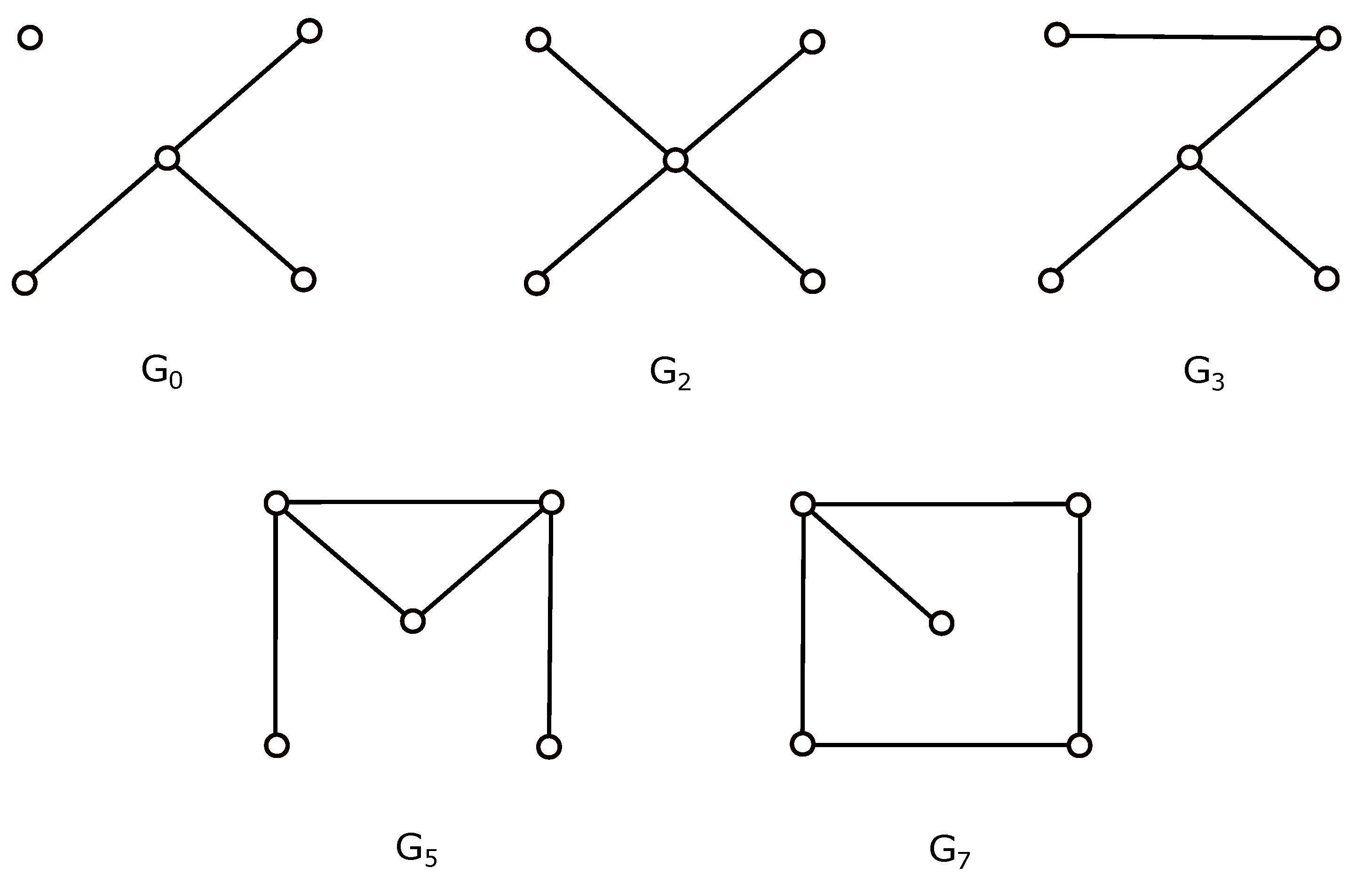
:1. Introduction
2. Cyclic Permutations and Possible Drawings of
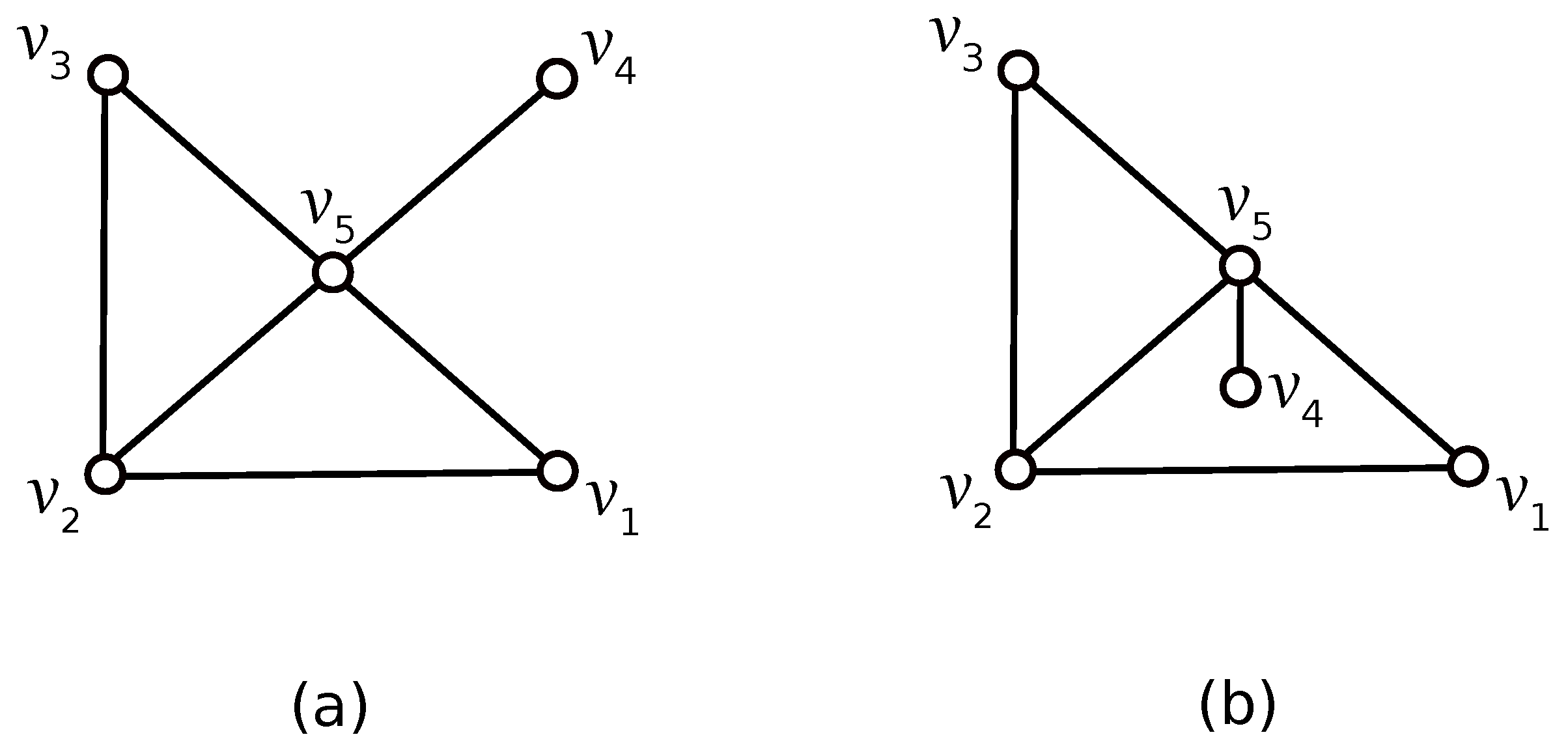
3. The Crossing Number of
4. The Crossing Number of
- (a)
- holds for any subgraph , ; and
- (b)
- holds for any subgraph , such that the edge of is not crossed by the edges of .
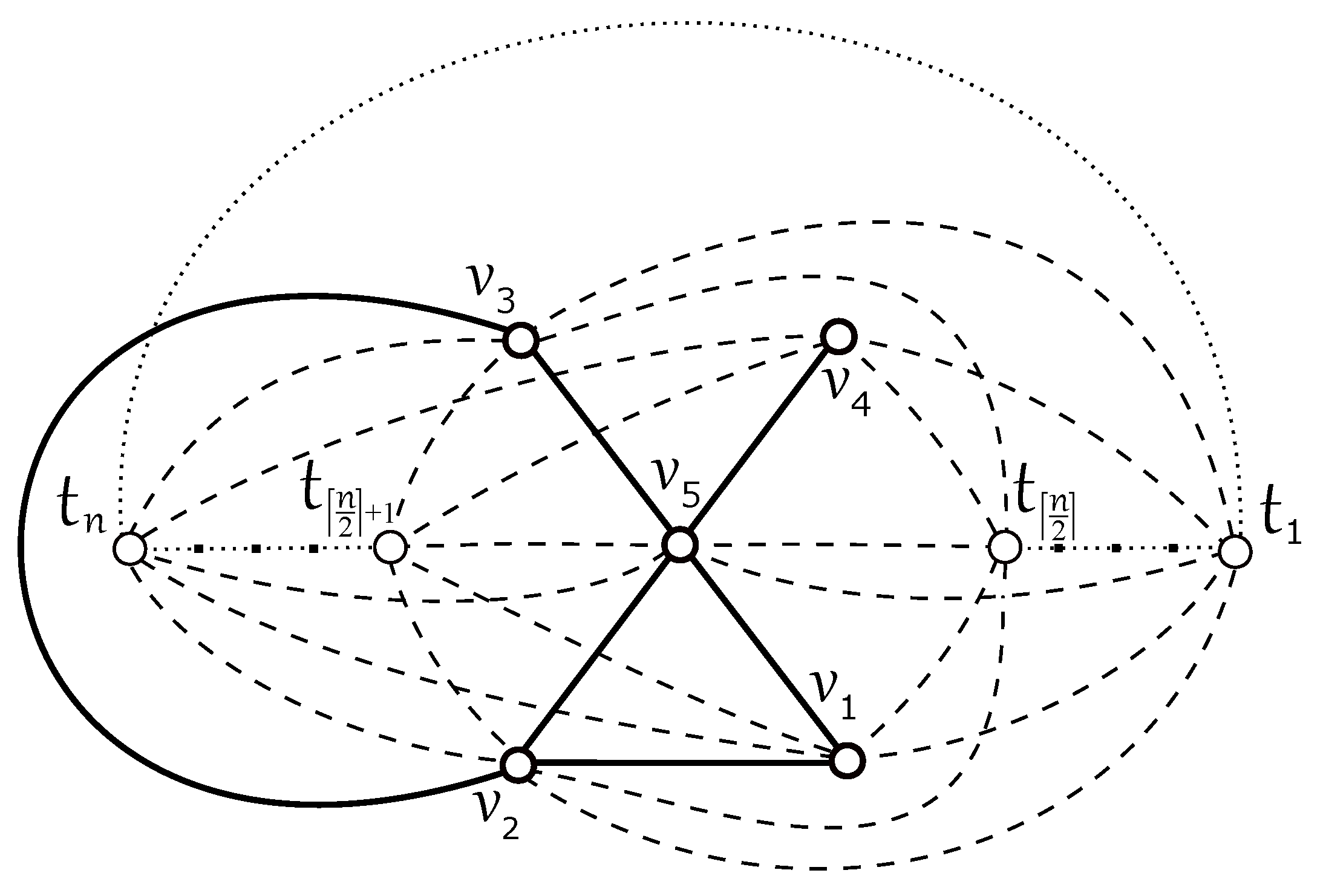
- (a)
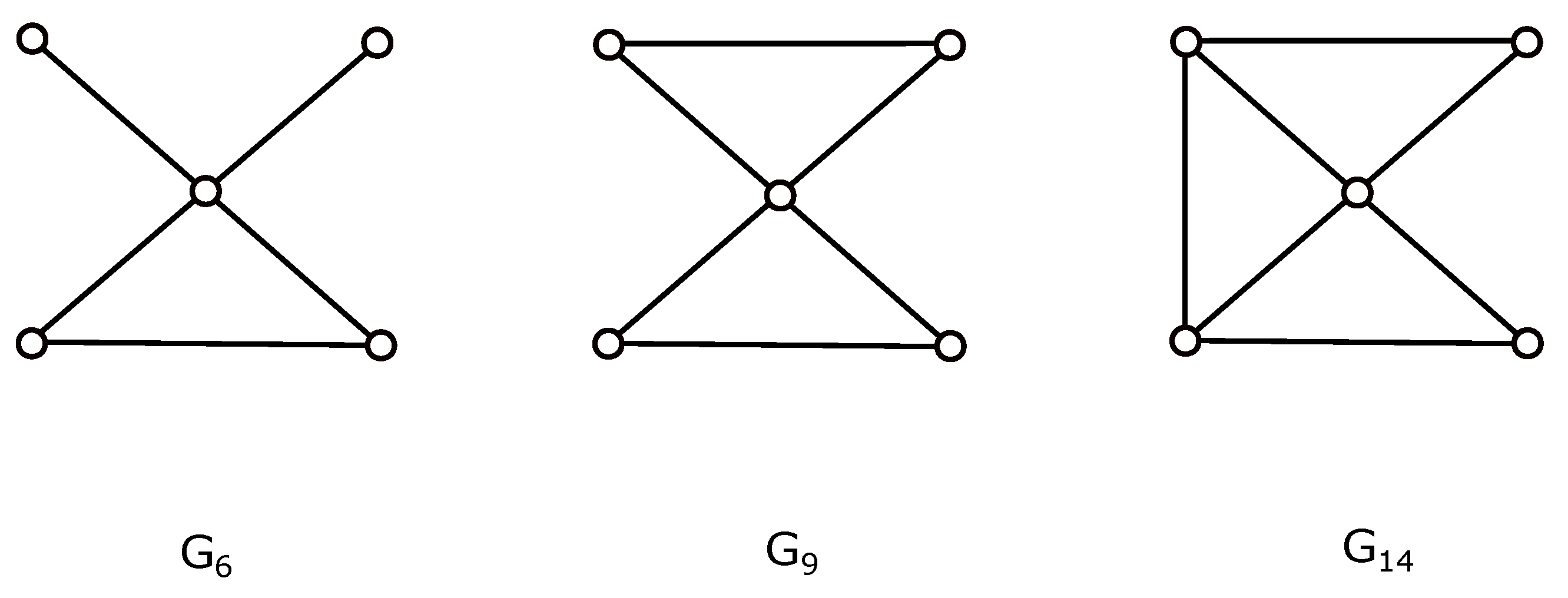
- Let be a subgraph with . If we suppose the drawing of subgraph as shown in Figure 4a, then . For with , the possible configurations and are uniquely represented by the cyclic permutations and , respectively. Using the distances between two cyclic permutations, we are able to determine the minimum numbers of crossings of with the subgraphs and in the first two columns of Table 1. The smallest value in the last column of Table 1 gives the required minimum number of crossings. Of course, the same idea for the case of forces the same result.
- (b)
- For , let be a subgraph with respect to the restriction that the edges of does not cross the edges , , and of the graph . Since the considered drawing D is antipode-free and can cross only some of edges , , and of , one can easily determine, in all possible regions of the subdrawing , that is fulfilling for such a subgraph .
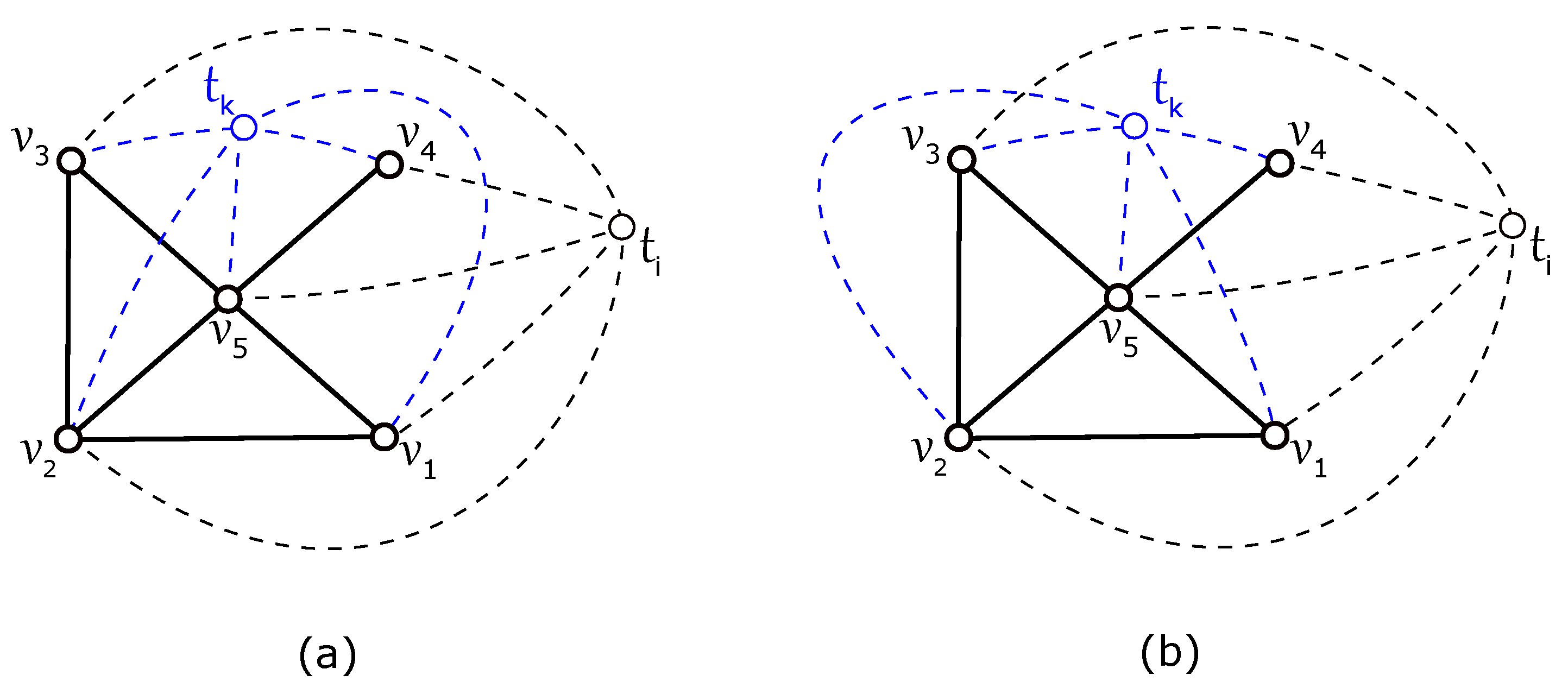
- (a)
- . For with the configuration of , there is the possibility of obtaining a subdrawing of in which holds for some . For this case by Lemma 4, the edges of the graph are crossed by each subgraph , at least six times except in cases where the edge of is crossed by the edges of . Thus, by fixing the subgraph , we haveThis also contradicts the assumption of D, and therefore, in the next part, suppose that holds for each . Notice that if and there are two different subgraphs such that and have configurations and , respectively, then is fulfilling for any , and holds for any . Therefore, in such a contemplated case, by fixing the graph , we receive the following contradiction with the assumption in DFurther, if there is a subgraph such that , then the edges and of the graph are crossed by the edges and , respectively, which yields by the result in [11] that for n at least 5. Finally, if either and or , by fixing the subgraph , we have
- (b)
- . Let be any subgraph from the nonempty set . Then, holds for each subgraph , provided by . Moreover, we can easily verify in five possible regions of that is fulfilling for any , if the edge of is not crossed by the edges of . Thus, by fixing the subgraph , we haveAll these subcases confirm a contradiction with the assumption in D.
5. Some Consequences of the Main Result
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klešč, M. The crossing numbers of join of the special graph on six vertices with path and cycle. Discret. Math. 2010, 310, 1475–1481. [Google Scholar] [CrossRef] [Green Version]
- Garey, M.R.; Johnson, D.S. Crossing number is NP-complete. SIAM J. Algebraic. Discret. Methods 1983, 4, 312–316. [Google Scholar] [CrossRef]
- Kleitman, D.J. The crossing number of K5,n. J. Comb. Theory 1970, 9, 315–323. [Google Scholar] [CrossRef] [Green Version]
- Klešč, M. The join of graphs and crossing numbers. Electron. Notes Discret. Math. 2007, 28, 349–355. [Google Scholar] [CrossRef]
- Klešč, M. The crossing numbers of join of cycles with graphs of order four. In Proceedings of the Aplimat 2019: 18th Conference on Applied Mathematics, Bratislava, Slovakia, 5–7 February 2019; pp. 634–641. [Google Scholar]
- Klešč, M.; Schrötter, Š. The crossing numbers of join products of paths with graphs of order four. Discuss. Math. Graph Theory 2011, 31, 321–331. [Google Scholar] [CrossRef]
- Berežný, Š.; Staš, M. Cyclic permutations and crossing numbers of join products of two symmetric graphs of order six. Carpathian J. Math. 2019, 35, 137–146. [Google Scholar] [CrossRef]
- Draženská, E. On the crossing number of join of graph of order six with path. In Proceedings of the CJS 2019: 22nd Czech-Japan Seminar on Data Analysis and Decision Making, Nový Světlov, Czech Republic, 25–28 September 2019; pp. 41–48. [Google Scholar]
- Klešč, M.; Petrillová, J.; Valo, M. On the crossing numbers of Cartesian products of wheels and trees. Discuss. Math. Graph Theory 2017, 71, 399–413. [Google Scholar] [CrossRef]
- Klešč, M.; Schrötter, Š. The crossing numbers of join of paths and cycles with two graphs of order five. In Lecture Notes in Computer Science: Mathematical Modeling and Computational Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7125, pp. 160–167. [Google Scholar]
- Klešč, M.; Staš, M. Cyclic permutations in determining crossing numbers. Discuss. Math. Graph Theory 2020. to appear. [Google Scholar]
- Staš, M. Alternative proof on the crossing number of K1,4,n. In Proceedings of the CJS 2019: 22nd Czech-Japan Seminar on Data Analysis and Decision Making, Nový Světlov, Czech Republic, 25–28 September 2019; pp. 165–174. [Google Scholar]
- Staš, M. Join Products K2,3 + Cn. Mathematics 2020, 8, 925. [Google Scholar] [CrossRef]
- Staš, M.; Valiska, J. On the crossing numbers of join products of W4 + Pn and W4 + Cn. Opusc. Math. 2021, 41, 95–112. [Google Scholar] [CrossRef]
- Draženská, E. Crossing numbers of join product of several graphs on 6 vertices with path using cyclic permutation. In Proceedings of the MME 2019: Proceedings of the 37th International Conference, České Budějovice, Czech Republic, 11–13 September 2019; pp. 457–463. [Google Scholar]
- Klešč, M. The crossing numbers of Cartesian products of paths with 5-vertex graphs. Discret. Math. 2001, 233, 353–359. [Google Scholar] [CrossRef]
- Li, M. The Crossing Numbers of Join of Some 5-Vertex Graphs with Paths and Cycles. J. Henan Norm. Uni. Nat. Sci. Ed. 2013, 41, 40–44. [Google Scholar]
- Yue, W.; Huang, Y.; Tang, L. The crossing number of join products of three 5-vertex graphs with Cn. J. Hunan Uni. Arts Sci. Nat. Sci. Ed. 2013, 25, 1–7. [Google Scholar]
- Clancy, K.; Haythorpe, M.; Newcombe, A. A survey of graphs with known or bounded crossing numbers. Australas. J. Comb. 2020, 78, 209–296. [Google Scholar]
- Berežný, Š.; Buša, J., Jr. Algorithm of the Cyclic-Order Graph Program (Implementation and Usage). J. Math. Model. Geom. 2019, 7, 1–8. [Google Scholar] [CrossRef]
- Hernández-Vélez, C.; Medina, C.; Salazar, G. The optimal drawing of K5,n. Electron. J. Comb. 2014, 21, 29. [Google Scholar]
- Chimani, M.; Wiedera, T. An ILP-based proof system for the crossing number problem. In Proceedings of the 24th Annual European Symposium on Algorithms (ESA 2016), Aarhus, Denmark, 22–24 August 2016; Volume 29, pp. 1–13. [Google Scholar]
- Woodall, D.R. Cyclic-order graphs and Zarankiewicz’s crossing number conjecture. J. Graph Theory 1993, 17, 657–671. [Google Scholar] [CrossRef]
- Berežný, Š; Staš, M. On the crossing number of join of the wheel on six vertices with the discrete graph. Carpathian J. Math. 2020, 36, 381–390. [Google Scholar] [CrossRef]

| 4 | 2 | 6 | 6 | |
| 3 | 3 | 6 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staš, M. The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five. Mathematics 2021, 9, 1277. https://doi.org/10.3390/math9111277
Staš M. The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five. Mathematics. 2021; 9(11):1277. https://doi.org/10.3390/math9111277
Chicago/Turabian StyleStaš, Michal. 2021. "The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five" Mathematics 9, no. 11: 1277. https://doi.org/10.3390/math9111277
APA StyleStaš, M. (2021). The Crossing Numbers of Join Products of Paths and Cycles with Four Graphs of Order Five. Mathematics, 9(11), 1277. https://doi.org/10.3390/math9111277






