A Review of Software for Spatial Econometrics in R

Abstract

The software for spatial econometrics available in the R system for statistical computing is reviewed. The methods are illustrated in a historical perspective, highlighting the main lines of development and employing historically relevant datasets in the examples. Estimators and tests for spatial cross-sectional and panel models based either on maximum likelihood or on generalized moments methods are presented. The paper is concluded reviewing some current active lines of research in spatial econometric software methods.

1. Introduction

The term spatial econometrics was coined by the Belgian economist Jean Paelinck in 1974 during an address to the Dutch statistical association. A few years later with his famous book “Spatial Econometrics: Methods and Models” Luc Anselin was instrumental to lay down the foundation of the field [1]. His book was (and still is after many years) a very well organized collection of tools for the analysis of spatial data. The  use of spatial econometrics in empirical applications was facilitated and extended by how easily the methods and examples presented in [1] could be reproduced in SpaceStat software. In  the early years, most of the attention given to spatial econometrics was from researchers in quantitative geography and regional science. Sessions of the North American Regional Science Association annual meetings were populated by research analyzing regional data from a spatial econometric perspective. This was probably due also to certain similarities between spatial econometrics and methods typically adopted in regional science as for example Input-Output analysis. At the same time SpaceStat was complemented by other tools such as the MATLAB spatial econometrics toolbox by LeSage (http://www.spatial-econometrics.com/) and the package spdep in R. In  recent years, the field of spatial econometrics has experienced a rapid growth in conjunction with the interest and attention received by researchers in mainstream economics and econometrics. A multiplicity of methods and models have been developed for cross-sectional as well as panel data [2,3,4]. Currently, spatial econometrics routines to estimate spatial models are available from many commercial (and non commercial) software, as for example Stata and the PySal module spreg [5]. R [6] is with no doubt the open source environment that contains the richest variety of options.

The aim of this paper is to survey all the available spatial econometrics packages and methods in R that deal with polygon spatial data, presenting the interested researchers with an up-to-date and comprehensive review of methods in both the cross-sectional and the panel data domains. All examples are meant to be replicable with resources from the public domain, allowing the reader to immediately put the relevant method into practice.

The rest of the paper is organized as follows: in Section 2 we present four data sets that will be then used to illustrate the libraries introduced. Section 3 is entirely devoted to cross sectional models and R libraries that deal with them. We present those libraries following as close as possible the chronological order in which they appeared in R. Section 4 describes static panel data model and the library splm, which implements maximum likelihood (ML) and generalized moments (GM) estimation. Section 5 deals with further developments and alternative methods and approaches both for cross-sectional and panel models. Section 6 concludes the paper.

2. Preliminaries and Data

2.1. Used Car Prices

In the 1960s, Hanna [7] wanted to examine the effects of regional differences in state taxes and transportation charges on used car prices. The  article lists data for the 48 coterminous US states and the District of Columbia. The  data set was used by Hepple [8] in developing ML estimation methods for spatial series, as cross-sectional spatial data were then known. We may read a copy of the data, punched from the article and stored in a GeoPackage file with the state boundaries, into R in this way:

Figure 1 shows why Hanna and Hepple saw the spatial nature of the problem: the used car prices in 1960 of vehicles first sold 1955–1959 (standardized as described by Hanna [7]) are lowest in Kentucky and in surrounding states northward towards Detroit. The  lower panel shows the transport costs, which are lowest in Michigan for obvious reasons, because Detroit was then Motor City. State sales taxes are set by political decisions, and were considered carefully by Hanna as a driver for differences in used car prices. One might expect some leakage of demand for used cars across state boundaries; the figure also shows some variation in sales taxes between neighbouring states that might provoke leakage.

The upper panel of Figure 1 also shows the graph of contiguous states, that is states sharing at least one boundary point. Some links are counter-intuitive, such as Wisconsin-Michigan, but here it is Upper Michigan that shares a boundary with Wisconsin. It is this symmetric neigbour graph that forms the basis for measuring the relationships between values at observations (here states) and aggregate values at neighbouring observations.

The aggregate values here are taken as the average of values in neighbouring states, with edge weights summing to unity for each state, denoted by style="W" in the definition of the list of weights object. Spatial weights matrices are typically very sparse, and while formulae often show them as matrices, they are seldom used as dense matrices.

To get an impression of the level of spatial dependence in these variables, we may use the approximate profile likelihood estimator [9,10] [APLE], which may be viewed somewhat like a correlation coefficient between the values observed for each state and the average values for neighbouring states. For the 1960 used car prices, APLE is $0.7579$, for transport costs unsurprisingly a little stronger: $0.8404$. The  coefficient for sales taxes is negative: $-0.3625$, and for both transport costs and sales taxes taken together it is more moderate: $0.5317$.

2.2. Driving under the Influence

One of the main advantages of GMM methods in space is that this technique is able to handle additional endogenous variables (other than the spatial lag). For this reason we choose to employ the simulated county data set US Driving Under the Influence (DUI) from in [11,12,13] for our demonstration. The  data for 3109 counties (excluding Alaska, Hawaii, and US territories), was constructed simulating from variables in Powers and Wilson [14]. The  counties were available from an ESRI Shapefile downloaded in 2102 from the US Census. (https://www2.census.gov/geo/tiger/TIGER2008/tl_2008_us_county00.zip). The dependent variable dui is defined as the alcohol-related arrest rate per 100,000 daily vehicle miles traveled (DVMT). The  regressors include police (measured in terms of number of sworn officers per 100,000 DVMT); nondui (non-alcohol-related arrests per 100,000 DVMT); vehicles (number of registered vehicles per 1000 residents), and dry (a dummy for counties that prohibit alcohol sale within their borders, about 10% of counties). An additional dummy variable elect is 1 if a county government faces elections, 0 otherwise, and has 295 non-zero entries.

More than likely, the size of the police force is related with the alcohol-arrest rates. Therefore, police is treated as an endogenous variable. [12] also assume that the dummy variable elect make a proper instrument for police.

We first read the shape file and the list of neighbors. Then, the function nb2listw serves to transform the neighbors into an actual (row-standardized) weights matrix. The last three lines of code define the formulas. In  particular, fm2 is the main formula that relates dui to the explanatory variables from which police is excluded because of endogeneity and is added separately. Finally, the last line of code below defines that the variable elect should be used as instrument.

2.3. Rice Farming

The famous Econometrica paper of Case [15] has introduced spatial panel data to a large audience and the mainstream profession. She applied a comprehensive spatial panel data framework to the empirical analysis of rice production in Indonesia, a subject panel data econometricians would come back to in more recent years. In  another seminal paper [16] 171 rice farms in Indonesia are observed over six growing seasons, three wet and three dry, between 1975 and 1983. The  farms are located in six different villages of the Chimanuk River basin in West Java. Following Druska and Horrace [16], the proximity matrix is constructed considering all the farms of the same village as neighbours.

Data and weights matrix are available in the splm package as, respectively, RiceFarms and riceww; the spatial weights do not change over time, and are of size $N\times N$, while there are $N\times T$ observations.

Druska and Horrace [16] estimated a production frontier equation where rice output depends on the inputs: seed, urea, phosphate (tsp), labour hours (lab) and land (size); all variables in logs but phosphate. Dummy variables are added for:the use of high yield varieties of seed (high); for a mix of seed varieties (mixed); and for the use of pesticides. Dummy variables are also included for each of the six villages, and for wet season (as opposed to dry):

As per Druska and Horrace [16], “[o]f the six villages included in the sample, two are on the north coast of the island in an area with average altitudes of 10–15 m above sea level. Another three villages are in an area (600–1100 m above sea level) in the central part of West Java. The last village is in the center of the island with an average altitude of 375 m. The infrastructure in the Cimanuk River Basin is fairly heterogeneous. Some of the villages (in both high and lowland areas) lack reliable transportation systems, and local roads are almost impassable in the wet (rainy) season. Other villages, located in close proximity to province capital cities, are highly accessible along paved, all-weather roads.” Therefore, both village-level heterogeneity and spatial correlation between farms belonging to the same village can be expected. Of the two possible spatial effects, spatial dependence in the errors is more likely, because of the similarity in idiosyncratic factors and climate conditions between neighbouring farms; the inclusion in the model of a spatial lagged response is harder to justify, as it seems unrealistic for one farm’s production to influence those of neighbours.

2.4. Crime in North Carolina

The second panel data set considered is based on a well known economic model of crime estimated by [17]. (The data are available from the website associated with Baltagi’s book [18].) They use a panel data on 90 counties in North Carolina over the period 1981–1987. The empirical model relates the crime rate (lcrmrte) to a set of controls for the return to legal activities, and to a number of deterrent variables (probability of arrest, probability of conviction conditional on arrest, and probability of imprisonment conditional on conviction). The crime rate variable is the ratio between an FBI index that measures the number of crimes, and  county population (i.e., crime per-capita in the county). The ratio of arrest to offenses is a proxy for the probability of arrest (lprbarr); the ratio of convictions to arrest is a proxy for the probability of conviction (lprbconv), and, finally, the proportion of total convictions resulting in prison sentences is a proxy for the probability of imprisonment (lprbpris). A measure of sanction severity (lavgsen) measured by the average prison sentence length in days is included in the model as well.

All of the other variables are either observable county characteristic, or controls for the relative return to legal activities. The  relative returns to legal activities are captured by the average weekly wage in the county in various sectors, such as construction (lwcon); transportation, utilities, and communications (lwtuc); wholesale and retail trade (lwtrd); finance, insurance, and real estate (lwfir); services (lwser); manufacturing (lwmfg); and federal (lwfed), state (lwsta), and local government (lwloc). The  dummy variable (urban) controls for differences in participation in the legal sector that may occur between urban and rural environment. A similar role is played by the density variable (ldensity) which measures the ratio between county population and county land area.

It is well known that crime rates tend to change with demographic characteristics of the population. The  model incorporates the proportion of male population between the ages of 15–24 (lpctymle), as well as the proportion of the population that is minority (lpctmin). Finally, regional or cultural factors that may affect the crime rate are picked up with the inclusion of a central and western dummies. Ref. [17] estimates the model both by the between and the within estimators and find quite impressive differences. Since they are concerned by the heterogeneity in their sample, they reject estimators that do not condition on country effects. This decision is clearly based on the evidence of a Hausman test.

Additionally, ref. [17] are concerned about the endogeneity of police per-capita and the probability of arrest. Hence those two variables are instrumented using per-capita tax revenue and a mix of different offense types. The  following lines of code read the data and the shape file, generate a spatial weight matrix based on the five-nearest neighbours criterion, and define the formulas to estimate the model.

3. Cross Sectional Models

The general model presented in this section allows for endogeneity of (some of) the regressors. The  point of departure is the Cliff–Ord spatial model:

$$\mathbf{y}=\mathbf{Y}\pi +\mathbf{X}\beta +\mathbf{WX}\gamma +\lambda \mathbf{W}\mathbf{y}+\mathbf{u}$$

(1)

where $\mathbf{y}$ is an $n\times 1$ vector of observations on the dependent variable, $\mathbf{Y}$ is an $n\times p$ matrix of observations on p endogenous variables, $\mathbf{X}$ is a $n\times k$ matrix of observations on k exogenous variables, $\mathbf{W}$ is an $n\times n$ observed and non-stochastic spatial weight matrix and, consequently, $\mathbf{Wy}$ is an $n\times 1$ variable that is generally referred to as the spatial lag of the dependent variable; $\pi$ and $\beta$ are corresponding parameters; and $\lambda$ is the spatial autoregressive coefficient. Given the presence of $\mathbf{Y},$ the model can be viewed as a representation of a single equation of a system of equations.

The error vector $\mathbf{u}$ follows a spatial autoregressive process of the form:

$$\mathbf{u}=\rho \mathbf{Mu}+\epsilon$$

(2)

where $\rho$ is a scalar spatial autoregressive parameter, $\mathbf{M}$ is an $n\times n$ spatial weights matrix that may or may not be the same as $\mathbf{W},$ $\mathbf{Mu}$ is an $n\times 1$ vector of observation on the spatially lagged vector of residuals.

An alternative, more compact way to express the same model is:

$$\mathbf{y}=\mathbf{Z}\delta +\mathbf{u}$$

(3)

where $\mathbf{Z}=[\mathbf{Y},\mathbf{X},\mathbf{Wy}]$ is the set of all (endogenous and exogenous) explanatory variables, and $\delta ={[{\pi }^{\top },{\beta }^{\top },\lambda ]}^{\top }$ is the corresponding vector of parameters. Finally, the assumption on which the ML relies is that $\epsilon \sim N(0,{\sigma }^2)$.

The general model (Equation (1)) may be restricted in various ways. Particularly in ML applications, $\pi$ is generally set to zero.

The spatial error model (SEM) is generated from the general model when $\lambda =\gamma =\pi =0$:

$$\mathbf{y}=\mathbf{X}\beta +\mathbf{u},\mathbf{u}=\rho \mathbf{Mu}+\epsilon$$

(4)

The spatial lag model (SLM) or spatial autoregressive model (SAR) is generated from the general model when $\rho =\gamma =\pi =0$:

$$\mathbf{y}=\mathbf{X}\beta +\lambda \mathbf{W}\mathbf{y}+\epsilon$$

(5)

The spatial Durbin model (SDM) is generated from the general model when $\rho =\pi =0$:

$$\mathbf{y}=\mathbf{X}\beta +\mathbf{WX}\gamma +\lambda \mathbf{W}\mathbf{y}+\epsilon$$

(6)

It is also possible to define the spatial error model with lags of the explanatory variables (henceforth SDEM) when $\lambda =\pi =0$:

$$\mathbf{y}=\mathbf{X}\beta +\mathbf{WX}\gamma +\mathbf{u},\mathbf{u}=\rho \mathbf{Mu}+\epsilon$$

(7)

If the only restriction are $\gamma =\pi =0$ we have a spatial autoregressive model with autoregressive error term (SARAR):

$$\mathbf{y}=\mathbf{X}\beta +\lambda \mathbf{Wy}+\mathbf{u},\mathbf{u}=\rho \mathbf{Mu}+\epsilon$$

(8)

Finally, the SARAR model can also include lagged explanatory variables. In this case the only restriction on the general model is $\pi =0$, that corresponds to the following specification:

$$\mathbf{y}=\mathbf{X}\beta +\mathbf{WX}\gamma +\lambda \mathbf{Wy}+\mathbf{u},\mathbf{u}=\rho \mathbf{Mu}+\epsilon$$

(9)

Over time, a characteristic of spatial lag models (and, by extension, of any model including the spatially lagged response) has become clear: that, unlike the spatial error model, the spatial dependence in the parameter $\lambda$ feeds back. The  interpretation of marginal effects should therefore not be based on the fitted parameters $\beta$, but rather on correctly formulated impact measures, as discussed in references given further on.

The reason for the feedback lies with the data generation process of the spatial lag model (and by extension in the general model). Rewriting:

$$\begin{array}{ccc}\hfill \mathbf{y}-\lambda \mathbf{W}\mathbf{y}& =& \mathbf{X}\beta +\epsilon \hfill \\ \hfill (\mathbf{I}-\lambda \mathbf{W})\mathbf{y}& =& \mathbf{X}\beta +\epsilon \hfill \\ \hfill \mathbf{y}& =& {(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{X}\beta +{(\mathbf{I}-\lambda \mathbf{W})}^{-1}\epsilon \hfill \end{array}$$

where $\mathbf{I}$ is the $n\times n$ identity matrix. This means that the expected impact of a unit change in an exogenous variable r for a single observation i on the dependent variable $y_i$ is no longer equal to ${\beta }_r$, unless $\lambda =0$. The  awkward $n\times n$$S_r\left(\mathbf{W}\right)=\left({(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{I}{\beta }_r\right)$ matrix term is needed to calculate impact measures for the spatial lag model, and similar forms for other models including the general model, when $\lambda \ne 0$.

3.1. Initial Development in R: The spdep Package

Bivand and Gebhardt [19] discusssed initial approaches to handling and analysing spatial data using R, based on a presentation at the 1998 European Reagional Science Association (ERSA) Congress in Vienna. A specialist meeting in Santa Barbara in May 2002 turned out to be very fruitful, but the contribution covering R took a little while to appear [20]; the meeting proceedings were online directly. Further discussion of spatial regression for areal/lattice data was presented at the 2002 ERSA Congress in Dortmund and published straight away [21]. The  main traits of the development of spatial data handling are described by Bivand [22]. The spdep package was first published on the Comprehensive R Archive Network (CRAN) in March 2002, replacing and merging spweights and sptests first available from September 2001, and the short-lived spsarlm package on CRAN in February 2002. spdep inherited the ML estimation functions from spsarlm; there have been other simpler implementations, for instance [23].

3.1.1. Spatial Dependence and the OLS Model

Initial concerns about the presence of spatial dependence in variables included in standard Gaussian linear models concentrated on the interpretation of tests on regression coefficients. Since positive spatial dependence may signal fewer effective degrees of freedom, could one trust standard tests assuming that no spatial dependence was present?

Table 1. Simulation of the power of a t-test on the regression coefficient at the nominal level of $0.05$ for uncorrelated y and x and spatial dependence for the response ${\rho }_y$ and the covariate ${\rho }_x$, following Smith and Lee [24].

	${\mathit{\rho }}_{\mathit{x}}$ 0	${\mathit{\rho }}_{\mathit{x}}$ 0.2	${\mathit{\rho }}_{\mathit{x}}$ 0.5	${\mathit{\rho }}_{\mathit{x}}$ 0.8
${\rho }_y$ 0	0.0505	0.0504	0.0499	0.0502
${\rho }_y$ 0.2	0.0497	0.0561	0.0647	0.0802
${\rho }_y$ 0.5	0.0496	0.0647	0.1002	0.1625
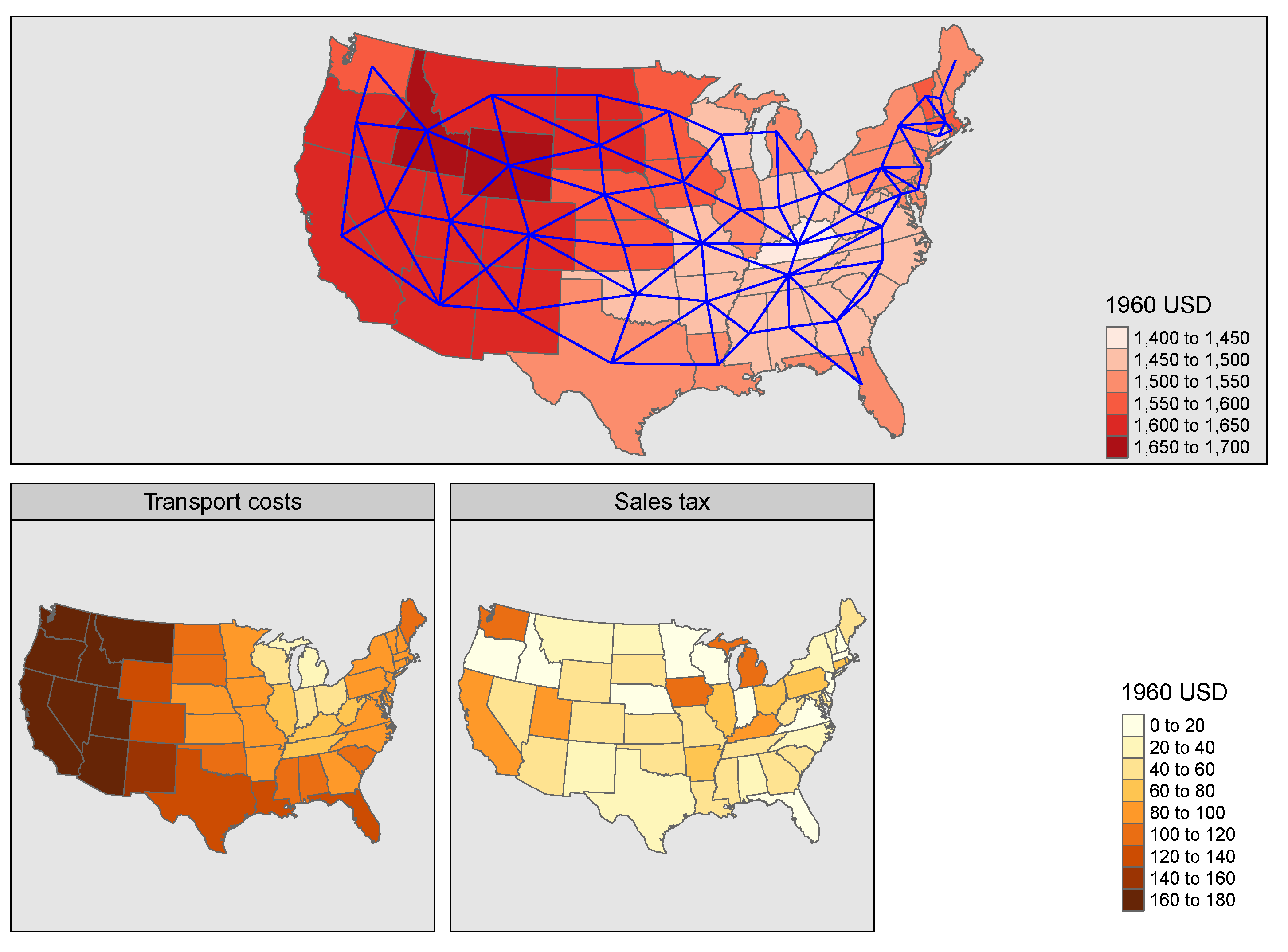
${\rho }_y$ 0.8	0.0532	0.0848	0.1650	0.3134

shows a small part of the findings of Smith and Lee [24], using the 49 coterminous states neighbour graph (Figure 1) and 10,000 draws. If both y and x show spatial dependence, standard test assumptions should not be used. If either is free of spatial dependence, standard test assumptions may be used. Here, we impose the levels of spatial dependence, and also know the scheme used to do this. With empirical data, we do not know where the spatial dependence is coming from, including the actual footprint of the variables. While sales taxes are determined here by states, neither prices nor transport costs are; they are aggregates.

Hepple [8] questioned whether the relationships described by Hanna held up when spatial dependence was taken into account. He used the sum of transport costs and sales taxes as the covariate, but we can also use the two covariates directly:

Table 2. Output of linear model estimates (standard error estimates in parentheses).

	(1)	(2)	(3)
(Intercept)	1435.971	1404.473	1436.256
	(27.178)	(23.200)	(11.515)
I(transp + salesTax)	0.686
	(0.173)
transp		1.297
		(0.189)
salesTax		−0.073	−0.080
		(0.211)	(0.214)
${\sigma }^2$	3181.985	2139.748	2206.494

shows that the simpler model, summing the costs and taxes, appears to perform less well than the model with two separate covariates. However, we know that transport costs might be offset rather than fitted, so the third model implicitly imposes a coefficient of unity on transport costs. McMillen [25] stresses the importance of considering whether apparent spatial dependence is in fact engendered by model mis-specification, such as the erroneous inclusion or omission of covariates, and the inappropriate functional form of included covariates.

3.1.2. The Development of the Moran and LM Tests for Spatial Dependence (Error and Lag)

When Cliff and Ord [26,27] proposed an extension of the Moran’s I spatial autocorrelation test for regression residuals, there was already some confusion associated with the choice facing analysts between the spatial error model and the spatial lag model. The  test was, like the Durbin–Watson test, based on testing a linear model against an alternative of omitted spatial autocorrelation in the error term.

Table 3. Tabulation of Moran’s I for regression residuals for three model specifications; alternative hypothesis: spatially autocorrelated residuals.

	(1)	(2)	(3)
Observed Moran I	0.5738	0.5385	0.5917
Expectation	−0.0297	−0.0361	−0.0175
Variance	0.0089	0.0090	0.0094
Standard deviate	6.4071	6.0731	6.2897
Pr(z != 0)	1.4830e−10	1.2543e−09	3.1804e−10

shows that all of the fitted models appear to show significant spatial autocorrelation in the error. Hepple [8] draws the same conclusion from a similar test, and fitted a spatial error model. This test may also be used when a weighted linear model is used; here no major differences are observed although the level of residual spatial autocorrelatiion is not so strong when counts of cars held by households from the 1960 US Census are used as weights.

Because Moran’s I for regression residuals gives no guidance in choosing between spatial error and spatial lag models, ref. [28] and Anselin and Bera [29] introduced Lagrange multiplier (LM) tests. The re are five tests, a test for residual autocorrelation (LMerr) with a robust version (RLMerr) for error dependence in the presence of spatial dependence in the response, conversely LMlag for an omitted spatially lagged response with RLMlag robust to the simulatneous presence of residual dependence, and the portmanteau test SARMA which is the sum of LMlag and RLMerr or LMerr and RLMlag.

Table 4. Lagrange multiplier test probability values for five tests and three models.

	(1)	(2)	(3)
LMerr	1.4160e−08	1.0208e−07	4.9702e−09
LMlag	1.5194e−10	6.4062e−09	8.8371e−09
RLMerr	0.839688	0.615013	0.015588
RLMlag	0.0028841	0.0176952	0.0296537
SARMA	1.2226e−09	4.2232e−08	3.5187e−09

shows the conventional probability values for the three models and the five tests. While SARMA, LMlag and LMerr indicate strong autocorrelation mis-specification, the contrasts between the robust RLMerr and RLMlag suggest that models (1) and (2) might be suffering from an omitted spatially lagged response, while the picture for model (3) is unclear. Until the last decade, it has been felt reasonable to use the balance between the robust LM tests as a guide, because the spatial lag and spatial error models are not nested, so cannot be tested against each other using likelihood ratio tests.

3.1.3. Early ML Estimation

The ML estimation methods for spatial lattice regression models grew from developments in Cliff and Ord [26], soon afterwards refined in Ord [30]. In  these and in [8,31], short-cuts were sought but largely rejected, in favour of optimizing the appropriate likelihood function. The implementation in spdep uses line search over the single spatial coefficient, calculating the other coefficients once that is found. The  development in [26] only addresses the simultaneous autoregressive (SAR) approach, but [32] and the rich literature based on his work prefers to treat spatial lattice regression in a Markov random field setting (conditional autoregressive, CAR), with spatially structured random effects included in an otherwise aspatial model. Reference [33] summarizes these developments and relates the SAR and CAR approaches.

The log-likelihood function for the spatial error model is:

$$\begin{array}{c}\hfill \ell (\beta ,\rho ,{\sigma }^2)=-\frac{N}{2}ln2\pi -\frac{N}{2}ln{\sigma }^2+ln|\mathbf{I}-\rho \mathbf{W}|\\ \hfill -\frac{1}{2{\sigma }^2}\left[{(\mathbf{y}-\mathbf{X}\beta )}^{\top }{(\mathbf{I}-\rho \mathbf{W})}^{\top }(\mathbf{I}-\rho \mathbf{W})(\mathbf{y}-\mathbf{X}\beta )\right].\end{array}$$

$\beta$ may be concentrated out of the sum of squared errors term, for example as:

$$\begin{array}{c}\hfill \ell (\rho ,{\sigma }^2)=-\frac{N}{2}ln2\pi -\frac{N}{2}ln{\sigma }^2+ln|\mathbf{I}-\rho \mathbf{W}|\\ \hfill -\frac{1}{2{\sigma }^2}\left[{\mathbf{y}}^{\top }{(\mathbf{I}-\rho \mathbf{W})}^{\top }(\mathbf{I}-{\mathbf{Q}}_{\rho }{\mathbf{Q}}_{\rho }^{\top })(\mathbf{I}-\rho \mathbf{W})\mathbf{y}\right]\end{array}$$

where ${\mathbf{Q}}_{\rho }$ is obtained by decomposing $(\mathbf{X}-\rho \mathbf{W}\mathbf{X})={\mathbf{Q}}_{\rho }{\mathbf{R}}_{\rho }$.

The first published versions of the eigenvalue method for finding the Jacobian [30] (p. 121) is:

$$ln\left(\right|\mathbf{I}-\lambda \mathbf{W}\left|\right)=\sum _{i=1}^{N}ln(1-\lambda {\zeta }_i)$$

where ${\zeta }_i$ are the eigenvalues of $\mathbf{W}.$

One specific problem addressed by [30] (p. 125) is that of the eigenvalues of the asymmetric row-standardized matrix $\mathbf{W}$ with underlying symmetric neighbour relations $c_{ij}=c_{ji}$. If we write $\mathbf{w}=\mathbf{C}\mathbf{1}$, where $\mathbf{1}$ is a vector of ones, we can get: $\mathbf{W}=\mathbf{C}\mathbf{D}$, where $\mathbf{D}=\mathrm{diag}(1/\mathbf{w})$; by similarity, the eigenvalues of $\mathbf{W}$ are equal to those of: ${\mathbf{D}}^{\frac{1}{2}}\mathbf{C}{\mathbf{D}}^{\frac{1}{2}}$. From the very beginning in spdep, sparse Cholesky alternatives were available for cases in which finding the eigenvalues of a large weights matrix would be impracticable.

The log-likelihood function for the spatial lag model is:

$$\begin{array}{c}\hfill \ell (\beta ,\lambda ,{\sigma }^2)=-\frac{N}{2}ln2\pi -\frac{N}{2}ln{\sigma }^2+ln|\mathbf{I}-\lambda \mathbf{W}|\\ \hfill -\frac{1}{2{\sigma }^2}\left[{((\mathbf{I}-\lambda \mathbf{W})\mathbf{y}-\mathbf{X}\beta )}^{\top }((\mathbf{I}-\lambda \mathbf{W})\mathbf{y}-\mathbf{X}\beta )\right]\end{array}$$

and by extension the same framework is used for the spatial Durbin model when $\left[\mathbf{X}\right(\mathbf{W}\mathbf{X}\left)\right]$ are grouped together. The  sum-of-squared errors (SSE) term in the square brackets is found using auxilliary regressions $\mathbf{e}=\mathbf{y}-\left({\mathbf{X}}^{\top }\mathbf{X}\right)\mathbf{X}\mathbf{y}$ and $\mathbf{u}=\mathbf{W}\mathbf{y}-\left({\mathbf{X}}^{\top }\mathbf{X}\right)\mathbf{X}\mathbf{W}\mathbf{y}$, and $SSE={\mathbf{e}}^{\top }\mathbf{e}-2\lambda {\mathbf{u}}^{\top }\mathbf{e}+{\lambda }^2{\mathbf{u}}^{\top }\mathbf{u}$. The cross-products of $\mathbf{u}$ and $\mathbf{e}$ can conveniently be calculated before line search begins.

The spatial error model (SEM, Equation (4)) was fitted to Hanna’s data by Hepple [8]; here we separate the two covariates, but if estimated using the sum of the two, the errorsarlm() function yields the same results at those reported in the article. All the model estimation functions from the spdep package have been split out into spatialreg [34], mostly because most users need spdep for creating spatial neighbour objects and for testing for autocorrelation. A separate model estimation package permits faster development of the model fitting functions without disturbing other work. The  model fitting functions follow the structure for R functions of this kind, using a formula interface. The  list of weights object is required, and when no method is specified for the computation of the log Jacobian to which we will return later, the  eigenvalues of the spatial weights matrix are used [30].

While each iteration of the line search of SEM involves a regression, the spatial lag model (SLM, Equation (5)), and the spatial Durbin model (SDM, Equation (6)) use intermediate values from two pre-computed regressions in each iteration. Again, the implementations use the eigenvalues of the spatial weights matrix to compute the log Jacobian at each iteration. Setting the Durbin= argument to TRUE adds the spatially lagged covariates, omitting the lagged intercept when the spatial weights are row standardized.

Table 5. Fitted spatial regression model coefficients for model (2): average 1960 prices of 1955–1955 cars, with transport cost and sales tax covariates (standard error estimates in parentheses).

	OLS	SEM	SLM	SDM
(Intercept)	1404.473	1445.411	441.828	516.990
	(23.200)	(36.934)	(150.080)	(166.969)
transp	1.297	0.873	0.466	0.230
	(0.189)	(0.299)	(0.168)	(0.454)
salesTax	−0.073	0.043	−0.053	−0.161
	(0.211)	(0.122)	(0.143)	(0.156)
lag(transp)				0.317
				(0.536)
lag(salesTax)				−0.474
				(0.301)
$\rho$		0.721
		(0.100)
$\lambda$			0.683	0.645
			(0.105)	(0.115)
${\sigma }^2$	2139.748	999.691	974.969	942.052

shows the fitted model output as it would have been presented until about 10 years ago. All the spatial models improve the fit of the model compared with the aspatial model in the first column. In  addition, a Lagrange multiplier test of the residuals of the SLM for spatial autocorrelation has a probability value of $0.1578$ (SDM: $0.4471$), neither of which appear to indicate any further spatial patterning. Pace and LeSage [35] propose a Hausman test assessing whether SEM coefficients are as close to the OLS coefficients as they should be in a well-specified model; the probability value here is $0.0293$. Had they been more different, one could find that the model was more seriously mis-specified. All of these tests are borderline, so all open for more analysis but do not point clearly in a single direction.

Finally, the examples of spatial regression in Waller and Gotway [36], using both SAR and CAR approaches, and introducing case weights to try to handle heterogeneity, led to the re-implementation of the spatial error model in the spautolm() function, which will not be presented here.

3.2. The “Advent” of The GMM

In two seminal papers [37,38] suggested a generalized method of moments (GMM) approach to the estimation of a SARAR model (Equation (8)) and established asymptotic results for the estimator. The main motivation for the success of this approach was, and in part still is, the computational simplicity even for large samples compared to ML. Additionally, at the time the GMM was proposed, one further problem was the lack of formal results concerning the asymptotic properties of ML, that were only derived later in a paper by [39]. The  original approach is based on a three steps procedure:

• In the first step, the first equation in (8) is estimated by two-stage least square (2SLS) using the matrix of instruments

  $$\mathbf{H}=(\mathbf{X},\mathbf{WX},{\mathbf{W}}^{\mathbf{2}}\mathbf{X},\cdots ,{\mathbf{W}}^q\mathbf{X})$$

  where, generally, $q=2.$
• In the second step, the residuals from the first step are employed to obtain an estimate of $\rho$ by solving a non-linear system of three equations resulting from the specification of the three following quadratic moment conditions:

  $$E{n}^{-1}{\epsilon }^{\prime }\epsilon ={\sigma }^{2}E{n}^{-1}{\overline{\epsilon }}^{\prime }\overline{\epsilon }={\sigma }^2{n}^{-1}tr{\mathbf{M}}^{\prime }\mathbf{M}E{n}^{-1}{\overline{\epsilon }}^{\prime }\epsilon =0$$

  (10)

  where $\overline{\epsilon }=\mathbf{M}\epsilon .$
• With the estimate of $\rho$ obtained in the second step, a transformation of the model is taken to filter out the spatial parameter and the transformed model is estimated again by 2SLS.

The estimator described by these three steps is generally referred to as the feasible generalized spatial two-stage least square (FGS2SLS) estimator. One issue to emphasize is that $\rho$ is treated as a nuisance parameter. Basically, the idea is to filter out spatial autocorrelation in the errors that is potentially dangerous for statistical inference on the model parameters, but there is no interest to make inference on the spatial error parameter itself. (In a later unpublished document, the authors demostrated how to compute the variance for the spatial error parameter in order to make inference on it. The  GMerrorsar function takes advantage of this and therefore in the demonstration below there will be a standard error for $\rho$.)

At this point it should be also evident that the nested models (i.e., the SLM, SEM, SDM and SDEM) can be estimated easily by modifyng the three steps described above. On the one hand, in the SEM and SDEM models the first and third steps are simply OLS, since there is not any endogeneity deriving from the presence of the spatial lag of y. On the other hand, the SLM and SDM models can be estimated by 2SLS since the error term is no longer spatially autocorrelated.

There were three separate functions in spdep: stsls for the SLM, GMerrorsar for the SEM, initially contributed by Luc Anselin, and  gs2sls for the SARAR model. These functions, along with many others, recently migrated into spatialreg.

The estimation of the lag model, as well as those of the error and SARAR models, of the DUI data cannot use the formula defined in Section 2, since none of the functions in spdep allow for additional endogenous variables.

Table 6. Fitted spatial regression model coefficients for SLM, SEM, and SARAR: DUI data (standard error estimates in parentheses).

	SEM	SLM	SARAR
(Intercept)	−5.432	−6.410	−6.410
	(0.229)	(0.418)	(0.418)
nondui	0.000	0.000	0.000
	(0.001)	(0.001)	(0.001)
vehicles	0.016	0.016	0.016
	(0.001)	(0.001)	(0.001)
dry	0.104	0.106	0.106
	(0.035)	(0.035)	(0.035)
police	0.600	0.598	0.598
	(0.015)	(0.015)	(0.015)
$\rho$	0.051		0.001
	(0.080)
$\lambda$		0.047	0.047
		(0.017)	(0.017)

reports results for the three implementations. A glance at the table shows that, out of the regressors, only non-alcohol related arrests is not statistically significant. The  presence of police force is the larger deterrent to driving under the influence of alcohol. It is also noteworthy that the coefficient estimates are very stable across different models. The  value of $\lambda$ for the SLM is higly statistically significant (even though it is quite small in magnitude). The spatial error coefficient $\rho$ in the SEM model is similar in magnitude, but it is not statistically significant. Finally, the estimated value and inference for $\lambda$ in the SARAR model is (almost) identical to the SLM, while $\rho$ is smaller than the SEM coefficient estimates and, as we mentioned previously, inference is not available.

An Early Version of sphet

Few years later that the GM approach was implemented in spdep, [40] developed a new package for estimating and testing spatial models with heteroskedastic innovations. The library was mainly based on GM estimators and semi-parametric methods for the estimation of the coefficient’s variance-covariance matrix. sphet was complementing but not overlapping with spdep. In fact, sphet focused only on GM and instrumental variables (IV) methods, leaving aside ML, and dealt with potential heteroskedasticity in the error term, features that was only partly taken into account in stsls. From a theoretical point of view, the procedures implemented in sphet were derived in [41,42]. The  point of departure of [41] was the SARAR model with potential heteroskedasticity in the innovations. A noticeable difference of [41] is that they gave results for the spatial error coefficient for both consistency and asymptotic normality. Of course, this enabled to perform statistical inference on both spatial parameters. Moreover, the moment conditions were slightly different from their earlier paper, thus leading to a different system of equations, that, in turn, resulted in a different estimates for the spatial error parameter.

The corresponding function in sphet is called gstslshet. The  syntax of the function is pretty straightforward: the first argument is a description of the model to be estimated, then the optional argument containing the data set, and, finally, the (mandatory) object of class "listw".

Table 7. Fitted spatial regression model coefficients for SARAR using gstslshet: DUI data (standard error estimates in parentheses).

	SARAR Het
(Intercept)	−6.410
	(0.446)
nondui	0.000
	(0.001)
vehicles	0.016
	(0.001)
dry	0.106
	(0.034)
police	0.598
	(0.018)
$\lambda$	0.047
	(0.018)
$\rho$	−0.000
	(0.037)

reveals that, besides the different moment conditions (that influence the estimated value of $\rho$), the model coefficients estimates, including the coefficient of the spatially lagged dependent variable, are very stable. The  spatial error coefficient can be tested although, in this case, it is not statistically significant.

Reference [42] propose a semi-parametric method for the estimation of the coefficient’s variance-covariance matrix that is robust against possible misspecifications of the disturbances and allows for unknown forms of heteroskedasticity and correlation across spatial units (HAC estimation). Instead of assuming a specific spatial structure for the error term, they assume a general form that nests many different spatial processes such as spatial autoregressive or spatial moving average. The  rationale behind this idea is that the error term, being the unknown part of the model, should not be specified a priori in terms of a specific spatial process, but rather assume a very general flexible form. However, the spatial HAC estimator is not immune from possible criticisms related to the type of kernel and the bandwidth selection. If the decision about the kernel choice has been proven not to be very relevant in that different kernels lead to negligible differences in practical applications, the same does not apply for the bandwith.

The function to produce the 2SLS with HAC standard errors available from sphet is stslshac. The  procedure is based on the choice of a distance function that along with a kernel determines the non-zero observations in the variance-covariance matrix.

Clearly, the results of the estimated coefficients in

Table 8. Fitted spatial regression model coefficients for LAG: dui data (standard error estimates in parentheses).

	LAG HAC	s.e. (2SLS)	s.e. (HAC)
(Intercept)	−6.410	(0.418)	(0.466)
nondui	0.000	(0.001)	(0.001)
vehicles	0.016	(0.001)	(0.001)
dry	0.106	(0.035)	(0.034)
police	0.598	(0.015)	(0.020)
$\lambda$	0.047	(0.017)	(0.019)

are not different from those obtained using the stsls in spatialreg. The  table reports two standard errors (second and third columns): For each coefficient, the second column has the usual 2SLS standard error, while the third is produced with the HAC. Interestingly, the differences in standard errors do not change the overall conclusions that all but one variable are statistically significant.

3.3. Further Development in R: The spdep Package and the Improvement of sphet

When [43] was published, the treatment of spatial econometrics covered the available software implementations in spdep. LeSage and Pace [2] appeared shortly afterwards, significantly “raising the bar” as expressed by Elhorst [44] in an extended review. Reference [45] discussed in detail both how to estimate an extended range of nested models using ML, and how to handle model interpretation, pursuing topics presented in Halleck Vega and Elhorst [46] and LeSage [47].

Work began in 2019 to split model fitting functions out from the spdep package, moving these components to the new spatialreg package. At about the same time, Bayesian fitting methods were added, based on porting of MATLAB Spatial Econometrics Toolbox code carried out by Virgilio Gómez-Rubio and Abhirup Mallik.

At the same time, the theoretical development of the generalized methods of moments in spatial econometric models was flourishing and gave rise to many important contributions. This corresponded to a series of major revisions of sphet, and, in particular, the inclusion of the wrapper function spreg. We will turn to this after describing the evolution of the ML estimation in the next subsection.

3.3.1. Evolution of the ML Estimation

Bivand et al. [48] review the technical issues around the calculation of the log Jacobian term in ML and Bayesian model estimation. It had been established from the mid-1990s that sparse matrix decomposition (Cholesky for symmetric weights matrices and LU for intrinsically asymmetric weights matrices) was feasible [49,50]. This was extended to cover the initial decomposition step in sparse Cholesky decomposition, which does not need to be repeated to look up log Jacobian values for successive values of the spatial coefficient.

Gomez-Rubio et al. [51] also show that these kinds of models may be estimated using integrated nested Laplacian approximation, yielding estimates of n spatially structured random effects over and above the spatial coefficient itself. The  domain of the spatial coefficient is transformed internally to $[0,1)$, so the bounds of the domain need to be known or calculated; here the extreme eigenvalues were previously calculated when fitting with ML and the eigenvalue-based log Jacobian.

Table 9. Spatial error model estimates and timings for the DUI data set: GMM, ML (eigenvalue and sparse Cholesky log Jacobian), MCMC using sparse LU griddy Gibbs log Jacobian and INLA using the experimental "slm" latent model.

	GMM	Eigen	Cholesky	MCMC	INLA
$\rho$	0.0509	0.0459	0.0459	0.0464	0.0461
(Intercept)	−5.4319	−5.4329	−5.4329	−5.4344	−5.4331
nondui	0.0003	0.0003	0.0003	0.0003	0.0003
vehicles	0.0156	0.0156	0.0156	0.0156	0.0156
dry	0.1037	0.1039	0.1039	0.1049	0.1039
police	0.5999	0.5998	0.5998	0.5995	0.5998
$\rho$ s.e.	0.0805	0.0299		0.0302	0.0299
LR test		0.1287	0.1287
Set up		11.8420 s	0.0390 s	4.3530 s	0.6579 s
Fitting		0.0170 s	0.0820 s		25.1193 s
Sampling				2.9090 s
Completion		92.8660 s	0.1140 s	0.0000 s	0.6290 s

shows clearly that the coefficients of the covariates are very much the same for all estimation methods. The  values of $\rho$ differ a little, but all of those based on the likelihood are very close. For comparison of estimation methods, the standard error of $\rho$ is more interesting. When eigenvalues are used to compute the log Jacobian, it is assumed that the data set is small enough to compute the asymptotic variance-covariance matrix of the coefficients. The  estimated value in this case matches those from MCMC and INLA very well, but when the sparse Cholesky is used for the log Jacobian, inverting $(\mathbf{I}-\rho \mathbf{W})$ is not attempted, and a finite difference Hessian approach is tried instead. This may lead, as  in this case, to there being marginally negative values on the diagonal of the estimated variance-covariance matrix, leading to failures when taking square roots. Problems with estimating the variance-covariance matrix can also occur in general when the scaling of the spatial coefficient and the remaining coefficients differ greatly. In this case the problem may be avoided by dividing the response by 1000, but the introduction of sensitivity tests to the poor conditioning of these matrices may be required. The  standard error of $\rho$ seems to be estimated well by MCMC and INLA. The  likelihood ratio test on $\rho$ return the same probability value in both the eigenvalue and sparse Cholesky cases, however, so resolving numerical issues in the variance-covariance matrix has not been seen as critical, although it also impacts the Hausman test as well.

Turning to the timings reported in Table 9, the set up times for the ML eigenvalue method, involving finding the eigenvalues of $\mathbf{W}$, and for MCMC conducting many LU decompositions for a coarse grid of values of the spatial coefficient to prepare for griddy Gibbs sampling, are longer than for the other estimation methods. Fitting for INLA is much longer because the n random effects are computed as coefficients, so that the dimensionality of the problem is bigger. MCMC here took 2500 draws only, discarding the first 500; more draws would increase the run time. Completion for the ML eigenvalue method includes the calculation of the asymptotic variance-covariance matrix of the coefficients, which could be speeded up somewhat with multi-threaded linear algebra.

There are a number of loose ends in the implementations, especially where numerical issues can appear, or where approximations lead to degradations when the spatial coefficient is near the extremities of its domain.

3.3.2. Interpretation and Impacts Evaluation

A fuller comparative treatment of model interpretation and the calculation of impacts is given by Bivand and Piras [52]. Difficulties arise from interaction between the spatial dependence modelled in the response, parameterized as $\lambda$ and the coefficients on the covariates.

Here, we run into trouble with: $\mathbf{y}=\lambda \mathbf{W}\mathbf{y}+\mathbf{X}\beta +\epsilon$, and rewriting: $(\mathbf{I}-\lambda \mathbf{W})\mathbf{y}=\mathbf{X}\beta +\epsilon$, and: $\mathbf{y}={(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{X}\beta +{(\mathbf{I}-\lambda \mathbf{W})}^{-1}\epsilon$, with the interaction between the coefficients in ${(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{X}\beta$ when $\lambda \ne 0$ potentially causing confusion unless clearly motivated.

As observed before, in the spatial lag mode—unlike the spatial error case—the spatial dependence in the parameter $\lambda$ feeds back. These difficulties are discussed as emanating effects [53], also known as impacts [2,54], simultaneous spatial reaction function/reduced form [55] and equilibrium effects [56].

This feedback comes from the fact that, while the elements of the Hessian matrix for the ML spatial error model linking $\rho$ and $\beta$ are zero (${\partial }^2\ell /(\partial \beta \partial \lambda )=\mathbf{0}$), in the spatial lag model (and by extension in the spatial Durbin model): ${\partial }^2\ell /(\partial \beta \partial \lambda )\ne \mathbf{0}$. In  the spatial error model, for exogenous variable r, $\partial y_i/\partial x_{ir}={\beta }_r$ and $\partial y_i/\partial x_{jr}=0$ for $i\ne j$. In  the spatial lag model, $\partial y_i/\partial x_{jr}={\left({(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{I}{\beta }_r\right)}_{ij}$, where $\mathbf{I}$ is the $N\times N$ identity matrix, and ${(\mathbf{I}-\lambda \mathbf{W})}^{-1}$ is known to be dense. The awkward $S_r\left(\mathbf{W}\right)=\left({(\mathbf{I}-\lambda \mathbf{W})}^{-1}\mathbf{I}{\beta }_r\right)$ matrix term needed to calculate impact measures for the lag model, and $S_r\left(\mathbf{W}\right)=\left({(\mathbf{I}-\lambda \mathbf{W})}^{-1}(\mathbf{I}{\beta }_r-\mathbf{W}{\gamma }_r)\right)$ for the spatial Durbin model, may be approximated using traces of powers of the spatial weights matrix as well as analytically.

The average direct impacts are represented by the sum of the diagonal elements of the matrix divided by n for each exogenous variable. The  average total impacts are the sum of all matrix elements divided by n for each exogenous variable. The  average indirect impacts are the differences between the direct and total impact vectors.

The development for approximation using traces of powers of the spatial weights matrix in [2] (pp. 114–115) for the lag model and q traces is as follows:

$$\mathbf{T}=[1,0,n^{-1}tr\left({\mathbf{W}}^2\right),n^{-1}tr\left({\mathbf{W}}^3\right),\dots ,n^{-1}tr\left({\mathbf{W}}^q\right)]$$

$$\mathbf{g}=[1,\lambda ,{\lambda }^2,{\lambda }^3,\dots ,{\lambda }^q];{\mathbf{G}}_{ii}=g_i,i=1,\dots ,q+1$$

$$\mathbf{P}={[{\beta }_1,{\beta }_2,\dots ,{\beta }_p]}^T,$$

where the intercept ${\beta }_0$ is dropped, and with $\mathbf{a}$ a p-vector of ones:

$$\mathrm{Direct}=\mathbf{P}\mathbf{T}\mathbf{G}\mathbf{a}$$

$$\mathrm{Total}=\beta \mathbf{g}\mathbf{a}.$$

Let us revert to the smaller used car data set, and show the important difference between predictions from the OLS model for the base data set and a new data set with the transport cost variable incremented by one: and the spatial lag model (SLM):

In the OLS case, the mean difference between the predictions is (of course) the value of the coefficient for the transport cost variable. In  the SLM case, $\lambda$ is far from zero, so the feedback is strong, and the difference between predictions is much larger than the coefficient value.

If we pick apart the model output, we can calculate the $S_r\left(\mathbf{W}\right)$ matrix for the transport cost variable, and see that the mean difference between predictions is the average total impact:

We can further check that the average direct and total impacts calculated in this way match the values returned by the impacts() method, when the spatial weights matrix is inverted inside the method:

When the eigenvalues of the spatial weights matrix are used, the results are identical.

However, these methods do not scale to larger data sets, so the traces of the power series of the spatial weights matrix may be used instead, noting a minor degradation in accuracy caused by the limited length of the power series q (here argument m=):

The eigenvalue and trace methods make it possible to conduct Monte Carlo tests on the impacts using draws from the fitted model coefficients and their variance-covariance matrix.

3.3.3. Evolution of the GMM and Recent Developments

The theoretical development of the generalized methods of moments in spatial econometric models has been flourishing over the last 15 years. Many important scholars in the field got involved and major commercial software (like, for example, Stata) started implementing codes to estimate the techniques that were under development. In  this context, [52] presented a comparison of the implementations available for spatial econometric models. In  the meanwhile, sphet had gone under a process of serious revisions that culminated with the inclusion of the wrapper function spreg. Specifyfing a model argument, spreg allows to estimate all of the specifications nested in the general model of Equation (1). The re are mainly two advantages of GMM compared to ML: On the one hand, GMM can deal with very large sets of data since it does not require inversion of large matrices. On the other hand, dealing with additional (other than the spatial lag) endogeneous variables is simple, provided that one has proper and valid instruments.

For the DUI data, the size of the police force is most likely related with the alcohol-arrest rates. The refore, police can be treated as an endogenous variable. As we anticipated earlier, ref. [12] also assume that the dummy variable elect (where elect is 1 if a county government faces an election, 0 otherwise) make a valid instrument for police.

Table 10. Fitted spatial regression model coefficients for SLM, SEM, and SARAR: dui data (standard error estimates in parentheses).

	SEM	SEM-End	SLM	SLM-End	SARAR	SARAR-End
(Intercept)	−5.432	15.782	−6.410	11.850	−6.410	11.920
	(0.229)	(1.606)	(0.418)	(1.724)	(0.416)	(1.696)
nondui	0.000	−0.000	0.000	−0.000	0.000	−0.000
	(0.001)	(0.003)	(0.001)	(0.003)	(0.001)	(0.003)
vehicles	0.016	0.094	0.016	0.094	0.016	0.094
	(0.001)	(0.006)	(0.001)	(0.006)	(0.001)	(0.006)
dry	0.104	0.400	0.106	0.400	0.106	0.401
	(0.035)	(0.092)	(0.035)	(0.092)	(0.035)	(0.092)
police	0.600	−1.365	0.598	−1.366	0.598	−1.367
	(0.015)	(0.144)	(0.015)	(0.143)	(0.015)	(0.142)
$\rho$	0.047	−0.005			−0.006	−0.0819
	(0.030)	(0.025)			(0.035)	(0.0304)
$\lambda$			0.047	0.188	0.047	0.186
			(0.017)	(0.047)	(0.017)	(0.046)

compares the SEM, the SLM, and the SARAR models with the corresponding models assuming that police force is endogenous.

Let us focus first on the three models with no additional endogeneity. While the SLM is the same as the one presented in Table 6, the SEM and the SARAR models are sligthly different since spreg uses different moment conditions. Despite this fact, results are very close to the one presented before and similar conclusions can be drawn. In  particular, the spatial error parameter is not statistically significant, while the positive spatial lag coefficient is small but strongly statistically significant. This means that the DUI related arrests in neighbouring counties affects the alcohol related arrests for a given county. This result can be explained in terms of copycat policies or a certain level of coordination in police enforcement between counties. In terms of the explanatory variables in the model, nondui is the only one that is not statistically signicant. The  estimated coefficient for police is large and positive in all three models. Moving to the specifications that treat police as endogenous the results are quite different particularly in terms of the magnitude of the coefficient estimates. Moreover, police turns out to be negative once endogeneity is controlled for. Two additional things have to be noted. The  first relates to the SARAR model. The  summary method for SARAR models automatically performs a Wald test that both $\rho$ and $\lambda$ are statistically significant. The  second relates to the SLM as well as to the SARAR model. Once again for models that are specified in terms of a spatial lag of the dependent variable appropriate summary measures needs to be used to take into account for simultaneity. This is the reason why appropriate spatial effects are calculated for the SAR and SARAR models. However, when additional endogenous variables are present, the calculation of the impacts is quite complicated. Ref. [57] show how to approximate that calculation but since is very case specific, it has not been implemented (yet) in sphet.

4. Spatial Panel Data Models

The econometric literature has considered panel regression models with spatially autocorrelated outcomes or disturbances and random or fixed individual effects for more than three decades now.

The pioneering book of Anselin [1] and the famous Econometrica paper of Case [15] have introduced the subject to a large audience. The  former reserved a minor part of a book-length treatment to the SEM model in a random effects setting, while the second applied a comprehensive spatial panel data framework to the empirical analysis of rice production in Indonesia, a subject panel data econometricians would come back to in more recent years. Nevertheless, few spatial panel data applications have followed, mainly because of the computational difficulties and the lack of ready-made, user-friendly software.

The more recent methodological contributions by [58,59] and the first comprehensive treatments of the subject in [60,61] have further helped the diffusion of spatial panel methods in applied practice, this time helped by the circulation of the first general-purpose routines, written in MATLAB by J. Paul Elhorst and kindly provided for public use by the author.

Nevertheless, the number of empirical applications has constantly trailed that of theoretical developments in this particular subject. Although clearly written, well tested and not difficult to adapt to one’s problem, Elhorst’s MATLAB routines were still primarily written for the author’s own use; moreover, if the specific routines were provided free for general use, MATLAB was, and is, non-free. The  availability of estimators and tests of production-quality usability (i.e., devoting much of the functionality to data and modelling interfaces, results’ presentation and consistency checks) within an open source environment would boost the number of spatial panel applications in the empirical literature. This happened with the emergence of the dedicated R package splm described here (see [62]); and, some years later, with the Stata add-on package ’xsmle’ [63] (in this latter case, while the package is provided in the open domain, the base software system is not; still, Stata is a de facto standard in econometrics and most researchers are likely to have access to a copy).

4.1. Static Spatial Panels

Spatial panel data models capture spatial interactions across spatial units observed over time. A general static panel model includes a spatial lag of the dependent variable and spatial autoregressive disturbances:

$$\mathbf{y}=\lambda ({\mathbf{I}}_T\otimes \mathbf{W})\mathbf{y}+\mathbf{X}\beta +\mathbf{u}$$

where $\mathbf{y}$ is an $nT\times 1$ vector of observations on the dependent variable, $\mathbf{X}$ is a $nT\times k$ matrix of observations on the non-stochastic exogenous regressors, ${\mathbf{I}}_T$ an identity matrix of dimension T, $\mathbf{W}$ is the $n\times n$ spatial weights matrix of known constants whose diagonal elements are set to zero, and $\lambda$ the corresponding spatial parameter. The disturbance vector is the sum of two terms

$$\mathbf{u}=({\iota }_T\otimes {\mathbf{I}}_n)\mu +\epsilon$$

where ${\iota }_T$ is a $T\times 1$ vector of ones, ${\mathbf{I}}_n$ an $n\times n$ identity matrix, $\mu$ is a vector of time-invariant individual specific effects and $\epsilon$ a vector of spatially autocorrelated idiosyncratic errors that follow a spatial autoregressive process of the form

$$\epsilon =\rho ({\mathbf{I}}_T\otimes \mathbf{W})\epsilon +e$$

with $\rho$ as the spatial autoregressive parameter, $\mathbf{W}$ the spatial weights matrix and $e\sim IID(0,{\sigma }_e^2)$. The  spatial weights matrices in the lag and the error term can differ (see the following). ${\mathbf{I}}_n-\rho \mathbf{W}$ is assumed non-singular.

The spatial panel model described above draws on panels of n data points observed over T time periods. Contrary to standard panel data practice, data are stacked by time, then by cross-section (so that the individual index is the “fastest” one). The spatial weight matrix $\mathbf{W}$ is assumed time invariant, as customary in the literature, and enters spatial panel models as ${\mathbf{I}}_T\otimes \mathbf{W}$ where ⊗ is the Kronecker product. In  the following, the models are illustrated based on the Rice Farming data.

The Pooled Spatial Model

If one could safely assume out any individual heterogeneity, spatial panels could be estimated by simply applying cross-sectional estimation techniques to the pooled dataset, employing an extended $\mathbf{W}$ matrix as specified above. This hypothesis, nevertheless, is extremely unlikely to hold. Below we estimate the pooled model; results will be reported later, comparing them to those considering individual effects.

4.2. Tests

In principle, spatial correlation in the residuals of panel models can be tested through a Moran test, treating all observations as a pool and employing a panel extension of the neigbourhood matrix, where as discussed above ${\mathbf{W}}_{nT}={\mathbf{I}}_T\otimes \mathbf{W}$. This approach nevertheless depends on the pooling assumption, i.e., assuming out any form of individual effect: which is inappropriate in the vast majority of cases. Specific test statistics have therefore been devised for spatial panels.

4.2.1. LM Tests

The Lagrange multiplier (LM), or score, test procedure on verifying whether the score of the likelihood of a restricted model is significantly different from the zero vector. If this is not the case, then the restriction is not binding w.r.t. the problem at hand and the corresponding null hypothesis is not rejected. Differently from its siblings, the asymptotically equivalent Likelihood Ratio and Wald tests, the LM test only requires to estimate the restricted model, therefore is often the procedure of choice in econometrics because of its computational parsimony, especially when estimation of the unrestricted model is complicated, costly or even problematic.

Since the seminal work of [64], LM tests have been extensively employed to test for random effects and serial or cross-sectional correlation in panel data models. For the above reasons, LM tests are particularly appealing in a spatial random effects setting because estimates for the full model are often much more difficult to compute than those for the restricted one.

Conditional and Joint Tests for Spatial or Random Effects

Building on the earlier literature, ref. [59] have extended the ML-based testing framework deriving joint, marginal and conditional tests for all combinations of random effects and spatial correlation. While the marginal tests are those already known, and the joint test is of little practical value because it will be a signal either of spatial or random effects without giving directions regarding which one is actually present, the conditional tests are particularly important because they allow to test for one of the two effects allowing for the presence of the other. The  comparative disadvantage of conditional tests is that their implementation is slightly more complicated as being based on the ML residuals from the model containing the “other” effect–the one the test is conditional on–instead of on OLS residuals.

Specifically, the hypotheses under consideration are:

• $H_0^a:\lambda ={\sigma }_{\mu }^2=0$ under the alternative that at least one component is not zero
• $H_0^b:{\sigma }_{\mu }^2=0$ (assuming $\lambda$ = 0), under the one-sided alternative that the variance component is greater than zero
• $H_0^c:\lambda =0$ assuming no random effects (${\sigma }_{\mu }^2=0$), under the two-sided alternative that the spatial autocorrelation coefficients is different from zero
• $H_0^d:\lambda =0$ assuming the possible existence of random effects (${\sigma }_{\mu }^2$ may or may not be zero), under the two-sided alternative that the spatial autocorrelation coefficient is different from zero
• $H_0^e:{\sigma }_{\mu }^2=0$ assuming the possible existence of spatial autocorrelation ($\lambda$ may or may not be zero)and the one-sided alternative that the variance component is greater than zero.

In the following we compute the full suite of tests from the [59] paper:

The presence of both spatial error dependence and random effects are confirmed, the spatial effect giving rise to the “most forceful” rejection.

Local CD Test

An alternative testing procedure from the heterogeneous panel literature can be applied to homogeneous panels as well, containing either fixed or random effects. This is based on a particularization of Pesaran’s ([65]) CD test for global spatial dependence. The CD test is based on an average (across the sectional dimension) of sample estimates of the pairwise correlations of residuals of the separate (timewise) regressions for every cross sectional unit:

$$CD=\sqrt{\frac{2T}{N(N-1)}}\left(\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\widehat{\rho }}_{ij}\right);\phantom{pi}{\widehat{\rho }}_{ij}=\frac{{\sum }_t{e}_{it}{e}_{jt}}{{\left({\sum }_t{e}_{it}^2\right)}^{1/2}{\left({\sum }_t{e}_{jt}^2\right)}^{1/2}}$$

The CD test is asymptotically standard Normal distributed under the null of no cross-sectional correlation; moreover, it does not depend on the heterogeneity assumption. In  general, residuals from any appropriate model (pooled, FE, RE) can be employed.

A variant of the $CD$ test, called $CD\left(p\right)$ test, has been designed to test for local cross-sectional dependence, i.e., dependence between neighbours only: in other words, for spatial dependence. It works by considering only the subset of “neighbouring” pairs of cross-sectional units, selected by means of the familiar binary proximity matrix. Originally, a regular ordering of observations was assumed, so that the m-th cross-sectional observation was a neighbour to the $(m-1)$-th and to the $(m+1)$-th. Reference [66] first extended the application of the $CD\left(p\right)$ test to an irregular lattice. The formula for the local test is an adaptation of the original $CD$ statistic where, as observed, the binary proximity matrix is employed as a selector for discarding the correlation coefficients relative to pairs of observations that are not neighbours (corresponding to zeros in $\mathbf{W}$):

$$CD\left(p\right)=\sqrt{\frac{T}{{\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^{N}w{\left(p\right)}_{ij}}}\left(\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}w{\left(p\right)}_{ij}{\widehat{\rho }}_{ij}\right)$$

where $w{\left(p\right)}_{ij}$ is the $(i,j)$-th element of the p-th order proximity matrix, so that if $h,k$ are not neighbours, $w{\left(p\right)}_{hk}=0$ and ${\widehat{\rho }}_{hk}$ is canceled out. Both the global (i.e., non-spatial) and the local CD tests have been available since 2008 in the plm package [67]. In the following we compute the local CD test on the residuals of the random effects panel model:

Again, spatial dependence is clearly present regardless of which kind of individual effects, if any, are included.

4.2.2. Individual Effects: Fixed or Random

The spatial panel data literature, following the mainstream non-spatial approach, distinguishes between treating the unobserved individual effects as fixed or random. In a random effects specification, these are assumed uncorrelated with the regressors, so that they can be safely treated as components of the error term: see, e.g., Assumption RE.1.b in Wooldridge [68] (10.4). Should this hypothesis not hold, then the latter strategy would introduce endogeneity and produce inconsistent estimates; the individual effects would either have to be estimated out or, which is more often the case, eliminated by first differencing or time-demeaning the data (see [68] 10.5). The  standard device for assessing the hypothesis of no correlation (i.e., for testing the appropriateness of random effects methods), is the Hausman [69] test. In  a spatial setting, Mutl and Pfaffermayr [70] derived an appropriate Hausman test for spatial panels.

From another viewpoint, the random effects hypothesis is considered consistent with sampling individuals from a potentially infinite population. for this reason Elhorst [61] dismissed its practical utility in spatial econometric contexts, where sampling typically takes place over a fixed set of countries or regions.

4.3. ML Estimation

For all the popularity of either the SAR and the SEM specification, econometric practice generally focuses on one effect only. With an exception made for the pioneering work of [15], few applications in the literature allow for both. Nevertheless, the expression for the likelihood of a model combining a spatial lag with any error structure $\Sigma$, including spatial dependence ones, is easily written as a panel version of the general likelihood in Anselin [1]:

$$\begin{array}{c}\ell (\lambda ,\beta ,{\sigma }^2,\Sigma )=-\frac{nT}{2}ln\left(2\pi {\sigma }_e^2\right)-\frac{1}{2}ln|\Sigma |+Tln\left|\mathbf{A}\right|\hfill \\ \phantom{logL=}-\frac{1}{2{\sigma }_e^2}{[({\mathbf{I}}_T\otimes \mathbf{A})\mathbf{y}-\mathbf{X}\beta ]}^{\prime }{\Sigma }^{-1}[({\mathbf{I}}_T\otimes \mathbf{A})\mathbf{y}-\mathbf{X}\beta ].\hfill \end{array}$$

(11)

As such, the spatial lag model can be estimated combining the SAR filter with any spatial or non-spatial structure, e.g., random effects:

4.3.1. Individual Effects and Spatial Errors

What differentiates the panel estimators from their cross-sectional counterparts is their ability to deal with the individual effects. In  the MATLAB routines due to [58], which have long been the de facto standard in the econometric analysis of spatial panel data, the partial time-demeaning technique familiar from standard panel data (see, e.g., [68] Ch. 10) is combined with Anselin’s ML framework: the data are either time-demeaned (FE) or partially time-demeaned (RE) in order to eliminate the individual effects, then standard SAR or SEM estimators are applied to the transformed data (see [61]).

Computationally, the fixed effects case is simpler, being encompassed by the pooled case: fixed effects models are generally estimated by pre-demeaning the data, according to the framework described in Elhorst [58]. This procedure has been criticized by [60] because time-demeaning alters the properties of the joint distribution of errors, introducing serial dependence: ([71] p.257) also discuss the issue; see also [62] (p.33) for Monte Carlo evidence of the magnitude of the bias. [72] (3.2) suggest to either correct the estimates ex post or to circumvent the problem using a different orthonormal transformation of the data. The  current implementation in splm can perform the Lee and Yu correction.

In the random effects case, following [58], to estimate the SARRE model one can add spatial filtering on $\mathbf{y}$ using ${\mathbf{I}}_T\otimes \mathbf{A}={\mathbf{I}}_T\otimes ({\mathbf{I}}_n-\lambda \mathbf{W})$ and the determinant of the spatial filter matrix, $|{\mathbf{I}}_T{\otimes \mathbf{A}|=|\mathbf{A}|}^T$, to the likelihood of the random effects model. Concentrating the likelihood with respect to $\beta$ and ${\sigma }_e^2$ as

$$\ell (\lambda ,\theta )=-\frac{nT}{2}ln\left(2\pi {\sigma }_e^2\right)+\frac{N}{2}ln\theta +Tln\left|\mathbf{A}\right|-\frac{nT}{2}ln\left({\tilde{e}}^{\prime }\tilde{e}\right)$$

(12)

where $\theta$ is the quasi-demeaning parameter and the residuals $\tilde{e}$ are those of the demeaned model with a spatial filter on $\mathbf{y}$

$$\tilde{e}=({\mathbf{I}}_T\otimes \mathbf{A})\tilde{\mathbf{y}}-\tilde{\mathbf{X}}\beta ,$$

and maximizing it w.r.t. $\lambda$ and $\theta$; then iterating until convergence between this maximization and the GLS step, whose first order conditions are

$$\begin{array}{c}\widehat{\beta }={\left({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}\right)}^{-1}\tilde{\mathbf{X}}({\mathbf{I}}_T\otimes \mathbf{A})\tilde{\mathbf{y}}\hfill \\ {\widehat{\sigma }}_e^2=\frac{{\tilde{e}}^{\prime }\tilde{e}}{nT}.\hfill \end{array}$$

yields an efficient two-step estimation procedure.

The transformation procedure for the SEM model (which employs a spectral decomposition of the errors covariance) is omitted here: see [58] (pp. 19–21). Although not explicitly stated by the author, [58]’s methodology is also easily extended, by combination, to the SAREM specification (for an application see [73]); on the other hand, it does not lend itself as easily to extensions in the direction of serially correlated errors (see the following).

The implementation in splm works instead on untransformed data and approaches random effects together with any other feature of the error covariance, spatial dependence included [74]. This has the advantage of keeping some components of the error term (most notably, the random effects) out of the spatial dependence, which can remain a feature of the idiosyncratic error only, as in most applications in the literature (see, e.g., [44,58,59,60,61,70,71,72,75,76,77,78,79,80,81,82,83,84,85]) but entails some computational complications. The alternative specification where the individual effects follow the same spatial process as the idiosyncratic errors, as in [86], which is also considered below, is much easier to compute.

4.3.2. Fixed Effects

Consistently with the conventions of the standard panel package plm, the most robust specification—the FE—is the default choice in the estimator function:

Spatial error correlation is remarkably high, as expected. What about spatial lag correlation? In his seminal papers which laid the foundations for practical estimation of spatial panel data models both under the fixed and the random effects assumptions, [58,61] does not consider combinations of spatially lagged response and spatially autocorrelated error term; while the original contribution of Case [15] did. With splm it is indeed possible to estimate a model containing both effects to assess the significance of each through a Wald test. We only report estimation results for the relevant coefficients:

The results confirm the relevance of the spatial error process, while the spatial lag is only marginally significant.

4.3.3. Independent Random Effects

The Rice Farms dataset, with observations coming from a large number of small villages employing the same standard technology, is a good candidate for a random effects analysis, perhaps after controlling for the region (which itself is likely to be a source of systematic differences in soil quality and climate).

Two kinds of random effects specifications are possible in spatial error panels: one where the spatial process in the error includes the random effects, the other where the individual random effects are idiosyncratic and independent of the neighbours’ ones. In the latter case, $\mu \sim IID(0,{\sigma }_{\mu }^2)$, and the error term can be rewritten as:

$$\epsilon =({\mathbf{I}}_T\otimes {\mathbf{B}}_n^{-1})e$$

where ${\mathbf{B}}_n=({\mathbf{I}}_n-\rho \mathbf{W})$. As a consequence, the composite error term becomes

$$\mathbf{u}=({\iota }_T\otimes {\mathbf{I}}_n)\mu +({\mathbf{I}}_T\otimes {\mathbf{B}}_n^{-1})e$$

and its variance-covariance matrix, if ${\mathbf{J}}_T={\iota }_T{\iota }_T^{\top }$ is a $T\times T$ matrix of ones, is

$${\Omega }_u={\sigma }_{\mu }^2({\mathbf{J}}_T\otimes {\mathbf{I}}_n)+{\sigma }_e^2[{\mathbf{I}}_T\otimes {\left(B_n^{\top }{B}_n\right)}^{-1}].$$

(13)

The hypothesis of independent random effects is the most natural to assume in many cases, including the one at hand; the idea being that random shocks, possibly related to weather, economic or health conditions, are likely to affect farms within the same village; while the individual heterogeneity captures the persistent random differences between individual farms in terms of soil quality or ability of the farmers.

The estimated variance of the random effect is small in proportion of that of the idiosyncratic error (about one fifth); the spatial error correlation is confirmed as very strong.

4.3.4. Spatially Correlated Random Effects

The specification for the disturbances of [86] assumes that spatial correlation applies to both the individual effects and the idiosyncratic errors. Although the “Baltagi” and “KKP” data generating processes look similar, they do imply different spatial spillover mechanisms. The economic meaning of the two models is also different: in the first model only the time-varying components diffuse spatially, in the second spatial spillovers too have a permanent component [76]. Reference [87] (see also 2.4) on the difference between these two RE specifications. In this latter case, commonly referred to as “KKP”, the composite disturbance term

$$\mathbf{u}=({\iota }_T\otimes {\mathbf{I}}_n)\mu +\epsilon$$

follows a first order spatial autoregressive process of the form:

$$\mathbf{u}=\rho ({\mathbf{I}}_T\otimes \mathbf{W})\mathbf{u}+e.$$

Then the variance-covariance matrix of $\mathbf{u}$ is:

$${\Omega }_u=[{\mathbf{I}}_T\otimes {\mathbf{B}}_n^{-1}]{\Omega }_{\epsilon }[{\mathbf{I}}_T\otimes {\left({{\mathbf{B}}_n}^{\top }\right)}^{-1}]$$

(14)

where ${\Omega }_{\epsilon }=[{\sigma }_e^2{\mathbf{I}}_T+{\sigma }_{\mu }^2{\mathbf{J}}_T]\otimes {\mathbf{I}}_n$ is the typical variance-covariance matrix of a one-way error component model.

It is not obvious why the spatial process should carry over to the individual effects in the case of the Rice Farms data; although one plausible hypothesis is that if the random individual heterogeneity is related to the quality of soil or to the working ability of the farmers—perhaps through tradition and cultural affinity—then one might see this as leading to a spatial process in the individual effects as well.

The practical difference between the two approaches turns out to be quite small. Again, models containing both a spatial lag and a spatial error (plus individual effects) can be estimated: the encompassing models’ results confirming the preference for a spatial error specification, given that the spatial lag coefficient is not significant.

4.4. Serial and Spatial Correlation

Serial correlation in spatial panel data has long been overlooked, if not for the very special case of persistent random effects. Nevertheless, if autocorrelation of the autoregressive type were present it would bias ML estimates, and may be a symptom of more serious misspecification: unit roots or missing dynamics. Ref. [75] further generalized the structure of the errors, introducing serial correlation in the remainder of the error term together with the spatial correlation and random effects. They derived a number of LM tests for the different effects, either marginal (i.e., assuming the other effects out) or conditional (i.e., allowing for their presence). The  general model is:

$$\begin{array}{c}\mathbf{y}=\mathbf{X}\beta +u\hfill \\ \mathbf{u}=({ı}_T\otimes \mu )+\epsilon \hfill \\ \epsilon =\rho ({\mathbf{I}}_T\otimes \mathbf{W})\epsilon +\nu \hfill \\ {\nu }_t=\psi {\nu }_{t-1}+e_t.\hfill \end{array}$$

While the marginal tests are already established testing procedures in the literature, the main contribution lies with the three-way joint test J and the one-way conditional tests C.1-3. The hypotheses under consideration are:

• $H_0^a:\lambda =\rho ={\sigma }_{\mu }^2=0$ under under the alternative that at least one component is not zero (J)
• $H_0^h:\lambda =0$, assuming $\rho \ne 0,{\sigma }_{\mu }^2>0$: test for spatial correlation, allowing for serial correlation and random individual effects (C.1)
• $H_0^i:\rho =0$, assuming $\lambda \ne 0,{\sigma }_{\mu }^2>0$: test for serial correlation, allowing for spatial correlation and random individual effects (C.2)
• $H_0^j:{\sigma }_{\mu }^2=0$, assuming $\lambda \ne 0,\rho \ne 0$: test for random individual effects, allowing for spatial and serial correlation (C.3)

An early application of the $C.2$ conditional test for spatial correlation in RE panels with serially correlated errors, based on a prototype of the R code, appeared at the same SEA conference as the [75] paper and was later published as (see 0.290 [66]). Production versions of the test resulted in the function bsjktest with J and C.1-3 appearing in the new splm package for R [62].

In the following we illustrate a possible specification search based on performing the joint test—which will obviously reject—and, most importantly, all three conditional tests from the [75] paper, which will give indications on whether any of the three possible effects (random, serial or spatial) is absent:

Although all three the conditional tests reject, the p-values make it very clear that the strongest effect is the spatial correlation, then the individual heterogeneity; lastly, there is also evidence of serial correlation but this is much weaker.

ML Estimation of Models with Serially Correlated Errors

In the splm package, Millo et al. [62]—also based on the early empirical work of Case [15]—realized that the estimation framework allowed for the coexistence of spatial lag and spatial error, and introduced the possibility of combining them into the so-called SAREM (or SARAR) model, so that functionality of this kind was available in the package from the outset (i.e., before 2010). In  the same fashion, it is possible to combine a spatial lag with a further generalization of the errors according to the Baltagi et al. [75] model outlined above. Extending Baltagi et al. [75] to the spatial lag, Millo [74] formalizes the estimation procedure for this kind of specification; he also presents a similar extension to serial correlation of the errors a la Kapoor et al. [86].

The encompassing model’s estimates confirm that the relevant spatial process is the error; and that random effects of modest magnitude are present, together with an even weaker form of autocorrelation in the remainder errors. Again, the practical difference between independent or spatially correlated random effects turns out to be minimal.

The estimates from all the spatial panel models in the previous paragraphs are presented in the following

Table 11. Parameter estimates from all spatial panel models for the Rice Farming dataset; left to right: pooled SEM, SAR-RE, SEM-FE, SAREM-FE, SEM-RE, SEM-RE (KKP version), SAREM-AR(1)-RE and SAREM-AR(1)-RE (KKP version). Standard errors are reported only for the spatial parameters.

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
(Intercept)	5.2240	2.9114			5.2359	5.2400	4.7440	4.5834
log(seed)	0.1224	0.0916	0.1025	0.1033	0.1153	0.1155	0.1146	0.1151
log(urea)	0.1430	0.1301	0.1043	0.1045	0.1280	0.1286	0.1266	0.1270
phosphate	0.0006	0.0014	0.0006	0.0006	0.0006	0.0006	0.0006	0.0006
log(totlabor)	0.2200	0.2370	0.2350	0.2344	0.2301	0.2289	0.2336	0.2326
log(size)	0.5076	0.4547	0.4830	0.4859	0.5021	0.5031	0.5021	0.5035
pesticide	−0.0117	0.0366	−0.0178	−0.0152	−0.0106	−0.0109	−0.0110	−0.0111
high yield	0.1212	0.0260	0.0983	0.0983	0.1149	0.1178	0.1107	0.1133
mixed	0.0894	0.0798	0.1073	0.1075	0.0980	0.0990	0.0954	0.0962
wet season	0.0630	−0.0390	0.0849	0.0165	0.0689	0.0687	0.0488	0.0405
lambda		0.3433		0.2135			0.0734	0.0984
S.E.lambda		0.0286		0.0956			0.0835	0.0842
rho	0.7225		0.7691	0.6902	0.7488	0.7421	0.7192	0.7039
S.E.rho	0.0332		0.0275	0.0531	0.0304	0.0310	0.0433	0.0454
psi							0.0899	0.0943
S.E.psi							0.0409	0.0411

:

4.5. Endogeneity in Static Panel Data Models

As we mentioned early, the initial contribution to the application of GM methods for spatial panels dates back to [86]. The y considered a panel data model involving a first order spatially autoregressive disturbance term that, in turn, allowed for an error component structure in the innovations. The  proposed methodology was based on an extension of the moment conditions put forth from the same authors in the context of a cross-sectional model. A few years later while considering a spatial panel version of the Hausman test, ref. [70] extended the estimation procedure to a Cliff and Ord type model including the spatial lag of the dependent variable as well as a spatially lagged one-way error component model. The y implemented instrumental variables estimation under both the fixed and the random effects specifications. However, Piras [88] noted that they were not taking full advantage of the six moment conditions derived in [86] since they were using only a subset of those moment conditions.As a consequence, ref. [88] suggested an improvement that included all six moment conditions in [86]. The  approach taken by [88] followed more closely the fixed and between effects two stage least squares estimator for spatial panel models proposed by [89]. (This was in turn an extension of the [90] error component 2SLS estimator to a spatial panel model.) The function spgm implements the procedure described in [88] with the extra feature of considering additional (other than the spatial lag) endogenous variables.

Table 12. Results from the EC2SLS and the spatial version of the EC2SLS.

	EC2SLS	(std. err.)	Spatial EC2SLS	(std. err.)
lprbarr	−0.413	(0.097)	−0.340	(0.059)
lpolpc	0.435	(0.090)	0.354	(0.050)
(Intercept)	−0.954	(1.284)	−0.698	(1.144)
lprbconv	−0.323	(0.054)	−0.275	(0.031)
lprbpris	−0.186	(0.042)	−0.164	(0.033)
lavgsen	−0.010	(0.027)	−0.014	(0.025)
ldensity	0.429	(0.055)	0.446	(0.049)
lwcon	−0.007	(0.040)	−0.005	(0.037)
lwtuc	0.045	(0.020)	0.039	(0.017)
lwtrd	−0.008	(0.041)	−0.012	(0.039)
lwfir	−0.004	(0.029)	−0.006	(0.027)
lwser	0.006	(0.020)	0.004	(0.019)
lwmfg	−0.204	(0.080)	−0.185	(0.074)
lwfed	−0.164	(0.159)	−0.067	(0.141)
lwsta	−0.054	(0.106)	−0.041	(0.097)
lwloc	0.163	(0.120)	0.118	(0.110)
lpctymle	−0.108	(0.140)	−0.066	(0.116)
lpctmin	0.189	(0.041)	0.185	(0.036)
west	−0.227	(0.100)	−0.224	(0.089)
central	−0.194	(0.060)	−0.210	(0.056)
urban	−0.225	(0.116)	−0.179	(0.100)
d82	0.011	(0.026)	0.006	(0.020)
d83	−0.084	(0.031)	−0.064	(0.026)
d84	−0.103	(0.037)	−0.077	(0.032)
d85	−0.096	(0.049)	−0.073	(0.044)
d86	−0.069	(0.060)	−0.057	(0.054)
d87	−0.031	(0.071)	−0.034	(0.064)
$\lambda$			0.268	(0.069)

compares results from the “classical" error component two stage least square (EC2SLS) in [90] and the spatial version of the EC2SLS. The  first model can be obtained by setting both lag and error arguments to FALSE and specifying endogenous variables along with instruments. To obtain the second model the user has to include both spatial lag and error parameters. The  data set to produce Table 12 where presented in Section 2.4 and relates to an economic model of crime estimated by [17]. Keep in mind that [17] had a genuine concern about the endogeneity of police per-capita ad the probability of arrest. The refore, those two variables are instrumented using per-capita tax revenue and a mix of different types of offense. The  spatial lag parameter at the bottom of the second column in Table 12 is positive and statistically significant and then justifies the spatial specification. The  spatial connection are driven from the fact that counties with high (low) levels of crime are generally clustered. This may be due to some sort of copy-cat policies occurring within the counties.

5. Developments and Alternative Approaches

Before concluding, we will draw attention to work in progress, and to alternative approaches to spatial regression for area data, first for cross-sectional models, later for spatial panel models.

5.1. Developments and Alternative Approaches in Cross-Sectional Models

One of many implementations of Markov Random Field (MRF) spatially structured random effects in generalized additive models (GAM) is found in Wood [91], implemented in [92]. The  neighbour objects needs to be matched to the variable expressing the random effect, here State. The  MRF smooth requires manual adjustment of the number of knots, because here we are not using a multi-level approach and so approach the upper bound on the number of parameters to be estimated. In  addition, the MRF approach does not row-standardize the spatial weights, using a conditional rather than a simultaneous autoregression.

Another approach is through hierarchical generalized linear models (HGLM), presented by [93] and implemented in [94]. Both GAM and HGLM can fit Gaussian responses, but can also fit discrete responses. This implementation can accommodate either SAR or CAR spatially structured random effects. All such approaches estimate the per-observation random effects and their standard errors, so are somewhat constrained as the number of observations increases.

Figure 2 shows the spatially structured random effects, where the HGLM SAR and GAM MRF values are very similar indeed (

Table 13. Correlation coefficients between HGLM and GAM random effects and cumulated spatial filtering effects (eigenvector values multiplied by their regression coefficients and summed by observation, SF: [114], ESF: [119], ME: [115]); SAR are the implied values from the SEM model fitted by ML.

	HGLM	GAM	SF	ESF	ME	SAR
HGLM	1.0000	0.9593	0.4443	0.9046	0.9588	0.9500
GAM	0.9593	1.0000	0.4064	0.8833	0.8856	0.8462
SF	0.4443	0.4064	1.0000	0.2635	0.4570	0.4992
ESF	0.9046	0.8833	0.2635	1.0000	0.8751	0.8336
ME	0.9588	0.8856	0.4570	0.8751	1.0000	0.9410
SAR	0.9500	0.8462	0.4992	0.8336	0.9410	1.0000

).

In an extension of work handling missing observations of the response variable, ref. [95] began a series of articles, followed by [96,97]. Reference [98] give a complete survey of the challenges raised in predicting from models when the observations are autocorrelated (implemented in spatialreg for ML estimators); this has obvious extensions to spillover between training, validation and test data sets in machine learning contexts.

5.1.1. Limited Dependent Variables Models

In addition to the resolutions shown above using GAM or HGLM, a number of other approaches have been proposed for limited dependent variables, in particular discrete dependent variables. Ref. [99] follow [2] in fitting spatial probit models using MCMC, implemented in [100]. The link function used in this approach differs in character from those used in generalized additive and linear mixed models, such as those fitted using standard Bayesian techniques, which dominate the application of such approaches outside spatial econometrics. It is also possible to use GMM approaches, as shown by Klier and McMillen [101] and implemented in [23]. The  same package also provides implementations od spatial quantile regression [102].

5.1.2. Multi-Level Models

Multi-level models involve the grouping of observations within nested containers, where the spatial processes may play out at the finest level, or at coarser spatial scales. Recent work has been undertaken by [103,104,105], and is implemented in [106] using MCMC. Many of the general packages for Bayesian model fitting, such as [107] implemented in [108] can also be used for fitting multi-level models. A comparative review is given by [109].

5.1.3. Spatial Filtering Methods

Spatial filtering methods as developed by Griffith [110] build on using standard linear and generalized linear models supplemented with selected eigenvectors from the spatial weights matrix. In [111,112,113], examples were given of how standard and non-standard spatial econometric problems could be approached using spatial filtering. Tiefelsdorf and Griffith [114] proposed that the eigenvectors for inclusion should be selected by their ability to reduce residual autocorrelation rather than to increase model fit. This approach was implemented by Chun and Tiefelsdorf in spdep and moved to spatialreg [34], with two steps, first to select eigenvectors taken from the spatial weights matrix doubly centred using the hat matrix of the actual regression, then using lm to fit the model, effectively removing residual autocorrelation:

Figure 3 shows the products of the selected eigenvectors and their estimated regression coefficients in map form. Typically, the small subset of eigenvectors selected mops up spatial autocorrelation in the residual. References [115,116] adopt a similar approach in a generalized linear model context, implemented in spdep by Pedro Peres-Neto and moved now to spatialreg as ME analogous with SpatialFiltering, but centering the spatial weights matrix on the null model hat matrix, and using bootstrap methods in evaluating the the choice of eigenvectors. The correlations between the implied cumulated outcomes of these methods are shown in Table 13. Reference [117] describe many of the underlying motivations, including the view that Moran eigenvector spatial filtering approaches may permit both spatial autocorrelation and spatial scale tto be accommodate in a single model; a further implementation is given in [118].

Murakami and Griffith [119] provide a fresher version of spatial filtering implemented in [120]. This also appears to centre the spatial weights matrix on the null model hat matrix, and chooses eigenvectors not to reduce residual autocorrelation, but chooses those among the eigenvectors with positive eigenvalues that increase model fit most up to a threshold to control overfitting. The  default approach uses an exponential variogram model to generate the weights matrix from planar coordinates. The  meigen function subsets the full set of eigenvectors before the data are seen, then esf calls lm itself while further subsetting the eigenvectors.

Figure 4 shows the products of the first four eigenvectors chosen and their regression coefficients, and differs from the approaches shown above mostly in using a distance model to relate the observations to each other rather than the graph of neighbours, and in selecting to improve fit rather than reduce residual autocorrelation.

Table 13 shows the correlations between the two estimates of spatially structured random effects, three cumulated spatial filtering approaches, and the spatially structured term implied by the ML estimates of the spatial error model. As can be seen, they are very similar to each other, so the choice of approach may be fairly flexible and relate more to the needs of users and their domain usages that to a single body of theory.

5.1.4. Heterogeneity in Space: GWR and Regime Models

While the presence of spatial dependence has been widely recognized as an issue to address in econometric models, spatial heterogeneity has not received that much attention ans, therefore, is not always adequately taken into account. Possible reasons for this should be searched not only in the theoretical and practical difficulties to identify spatial heterogeneity separately from spatial dependence in empirical models, but also (and perhaps primarily) to the lack of readily available software to perform this kinds of analysis. There is a wide array of models to account for spatial heterogeneity, but only few of them are available in R. (An interesting overview can be found in [1].) One can model heterogeneity allowing for a different parameter for each observations. This is the idea embedded in the so-called geographically weighted regression [121] available in R from the package spgwr. A different approach to this extreme case would be assuming that spatial heterogeneity can be classified into a limited number of spatial regimes characterized by different values of the regression parameters. One of the future directions for spatial models in R would be geared towards the development of such regime models.

5.1.5. Higher Order Spatial Models

A natural extension of the techniques in sphet would be considering higher order spatial models [122,123]. The presence of additional lags (either of the dependent variable, of the regressors, or of the error term) would allow to test different types of interactions and make the model interpretation richer.

5.1.6. Systems of Spatial Equations

An earlier version of the package splm included codes to estimate spatial simultaneous equation and spatial seemingly unrelated regression equations. By the time splm was published the routine for those models migrated into a new package spse that, unfortunately, never saw the light. spse contained two major functions: spsegm and spseml. spsegm implemented the feasible generalized three stages least square estimator (FGS3SLS) for simultaneous systems of spatially interrelated cross sectional equations put forward by [124], while spseml implemented ML estimation of simultaneous systems of spatial seemingly unrelated regression equation following the lines in [1]. The package is now hosted on Github (https://github.com/gpiras/spse) and is (again) under development. Future plans will include the extension to simultaneous equation combined with higher order spatial interactions [125]. (In a similar context, the package spsur [126] also deals with seemingly unrelated regression equations.)

5.1.7. Machine Learning and Spatial Econometrics

A first attempt to insert a spatial lag model into a regression tree has been presented by Wagner and Zeileis [127], and is implemented in [128].

5.2. Developments and Alternative Approaches in Spatial Panels

Here two important developments will be mentioned briefly, referring the interested reader to the cited references for futher details.

5.2.1. Dynamic Spatial Panels

Many economic phenomena are inherently dynamic in nature and therefore call for estimators allowing for time lags of the included objects, most notably for a lagged dependent variable. Nevertheless, the abundant results from the time series literature do not easily carry over to the spatial panel case. The estimation of panel models containing both individual effects and a lagged dependent variable is well known to be problematic because of the serial correlation induced in the error terms by the transformation procedures employed to eliminate the individual heterogeneity (either time-demeaning or first differencing), so that e.g., the fixed effects estimator for a dynamic model would be biased [129]. Arellano and Bond [130] famously proposed a GMM procedure for consistently estimating the dynamic model with individual effects; yet their estimator assumes cross-sectionally uncorrelated errors and is hence not appropriate in a spatial context.

Research on dynamic spatial panels has been quite recent and is mostly associated with Elhorst. His first paper on the subject [131] set the stage in 2001; then he provided a first solution based on approximating the initial conditions (complete with MATLAB routines in the public domain) some years later [132]. Still, the ML estimator of [132] has a number of caveats: refs. [83,133] derive the asymptotic properties and a bias correction. The review paper of [134] discusses the general space-time specification, the different estimation approaches of ML/QML, GMM and Markov Chain Monte Carlo (MCMC). In general, despite the existence of some solutions, estimation of spatial dynamic panels can be said to be a still developing field. R software for this task is still lacking but is likely to be developed in the near future.

5.2.2. Heterogeneous SAR Panels

Another recent extension of the mainstream spatial panel is the heterogeneous spatially autoregressive (HSAR) estimator of [135] which, in the general framework of the SAR panel with fixed effects, relaxes the assumptions of parameter homogeneity and of error homoscedasticity, so that the model becomes

$$\begin{array}{cccc}\hfill y_{it}& =\lambda \left(\sum _{j=1}^N{w}_{ij}{y}_{jt}\right)+{\beta }^{\prime }{x}_{it}+u_{it},\hfill & \hfill i& =1,2,\cdots ,N;t=1,2,\cdots ,T\hfill \end{array}$$

(15)

where $y_{it}$ is the response variable for unit i observed at time t, $x_{it}={\left(x_{i1,t},x_{i2,t},\cdots ,x_{ik,t}\right)}^{\prime }$ is a $k\times 1$ vector of exogenous explanatory variables, with the associated $k\times 1$ vector of slope parameters, $\beta ={\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_k\right)}^{\prime }$, $w_{ij}$ is the element $(i,j)$ of W; and the vector of individual SAR coefficients $\lambda ={\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k\right)}^{\prime }$. As in a standard linear panel data model, the idiosyncratic error is in turn the sum of two terms

$$\begin{array}{cccc}\hfill u_{it}& ={\mu }_i+{\epsilon }_{it},\hfill & \hfill i& =1,2,\cdots ,N;t=1,2,\cdots ,T\hfill \end{array}$$

(16)

where ${\mu }_i$ is a time-invariant unit specific effect and ${\epsilon }_{it}$ is the idiosyncratic error. $\mu$ are allowed to be correlated with the regressors, and $\epsilon$ to be heteroscedastic.

ML estimators are provided for the individual coefficients; then the latter can be averaged according to the mean groups (MG) method of Pesaran and Smith [136] to obtain average coefficients and their dispersion matrix. A project to produce a multilanguage implementation, including an R package, is nearing completion [137].

6. Conclusions

This paper was dedicated to a review of the functionality for spatial econometric methods available in the R system for statistical computing, in the light of the historical developments of methods, mostly following a chronological order and hinting when appropriate at implementations in different software environments. It addressed estimators and tests for: spatial econometric models on cross sectional data, both based on ML and on GM; spatial panel models with either correlated or independent unobserved heterogeneity; spatial panel models with possibly endogenous explanatory variables. The methods have been presented through empirical examples based on four well-known and historically relevant datasets. At the end of the paper, several active areas of development are hinted at.

Although some specific areas of spatial econometric modelling have been covered in recent books—cross-sectional methods in [3] (Appendix B), panel data in [138] (Ch. 10)—this is the first comprehensive review addressing the development of spatial methods in R in a historical perspective and trying to cover all relevant functionality in both the cross-sectional and the panel domain.

R is considered the lingua franca of statistical computing. As such, most available statistical functionality is available under form of R packages, including very powerful optimization features. Moreover, the R system offers a wide range of tools for dealing with spatial data, including mapping and automated computing of spatial weights. Therefore, although there are several other viable and powerful options, R is arguably the ideal development environment for spatial regression modelling. Finally, two aspects that need to be taken into consideration are that R, unlike other software, is open-source and cross-platform.

The R infrastructure described in the paper is entirely open source and packaged into the standard, user-friendly and documented packages so that it is ready for the perusal of empirical researchers. The paper itself is entirely replicable in its computational aspects, based on open source code and data from the R project. As such, it complies with the reproducibility requirements of Peng [139], the “gold standard of full replication”, as providing “a detailed log of every action taken by the computer” which can be reproduced by anybody on any system.