Abstract
The paper presents a tuning method for PID controllers with higher-order derivatives and higher-order controller filters (HO-PID), where the controller and filter orders can be arbitrarily chosen by the user. The controller and filter parameters are tuned according to the magnitude optimum criteria and the specified noise gain of the controller. The advantages of the proposed approach are twofold. First, all parameters can be obtained from the process transfer function or from the measured input and output time responses of the process as the steady-state changes. Second, the a priori defined controller noise gain limits the amount of HO-PID output noise. Therefore, the method can be successfully applied in practice. The work shows that the HO-PID controllers can significantly improve the control performance of various process models compared to the standard PID controllers. Of course, the increased efficiency is limited by the selected noise gain. The proposed tuning method is illustrated on several process models and compared with two other tuning methods for higher-order controllers.
1. Introduction
The PID controllers are widespread in many industries and are frequently included in embedded solutions [,,,]. This is not surprising, since the basic PID control algorithm is very simple and the control performance, when the controller is tuned appropriately, is usually very good. However, the control performance can be improved by increasing the controller order. The improvement depends on the process order. While the first-order process can be efficiently controlled by the PI controller and the second-order process by the PID controller, the control efficiency for higher-order processes can be improved by increasing the controller order beyond the PID control.
In practice the PI controllers are used more often than the PID controllers, since the latter significantly increase the controller output noise. Naturally, with higher degrees of controllers, the problem becomes aggravated. Therefore, the appropriate higher-order controller filter is inevitable in practical applications.
For easier classification of the HO-PID controllers according to the controller (m) and filter (n) order, let us denote them as . A general controller transfer function GCF(s) can be defined as follows:
where K−1, K0, K1, … Km are controller gains, and GF(s) is the binomial filter with filter time constant TF. In practical applications, in order to limit the higher-frequency controller output noise, n ≥ m. Note that denotes the PI controller (KI = K−1, KP = K0) and denotes the PID controller (KI = K−1, KP = K0, KD = K1) with the first-order filter (n = 1).
Several tuning methods for HO-PID controllers have been proposed so far. The majority of them are made for proportional-integrative-derivative-accelerative (PIDA) controllers (). The controller structure is either 1 degree of freedom (1-DOF) [,,,,,,,,,,,,,,,] or 2 degrees of freedom (2-DOF) [,,] which can optimise the tracking and control performance.
The tuning methods for the mentioned PIDA controllers are derived either for the first-order process with delay [,,], third order process [,,,,], first-order double integrating process [,,], second-order integrating process [,,,], double integrating process with time delay [], fourth-order system [], for different types of process models [,,] or for the automatic voltage regulator (AVR) in the generator excitation system [,,]. Unfortunately, only a few of the mentioned PIDA controller tuning methods take into account the controller filter in the controller design stage [,,,,,]. Therefore, the practical implementation of other PIDA tuning methods remains questionable.
Besides PIDA controllers, some higher-order controller tuning methods also exist [,,,]. The tuning method for the controller (the controller filter is not considered), where the controlled process is a model of the ship power plant, including the heat exchanger, is given in []. The method optimises the IAE for disturbance rejection while limiting the peak of the closed-loop amplitude frequency response.
Tuning methods for even higher-order controllers (m > 3) were developed for the integrating process model with a time delay (IPTD) [,,]. Although the type of the process model seems to be limited, we have to mention that many stable process models can be modelled as IPTD processes []. For HO-PID control of stable time-delayed processes, a new method was also proposed by generalizing Skogestad’s method SIMC []. The basic version is based on the approximation of processes by transfer functions with multiple time constants (obtained, for example, by an appropriate identification method); however, a suitable model can also be obtained from a more general description of the process reduced by the modified “half-rule” method []. Although not specifically designed for HO-PID controllers, we should also mention that the tuning approach is based on the design of multiple dominant closed-loop poles for delayed processes, applied to the PI and PID controllers [], which can be easily extended to HO-PID controllers.
The developed tuning methods for the controllers reveal that the HO-PID controllers can be much more efficient than the ordinary PID controllers without significant increase of the controller output noise.
This paper presents the controller and filter tuning method, which is based on the parametric or the non-parametric process description. It means that the process can be given by the general transfer function (of the arbitrary order and time delay) or by the process input and output time-responses during the steady-state change of the process. The only user-defined parameters will be the controller (m) and the filter (n) order and the desired high-frequency gain of the controller. As will be shown later, the controller parameters will be calculated analytically.
Therefore, the main advantages of the proposed method are the flexibility of the process description (the process model is not required), simple specifications by the user and simple calculation of the controller and filter parameters.
The content of the paper is as follows. The tuning method for the controllers is covered in Section 2. The calculation of the controller and controller filter time constant, according to the desired closed-loop high-frequency gain, is derived in Section 3. The comparison with some other tuning methods is carried out in Section 4. The paper concludes with Section 5.
2. HO-PID Controller Tuning
The HO-PID controller parameters will be derived according to the magnitude optimum multiple integration (MOMI) tuning method, which is based on the magnitude optimum (MO) criteria [,,,,,,]. The main advantages of the MOMI method are that it combines frequency-domain MO tuning criterion (providing a fast and non-oscillatory closed-loop process output response) with the time-domain method of moments (the calculation of the process characteristic areas directly from the process time responses).
The process
The general order process transfer function with time delay is defined by the following expression:
where KPR is the process gain, Tdel is the process time delay and a1 to ap and b1 to br are the process dynamic parameters. To simplify the derivation, let us assume that the process transfer function is developed into an infinite Taylor series around s = 0:
where GPk are the k-th derivatives of the GP(s) over s around s = 0. The moments can be calculated from the process impulse response h(t) in the following way [,]:
Besides measuring the process impulse response, the moments can also be calculated from the process steady-state change by measuring the process input and output time responses [,]. By integrating the process input and output time responses, the so-called characteristic areas Ak are obtained, which are related to the process moments as follows:
The process transfer function, based on the characteristic areas, can be derived from (3) and (5) as follows:
Since the calculation of the mentioned areas from the process input and output time responses, during arbitrary steady-state change, are already covered in detail in [], it will not be repeated herein.
The process moments (4) and, therefore, the characteristic areas Ak (5), can also be calculated from the process transfer function (2) by calculating the derivatives of GP(s) over s around s = 0. The result is the following [,]:
Therefore, the characteristic areas in expression (6) can be calculated either from the process time response or from the process transfer function. This is a very important advantage, since the actual process model can be used, but is not required.
In order to simplify the derivation of the controller parameters, the controller binomial filter GF(s) (1) will be considered as a part of the process. Since the above areas are calculated for the process without the filter, the areas Ai should be modified, accordingly. If the filter GF(s) (1) is added to the process (2) and developed into a Taylor series, it can be derived that the new areas, denoted by AiF, can be simply calculated as:
Note that n is the binomial filter order (1). Naturally, the chosen size of the matrix and the vectors depends on the number of the required areas.
Note that the characteristic areas with the included controller filter can be obtained a-posteriori, when the process areas Ai are already measured either from the process time response (5) or calculated from the process transfer function (7).
For further reference, please note that the process areas with the included controller binomial filter are denoted with index F (AiF) and the process areas without the controller filter are denoted without index F (Ai).
The closed-loop transfer function
In the paper, the process and the HO-PID controller (1) will be considered, as shown in Figure 1. Signals r, rf, e, u, d, n and y stand for the reference, filtered reference, control error, controller output, process input disturbance, process output noise and the process output, respectively. Block GFR represents the second order filter for the reference signal in order to reduce excessive controller output change on reference changes:
where TFR denotes the reference filter time constant. Due to simplicity, the filter order in (9) is fixed. However, note that the filter order may be increased by increasing the controller order so as to additionally attenuate the swings of the signal u for step-like changes of the reference signal r.
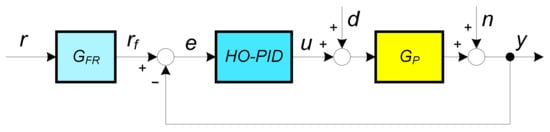
Figure 1.
The control loop with HO-PID controller and the process.
Let us now calculate the process closed-loop transfer function GCL(s) from the filtered reference (rf) to the process output (y). The closed-loop transfer function is then defined as:
where Y(s) and R(s) are the Laplace transforms of the process output and the reference signals, respectively.
When applying the process (6) and the controller (1) transfer functions to (10), and considering that the controller binomial filter is a part of the process (in the process transfer function (6) the areas Ai are replaced by AiF), the closed-loop transfer function becomes:
where GOL(s) denotes the open-loop transfer function GOL(s) = GC(s)GP(s).
The MO criteria
According to [], the MO tuning criterion states that the closed-loop amplitude (magnitude) should be 1 in as wide a frequency bandwidth as possible (starting from frequency ω = 0). This can be achieved if the open-loop transfer function GOL(jω), in the Nyquist diagram, follows the vertical line with the real value −0.5 (according to M and N circles in control theory).
Replacing s with complex frequency jω in GOL(s) (11) yields:
where j denotes the imaginary component .
Since merely the real part of the open-loop transfer function is required, only the even powers over frequency in (12) are needed. Therefore:
In order to achieve that the Re{GOL(s)} = −0.5 for as high frequencies as possible, the following conditions should be fulfilled:
or in matrix form:
Note that the matrix and vector dimensions depend on the number of controller parameters (m + 2):
The controller parameters (gains) can then be simply calculated from (15):
The calculation of the controller and filter parameters is straightforward. However, to make it even simpler, we have provided online MATLAB/Octave scripts via the OctaveOnline Bucket website []. The provided scripts calculate all the controller parameters for the given process transfer function and the filter time constant. The website layout is shown in Figure 2. The calculation procedure proceeds as follows:
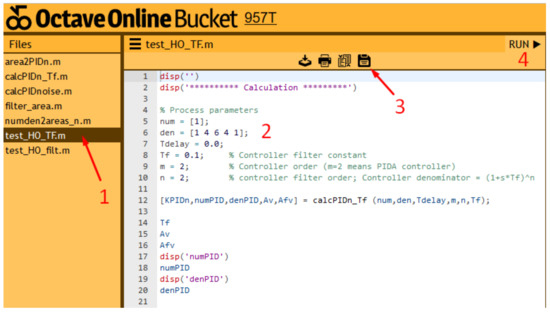
Figure 2.
The layout of the OctaveOnline Bucket website (function test_HO_TF.m).
- Select the appropriate Octave (MATLAB) script (test_HO_TF.m).
- Provide the process parameters, the filter time constant, the controller order and filter order,
- press the “Save” button, and
- press the “Run” button.
The script then calculates the characteristic areas, the controller and the filter parameters. The results are then shown on the right panel of the website.
Illustrative example 1
The , and controller parameters will be calculated for the following processes:
The chosen controller filter time constants is TF = 0.1. The characteristic areas, without (7), and with controller filter (8) are given in Table 1.

Table 1.
The calculated areas for the processes (18) without and with the controller filter.
The calculated controller parameters (17) are given in Table 2.

Table 2.
The calculated controller parameters.
In order to reduce the excessive swing of the controller output when changing the reference, the following reference filter time constant (9) is used for both processes:
Note that the second order reference filter is used (9).
The closed-loop responses for the processes GP1(s) and GP2(s), for all three types of controllers, are shown in Figure 3 and Figure 4. It is clear that tracking and control performance increase by the controller order. Note that the controller output response of controller is not shown entirely in order to see the responses of and controllers more clearly.
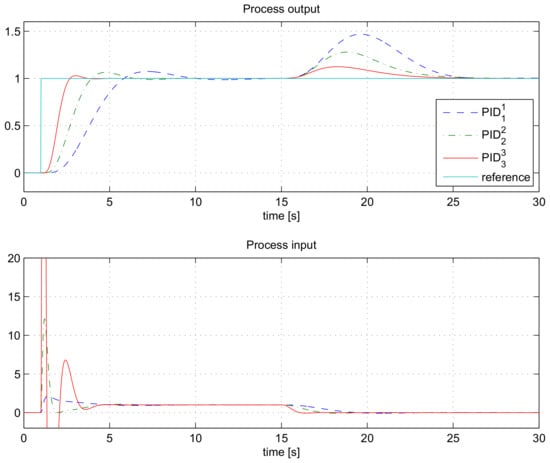
Figure 3.
The closed-loop responses for the process GP1(s) when using controllers , and .

Figure 4.
The closed-loop responses for the process GP2(s) when using controllers , and .
When comparing process output responses when using controllers and in Figure 3 and Figure 4, it can be seen that the relative difference in performance is larger on higher-order process GP1(s). This is expected, since lower-order processes can already be optimally controlled by lower-order controllers (e.g., the first-order process with and the second-order process with the controller). Since the second-order process GP2(s) has an additional delay, the closed-loop performance can still be slightly increased with the controller.
According to the closed-loop responses, it can be concluded that HO-PID controllers can significantly improve the closed-loop performance, especially for higher-order processes. The only required parameter from the user is the controller filter time constant TF. Namely, the amplification of the process output measurement noise depends on the chosen TF. However, the relation between TF and the actual amplification of the high-frequency (HF) noise depends on several other controller parameters and is a rather complex function. Therefore, in practice, it would be more appropriate to define the desired HF noise amplification than the controller filter time constant.
3. HO-PID Controller with Specified HF Noise Amplification
As mentioned in the previous section, the n-th order controller filter GF(s) (1) is primarily used to decrease the controller output noise due to the measurement noise (in addition to making the entire controller transfer function proper or strictly proper and, therefore, realisable in practice). High controller amplification of the measurement noise is never desired, since it may also cause large swings of the control output signals and thus may decrease the actuator’s life span. In order to limit the amplification of the process measurement noise, the user can try different values of TF until the desired amplification (attenuation) of the noise is achieved. In practice, this may take too long, since the function between TF and the noise amplification is complex and non-linear. Therefore, from the user’s perspective, it is easier to define the desired noise amplification of the controller than select filter time constant TF.
The process output noise (ny) is amplified by the controller (1) in the closed-loop configuration as follows:
where Ny and UN are Laplace transforms of the measurement noise and the controller output noise, respectively. The negative sign is omitted to simplify the derivation. From (20) it can be seen that at lower frequencies, the transfer function GCN(s) is mostly dominated by the process transfer function GP(s), while at higher frequencies, it is mostly dominated by the controller transfer function GCF(s). At lower frequencies, the process can be approximated by its gain KPR, while at higher frequencies the controller gains K−1 and K0 can be neglected. Therefore, GCN(s) can be approximated by the following transfer function:
On the other hand, the desired controller output noise (UND) should be similar to:
where KHF is a chosen noise amplification factor. Since amplitudes UN and UND cannot be compared directly due to different frequency characteristics, it is easier to compare noise powers of both signals in some chosen frequency bandwidth (from ω1 to ω2). Namely, due to Parseval theorem, the power of the controller output signal (PUN) is proportional to:
The desired noise power is, according to (22), proportional to:
When considering the Ny as a white noise with amplitude over frequency as Ny(ω) = 1, the powers PUN and PUND would become the same when:
However, the solution of the integral in (25), due to the denominator (controller filter), becomes very complex and highly non-linear in respect to TF. Therefore, some search algorithm (optimization) must be applied for each calculation of the TF.
This would seriously impact the simplicity of the proposed method. Therefore, it is decided to simplify the function inside the above integral. Since at higher frequencies, the most dominant controller term becomes the one with the highest derivative (Km), the function can be simplified as follows:
According to (26), the expression (25) simplifies into:
The contribution of noise power in the frequency region below ωF is usually much smaller than at higher frequencies. Therefore, in order to even further simplify the derivation, we can choose ω1 = 0 without making any significant error in the calculation. Selection of the upper frequency (ω2) in the integral, due to the Shannon theorem, depends on the controller sampling frequency. Without loss of generality, the upper frequency can be selected as:
where ωS is controller sampling frequency (in rad/s) and TS is controller sampling time. By taking into account that:
and ω1 = 0, the expression (27) simplifies even further:
Therefore, the final expression, when taking into account that Fm = Km2, reads as:
Therefore, the filter time constant (TF =1/ωF) can be estimated as follows:
Note that the above derivation of the filter time constant takes into account approximations (26) and (29). This means that the final output noise power of the controller may differ from that defined by the selected high frequency gain KHF. However, if the above approximations are not taken into account, then the final expressions for the calculation of ωF in (31) would become those of the higher order without analytic solution for TF. This would significantly complicate the filter calculation.
The entire procedure for the calculation of the controller parameters for a given process is given in Figure 5.

Figure 5.
Calculation of the filter and controller parameters.
As shown in Figure 5, the calculation of the controller and filter parameters is straightforward. However, to make it even simpler, as mentioned before, we have provided online MATLAB/Octave scripts via OctaveOnline Bucket website []. The website layout is shown in Figure 6. The calculation procedure proceeds as follows:
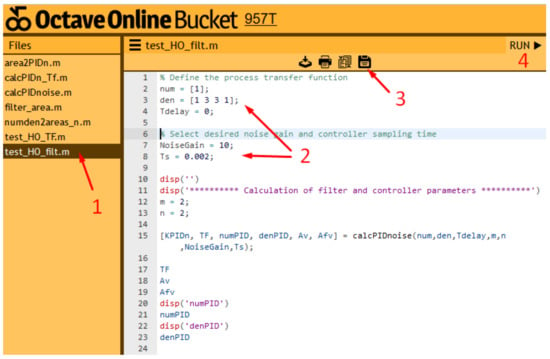
Figure 6.
The layout of the OctaveOnline Bucket website (function test_HO_filt.m).
- Select the appropriate Octave (MATLAB) script (test_HO_filt.m).
- Provide the process parameters, the desired noise gain, the controller sampling time, the controller order and filter order,
- press the “Save” button, and
- press the “Run” button.
The script then calculates the filter time constant, the characteristic areas and the controller parameters. The results are shown on the right panel of the website.
Illustrative example 2
Consider the following fourth-order process transfer function GP3(s) (18):
The initially chosen controller filter time constants is TF = 0.1. For all the experiments in this section, the chosen sampling time is TS = 0.002 s. In order to retain clarity of the derivations, the characteristic areas of the process are not mentioned herein; however, they can be calculated (besides all the controller and the filter parameters) on the aforementioned website [].
a. Changing the parameter KHF
According to the procedure given in Figure 5, when choosing parameter KHF, controller and repeating steps 3–5 a few times (in our case, 3 times), the calculated filter time constants, and the calculated controller parameters (17) are given in Table 3.

Table 3.
The calculated filter time constants TF and controller parameters at different noise gains KHF.
Again, in order to reduce the excessive swing of the controller output when changing the reference, the following second-order reference filter time constant (9) is used:
The closed-loop responses for different values of KHF are given in Figure 7.
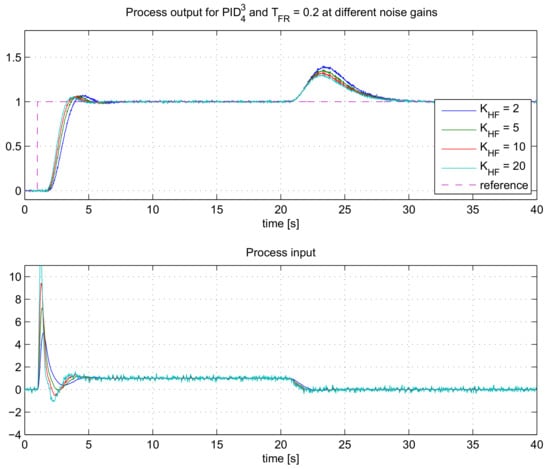
Figure 7.
The closed-loop responses for the process GP3(s) when using controllers , at different KHF.
As expected, the speed of the closed-loop response and the controller output signal noise increases by increasing the noise gain factor KHF. However, the improvement of the closed-loop speed is not so significant at the highest factors KHF. On the other hand, the controller output noise increases at higher factors KHF. As expected, there is a trade-off between the closed-loop speed and the amount of the controller output noise. Therefore, in practice, the allowed noise gain should be chosen wisely according to the amount of noise present in the system.
The actual “amplification” of the measurement noise (the actually achieved noise gain KHF) is measured by dividing standard deviations of the controller output signal (u) and the process output (n) when the process is in the steady-state:
The actual amplifications of the measurement noise signals are given in Table 3. It is obvious that the actual gains of the noise () are very similar to the desired ones (KHF).
b. Changing the filter order (n)
On the other hand, the speed of the closed-loop response, for the same KHF and the controller order (m), can also be altered by changing the filter order. In this regard, we tested the performance of the controllers , where n varies from 3 to 6.
According to the procedure given in Figure 5, when choosing KHF = 10 and repeating steps 3–5 3 times, the calculated filter time constants and the controller parameters (17) are given in Table 4.

Table 4.
The calculated filter time constants TF and controller parameters at different n.
The closed-loop responses for different controller filter orders (n = 3 to 6) are given in Figure 8.
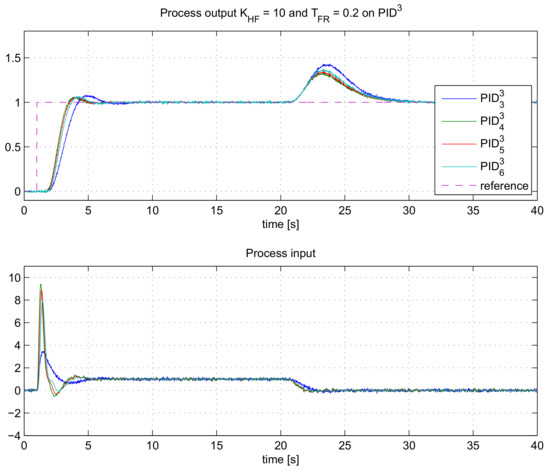
Figure 8.
The closed-loop responses for the process GP3(s) when using controllers with different filter orders , at KHF = 10.
As can be seen, the speed of the closed-loop response is the highest for controller . The speed of controllers with higher-order filters (n > 4) are slightly slower. The speed of response for n > 4 is not improving since a higher-order filter also adds some complexity to the closed-loop transfer function. This, in return, may result in lower closed-loop speeds.
The practical question is how to find the most optimal controller filter order in advance, before making the closed-loop experiment on the process. This can be answered by calculating the integral of control error (IE), which can be considered as a measure of the closed-loop speed:
If the closed-loop responses have small overshoots, the higher values of IE indicate slower closed-loop responses. For such responses, the IE can be a useful tool to measure the closed-loop speed. The IE value can be relatively easily calculated by transforming the equation (36) into Laplace domain. It can be shown that:
Therefore, for the process with the same steady-state gain KPR (2), the closed-loop speed is inversely proportional to the integrating gain (K−1) of the controller. Therefore, the controller with the highest gain K−1 will produce the fastest closed-loop response (providing that the closed-loop responses have small or negligible overshoots). Indeed, from Table 4 it is evident that the highest gain K−1 is calculated for controller This corresponds to our previous observations.
The actual amplifications of the measurement noise signals, according to (35), are given in Table 4. The actual noise gains () are very similar to the desired ones (KHF) for filter orders 3 and 4, while for higher-order filters the actual noise gain is lower. This is due to various assumptions (simplifications) made when deriving the filter time constant (32).
c. Changing the controller order (m)
As is already known, the speed of the closed-loop response can also be altered by changing the controller order. In this regard, we tested the performance of the controllers , where m varies from 1 to 4. In all cases the controller filter is chosen to be 1 order higher than the controller order (n = m + 1). The desired noise gain remains the same as in the previous experiment (KHF = 10).
The calculated filter time constants and the controller parameters (17) are given in Table 5.

Table 5.
The calculated filter time constants TF and controller parameters at different controller order m (n = m + 1).
The closed-loop responses for different controller orders (m = 1 to 4) are given in Figure 9.
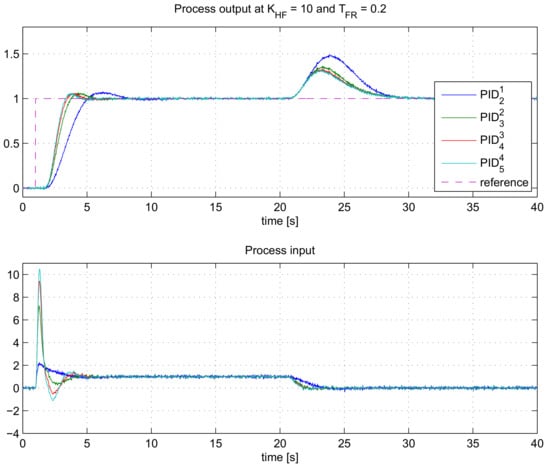
Figure 9.
The closed-loop responses for the process GP3(s) when using controllers with different controller orders , at KHF = 10 and n = m + 1.
As can be seen, the closed-loop speed increases by increased controller order, similar to the results in Figure 3 and Figure 4. The difference is that now the controller output noise is under control (KHF = 10), so the level of control noise is similar for all of the controllers. The fastest responses are obtained with . In a similar manner as in the previous case, the speed of responses can be estimated by comparing the values of the calculated integrating gains (K−1) in Table 5. Indeed, K−1 is the highest for .
The actual amplifications of the measurement noise signals, according to (35), are given in Table 5. The actual gains of the noise () are very similar to the desired ones (KHF) for all controller orders.
4. Robustness
The proposed design of HO-PID controllers results in a relatively fast and non-oscillatory response. In addition, the controller noise is under control by choosing parameter KHF. However, the designed closed-loop system can still be not robust enough to process variations. Namely, due to nonlinearity or time-variations of the process, its characteristics (gain, delay, time constants, etc.) can vary by working point or by time.
The robustness of a stable closed-loop system is usually measured by maximum sensitivity (MS) [,]. Maximum sensitivity is related to the distance of the open-loop transfer function GC(jω)GP(jω) from the critical point (−1+j0). Namely, MS is the inverse of the minimum distance between the open-loop transfer function and the critical point. Generally, a smaller value of MS denotes a more robust closed-loop system to process variations. Usual values of MS for stable processes are between 1.4 and 2.0 [,].
The robustness of the closed-loop system for the proposed HO-PID controllers has been tested on the following third-order process with delay:
where the nominal values are KPR = 1, Tdel = 1 and T = 1. Three different HO-PID controllers are selected: , , and . The calculated controller parameters, when choosing KHF = 10, TS = 0.002 s and according to the proposed tuning method, are shown in Table 6. The calculated values of the maximum sensitivity MS, for all three controllers, are shown in the same table. It can be seen that the MS values slightly increase with the increased controller order. However, the differences are not large and all the values are below 2.0.

Table 6.
The calculated filter time constants TF and controller parameters at different controller orders m (n = m + 1) for GP4(s).
Besides calculating the MS values, we were also simulating the closed-loop responses using all three controllers on the nominal process, and on the changed process (±10% change of process gain KPR, time-delay Tdel and time constant T). The closed-loop responses are shown in Figure 10, Figure 11 and Figure 12. It is evident that the closed-loop responses under perturbed parameters are still stable without significant oscillations. When comparing Figure 10 and Figure 12 it can be noticed that the perturbed parameters with controller result in slightly more deviation from the nominal response than with controller . This is all in accordance with the calculated values of MS in Table 6.
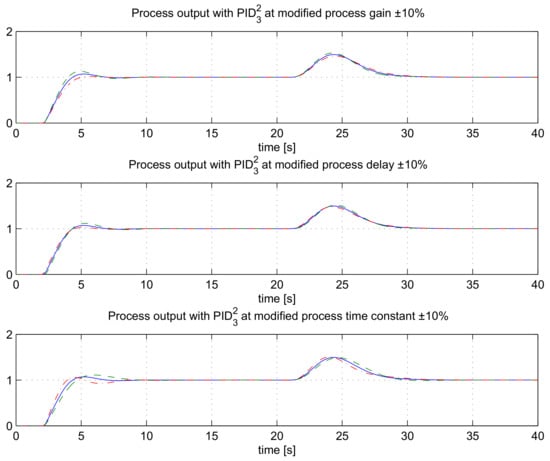
Figure 10.
The closed-loop responses for the process GP4(s), using controller at KHF = 10 for nominal (solid line), 10% increased (dashed line) and 10% decreased (dash-dotted line) process parameters.

Figure 11.
The closed-loop responses for the process GP4(s), using controller at KHF = 10 for nominal (solid line), 10% increased (dashed line) and 10% decreased (dash-dotted line) process parameters.

Figure 12.
The closed-loop responses for the process GP4(s), using controller at KHF = 10 for nominal (solid line), 10% increased (dashed line) and 10% decreased (dash-dotted line) process parameters.
5. Comparison with Other Tuning Methods
The proposed tuning method was compared with some other methods for PIDA controllers. The chosen methods, which were tested on a particular process model, are from Lurang and Puangdownreong [] (denoted as the Lurang method from here on) and Jung and Dorf [] (denoted as the Jung method from here on). The Lurang method involves calculating the PIDA controller parameters by optimizing the tracking and disturbance rejection response under several limitations given on rise time, overshoot, settling time, steady-state error and similar. The optimization is carried out with a modified bat algorithm proposed by the authors. The Jung method analytically calculates the PIDA controller parameters for the third-order process according to provided desired overshoot and settling time. Both methods do not take into account the controller’s filter. Therefore, the actual implementation in practice could be questionable if the filter dynamics become slower.
Case 1
The following process model has been selected, according to []:
The Lurang method suggests the following PIDA controller parameters:
The chosen controller filter time constant was very low (TF = 0.01), since we did not want to spoil the closed-loop response of the Lurang method. Namely, as already mentioned, the Lurang method does not take into account the controller filter in the design phase.
For comparison, we chose the controller structures with the lowest possible controller filter order n: . For illustrative purposes, the one-order higher controller structure () was also tested. Note that the closed-loop results of our proposed method, for the same level of controller noise, can be improved by using n > m.
The calculated controller parameters, for the given process and controller filter were the following:
We tested, separately, the tracking response and the disturbance rejection when using all three controllers. For tracking response, the reference (r) changed from 0 to 1 at t = 1 s and for disturbance response the process input disturbance (d) changed from 0 to 1 at t = 1 s.
The closed-loop responses are shown in Figure 13.
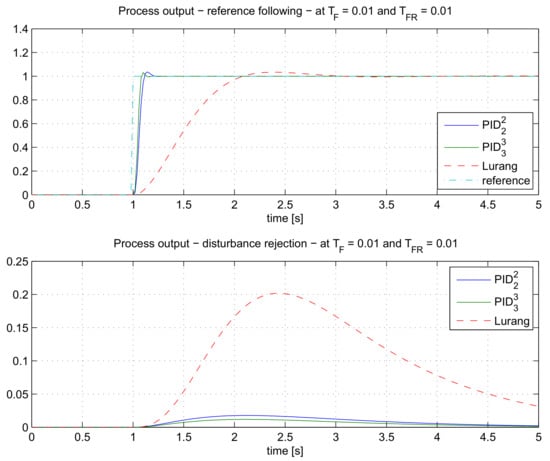
Figure 13.
The comparison of the closed-loop responses for the process GP5(s) when using , and the Lurang controller.
As can be seen, the responses of the proposed method with controller are superior to the Lurang method. Certainly, the one-order higher controller () has a better result.
For a more objective comparison, the integral of squared error (ISE) signal has been calculated for all three controllers. The results are shown in Table 7. It is obvious that the ISE values for the controller are much lower than the ones for the Lurang controller.

Table 7.
The ISE values for all three controllers in tracking and disturbance rejection.
Case 2
The second process model has been selected according to []:
The Jung method suggests the following PIDA controller parameters:
As before, the controller filter time constant was chosen very low (TF = 0.005), since we wanted to preserve the closed-loop response of the Jung method, which was obtained without the controller filter.
The calculated and controller parameters, for the given process and controller filter were the following:
As in the previous case, the closed-loop responses were tested on the tracking response and the disturbance rejection. The closed-loop responses are shown in Figure 14.
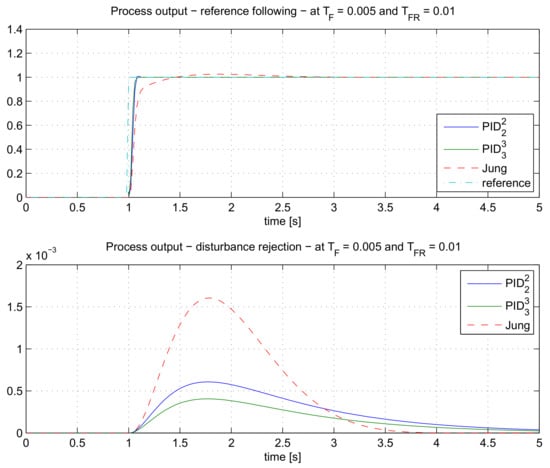
Figure 14.
The comparison of the closed-loop responses for the process GP6(s) when using , and the Jung controller.
Again, the responses of the proposed method with and controllers are superior to the Jung method. The comparison of ISE values in Table 8 shows controller has lower values than the Jung controller. However, note that the disturbance rejection settling time is the best with the Jung method.

Table 8.
The ISE values for all three controllers in tracking and disturbance rejection.
Case 3
The fourth-order process model has been selected according to []:
The Puangdownreong method suggests the following PIDA controller parameters:
The method calculated the following controller filter:
which was also used in design of the proposed controller parameters. For the given process and controller filter transfer function, the following controller parameters were calculated:
As in the previous case, the closed-loop responses were tested on the tracking response and the disturbance rejection. The closed-loop responses are shown in Figure 15.
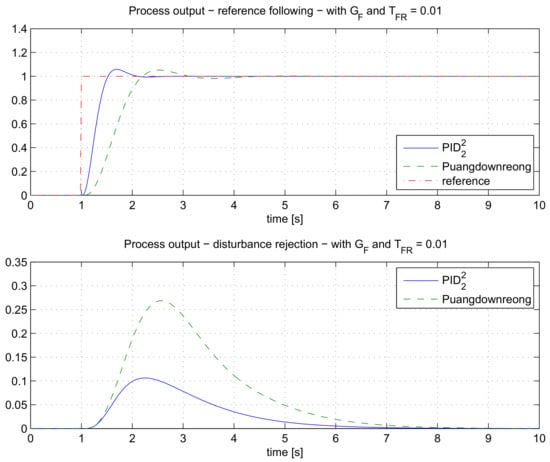
Figure 15.
The comparison of the closed-loop responses for the process GP6(s) when using and the Puangdownreong controller.
Again, the responses of the proposed method with the controller are superior to the Puangdownreong method. The comparison of ISE values in Table 9 shows the controller has lower values than the Puangdownreong controller.

Table 9.
The ISE values for both controllers in tracking and disturbance rejection.
6. Conclusions
In the paper, the method for tuning the parameters of the m-th order controller with the n-th order binomial filter has been presented. The proposed tuning method is based on the MO criteria which aims to produce non-oscillatory and fast closed-loop reference step responses. The calculation of the controller parameters is analytical and does not require any kind of optimization. An additional advantage of the proposed method is that the process can be described either by the process model or by the process time responses during the steady-state change.
To keep the noise gain of the controller under control, the filter time constant of the controller can also be calculated according to the specified noise gain. The calculation procedure is still analytical, and the results confirm that the level of controller noise is consistent with the given noise gain. The only exception is the use of larger relative degrees between the controller and the filter order, which is the consequence of some simplifications in the calculation of the filter time constant.
The proposed method was tested on six different process models (from second to fourth-order process models with or without time delay). The results confirmed that the control performance can be improved by increasing the controller order or by selecting the filter order appropriately without increasing the controller output noise. The study shows that increasing the filter order improves the performance only up to a certain level, after which the performance starts to decrease. The optimum degree of controller and filter order can be easily determined by the value of integral gain of the controller.
The tuning method was compared with three other tuning methods for PIDA controllers (Lurang [], Jung [] and Puangdownreong [] methods). Although the selected process models were the same as in the aforementioned methods, the proposed method resulted in a better control performance.
Therefore, the proposed higher-order controller design is efficient, and the controller output noise gain is under control. However, it does not mean that the proposed method cannot be improved. Indeed, the proposed method is based on optimizing the reference tracking performance. In our further research, we plan to improve the disturbance rejection performance as well. Namely, the article shows that the MO controller design leads to a strong asymmetry in the dynamics of tracking and disturbance rejection behaviour. While the HO-PID controller design leads to an increase in the number of pulses of the control signal after reference step changes, the responses of the control signal after the change of disturbance remain monotonic. This motivates us to deal with the modification of the MO controller design with regard to a faster response to disturbances.
Moreover, we also plan to design a method that will find the most optimal controller and filter order for the given process and noise amplification considering the complexity of the controller and filter order. We plan to calculate the optimal parameters of the reference filter to control the change of the controller output signal when the reference signal is changed.
Another planned modification is adding a user-defined parameter for changing the speed of the closed-loop control. Slowing down the control speed would further increase the robustness of the system.
Author Contributions
Writing-original draft preparation, D.V. and M.H. Simulations, D.V. and M.H. Editing, D.V. and M.H. Project administration, D.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the grants P2-0001 financed by the Slovenian Research Agency, APVV SK-IL-RD-18-0008 platoon modelling and control for mixed autonomous and conventional vehicles: a laboratory experimental analysis, and VEGA 1/0745/19 control and modelling of mechatronic systems in e-mobility.
Acknowledgments
Supported by Slovenská e-akadémia, n. o.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; Instrument Society of America: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Vilanova, R.; Visioli, A. PID Control in the Third Millennium, 1st ed.; Vilanova, R., Visioli, A., Eds.; Advances in Industrial Control; Springer: London, UK, 2012; ISBN 978-1-4471-2424-5. [Google Scholar]
- Alfaro, V.M.; Vilanova, R. Model-Reference Robust Tuning of PID Controllers; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Springer: London, UK, 2016. [Google Scholar] [CrossRef]
- Jung, S.; Dorf, R.C. Analytic PIDA controller design technique for a third order system. In Proceedings of the 35th IEEE on Decision and Control, Kobe, Japan, 13 December 1996; Volume 3. [Google Scholar] [CrossRef]
- Puangdownreong, D. Application of Current Search to Optimum PIDA Controller Design. Intell. Control Autom. 2012, 3, 303–312. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Paliwal, D. Design of PIDA Controller Using Bat Algorithm for AVR Power System. Adv. Energy Power 2016, 4, 1–6. [Google Scholar] [CrossRef]
- Ukakimaparn, P.; Pannil, P.; Boonchuay, P.; Trisuwannawat, T. PIDA Controller Designed by Kitti’s Method. In Proceedings of the ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 1547–1550. [Google Scholar]
- Smerpitak, K.; Ukakimaparn, P.; Trisuwannawat, T.; La-orsri, P. Discrete-time PIDA Controller designed by Kitti’s method with Bilinear transform. In Proceedings of the 12th International Conference on Control, Automation and Systems, JeJu Island, Korea, 17–21 October 2012; pp. 1585–1590. [Google Scholar]
- Huba, M. Filtered PIDA Controller for the Double Integrator Plus Dead Time. IFAC PapersOnLine 2019, 52, 106–113. [Google Scholar] [CrossRef]
- Jung, A.; Dorf, R.C. Novel Analytic Technique for PID and PIDA Controller Design. IFAC Proc. Vol. 1996, 29, 1146–1151. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, H.; Bhargava, A.; Sharma, N. Optimal design of PIDA controller for induction motor using Spider Monkey Optimization algorithm. Int. J. Metaheuristics 2016, 5, 278–290. [Google Scholar] [CrossRef]
- Jitwang, T.; Nawikavatan, A.; Puangdownreong, D. Optimal PIDA Controller Design for Three-Tank Liquid-Level Control System with Model Uncertainty by Cuckoo Search. Int. J. Circuits Syst. Signal Process. 2019, 13, 60–65, ISSN 1998-4464. [Google Scholar]
- Kumar, M.; Hote, Y.V. Robust CDA-PIDA Control Scheme for Load Frequency Control of Interconnected Power Systems. IFAC PapersOnLine 2018, 51, 616–621. [Google Scholar] [CrossRef]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y. Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng. J. 2019, 10, 755–767. [Google Scholar] [CrossRef]
- Dal-Young, H.; Ihn-Yong, L.; Young-Seung, C.; Young-Do, L.; BooKwi, C. The design of PIDA controller with pre-compensator [for induction motors]. In Proceedings of the 2001 IEEE International Symposium on Industrial Electronics Proceedings (Cat. No.01TH8570), Pusan, Korea, 12–16 June 2001; Volume 2, pp. 798–804. [Google Scholar] [CrossRef]
- Raju, M.; Saikia, L.C.; Sinha, N. Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller. Int. J. Electr. Power Energy Syst. 2016, 80, 52–63. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Multi-verse optimisation: A novel method for solution of load frequency control problem in power system. IET Gener. Transm. Distrib. 2017, 11, 3601–3611. [Google Scholar] [CrossRef]
- Sahib, M.A. A novel optimal PID plus second order derivative controller for AVR system. Eng. Sci. Technol. Int. J. 2015, 18, 194–206. [Google Scholar] [CrossRef]
- Bisták, P.; Huba, M. Analysis of Higher Derivative Degree PID Controllers via Virtual Laboratory. In Proceedings of the 27th Mediterranean Conference on Control and Automation (MED), Akko, Israel, 1–4 July 2019; pp. 256–261. [Google Scholar] [CrossRef]
- Lurang, K.; Puangdownreong, D. Two-degree-of-freedom PIDA controllers design optimization for liquid-level system by using modified mat algorithm. Int. J. Innov. Comput. Inf. Control 2020, 16, 715–732. [Google Scholar] [CrossRef]
- Ozbey, N.; Yeroglu, C.; Baykant Alagoz, B.; Herencsar, N.; Kartci, A.; Sotner, R. 2DOF multi-objective optimal tuning of disturbance reject fractional order PIDA controllers according to improved consensus oriented random search method. Int. J. Innov. Comput. J. Adv. Res. 2020, 25, 159–170. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D. Comparing filtered PI, PID and PIDD control for the FOTD plants. IFAC PapersOnLine 2018, 51, 954–959. [Google Scholar] [CrossRef]
- Simanenkov, A.L.; Rozhkov, S.A.; Borisova, V.A. An algorithm of optimal settings for PIDD2D3-controllers in ship power plant. In Proceedings of the 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 18–20 April 2017; pp. 152–155. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D. Introduction to the Discrete Time PIDmn Control for the PDT Plant. In Proceedings of the 15th IFAC International Conference on Programmable Devices and Embedded Systems, Ostrava, Czech Republic, 23–25 May 2018. [Google Scholar]
- Bistak, P. Disturbance Analysis Virtual Laboratory for PID Controllers with Higher Derivative Degrees. In Proceedings of the 2018 16th International Conference on Emerging eLearning Technologies and Applications (ICETA), Stary Smokovec, Slovakia, 15–16 November 2018; pp. 69–74. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D.; Bisták, P. PIDmn Control for IPDT Plants. Part 1: Disturbance Response. In Proceedings of the 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Huba, M.; Vrancic, D. Extending the Model-Based Controller Design to Higher-Order Plant Models and Measurement Noise. Symmetry 2021, 13, 798. [Google Scholar] [CrossRef]
- Vítečkova, M.; Víteček, A. 2DOF PI and PID controllers tuning. In Proceedings of the 9th IFAC Workshop on Time Delay Systems, Prague, Czech Republic, 7–9 June 2010; Volume 9, pp. 343–348. [Google Scholar]
- Vrančić, D.; Strmčnik, S.; Hanus, R. Magnitude optimum tuning using non-parametric data in the frequency domain. In Proceedings of the PID’00: Preprints: IFAC Workshop on Digital Control: Past, Present and Future of PID Control, Terrassa, Spain, 5–7 April 2000; pp. 438–443. [Google Scholar]
- Vrančić, D.; Strmčnik, S.; Juričić, Đ. A magnitude optimum multiple integration method for filtered PID controller. Automatica 2001, 37, 1473–1479. [Google Scholar] [CrossRef]
- Vrančić, D.; Strmčnik, S.; Kocijan, J.; de Moura Oliveira, P.B. Improving disturbance rejection of PID controllers by means of the magnitude optimum method. ISA Trans. 2010, 49, 47–56, ISSN 0019-0578. [Google Scholar] [CrossRef]
- Vrančić, D. Magnitude optimum techniques for PID controllers. In Introduction to PID Controllers: Theory, Tuning and Application to Frontiers Areas; Panda, R.C., Ed.; InTech Cop.: Rijeka, Croatia, 2011; pp. 75–102. [Google Scholar]
- Whiteley, A.L. Theory of servo systems, with particular reference to stabilization. J. IEE Part II 1946, 93, 353–372. [Google Scholar]
- Preuss, H.P. Model-free PID-controller design by means of the method of gain optimum. Automatisierungstechnik 1991, 39, 15–22. (In German) [Google Scholar] [CrossRef]
- Kessler, C. Über die Vorausberechnung optimal abgestimmter Regelkreise Teil III. Die optimale Einstellung des Reglers nach dem Betragsoptimum. Regelungstechnik 1955, 3, 40–49. [Google Scholar]
- Åström, K.J.; Panagopoulos, H.; Hägglund, T. Design of PI Controllers based on Non-Convex Optimization. Automatica 1998, 34, 585–601. [Google Scholar] [CrossRef]
- Octave Online Bucket Website. Available online: https://octave-online.net/bucket~957TukXTyYuXNMsxeL75FP (accessed on 8 April 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).