1. Introduction
The dynamics of the interactions between the individuals of different categories of a population may be modeled by autonomous first-order differential equations. For a period of time, there are situations when the total size of the population can be assumed constant, that is, the model is a dynamical system with constant population. For instance, we recall here the SIR model [
1], a model of the opiate-using career [
2], and the NERA model of drug consumption in a given population [
3]. Additionally, there are cases of high-dimensional Lotka–Volterra systems with constant population [
4,
5].
A dynamical system with constant population always has a constant of motion. In the three-dimensional case, if the system has a second constant of motion, then it admits a Hamilton–Poisson formulation. In addition, controlled versions of such a system that are also Hamilton–Poisson may be obtained by integrable deformations [
6,
7,
8].
The paper is organized as follows. In
Section 2, we particularize some known results about Hamilton–Poisson formulations and integrable deformations in the case of a three-dimensional dynamical system with constant population. In
Section 3, we consider three-dimensional Kolmogorov systems. We deduce the general form of a Lotka–Volterra system with constant population and we present a Hamilton–Poisson formulation of it. We give integrable deformations that are also with a constant population. Then, we obtain the general form of a polynomial Kolmogorov system of degree 3 with constant population and a particular version of it, which is Hamilton–Poisson. In
Section 4, we study the stability of the equilibrium states of the Lotka–Volterra system with a constant population restricted to
, the existence of periodic orbits, and we point out the heteroclinic orbits. We also study the properties of the energy-Casimir mapping associated with this system and their connections with the dynamics of the system.
2. Hamilton–Poisson Formulations and Integrable Deformations
In this section, we consider a system of three autonomous first-order differential equations:
where
such that the function
is a constant of motion. In this case, we say that (
1) is a three-dimensional dynamical system with constant population. System (
1) has only one constant of motion, namely
H, or there may exist another functionally independent constant of motion, denoted by
C.
In the following, we particularize some known results about Hamilton–Poisson formulations and integrable deformations in the case of system (
1). For the sake of completeness, we present some proofs. For details about Poisson geometry see, for example, [
9,
10,
11].
Proposition 1. Let where is a manifold, such that H and C are functionally independent on P, where . Then:
- (i)
Systemwhere is a dynamical system with constant population. - (ii)
C is also a constant of motion of system (2). - (iii)
is a Hamilton–Poisson formulation of system (2), where the Poisson structure is given byand H is the Hamiltonian. Furthermore, C is a Casimir of the Poisson structure .
Proposition 2. Let where is a manifold. If H and C are functionally independent on P, where , then systemis a dynamical system with constant population. Moreover, C is also a constant of motion and is a Hamilton–Poisson formulation of system (4), where is given by (3) and H is the Hamiltonian. Furthermore, C is a Casimir of the Poisson structure . The next result follows by [
13,
14].
Proposition 3. Let where is a manifold, and .
- (i)
If H and C are constants of motion of system (1) and they are functionally independent on P, then there is a differentiable function ν on an open and dense subset of P such that system (1) takes the form (4). - (ii)
If H and are functionally independent on P, then a family of integrable deformations of system (1) is given by:where g is a deformation parameter. Moreover, H and are constants of motion of system (5). - (iii)
If H is the only constant of motion of system (1), then a family of deformations of system (1) for which H is also a constant of motion is given by (5).
Proof. (
i) By hypothesis,
H and
C are functionally independent on
P, and thus at least one of the following inequalities
holds.
Let us consider
. Since
H and
C are constants of motion of system (
1), it follows that
Therefore . Considering , the conclusion follows.
From
we have
. Then
. Therefore system (
5) is obtained. It is easy to see that
H and
are constants of motion of system (
5). Then, by Proposition 2, where
C is replaced by
, (
5) is a Hamilton–Poisson system. Moreover, if the deformation parameter
g vanishes then system (
5) becomes (
1), as required.
Using (
5), it immediately follows that
. □
We end this section with some considerations about the dynamics of a three-dimensional dynamical system with constant population.
Let
be an initial condition of the system with constant population (
1) and
Since
H is a constant of motion, that is
for all
t, it follows that
for all
t. Therefore, it is clear that the dynamics of such a system takes place in the level surface
Moreover, if
C is the second constant of motion, then the trajectories belong to the intersection of the level surfaces
S and
As A. J. Lotka himself highlighted, “Periodic phenomena play an important role in nature, both organic and inorganic” [
15]. In our case, if
H and
C are functionally independent constants of motion and the intersection of the corresponding level surfaces is a closed curve, then the trajectory may be a periodic orbit. On the other hand, if
H is the only one constant of motion of system (
1) the Bendixon condition div
in a simply connected region of
S precludes periodic solutions in that region (see, e.g., [
16] and references therein).
3. A Particular Case: Polynomial Kolmogorov Systems
Let
be three continuously differentiable functions on
Consider the differential equations
called the three-dimensional ecological equations or Kolmogorov equations [
17,
18]. If
are polynomial such that the maximum of their degrees is
, then (
6) is a three-dimensional polynomial Kolmogorov system of degree
k. Particularly, if
, then (
6) is a three-dimensional Lotka–Volterra system. In this section, we deal with Kolmogorov systems of degree
with constant population. More precisely, we deduce the general forms of such systems that admit Hamilton–Poisson formulations. We recall here that the Liouville, Darboux integrability, respectively, of Kolmogorov and Lotka–Volterra systems and their dynamical behavior have been widely investigated (see, e.g., [
19,
20,
21,
22,
23,
24,
25] and references therein).
Proposition 4. If is a constant of motion of the three-dimensional Lotka–Volterra Equation (6), thenwhere . Proof. Let
. The condition
implies
or equivalently,
Then , and denoting , the conclusion follows. □
Remark 1. We obtained that a three-dimensional Lotka–Volterra system with constant population has the form Moreover, the function is a constant of motion of this system (see also [26]). In Section 4, we will study this system from some standard and nonstandard Poisson geometry points of view (for details about such approach see, e.g., [27]). The next result is a consequence of Propositions 2 and 3.
Proposition 5. Let .
- (i)
The three-dimensional Lotka–Volterra system with constant population (8) has the Hamilton–Poisson formulation where and the Poisson structureIn addition, system (8) reads , where and the rescaling function ν is given by - (ii)
If such that H and are functionally independent on P, then a family of integrable deformations of Lotka–Volterra system (8) is given bywhere is a deformation parameter. Moreover, (10) is also a system with constant population and is a constant of motion.
Taking into account the form of system (
10), it is natural to ask whether there are functions
such that (
10) is a polynomial Kolmogorov system. The answer is affirmative. Indeed, let us consider
where
Q is an arbitrary polynomial of degree
n. Then we obtain that system (
10) becomes
which is a polynomial Kolmogorov system of degree
. Moreover, by Proposition 5, it is a system with constant population for which
is a constant of motion.
In the sequel, we deduce the general form of a three-dimensional polynomial Kolmogorov system of degree 3 with a constant population. In addition, we present a family of such systems that are Hamilton–Poisson.
Proceeding as in the proof of Proposition 4, we obtain the following.
Proposition 6. The family of three-dimensional polynomial Kolmogorov systems of degree 3 with constant population is given by We note that system (
12) is a deformation of the Lotka–Volterra system (
8). Therefore, if this deformation is an integrable deformation, then system (
12) has a second constant of motion and, consequently, it is a Hamilton–Poisson system.
Proposition 7. A family of three-dimensional Hamilton–Poisson polynomial Kolmogorov systems of degree 3 with constant population is given by
where, . Moreover, is also a constant of motion of the above system. Proof. Using Proposition 6, it is obvious that (
13) is a three-dimensional Kolmogorov system with constant population. In order to prove that (
13) is a Hamilton–Poisson system, we show that it is a particular case of system (
10). Let
be as in Proposition 5 such that system (
10) becomes (
12). We obtain
and
Adding the above relations and equating the coefficients of the obtained polynomial to zero, we obtain
We denote
where
. Using (
14), we obtain that system (
12) becomes (
13). We also consider the function
given by
where
such that
. Now, on one the hand, function
fulfills the above conditions regarding partial derivatives. On the other hand, we have already seen that for such a function
, system (
10) becomes (
11), which also takes the particular form (
13).
By Proposition 5 it follows that
is a constant of motion and, consequently, (
13) is a Hamilton–Poisson system, as required. □
4. Dynamical Properties of the Three-Dimensional Lotka–Volterra System with Constant Population
In this section we study the dynamical properties of the three-dimensional Lotka–Volterra system with constant population (
8) and their connections with the corresponding energy-Casimir mapping. Lotka–Volterra systems [
28] are widely investigated from dynamical point of view (see, e.g., [
29,
30,
31] and references therein).
As we have seen in
Section 3, the three-dimensional Lotka–Volterra system with constant population is given by
In addition, the constants of motion of this system is
In the following we consider and we restrict our study on the set which is the region of ecological interest.
System (
15) has the Hamilton–Poisson formulation given by Proposition 5. Therefore, the corresponding energy-Casimir mapping is given by
There are some connections between the dynamics of a Hamilton–Poisson system and the properties of the corresponding energy-Casimir mapping (see, e.g., [
27,
32,
33,
34,
35,
36,
37,
38]). Most of the connections are provided by the partition of the image of the energy-Casimir mapping given by the equilibrium states. In the abovementioned papers, the energy-Casimir mapping is defined on
; thus, we are interested to see which of the properties remain true in our case.
Lemma 1. Moreover, the equality holds if and only if .
Proof. If
, then the inequality holds. Let
. We apply Jensen’s inequality for a real concave function
, namely
The equality holds if and only if or is linear.
Let and , . Then the conclusion follows. □
Remark 2. For and , the inequality from Lemma 1 becomesand the equality holds if and only if . Now, we can present the image of the energy-Casimir mapping (
17).
Proposition 8. The image of the energy-Casimir mapping (17) is the set Proof. Using Lemma 1, we obtain the conclusion. □
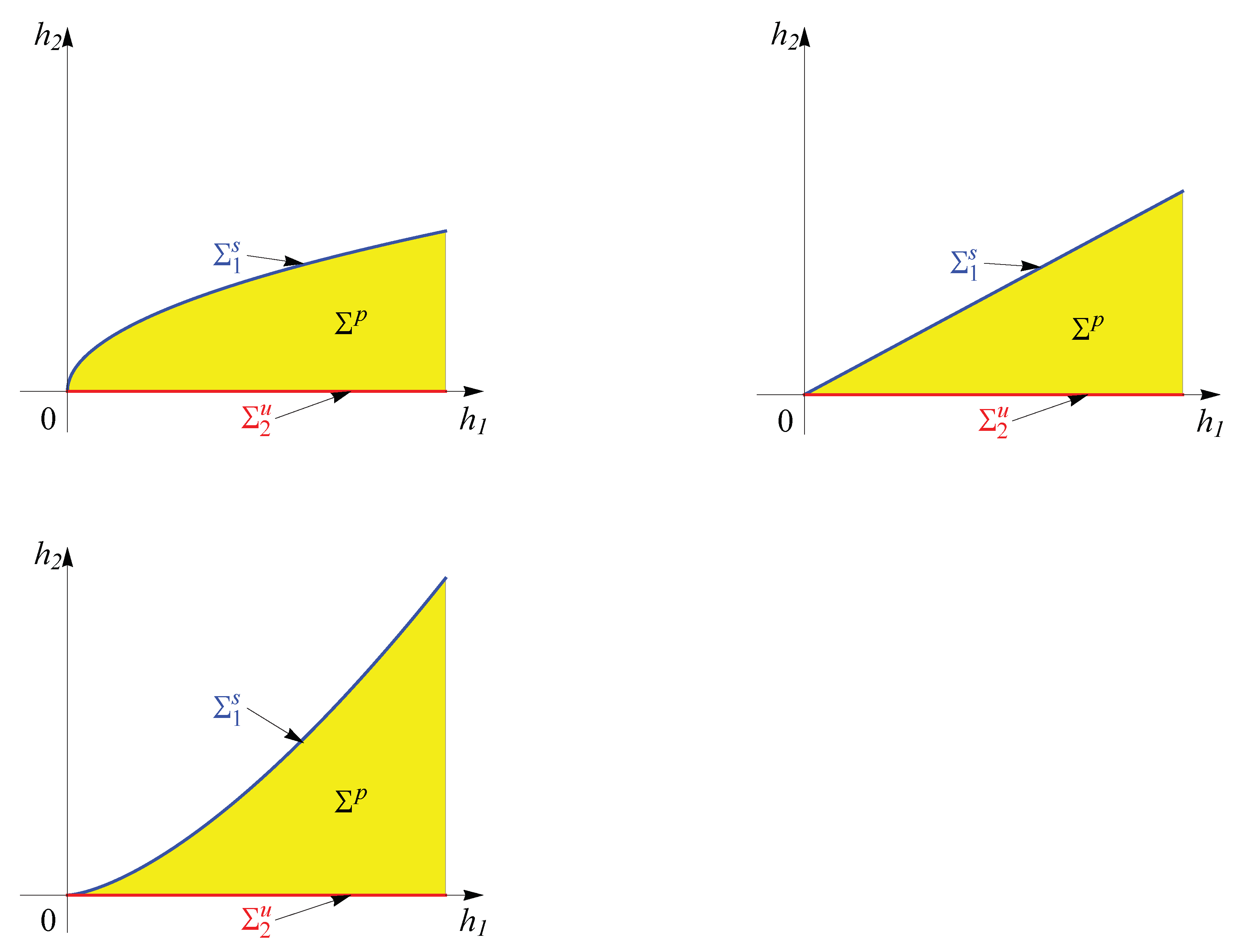
Remark 3. The image of the considered energy-Casimir mapping is drawn in Figure 1. In the abovementioned papers, if Im is a proper subset of , then its boundary is given by the images of the stable equilibrium states through . Moreover, a partition of Im is given by the images of all equilibrium states through . If the image of an unstable family of equilibrium states through is a half-line, then there are heteroclinic orbits that connect pairs of such states. Furthermore, if denotes an open subset of the partition of that has dimension 2, then each point of is the image of at least one periodic orbit through . In our case, because is restricted to , the image of the energy-Casimir mapping is a proper subset of , but without this restriction, it is . If the image of the energy-Casimir mapping is , the dynamics is more complicated, but we can expect to find periodic orbits and heteroclinic orbits. In the following we study the abovementioned connections.
The equilibrium states of system (
15) are given by the families
Proposition 9. If , the equilibrium states of system (15) that belong to the family (20) are Lyapunov stable. Proof. Let
. We use the Arnold method [
39]. Consider the function
and let
. For
, we obtain:
- (i)
- (ii)
, which is negative definite for all
Therefore the equilibrium state is nonlinearly stable. □
Proposition 10. For every , the equilibrium states of system (15) that belong to the families (20) are unstable. Proof. Let
J be the Jacobian matrix of system (
15). Then
The eigenvalues of are given by . Since , the equilibrium state is unstable for all . Analogously, we study the stability of the other equilibrium states. □
It remains to study the stability of , the common point of all families of equilibrium states.
Consider that system (
15) is without the restriction
We choose the initial conditions
, where
is near to zero. Then we obtain the particular solution of system (
15) given by
Therefore, the equilibrium state
is unstable.
On the other hand, our system is restricted to
. The coordinate axes and the subspaces spanned by them, and also the first octant, are all invariant sets for a Lotka–Volterra system with constant population (
15). Hence, populations that start non-negative remain non-negative. If
V is a neighborhood of
, then we say that
is a positive neighborhood of
.
The next result shows the behavior of a trajectory that starts in a positive neighborhood of .
Proposition 11. For every positive neighborhood U of there is a positive neighborhood V of such that the trajectories of system (15) initially in V never leave . Proof. Consider the initial conditions of system (
15) given by
. Thus
for
. We have to prove that for all
there is
such that if
, then
for
.
For every
let
such that
. Then the following relations hold:
for every
as required. □
Remark 4. In the case when system (15) is restricted to , Proposition 11 tells us that behaves as a Lyapunov stable equilibrium state. Remark 5. For every , the sets of images of the equilibrium states through are given bywhere “s” and “u” stand for stable and unstable, respectively. We note that in our case the boundary of Im is given by . We also denote by the interior of Im (see Figure 1). Therefore, In the next result we prove that there are periodic orbits of the considered system around the stable equilibrium states. In [
40], the existence of periodic orbits of a similar system has been proven by another approach.
Proposition 12. Let be such that . Then, for each sufficiently small , any integral surfacecontains at least one periodic orbit of system (15) whose period is close to . Proof. We apply a version of Moser’s theorem in the case of a zero eigenvalue [
41]. By (
21),
has the eigenvalues
,
and the eigenspace corresponding to the eigenvalue zero has dimension 1. Consider the constants of motion
and
. We obtain
,
, and
, which is positive definite for all
.
By Theorem 2.1 from [
41], for each sufficiently small
, any integral surface
contains at least one periodic solution of system (
15) whose period is close to the period of the corresponding linear system around
which finishes the proof. □
Another special orbit of a Hamilton–Poisson system is the heteroclinic orbit. In our case we have the following.
Proposition 13. For each there is a cycle of heteroclinic orbits that connect the unstable equilibrium states given bywhere and . Proof. To obtain a parametric form of the heteroclinic orbit
, we first reduce our system from three degrees of freedom to one degree of freedom by using the level sets
and
and then integrate the resulting reduced differential equation. We have
Consider
. Thus,
and system (
15) reduces to
. Let
be the initial condition of the above equation. We obtain the solution
and then
. We similarly obtain the other parametric forms of the heteroclinic orbits. □
Remark 6. By geometrical point of view, the heteroclinic orbits given in Proposition 13 are open line segments with endpoints given by the unstable equilibrium states. Another approach in the study of the existence of heteroclinic orbits of a similar system has been used in [40]. The dynamics of system (
15) takes place at the intersection of the level sets
where
The fiber of the energy-Casimir mapping
corresponding to
is the set
Then, in other words, the dynamics of system (
15) takes place on the fibers of the corresponding energy-Casimir mapping. In the following we give a topological classification of these fibers and, as a consequence, we point out the connections between the partition of Im
and the dynamics of the considered system. This classification is provided by the partition of the image of the energy-Casimir mapping (
22).
Proposition 14. Let (19) and (23) be the corresponding fiber of the energy-Casimir mapping. - (i)
If , then where that is, a stable equilibrium state. In addition,
- (ii)
If , then is the triangle with vertices at where that is, three unstable equilibrium states and the cycle of heteroclinic orbits that connect them (see Proposition 13).
- (iii)
If , then that is, a periodic orbit.
Proof. (
i) Let
(
23),
where
is given in Remark 5. Using Lemma 1, we obtain
Since
we obatin the conclusion.
We have and . Using Proposition 13 and Remark 6, the conclusion follows.
The dynamics of system (
15) takes place at the intersection of the level sets
and
which is the closed curve drawn in
Figure 2. On the other hand, by Proposition 12 we know that there are periodic orbits around the stable equilibrium
for every
. Hence, in this case, we conclude that the fiber is a periodic orbit. □
We notice that the level set
is locally foliated by the periodic orbits that expand from the stable equilibrium
Moreover, these orbits tend to the heteroclinic cycle given by the boundary of
(see
Figure 2, right).
Remark 7. Consider that system (15) describes the dynamics of the interactions between three categories of a constant population of total size h. After an interaction between individuals from distinct categories, they can change their category. At a moment t, we denote by the number of individuals of these categories. At , the initial conditions are such that and . The above analysis shows the following types of behaviors. First, if , then we obtain a periodic behavior around the stable equilibrium . Second, if , then for all since the plane of equation is an invariant set of our system. In this case, system (15) reduces to , and hence x increases in time and y decreases, that is approaches in infinite time (the heteroclinic orbit ). Analogously, if then approaches , and if then approaches . Finally, if is an equilibrium state, then the number of individuals from each category stays unchanged.