Abstract
The dynamics of a specific consumer-resource model for Daphnia magna is studied from a numerical point of view. In this study, Malthusian, chemostatic, and Gompertz growth laws for the evolution of the resource population are considered, and the resulting global dynamics of the model are compared as different parameters involved in the model change. In the case of Gompertz growth law, a new complex dynamic is found as the carrying capacity for the resource population increases. The numerical study is carried out with a second-order scheme that approximates the size-dependent density function for individuals in the consumer population. The numerical method is well adapted to the situation in which the growth rate for the consumer individuals is allowed to change the sign and, therefore, individuals in the consumer population can shrink in size as time evolves. The numerical simulations confirm that the shortage of the resource has, as a biological consequence, the effective shrink in size of individuals of the consumer population. Moreover, the choice of the growth law for the resource population can be selected by how the dynamics of the populations match with the qualitative behaviour of the data.
Keywords:
size-structured population; numerical methods; characteristics method; growth laws; asymptotic behaviour; Daphnia magna MSC:
92D25; 92D40; 65M25; 65M12; 35B40
1. Introduction
Population dynamics is a very active field with different disciplines (epidemiology, ecology, etc.) in which a variety of theoretical studies and different numerical approaches arise. The purpose of this work is to analyse, from a numerical point of view, some aspects of the dynamics of a problem that describes the evolution of a Daphnia magna population, as an example of a consumer-resource model. As, in general, it is not feasible to obtain its dynamics from a theoretical point of view, the behaviour of the solutions to the problem is analysed with numerical techniques. The model is solved by means of an efficient numerical method adapted to the problem, which was proposed and analysed in [1]. It is a second-order method that has been used successfully to obtain numerical approximations to solutions of a wide range of physiologically structured population problems [1,2,3]. The numerical method provides the size dependence of the density of the consumer population and can afford numerical approximations even in the situation of unbounded density functions. With this help, the evolution of the consumer-resource model of the Daphnia magna is studied to evaluate the effect of different biological growth laws for the resource on the dynamics of the model. The method allows achieving certainty regarding different conclusions on the dynamics of the model.
Many population dynamics models can be formulated and analysed as a specific physiologically structured consumer-resource model. In de Roos and Persson [4], a trophic chain population model with a resource, a consumer, and a top predator is considered, and its stability analysis was performed in Sanchez and Getto [5]. Cuesta et al. [6] studied the stability of a problem for phytoplankton cell dynamics and allometry in the growth rate and a top predator. Pang et al. [7], also studied the stability of models structured by the age of infection for HIV transmission. The group of Lafferty approach to these models is through the formulation of a general complete macrostructured population model [8]. Aylaj and Noussair [9] analysed the convergence of a numerical method for the approximation to the solution of a multistage kinetic model of a physiologically structured population of insects with four stages in their life-cycle. The numerical integration for an erythropoiesis model with two dynamical growth factors (erythropoietin and glucocorticoids) was proposed in [10].
The pioneering work of Kooijman and Metz [11] was the beginning of the theoretical study of consumer-resource models. These authors presented a mathematical model for the development of an ectothermic population (Daphnia magna, water flea) in which the amount of food they are supplied with represented a regulatory mechanism for the population density. The model was length-structured and also included a stage of maturity: the difference between juveniles and adults in the population. A few years later, this model was studied by Thieme [12]. He described the population as a distributional solution of a classical partial differential equation formulation and explained heuristically why the well-posedness was a problem and to what extent it could be solved. He also included a dynamical environment in which individuals fed and that evolved with a general growth law in absence of a consumer. In [13], Diekmann et al. proved that, under appropriate assumptions, the local stability of a steady-state was determined by the spectral properties of the linearised semigroup. They applied this theory to the consumer-resource model that was transformed into a delay ordinary differential equation coupled with a birth law (Volterra functional formulation). They employed the age of individuals as the structuring variable with a finite life span and a finite delay in the description of the birth law. These results were extended to the infinite delay case in [14], which allowed them to study problems with infinite life span. The properties of the stability of the former model proposed by Kooijman and Metz, including the maturation stage, were studied in [15]. This work led to the theoretical support of [16], where de Roos et al. performed a numerical study of such equilibria. This analysis assumed positive continuously differentiable vital rates and only continuous at the value of maturity.
On the other hand, the numerical study of the dynamics of the model is also important because it gives an answer to problems that cannot be addressed theoretically. With respect to the research on the dynamics of the model, recent papers [17,18], tried to compute the roots of the characteristic equation numerically by means of pseudoespectral discretisation and then determine the stability properties. This last procedure was also applied to a more complex model that introduced to the system a superconsumer (predator) [5]. Moreover, suitable numerical methods were proposed to approximate the solution of the problem and were used to study its dynamics by means of a long-time integration. These studies concerned different cases that also included an unbounded consumer population [1,2,3,19].
Consumer-resource models with undefined sign growth rates for the consumer population still have to be considered theoretically concerning the existence, uniqueness, and regularity of solutions. Numerically, only [1,2,3] dealt with this problem but by employing a logistic growth law for the resource. The numerical method used in the simulations is well adapted to this situation in which the growth rate is allowed to change the sign, and therefore, individuals in the consumer population can shrink in size as time evolves.
The remainder of the paper is organised as follows. Section 2 describes a general consumer-resource model of a physiologically structured population and the growth laws for the resource considered in the numerical experiments. In this model, the maximum size of individuals in the population is not fixed and they are allowed to shrink. The main contribution is included in Section 3, where an extensive numerical experimentation, for the case of the Daphnia magna, is reported using vital rates and initial conditions selected from the literature. The simulations will show the complexity of the dynamics of both populations (consumer—Daphnia magna—and resource—algae) under different biological growth laws and parameter values in the model. The numerical experimentation is developed with an efficient numerical scheme, which is completely described in Appendix A to make the paper self-contained.
2. The Daphnia magna Model and the Growth of the Resource
The problem studied is in the form introduced by de Roos [19]: he did not consider a maturation stage to distinguish between juveniles and adults (therefore individuals started reproducing immediately after they were born), and for the first time, he described the growth rate of the consumer population with a function that had an undefined sign. This difficult issue, from a mathematical point of view, provided an answer to the modelisation of rare species that could diminish their size.
A size-structured consumer-resource model that represents the evolution of a single consumer population preying on a single resource (for instance, a Daphnia magna feeding on an algal population) is employed. In general, this model is composed of two nonlinear coupled problems. On the one hand, the evolution of the consumer population, which is structured by the length of the individuals. On the other hand, the evolution of a resource, which is seen as an unstructured population. Henceforth, the model is composed of a classical size-structured problem driven by a nonlinear hyperbolic partial differential equation (conservation law), a nonlocal boundary condition (the birth law), and an initial condition:
and by the following nonlinear initial value problem
Here t and x represent, respectively, the time and the length of the consumer individuals, and and denote the minimum and maximum consumer individual length at the initial distribution, respectively. Functions and mean the available resource and the density of individuals with length x at time t, respectively. The solution of this evolution problem depends on the initial conditions , , and , the vital rates that define the evolution of the consumer (growth, birth, and death), and the biological growth law of the resource. The fertility and mortality rates, and , respectively, are non-negative functions. The growth rate, g, has the following special properties: it has an undetermined sign but 0 at any time . These conditions on the growth rate mean that, on the one hand, individuals grow from their birth and, on the other hand, individuals in the population can shrink under food scarcity conditions. These vital rates are influenced by the time, the length of an individual and the available resource. Next, the biological growth law of the resource is represented as the sum of two terms to fulfil the requirements of the further numerical experimentation. The first one, , introduces the evolution of the resource without the consumer influence; the second one, , takes into account the intake of resources by the consumer-population individuals through a quantity, , that represents its consumption along time. It is described with the following nonlocal term,
where represents the intake of individuals of size x in the consumer population at time t and also depends on the available resource. Thus, the evolution of the individuals in the consumer population is affected by the competition for food through the vital rates, which depends on the available resource itself. The evolution of the feeding resource is modified by the individuals through (2).
Finally, the maximum individual length, , is not fixed and can evolve in a non-monotonical way with time due to the lack of restriction on the growth rate sign. Its evolution follows the corresponding characteristic curve. It is the solution of the next initial value problem,
To close this section, different alternatives for the growth of the resource in the absence of a consumer, which is given by , will be discussed. The analysis is focused on the growth phenomena with the introduction of three basic distributions which provide the main mathematical frameworks.
- (1)
- The exponential growth: , .This is the most basic and simplest growth function and, in essence, it is the growth relationship considered by Malthus (see [20], for instance). The parameter r is the specific growth rate. When , there is only an equilibrium for the differential equation associated: the trivial solution. If , the trivial equilibrium is an attractor. If , this solution is unbounded.
- (2)
- The chemostat growth function: , , .This is a modification of the exponential growth function with a limited increment that depends on the carrying capacity K. There is a stable nontrivial equilibrium that corresponds with the carrying capacity. When the population increases, and the growth is slower because the available resources decrease. In the case , population decreases to the carrying capacity. It also can represent a population, given by s, that is growing up in an environment in which a constant quantity of feeding is provided (the carrying capacity) and r represents the dilution rate [20].
- (3)
- The Gompertz growth function: , , .The Gompertz equation was formulated originally as a law of decreasing survivorship, but it has also been employed to model the growth of plants, tumours, and fisheries [20]. There is a limited carrying capacity. The population has a similar behaviour as when the biological growth is described with the well-known logistic growth law because there are two equilibria: the unstable trivial equilibrium and a stable nontrivial one.
Although there are other possibilities (logistic, power laws, Ricker’s, Weibull or Gaussian distributions, etc., or diverse combinations among them) the results will show enough variability to consider that the discussion is enough with these choices. The logistic growth, which was studied in [1,2,3,19], deserves a special mention. Numerical simulations for this growth law will not be reported because the dynamics obtained with the numerical method are basically not different from the numerical results discussed for the Gompertz growth law.
3. Numerical Experimentation
As it was previously stated, the main interest is to discover the dynamics of the particular case introduced in [19] to describe the evolution of the Daphnia magna population, by using different growth laws for the resource. Therefore, most of the parameter data and functions that were employed in that work are considered in this study. The growth rate is given as , the mortality rate function is chosen constant, , and the fertility rate is defined . The function that controls the way in which consumer individuals use the resource, in the definition of the nonlocal term (3), is considered . The functional that depends on the consumer is given by . It has to be noted that the growth and fertility rates, and the nonlocal term weight function depend on the resource through the Micaelis–Menten law. Lastly, the parameters employed are , , and , as in [19].
The numerical method used in the simulations was analysed in [1] and, for the sake of completeness, is fully described in Appendix A. The second order of convergence was proven under enough regularity hypotheses on the function data. It should be pointed out that the following numerical results are performed beyond the limits of the numerical convergence theorem because the integration could be made on unbounded problems. On the one hand, the search of the asymptotic behaviour of the problem compels to employ an undetermined large time interval. On the other hand, some combination of the parameter values (as the one employed in [19]) makes the population density unbounded close to the maximum size , . This last case was explored in [3], and it arises from the relationship , which makes the equilibrium solution unbounded when the size of individuals tends to the maximum size. It should be argued that this situation is fully admitted because most of the theoretical analysis made for the model asks for solutions on , (see [13], for instance). Although the study performed in the following avoids this kind of unboundness, the numerical approximation given in [3] was based on modifying the removing procedure (see Equation (A3), Appendix A) to adapt it to the behaviour of the solution. Therefore, the value is employed, that ensures both the boundedness of the solution without affecting the behaviour of the model and the non-negativity of the resource at equilibrium.
In addition to the fixed parameters previously introduced in the vital functions, different experiments with diverse values of the parameters , the specific growth rate of the resource, and , the carrying capacity, are performed. In each trial, the following initial conditions are employed: ( in the case of Malthusian growth, where there is no declared carrying capacity), and
where and are chosen to fulfil the compatibility between initial and boundary conditions.
If the growth rate of the resource is autonomous, the computation of the theoretical equilibrium of (1)–(4) is possible, due to the choice of the function data in this test problem (note that all the growth functions described in Section 2 are independent of time). Thus, when is defined as the autonomous representation of , whenever a nontrivial steady state of (2), , exists, the nontrivial equilibrium state for the coupled problem (the maximum size, consumer, and resource) is given by the following formulae [1]:
This nontrivial equilibrium state could be stable, unstable or even not exist. The initial values considered in (5) are different enough from this state to observe the convergence of the solution towards such a nontrivial equilibrium state when it happens.
The numerical integration is carried out in an undetermined finite time interval that varies in different circumstances (for instance, in the case of the Malthusian growth, the integration time is left free to arrive to extinction or an unbounded solution). In previous works [1], the convergence of the numerical approximation to the theoretical nontrivial equilibrium (when it exists) was stated. The good behaviour of the numerical scheme allows reaching the possible behaviours: unbounded solutions, trivial equilibrium (extinction of the consumer population), nontrivial equilibrium (coexistence of both populations), and periodical solutions (stable limit cycles). It is observed that it is enough to consider the discretisation parameters values as to describe the full asymptotic dynamics of the problem.
All in all, different scenarios of the growth of the resource in the absence of the population will be considered, and the influence of the consumer population on the dynamics will be discussed. Therefore, although the original work of de Roos [19] introduced a feeding resource that evolved with a logistic function, its behaviour is challenged with the three other new possibilities presented in the previous section.
3.1. Malthusian Growth
The first choice consists of considering an unlimited growth. The evolution of the resource is given by the Malthusian growth, with a constant intrinsic rate of growth, , . Therefore, the resource grows exponentially when and declines to extinction when r is negative. It would only remain constant when births balance deaths ().
This kind of growth is introduced into the model. The main consequence expected would be that the consumer expedites the decline of the resources, due to the consumption effect produced by . Therefore, it could be thought that will remain the threshold value of the intrinsic rate of growth that separates the exponential growth from the extinction of the resource.
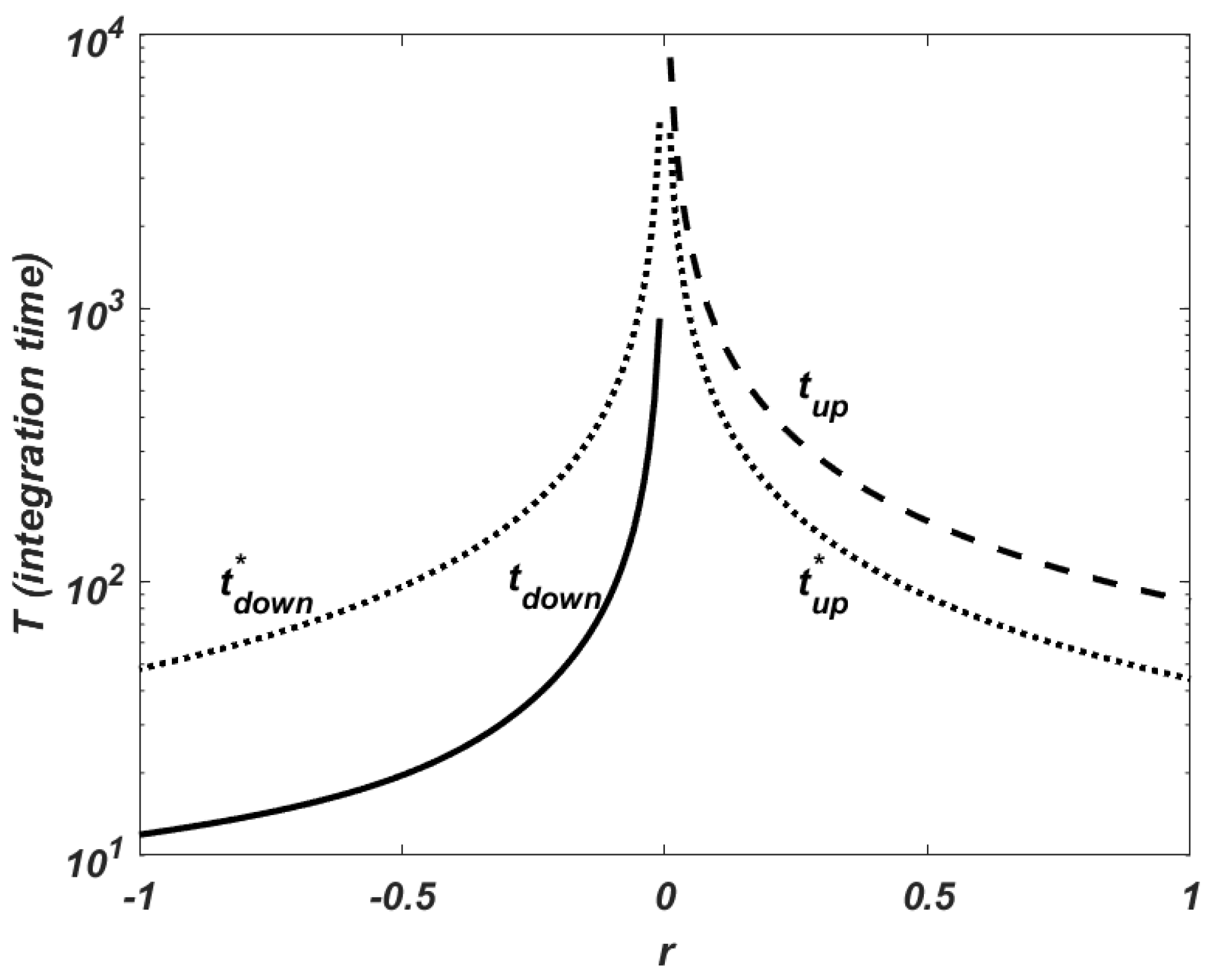
In order to validate this assumption, and are computed. is the integration time at which the approximated value of the resource is higher than , a sufficiently large value to represent an exponential growth, i.e., an unbounded solution. is the integration time at which the numerical approximation is lower than , a small enough value to represent the extinction of the population. It is obvious that both values are mutually exclusive. In addition, the theoretical time values that correspond to these integration times but when there is no consumption of the resource are computed. The following formula is employed or . In Figure 1, the results obtained with the numerical experimentation are plotted. The intrinsic rate of growth r is in the set and r is drawn versus and or and , in a semilogarithmic scale. It is observed that the consumer influence is interpreted as a modification of the response speed. It decreases the time the resource takes to arrive to extinction and increases the time that the numerical approximation needs to reach the fixed upper bound. Furthermore, the value of the intrinsic growth at which the population remains constant disappears, and when , the resource tends to extinction slowly. This behaviour shows the small influence of the consumer population on the resource evolution with this kind of growth function. Finally, the evolution of the consumer population is closely related to the behaviour of the resource and it grows exponentially in the case of unlimited resources and decays to extinction with scarce resources.
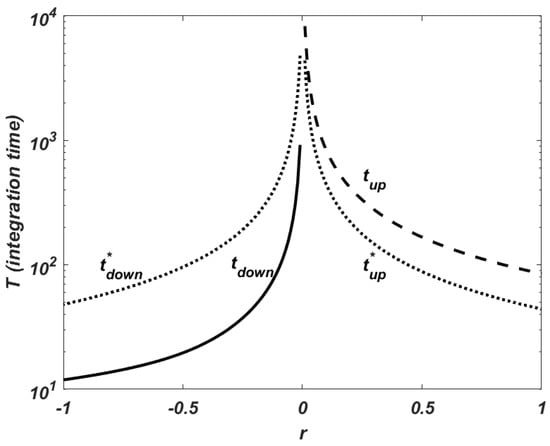
Figure 1.
Malthusian growth. Behaviour of the numerical solution depending on r. (solid line): time at which the approximated resource shows an exponential decay, its value is lower than (extinction). (dashed line): time at which it shows an exponential growth, its value is higher than (unbounded solution). Theoretical values in the absence of the consumer (dotted line): , , and , .
This is a signal of the limitations of exponential growth that could describe accurately the growth for small values of time. After a certain period, other factors become involved and the growth is retarded and limited.
3.2. Chemostat Growth
A growth law that circumvents some of the disadvantages of the Mathusian growth is introduced. It is clear that the effect of the limitation of the growth of the resource imposed by the carrying capacity of the environment affects its evolution. The chemostat growth law is a simple choice to modelise this situation. It is also called exponential confined growth law because the curve defined by the differential equation maintains the sign of the curvature along time as it approaches the carrying capacity; therefore, it is always confined to a region bounded by K. In terms of growth, it means that the resource rate of the growth is proportional to the available space. Thus, the dynamics of the resource in the absence of a consumer population are reduced to a stable nontrivial equilibrium that matches the carrying capacity.
An extensive numerical experimentation with different values of both parameters has been performed. It is observed that the size-structured consumer population defined in (1) modifies the nontrivial equilibrium to which the resource population tends to, but it does not modify its behaviour. Regardless of the value of parameters K and r employed, the resource grows very fast to a value close and below the carrying capacity of the environment (note that is lower than K, otherwise it would decrease) followed by a smooth transition to the stable nontrivial equilibrium.
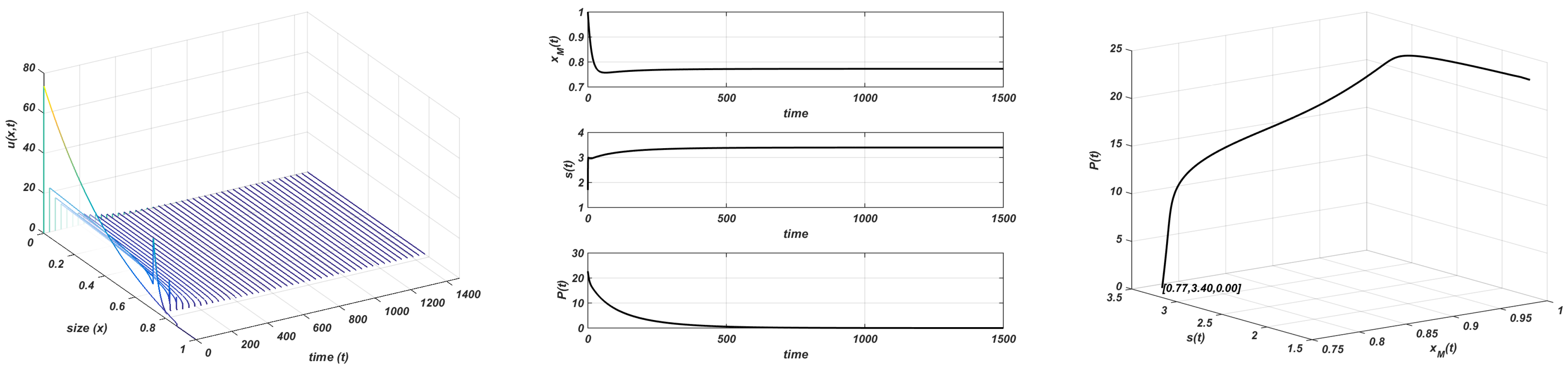
Figure 2, Figure 3, Figure 4 and Figure 5 confirm that statement. Three kinds of plots are shown. First, a 3D plot in which the density function is drawn versus the size of individuals and time. Second, the evolution of the maximum size, the resource, and the total population of consumers, , , and , respectively, are represented versus time. This last quantity is computed numerically with the quadrature rule employed in the numerical scheme. In the last plot, the transition that these three quantities follow to the equilibrium is shown. It is a 3D plot in which the total population versus the resource and the maximum size, for every value of the time integration interval is drawn. Furthermore, the equilibrium value is shown.

Figure 2.
Chemostat growth. and . Stable equilibria: consumer extinction. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .
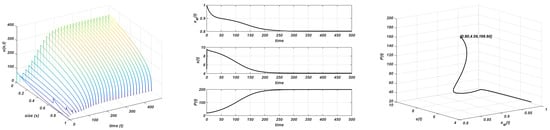
Figure 3.
Chemostat growth. and . Stable equilibria. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .
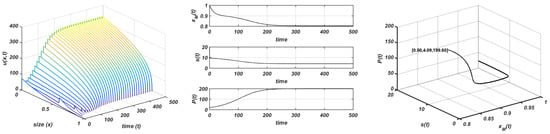
Figure 4.
Chemostat growth. , , and . Stable equilibria. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .

Figure 5.
Chemostat growth. and . Stable equilibria. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .
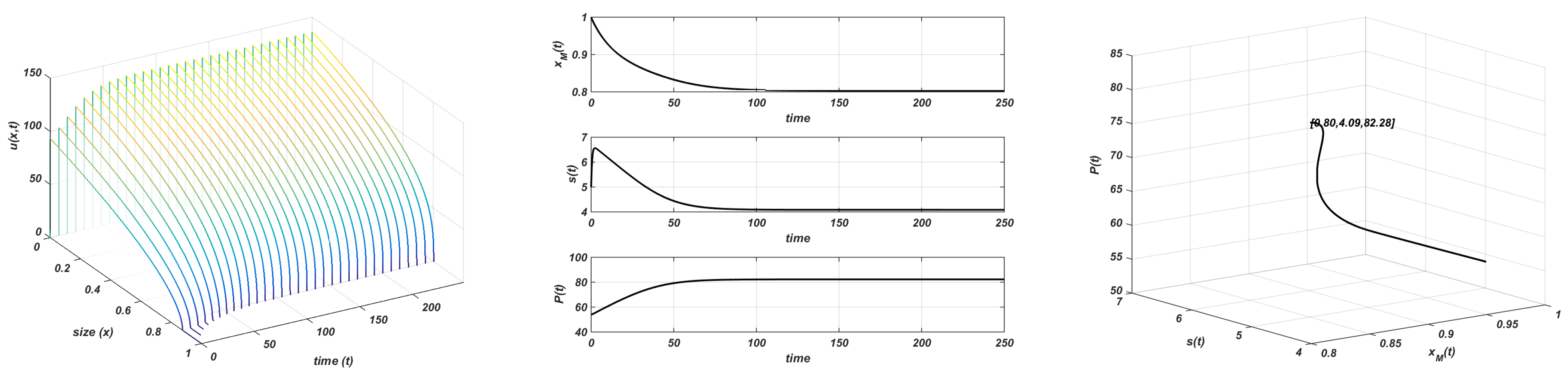
This growth function confers stability to the equilibrium. However, the equilibrium reached by the resource population is modified by the action of the consumer population. It is observed that there is a threshold value of the carrying capacity (whose value is in (6)), below which the consumer population tends to extinction, probably due to the lack of enough resources to survive (Allee effect type), and the resource tends to the carrying capacity. Therefore, the existence of a trivial equilibrium of the system corresponding to the extinction of the consumer population and a value equal to the carrying capacity for the resource population, can be assessed. This behaviour is shown in Figure 2, with and .
However, if , both populations tend to nontrivial steady states, which seem to be stable, and are given by the expressions in (6). It should be assumed that the trivial equilibrium for the consumer population becomes unstable and a new stable nontrivial equilibrium appears; then we can affirm the existence of a transcritical bifurcation point for the consumer population at . The emergence of this nontrivial consumer equilibria modifies the behaviour of the resource (and the maximum size) because, in these conditions, it never reaches the carrying capacity and tends to the nontrivial equilibrium (6). In this case, the nontrivial equilibrium reached by the system is modified and changes with the value of K. This coexistence pattern between both populations is shown in Figure 3 (experiment made with and ). Figure 4 shows that the same dynamics occur when the initial resource is larger than the carrying capacity, with the only novelty of a continuous decline to the asymptotic state. In this experiment the following values of parameters have been employed , , and .
Finally, no other change is noted when the value of the carrying capacity K is augmented. It is only noticeable that the consumer population increases its size without any other related changes in the other variables and . This is shown in a final experiment with and , as shown in Figure 5.
3.3. Gompertz Growth
The last growth law in this study also presents an effect of limitation on the growth of the resource. Unlike the chemostat growth law, there are two possible theoretical equilibria in the system: an unstable trivial equilibrium state and a stable nontrivial equilibrium state that corresponds to the carrying capacity of the environment. Therefore, in this case, the evolution of the resource in the absence of the consumer population is towards the carrying capacity.
An exhaustive numerical experimentation with different values of both parameters has also been performed and the results are represented with similar figures as in the chemostat growth section. First, the evolution of the density function is plotted versus the size of individuals and the time. The three plots in the middle of the figure represent the evolution of the maximum size, the resource, and the total population of consumers versus time, respectively. The right-hand size 3D plot in the figure shows the orbit that these three previously introduced quantities follow for every value in the time integration interval. When the system arrives to a stable equilibrium, its value is also shown.
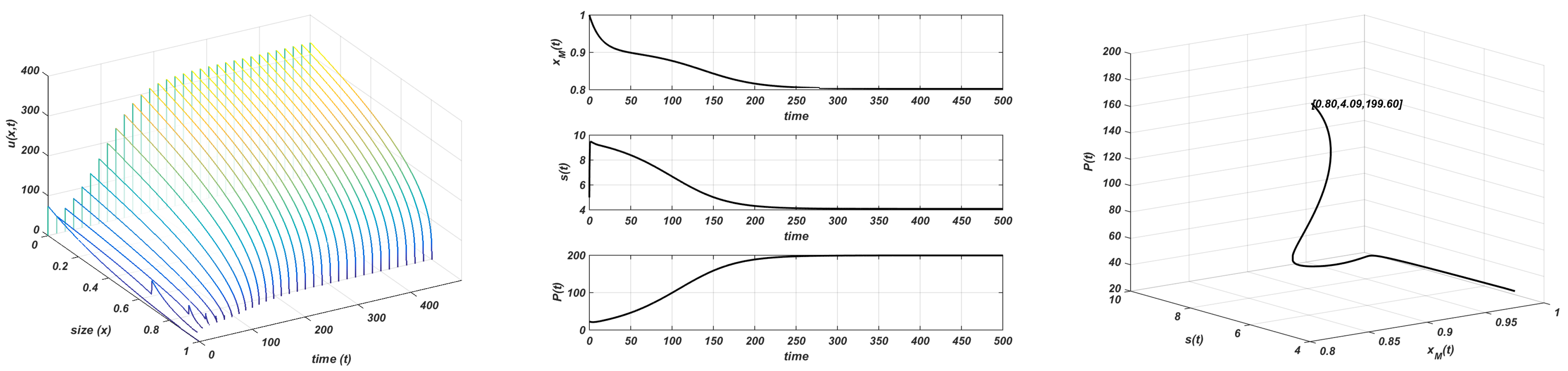
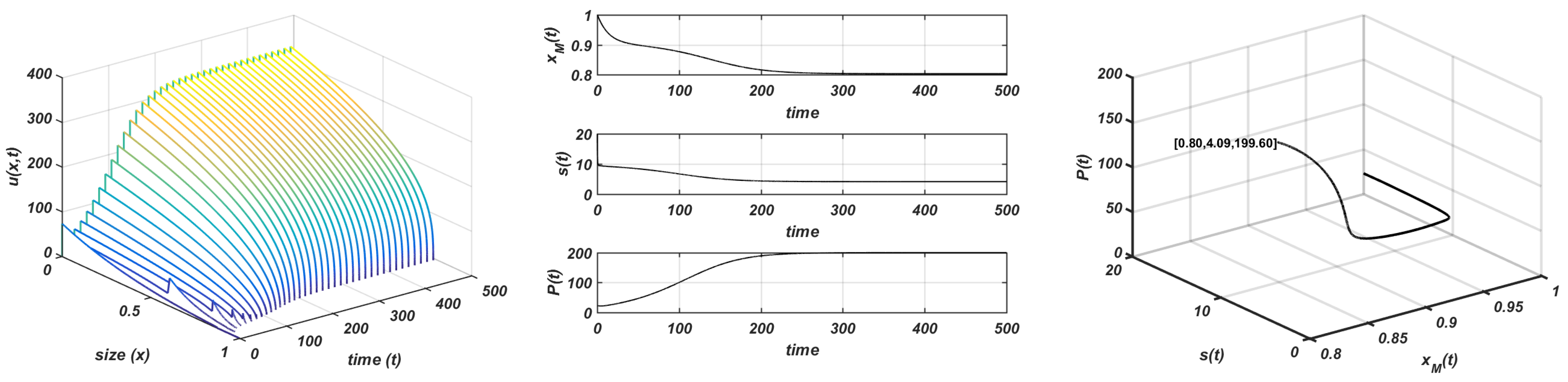
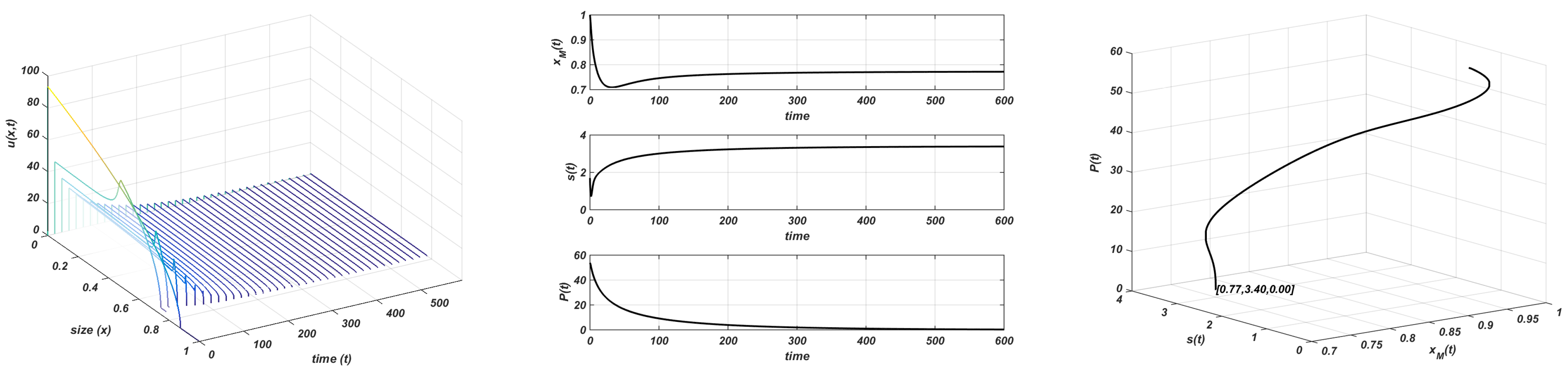
Initially, a situation in which the consumer population does not affect the unstructured resource is observed. This happens when the carrying capacity is lower than a threshold value (whose value is again in (6)). This case is similar to the corresponding one in the chemostat growth law. The resource approaches the carrying capacity while the consumer population tends to extinction, probably the consumer population does not find enough resources to survive. In Figure 6, the use of and allows showing how the whole system tends to a so-called stable trivial equilibrium state, and , . Note that this situation happens regardless of the value of r.

Figure 6.
Gompertz growth. and . Stable equilibria. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .
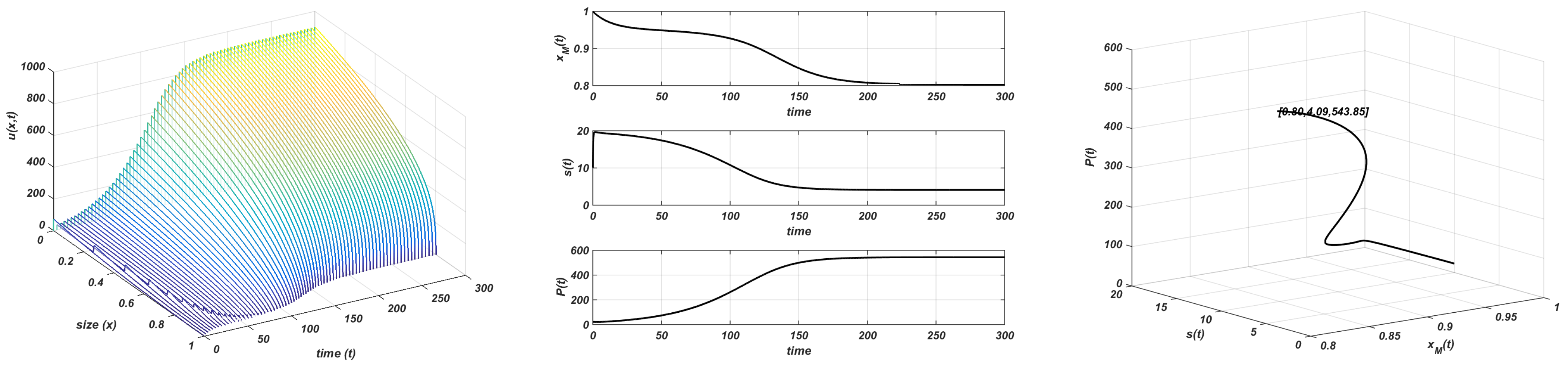
When the carrying capacity increases, the resource does as well. As a consequence, the consumer population is able to survive, and when the consumer population appears in the system, the dynamics of the resource population change. Thus, when , the resource population converges to the nonlinear steady-state given by in (6), and the carrying capacity will never be a steady-state again. With respect to the consumer population, it tends to the nontrivial equilibrium , given by (6). Therefore, the existence of a transcritical bifurcation at can be stated for the consumer population: the trivial equilibrium becomes unstable and a nontrivial stable equilibrium emerges. In Figure 7, the parameter values employed are and , and it is shown how both populations and the maximum size approach the stable steady-state given by (6). Thus, the consumer affects the resource, but the stability of the asymptotic state is maintained and, as a consequence, both populations coexist.

Figure 7.
Gompertz growth. and . Stable equilibria. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: orbit followed towards the equilibrium .
Thus far, the behaviour is quite similar to what we have described before with the chemostat growth law. However, the stable nontrivial equilibrium lingers until the carrying capacity reaches a second threshold , and then, it becomes unstable and a stable limit cycle emerges. The value of the threshold depends on r and decreases as r increases. Its existence was previously reported when the logistic growth law was employed [1]. Thus, the consumer population affects the behaviour of the resource and modifies the stability of its nontrivial equilibrium. We could describe as a Hopf bifurcation.
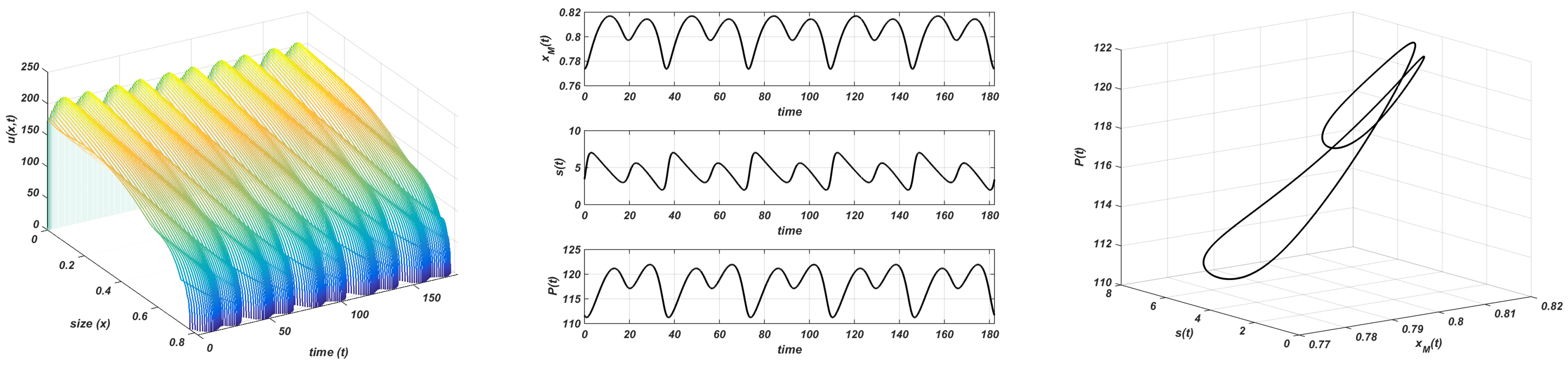
The following figures are slight modifications of the others shown above: now the evolution of the involved quantities (, , , and ) with respect to the full time-integration interval is not presented. Instead, the period, , and the amplitude of the resource oscillations, , of the corresponding limit cycle are computed numerically for each experiment. The time interval, in which the involved quantities are displayed, corresponds to , i.e., five periods once the limit cycle reaches its stability. The right-hand picture is completely different. It represents a 3D plot of the stable limit cycle at which the evolutions of , , and converge.
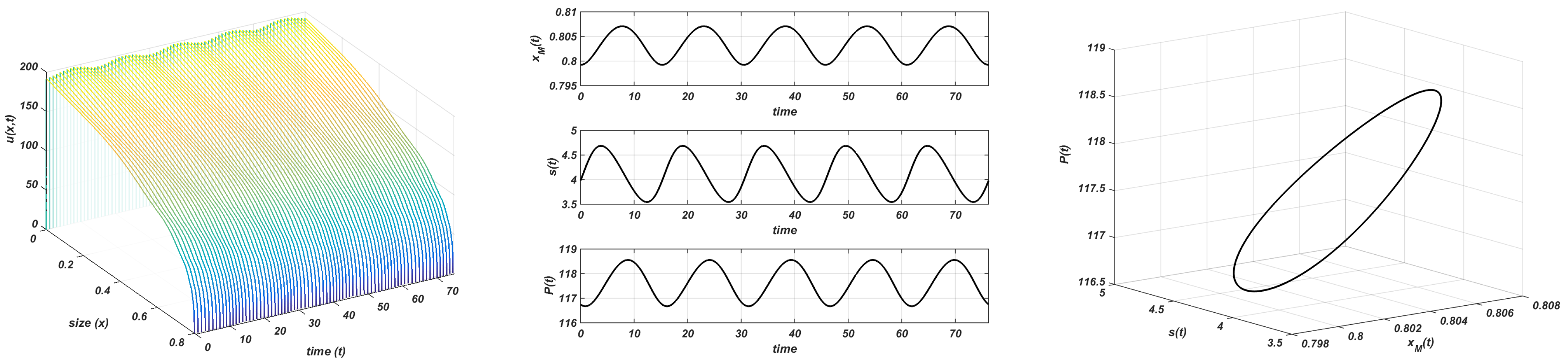
The following experiments are carried out with and different values of the carrying capacity, . In Figure 8, the announced behaviour for is observed: the nontrivial equilibrium is unstable and a stable limit cycle emerges with and . The nontrivial steady-state loses its stability, and both populations and the maximum size oscillate around the nontrivial equilibrium. It should be pointed out the free behaviour of the maximum size as was done in [1] with the logistic growth law.
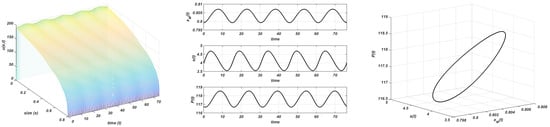
Figure 8.
Gompertz growth. and . Stable limit cycle. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: stable limit cycle.
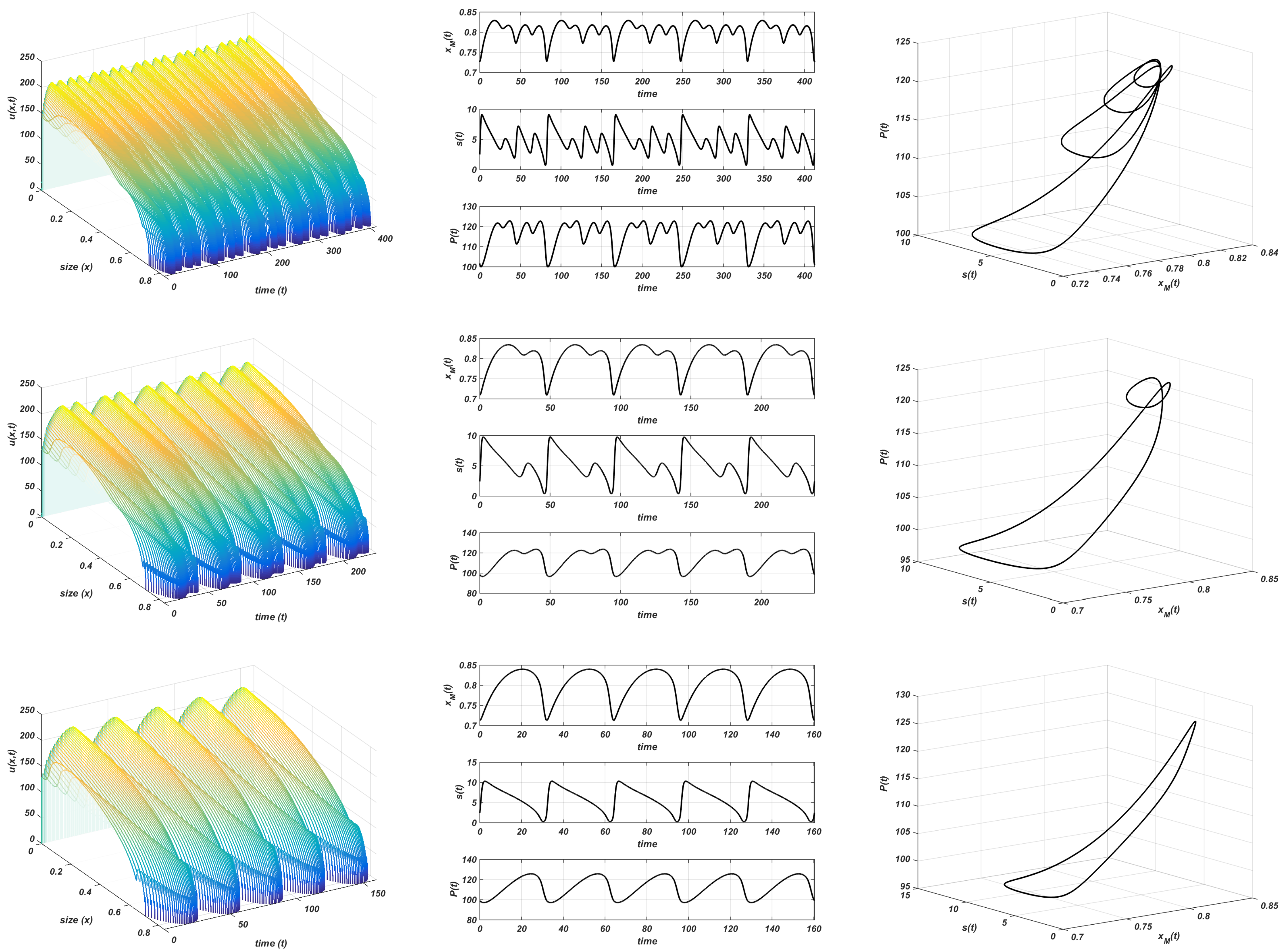
Beyond this new threshold , a complex dynamic, which has never been described in this kind of model so far, arises. It is shown in Figure 9, where simulations are made with , , , and . The instability of the nontrivial equilibrium and the convergence to a stable limit cycle is observed. However, the period of the oscillations increases from to and diminishes again to (see Figure 9). This means that the period is doubled twice and, after that, it is also split twice. This is a common doubling period cascade. The amplitude of the oscillations (in the resource population) increases from to .
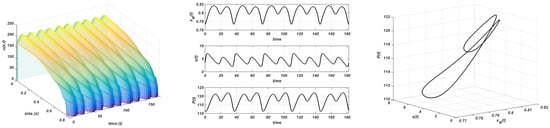
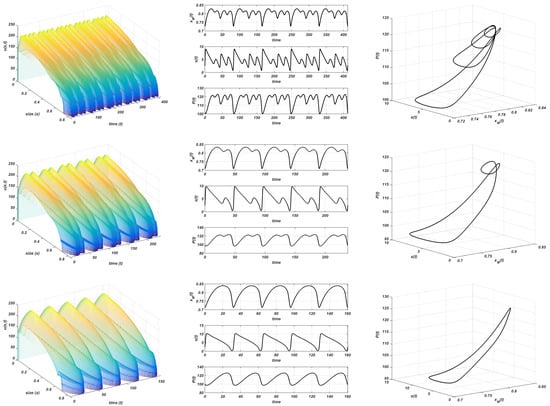
Figure 9.
Gompertz growth. . Stable limit cycle. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: stable limit cycle. Values of K from top to bottom: , , , and .
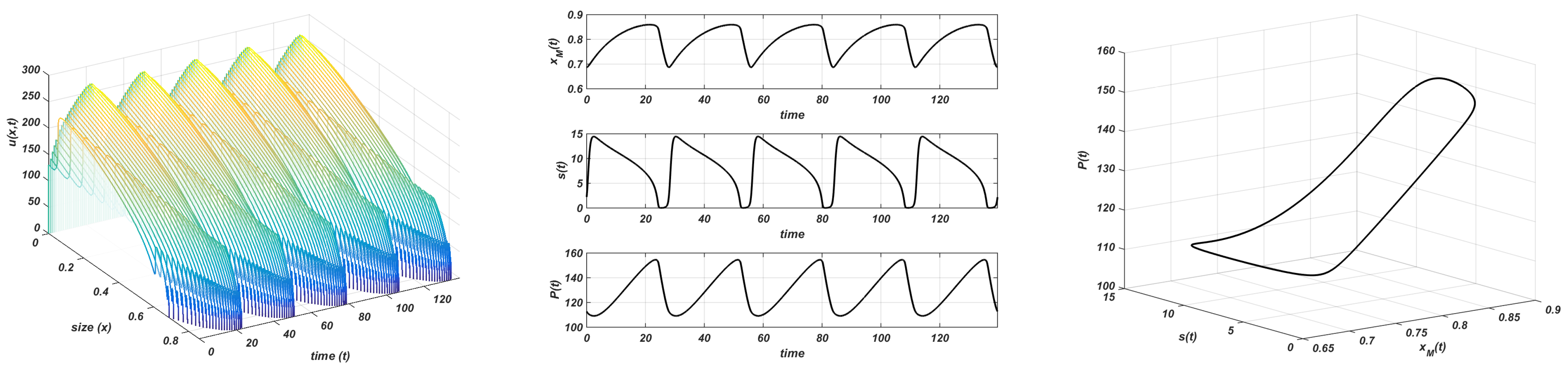
Finally, there are no different situations beyond this value. In Figure 10, we show the numerical results we obtain with . The only statement is that the amplitude increases with K, . A final influence of parameter r reveals the increments of the consumer population (figure not shown).
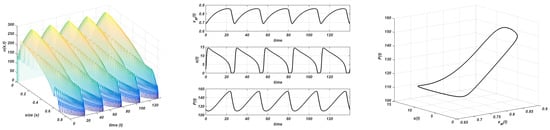
Figure 10.
Gompertz growth. and . Stable limit cycle. Plot on the left: evolution of the structure of the consumer; plot in the centre: evolution of the maximum size, resource, and total consumer population to the equilibrium; plot on the right: stable limit cycle.
4. Conclusions
In this work, the mutual interaction between the dynamics of a consumer population and an unstructured resource is considered. Through the study of a specific consumer-resource model for the dynamics of the Daphnia magna, we cope with the numerical difficulties due to an undefined sign growth law for the individual consumers. The numerical method employed is well adapted to this kind of size-structured population model: it efficiently provides the density function for the individuals in the consumer population without the numerical dissipation of first-order finite difference methods (the upwind, for instance) and the spurious oscillations from second-order finite difference methods.
Although existence, uniqueness, and regularity results about this model with a non-negative growth rate [12,13,14,15] have not been extended to the case of an undefined sign growth law yet, these properties are assumed under usual hypotheses that include enough smoothness on the function data. We focus on the numerical study of the long-time behaviour of both populations. In this case, a numerical method, that deals efficiently with the complex dynamics that arise, has been employed. With meaningful biological vital rates for the function data for the Daphnia magna model [19], the complex dynamics, which the model presents, are shown for each of three different growth laws.
The model behaves as a typical Malthusian population when this kind of growth law is chosen. The only influence of the consumer population is to slow down or to increase the speed at which the resource is unbounded or tends to extinction.
For the chemostat growth law, the consumer population does not influence the stable behaviour of the resource. On the one hand, the whole system stabilises the resource population towards the carrying capacity, and the consumer population tends to extinction, and on the other hand, the system stabilises towards the nontrivial steady-state given by (6). It should be pointed out that the consumer population increases with the increment of both parameters r and K.
With respect to the Gompertz growth law, the model exhibits many of the same properties as in the analysis of models that include the logistic growth law. In particular, several features have been presented, such as: stable and unstable equilibria, and stable periodical behaviours for different values of the parameters r and K of the resource growth law. However, in the extensive numerical experimentation with different values of r and K, a period cascade it is also obtained, short and long oscillations and short and long periods that have not been presented in this model before. These results could indicate the use of the Gompertz growth when other distributions do not match the real behaviour.
As the numerical simulations for each of the growth laws considered show, we can argue that the shortage of the resource has, as a biological consequence, not only the reduction in the total number of individuals of the stationary equilibria but also the effective shrink in size of the individuals of the population. This second effect has to be exclusively attributed to the undefined sign of the growth law of the consumer population. A future work in this direction is to confirm this effect as a general pattern for other consumer-resource population models in which an undefined sign growth rate is presented. Furthermore, we should expect some confirmation with real data from field experiments for these kinds of dynamics.
Author Contributions
All authors contributed equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by project MTM2017-85476-C2-1-P of the Spanish Ministerio de Economía y Competitividad, and European FEDER Funds, research grant RED2018-102650-T of the Spanish Ministerio de Economía y Competitividad, and research grant VA193P20 of the Junta de Castilla y León, Spain, and European FEDER funds (EU).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Authors are very grateful to the referees for their careful reading of the original manuscript and their aid to improve it.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Numerical Method
The description of the numerical scheme used in the simulations is introduced. This was built “ad hoc” for the problem in the current conditions in [1]. It also could be used in a long time integration searching for equlibria or periodicity.
The problem (1)–(4), ready to perform the numerical integration, is composed of four fully coupled problems:
where ,
Their discretisation will provide numerical approximations for the physiological states, the evolution of the resource, and the solution at the grid points at each time level.
In the following, the equations of the numerical scheme are introduced. It is a second order method, based on the trapezoidal quadrature rule (both integral and differential versions). This is an implicit rule but an explicit predictor–corrector transformation is used to compute a first aproximation and, in the second stage, to obtain the right value (with higher order of convergence). The integration is made on a finite time interval . Therefore, given and , the discretisation parameters are defined as , . Thus, the number of time levels are given by , and the time discretisation levels are , .
Now, to perform the numerical integration, initial values are provided: the initial space discretisation, , , , the initialisation of the resource and the initial condition on the initial grid, , , . Then, the computation of the general step , , , is built after the corresponding values at the previous time step , , , , are known, by means of the following procedure. The equations of the first stage are given by,
The equations in the second stage are
The discretisation of the nonlocal terms is made by means of a composite quadrature rule (in this case based on the trapezoidal one), .
The grid of the scheme is built following the characteristic curves and, therefore, a new node appears after each time level. For efficiency reasons, the number of grid nodes is kept constant by removing one grid node after every time step as in the following procedure: first, such that
is selected. Next, the selected node is removed and the nodes are renamed. Thus, the quadrature is performed on this subgrid with a fixed number of nodes. Other versions of this procedure could be possible if the integration interval increases or decreases due to the variable maximum size. Finally, , , , and are the vectors whose components are , , , and , respectively, ; and the vector products in (A1) and (A2) are considered component-wise.
The analysis of this numerical method was performed in [1], where the corresponding smoothness properties demanded by this second-order numerical scheme were specified.
References
- Angulo, O.; López-Marcos, J.C.; López-Marcos, M.A. Analysis of an efficient integrator for a size-structured population model with a dynamical resource. Comput. Math. Appl. 2014, 68, 941–961. [Google Scholar] [CrossRef]
- Abia, L.M.; Angulo, O.; López-Marcos, J.C.; López-Marcos, M.A. Long-Time Simulation of a Size-Structured Population Model with a Dynamical Resource. Math. Model Nat. Phenom. 2010, 5, 1–21. [Google Scholar] [CrossRef]
- Angulo, O.; López-Marcos, J.C.; López-Marcos, M.A. Numerical approximation of singular asymptotic states for a size-structured population model with a dynamical resource. Math. Comput. Model. 2011, 54, 1693–1698. [Google Scholar] [CrossRef]
- de Roos, A.M.; Persson, L. Size-dependent life-history traits promote catastrophic collapses of top predators. Proc. Nat. Acad. Sci. USA 2002, 99, 12907–12912. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Sanz, J.; Getto, P. Numerical bifurcation analysis of physiologically structured populations: Consumer–resource, cannibalistic and trophic models. Bull Math. Biol. 2016, 78, 1546–1584. [Google Scholar] [CrossRef] [PubMed]
- Cuesta, J.A.; Delius, G.W.; Law, R. Sheldon spectrum and the plankton paradox: Two sides of the same coin—A trait-based plankton size-spectrum model. J. Math. Biol. 2017, 76, 67–96. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Chen, J.; Liu, Z.; Bi, P.; Ruan, S. Local and global stabilities of a viral dynamics model with infection-age and immune response. J. Dyn. Diff. Equat. 2019, 31, 793–813. [Google Scholar] [CrossRef]
- Lafferty, K.; De Leo, G.; Briggs, C.; Dobson, A.; Gross, T.; Kuris, A. A general consumer-resource population model. Science 2015, 349, 854–857. [Google Scholar] [CrossRef] [PubMed]
- Aylaj, B.; Noussair, A. Global weak solution for a multistage physiologically structured population model with resource interaction. Nonlinear Anal. Real. World Appl. 2010, 11, 1670–1684. [Google Scholar] [CrossRef]
- Angulo, O.; Crauste, F.; López-Marcos, J.C. Numerical integration of an erythropoiesis model with explicit growth factor dynamics. J. Comput. Appl. Math. 2018, 330, 770–782. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M.; Metz, J.A.J. On the dynamics of chemically stressed populations: The deduction of population consequences from effects on individuals. Ecotoxicol. Environ. Saf. 1984, 8, 254–274. [Google Scholar] [CrossRef]
- Thieme, H.R. Well-posedness of physiologically structured population models for daphnia magna. J. Math. Biol. 1988, 26, 299–317. [Google Scholar] [CrossRef][Green Version]
- Diekmann, O.; Getto, P.; Gyllenberg, M. Stability and bifurcation analysis of volterra functional equations in the light of suns and stars. SIAM J. Math. Anal. 2007, 39, 1023–1069. [Google Scholar] [CrossRef][Green Version]
- Diekmann, O.; Gyllenberg, M. Equations with infinite delay: Blending the abstract and the concrete. J. Differential. Equat. 2012, 252, 819–851. [Google Scholar] [CrossRef]
- Diekmann, O.; Gyllenberg, M.; Metz, J.A.J.; Nakaoka, S.; de Roos, A.M. Daphnia revisited: Local stability and bifurcation theory for physiologically structured population models explained by way of an example. J. Math. Biol. 2010, 61, 277–318. [Google Scholar] [CrossRef] [PubMed]
- de Roos, A.M.; Metz, J.A.J.; Evers, E.; Leipoldt, A. A size dependent predator-prey interaction: Who pursues whom? J. Math. Biol. 1990, 28, 609–643. [Google Scholar] [CrossRef]
- Breda, D.; Diekmann, O.; Gyllenberg, M.; Scarabel, F.; Vermiglio, R. Pseudospectral discretization of nonlinear delay equations: New prospects for numerical bifurcation analysis. SIAM J. Appl. Dyn. Syst. 2016, 15, 1–23. [Google Scholar] [CrossRef]
- Breda, D.; Getto, P.; Sánchez-Sanz, J.; Vermiglio, R. Computing the eigenvalues of realistic Daphnia models by pseudospectral methods. SIAM J. Sci. Comput. 2015, 37, A2607–A2629. [Google Scholar] [CrossRef]
- de Roos, A.M. Numerical methods for structured population models: The escalator boxcar train. Numer. Methods Partial Differ. Equat. 1988, 4, 173–195. [Google Scholar] [CrossRef]
- Banks, R.B. Growth and Diffusion Phenomena; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).