An α-Monotone Generalized Log-Moyal Distribution with Applications to Environmental Data
Abstract
1. Introduction
2. Background Information
2.1. The GlogM Distribution
- i.
- If and , the pdf of the random variable X reduces to the invGHN distribution
- ii.
- If and , the pdf of the random variable X reduces to the invHN distribution
- i.
- If and , the pdf of the random variable Z reduces to the generalized half-normal (GHN) distribution proposed by Cooray and Ananda [16];
- ii.
- If and , the pdf of the random variable Z reduces to the half-normal (HN) distribution.
2.2. The Slash and -Monotone Distributions
3. The -GlogM Distribution
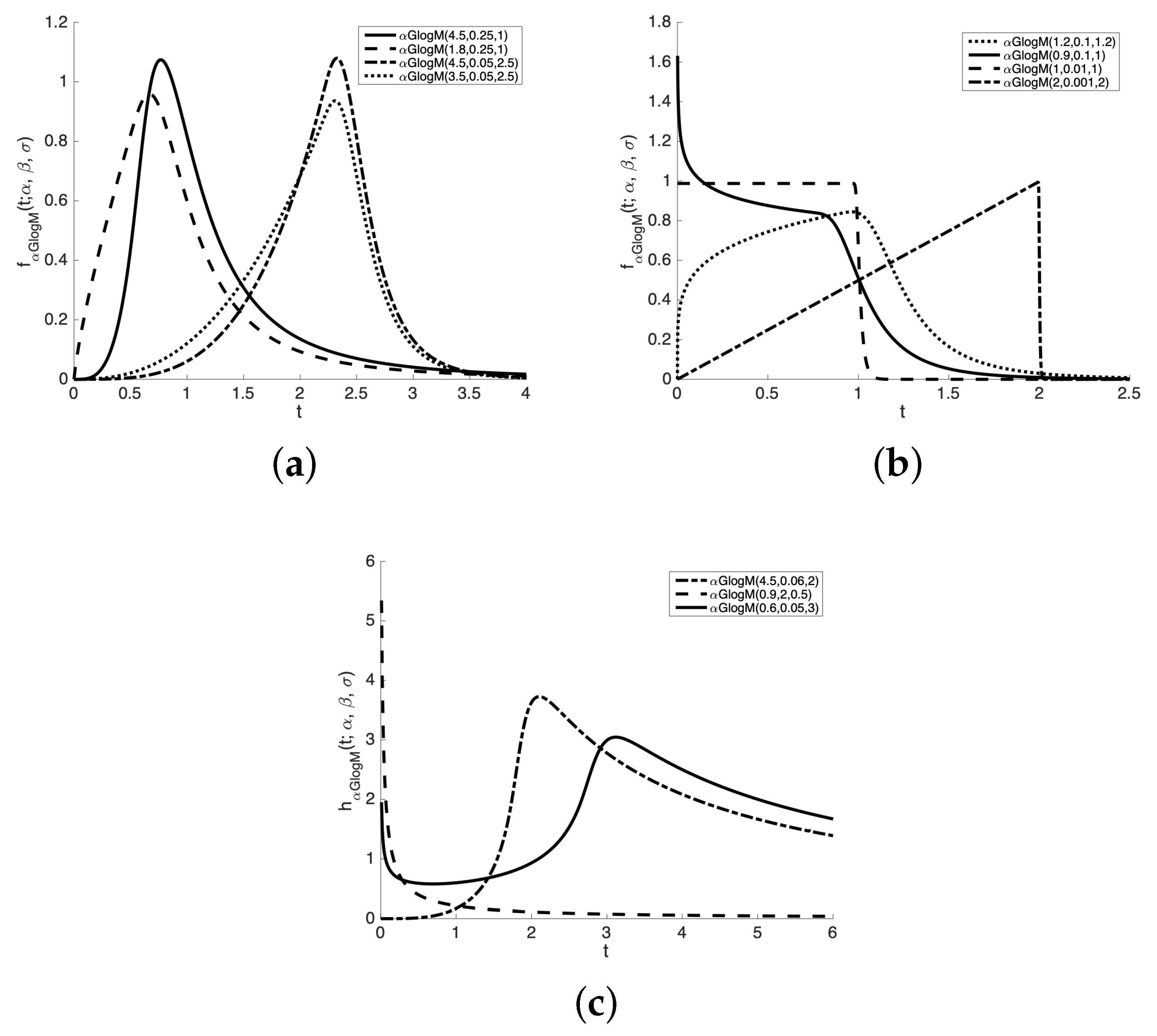
3.1. Density Function and Some Statistical Properties
- i.
- ∼α-GlogM().
- ii.
- The pdf of is
- iii.
- The pdf of is
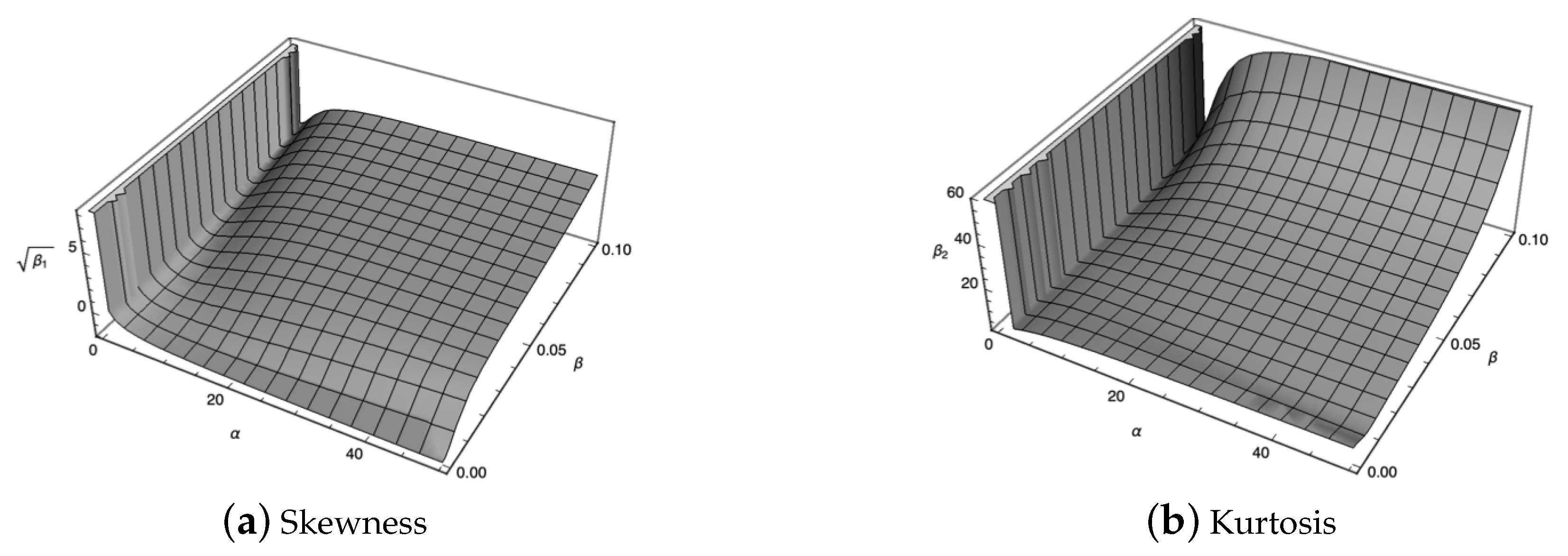
3.2. Moments
3.3. Related Distributions
3.3.1. Submodels
3.3.2. Limiting Distributions
- i.
- If , then the -GlogM() converges to the GlogM() distribution given in (1), i.e.,
- ii.
- If , and and , then the -GlogM() converges to the invGHN distribution.
- iii.
- If , and and , then the -GlogM() converges to the invHN distribution.
- iv.
- Let . If and and , then the pdf of the random variable Z converges to the GHN distribution proposed by Cooray and Ananda [16].
- v.
- Let . If , and and , then the pdf of the random variable Z converges to the HN distribution.
3.4. Data Generation
- Step 1.
- Generate a p from U distribution and incorporate it into the equationto generate a random number x from the distribution. Here, is inverse of the upper-incomplete gamma function.
- Step 2.
- Generate a y from a U distribution and incorporate it into the equationto generate the random varaites from the -GlogM distribution.
4. Estimation
4.1. ML Estimation
4.2. MoM Estimation
4.3. Monte-Carlo Simulation
| Scenario | |||||||
| I | 1.8 | 0.10 | 1.0 | 0.7506 | 0.1325 | 1.3991 | 16.7429 |
| II | 3.5 | 0.05 | 2.5 | 2.0856 | 0.2945 | −0.1339 | 4.1345 |
| III | 1.2 | 0.01 | 1.2 | 0.6631 | 0.1148 | −0.1489 | 1.8828 |
| IV | 0.9 | 0.10 | 5.0 | 2.7655 | 3.7250 | 1.1570 | 10.1785 |
5. Applications
| AIC= | |
| AICc= | |
| RMSE= | |
| = | |
| KS= | |
| AD= |
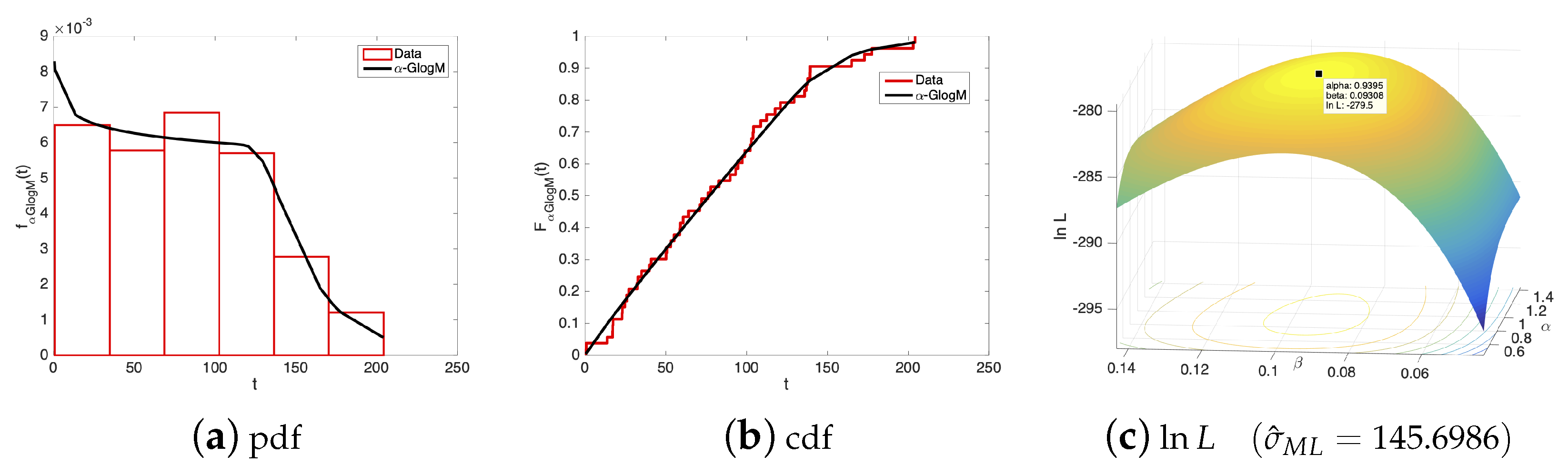
5.1. Application-I
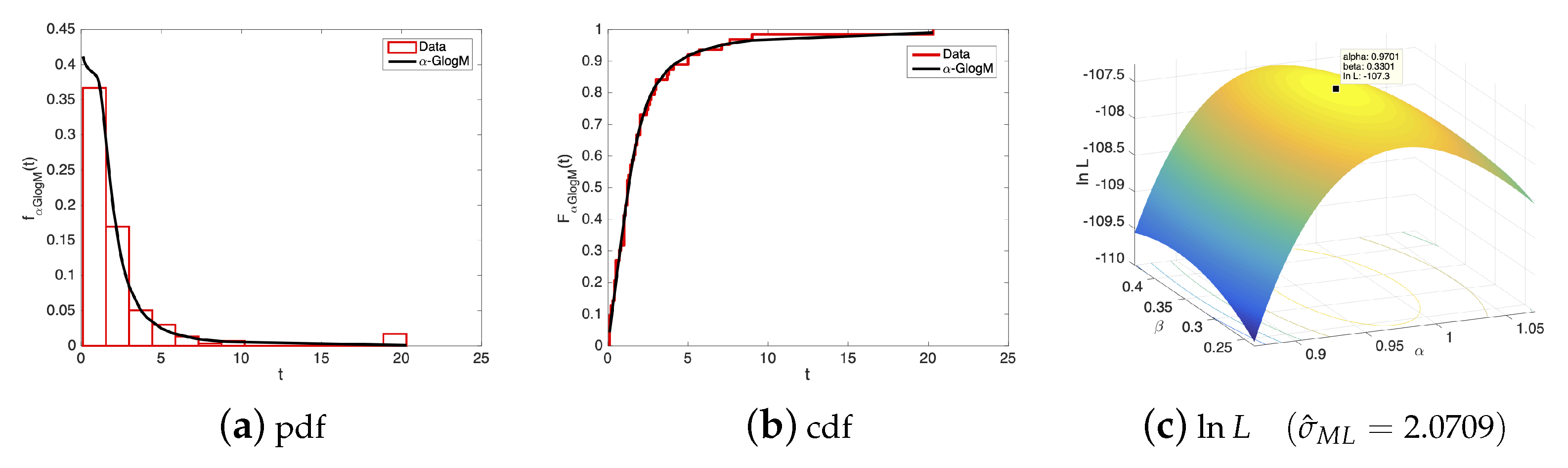
5.2. Application-II
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Gómez, H.W.; Venegas, O.; Bolfarine, H. Skew-symmetric distributions generated by the distribution function of the normal distribution. Environmetrics 2007, 18, 395–407. [Google Scholar] [CrossRef]
- Leiva, V.; Barros, M.; Paula, G.A.; Sanhueza, A. Generalized Birnbaum-Saunders distributions applied to air pollutant concentration. Environmetrics 2007, 19, 235–249. [Google Scholar] [CrossRef]
- Nadarajah, S. A truncated inverted beta distribution with application to air pollution data. Stoch. Environ. Res. Risk. Assess. 2008, 22, 285–289. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. The log-power-normal distribution with application to air pollution. Environmetrics 2014, 25, 44–56. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Dey, S.; Ramos, P.L.; Louzada, F. Binomial-exponential 2 distribution: Different estimation methods with weather applications. TEMA (São Carlos) 2017, 18, 233–251. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Bakouch, H.S.; Habibi, M. A generalized binomial-exponential 2 distribution: Modeling and applications to hydrologic events. J. Appl. Stat. 2017, 44, 2368–2387. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Bolfarine, H.; Gomez, H.W. Gumbel distribution with heavy tails and applications to environmental data. Math. Comput. Simul. 2019, 157, 115–129. [Google Scholar] [CrossRef]
- Bahti, D.; Ravi, S. On generalized log-Moyal distribution: A new heavy-tailed size distribution. Insur. Math. Econom. 2018, 79, 247–259. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Alzaatreh, A.Y. Methods for generation families of univariate continuous distributions in the recent decades. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 219–238. [Google Scholar] [CrossRef]
- Moyal, J.E. Theory of ionization fluctuations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1955, 46, 263–280. [Google Scholar] [CrossRef]
- Walck, C. Hand-Book on Statistical Distributions for Experimentalists; Particle Physics Group, Fysikum, University of Stockholm: Stockholm, Sweden, 2007. [Google Scholar]
- Cordeiro, G.M.; Nobre, J.S.; Pescim, R.R.; Ortega, E.M.M. The beta Moyal: A useful skew distribution. Int. J. Res. Rev. Appl. Sci. 2012, 10, 171–192. [Google Scholar]
- Genc, A.A.; Korkmaz, M.C.; Kus, C. The Beta Moyal-Slash distribution. J. Selçuk Univ. Nat. Appl. Sci. 2014, 3, 88–104. [Google Scholar]
- Olmos, N.M.; Varela, H.; Bolfarine, H.; Gómez, H.W. An extension of the half-normal distribution. Stat. Pap. 2012, 53, 875–886. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Bolfarine, H.; Gómez, H.W. An extension of the generalized half-normal distribution. Stat. Pap. 2014, 55, 967–981. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.A.M. A generalization of the half-normal distribution with applications to lifetime data. Commun. Stat. Theory Methods 2008, 37, 1323–1337. [Google Scholar] [CrossRef]
- Andrews, D.D.; Bickel, P.J.; Hampel, F.Y.; Huber, P.J.; Rogers, W.H.; Tukey, J.W. Robust Estimates of Location: Survey and Advances; Princeton University Press: Princeton, NJ, USA, 1972. [Google Scholar]
- Rogers, W.H.; Tukey, J.W. Understanding some long-tailed symmetrical distributions. Stat. Neerl. 1972, 26, 211–226. [Google Scholar] [CrossRef]
- Mosteller, F.; Tukey, J.W. Data Analysis and Regression; Addison-Wesley: Reding, MA, USA, 1977. [Google Scholar]
- Jones, M.C. On univariate slash distributions, continuous and discrete. Ann. Inst. Stat. Math. 2020, 72, 645–657. [Google Scholar] [CrossRef]
- Gómez, H.W.; Quintana, F.A.; Torres, J. A new family of slash-distributions with elliptical contours. Stat. Probab. Lett. 2007, 77, 717–725. [Google Scholar] [CrossRef]
- Genc, A.I. A generalization of the univariate slash by a scale-mixtured exponential power distribution. Commun. Stat. Simul. Comput. 2007, 36, 937–947. [Google Scholar] [CrossRef]
- Punathumparambath, B. A New Family of Skewed Slash Distributions Generated by the Cauchy Kernel. Commun. Stat. Theory Methods 2013, 42, 2351–2361. [Google Scholar] [CrossRef]
- Astorga, J.M.; Gomez, H.W.; Bolfarine, H. Slashed generalized exponential distribution. Commun. Stat. Theory Methods 2017, 46, 2091–2102. [Google Scholar] [CrossRef]
- Korkmaz, M.C. A generalized skew slash distribution via gamma-normal distribution. Commun. Stat. Simul. Comput. 2017, 46, 1647–1660. [Google Scholar] [CrossRef]
- Arslan, O. An alternative multivariate skew-slash distribution. Stat. Probab. Lett. 2008, 78, 2756–2761. [Google Scholar] [CrossRef]
- Arslan, O.; Genc, A.I. A generalization of the multivariate slash distribution. J. Stat. Plan. Inference 2009, 139, 1164–1170. [Google Scholar] [CrossRef]
- Reyes, J.; Gómez, H.W.; Bolfarine, H. Modified slash distribution. Statistics 2013, 47, 929–941. [Google Scholar] [CrossRef]
- Iriarte, Y.A.; Castillo, N.O.; Bolfarine, J.; Gómez, H.W. Modified slashed-Rayleigh distribution. Commun. Stat. Theory Methods 2018, 47, 3220–3233. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gómez, H.W. Generalized modified slash distribution with applications. Commun. Stat. Theory Methods 2020, 49, 2025–2048. [Google Scholar] [CrossRef]
- Rojas, M.A.; Bolfarinei, H.; Gómez, H.W. An extension of the slash-elliptical distribution. SORT 2014, 38, 215–230. [Google Scholar]
- Zörnig, P. On generalized slash distributions: Representation by hypergeometric functions. Stats 2019, 2, 371–387. [Google Scholar] [CrossRef]
- Arslan, T. Scale-Mixture Extension of Inverse Weibull Distribution, Olomoucian Days of Applied Mathematics 2019; ODAM: Olomouc, Czech Republic, 2019; p. 12. [Google Scholar]
- Iriarte, Y.A.; Vilca, F.; Varela, H.; Gómez, H.W. Slashed generalized Rayleigh distribution. Commun. Stat. Theory Methods 2017, 46, 4686–4699. [Google Scholar] [CrossRef]
| Scenario-I | |||||||
|---|---|---|---|---|---|---|---|
| n | ML | MoM | |||||
| Bias | Variance | MSE | Bias | Variance | MSE | ||
| −0.13153 | 0.19941 | 0.21651 | 0.13275 | 0.31909 | 0.33671 | ||
| 20 | 0.00139 | 0.00192 | 0.00192 | 0.03010 | 0.00077 | 0.00168 | |
| 0.01034 | 0.01652 | 0.01663 | −0.10730 | 0.02837 | 0.03988 | ||
| −0.11841 | 0.16049 | 0.17443 | 0.12084 | 0.10649 | 0.12104 | ||
| 50 | −0.00167 | 0.00080 | 0.00080 | 0.01888 | 0.00042 | 0.00078 | |
| 0.00215 | 0.00738 | 0.00738 | −0.08608 | 0.00940 | 0.01680 | ||
| −0.03556 | 0.05736 | 0.05857 | 0.13539 | 0.04900 | 0.06729 | ||
| 100 | −0.00017 | 0.00042 | 0.00042 | 0.01485 | 0.00034 | 0.00056 | |
| −0.00157 | 0.00352 | 0.00352 | −0.06626 | 0.00394 | 0.00833 | ||
| −0.02077 | 0.02844 | 0.02882 | 0.11269 | 0.02589 | 0.03854 | ||
| 200 | −0.00133 | 0.00020 | 0.00020 | 0.01107 | 0.00024 | 0.00036 | |
| 0.00140 | 0.00167 | 0.00167 | −0.04923 | 0.00192 | 0.00434 | ||
| Scenario-II | |||||||
| n | ML | MoM | |||||
| Bias | Variance | MSE | Bias | Variance | MSE | ||
| −0.51300 | 1.55340 | 1.81657 | −0.41089 | 1.26007 | 1.42368 | ||
| 20 | −0.00017 | 0.00066 | 0.00066 | 0.00789 | 0.00059 | 0.00064 | |
| 0.02281 | 0.03283 | 0.03321 | −0.01732 | 0.03025 | 0.03042 | ||
| −0.16020 | 0.50873 | 0.53414 | −0.08283 | 0.47270 | 0.47932 | ||
| 50 | −0.00129 | 0.00023 | 0.00023 | 0.00450 | 0.00036 | 0.00038 | |
| 0.00035 | 0.01267 | 0.01267 | −0.03229 | 0.01652 | 0.01756 | ||
| −0.10093 | 0.24034 | 0.25029 | −0.06002 | 0.29182 | 0.29513 | ||
| 100 | −0.00134 | 0.00011 | 0.00011 | 0.00155 | 0.00017 | 0.00017 | |
| 0.00443 | 0.00522 | 0.00524 | −0.01462 | 0.00873 | 0.00893 | ||
| −0.06286 | 0.09844 | 0.10219 | −0.03714 | 0.11643 | 0.11758 | ||
| 200 | −0.00109 | 0.00005 | 0.00005 | 0.00078 | 0.00007 | 0.00007 | |
| 0.00295 | 0.00230 | 0.00230 | −0.00865 | 0.00396 | 0.00403 | ||
| Scenario-III | |||||||
| n | ML | MoM | |||||
| Bias | Variance | MSE | Bias | Variance | MSE | ||
| −0.13570 | 0.10631 | 0.12462 | −0.26612 | 0.19742 | 0.26812 | ||
| 20 | −0.03644 | 0.00072 | 0.00205 | −0.02095 | 0.00099 | 0.00143 | |
| 0.15882 | 0.01057 | 0.03579 | 0.12531 | 0.01390 | 0.02959 | ||
| −0.09049 | 0.04164 | 0.04981 | −0.09361 | 0.04758 | 0.05631 | ||
| 50 | −0.02101 | 0.00027 | 0.00071 | −0.01392 | 0.00070 | 0.00089 | |
| 0.09206 | 0.00414 | 0.01262 | 0.07876 | 0.00807 | 0.01427 | ||
| −0.04574 | 0.01675 | 0.01882 | −0.05437 | 0.01966 | 0.02260 | ||
| 100 | −0.01440 | 0.00009 | 0.00030 | −0.01046 | 0.00051 | 0.00062 | |
| 0.05926 | 0.00167 | 0.00518 | 0.05553 | 0.00516 | 0.00824 | ||
| −0.03068 | 0.00843 | 0.00936 | −0.04136 | 0.01091 | 0.01260 | ||
| 200 | −0.01024 | 0.00002 | 0.00013 | −0.00801 | 0.00046 | 0.00052 | |
| 0.04120 | 0.00052 | 0.00222 | 0.04334 | 0.00323 | 0.00510 | ||
| Scenario-IV | |||||||
| n | ML | MoM | |||||
| Bias | Variance | MSE | Bias | Variance | MSE | ||
| −0.11095 | 0.08495 | 0.09718 | −0.01709 | 0.06358 | 0.06381 | ||
| 20 | 0.02055 | 0.00438 | 0.00480 | 0.04348 | 0.00140 | 0.00329 | |
| −0.00458 | 0.89955 | 0.89867 | −0.48331 | 0.77694 | 1.00975 | ||
| −0.02869 | 0.02844 | 0.02918 | 0.07019 | 0.02352 | 0.02838 | ||
| 50 | −0.01916 | 0.00137 | 0.00173 | 0.01161 | 0.00041 | 0.00055 | |
| 0.01344 | 0.42467 | 0.42354 | −0.60497 | 0.43470 | 0.79936 | ||
| −0.02454 | 0.01245 | 0.01302 | 0.05199 | 0.01208 | 0.01476 | ||
| 100 | −0.01551 | 0.00065 | 0.00089 | 0.00791 | 0.00037 | 0.00043 | |
| 0.02554 | 0.19268 | 0.19285 | −0.44551 | 0.14778 | 0.34589 | ||
| −0.00952 | 0.00617 | 0.00625 | 0.04917 | 0.00687 | 0.00928 | ||
| 200 | −0.01128 | 0.00026 | 0.00038 | 0.00507 | 0.00028 | 0.00030 | |
| 0.00976 | 0.07829 | 0.07823 | −0.32986 | 0.07196 | 0.18063 | ||
| n | Scenario-I | Scenario-II | Scenario-III | Scenario-IV | |
|---|---|---|---|---|---|
| 0.96 | 0.97 | 0.96 | 0.93 | ||
| 20 | 0.89 | 0.91 | 0.87 | 0.96 | |
| 0.90 | 0.93 | 0.90 | 0.87 | ||
| 0.95 | 0.95 | 0.95 | 0.94 | ||
| 50 | 0.94 | 0.92 | 0.88 | 0.95 | |
| 0.99 | 0.90 | 0.98 | 0.88 | ||
| 0.96 | 0.95 | 0.96 | 0.94 | ||
| 100 | 0.93 | 0.95 | 0.89 | 0.95 | |
| 0.99 | 0.93 | 0.99 | 0.91 | ||
| 0.94 | 0.96 | 0.94 | 0.94 | ||
| 200 | 0.95 | 0.95 | 0.90 | 0.97 | |
| 0.99 | 0.96 | 0.98 | 0.94 |
| 59.00 | 102.20 | 17.30 | 23.00 | 50.60 | 27.00 | 203.00 | 40.90 | 53.00 | 177.40 | 94.60 |
| 129.40 | 76.00 | 93.20 | 22.80 | 98.80 | 77.70 | 204.20 | 16.90 | 55.10 | 103.90 | 34.90 |
| 39.70 | 137.70 | 104.20 | 117.60 | 17.10 | 120.80 | 164.90 | 50.20 | 172.80 | 58.50 | 112.40 |
| 24.50 | 32.80 | 64.00 | 72.10 | 139.30 | 0.50 | 70.90 | 0.80 | 82.70 | 108.60 | 32.30 |
| 13.60 | 25.70 | 135.80 | 136.80 | 89.70 | 139.20 | 102.80 | 97.30 | 60.60 |
| -GlogM Distribution | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | AICc | AD | KS | RMSE | |||||
| 0.9390 | 0.0931 | 145.6986 | −279.4682 | 564.9364 | 565.4262 | 0.2563 | 0.0638 | 0.0201 | 0.9950 |
| AIC | AICc | AD | KS | RMSE | |||||
| 0.9407 | 0.0726 | 150.0158 | — | — | — | 0.3088 | 0.0622 | 0.0223 | 0.9938 |
| BE2 Distribution | |||||||||
| AIC | AICc | AD | KS | RMSE | |||||
| 0.9100 | 0.0227 | −281.2113 | 566.4226 | 566.6626 | 0.5986 | 0.1002 | 0.0407 | 0.9796 | |
| SGR Distribution | |||||||||
| AIC | AICc | AD | KS | RMSE | |||||
| 0.0001 | −0.4161 | 22.4821 | −279.9818 | 565.9637 | 566.4534 | 0.4296 | 0.0888 | 0.0334 | 0.9865 |
| 1.0 | 2.5 | 1.2 | 1.2 | 4.1 | 9.0 | 3.0 | 1.0 | 1.4 | 2.0 | 3.0 | 1.7 | 1.2 | 1.2 | 1.1 | 1.5 | 5.0 |
| 1.6 | 2.0 | 0.1 | 0.4 | 0.8 | 3.7 | 1.3 | 3.8 | 0.1 | 0.1 | 0.2 | 2.0 | 7.6 | 0.1 | 1.8 | 0.5 | 0.5 |
| 0.5 | 1.1 | 1.4 | 1.0 | 1.0 | 0.7 | 5.7 | 0.4 | 0.3 | 1.8 | 0.4 | 1.0 | 1.2 | 2.6 | 1.0 | 5.0 | 1.7 |
| 2.4 | 0.1 | 0.5 | 7.1 | 0.2 | 0.7 | 0.1 | 2.7 | 2.9 | 0.4 | 2.0 | 20.3 |
| -GlogM Distribution | ||||||||
|---|---|---|---|---|---|---|---|---|
| AD | KS | RMSE | ||||||
| 0.9706 | 0.3332 | 2.0709 | −107.2595 | 220.5190 | 0.2999 | 0.0790 | 0.0247 | 0.9929 |
| AIC | AD | KS | RMSE | |||||
| 1.9497 | 0.1623 | 2.4131 | — | — | 15.4246 | 0.3175 | 0.1754 | 0.7543 |
| SG Distribution | ||||||||
| AD | KS | RMSE | ||||||
| 0.876 | 0.557 | 1.637 | −116.496 | 238.992 | 1.0556 | 0.1105 | 0.043 | 0.9783 |
| SGR Distribution | ||||||||
| AIC | AD | KS | RMSE | |||||
| 0.4423 | −0.4779 | 1.5611 | −107.3915 | 220.7830 | 0.3131 | 0.0891 | 0.0253 | 0.9925 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arslan, T. An α-Monotone Generalized Log-Moyal Distribution with Applications to Environmental Data. Mathematics 2021, 9, 1400. https://doi.org/10.3390/math9121400
Arslan T. An α-Monotone Generalized Log-Moyal Distribution with Applications to Environmental Data. Mathematics. 2021; 9(12):1400. https://doi.org/10.3390/math9121400
Chicago/Turabian StyleArslan, Talha. 2021. "An α-Monotone Generalized Log-Moyal Distribution with Applications to Environmental Data" Mathematics 9, no. 12: 1400. https://doi.org/10.3390/math9121400
APA StyleArslan, T. (2021). An α-Monotone Generalized Log-Moyal Distribution with Applications to Environmental Data. Mathematics, 9(12), 1400. https://doi.org/10.3390/math9121400






