A General Mechano-Pharmaco-Biological Model for Bone Remodeling Including Cortisol Variation
Abstract
1. Introduction
2. Materials and Methods
2.1. Development of the Bone Remodeling Mathematical Model
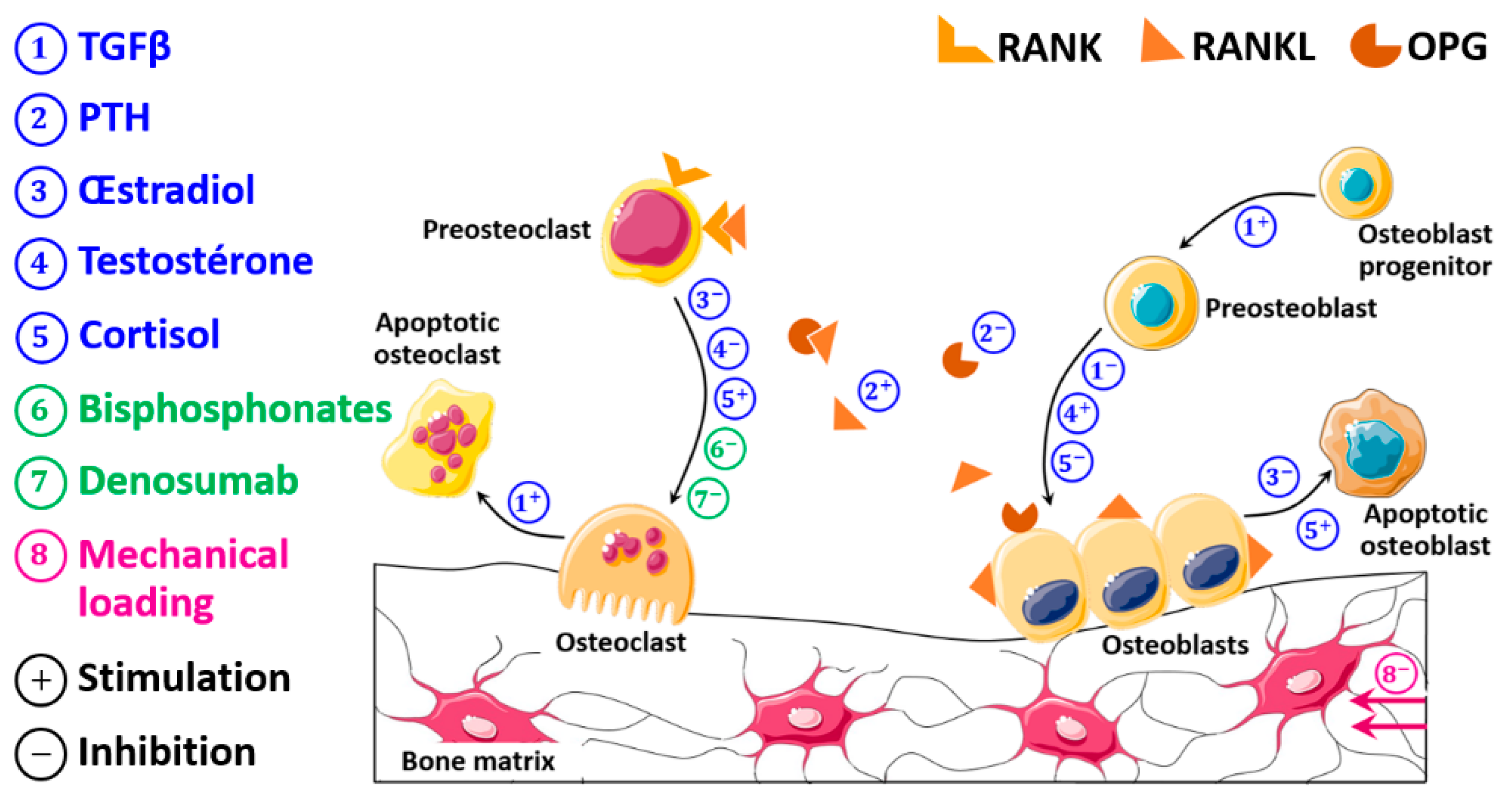
2.1.1. Development of the Pharmaco-Biological Model
- Transforming growth factor beta (TGFβ)
- Parathyroid hormone (PTH)
- Estradiol (Es)
- Testosterone (Ts)
- Cortisol (Co)
- Bisphosphonates (Bp)
- Denosumab (De)
2.1.2. Mechanical Model
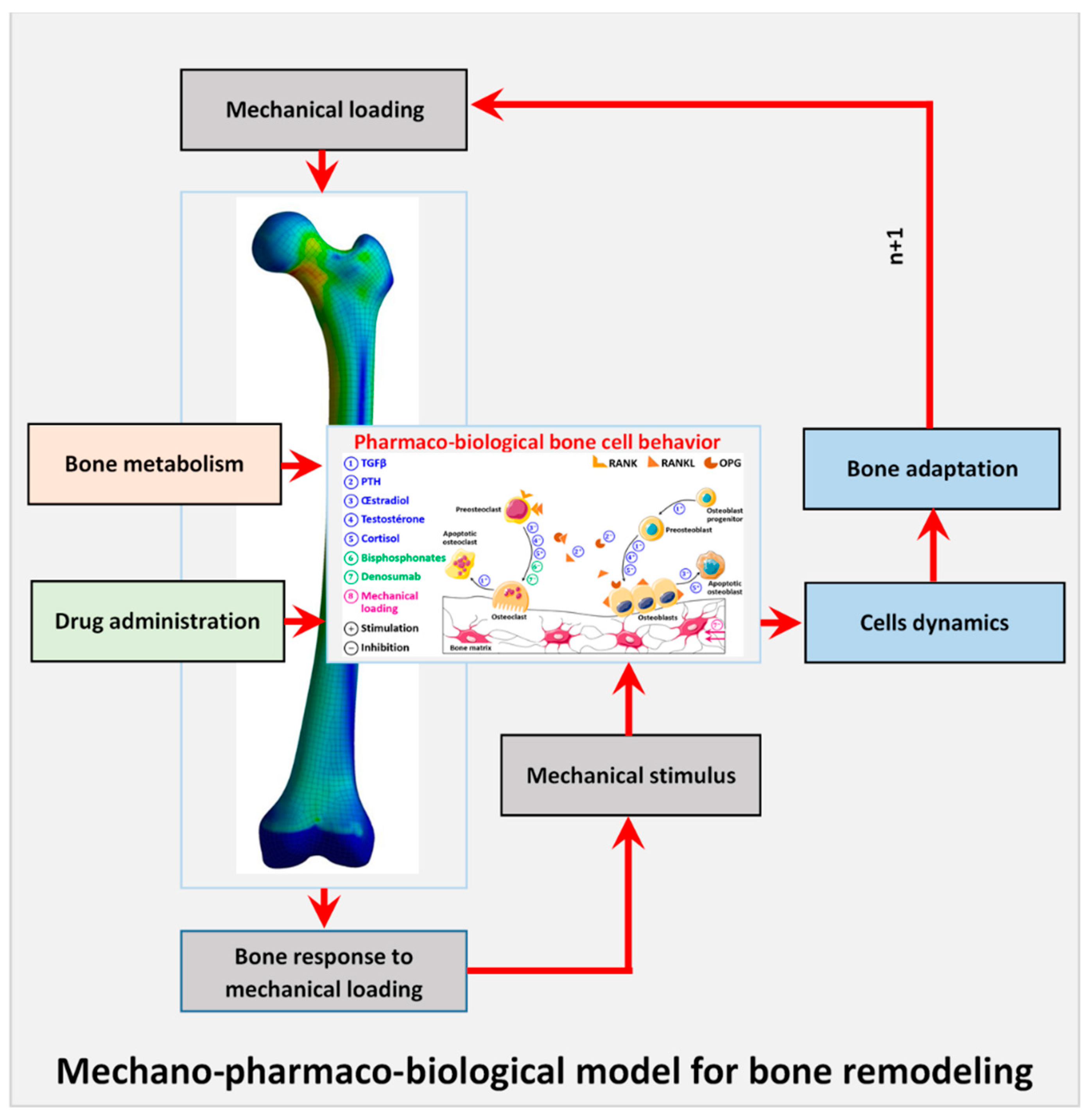
2.2. Overview of the Whole Model
2.3. Mechanobiological Coupling
2.4. Bone Mass Evolution
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Borgström, F.; Karlsson, L.; Ortsäter, G.; Norton, N.; Halbout, P.; Cooper, C.; Lorentzon, M.; McCloskey, E.V.; Harvey, N.C.; Javaid, M.K.; et al. Fragility fractures in Europe: Burden, management and opportunities. Arch. Osteoporos. 2020, 15, 1–21. [Google Scholar] [CrossRef]
- Beaupre, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling-theoretical development. J. Orthop. Res. 1990, 8, 651–661. [Google Scholar] [CrossRef]
- Carter, D.R.; Fyhrie, D.P.; Whalen, R. Trabecular bone density and loading history: Regulation of connective tissue biology by mechanical energy. J. Biomech. 1987, 20, 785–794. [Google Scholar] [CrossRef]
- Carter, D.; Orr, T.; Fyhrie, D. Relationships between loading history and femoral cancellous bone architecture. J. Biomech. 1989, 22, 231–244. [Google Scholar] [CrossRef]
- Doblaré, M.; García, J. Anisotropic bone remodelling model based on a continuum damage-repair theory. J. Biomech. 2002, 35, 1–17. [Google Scholar] [CrossRef]
- Jacobs, C.R.; Levenston, M.E.; Beaupré, G.S.; Simo, J.C.; Carter, D.R. Numerical instabilities in bone remodeling simulations: The advantages of a node-based finite element approach. J. Biomech. 1995, 28, 449–459. [Google Scholar] [CrossRef]
- Mullender, M.; Huiskes, R.; Weinans, H. A physiological approach to the simulation of bone remodeling as a self-organizational control process. J. Biomech. 1994, 27, 1389–1394. [Google Scholar] [CrossRef]
- Mullender, M.; Huiskes, R. Osteocytes and bone lining cells: Which are the best candidates for mechano-sensors in cancellous bone? Bone 1997, 20, 527–532. [Google Scholar] [CrossRef]
- Frost, H.M. The mechanostat: A proposed pathogenic mechanism of osteoporoses and the bone mass effects of mechanical and non mechanical agents. Bone Miner. 1987, 2, 73–85. [Google Scholar] [PubMed]
- Wolff, J. Das Gesetz der Transformation der Knochen. DMW Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Huiskes, H.R.; Ruimerman, R.R.; Van Lenthe, G.H.; Janssen, J.D. Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature 2000, 405, 704–706. [Google Scholar] [CrossRef]
- Rouhi, G.; Vahdati, A.; Li, X.; Sudak, L. A three-dimensional computer model to simulate spongy bone remodeling under overload using a semi-mechanistic bone remodeling theory. J. Mech. Med. Biol. 2015, 15, 1550061. [Google Scholar] [CrossRef]
- Van Schaick, E.; Zheng, J.; Ruixo, J.J.P.; Gieschke, R.; Jacqmin, P. A semi-mechanistic model of bone mineral density and bone turnover based on a circular model of bone remodeling. J. Pharmacokinet. Pharmacodyn. 2015, 42, 315–332. [Google Scholar] [CrossRef]
- Komarova, S.V.; Smith, R.J.; Dixon, S.; Sims, S.M.; Wahl, L.M. Mathematical model predicts a critical role for osteoclast autocrine regulation in the control of bone remodeling. Bone 2003, 33, 206–215. [Google Scholar] [CrossRef]
- Ryser, M.D.; Nigam, N.; Komarova, S.V. Mathematical Modeling of Spatio-Temporal Dynamics of a Single Bone Multicellular Unit. J. Bone Miner. Res. 2009, 24, 860–870. [Google Scholar] [CrossRef]
- Ayati, B.P.; Edwards, C.M.; Webb, G.F.; Wikswo, J.P. A mathematical model of bone remodeling dynamics for normal bone cell populations and myeloma bone disease. Biol. Direct 2010, 5, 28. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, V.; Tobin, F.L.; Greller, L.D.; Cho, C.R.; Suva, L.J. Modeling the interactions between osteoblast and osteoclast activities in bone remodeling. J. Theor. Biol. 2004, 229, 293–309. [Google Scholar] [CrossRef]
- Maldonado, S.; Borchers, S.; Findeisen, R.; Allgower, F. Mathematical modeling and analysis of force induced bone growth. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 3154–3157. [Google Scholar]
- Pivonka, P.; Zimak, J.; Smith, D.W.; Gardiner, B.S.; Dunstan, C.; Sims, N.A.; Martin, T.J.; Mundy, G.R. Model structure and control of bone remodeling: A theoretical study. Bone 2008, 43, 249–263. [Google Scholar] [CrossRef] [PubMed]
- Peyroteo, M.M.A.; Belinha, J.; Dinis, L.M.J.S.; Jorge, R.M.N. Bone remodeling: An improved spatiotemporal mathematical model. Arch. Appl. Mech. 2019, 90, 635–649. [Google Scholar] [CrossRef]
- Ghiasi, M.S.; Chen, J.; Vaziri, A.; Rodriguez, E.K.; Nazarian, A. Bone fracture healing in mechanobiological modeling: A review of principles and methods. Bone Rep. 2017, 6, 87–100. [Google Scholar] [CrossRef] [PubMed]
- Aitoumghar, I.; Barkaoui, A.; Chabrand, P. Mechanobiological Behavior of a Pathological Bone. In BioMechanics and Functional Tissue Engineering; IntechOpen: London, UK, 2021. [Google Scholar]
- Kahla, R.B.; Barkaoui, A.; Salah, F.Z.B.; Chafra, M. Cell Interaction and Mechanobiological Modeling of Bone Remodeling Process. In BioMechanics and Functional Tissue Engineering; IntechOpen: London, UK, 2020. [Google Scholar]
- Anderson, D.D.; Thomas, T.P.; Marin, A.C.; Elkins, J.M.; Lack, W.D.; Lacroix, D. Computational techniques for the assessment of fracture repair. Injury 2014, 45, S23–S31. [Google Scholar] [CrossRef]
- Betts, D.C.; Müller, R. Mechanical regulation of bone regeneration: Theories, models, and experiments. Front. Endocrinol. 2014, 5, 211. [Google Scholar] [CrossRef]
- Isaksson, H. Recent advances in mechanobiological modeling of bone regeneration. Mech. Res. Commun. 2012, 42, 22–31. [Google Scholar] [CrossRef]
- Avval, P.T.; Klika, V.; Bougherara, H. Predicting bone remodeling in response to total hip arthroplasty: Computational study using mechanobiochemical model. J. Biomech. Eng. 2014, 136, 051002. [Google Scholar] [CrossRef] [PubMed]
- Klika, V.; Pérez, M.A.; García-Aznar, J.M.; Maršík, F.; Doblaré, M. A coupled mechano-biochemical model for bone adaptation. J. Math. Biol. 2014, 69, 1383–1429. [Google Scholar] [CrossRef]
- Lerebours, C.; Buenzli, P.R.; Scheiner, S.; Pivonka, P. A multiscale mechanobiological model of bone remodelling predicts site-specific bone loss in the femur during osteoporosis and mechanical disuse. Biomech. Model. Mechanobiol. 2016, 15, 43–67. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Sansalone, V.; Cooper, D.M.L.; Forwood, M.R.; Pivonka, P. Mechanobiological osteocyte feedback drives mechanostat regulation of bone in a multiscale computational model. Biomech. Model. Mechanobiol. 2019, 18, 1475–1496. [Google Scholar] [CrossRef]
- Pastrama, M.-I.; Scheiner, S.; Pivonka, P.; Hellmich, C. A mathematical multiscale model of bone remodeling, accounting for pore space-specific mechanosensation. Bone 2018, 107, 208–221. [Google Scholar] [CrossRef]
- Rouhi, G.; Epstein, M.; Sudak, L.; Herzog, W. Modeling bone resorption using Mixture Theory with chemical reactions. J. Mech. Mater. Struct. 2007, 2, 1141–1155. [Google Scholar] [CrossRef]
- Scheiner, S.; Pivonka, P.; Hellmich, C. Coupling systems biology with multiscale mechanics, for computer simulations of bone remodeling. Comput. Methods Appl. Mech. Eng. 2013, 254, 181–196. [Google Scholar] [CrossRef]
- Rouhi, G.; Vahdati, A.; Li, X.; Sudak, L.J. An investigation into the effects of osteocytes density and mechanosensitivity on trabecular bone loss in aging and osteoporotic individuals. Biomed. Eng. Lett. 2015, 5, 302–310. [Google Scholar] [CrossRef]
- Hinton, P.V.; Rackard, S.M.; Kennedy, O.D. In Vivo Osteocyte Mechanotransduction: Recent Developments and Future Directions. Curr. Osteoporos. Rep. 2018, 16, 746–753. [Google Scholar] [CrossRef]
- Klein-Nulend, J.; Bakker, A.D.; Bacabac, R.G.; Vatsa, A.; Weinbaum, S. Mechanosensation and transduction in osteocytes. Bone 2013, 54, 182–190. [Google Scholar] [CrossRef]
- Ashrafi, M.; Gubaua, J.E.; Pereira, J.T.; Gahlichi, F.; Doblaré, M. A mechano-chemo-biological model for bone remodeling with a new mechano-chemo-transduction approach. Biomech. Model. Mechanobiol. 2020, 19, 2499–2523. [Google Scholar] [CrossRef]
- Barkaoui, A.; Ben Kahla, R.; Merzouki, T.; Hambli, R. Age and gender effects on bone mass density variation: Finite elements simulation. Biomech. Model. Mechanobiol. 2016, 16, 521–535. [Google Scholar] [CrossRef]
- Ben Kahla, R.; Barkaoui, A.; Merzouki, T. Age-related mechanical strength evolution of trabecular bone under fatigue damage for both genders: Fracture risk evaluation. J. Mech. Behav. Biomed. Mater. 2018, 84, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Barkaoui, A.; Ben Kahla, R.; Merzouki, T.; Hambli, R. Numerical Simulation of Apparent Density Evolution of Trabecular Bone under Fatigue Loading: Effect of Bone Initial Properties. J. Mech. Med. Biol. 2019, 19, 1950041. [Google Scholar] [CrossRef]
- Hill, A.V. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. 1910, 40, 4–7. [Google Scholar]
- Tamma, R.; Zallone, A. Osteoblast and osteoclast crosstalks: From OAF to Ephrin. Inflamm. Allergy Drug Targets 2012, 11, 196–200. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, X.; Lei, W.; Pang, L.; Wan, C.; Shi, Z.; Zhao, L.; Nagy, T.; Peng, X.; Hu, J.; et al. TGF-β1–induced migration of bone mesenchymal stem cells couples bone resorption with formation. Nat. Med. 2009, 15, 757–765. [Google Scholar] [CrossRef]
- Oumghar, I.A.; Barkaoui, A.; Chabrand, P. Toward a Mathematical Modeling of Diseases’ Impact on Bone Remodeling: Technical Review. Front. Bioeng. Biotechnol. 2020, 8, 1236. [Google Scholar] [CrossRef]
- Erlebacher, A.; Filvaroff, E.H.; Ye, J.-Q.; Derynck, R. Osteoblastic Responses to TGF-β during Bone Remodeling. Mol. Biol. Cell 1998, 9, 1903–1918. [Google Scholar] [CrossRef]
- Janssens, K.; Dijke, P.T.; Janssens, S.; Van Hul, W. Transforming Growth Factor-β1 to the Bone. Endocr. Rev. 2005, 26, 743–774. [Google Scholar] [CrossRef]
- Alliston, T.; Choy, L.; Ducy, P.; Karsenty, G.; Derynck, R. TGF-β-induced repression of CBFA1 by Smad3 decreases cbfa1 and osteocalcin expression and inhibits osteoblast differentiation. EMBO J. 2001, 20, 2254–2272. [Google Scholar] [CrossRef] [PubMed]
- Bonewald, L.F.; Dallas, S.L. Role of active and latent transforming growth factor β in bone formation. J. Cell. Biochem. 1994, 55, 350–357. [Google Scholar] [CrossRef]
- Mundy, G.R.; Boyce, B.F.; Yoneda, T.; Bonewald, L.F.; Roodman, G.D. Osteoporosis; Marcus, R., Feldman, D., Kelsey, J., Eds.; Academic Press: New York, NY, USA, 1996. [Google Scholar]
- Siddiqui, J.A.; Johnson, J.; Le Henaff, C.; Bitel, C.L.; Tamasi, J.A.; Partridge, N.C. Catabolic Effects of Human PTH (1–34) on Bone: Requirement of Monocyte Chemoattractant Protein-1 in Murine Model of Hyperparathyroidism. Sci. Rep. 2017, 7, 15300. [Google Scholar] [CrossRef]
- Wein, M.N.; Kronenberg, H.M. Regulation of Bone Remodeling by Parathyroid Hormone. Cold Spring Harb. Perspect. Med. 2018, 8, a031237. [Google Scholar] [CrossRef]
- Khosla, S.; Monroe, D.G. Regulation of Bone Metabolism by Sex Steroids. Cold Spring Harb. Perspect. Med. 2018, 8, a031211. [Google Scholar] [CrossRef] [PubMed]
- Okman-Kilic, T. Estrogen deficiency and osteoporosis. In Advances in Osteoporosis; IntechOpen: London, UK, 2015. [Google Scholar]
- Mohamad, N.V.; Soelaiman, I.-N.; Chin, K.-Y. A concise review of testosterone and bone health. Clin. Interv. Aging 2016, 11, 1317–1324. [Google Scholar] [CrossRef]
- Chiodini, I.; Torlontano, M.; Carnevale, V.; Trischitta, V.; Scillitani, A. Skeletal involvement in adult patients with endogenous hypercortisolism. J. Endocrinol. Investig. 2008, 31, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Mathis, S.L.; Farley, R.S.; Fuller, D.K.; Jetton, A.E.; Caputo, J.L. The Relationship between Cortisol and Bone Mineral Density in Competitive Male Cyclists. J. Sports Med. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Çetin, A.; Gökçe-Kutsal, Y.; Çeliker, R. Predictors of bone mineral density in healthy males. Rheumatol. Int. 2001, 21, 85–88. [Google Scholar] [CrossRef]
- Reynolds, R.M.; Dennison, E.M.; Walker, B.R.; Syddall, H.E.; Wood, P.J.; Andrew, R.; Phillips, D.I.; Cooper, C. Cortisol Secretion and Rate of Bone Loss in a Population-Based Cohort of Elderly Men and Women. Calcif. Tissue Int. 2005, 77, 134–138. [Google Scholar] [CrossRef]
- Osella, G.; Ventura, M.; Ardito, A.; Allasino, B.; Termine, A.; Saba, L.; Vitetta, R.; Terzolo, M.; Angeli, A. Cortisol secretion, bone health, and bone loss: A cross-sectional and prospective study in normal nonosteoporotic women in the early postmenopausal period. Eur. J. Endocrinol. 2012, 166, 855–860. [Google Scholar] [CrossRef]
- Siggelkow, H.; Etmanski, M.; Bozkurt, S.; Groβ, P.; Koepp, R.; Brockmöller, J.; Tzvetkov, M.V. Genetic polymorphisms in 11β-hydroxysteroid dehydrogenase type 1 correlate with the postdexamethasone cortisol levels and bone mineral density in patients evaluated for osteoporosis. J. Clin. Endocrinol. Metab. 2014, 99, E293–E302. [Google Scholar] [CrossRef]
- Anastasilakis, A.D.; Polyzos, S.A.; Makras, P. Therapy of endocrine disease: Denosumab vs bisphosphonates for the treatment of postmenopausal osteoporosis. Eur. J. Endocrinol. 2018, 179, R31–R45. [Google Scholar] [CrossRef]
- Bonfoh, N.; Novinyo, E.; Lipinski, P. Modeling of bone adaptative behavior based on cells activities. Biomech. Model. Mechanobiol. 2010, 10, 789–798. [Google Scholar] [CrossRef] [PubMed]
- García-Aznar, J.M.; Rueberg, T.; Doblare, M. A bone remodelling model coupling microdamage growth and repair by 3D BMU-activity. Biomech. Model. Mechanobiol. 2005, 4, 147–167. [Google Scholar] [CrossRef] [PubMed]
- Martin, B. A theory of fatigue damage accumulation and repair in cortical bone. J. Orthop. Res. 1992, 10, 818–825. [Google Scholar] [CrossRef]
- Nagaraja, S.; Couse, T.L.; Guldberg, R.E. Trabecular bone microdamage and microstructural stresses under uniaxial compression. J. Biomech. 2005, 38, 707–716. [Google Scholar] [CrossRef] [PubMed]
- Zioupos, P.; Casinos, A. Cumulative damage and the response of human bone in two-step loading fatigue. J. Biomech. 1998, 31, 825–833. [Google Scholar] [CrossRef]
- Chaboche, J.-L. Continuous damage mechanics—A tool to describe phenomena before crack initiation. Nucl. Eng. Des. 1981, 64, 233–247. [Google Scholar] [CrossRef]
- Pattin, C.A.; Caler, W.E.; Carter, D.R. Cyclic mechanical property degradation during fatigue loading of cortical bone. J. Biomech. 1996, 29, 69–79. [Google Scholar] [CrossRef]
- Martin, R.B.; Burr, D.B.; Sharkey, N.A. Skeletal Tissue Mechanics; Springer: Berlin/Heidelberg, Germany, 1998; Volume 190. [Google Scholar]
- Martin, R.B. Fatigue damage, remodeling, and the minimization of skeletal weight. J. Theor. Biol. 2003, 220, 271–276. [Google Scholar] [CrossRef]
- Hambli, R. Connecting mechanics and bone cell activities in the bone remodeling process: An integrated finite element modeling. Front. Bioeng. Biotechnol. 2014, 2, 6. [Google Scholar] [CrossRef]
- Baste, S.; el Guerjouma, R.; Gérard, A. Mesure de l’endommagement anisotrope d’un composite céramique-céramique par une méthode ultrasonore. Rev. Phys. Appliquée 1989, 24, 721–731. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Duan, N.; Zhu, G.; Schwarz, E.M.; Xie, C. Osteoblast–osteoclast interactions. Connect. Tissue Res. 2018, 59, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Buckland-Wright, J. Sensitivity analysis of a novel mathematical model identifies factors determining bone resorption rates. Bone 2004, 35, 918–928. [Google Scholar] [CrossRef]
- Bahia, M.T.; Hecke, M.B.; Mercuri, E.G.F. Image-based anatomical reconstruction and pharmaco-mediated bone remodeling model applied to a femur with subtrochanteric fracture: A subject-specific finite element study. Med. Eng. Phys. 2019, 69, 58–71. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S.; Pivonka, P.; Smith, D.W.; Dunstan, C.; Hellmich, C. Mathematical modeling of postmenopausal osteoporosis and its treatment by the anti-catabolic drug denosumab. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 1–27. [Google Scholar] [CrossRef]
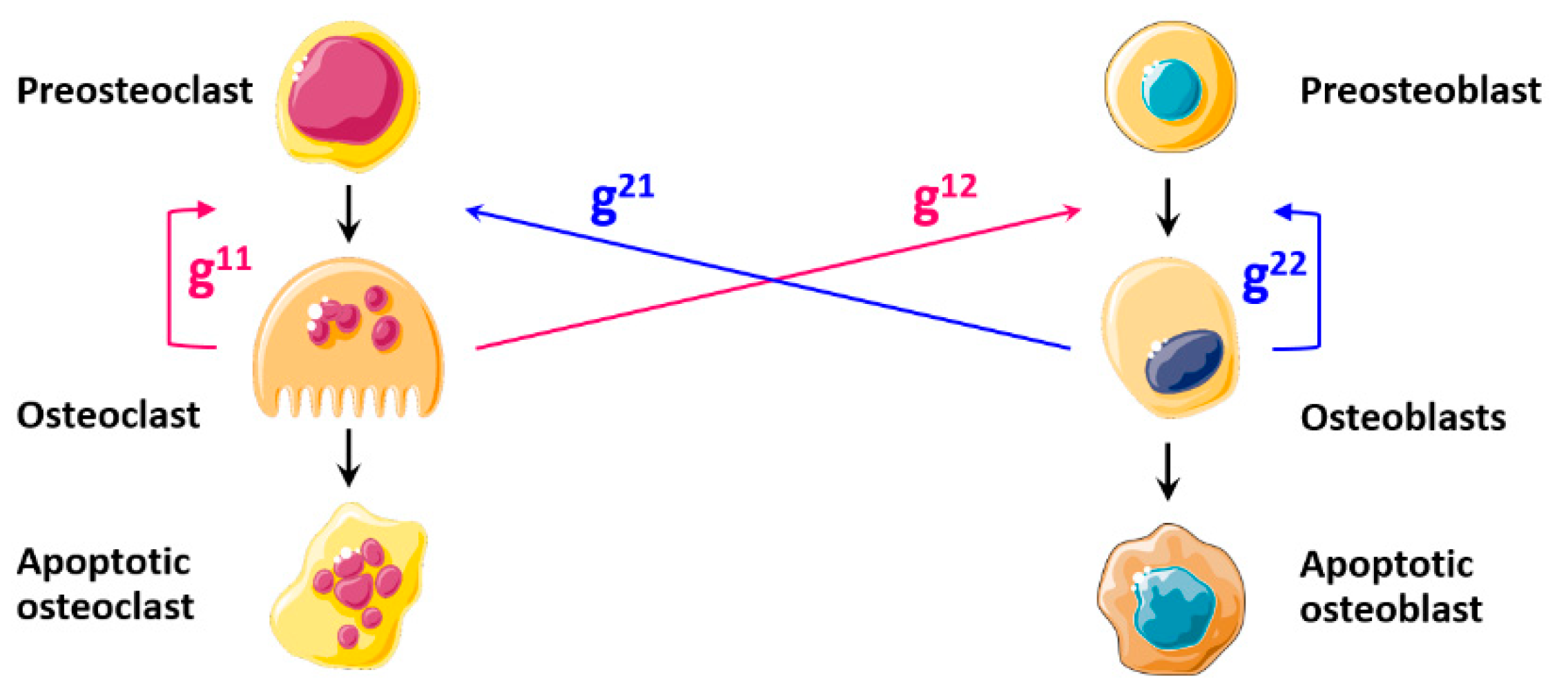
| TGFβ | |
|---|---|
| Actions | ). ). ). |
| Diagram |  |
| Formulation | |
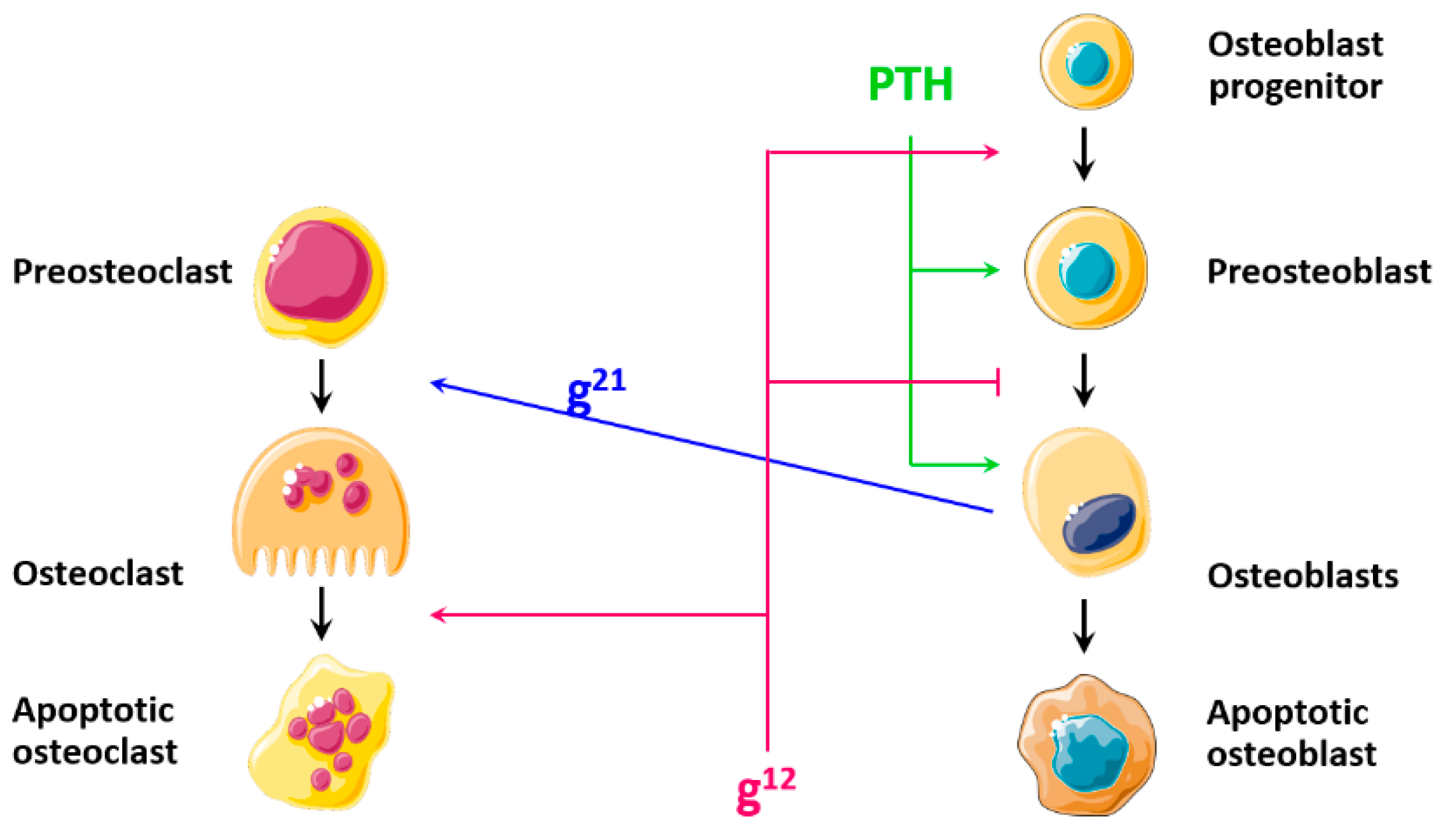
| PTH | |
|---|---|
| Actions | ). ). |
| Diagram | 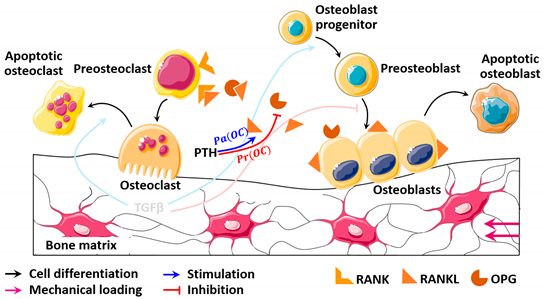 |
| Formulation | |
| Estradiol | |
|---|---|
| Actions | ). ). |
| Diagram | 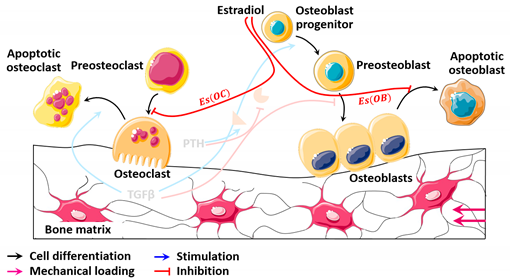 |
| Concentration evolution | 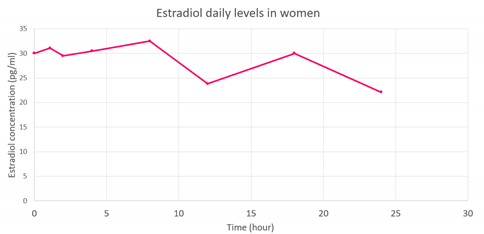 |
| Formulation | |
| Testosterone | |
|---|---|
| Actions | ). ). |
| Diagram |  |
| Concentration evolution | 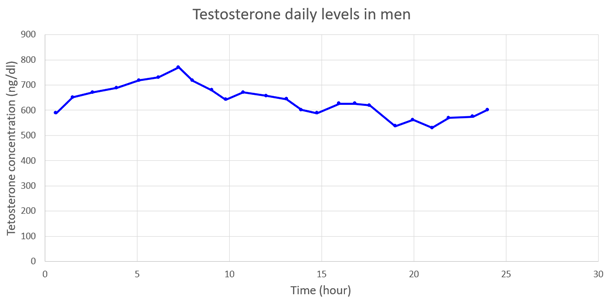 |
| Formulation | |
| Cortisol | |
|---|---|
| Actions | ). ). ). ). |
| Diagram |  |
| Concentration evolution | 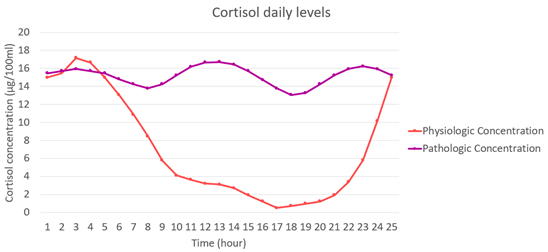 |
| Formulation | |
| Bisphosphonates | |
|---|---|
| Actions | ). |
| Diagram |  |
| Formulation | |
| Denosumab | |
|---|---|
| Actions | ). |
| Diagram | 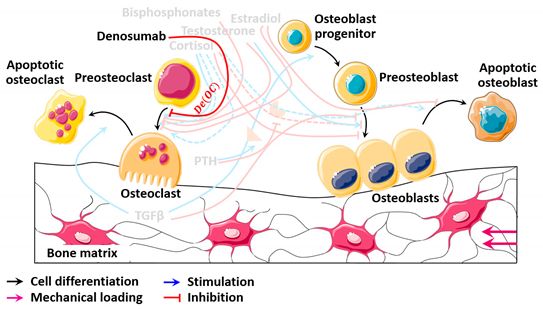 |
| Formulation | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahla, R.B.; Barkaoui, A.; Chafra, M.; Tavares, J.M.R.S. A General Mechano-Pharmaco-Biological Model for Bone Remodeling Including Cortisol Variation. Mathematics 2021, 9, 1401. https://doi.org/10.3390/math9121401
Kahla RB, Barkaoui A, Chafra M, Tavares JMRS. A General Mechano-Pharmaco-Biological Model for Bone Remodeling Including Cortisol Variation. Mathematics. 2021; 9(12):1401. https://doi.org/10.3390/math9121401
Chicago/Turabian StyleKahla, Rabeb Ben, Abdelwahed Barkaoui, Moez Chafra, and João Manuel R. S. Tavares. 2021. "A General Mechano-Pharmaco-Biological Model for Bone Remodeling Including Cortisol Variation" Mathematics 9, no. 12: 1401. https://doi.org/10.3390/math9121401
APA StyleKahla, R. B., Barkaoui, A., Chafra, M., & Tavares, J. M. R. S. (2021). A General Mechano-Pharmaco-Biological Model for Bone Remodeling Including Cortisol Variation. Mathematics, 9(12), 1401. https://doi.org/10.3390/math9121401








