A Tool for the Analysis and Characterization of School Mathematical Models

Abstract

This paper shows a tool for the analysis of written productions that allows for the characterization of the mathematical models that students develop when solving modeling tasks. For this purpose, different conceptualizations of mathematical models in education are discussed, paying special attention to the evidence that characterizes a school model. The discussion leads to the consideration of three components, which constitute the main categories of the proposed tool: the real system to be modeled, its mathematization and the representations used to express both. These categories and the corresponding analysis procedure are explained and illustrated through two working examples, which expose the value of the tool in establishing the foci of analysis when investigating school models, and thus, suggest modeling skills. The connection of this tool with other approaches to educational research on mathematical modeling is also discussed.

1. Introduction

The current socio-educational context exposes the need for individuals to acquire a strong mathematical education that enables them to develop active citizenship [1]. Modeling is a school activity that contributes to this aim, since it promotes mathematical skills such as problem solving [2], mathematical connections [3] and the use of multiple representations [4]. Furthermore, modeling adds meaning to mathematical activities [5] and stimulates critical thinking and reflection on the importance of mathematics [6], thereby increasing students’ commitment to understanding and applying mathematical content [7].

Modeling is, therefore, a specific focus of interest in mathematics education [8] that has been approached from different perspectives (a review of some of these was provided in [9]). Each of them emphasizes different issues that together characterize what is meant by mathematical modeling in education: (i) modeling is a school activity. As a matter of fact, papers such as [10] claimed that a large part of mathematical activity is modeling. Under this perspective, [11] described it as a functional mathematical activity, in contrast to formal mathematical activity. (ii) Modeling arises from a question about a certain system [12]. In this regard, some authors identify modeling and problem solving [13], while others claim that modeling is intended to produce knowledge about the system under study, without restricting itself to answering a specific question [3]. A third perspective integrates these two approaches [14] in such a way that “modeling for” (oriented to specific problem solving) emerges at more basic learning stages, while “modeling of” (oriented to develop knowledge) emerges at more advanced learning stages. (iii) Modeling is a process that involves different steps [15,16], which may describe the stages necessary to create, implement and evaluate a mathematical model (e.g., [17]), or the observable school activities that students carry out during the process, such as reading, estimating, or calculating (e.g., [18]). (iv) Modeling involves working with a mathematical model, or the output of modeling [19]. This entails a language shift between the real world and mathematics [20], or also between different mathematical descriptions [21]. (v) Modeling involves the acquisition of specific mathematical skills. In this sense, [2] and [22] provided conceptualizations of modeling competence based on different descriptions of such skills. Synthesizing all these ideas leads one to understand mathematical modeling as the school activity that arises from a question about a certain system, which is developed through the process of creating, applying and evaluating a mathematical model useful for building knowledge about the system, and contributes to the development of mathematical skills linked to the process. This conception, which is assumed throughout the paper, relies on three dimensions whose analysis is crucial in educational research on modeling: the type of mathematical skills associated with modeling, the activities involved in the process, and the concept of mathematical model that is assumed. This paper focuses on the latter, specifically on the characterization of the underlying models in written productions developed by students.

The reasons that lead one to considering the mathematical model as a key focus of interest in empirical research are diverse. The first one relates to the size of the samples that can be investigated. Indeed, studies centered on the analysis of written productions require simpler data gathering procedures compared to studies that involve the entire modeling process. This allows for easier access to a larger number of models for a given modeling task, thereby increasing the educational potential of the research. The second reason has to do with the kind of data to be dealt with. On the one hand, the study of the mathematical model from a written production forces researchers to interpret a smaller amount of information than studies that investigate students’ actions during the modeling process. On the other hand, the analysis of the model encompasses the complete students’ response to a given task, thereby exposing the variety of representations, reasoning and variables autonomously used by them for modeling. This allows researchers to observe the overall character of the modeling activity, as opposed to instrument-based studies (e.g., [23]), that atomize observation. The third reason for focusing research on the mathematical model is the low proliferation of empirical studies that do so to draw educational implications. Despite the reasons for analyzing the model presented above, there is no consensus among researchers on what the nature of a mathematical model is, nor is there a wealth of empirical results that gather evidence on the learning of modeling from the analysis of school models. The importance of obtaining these types of results requires the development of analytical tools for studying school models, thus motivating this paper.

Considering all the above, the research questions to be addressed are as follows: what components should research consider when characterizing a school mathematical model? What evidence should be recorded in a tool for analyzing written productions? What is the associated analysis procedure and what kind of results does it provide? To answer these questions, this paper aims to:

• Define a set of categories that altogether make it possible to characterize the school mathematical model underlying a written production.
• Provide an analysis tool based on these categories, as well as an appropriate analysis procedure associated with such tool.
• Illustrate the use and results provided by the tool by applying it to two different modeling tasks.

Research Background

As commented above, the value of analyzing school models for empirical research had not so far led to a great number of papers that develop tools for this purpose. One of the most noteworthy is that of [24], who took the conceptualization of model in [25] as a starting point to design a tool for characterizing models. This is based on the observation of (i) conceptual systems, which include mathematical objects, relations between them and patterns or regularities in the data, (ii) procedures, which can be algebraic or functional, calculation algorithms and measurements, and (iii) languages (symbolic, written, graphic) and diagrams/schemes. This scheme has proved to be useful when investigating the so-called Fermi problems [26]. Beyond that, unfortunately, research in mathematics education has not been concerned with developing a wide variety of instruments to investigate school models. However, the idea in [24] of basing the analysis tool on a certain conceptualization of a mathematical model can be followed to develop a new tool applicable to diverse modeling situations. This leads to the exploration of different conceptualizations in the search of components that characterize a mathematical model according to the literature.

The first component to take into consideration was suggested by [27], who thought of a model as an object that abstracts the relevant properties of a certain system and allows decisions to be made to deal with a problematic situation. This perspective focuses on the predictive value, in contrast to the descriptive–explanatory duality of the mathematical models proposed by [28]. In any case, these two papers illustrate that the system that motivates its creation should be considered as a relevant component of the model.

The second and third components of interest relate to the conceptual (mathematical) structure underlying a model. As mentioned above, [25] proposed a definition based on two components: a conceptual system and the procedures associated with it. Both are expressed through different representations and are linked to a problem situation. Similarly, [4] conceived models as conceptual systems that are expressed through external notation systems. In this case, the conceptual system involves operations, relations and rules that govern interactions. In [29], a model was conceived as a representation of the structure in a given system, where the system is a set of interrelated objects, and the structure of the system is a set of relations between its objects. This representation consists of a set of words, symbols or figures completed with a set of rules and conventions that allow the model to be expressed. The conceptualizations by [4,25,29] introduce two components of interest: the mathematical structure underlying the system being modeled and the representations used to express this structure.

Another matter of interest found in the literature is the consideration of conceptualizations based on indivisible components that are indissoluble, but which can be studied separately to understand the model, thus facilitating its analysis. In this regard, [12] provided a conceptualization based on the usefulness of the model to solve problems. Indeed, this author defined a mathematical model as the term (S, Q, M), where S is a system, Q is a question related to S and M is a set of mathematical statements that can be used to answer Q. In [30], a model was considered to be the triplet (S, M, R), where S is the (real) problem situation, M is a collection of mathematical entities and R the relations between the elements of S and those of M. Subsequently, [31] took up this idea to define a mathematical model as a new triplet (D, f, M) that includes an extra-mathematical domain D, a mathematical realm M and an application f (the mathematization) that maps D into M. These approaches decouple the model from a concrete problem and bring the novelty of introducing the application f to materialize the intuitive idea of a model as a mathematical description of reality. The ideas brought into play by [12,30,31] were taken up by [32], who defined a mathematical model by the quartet (S, Q, M, R), where S is a system, Q is a question about S, M is a set of mathematical statements that arise to give an answer to Q, and R is the relation between the objects of S and M.

In summary, the background review highlights the relevance of grounding the analysis tool in an adequate conceptualization of a mathematical model. The different approaches found in the literature provide the idea of considering a model as a conjunction of several components that include the starting system, the mathematical structure and the representations used. In [33], these ideas were taken to articulate a definition of a model based on three components: the system that motivates the creation of the model, its mathematization and the representations used to describe a system and mathematization. The tool proposed in this paper builds on this definition and is explained and exemplified below.

2. Materials and Methods

The development of a tool for the analysis of school models based on the definition in [33] requires the specification of the meanings of the system, the mathematization and the representations within a written production, in order to make such components operational for the research. In the following, the specification of these meanings is explained, and the categories of the tool are specified. Next, the associated analysis procedure is described. This is illustrated for two written productions in the Results section. Each of the productions were developed by a different group of students enrolled in the Elementary Teacher degree studies at two Andalusian universities. Both groups were composed of five students (18–19 years old) who attended courses focused on mathematical content knowledge.

2.1. The Tool

When considering a modeling task and a written production that seeks to solve it, the mathematical model developed in the production can be known through the study of the system, its mathematization, and the representations, where:

(i) the system comprises those relations and real objects in the context of the task that are used to obtain knowledge about such context, as well as the explicit questions that stimulate the creation of knowledge. The relations are understood as all those statements without mathematical content that express relevant information about the context, while the objects are the elements of the context to which the relations refer to. Finally, the questions are those explicit ones that seek to be answered in the written production. For example, in the task “the President’s supporters”, which consists of estimating the number of people who attended Obama’s inauguration from a satellite image of the event (see Appendix A), a statement indicating the number of people who fit on the floor area of the Capitol is a relation of the system. It alludes to the Capitol, which is an object of the system. In turn, the request of estimating the number of people attending the inauguration is a question of the system.

The system is determined by the context in which the model is created, and therefore, it has the same level of abstraction. Like the question that motivates the development of the model, the knowledge about the context obtained from applying it may also be considered part of the system.

(ii) The mathematization contains those statements and mathematical entities abstracting the information of the system which is relevant for modeling. Within it, four types of elements can be distinguished: results, variables, properties and concepts. The results are all those statements that involve mathematical content and that lead to an answer to the task or situation that motivates the development of the model, while the variables are those relevant quantities involved in the results. In turn, the properties are the purely mathematical abstract statements that support the results, while the concepts are all those to which the properties refer to.

Table 1. Classification of the statements and entities in the mathematization, as organized in this paper (source: prepared by the authors).

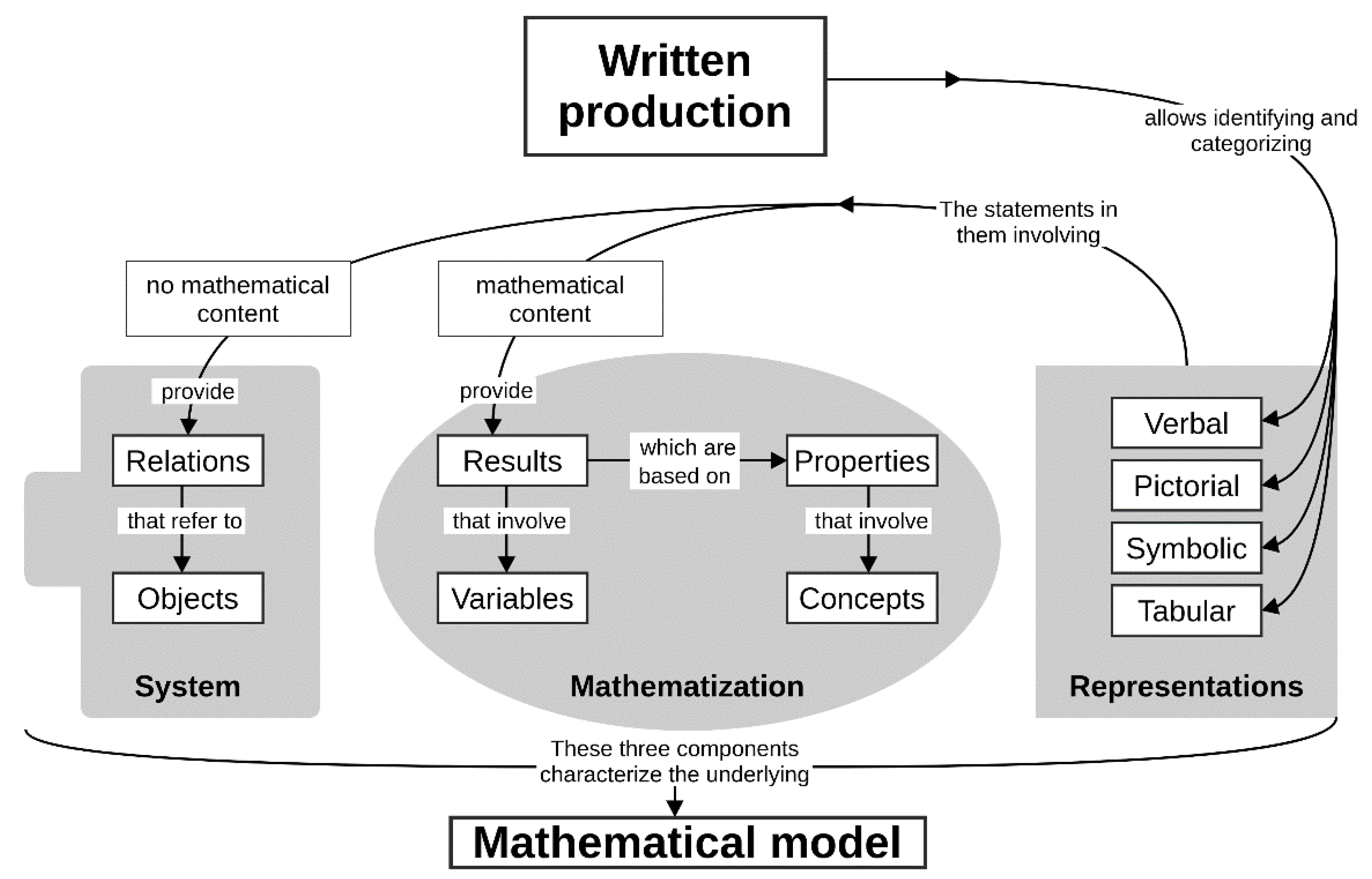
	Statements	Entities They Refer to
Knowledge applied to the system	Results	Variables
Conceptual mathematical knowledge	Properties	Concepts

shows the classification of these subcomponents of the mathematization according to their nature (statements or entities) and their level of abstraction.

For example, in the task “the President’s supporters” (Appendix A), the statement that the area occupied by people can be approximated by 15 and a half times the area of the Capitol would be a result, which refers to two variables: the area occupied by people and the number of times the Capitol fits within the area occupied by people. The extensive character of the area would be a property that underlies the result and that refers to the concept of area.

The mathematization describes any mathematical knowledge that is applied to the system to generate knowledge about the situation at hand. It incorporates the abstract mathematical ideas of the model and may sometimes be implicit. For example, the extensive character of the area is a property that is implicit in the written production shown in Appendix A.

(iii) The representations comprise the evidence that expresses knowledge or reasoning about the model: fragments of text containing natural language statements (verbal representations), numerical or algebraic expressions (symbolic), graphs, drawings or diagrams (pictorial), tables (tabular), etc. For example, in the task “the President’s supporters” (Appendix A), a statement such as “…so that the rectangle on which the Capitol sits has been reproduced 15 and a half times on the attached plan” would be a verbal representation, while a drawing in which the surface area occupied by people is covered using copies of the floor plan of the Capitol would be a pictorial representation (Table 3 in Section 3.1. shows all the representations in the written production associated with this task).

The representations contain the directly observable evidence of a written production, and their analysis allows access to the rest of the components of a school model and, therefore, allows one to characterize it.

Table 2. Analysis template proposed for the investigation of school models (source: prepared by the authors).

System	Mathematization	Representations
Relations (may include new knowledge obtained)	Results	Verbal (written)
	Variables	Pictorial
Objects	Properties	Symbolic
Questions	Concepts	Tabular
Characterization of the model

shows the analysis template for the investigation of school models from written productions according to the three components previously discussed. Therefore, this tool includes three main categories: system, mathematization and representations, and each category includes the subcategories defined and explained above.

2.2. Analysis Procedure

Prior to analysis, it should be noted that the system and the mathematization are clearly distinguished entities, according to Table 2. Since this distinction can sometimes be blurred, it is proposed to include in the mathematization all those statements and entities that explicitly use mathematical content. This forces researchers to decide beforehand what they consider to be mathematical content, depending on the context, the educational level in which the study is carried out, and the objectives of their research. The examples in Section 3 below illustrate such selection of criteria.

In view of the above, the analysis procedure starts by deciding what is to be considered mathematical content. Next, the study of the model begins with the identification and categorization of the representations. The statements involved in each of them lead one to identify the relations of the system (those not involving mathematical content) and mathematical results (those involving mathematical content) of the model. Then, the objects of the system are the entities the relations refer to, and the variables of the mathematization are the relevant quantities involved in the results. Finally, the results are analyzed in order to identify the underlying mathematical properties, and hence, the concepts involved. Following this strategy throughout all the representations leads one to obtain the system and the mathematization that make up the mathematical model under study. The synthesis of all of them included in a written production enables one to conjecture a characterization (bottom row of Table 2) which gives an overall idea of the model developed and highlights its main attributes. Figure 1 sketches this procedure as a flux diagram.

Finally, it is noteworthy that this analysis procedure facilitates the observation of the impact of a task on the models that are developed to solve it. Small changes in the specific wording (e.g., numerical data provided, type of representations used, use made of certain terms) can impact the entire modeling process, and thus, its output. Therefore, it is convenient that the analysis of school mathematical models also pays attention to the stimulus provided for modeling, in order to expose the actual contribution of students to the model they develop. In the present proposal, this can be carried out by following the same analysis procedure for the statement of the task and differentiating those elements of the model included in it from those provided by the students. For example, in the analysis for the task “the President’s supporters” shown in

Table 3. Analysis of the written production for the task “the President’s supporters.” The elements shaded in gray were explicitly provided in the statement of the task (source: prepared by the authors).

System	Mathematization	Representations
Relations	Results	Verbal
-The surface area of the Capitol holds 97,096 people. -Obama’s inauguration was attended by 1,504,988 people (answer to the question).	-The ground plan of the building (Capitol) is rectangular, measuring 106 m × 229 m and 24.274 m2 in area. -The area occupied by people is about 15 and a half times that occupied by the ground plan of the Capitol. -There is room for 4 people per square meter.	-”Provide an estimate of the number of people who attended Obama’s inauguration ceremony.” -“Estimating that the building is rectangular in shape”. -“…so that the rectangle on which the capitol sits has been reproduced 15 and a half times on the enclosed plan”. -“…considering that each square meter has room for 4 people”.
Objects	Variables	Pictorial
-Capitol Park -People who attended the inauguration -Capitol building	-Area of the Capitol (AC) -Total area occupied by people in the park (AP) -Number of times the capitol fits in the area occupied by people (nC) -Number of people that fit in 1 m2 (d)	(Satellite image of a moment of the inauguration)
Questions	Properties	Symbolic (integrated into verbal discourse):
-Estimate the number of people who attended Obama’s inauguration	-Formula for the area of the rectangle -Extensive property of the area -Invariance of area to rigid motion	They include some non-numerical symbols such as the formula for the area of the rectangle and “m2”. They do not use proper symbols for persons as a unit of measurement or for the variables used.
	Concepts	Tabular 1
	-Rectangle -Area -Density (people/m2)
Characterization of the model used: the number of people p who attended the inauguration can be estimated using p = AP d = AC nC d

¹ Blank space indicates that no items were found in the subcategory.

below, the satellite image of Capitol Park is a representation provided in the task (and thus, it is shaded in grey), while the rectangle overlay along the park is a representation introduced by the students.

3. Results

3.1. Analysis of a Model for the Task “The President’s Supporters”

The first task consisted of a synthetic question similar to a Fermi problem [34]. The specific statement provided to the students as well as the full content of the written production to be analyzed can be found in Appendix A.

Regarding the decision on what is considered mathematical content, it should be emphasized that the subject the students were enrolled in includes plane figures, the use of units of measurement and the quantification of measurements as specific contents. Hence, any statement or entity that involves these contents is assumed to be mathematical content, thus belonging to the mathematization. Table 3 shows the analysis of the students’ written production for this task. To exemplify the development of the analysis of the written production, an episode is detailed as follows.

Firstly, a pictorial representation was observed in which the students had used the ground plan of the Capitol as a pattern to cover the surface occupied by people (Table 3). The rest of the production is based on verbal reasoning with integrated symbolic expressions. Within this verbal representation, we found statements such as “…so that the rectangle on which the capitol sits has been reproduced 15 and a half times on the attached plan”. This statement involves the following result: the area occupied by the people approximates by 15 and a half times the area occupied by the Capitol. This result provides information on the following variable: number of times the Capitol fits in the area occupied by people (nC). Moreover, the extensive character of the area is a property underlying this result, which has the concept of area as an associated concept.

The same procedure was carried out with the rest of the representations to produce the contents of Table 3. The complete analysis leads to the following characterization of the model: the number of people attending the inauguration can be estimated by the product of the area of the Capitol, nC, and the number of people that fit in one square meter.

3.2. Analysis of a Model for the Task “The Play Center”

The second task, which was designed following the design principles of the Modeling Eliciting Activities [35], places greater emphasis on geometric visualization and the use of units of measurement. Both its statement and the full content of the written production analyzed can be found in Appendix B.

Regarding the decision on what is considered mathematical content, the educational context is similar to the other task, so any statement or entity in the analyzed production that involves the use of fractions, plane figures, units of measurement, or measurement strategies is assumed to be mathematical content, thus belonging to the mathematization.

Table 4. Analysis of the written production for the task “the play center.” The elements shaded in gray were explicitly provided in the statement of the task (Source: prepared by the authors).

System	Mathematization	Representations
Relations	Results	Verbal
-Taking advantage of a corner of the classroom allows play centers to be set up in both classrooms	-The play center should occupy a quarter of the classroom. -The maximum amount of 10 m of fencing. -One wall in the first classroom measures 7.6 m and one wall in the second classroom measures 8.7 m (these data allow one to calculate the measurements using the grid). -The side of the grid in classroom 1 is 1.27 m (actual measurement). -The dimensions of the rectangle that divides the first classroom into four equal parts are 3.8 m and 6.35 m. Its area is 24.13 m2. -This rectangle cannot be the play center, since there is no fence (this is implicit). -The square root of 24, 13 is 4, 91. -A square (leaning on the corner) of side 4.91 m is an admissible play center in classroom 1. -With this play center, there would be 0.18 m of fence left over. -The side of the grid in classroom 2 is 1.24 m (actual measurement). -Classroom 2 is divided into two shapes: (i) a rectangle of dimensions 9.94 m × 6.21 m, whose area is 61.77 m2 and (ii) a right triangle whose legs are 2.48 m and 9.94 m, and whose hypotenuse is 10.23 m. The area of this triangle is 12.37 m2. -The area of classroom 2 is 74.14 m2. -The area of the play center to be located in classroom 2 is 18.53 m2. -The square root of 18, 53 is 4, 30. -A square (leaning on the corner) of side 4.30 m is an admissible play center in classroom 2. -With this play center there would be 1.40 m of fencing left over.	-“…the play centers must occupy exactly a quarter of the classroom.” -“The school has 10 m of this fence, but cannot afford to spend money on more.” -“…you have a scaled map of the classroom below.” -“…explain how the fence could be placed and how much fence would be left over.” -“…if the play center can be set up in the 4-year-old classroom with the ten meters of fence and how much fence would be left over.” -“…invent a new one that does work in both classrooms. Use it to explain how the fence should be placed in each of the classrooms and how much fence would be left over in each case.” -“By calculating the area, we can see that there is not enough meters of fence [Classroom 1].” -“Therefore, in order to use it [the fence], it would have to be in the shape of a square of side 4.91 m.” -“Thus, 0.18 m [of fence] would be left over.” -“By calculating the area of the figure, we can see that there are not enough meters of fence [Classroom 2]” -“In order to use it [the fence], it would have to be in the shape of a square of side 4.30 m” -“Thus, there would be 1.40 m [of fence] left over.” -“In both cases we have to put the play center in a square in one corner of the classroom.” -“Thus, the play center will be square in shape.”
Objects	Variables	Pictorial
-Play center -Fence	-Classroom area (A) -Side of the square defining the play center (l)	(Plans of classrooms provided)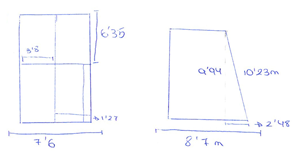
Questions	Properties	Symbolic
-Can the play center be set up in the first classroom? If so, how can it be done? How much fence is left over? -Is the method used also applicable to the second classroom? If so, how? How much fence is left over? -If the method applied in the first classroom is not valid for the second one, explain why and find a method to place the fence that works in both classrooms.	-Extensive property of length -Formula of the area of the rectangle and the square -Extensive property of area -Taking the square root is the inverse operation of squaring	-Integrated into verbal discourse: -Calculations not integrated in the text 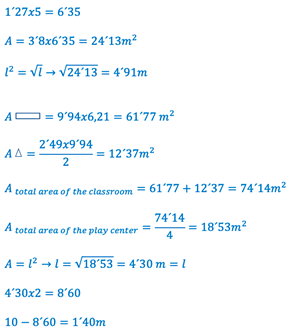Proper symbolism for the area of a rectangle Usual notation for the area (A) and for the side of the square (l)
	Concepts	Tabular 1
	-Plane figure -Length of a segment (the fence) -Unit of measure/scale -Fraction -Length of the perimeter of a plane figure -Area of a plane figure -Square root -Square of a number
Characterization of the model used: a square of side the root of a quarter of the area of the classroom located in a corner of the classroom is a play center that complies with the regulations

¹ Blank space indicates that no items were found in the subcategory.

shows the analysis of the students’ written production for this task. To exemplify the development of the analysis of the written production, an episode is detailed below.

Firstly, pictorial, symbolic and verbal representations were found, complementary to each other. In one of the symbolic representations, the students calculate the square root of the fourth part of the classroom to find the side of the square that constitutes the play center (Table 4). This calculation, together with the statement “therefore, in order to be able to use it [the fence], it would have to be in the form of a square of side 4.91 m” leads to the following result: a square leaning against the corner and of side 4.91 m would be an admissible play center in classroom 1. This result provides information on the following variable: side of the square defining the play center. One of the properties supporting this result is that making the square root is the inverse of squaring, and the concepts square root and square of a number are associated with this property.

This procedure was repeated with the rest of the written production representations to produce Table 4. The result of the analysis leads to the following characterization of the model used: a square whose side is the root of a quarter of the classroom area, and which is located in a corner of the classroom is suitable for designing a play center that complies with the regulations.

4. Discussion

4.1. What Does the Tool Provide for the Analysis of School Models?

The categorization based on the system, the mathematization and the representations makes it possible to systematize the analysis of written productions in order to provide valuable information not only for research but also for educational purposes.

From the research point of view, the proposed tool aims to provide a flexible structure that helps researchers to organize the foci of analysis on a mathematical model according to the purpose of each study. In this regard, the categories in Table 2 above allow the creation of hierarchies of terms or statements within each component of a model (e.g., different types of results, or different notations within the symbolic representations). These categories also allow the merging of subcategories according to the objectives of their research or the task or situation that stimulates the modeling activity. In particular, the properties of the elements in the system, the mathematization and the representations provide useful variables for research. For example, the study of assumed relations and results, whose validity is not explicitly justified in the model (premises), versus those that are explicitly justified (deductions) allow one to study the knowledge that a group of students spontaneously applied during a modeling activity [36]. Similarly, the assessment of concepts, properties or richness of representations can be used to measure the quality of applied mathematical knowledge. Finally, the characterization derived from the proposed analysis (final rows in Table 3 and Table 4) provides criteria to classify the models created by a group of students.

From the educational point of view, the analysis template shown in Table 2 above is a tool for monitoring students, since the identification of the elements of its categories allows the final product of the students’ activity to be used to infer the modeling skills exhibited. Specifically, the relations and objects of the system reveal those characteristics of a context-based situation that the students considered useful for generating knowledge by applying mathematics to that situation, showing their ability to abstract and organize relevant information from the context. In turn, the results and variables account for the strategy employed, whereas the properties and concepts record the mathematical content that the students used, thus showing their ability to apply mathematics to generate knowledge within a context. Likewise, the representations record the way students express their ideas, which gives clues about their understanding of the situation and their ability to express it. On the other hand, identifying the part of the model which is provided in the task contributes to raising teachers’ awareness of the information provided to the learners and the selection of task variables to stimulate different modeling activities within the same situation.

4.2. Connection with Other Approaches

The tool for the analysis of school models explained in this paper is based on three components: system, mathematization and representations. Previous research highlights that the wide variety of contexts in which modeling can take place makes it difficult to establish a priori criteria to discriminate and specify the complexity of entities that may be present in the system [12] and in the mathematization [31]. The tool presented in this paper proposes criteria for organizing the elements within each category, thus facilitating the analysis of written productions. Within the system and the mathematization, the proposal takes up the ideas of [12,30,32] to distinguish between statements (relations and results in the system and properties in the mathematization) and terms to which these statements refer to (objects and variables in the system and concepts in the mathematization). Furthermore, in line with the proposals of [12,25], the question that motivates the modeling activity or any other questions that arise about the starting context are considered to be part of the system, and therefore, part of the model, since these questions largely determine the final outcome of the modeling.

Another relevant aspect of the proposal presented is the inclusion of representations as part of the analysis of a mathematical model, which is aligned with the notions of model of [4,25,29]. From an operational point of view, the analysis of representations, which is organized according to the usual representation systems (verbal, pictorial, symbolic, tabular), provides access to the other components of the model. Conceptually, considering representations as part of the model implies the assumption that two individuals using different representations to express the same mathematization of the same system have developed a different modeling activity. This idea is in line with the work of [37], who used the representational systems employed during the modeling process to suggest the activation of different mathematical thinking styles: a greater richness of pictorial representations indicates a predominance of visual thinking, a greater richness of symbolic and verbal representations indicates a predominance of analytical thinking, and a balance between the different types of representation indicates integrated thinking.

With regard to the comparison of the tool presented and that of [24], two clear analogies can be observed. The components such as languages and conceptual systems proposed by these authors are comparable to the categories representations and mathematization of the present proposal, although this includes statements and entities that are not purely conceptual (results and variables, respectively). As for the differences between the two approaches, the tool in [24] gives relevance to the procedures, considering them fundamental components of the model. However, the proposal in this paper gives prominence to the information provided by the procedure as part of the model, rather than to the procedure per se. For example, in the task “the President’s supporters”, the procedure used to calculate the area of the Capitol is not part of the model, but the information provided by the statement “the ground plan of the building (Capitol) is rectangular, with dimensions 106 m × 229 m and 24.274 m² of area” is part of the model (it is a result in the mathematization, see Table 3). On the other hand, the tool of [24] sticks to the strictly mathematical model and does not refer to the context for which the model is designed, so it does not contain components comparable to the system.

5. Conclusions

This paper presents and discusses a tool for the analysis and characterization of school mathematical models. Research based on this tool has two main advantages. First, it makes visible and organizes the evidence contained in a written production that characterizes the underlying mathematical model, which facilitates the inference of the skills put into play by the students to develop the modeling activity. Secondly, it facilitates the formulation of variables useful for empirical research.

Despite the educational value of the results of studies based on the analysis of mathematical models, the literature does not include a wide variety of instruments to develop these types of studies. This resulted in developing a novel tool based on a conceptualization of the mathematical model, which is articulated from the system–mathematization–representations triad, whose subcomponents collect the relevant information about the mathematical model that contains a written production at different levels of abstraction: the system describes the contextual information, the mathematization encompasses all the relevant mathematical entities and statements of the system, and the representations collect the evidence of work on the system and the mathematization. Each of these components provide specific foci of attention based on the observation of statements and entities, which are flexible for the researcher and, taken together, characterize a mathematical model. The relationships between the three categories in the tool entail a suitable analysis procedure for the investigation of school models (Figure 1). Its application to the analysis of students’ written productions gives an account of the knowledge that students use to create the model and provides a characterization of such a model. This paper also presents two examples of the analysis of school models that illustrate the application of the proposed tool. Its characteristics, its suitability as an effective research tool and its connection with other previously argued ideas in mathematics education are also discussed.

Finally, it should be noted that the added value of this proposal could be strengthened by following two ways of working. Firstly, it would be desirable for the characterizations offered by this tool to be similar to those obtained with other tools or perspectives, which requires the investigation of the comparative nature of these results. Similarly, it would be necessary to assess the degree of agreement between different researchers who are users of the tool when analyzing the same production. This type of study will be considered for future research.